DOI:
https://doi.org/10.14483/23448350.16270Publicado:
09/01/2020Número:
Vol. 39 Núm. 3 (2020): Septiembre-Diciembre 2020Sección:
Educación científica y tecnológicaNociones matemáticas evidenciadas en la práctica cotidiana de un carpintero del sur de Chile
Mathematical notions evidenced in the daily practice of a carpenter from south Chile
Palabras clave:
mathematical notions, daily practice, carpenter, ethnomathematics (en).Palabras clave:
nociones matemáticas, práctica cotidiana, carpintero, etnomatemática (es).Descargas
Referencias
Albanese, V., Santillán, A., Oliveras, M. (2014). Etnomatemática y formación docente: el contexto argentino. Revista Latinoamericana de Etnomatemática, 7(1), 198-220.
Albis, V. (1986). Arte prehispánico y matemática. Revista de la Universidad Nacional, 1(7), 457-465.
Aroca, A. (2008). Análisis a una figura tradicional de las mochilas arhuacas. Comunidad Indígena Arhuaca. Sierra Nevada de Santa Marta, Colombia. Boletim de Educação Matemática, 21(30).
Aroca, A. (2012). Las formas de orientación espacial de los pescadores de Buenaventura, Colombia. Revista U.D.C.A Actualidad & Divulgación Científica, 15(2), 457-465. https://doi.org/10.31910/rudca.v15.n2.2012.847
Aroca, A. (2013). Los escenarios de exploración en el Programa de Investigación en Etnomatemáticas. Educación Matemática, 25(1), 111-131.
Aroca, A. (2016). La definición etimológica de Etnomatemática e implicaciones en Educación Matemática. Educación matemática, 28(2), 175-195. https://doi.org/10.24844/EM2802.07
Bishop, A. (1999). Enculturación matemática. La educación matemática desde una perspectiva cultural. Paidós.
Blanco, H. (2006). La Etnomatemática en Colombia: un programa en construcción. Boletim de Educação Matemática, 19(26), 1-19.
Blanco, H. (2011). La postura sociocultural de la educación matemática y sus implicaciones en la escuela. Revista Educación y Pedagogía, 23(59), 59-66. https://doi.org/10.35362/rie590455
Braun, V., Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3(2), 77-101. https://doi.org/10.1191/1478088706qp063oa
D’Ambrosio, U. (1997). Ethnomathematics and its place in the history and pedagogy of mathematics. Ethnomathematics: Challenging Eurocentrism in mathematics education, 13-24.
D’Ambrosio, U. (2001). Etnomatemática: Elo entre las tradições e a modernidad. Colección: Tendencias en educación matemática. Autêtica.
D’Ambrosio, U. (2014). Las bases conceptuales del Programa Etnomatemática. Revista Latinoamericana de Etnomatemática, 7(2), 100-107.
Diario Oficial de la República de Chile (2012). Decreto 439. Santiago, Chile.
Diario Oficial de la República de Chile (2014). Decreto 614. Santiago, Chile.
Fuentes, C. (2012). La Etnomatemática como mediadora en los procesos de la reconstrucción de la historia de los pueblos. El caso de los artesanos del municipio de Guacamayas en Boyacá, Colombia. Revista Latinoamericana de Etnomatemática, 5(2), 66 -79.
Gavarrete, M. (2013). La Etnomatemática como campo de investigación y acción didáctica: su evolución y recursos para la formación de profesores desde la equidad. Revista Latinoamericana de Etnomatemática, 6(1), 127-149.
Gavarrete, M. E., Casis, L. (2014). La cosmovisión indígena y sus perspectivas didácticas: visión etnomatemática de dos grupos étnicos. En P. Leston (ed.), Acta Latinoamericana de Matemática Educativa (vol. 27, pp. 1423-1429). Comité Latinoamericano de Matemática Educativa.
Gerdes, P. (2013). Geometría y Cestería de la Bora en la Amazonía Peruana. Ministerio de Educación.
Giesecke, F. E. (2006). Dibujo y comunicación gráfica. Pearson Educación.
González, J., Zambrano, J. (2011). Representaciones sociales y prácticas matemáticas en un grupo laboral de Corabastos (tesis de grado). Universidad Distrital Francisco José de Caldas, Bogotá.
Hernández, R., Fernández, C., Baptista, P. (2010). Metodología de la investigación. McGraw Hill.
Huencho, A. (2015). Estudio de las Orientaciones curriculares del Programa Intercultural Bilingüe: un análisis emergente en función de la matemática y la cultura mapuche. Revista Latinoamericana de Etnomatemática, 8(2), 214-236.
Kawulich, B. (2006). La observación participante como método de recolección de datos. Forum: Qualitative Social Research, 6(2).
http://nbnresolving.de/urn:nbn:de:0114-fqs0502430
Longhurst, R. (2010). Semi-structured intervews and Focus Groups. En N. Clifford, S. French y G. Valentine, Key Methods in Geography (pp. 103-115). Sage Publications Ltd.
Martínez, M. (2004). El método etnográfico de investigación.
http://prof.usb.ve/miguelm/metodoetnografico.html.
Martínez-Padrón, O. (2013). Etnomatemática: una reseña crítica de sus acepciones. Revista Científica, 427-431. https://doi.org/10.14483/23448350.4799
Millroy, W. (1991). An ethnographic study of the mathematical ideas of a group of carpenters. Learning and Individual Differences, 3(1), 1-25. https://doi.org/10.1016/1041-6080(91)90002-I
Ministerio de Educación Nacional (2006). Estándares básicos de competencias en Lenguaje, Matemáticas, Ciencia y Ciudadanas. Ministerio de Educación Nacional.
Ministerio de Educación (2012). Bases curriculares Educación Básica (Lenguaje; Matemáticas; Ciencias Naturales; Historia, Geografía y Ciencias Sociales; Idioma extranjero: inglés). Ministerio de Educación.
Ministerio de Educación (2013). Matemática Programa de Estudio Sexto Año Básico. Ministerio de Educación.
Ministerio de Educación (2016). Matemática Programa de Estudio Octavo Año Básico. Ministerio de Educación.
Mosquera, G., Rodríguez-Nieto, C., Suárez, S. (2015). Dos sistemas de medidas no convencionales en la pesca artesanal con cometas en bocas de ceniza y su potencial para la educación matemática (tesis de pregrado). Universidad del Atlántico, Barranquilla.
National Council of Teachers of Mathematics (2000). Principles and standards for school mathematics. Reston: National Council of Teachers of Mathematics.
Nagle, C., Moore-Russo, D. (2014). Slope across the curriculum: Principles and standards for school mathematics and common core state standards. The Mathematics Educator, 23(2).
Oliveira, B., Mendes, E. (2016). Etnomatemática: O ensino de medida de comprimento no 6º ano do ensino fundamental na Escola Indígena Kanamari Maraã-AM, Brasil. Revista Latinoamericana de Etnomatemática, 9(2), 53-66. https://doi.org/10.22267/relatem.1692.2
Oliveras, M., Blanco, H. (2016). Integración de las Etnomatemáticas en el aula de Matemáticas: posibilidades y limitaciones. Boletim de Educação Matemática, 30(55), 455-480. https://doi.org/10.1590/1980-4415v30n55a08
Peña-Rincón, P. A., Hueitra-Santibañez, Y. (2016). Conocimientos [matemáticos] mapuche desde la perspectiva de los educadores tradicionales de la comuna de El Bosque. Revista Latinoamericana de Etnomatemática, 9(1), 8-25. https://doi.org/10.22267/relatem.1691.16
Rey, M., Aroca, A. (2011). Medición y estimación de los albañiles, un aporte a la educación Matemática. Revista U.D.C.A Actualidad & Divulgación Científica, 14(1), 137-147. https://doi.org/10.31910/rudca.v14.n1.2011.766
Rodríguez-Nieto, C., Morales, L., Muñoz, A., Navarro, C. (2017). Medidas no convencionales: el caso del mercado Baltazar R. Leyva Mancilla, Chilpancingo, Gro. En Federación Española de Sociedades de Profesores de Matemáticas (ed.), VIII Congreso Iberoamericano de Educación Matemática (pp. 225-233). Madrid, España.
Rodríguez-Nieto, C., Mosquera, G., Aroca, A. (2019). Dos sistemas de medidas no convencionales en la pesca artesanal con cometa en Bocas de Cenizas. Revista Latinoamericana de Etnomatemática, 12(1), 6-24.
Rodríguez-Nieto, C., Aroca, A., Rodríguez-Vásquez, F. M. (en prensa). Procesos de medición en una práctica artesanal del caribe colombiano. Un estudio desde la Etnomatemática. Revista Latinoamericana de Etnomatemática.
Salas, S. S. (2014). Etnomatemática y multiculturalidad en la educación básica en Chile. El caso de la aritmética mapuche (tesis de maestría no publicada). Universidad de Granada.
Salas, S. S., Godino, J. D. (2016). Potencial Educativo de la Aritmética Mapuche en Chile. En A. M. Rosas (ed.), Avances en Matemática Educativa. Tecnología y matemáticas (pp. 72-84). Editorial Lectorum.
Souto, A. (2001). Nuevas herramientas de diseño de formas de buques basadas en códigos de flujo potencial (tesis de doctorado). Technical University of Madrid.
Soto, J. L. (2018). Nociones matemáticas en el sombrero Tampalkuari de la comunidad indígena Misak (tesis de pregrado). Universidad del Valle, Cali.
Gómez, J. (2007). Las matemáticas en los oficios y profesiones. Técnica Industrial, 273, 56-61.
Zambrano, J. (2012). Prácticas matemáticas en una plaza de mercado. Revista Latinoamericana de Etnomatemática, 5(1), 35-61.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: de mayo de 2020; Aceptado: de agosto de 2020
Resumen
A pesar de la riqueza cultural que existe en Chile, son escasos los estudios que relacionan las nociones matemáticas presentes en actividades culturales propias de las zonas como, por ejemplo, lo es la elaboración de muebles. Tomando como base las actividades universales propuestas por Bishop (1999), caracterizamos las nociones matemáticas presentes en el trabajo de un carpintero del sur de Chile mientras elaboraba un mueble tipo cama y en algunas explicaciones sobre la construcción de un barco. Basados en una metodología cualitativa exploratoria con un enfoque etnográfico, concluimos que en el trabajo de confección y elaboración de este tipo de mueble es posible identificar las actividades matemáticas universales. Finalmente, reflexionamos sobre cómo se podrían vincular estas nociones con el currículo chileno y la importancia de relacionar las matemáticas presentes en actividades propias de cada zona en el aula.
Palabras clave:
nociones matemáticas, práctica cotidiana, carpintero, etnomatemática.Abstract
Despite the cultural wealth that exists in Chile, there are few studies that relate the mathematical notions present in cultural activities typical of the areas, such as the making of furniture. Based on the universal activities proposed by Bishop (1999), we characterize the mathematical notions present in the work of a carpenter from the south of Chile when he makes a bed-type piece of furniture and in some explanations about the making of a ship. Based on an exploratory qualitative methodology with an ethnographic approach, we conclude that in the work of making and preparing this type of furniture it is possible to identify universal mathematical activities. Finally, we reflect on how these notions could be linked with the Chilean curriculum, and the importance of relating the mathematics present in activities typical of each area in the classroom.
Keywords:
mathematical notions, daily practice, carpenter, ethnomathematics.Resumo
Apesar da riqueza cultural existente no Chile, existem poucos estudos que relacionam as noções matemáticas presentes em atividades culturais típicas das áreas, como a confecção de móveis. Com base nas atividades universais propostas por Bishop (1999), caracterizamos as noções matemáticas presentes no trabalho de um carpinteiro do sul do Chile quando ele faz um móvel do tipo cama e em algumas explicações sobre a construção de um navio. Com base em uma metodologia qualitativa exploratória com abordagem etnográfica, concluímos que, no trabalho de fabricação e preparação desse tipo de móvel, é possível identificar atividades matemáticas universais. Por fim, refletimos sobre como essas noções poderiam ser vinculadas ao currículo chileno e a importância de relacionar a matemática presente em atividades típicas de cada área da sala de aula.
Palavras-chaves:
noções matemáticas, prática diária, carpinteiro, etnomatemática.Introducción
Desde hace varios años se ha reconocido la existencia de una matemática que es practicada entre grupos culturales o sociales identificables, la cual se denomina etnomatemática (D’Ambrosio, 1997; Martínez-Padrón, 2013). Esta estudia “las multifacéticas relaciones e interconexiones entre ideas matemáticas y otros elementos constituyentes culturales, como la lengua, el arte, la artesanía, la construcción, la educación” (Gerdes, 2013, p. 150).
En esta línea se han desarrollado diversos estudios que dan cuenta de las matemáticas presentes en prácticas desarrolladas por distintos grupos culturales y sociales, al elaborar productos artesanales (e. g., Aroca, 2008; Soto, 2018), asociadas al uso de medidas (e.g., Oliveira y Mendes, 2016; Mosquera et al., 2015; Rey y Aroca; 2011; Rodríguez-Nieto, et al., (2019a) ; Rodríguez-Nieto et al., (2019b), en prensa), así como en la comercialización de productos de algunas comunidades indígenas (Zambrano, 2012). Estos estudios proporcionan evidencia de que la matemática y la cultura están ligadas una con otra; asimismo, apoyan la idea de que no existe una forma de concebir las matemáticas, sino que existen tantas formas como grupos culturales o sociales puedan encontrarse (Aroca, 2012; 2013). A su vez proporcionan un valioso insumo para que los docentes puedan contextualizar los aprendizajes que esperan desarrollar en sus alumnos, sin necesidad de forzarlos a imaginar contextos inusuales para abordar el currículo escolar (Gavarrete, 2013).
Dado lo importante que es considerar los aspectos socioculturales propios del contexto en los que estudiantes están inmersos, se hace notable la necesidad de visualizar las matemáticas en el contexto educativo como una posibilidad para explorar la diversidad cultural existente en un país desde otra perspectiva (Decreto 614, 2014). Si bien en la nación se han desarrollado algunos estudios que analizan la relación entre grupos culturales específicos y las matemáticas (e. g., Gavarrete y Casis, 2014; Salas, 2014; entre otros), dada la diversidad cultural y social presente en Chile existen otras actividades típicas de cada zona, como lo es la carpintería.
La matemática de los carpinteros es una matemática socialmente construida y se comunica por medio del aprendizaje (Millroy, 1991). El razonamiento, el conteo y la medición presente en la carpintería, ebanistería, albañilería, modistería, entre otras actividades, han contribuido no solo a la preservación cultural de estas prácticas, sino que también en la enseñanza de las matemáticas a través de procesos de conteos y medición (Aroca, 2013). Los procesos realizados en la carpintería podrían beneficiar y tener implicaciones positivas en la enseñanza y aprendizaje de las matemáticas. Así, por ejemplo, instrumentos que son utilizados habitualmente en la carpintería como la cinta métrica (utilizada para la medición de longitudes largas), la escuadra de carpintero (empleada para comprobar el escuadrado de un mueble o de un ensamblado y el trazado de rectas perpendiculares considerando ángulos de 45º), el transportador de ángulos (empleado en la medición de ángulos no rectos y para hacer traslaciones) (Gómez, 2007) podrían ser utilizados en el aula para contextualizar la medición de longitudes, el trabajo con segmentos y rectas, así como con otros contenidos matemáticos propuestos en el currículo nacional (Ministerio de Educación, 2012).
Considerando que en algunas regiones del sur de Chile la carpintería es una actividad que está presente en la vida cotidiana de muchos estudiantes, este estudio se centra en identificar las nociones matemáticas que se encuentran presentes en la construcción de muebles. Tomando como base las actividades universales propuestas por Bishop (1999) caracterizamos las nociones matemáticas presentes en el trabajo de un carpintero del sur de Chile cuando elabora muebles y, resultado de ello, se analiza la forma en que se podrían vincular estas nociones con el currículo chileno.
Fundamento teórico
Etnomatemática
Una de las más reconocidas aproximaciones al término etnomatemática es la propuesta realizada por D’Ambrosio (2001), quien sostiene que la etnomatemática: “es la Matemática practicada por grupos culturales, tales como comunidades urbanas o rurales, grupos de trabajadores, clases profesionales, niños de cierta edad, sociedades indígenas y otros grupos que se identifican por objetivos y tradiciones comunes a los grupos” (p. 9). Etimológicamente, D’Ambrosio define la etnomatemática como una división de tres grandes raíces (figura 1).
Figura 1: Etimología del término etnomatemática.
A pesar de que diversos estudios en el área han tomado como base la definición de etnomatemática desde su concepción etimológica propuesta por D’Ambrosio (2001; 2014), también se ha señalado que las distintas interpretaciones de matemá y ticas se han distanciado de su origen etimológico, principalmente como consecuencia de la diversidad cultural implicada en las diversas formas de concebir y practicar las matemáticas (Aroca, 2016). En este sentido, para los fines de esta investigación consideramos que la etnomatemática:
No sólo es lo sociocultural, también es lo histórico, lo político, lo ético, su relación con la educación, la formación, la pedagogía, la didáctica, lo religioso, lo económico, lo psicológico, lo lingüístico que median en la enseñanza y aprendizaje de las matemáticas, y no a todas estas dimensiones las podemos interpretar mediante las ticas de mathema en una etno. (Aroca, 2016, p. 192).
Investigaciones en etnomatemática
En los últimos años se han desarrollado diversos estudios sobre etnomatemática. Por ejemplo, en Colombia Zambrano (2012) analizó las prácticas matemáticas que se utilizan en un mercado de Bogotá cuando algunas comunidades indígenas comercializar sus productos utilizando medidas de capacidad como el saco o bulto (unidad de medida). Este autor destaca el potencial matemático inmerso en las ventas de auyama y maíz para esbozar situaciones contextualizadas que permitan a los estudiantes diseñar, contar, medir, explicar, entre otras actividades.
De manera similar, Soto (2018) analizó las nociones matemáticas presentes en la elaboración del sombrero Tampalkuari y señala la presencia de nociones como medir, contar y diseñar. Este autor destaca el potencial de esta actividad como recurso didáctico para el aula de la matemática, el uso de traslaciones y rotaciones, así como conteos que involucran patrones en el trenzado. Rodríguez-Nieto et al., (2019a) describieron el uso de dos sistemas de medidas no convencionales en la pesca con cometas de Bocas de Cenizas, reportando el uso medidas como la brazada, la cuarta, el jeme y los dedos para la elaboración de la cometa y el aparejo de pesca, y lo utilizan en el proceso de enseñanza y aprendizaje de los sistemas métricos en el aula de educación secundaria (Mosquera et al., 2015).
En Brasil, Oliveira y Mendes (2016) estudiaron a una comunidad indígena Kanamari, la cual utiliza unidades de medidas (brazo, paso, pie, etc.) para desarrollar sus actividades cotidianas, que fueron llevadas al aula de clases para la conservación de la cultura y fortalecer la enseñanza de los sistemas de medidas. Da Silva y Farias (2020) indagaron sobre el conocimiento etnomatemático insertado en la práctica de medición de la tierra de los agricultores, en la que se utilizan unidades de medición propias del contexto como la braza y la vara para medir terrenos en forma de cuadriláteros, triangulares y elípticos.
En México, Rodríguez-Nieto et al. (2017) identificaron las formas de medir establecidas por comerciantes de un mercado, reconociendo las medidas de capacidad como el litro, el cuartillo y la arpilla, así como las equivalencias que se establecen entre ellas. Estos autores sugieren que a través de esta práctica se puede abordar el aprendizaje de conceptos geométricos como el área y el perímetro. García-García y Bernardino-Silverio (2019) exploraron los conocimientos geométricos (parábola, circunferencia, rectas paralelas y el uso de la cuarta) en la elaboración de un artefacto, el güilile, sugiriendo que, a través de actividades como la elaboración de una maqueta de este artefacto se pueden relacionar los conceptos geométricos identificados para crear situaciones matemáticas contextualizadas en el aula.
En Chile se han comenzado a hacer esfuerzos por matematizar la cultura de algunos pueblos originarios, centrándose esencialmente en la cultura mapuche (e. g. Gavarrete y Casis, 2014; Huencho, 2015, entre otros). Por ejemplo, Peña-Rincón y Hueitra-Santibañez (2016) analizan los conocimientos matemáticos que refieren a la ubicación espacial y temporal de la cultura mapuche basado en sol y la luna. Salas y Godino (2016) reconocieron la aritmética mapuche por medio de la numeración en mapunzugun. Sin embargo, los trabajos centrados en explorar los conocimientos matemáticos de otros grupos culturales en Chile (e. g., albañiles, carpinteros, pescadores, campesinos, entre otros) y su vinculación con el aula son muy escasos.
Actividades matemáticas universales
Bishop (1999) argumenta que existen ciertas actividades que están presentes en el accionar humano, en las cuales la cultura que rodea a la persona influye, y que corresponden a las actividades de contar, localizar medir, diseñar, jugar y explicar; a partir de las cuales es posible identificar matemática.
En este contexto, se han desarrollado algunos estudios que han demostrado la importancia de estas nociones evidenciadas en las prácticas cotidianas destacando su valor para el desarrollo del conocimiento matemático (e. g. Albis, 1986; Blanco, 2006; Fuentes, 2012; Soto, 2018). A pesar de que las nociones de medir, contar, localizar y explicar están presentes en diferentes currículos definidos desde los respectivos ministerios, como por ejemplo en el de Chile (Ministerio de Educación, 2012), el de Colombia (Ministerio de Educación Nacional, 2006) y los Estados Unidos de América (National Council of Teachers of Mathematics, 2000), las actividades universales descritas por Bishop (1999) presentes en el proceso de construcción de muebles han sido poco estudiadas.
Metodología
Con el objetivo de caracterizar las nociones matemáticas evidenciadas en la práctica de un carpintero del sur de Chile, se optó por una metodología cualitativa exploratoria con un enfoque etnográfico (Hernández et al., 2010). Este enfoque resulta conveniente cuando se requiere describir las costumbres o prácticas que se dan en una institución, una fábrica, un gremio de obreros, un aula de clases o de un sujeto en un contexto social determinado (Martínez, 2004).
Contexto y participantes
Se considera el caso de un carpintero de la zona sur de Chile al que hemos denominado en este estudio como Don Juan (DJ), quien ha manifestado su interés por participar de forma voluntaria. DJ tiene 62 años edad, comenzó a incursionar en la confección y realización de muebles desde temprana edad. Durante su niñez y adolescencia solo cursó hasta cuarto básico. A los 30 años se empezó a enfocar en la manufacturación de muebles, ya sea en trabajos particulares o como empleado por alguna empresa relacionada con el amoblamiento de catamaranes o embarcaciones menores. A los 40 años, a causa de exigencias laborales, decidió terminar su formación básica, siendo octavo básico el nivel escolar alcanzado con respecto a la educación formal en el sistema educativo chileno.
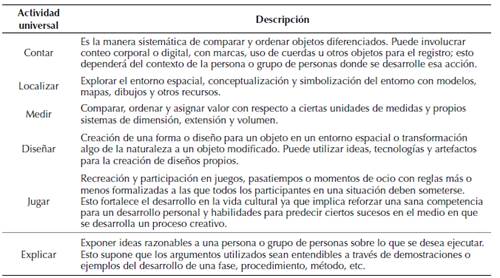
Fuente: información adoptada de Bishop (1999).
Tabla 1: Actividades matemáticas universales
Método y fases de la investigación
Nuestro estudio se centró en el seguimiento del proceso de construcción de un mueble tipo cama que realizó DJ y la explicación sobre algunas partes de un barco, lo cual se ha desarrollado en cinco fases:
Fase1: primer acercamiento con el objeto de estudio
En una primera fase, mediante la observación participante (Kawulich, 2006), se realizó un trabajo de campo el cual consistió en conocer de forma general la actividad cotidiana del carpintero y familiarizarse con él. En esta etapa solo se enfatizó en la presentación de los investigadores, se dialogó sobre los objetivos de la investigación y se obtuvo una carta de consentimiento informado para poder hacer uso de los datos recopilados en la práctica del mueblista.
Fase 2: elaboración de un instrumento de recolección de datos
La recolección y análisis de los datos se desarrolló con trabajos de campo. En el primero, con base en la revisión de la literatura sobre investigaciones similares (e. g.Albanese, Santillán y Oliveras, 2014; González y Zambrano, 2011; Soto, 2018; entre otros), se diseñó una entrevista semiestructurada para recoger los datos (Longhurst, 2010). Siguiendo lo propuesto por Bisquerra et al. (2009) en el guion de la entrevista, se incluyeron preguntas de inicio, introductorias, de transición, clave, de término y síntesis. Para establecer el contenido de nuestras preguntas tomamos como base las actividades matemáticas universales descritas por Bishop (1999) y establecimos seis dimensiones: D1. Contar; D2. Localizar; D3. Medir; D4. Diseñar; D5. Jugar, D6. Explicar (tabla 2).
Fuente: elaboración propia de los autores.
Tabla 2: Extracto de las preguntas incluidas en la entrevista

Fase 3: primera recolección de datos y aplicación de la entrevista
La entrevista semiestructurada aplicada a DJ se enmarcó en el primer trabajo de campo y fue conducida por dos de los autores de este estudio. Esta tuvo lugar en el taller de DJ al inicio del proceso de diseño de elaboración de un mueble tipo cama. Tuvo una duración de aproximadamente tres horas. La entrevista inició con preguntas centradas en la vida personal del participante (véase las preguntas de inicio en la tabla 2). Posteriormente, se realizaron preguntas centradas en el proceso de diseño y elaboración de muebles para incidir en la práctica. Cabe destacar que en el transcurso de la entrevista surgieron nuevas preguntas de profundización con base en la información que iba suministrando el carpintero, así como la elaboración de dibujos por parte de este para clarificar el proceso. Se hizo registro de audio para respaldar la información, así como fotografías de procesos relevantes que permitieran presentar evidencias para la fase de análisis.
Fase 4: segunda recolección de datos
Realizamos un segundo trabajo de campo con la finalidad de confirmar la objetividad de la información obtenida en la primera entrevista y profundizar en algunos aspectos que resultaron de gran interés. Se consideró pertinente realizar una nueva entrevista semiestructurada que incluyo preguntas como: ¿qué considera usted para la elaboración de un mueble?, ¿podría dibujar un mueble?, ¿cómo calcula el presupuesto de un mueble? Esta entrevista fue realizada, transcrita y estudiada siguiendo el formato de la primera entrevista.
Fase 5: análisis de datos
Utilizando el análisis temático propuesto por Braun y Clarke (2006) se hizo el correspondiente análisis de los datos. En la primera etapa de familiarización con los datos se transcribió la grabación de audio de la entrevista a texto utilizando una planilla Excel. Luego, en la segunda etapa de generación inicial de códigos, identificamos palabras o frases (códigos) que permitieran agrupar palabras clave mencionadas por el entrevistado, resaltándolos con colores distintos (figura 2).
Figura 2: Organización y codificación de la información en Excel.
En la tercera etapa de búsqueda de temas comparamos, discutimos y ajustamos nuestros códigos basados en nuestra conversación. Así, por ejemplo, las palabras centímetro, pulgada, metro, tolerancia y pendiente fueron asociadas a la categoría “medir” (tema) y agrupadas en esta. Después, en la cuarta etapa de revisión de temas, se identificaron los elementos más significativos que dan cuenta de la presencia de las actividades universales en cada grupo y se trianguló la información sobre los temas, verificando la presencia de las nociones matemáticas presentes en la práctica del carpintero.
En la quinta etapa de definición y nombramiento de temas realizamos una interpretación de las definiciones empleadas por Bishop (1999) para las actividades de contar, localizar, medir, diseñar, explicar y jugar, en el contexto del proceso de elaboración de muebles (tabla 3).
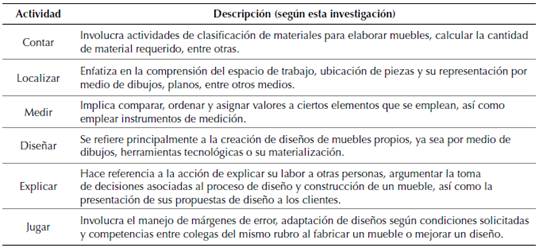
Fuente: elaboración propia de los autores.
Tabla 3: Actividades universales identificadas
Por último, en la sexta etapa del análisis temático concerniente a la producción de un reporte se presentan las nociones matemáticas identificadas en la elaboración de muebles por parte del carpintero.
Resultados
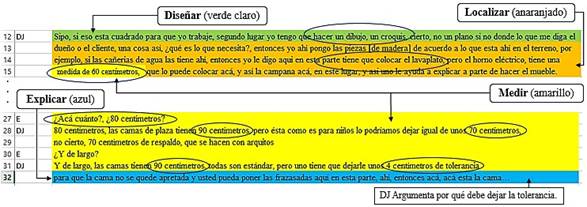
En este apartado se presentan las nociones matemáticas identificadas en el proceso de elaboración de un mueble tipo cama y en algunas explicaciones de DJ sobre la elaboración de un barco que utiliza para complementar sus respuestas. Los resultados se organizan en seis etapas identificadas durante el proceso seguido por DJ: 1) contacto con el cliente, 2) diseño del mueble, 3) localización del mueble, 4) cuantificación de materiales necesarios y presupuesto, 5) medidas del mueble y 6) explicación general sobre la confección y ensamble de las piezas del mueble.
Nociones matemáticas evidenciadas en la elaboración de muebles
Contacto con el cliente
Antes de iniciar la elaboración del mueble en sí, DJ se comunica con el cliente para tomar decisiones sobre el tipo de mueble que este desea. El cliente puede traer su propio diseño o elegir uno del registro de diseños y muebles que DJ ha realizado. En este proceso se identifican las nociones de diseñar y explicar de manera implícita en el siguiente extracto de la transcripción:
Pasa una cosa, llega un cliente, por ejemplo, ya sean tipos de la construcción de edificios, dice “yo quiero esto” te trae un plano [diseño]. Ahora uno tiene que darles en el gusto que quieren ellos para que, para que… Para que… Quede conforme el cliente. (DJ)
También se identifica la noción de medir en la comunicación de DJ con el cliente, cuando responde una pregunta sobre las dimensiones de la cama:
[…] de largo, las camas tienen 90 centímetros, todas son estándar, pero uno tiene que dejarle unos cuatro centímetros de tolerancia para que la cama no se quede apretada y usted pueda poner las frazasadas aquí en esta parte.
Diseño del mueble
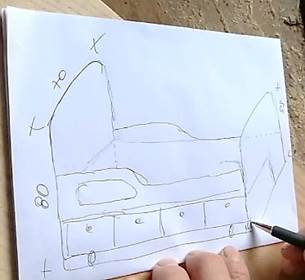
El diseño de la construcción del mueble en sí comienza con un dibujo del mueble que DJ quiere hacer, ya sea a partir de los requerimientos del cliente o producto de la adaptación de un diseño anterior de DJ a estos requerimientos:
Yo tengo que hacer un dibujo, un croquis, cierto, no un plano sino donde lo que me diga el cliente, una cosa así, ¿qué es lo que necesita?
Figura 3: Diseño de la cama.
DJ manifestó que los diseños son una guía para realizar los muebles, dado que se plasman las medidas, las formas y el tipo de madera como lo muestra el siguiente extracto:
A ti te mandan un plano, no cierto, por decir un camarote [una litera], que tiene dos metros, la cama tiene un metro noventa por una cama de plaza que tiene noventa centímetros también y tú haces la cama, el larguero de dos metros, o sea total, pero resulta que el arquitecto hace que ande todo bien.
En la entrevista se infiere que la idea de este diseño surge en gran parte por la experiencia propia o guiada por el deseo de no ocupar madera decorativa en lugares que no se aprecia su belleza como ocurre, por ejemplo, al realizar una puerta en la que utiliza madera de pino para el esqueleto y es forrada con madera nativa para darle un toque artístico y detallado.
Localización del mueble
En la elaboración de un mueble DJ considera que es necesario conocer dónde se ubicará el mueble, haciendo referencia a la noción de localización.
Entrevistador 1: ¿La localización del lugar, primero que todo?
DJ: Sipo, si eso [lugar] está cuadrado para que yo trabaje.
DJ se ubica en el espacio para entender dónde se ubicará el mueble, diseñarlo y orientar la elaboración del mismo respecto de dónde ubicar cada una de las piezas que lo conforman. Un ejemplo de ello es que, mientras explica cómo arma las partes de una escalera de interior, señala de qué manera van puesta algunas piezas y cómo determina la ubicación de estas. Además, DJ en la entrevista menciona que:
Este es el eje, donde yo voy a colocar esta pieza acá, entonces yo hago un eje, una línea, a ver…
En el extracto de transcripción anterior DJ explica que en la construcción de una escalera debe saber dónde ubicar determinadas piezas. Para ello, él (como se ve en la figura 4) realiza una línea simétrica (sin instrumento de medición) en el centro de la tabla de madera donde irán los bolillos de madera (figura 4).
Figura 4: Ubicación de las piezas sobre el eje (eje de simetría).
También, se evidencia cuando DJ complementa esta idea haciendo referencia al proceso que sigue para hacer muebles para barcos, señalando:
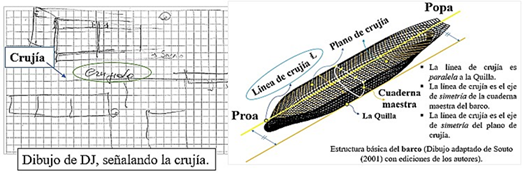
O sea, a uno le llevan un plano, dice por ejemplo en el caso de una consola de mando que, donde va todo, ese tiene un plano, y los planos no se miden, por ejemplo, como una casa, que tiene un cerco allí, hay una cota central, que es el eje del barco, de ese, por decir, aquí, este es el eje del buque, en el caso donde trabajo, y por ejemplo [comienza a elaborar la figura 5] de aquí hasta acá, aquí pasa un pasillo, una cosa así pongámosle, entonces aquí tenemos 10 centímetros hasta aquí, entonces tú dices de la crujía, esto se llama crujía, sí, de la crujía hasta acá tenemos cinco centímetros y de la crujía hasta acá tenemos, por ejemplo, ochenta centímetros.
Figura 5: Función de la línea de crujía en la estructura del barco.
En la figura 5 se observa que cuando DJ hace muebles para barcos enfatiza en la estructura básica del plano de crujía del barco para ubicar los muebles. Luego de observar el plano, DJ siente la necesidad de conocer el lugar físico donde se desea hacer un mueble. En este contexto, se observa que DJ implícitamente usa conceptos matemáticos como la simetría, al señalar:
[…] entonces tú, de esa crujía sacas todas las referencias, y por decir, hasta aquí un dormitorio, entiende que hay un dormitorio, acá hay un hall, y todo se mide desde ahí [señala la crujía en el dibujo], porque tú no lo puedes medir por los costados.
A su vez, deja entrever desde el punto de vista de las estructuras náuticas que la línea de crujía que menciona DJ es paralela a la quilla y es el eje de simetría de las cuadernas.
Cuantificación de materiales necesarios para el trabajo y presupuesto
Una vez determinado el diseño y las características del mueble es cuando uno de los entrevistadores le consulta a DJ “¿Cómo sabe la cantidad de material a ocupar?”, a partir de lo que surge la noción de contar.
Hay que cortarlo trabajando en serie, yo, por ejemplo, corto todas las puertas de una sola medida, corto todos los otros costados de otra medida, después los voy amontonando y después así ya sé cuánto…, y para la otra vez, ya me queda ese papel.
El carpintero plasma lo que desea cortar en una hoja, para tener certeza de los elementos necesarios para poder confeccionar un mueble. Utiliza un papel para realizar estos cálculos indicando: “para la otra vez, ya me queda ese papel”. Señala que este le servirá como un registro de conteo que le permite “un ordenamiento para futuros muebles que tengan características similares” y le ayudará a representar las cantidades de material que debe preparar para hacer un mueble: “corto todas las puertas de una sola medida, corto todos los otros costados de otra medida”.
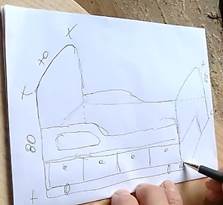
Además, DJ debe calcular cuántas planchas de un determinado material necesitará (conteos). Por ejemplo, mientras se habla sobre cómo lleva a cabo la elaboración de una cama explica cómo calcula la cantidad de planchas que necesitará:
Entonces que hago yo aquí [dibuja como se muestra en la figura 6], aquí voy a sacar, no cierto, estos 80 y estos 55 que me da, entonces esta yo voy a sacar ahí los 80 para calcular, y que me van a sobrar, ¿Cuánto me van a sobrar aquí? 125, 80, me van a sobrar 40, estos 40 necesito, estos 42 me van a servir para este larguero […].
Figura 6: Contando las planchas y encontrando las medidas.
En el extracto de transcripción anterior se evidencia cómo DJ distribuye los elementos que debe fabricar en una plancha según las medidas. Esto también se visualiza en la figura 6, en donde distribuye los elementos de la cama previamente diseñada en una plancha dibujada en otra hoja, en función de las áreas de estas y sus medidas.
DJ establece también realiza procesos de conteo cuando determina la cantidad de planchas necesarias para la elaboración del mueble y las medidas de cada una, señalando:
[…] con esta plancha no me da esto, porque tengo que comprar dos planchas y tengo que comprar otra plancha más delgada, que es de un metro, o sea la plancha es de 15 milímetros […]
Otros procesos de conteo identificados se observaron cuando DJ determinó la cantidad de clavos, tornillos y las tablas superpuestas una arriba de la otra. De manera similar, cuando se le preguntó a DJ sobre el precio de la cama, él respondió de forma detallada, especificando los materiales (la inversión) y cuánto cobra en general; lo que evidenció también la noción de contar.
E1: Otra pregunta, ¿los clientes al tiro le preguntan el precio de cuánto es el trabajo o algunos no preguntan?
DJ: Claro, me dicen yo necesito esto, yo más o menos hago un cálculo así mental y él [cliente] me dice, ¿Cuánto está saliendo esto? Yo por ejemplo estoy diciendo que me están saliendo tres planchas de terciado que pueden ser unos 60 mil pesos y yo le digo bueno esta cama, mi trabajo aquí yo tengo dos días de trabajo, saco mis días y mis materiales y le puedo decir yo, bueno esta camita le vale vendía 150 mil pesos.
Medidas del mueble
Otra noción matemática identificada en la práctica cotidiana de DJ fue la de medir. Primero, él toma las medidas (con un metro) del lugar donde se ubicará el mueble (ver el siguiente extracto de la transcripción).
E1: ¿Qué considera usted para la elaboración de un mueble?
DJ: La medida, tomar medidas del lugar donde va a estar el mueble.
Posteriormente, DJ mide las piezas que deberá elaborar para cada mueble a través de instrumentos de medición como la cinta de medir (metro). Se evidencia el uso de medidas convencionales y no convencionales por parte del DJ. Por ejemplo, al hablar de pulgadas y metros hace referencia al uso de unidades de medidas convencionales y equivalencias entre diferentes unidades que pertenecen a sistemas métricos distintos:
E1: ¿Más menos cómo calcula usted, o cómo se da cuenta qué tan largo tiene que ser el cajón hacía atrás, por ejemplo?
DJ: No debería ser mucho porque si usted tiene una pieza, no cierto, esta pieza, ya está cama dijimos que tiene 70 centímetros y esta pongámosle que tenga un metro, estas camas tienen un metro 90, pero como es para un niño, esta cama hay que mandarla a hacer a la medida pongámosle que tenga un metro con 50 centímetros, o sea un metro y medio. (figura 7)
Figura 7: DJ mide con el metro.
DJ en algunas ocasiones trabaja con el metro y en otras usa la pulgada, realiza conversiones entre unidades de un sistema a otro y considera sus equivalencias.
Madera de ocho pulgadas... empieza le iba a hacer esto al raulí le hago otro corte, pongo una lengüeta de otro color, tablas de raulí y lengüeta de mañío…da otro toque medio ostentoso dos piezas que se unen, dos piezas que se unen de dos pulgadas de madera al final terminen de hacer el trabajo yo.
También, utiliza unidades de medidas no convencionales como la tolerancia, evidenciada en su respuesta a los posibles inconvenientes que experimenta cuando realiza mediciones. Por ejemplo, casos en que la tolerancia en la madera queda corta o larga dependiendo del mueble. Esto sucede en las instalaciones de puertas, donde en la mayoría de los casos a la hoja (puerta) se le deja un poco de tolerancia corta, la cual es rebajada o cepillada hasta que encaje adecuadamente en el marco. La tolerancia larga se deja a los extremos del marco de la puerta, dado que en algunas situaciones hay desniveles en las paredes o se necesita empotrarlo en el piso.
Es que no podría quedar corto, ¿Por qué?, porque uno le da la tolerancia (con la mano señala una medida no convencional) que necesita, uno dice le vamos a dar cinco centímetros más, por si acaso. (figura 8)
Figura 8: Unidad de medida no convencional: “la tolerancia”.
De esta manera, DJ indicó que las camas tienen 1,90 m de largo (señala con el larguero); así, al realizar la preparación del material y no presentar problemas luego al ensamblar y ubicar la cama. DJ deja los largueros de dos metros, a esta acción él la denomina “darle tolerancia”, que incluso se puede interpretar como un margen de error para determinadas situaciones. Cabe destacar que esta tolerancia que él hace con un gesto con sus dedos varía dependiendo del mueble que se elabore. Por ejemplo, en algunos casos esta tolerancia es de cinco centímetros, mientras que en otros es aproximadamente 10 centímetros.
Por otra parte, para la elaboración de muebles para el interior de embarcaciones DJ mencionó que es importante interpretar planos donde se encuentran medidas, instancia que surgió mientras se hablaba de elaboración de alguna estrategia para la elaboración del mueble. Además, se reconoció el uso de otro instrumento de medida (escalímetro) y otras unidades de medidas convencionales como el centímetro y el milímetro:
E1: ¿Y ahí cómo desarrolló una estrategia?, ¿qué estrategia piensa usted que desarrolló?
DJ: No, porque por ejemplo ahí te dan un plano, un plano tiene sus medidas, por ejemplo, sus escalas de uno al diez que la mayoría se trabaja, del uno al cincuenta y así varias escalas que le trabajan, que están en un escalímetro y, a uno a veces le entregan un plano y no tienen una escala, lo hace nada más el arquitecto, hace el plano y por decir, se le olvida, entonces como tu sacas, tu buscas el escalímetro y mides, por decir, [comienza a realizar el dibujo de la figura 9], ya de aquí [señalando con el dedo], entonces ya aquí tengo un punto y hasta acá aquí no tengo una medida, pero yo busco un escalímetro y si esta escala es del uno al 50 yo tengo que tener, por ejemplo, en un metro, tengo que tener, o sea a ver, 50 cm medía un metro, o sea la cosa es que este metro me da, ucha esto 20 milímetros me da un centímetro... o sea, un metro, por eso del uno al 50.
Figura 9: Uso del escalímetro para medir e interpretar planos.
DJ da cuenta de la existencia de transformación de unidades de medida dentro del mismo sistema de medición, evidenciando relaciones entre milímetros, centímetros y metros. Asimismo, DJ explica el uso de escalas, enfatizando en una escala 1:2 (de reducción), lo cual significa que una unidad expresada en metros, centímetros o milímetros, en el plano (que está en la hoja) equivale a dos unidades en la realidad; es decir, para el caso de DJ, en el plano tiene una medida de 50 cm y el objeto en la realidad tiene 100 cm = 1 m. Podemos afirmar que DJ relaciona su práctica cotidiana de la carpintería con conocimientos clave de la arquitectura. A su vez, da cuenta de la presencia del manejo del concepto de punto, segmento y medida de la longitud del segmento:
[…] ya aquí tengo un punto y hasta acá aquí no tengo una medida, pero yo busco un escalímetro [para medir].
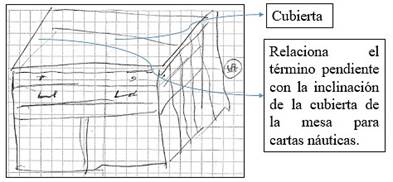
Por otra parte, otra noción matemática relacionada con la actividad de medir es identificada cuando DJ menciona el término pendiente, el cual comenta DJ en el siguiente extracto de transcripción:
No hacía otros trabajos, tanto con los closets tanto como las literas camas eh… los veladores, los mesones de cartas, las mesas de cartas, ósea las mesas de carta es una cubierta que tiene esta pendiente [hace un gesto con su mano, refiriéndose a la inclinación], pero tiene un cajoncito angostito donde se meten […].
DJ explica a los entrevistadores que la cubierta de las mesas de cartas náuticas (figura 10) tienen una pendiente. Este término se entiende en este caso de manera intuitiva como una inclinación (hace gestos con sus manos), la cual posee una razón fija y que DJ debe considerar para adaptar las medidas de los materiales que debe emplear en la elaboración de este mueble en particular. Consideramos que DJ en su práctica cotidiana usa implícitamente la conceptualización de la pendiente como propiedad física (Nagle y Moore-Russo, 2014).
Figura 10: Medida de la pendiente como inclinación.
Además, en esta investigación se destacan procesos de medición de ángulos realizados por DJ usando la escuadra. Estos los desarrolla estableciendo cortes a la madera de 45º y uniendo dos cortes para obtener un ángulo recto con una medida de 90º (figura 11).
Figura 11: Evidencia de medidas de ángulos de 45º y de 90º.
En la tabla 4 se presentan los instrumentos de medida y se sintetizan todas las unidades de medidas usadas por DJ en la elaboración del mueble.
Fuente: elaboración propia de los autores.
Tabla 4: Sistema de medida usado por DJ

Explicación general sobre la confección y ensamble de las piezas del mueble
La noción matemática de explicar se evidenció durante todo el proceso de construcción de DJ en los argumentos dados cuando diseña, localiza, cuenta y mide. Vemos que la explicación está involucrada tanto en la acción de explicar su labor a otras personas, argumentar la toma de decisiones asociadas al proceso de diseño y construcción de un mueble, así como la presentación de sus propuestas de diseño a los clientes. Por ejemplo, cuando explicó la medida no convencional la tolerancia y da un ejemplo apropiado de su uso; cuando explica cómo usa el escalímetro para medir e interpretar planos; o cuando se señala que las puertas de un mueble deben tener menor medida porque deben considerarse los marcos:
Si tú quieres hacer un mueble de 90 cm, debes tener unas puertas de 75 cm.
Discusión e implicaciones para la docencia
Nuestros hallazgos complementan resultados obtenidos en investigaciones similares centradas en otros grupos culturales y sociales (e. g. Fuentes, 2012; González y Zambrano, 2011; Soto, 2018). En esta investigación hemos identificado las nociones matemáticas presentes en el trabajo cotidiano de un carpintero cuando elabora muebles. Dichas nociones giraron en torno a las acciones de medir, contar, explicar, diseñar y localizar. Cabe destacar que la actividad de jugar no se vio involucrada explícitamente en la labor del carpintero; sin embargo, se reconocieron aspectos que podrían activar la noción de jugar cuando el carpintero usa estrategias en las relaciones interpersonales y desarrolla habilidades en la elaboración de un mueble.
También destacamos el uso de medidas convencionales como el metro, la pulgada y el centímetro y no convencionales como la tolerancia. Así como el papel fundamental que juega el escalímetro en los procesos de medición que realiza el carpintero, el uso de ángulos y la presencia de conocimientos geométricos como simetrías (cuando se habla de la crujía del barco), paralelismo, línea, punto, segmento y medida del segmento. Estos hallazgos son un valioso insumo para el diseño de actividades contextualizadas que relacionen prácticas cotidianas que se dan en el contexto de la construcción de muebles con los objetivos de aprendizaje del currículo.
Por ejemplo, la unión de cortes de ángulos de 45° grados para formar un ángulo de 90° que realiza DJ se puede relacionar con la identificación de ángulos que se forman entre dos rectas que se cortan y ángulos complementarios (Ministerio de Educación, 2013). También, se puede utilizar el concepto de pendiente empleado por DJ en las mesas de cartas náuticas que él elabora, en la interpretación gráfica de la pendiente al abordar los aprendizajes asociados a la función afín (Ministerio de Educación, 2016). En este sentido, se requiere más investigación en el área que permita analizar cuál es la mejor forma de poner en funcionamiento este tipo de propuestas en el aula a través de tareas matemáticas contextualizadas, así como el efecto que pueden tener en los aprendizajes alcanzados por los estudiantes.
Acknowledgements
Agradecimientos
Al carpintero participante de este estudio por suministrarnos la información sobre la elaboración de muebles para el desarrollo de esta investigación.
Referencias
Licencia
El (los) autor(es) al enviar su artículo a la Revista Científica certifica que su manuscrito no ha sido, ni será presentado ni publicado en ninguna otra revista científica.
Dentro de las políticas editoriales establecidas para la Revista Científica en ninguna etapa del proceso editorial se establecen costos, el envío de artículos, la edición, publicación y posterior descarga de los contenidos es de manera gratuita dado que la revista es una publicación académica sin ánimo de lucro.