DOI:
https://doi.org/10.14483/23448350.291Publicado:
11/30/2007Número:
Núm. 10 (2008): Enero-diciembreSección:
Ingeniería y TecnologíaDidáctica de la programación lineal con el método gráfico
Lineal programming didactic with the Graphic Method
Palabras clave:
Sensitividad, sensibilidad, postóptima, análisis gráfico, cotas, márgenes, variación de coeficientes, modelos, programación lineal (es).Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ingeniería y Tecnología
Revista Científica, 2008-08-00 nro:10 pág:17-21
Didáctica de la programación lineal con el método gráfico
Lineal programming didactic with the Graphic Method
Fernando León Parada
Magister en Ciencia Matemática, Universidad Nacional de Colombia. Licenciado en Ciencia de la Educación Matemática, Universidad Nacional de Colombia. Director del grupo de investigación DIMMIO, Universidad Distrital Francisco José de Caldas. E-mail: fleon@udistrital.edu.co
Análisis gráfico para la sensibilidad post-óptima de modelos de programación lineal con dos variables
Resumen
Todo modelo de programación lineal contiene una función objetivo determinada por los coeficientes de las variables de decisión. La función objetivo evaluada en un punto óptimo es una recta cuya pendiente depende de las variaciones de los coeficientes. El análisis geométrico de las pendientes de los segmentos, frontera de una región factible, permite establecer los márgenes de variación para esos coeficientes. Además, también se analizará el acotamiento de los bordes de la región factible manteniéndola como dominio de la función objetivo.
Palabras clave:
Sensitividad, sensibilidad, postóptima, análisis gráfico, cotas, márgenes, variación de coeficientes, modelos, programación lineal.
Abstract
Every Linear Programming model has a Objective Function determined by the coefficients of the decision variables. The Objective Function can be represented as a line evaluated on an optimal point which slope depends from the variation of the coefficients. The segments adjacent to the optimal point in the Feasible Region can also determine the variation of this slope. Finally a geometric analysis allows to establishing the constraining of the boundary for the Feasible Region keeping as a domain for the Objective Function.
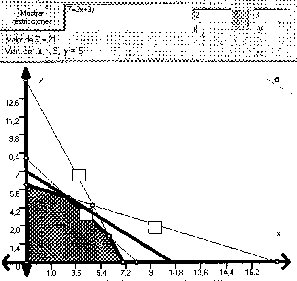
Gráfico 3.1
Key words:
Sensitivity, sensibility, post- optimal, graphical analysis, constraints, margins, coefficients variance, models, linear programming.
Objetivo
Una vez obtenida la solución a un problema se pretende determinar la variación de los coeficientes de la función objetivo que no afectan la decisión de continuar con el mismo punto óptimo, o del segmento óptimo en el caso de infinitas soluciones paramétricas; también se aplicará el concepto de paralelismo y puntos de corte entre rectilíneas para la variación de las fronteras de la región, de tal manera que siga siendo un dominio factible para la función objetivo del modelo de programación lineal.
Análisis sensitivo para los coeficientes de una función objetivo
Iniciamos la didáctica con dos preguntas.
a. ¿Cuáles son los márgenes entre los que pueden variar cada uno de los coeficientes de la función objetivo sin tener que modificar los puntos de la solución óptima previamente obtenida para un modelo de programación lineal?
b. ¿Cuáles serán las respectivas variaciones de los valores extremos de la función objetivo al modificar los coeficientes hasta esos márgenes?
La respuesta se dará al hacer variar la pendiente de la recta objetivo zo = c1 x + c2 Y, siendo constante el valor z(x0, Yo) = z0 extremo previamente obtenido en un punto óptimo. Tal variación debe limitarse entre las pendientes de los segmentos bordes o frontera adyacentes al punto óptimo. Los movimientos gráficos se presentan así:
Ejemplo 3.1 Respecto de la solución óptima z = 21 en el punto óptimo B = (3,5) del modelo maximizar z = 2x + 3Y sujeta a { 2x+Y ≤14, X+Y ≤ 8, x+3Y ≤ 18 }, analizar la sensibilidad de coeficientes de la función objetivo.
Solución:
A partir del gráfico 3.1, la recta objetivo apoyada en el punto B tiene ecuación: 21 = 2x + 3Y, su pendiente es - 2/3, y se encuentra entre las pendientes de los segmentos BC y AB, esto es: - 1≤ - 2/3 ≤ - 1/3.
Ahora, si se mantiene constante el coeficiente C2 = 3, se puede analizar la variación del coeficiente C1 en la desigualdad de las pendientes ya establecidas:
- 1 ≤ - C1 /3 ≤ - 1/3
Al resolver: 1 ≤ C1 ≤ 3
Al evaluar las funciones objetivo modificadas según los márgenes en el mismo punto B :
z = 1x + 3Y : z = 1(3) + 3(5) = 18
z'= 3x+ 3Y: z' = 3 (3) + 3 (5) = 24
Ahora, los gráficos 3.2 y 3.3 presentan las respectivas rectas objetivo coincidentes sobre cada uno de los segmentos adyacentes al punto óptimo; estos son efectos de rotación de la recta objetivo inicial anclada en B:
Para el análisis de los márgenes de sensibilidad del coeficiente C2 se mantiene constante el coeficiente C1= 2,
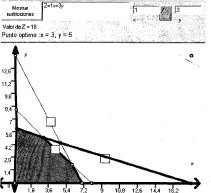
Gráfico 3.2
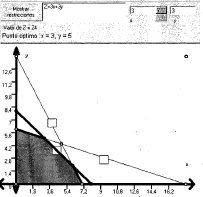
Gráfico 3.3
y se establece la desigualdad de las pendientes:
- 1 ≤ 2/ C2 ≤ - 1/3
Al resolver: 2 ≤C2 ≤6
Al evaluar las funciones objetivo modificadas según los márgenes en el mismo punto B; note que sigue el mismo efecto de rotación.
Ejemplo 3.2 Respecto de la solución óptima Z = 21 en el punto óptimo B = (3,5) del modelo maximizar Z = 2x + 3Y sujeta a { 2x+Y ≤ 14, X+Y ≤ 8, x+3Y ≤18 }, analizar la sensibilidad de cada cota en las restricciones.
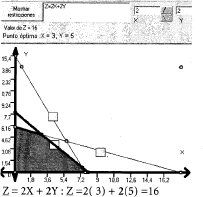
Gráfico 3.4
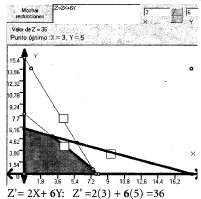
Gráfico 3.5
Solución:
Para la cota de valor constante 14 de la primera restricción:
Cuando se desplaza paralelamente el segmento frontera CD de la recta 2x+Y = 14, suceden dos casos:
Al aumentar el valor de 14, el segmento extiende la región hacia la derecha pero no acarrea el desplazamiento del punto óptimo B pues éste no pertenece al segmento CD; esto indica que no hay cota superior para la constante, lo cual se expresa como una indiferencia económica para el punto óptimo y el valor máximo sigue igual, Z = 21.
En cambio, al disminuir el valor desde 14, el segmento CD se desplaza paralelamente hasta hacer coincidir el punto C con el punto óptimo B; esto refleja que el valor de cota mínimo para la restricción es 11, pues al calcular el punto B en la expresión 2x + Y se obtiene: 2(3) + 5 = 11. El valor de z sigue igual al valor máximo 21. El gráfico 3.6 refleja esta nueva situación del lugar geométrico.
Para la cota de valor constante 8 de la segunda restricción:
Cuando se desplaza paralelamente el segmento frontera Bc de la recta x + Y = 8, suceden los dos casos:
Si se aumenta el valor desde 8, el segmento extiende la región hacia la derecha y acarrea el desplazamiento del punto óptimo B hacia el nuevo punto P solución del sistema simultáneo de las rectas que contienen los segmentos AB y Bc.
Como la solución del sistema { 2x+Y ≤ 14, x+3Y ≤ 18 } es el punto P = (24/5, 22/5), al sustituir en la expresión x + Y se obtiene el valor 24/5 + 22/5 = 46/5 = 9.2: este es el valor de cota superior para la restricción.
El valor máximo cambia pues al evaluar z en este nuevo punto se obtiene:
Z = 2 (24/5) + 3 (22/5) = 114/5 = 22.8.
Esta situación geométrica aparece en el gráfico 3.7.
En cambio, al disminuir el valor desde 8, el segmento BC se desplaza paralelamente hasta coincidir el punto óptimo B con el punto A, de modo que la cota inferior se obtiene al evaluar A = (0,6) en la expresión x + Y, esto da un valor de 6. El valor máximo ahora será de z = 2 (0) + 3 (6) = 18; esta nueva condición geométrica se representa en el gráfico 3.8.
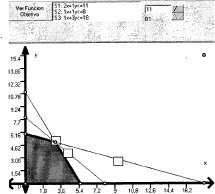
Gráfico 3.6
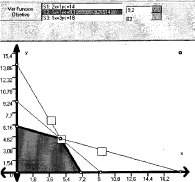
Gráfico 3.7
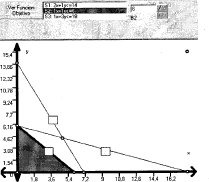
Gráfico 3.8
Para la cota de valor constante 18 de la tercera restricción, al desplazar paralelamente el segmento frontera AB de la recta x + 3Y = 18, suceden los dos casos siguientes:
Al disminuir el valor desde 18, el segmento AB restringe la región hacia abajo y acarrea el desplazamiento del punto óptimo B hacia el punto C = (6, 2); al sustituir las coordenadas de C en la expresión x + 3Y se obtiene el valor 6 + 3(2) = 12: este es el valor de cota inferior para la restricción.
El valor Mínimo cambia, pues al evaluar Z en este nuevo punto se obtiene:
Z = 2 (6) + 3 (2) = 18. Esta situación de la nueva Región Factible parece en el Gráfico 3.9
Si se aumenta el valor desde 18, el segmento AB extiende la región hacia arriba acarreando el desplazamiento del punto óptimo B hacia el nuevo punto Q = (0, 8) que es el corte con el eje vertical de la recta x + Y = 8; al sustituir las coordenadas de este nuevo punto óptimo Q en la expresión x + 3Y se obtiene el valor O + 3(8) = 24: este es el valor de cota superior para la restricción.
El valor m Máximo cambia porque al evaluar z en este nuevo punto Q y se obtiene:
z = 2 (0) + 3 (8) = 24. Esta situación geométrica aparece en el gráfico 3.10.
Una tarea sencilla de interés para el lector es la de plantear el análisis de sensibilidad tanto para los coeficientes de la función objetivo como para las cotas de las restricciones del ejemplo 3.2 sobre minimización; el modelo es
Minimizar z (x, Y) = 2x + Y sujeta a: + 2Y ≥ 7, x + Y≥ 5,3x + Y ≥ 7,x ≥ O, Y ≥ O.
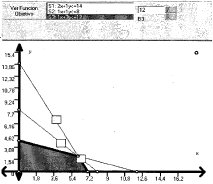
Gráfico 3.9

Gráfico 3.10
Ingrese a www.udistritaLedu.co/comunidad/grupos/ dimmio. Desde este enlace descargue el software Simplex2004 e ingrese al menú de Programación Lineal; escriba el planteamiento algebraico del modelo y seleccione la opción de minimizar. Después de resolver el problema planteado por el modelo, puede entrar al gráfico y analizar la sensibilidad de los parámetros de dos formas: haciendo variar la función objetivo desde el punto óptimo para determinar las cotas de variación de los coeficientes de la función objetivo, o desplazando las fronteras de la región factible para conocer los márgenes de variación de las cotas en las restricciones.
Licencia
El (los) autor(es) al enviar su artículo a la Revista Científica certifica que su manuscrito no ha sido, ni será presentado ni publicado en ninguna otra revista científica.
Dentro de las políticas editoriales establecidas para la Revista Científica en ninguna etapa del proceso editorial se establecen costos, el envío de artículos, la edición, publicación y posterior descarga de los contenidos es de manera gratuita dado que la revista es una publicación académica sin ánimo de lucro.



