DOI:
https://doi.org/10.14483/23448393.11825Published:
2018-01-10Issue:
Vol. 23 No. 1 (2018): January - AprilSection:
Industrial EngineeringDimensionamiento de Almacén a partir de la Planificación de Requerimiento de Materiales en una Fábrica de Revestimiento de Poliuretano
Warehouse Sizing based on Material Requirements Planning for a Polyurethane Coating Factory
Keywords:
Material requirements planning, warehouse layout, warehouse sizing (en).Keywords:
Dimensionamiento de almacenes, plan de requerimiento de materiales (es).Downloads
References
I. Sulírová, L. Závodská, M. Rakyta, V. Pelantová, "State-of-the-Art Approaches to Material Trans-portation, Handling and Warehousing". Procedia Engineering, vol. 192, pp. 857-862, 2017
https://doi.org/10.1016/j.proeng.2017.06.148
T. Sprock, A. Murrenho, L. F. McGinnis, "A Hierarchical Approach to Warehouse Design". Interna-tional Journal of Production Research, vol. 55, no. 21, pp. 6331-6343, octubre, 2016
https://doi.org/10.1080/00207543.2016.1241447
G. Zhang, T. Nishi, S. D.O. Turner, K. Oga, X. Li, "An Integrated Strategy for a Production Planning and Warehouse Layout Problem: Modeling and Solution Approaches". Omega, vol. 68, pp. 85-94, 2017.
https://doi.org/10.1016/j.omega.2016.06.005
E. Cakmak, N. S. Gunay, G. Aybakan, M. Tanyas, "Determining the Size and Design of Flow Type And U-Type Warehouses". in 8th International Strategic Management Conference, 2012, pp. 1425–1433.
https://doi.org/10.1016/j.sbspro.2012.09.1127
G. Jinxiang, M. Goetschalckx, L. F. McGinnis, "Research on Warehouse Design and Performance Evaluation: A Comprehensive Review". European Journal of Operational Research, vol. 203, no. 3, pp. 539-549, 2010.
https://doi.org/10.1016/j.ejor.2009.07.031
A. M. Hualpa, C. Suárez, "Ubicación y dimensionamiento como parámetros en el dise-o de alma-cenes: revisión del estado de arte". Ingeniería, vol. 18, no. 1, pp. 65-83, 2013.
Chachelson, L. C., Metodologías de dise-o de Almacenes: Fases, Herramientas y mejores prácti-cas. Donostia-San sebastian, Espa-a, 2013.
L. M. Thomas, R. D. Meller, "Developing design guidelines for a case-picking warehouse". Int. J. Production Economics, vol. 170, pp. 741-762, 2015.
https://doi.org/10.1016/j.ijpe.2015.02.011
L. F. Cardona, D.F. Soto, L. Rivera, H. J. Martínez, "Detailed Design of Fishbone Warehouse Layouts with Vertical Travel". Int. J. Production Economic, vol. 170, pp. 825-837, 2015.
https://doi.org/10.1016/j.ijpe.2015.03.006
K. Y. Tippayawong, A. Sopadang, P. Patitad, "Improving Warehouse Layout Design of a Chicken Slaughterhouse using Combined ABC Class Based and Optimized Allocation Techniques". In Proceed-ings of the World Congress on Engineering. London, 2013.
V. Rakesh, G.K. Adil, "Layout Optimization of a Three-Dimensional Order Picking Warehouse". IFAC – Papers on Line, vol. 48, no.3, pp. 1155 - 1160, 2015.
N. Mishra, V. Kumar, N. Kumar, M. Kumar, M.K. Tiwari, "Addressing Lot Sizing and Warehousing Scheduling Problem in Manufacturing Environment". Expert Systems with Applications, vol. 38, pp. 11751-11762, 2011.
https://doi.org/10.1016/j.eswa.2011.03.062
W. Jaruphongsa, S. Cetinkaya, C.Y. Lee, "Warehouse Space Capacity and Delivery Time Window Considerations in Dynamic Lot-Sizing for a Simple Supply Chain". Int. J. Production Economics, vol. 92, pp. 169-180, 2004.
https://doi.org/10.1016/j.ijpe.2003.10.012
S. Minner, "A Comparison of Simple Heuristics For Multi-Product Dynamic Demand Lot-Sizing with Limited Warehouse Capacity". Int.J. Production Economics, vol. 118, pp. 305-310, 2009.
https://doi.org/10.1016/j.ijpe.2008.08.034
S. Huang, Q. Wang, R. Batta, R. Nagi, "An Integrated Model for Site Selection and Space Determi-nation of Warehouses". Computers & Operations Research, vol. 62, pp. 169-176, 2015.
https://doi.org/10.1016/j.cor.2014.10.015
M. Klodawski, M. Jacyna, K. Lewczuk, M. Wasiak, "The Issues of Selection Warehouse Process Strategies". Procedia Engineering, vol. 187, pp. 451-457, 2017.
https://doi.org/10.1016/j.proeng.2017.04.399
A. M. Hualpa, C. A. López, "Algoritmo de dimensionamiento de almacenes para empresas de edificación en el sector de la construcción". Ingeniería, vol. 20, no. 1, pp. 189-208, 2015.
M. Horta, F. Coelho, S. Relvas, "Layout Design Modelling for a Real World Just-In-Time Ware-house". Computers & Industrial Engineering, vol. 101, pp. 1-9, 2016.
https://doi.org/10.1016/j.cie.2016.08.013
R. A. Gómez, A. A. Correa, "Métodos cuantitativos utilizados en el dise-o de la gestión de alma-cenes y centros de distribución". Revista Avances en Sistemas e Informática, vol. 7, no. 3, pp. 109-117, 2010.
R. Ballou, The Consideration of Angular Pallet Layout to Optimize Warehouse Space Utilization. 1963. Master´s Thesis. The Ohio State University.
M. S. Hung, J. C. Fisk, "Economic Sizing of Warehouses: a Linear Programming Approach". Com-puters & Operations Research, vol. 11, no. 1, pp. 13-18, 1984.
https://doi.org/10.1016/0305-0548(84)90003-0
G. Cormier, E. Gunn, "A Review of Warehouse Models". European Journal of Operational Re-search, vol. 58, pp. 3-13, 1992.
https://doi.org/10.1016/0377-2217(92)90231-W
T. N. Larson, H. March, A. Kusiak, "A Heuristic Approach to Warehouse Layout with Class Based Storage". IIE Transactions, vol. 29, no.4, pp. 337-348, 1997.
https://doi.org/10.1080/07408179708966339
A.K. Rao, M. R. RAO, "Solution Procedures for Sizing of Warehouses". European Journal of Oper-ational Research, vol. 108, no. 1, pp. 16-25, 1998.
https://doi.org/10.1016/S0377-2217(97)00159-8
G. Ghiani, G. Laporte, R. Musmanno, "Designing and Operating a Warehouse". in Introduction to Logistics Systems Planning Control, J. Wiley, Ed. England: 2004, pp. 157 - 166
L. Hsieh, L. Tsai, "The Optimum Design of a Warehouse System on Order Picking Efficiency". The International Journal of Advanced Manufacturing Technology, vol. 28, no. 5, pp. 626-637, 2006.
https://doi.org/10.1007/s00170-004-2404-0
D. Thornton, R. Francis, T. Loue, "Rectangular Layout Problems With Worst –Case Distance Measures". AIIE Transactions, vol.11, no.1, pp. 2 - 11, 1979.
https://doi.org/10.1080/05695557908974394
R.M. Venkata, K. A. Gajendra, "A branch and bound algorithm for class based storage location assignment". European Journal of Operational Research, vol. 189, no. 2, pp. 492-507, 2008.
https://doi.org/10.1016/j.ejor.2007.05.050
L. Choong, L. Careen, "A simulation study of warehouse loading and unloading systems using Arena". Journal of Quality Measurement and Analysis, vol.5, no. 2. pp. 45-56, 2009.
S. Huang, Q. Wang, R. Batta, R. Nagi, "An Integrated Model for Site Selection and Space Determi-nation of Warehouses". Computers & Operations Research, vol. 62, pp. 169-176, 2015.
https://doi.org/10.1016/j.cor.2014.10.015
G. Zhang, T. Nishi, S. Turner, K. Oga, L. Xindan, "An Integrated Strategy for a Production Planning and Warehouse Layout Problem: Modeling and Solution Approaches". Omega, vol. 68, pp. 85-94, 2016.
https://doi.org/10.1016/j.omega.2016.06.005
J. Bartholdi, S. Hackman, Warehouse & Distribution Science. The Supply Chain and Logistics Insti-tute. Georgia Institute of Technology, Release 094, pp. 219-222. 2011
D. Cárdenas, A. Urquiaga, "Administración de la producción". Revista de Ingeniería Industrial, vol.25, no. 3, 2004.
Z. Xiande, L. Kokin, "Lot-Sizing Rules and Freezing the Master Production Schedule in Material Requirements Planning Systems". Int. J. Production Economics, vol. 53, no.3, pp. 281-305, 1997.
https://doi.org/10.1016/S0925-5273(97)00111-4
Y. Hernández, "Aplicación del método de estudio de la gestión de la producción a un sistema productivo de medicamentos". Revista de Ingeniería Industrial, vol. 30, no.1, pp. 1 – 8, 2009.
Gue, K., Meller, R. D., "Aisle Configurations for Unit-Load Warehouses". IIE Transactions, 41, 3, 171-182, 2009.
https://doi.org/10.1080/07408170802112726
Celik, M., Sural, H., The Order Picking Problem in Fishbone Aisle Warehouses. Research Thesis. Georgia Institute of Technology. Atlanta, USA, 2012.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 5 de abril de 2017; Revisión recibida: 20 de octubre de 2017; Aceptado: 10 de noviembre de 2017
Resumen
Contexto:
El diseño del almacén es un factor clave en la configuración de los sistemas logísticos, pues facilita la gestión oportuna de materiales, productos intermedios o finales, mejorando el tiempo, costo y nivel de servicio al cliente. Para lograrlo se requiere el apoyo de expertos que integren en el diseño una combinación apropiada de almacenamiento, manipulación de materiales y selección n de pedidos; sin embargo, tal nivel de integración aún no se ha logrado ya que los avances en el tema han sido abordados desde diferentes aspectos del dimensionamiento y de manera independiente.
Método:
Se presenta un método de dimensionamiento de almacenes compuesto de dos fases. En la primera se definen variables y parámetros que son obtenidos a partir del proceso de planeación de la producción; en la segunda, se desarrollan cinco etapas que culminan con el diseño integral del almacén, en la cual se aplica un modelo matemático de dimensionamiento existente que incorpora una nueva ecuación.
Resultados:
El método de dimensionamiento de almacenes se aplica a una empresa que abastece poliuretano líquido en el sector de la construcción. Se generan cuatro opciones de configuración de muelles de recepción-envío y cinco opciones de almacenamiento; la mejor opción genera un área promedio, capacidad real promedio y porcentaje de utilización promedio de almacenamiento de 374,8 m2, 360 pallet y 93,8 % respectivamente, siendo estos resultados acordes con la dinámica de la empresa.
Conclusiones:
El método es funcional en la organización, puesto que permite evaluar opciones de configuración de flujo y su respectivo dimensionamiento, los cuales pueden influir en decisiones de gran importancia, por ejemplo, en determinar la capacidad operativa de la empresa a corto, mediano y largo plazo. Igualmente, para futuras investigaciones es de interés estudiar nuevas condiciones como es la compatibilidad del método propuesto con distribuciones diferentes a la configuración tradicional de estanterías paralelas.
Palabras clave:
Dimensionamiento de almacenes, plan de requerimiento de materiales., Idioma: Español.Abstract
Context:
The design of the warehouse is a key factor in the configuration of logistics systems, as it can facilitate the timely management of materials, intermediate and/or final products, improving the time, cost and levels of customer service. To achieve this, experts help is required to integrate within the design an appropriate combination of storage, manipulation of materials and selection of orders. This level of integration, however, has not yet been achieved since the advances in the subject have been addressed from different aspects of the storage problem, but independently.
Method:
The article presents a method for warehouse layout design in two phases. The first phase defines the variables and parameters that are obtained from the planning of the production; the second phase consists of five stages that culminate in the integral design of the warehouse. In this last phase a modified version of an existing mathematical model of sizing is applied, where a new equation is added.
Results:
The method is applied to a company that supplies liquid polyurethane in the construction sector. The design generates four options for configuration of shipping and receiving docks and five storage options, where the best option generates an average area, mean real capacity and percentage average of storage utilization of 374,8 m2, 360 pallet and 93,8 % respectively. These results are coherent with the dynamics of the company.
Conclusions:
The method allows evaluating options of the flow configuration and their respective sizing than may influence decisions of great importance in the operational capacity of the company in the short, medium and long term. In the future research is interesting to include new conditions, for example the compatibility of the method with different distributions to the traditional configuration of parallel shelves.
Keywords:
Material requirements planning, warehouse layout, warehouse sizing, Language: Spanish.1. Introducción
El diseño del almacén es un factor clave en la configuración de los sistemas logísticos, ya que promueve la gestión oportuna de materiales, productos intermedios o finales, los cuales a su vez permiten mejorar el tiempo, costo y nivel de servicio al cliente. Por lo tanto, uno de los objetivos de la gestión del almacén es hacer más eficientes los procesos logísticos, pues la edificación de un nuevo centro de almacenamiento requiere de una alta inversión; por esta razón, un almacén que presente la máxima utilización de los espacios, flujos de materiales claros y rápidos puede proporcionar un capital menos exigente. Además, una combinación apropiada de almacenamiento, manipulación de materiales y selección de pedidos puede reducir los tiempos de ciclo, aumentar la visibilidad del inventario y reducir los costos de su mantenimiento [1].
Asimismo, el desafío del almacén es un proceso complejo, requiere de expertos que ayuden a definir métodos para organizar e integrar su configuración. Es claro que este nivel de integración atún no existe, ya que los avances en el tema han sido orientados a resolver aspectos de diseño de almacenes de manera independiente; se requiere entonces una metodología ingenieril integrada que incorpore y de soporte a todas las decisiones de diseño [2]. Un ejemplo claro de lo anterior tiene que ver con los problemas que se presentan en la planeación de la producción, estos se analizan de forma aislada del almacenamiento, siendo este último un proceso final en el sistema de fabricación; una mejora en la utilización de este espacio puede aumentar los niveles de producción. De esta forma, la falta de coordinación entre la planificación de la producción y la gestión del almacén conduce a una ineficiencia significativa [3]. El proceso de almacenamiento no solo es importante en el sistema de fabricación sino en toda la gestión de la cadena de suministro, ya que refleja un vínculo entre el productor y el cliente en el cual las empresas se comprometen a entregar productos en el menor tiempo, siempre y cuando se tenga un número mínimo de existencias; además, permite manejar las cantidades cambiantes y decrecientes de la demanda, siendo esta una característica del día a día de las organizaciones [4].
Del mismo modo, el diseño del almacén se define en cinco grandes decisiones, a saber: la estructura, el dimensionamiento, el diseño interno, la selección de equipos y las estrategias operacionales en las que intervienen políticas de producción en términos de abastecimiento de material [5]. Sin embargo, varios expertos consideran que uno de los elementos críticos en esta etapa de diseño es determinar el dimensionamiento del almacén, debido a que una vez sea definido, se tiene una condición o restricción en las posibles configuraciones que se puedan efectuar posteriormente, es decir, en el caso de incrementar el flujo de materiales, se pueden presentar limitaciones de espacio para recepción, almacenamiento o despacho de materiales, restringiendo las operaciones normales de un centro de distribución, así como las actividades del área de producción. De acuerdo con lo anterior, se puede identificar la importancia que tienen los parámetros de ubicación y dimensionamiento en el diseño de almacenes [6]; es por ello por lo que se han desarrollado herramientas tecnológicas como Inventory Replenishment Expert System (IRES), el cual se enfoca en determinar la capacidad que debe tener un almacén de acuerdo con el nivel de servicio que desearía alcanzar [7]. A la vez, se resalta la importancia de que el dimensionamiento no puede ser trabajado en forma aislada, sino que debe integrarse a las funciones logísticas de la cadena.
En la literatura se encuentran diversos avances en el diseño del almacén, en [2] se presenta una metodología jerárquica de diseño, siendo un método poco explorado en esta área de conocimiento; la metodología consiste en la descomposición del problema en la que se aplica un modelo formal que integra las soluciones de estos subproblemas en un espacio de búsqueda exhaustiva. Igualmente, en el artículo [8] se proporciona un conjunto de directrices para llegar a una “buena” configuración de diseño para un almacén, para ello, se emplea una metodología basada en estadística y modelos analíticos, definiendo como variable de respuesta el número de horas de trabajo por cada uno de los diseños; de la misma manera, se postula que el almacén implica dos conjuntos de valores.
Teniendo en cuenta lo anterior, el primer conjunto describe los parámetros que se fijan para un determinado problema del almacén, estos parámetros se refieren a características como el numero requerido de ubicaciones de pallets, el número de referencia (SKU), los requisitos de rendimiento, entre otros; en cambio, el segundo conjunto son valores asociados con las opciones de diseño, haciendo referencia a variables de decisión como la forma del área del almacén, la configuración de la puerta del muelle, la disposición del área frontal y el tamaño. También se proporciona un método que genera un diseño tridimensional bajo una disposición en forma de espina de pescado; este método toma la capacidad de almacenamiento deseada e informa la ubicación en los ejes X-Y-Z a un costo total mínimo. Además, se determina como característica principal de diseño la distancia de viaje, logrando hasta un 20 % de reducción en comparación con los esquemas tradicionales para almacén de carga unitaria [9]. De igual modo, en [10] se propone un diseño del almacén que mejora el proceso de búsqueda y selección de productos, además de aumentar la utilización del espacio; en este diseño se aplica la clasificación del sistema ABC en los pedidos y la técnica de programación lineal, de tal manera que determina nuevas localizaciones para los productos. Es claro que las decisiones de disposición del almacén tales como altura, profundidad del carril, ancho, ubicación de pasillo, entre otros, son importantes, ya que afectan tanto al capital de inversión como los costos operacionales.
En [11] se presenta un modelo matemático apoyado con un algoritmo que decide cuatro de las decisiones más importantes en el diseño de un sistema de estanterías de almacén, las cuales corresponden a la profundidad del carril, numero de niveles de almacenamiento, profundidad lateral y ancho longitudinal. Por otra parte, se observan estudios aplicados al proceso de abastecimiento relacionados con el dimensionamiento de lote; por ejemplo, en [12] se explora el concepto de dimensionamiento de lotes en el contexto de la gestión de almacenes, ya que el problema de programación de tamaño de lote se ha centrado principalmente en la unidad de producción, razón por la cual el propósito es decidir el tamaño efectivo de lote que cumpla con las fechas de vencimiento, mientras que transfiere el producto desde el fabricante hasta el minorista a través del almacén. En este problema de dimensionamiento de lotes, el modelamiento utilizado para dar solución eficaz es el algoritmo de recocido simulado rápido (CBFSA), basado en restricciones donde los resultados demuestran la eficacia y la superioridad sobre otros enfoques (GA y SA).
Por su parte, en [13] se presenta un modelo de tamaño de lote dinámico de dos escalones con ventanas de tiempo de entrega, penalizaciones y limitaciones de capacidad en el espacio de almacén, en el que se aplica un algoritmo polinomial que reporta una solución óptima, esta incluye el plan de reposición y el plan de despacho. Este modelo es validado en la industria de la computación donde la capacidad de almacenamiento es limitada, siendo una restricción que debe considerarse explícitamente por la naturaleza de los productos terminados, pues son de alto valor económico. En cambio, los autores del artículo [3] proponen una estrategia que combina el problema de tamaño de lote capacitado con la disposición del almacén, esto con el fin de que el proceso de producción y el almacenamiento se puedan coordinar eficazmente; sin embargo, el problema de la disposición del almacén y del tamaño de los lotes capacitados ha sido abordado por separado en la literatura actual y no han sido considerados juntos en un modelo matemático, es por esta razón que el autor presenta un modelo que no solo combina un problema sobre asignación de ubicación de almacenamiento con un inventario dinámico, sino que también tiene en cuenta la planificación de la producción.
Otros estudios se han orientado a problemas como la reposición de múltiples productos para satisfacer demandas dinámicas cuando la capacidad del almacén es limitada, razón por la cual la sincronización ha de ser escalonado entre la reposición de los tamaños de los lotes y la capacidad, en la que es necesario proporcionar un espacio efectivo compartido [14]. Del mismo modo, se estudia un modelo integrado que busca resolver el problema sobre el número y ubicaciones de los almacenes a abrir, el tamaño de cada almacén que se edificara para satisfacer un nivel de servicio predeterminado, así como el flujo de producto a través de los almacenes abiertos con el objetivo de minimizar los costos totales (transporte, construcción fijos y variables del almacén), donde los resultados muestran que cuando el número de flujo de demanda es pequeño, es mejor usar el enfoque continuo de la variable tamaño del almacén porque presenta una menor brecha de error. En cambio, si el flujo de demanda es grande se recomienda usar el enfoque discreto de la variable tamaño, pues tarda menos tiempo y genera una solución satisfactoria [15].
En el artículo [4] se sugieren modelos que minimicen la distancia total de recorrido de los recolectores en almacenes tipo flujo (I-Shaped) y tipo U (U-Shaped) para determinar su tamaño, donde el número de muelles es la primera etapa del diseño del almacén al ser uno de los factores que más afectan la distancia media de viaje del selector y el tráfico de entrada y salida de los camiones; por lo tanto, se determinan los tamaños del almacén de acuerdo con los números de muelles (receptores y embarque) para cada tipo de almacén. Además, en el artículo [16] se caracteriza el proceso de almacén presentando un enfoque para seleccionar la estrategia de almacenamiento, ya que esta depende de factores técnicos y organizacionales como es el tipo de tareas básicas, la estructura y el tamaño de las ordenes de los clientes, los costos de manipulación de los materiales, disponibilidad de espacio de almacenamiento, recursos laborales, entre otros.
De manera específica, en la literatura se puede encontrar el diseño de un algoritmo aplicado en el dimensionamiento de almacenes, el cual permite asignar áreas de almacenamiento de manera dinámica en empresas dedicadas a la construcción de instalaciones residenciales. Esta propuesta se desarrolló con el propósito de disminuir el grado de informalidad que tiene este sector [17]. En el artículo [18] se expresa que la mayor parte de la literatura se centra en los almacenes tradicionales, donde el foco principal está en el almacenamiento de productos y la recogida; sin embargo, al operar sistemas de distribución recientes como es el cross-docking , se requieren nuevos enfoques para planificar el diseño interno del almacén, es por esta razón que el artículo propone un enfoque de programación matemática, basado en una formulación mínimo-máximo, la cual devuelve el diseño optimizado de un almacén de cross-docking que alimenta una operación de distribución just-in-time.
De acuerdo con lo anterior, se ha identificado que la gestión del almacén ha sido objeto de investigación por más de dos décadas, durante estas se han obtenido resultados asociados a la aplicación y modelamiento de técnicas cuantitativas, específicamente métodos analíticos, heurísticos, metaheurísticos, simulación discreta o continua y el diseño de experimentos [19]; sin embargo, se identifica que el tema de dimensionamiento como tal es una de las áreas de conocimiento que ha presentado menos investigaciones y que, hasta el momento, no se cuenta con un método de dimensionamiento de almacenes a partir del plan de requerimiento de materiales.
En la Tabla I se presentan algunos aportes y avances relevantes que están relacionados con el dimensionamiento de almacenes.
Tabla I: Avances en el dimensionamiento de almacenes
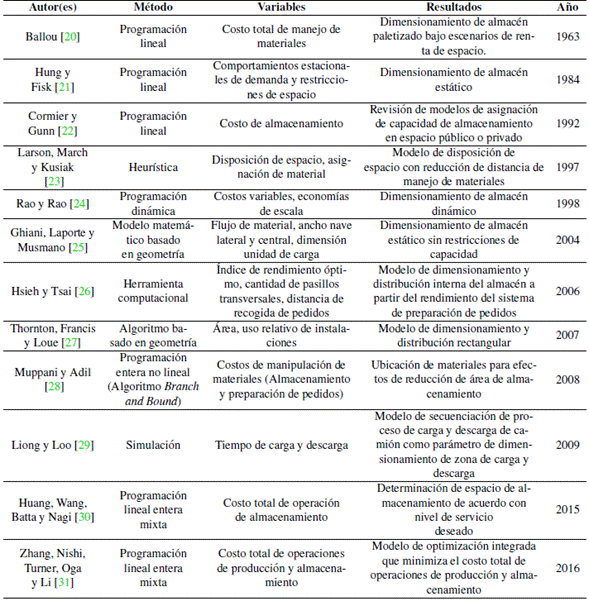
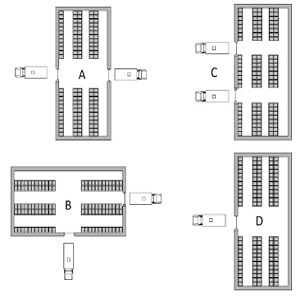
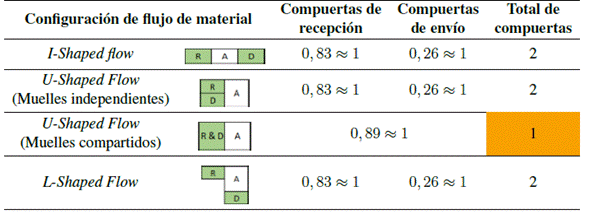
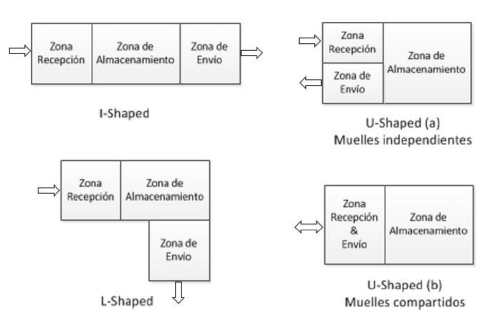
Varios han sido los estudios desarrollados en el tema gestión de almacenes, donde la aplicación de herramientas cuantitativas como alternativa de solución ha cobrado gran importancia en los últimos años. La programación lineal es uno de los modelamientos más utilizados para establecer el tamaño del almacén, se han encontrado estudios que definen como función objetivo la minimización de costos de operación, almacenamiento, manejo de materiales, entre otros [ Tabla I ). Asimismo, el dimensionamiento del almacén tiende a ser flexible debido a la dinámica que puede presentar el flujo de materiales, esto hace que las propuestas investigativas estén clasificadas en diseños estáticos, dinámicos y mixtos, debido a que las condiciones de flujo de material hacen que el tamaño de un almacén requiera flexibilidad en su dimensionamiento. En este orden de ideas, la configuración de flujo de material se considera como un parámetro para tener en cuenta en el diseño del almacén, puesto que establece la ubicación de los muelles de recepción y distribución. Existen tres configuraciones genéricas de flujo: I-Shaped (flow-type), U-Shaped y L-Shaped [32], en la Figura 1 se presentan las características de cada tipo de configuración de flujo en un almacén.
En la Figura 1 se identifica que en las configuraciones I-Shaped, U-Shaped (a) y L-Shaped , las operaciones de recepción y envío se realizan en muelles independientes; en este caso, el proceso de dimensionamiento de las zonas de recepción y envío se realiza de manera individual calculando el número de muelles para cada operación respectiva [4]. Por lo contrario, en la configuración U-Shaped (b) el cálculo de muelles se realiza de manera integrada, es decir, se generaliza a un solo movimiento promedio de material que se recibe y envía.
Figura 1: Configuraciones de flujo de material para diseño de almacenes.
De acuerdo con las anteriores referencias, se han presentado estudios que consideran la reubicación de materiales, la capacidad de equipos para manipulación de material, la capacidad de almacenamiento, la política de inventario, la dimensión de unidades de carga, el costo operativo, disponibilidad de espacio, entre otros; por lo anterior, el propósito de este artículo es brindar un método que facilite el dimensionamiento del almacén desde un enfoque integral, siendo una decisión estratégica y operativa que trasciende a corto, mediano y largo plazo los procesos de abastecimiento de la organización, asimismo, puede ser empleado para evaluar y proyectar nuevas políticas tanto en almacenes nuevos como en lo que se encuentran construidos.
2. Método para el dimensionamiento del almacén
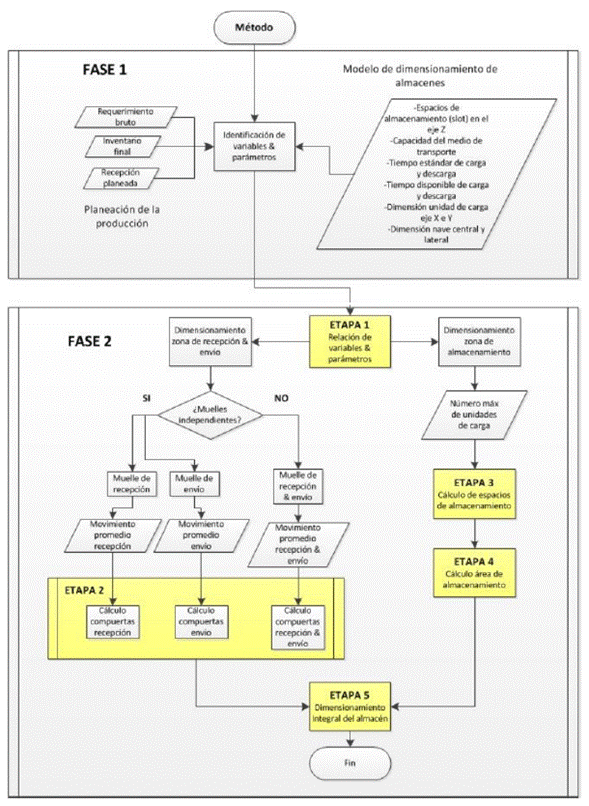
El método de dimensionamiento del almacén propuesto [ Figura 2) consta de dos fases. En la primera fase se observa la integración de dos grandes áreas operacionales de la organización: el área de producción y el área del almacenamiento. Es necesario contar con una continua retroalimentación para lograr una sincronización en el flujo de material, asimismo, suministrar información de variables y parámetros que se requieren para el desarrollo del método que se está presentando.
Figura 2: Método de dimensionamiento del almacén.
2.1. Fase I identificación de variables y parámetros
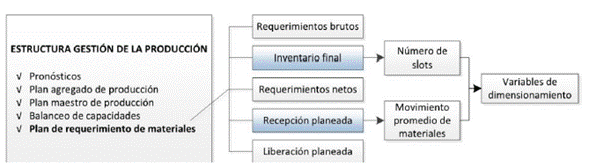
La primera fase del método propuesto tiene el objeto de recolectar la información necesaria de las variables y parámetros en el dimensionamiento del almacén; en este caso, los datos de entrada se agrupan en dos categorías principales que son los obtenidos a partir del proceso de planeación de la producción y los requeridos por el modelo de dimensionamiento de almacenes. Las características de cada categoría de datos se describen a continuación.
2.1.1. Variables y parámetros generados por el plan de producción
En el caso del primer grupo de datos, el plan de requerimiento de materiales (MRP) juega un papel muy importante para caracterizar los flujos de abastecimiento (entradas y salidas del sistema). De acuerdo con la literatura, el MRP se convirtió en un destacado enfoque para el manejo del flujo de materias primas y componentes en el proceso de fabricación en el siglo XX, que con la ayuda de los avances tecnológicos mejoro la toma de decisiones en la gestión de los materiales [19]. El funcionamiento del MRP consiste en la identificación de variables tal como requerimiento bruto, el inventario inicial, el stock seguridad, las necesidades netas, la liberación de «ordenes planificadas y la recepción de estas [20]; previamente, el plan maestro de producción (MPS) determina la cantidad de productos finales que se pueden fabricar, convirtiéndose en un requerimiento bruto del MRP, además de las restricciones de capacidad del sistema [33]. Esta proyección de unidades de producto es un insumo para realizar la explosión del MRP, en el cual se establecen los programas de reabastecimiento para todos los subconjuntos, componentes y materias primas que integran un producto terminado [34]. Es claro que a partir del proceso de planificación de la producción se obtienen múltiples ventajas en una organización, pues permite una mayor flexibilidad a cambios del entorno, a la vez incrementa la satisfacción del cliente y reduce los niveles de inventario [35].
2.1.2.Variables y parámetros necesarios para el modelo de dimensionamiento del almacén
En el caso del segundo grupo de datos, entre los diferentes modelos y técnicas de dimensionamiento identificados en la literatura se destaca el aporte de Ghiani, Laporte y Musmano [25], siendo uno de los referentes teóricos más importantes que se tienen en cuenta en el diseño del método de dimensionamiento. La Tabla II y la Tabla III relacionan las parámetros y variables que utiliza el modelo de dimensionamiento.
Tabla II: Variables de modelo de dimensiones para recepción y envío

Tabla III: Parámetros del modelo de dimensionamiento para zona de almacenamiento ((2), (3) (4 (5)

En la ecuación (1) se presenta el modelo inicial que permite dimensionar el número de compuertas que integran la zona de recepción o envío; esta ecuación contempla el movimiento promedio de materiales que es definido desde el proceso de planeación de la producción, a la vez considera parámetros previamente determinados por la organización como es el tiempo de carga y descarga del medio de transporte, la capacidad de transporte y el tiempo disponible de servicio en la zona de recepción. En la tabla II se presentan las variables de las que este modelo depende.
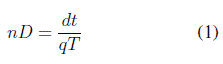
A continuación se presentan las ecuaciones que permiten calcular el número de espacios de almacenamiento (ecuaciones (2) y (3)) para determinar la distancia del almacén sobre el eje X (ancho) y sobre el eje Y (largo), con los cuales se puede obtener a su vez el área del almacén en la que incluye el área de pasillos para el desplazamiento del material. Los parámetros que integran este conjunto de ecuaciones contemplan el tamaño de la unidad de carga, el espacio entre pasillos de acuerdo con el equipo de alistamiento de pedidos y los niveles de altura en relación con el tipo de estantería a utilizar. Los parámetros del modelo se presentan en la Tabla III.
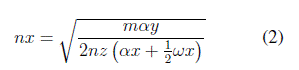
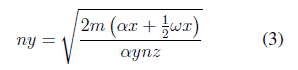
Al momento de diseñar el plano arquitectónico del almacén, se puede presentar la situación de que los resultados calculados mediante las ecuaciones anteriores no coincidan con las respectivas cotas del plano, es decir, si el resultado del cálculo de numero de espacios de almacenamiento en el eje X (nx) es un número par, las dimensiones de la cota y la distancia calculada del almacén sobre el eje X (Lx) van a coincidir. En el caso contrario, donde el resultado nx es un número impar, se modifica la ecuación (4) a la expresión matemática que se relaciona en la ecuación (6).
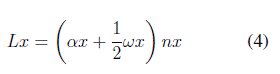
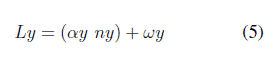
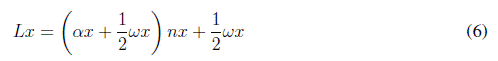
Por lo anterior, se indica que la ecuación (6) se aplica siempre y cuando el valor de nx sea un número impar, razón por la cual se presentan una adecuación a la técnica de dimensionamiento original.
2.2. Fase II dimensionamiento integral del almacén
La segunda fase del método de dimensionamiento está compuesta a su vez por cinco etapas que culminan en el dimensionamiento integral del almacén, en las que se integran los datos obtenidos durante la fase anterior. Las características de cada una de las etapas se presentan a continuación.
La primera etapa “relación de variables y parámetros” considera la información recolectada en la primera fase para identificar los datos de entrada que son necesarios en el modelo de dimensionamiento, específicamente el inventario registrado en el MRP es una variable de entrada que determina la cantidad de unidades que se almacena a lo largo de un periodo; posterior a esto, se aplica un factor de conversión para calcular el número de espacios (slots) necesarios para el almacenaje, en el que es necesario contemplar restricciones de disponibilidad de áreas en la zona de almacenamiento y las dimensiones de las unidades de carga (longitud, ancho y alto). Asimismo, el requerimiento bruto como la recepción planeada son variables que determinan el movimiento promedio de materiales en el muelle de carga y descarga (plataforma), que, junto con las características técnicas del medio de transporte (capacidad y tiempo), determina el número de compuertas requeridas en la zona de recepción del almacén. La relación de variables entre el plan de requerimiento de materiales y el modelo de dimensionamiento del almacén se presenta en la Figura 3.
Figura 3: Relación entre las variables MRP y dimensionamiento de almacenes.
Luego de haber realizado la primera etapa, se puede desarrollar de manera conjunta la segunda y tercera dado que son independientes.
La segunda etapa “cálculo de compuertas de recepción y envío”, mediante la aplicación de la ecuación (1), determina las características dimensionales de los muelles de carga y descarga (Tabla II); los parámetros que intervienen en esta etapa son capacidad del medio de transporte, tiempo estándar de carga y descarga y los tiempos disponibles para estas operaciones que normalmente son definidos bajo las condiciones logísticas de la empresa. La tercera etapa “cálculo de espacios de almacenamiento”, mediante la aplicación de las ecuaciones (2) y (3), determina el niñero de slots en el eje X y Y (Tabla III), donde el número máximo de unidades de carga es una variable de entrada. Los parámetros que intervienen en esta etapa son de tipo estantería, dimensiones de la unidad de carga y dimensiones para la nave central y lateral del almacén. La cuarta etapa “calculo área de almacenamiento”, utilizando las ecuaciones (4), (5) o (6), determina la distancia del almacén en el eje X y Y (Tabla III). Una vez calculada la distancia, se obtiene el área del almacén mediante el producto de los dos resultados anteriormente calculados. Finalmente, en la quinta etapa “dimensionamiento integral del almacén” se reinen los resultados obtenidos en la segunda y cuarta etapa para agrupar en un área general el dimensionamiento del almacén.
3. Resultados del caso de aplicación de método de dimensionamiento
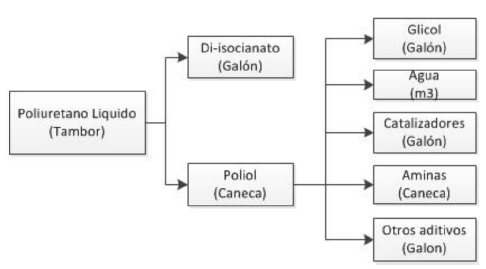
El método de dimensionamiento se aplicó a una empresa que abastece poliuretano líquido en sector de construcción con productos para acabados internos y sellantes. Los componentes de este producto se almacenan en diferentes presentaciones de acuerdo con las condiciones de abastecimiento (Figura 4). Es relevante mencionar que, por tema de confidencialidad de la organización, no se presentan datos específicos relacionados con el sistema de fabricación (mezcla y dosificación) de los componentes.
Figura 4: Presentaciones de poliuretano y sus componentes.
Para la aplicación del método de dimensionamiento de almacenes se desarrolló cada fase y etapas anteriormente presentadas. Los resultados se presentan a continuación.
3.1. Fase 1: identificación de variables y parámetros
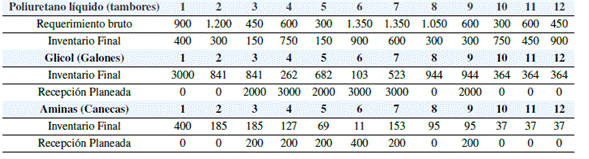
Para la identificación de variables se desarrolló un aplicativo computacional en el que se diseñaron tres módulos de información: pronóstico, plan maestro de producción y plan de requerimiento de materiales. De acuerdo con lo anterior, en el módulo de pronósticos se analizaron los datos de ventas de los dos años anteriores comparando diferentes modelos de proyección. Se identificó que el modelo que más se ajusta al comportamiento de la demanda es la regresión lineal con estacionalidad. Asimismo, en el módulo de plan maestro de producción se registraron los niveles de fabricación para doce meses, se tomó en cuenta el pronóstico en cada periodo y las políticas de inventario de producto final. En el módulo de plan de requerimiento de materiales, se ingresaron los resultados del plan maestro de producción y se tuvo en cuenta la estructura de fabricación de productos finales, las políticas de inventario de materia prima (stock de seguridad) y tamaños de lote. En la Tabla IV se presentan los resultados finales del MRP de las variables requerimiento bruto, inventario final, recepción planeada para el producto terminado y algunas materias primas, las cuales determinan el plan de recepción y almacenamiento en todos los componentes, así como la respectiva distribución para el producto terminado.
Tabla IV: Variables generadas por el plan de requerimiento de materiales.
Adicionalmente, la empresa presento las siguientes especificaciones para la definición de los parámetros del modelo de dimensionamiento (Tabla V).
Tabla V: Especificaciones de entrada para el método de dimensionamiento.
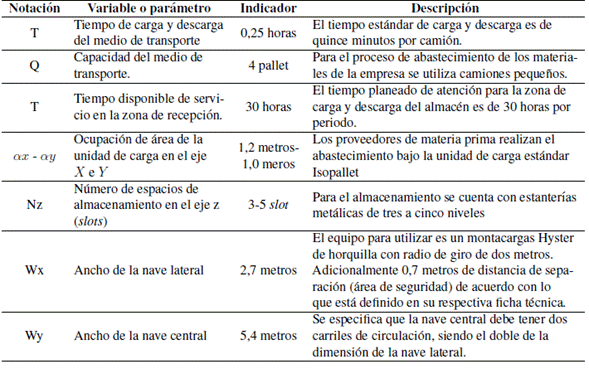
Algunos materiales están definidos en unidades de tambor, caneca y galón, cambiando sus empaques como unidades de carga para el almacenamiento; sin embargo, es necesario agrupar estas unidades de carga a pallet para calcular una dimensión general para el almacén. Estos materiales se almacenan manteniendo la relación cuatro tambores/pallet, 36 canecas/pallet y 180 galones/pallet.
3.2. Fase 2: relación de variables y parámetros (etapa 1)
De acuerdo con el método propuesto, la segunda fase se subdivide en cinco etapas. En la primera etapa se totalizaron las diferentes unidades en recepción planeada por cada producto y materiales, para obtener equivalencia a Isopallet como unidad de carga; para este caso, el movimiento promedio de materiales se caracteriza por recibir canecas y galones los cuales se unificarían a pallets. Esta conversión se presenta en la Tabla VI.
Tabla VI: Movimiento promedio de recepción de materiales como resultado del MRP.

A partir del total de pallet, se calculó el promedio mensual de materiales que ingresan al almacén, que en este caso es de 397 pallet. Los periodos 11 y 12 no se tienen en cuenta ya que registran valor igual a cero, esto hace determinar que en estos periodos el muelle de recepción no es necesario y, por lo tanto, estará cerrado. El resultado es considerado como variable de entrada para el cálculo de niñero de compuertas de recepción. El procedimiento de totalizar pallets de acuerdo con el factor de equivalencia y obtener el respectivo promedio también se aplica para los datos registrados de requerimiento bruto del producto terminado, dado que este será el promedio de materiales que se enviaran por periodo. Esta conversión se presenta en la Tabla VII.
Tabla VII: Movimiento promedio de distribución de materiales como resultado del MRP.

A partir del total de pallet se calculó el promedio mensual de materiales que se envían desde el almacén, que en este caso es de 191 pallet. Por último, se totalizaron las unidades en inventario final para cada producto y material, para obtener equivalencia a Isopallet como unidad de carga. El niñero máximo de unidades de carga que serán almacenados determina el “plan de almacenamiento” y sus resultados se presentan en la Tabla VIII.
Tabla VIII: Número máximo de unidades de carga como resultado del MRP.
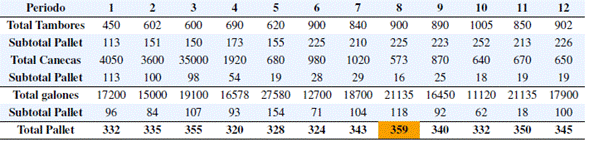
De acuerdo con la Tabla VII, se identificó que el niñero máximo de pallet en el plan de almacenamiento es de 359 pallet, al igual este número es una variable de entrada considerada para el modelo matemático de dimensionamiento de la zona de almacenamiento. Se selecciona el número máximo como capacidad necesaria y a su vez se fija a lo largo del periodo de planeación, debido a que esta se ajustaría a cualquier capacidad necesaria de otro periodo
3.3. Fase 2: calculo número de compuertas (etapa 2)
Para el cálculo del número de compuertas se tiene en cuenta la configuración de flujo. En este caso se evaluaran las cuatro opciones de acuerdo con la Figura 1, los resultados obtenidos se presentan en la Tabla IX.
Los resultados de la Tabla IX generan el niñero de compuertas de recepción y envío para cuatro opciones de configuración de flujo. Se aproximaron los resultados al entero siguiente debido a que se identificó una tendencia positiva que va incrementando el flujo de material para periodos de tiempo futuros; en este caso, se obtiene un total de dos compuertas para las configuraciones de flujo en las que se tiene muelles independientes. Por el contrario, en la configuración de muelles compartidos las actividades de recepción y envío se alternan en una sola compuerta. La selección de configuración de flujo de material finalmente dependerá de las restricciones de espacio para construir el almacén, recomendando principalmente para este caso la configuración U-Shaped flow con muelles compartidos, dado que requiere menor inversión por ser necesaria una sola compuerta.
Tabla IX: Número de compuertas para cada configuración de flujo
3.4. Fase 2: cálculo de espacios de almacenamiento (etapa 3)
Los espacios necesarios de almacenamiento (slots) determinan la capacidad total de almacenamiento, el cálculo de estos se obtiene mediante la aplicación de la ecuación (2) y (3). Los resultados obtenidos integran decimales que deben ser aproximados. En este caso, el diseñador debe ajustar al máximo o al mínimo dependiendo de la capacidad de almacenamiento que desee, es decir, evitar subdimensionamiento o sobredimensionamiento del almacén de acuerdo con las tendencias de demanda de los productos. Para el cálculo de la capacidad de almacenamiento se aplica la ecuación (7) en la que interviene los slots en los tres ejes X-Y-Z .
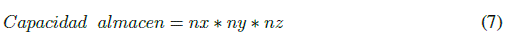
En la ecuación (7), la variable nz va a depender del tipo de estantería a utilizar, ya que su nivel de altura (slots en el eje z) modificaría la capacidad de almacenamiento, así como el área necesaria. A partir de lo anterior, el proceso de ajuste máximo-mínimo así como la determinación de los niveles de altura de almacenamiento, establecerán el niñero de slots en eje X e Y .La Tabla X presenta el proceso de ajuste o aproximación de acuerdo con la capacidad necesaria (359 slot ) identificada en la Tabla VII, teniendo en cuenta además la variación de uno a cinco niveles de altura.
Los resultados en la Tabla X presentan diferentes alternativas de configuración que pueden adoptarse al diseñar la zona de almacenamiento. Al aplicar las opciones de aproximación, es evidente que algunas deben ser descartadas, por ejemplo, en las primeras cuatro filas que corresponden a la asignación de un slot en el eje Z, la tercera y cuarta aproximación generan una capacidad real de almacenamiento de 344 y 336 slot estando por debajo de la capacidad necesaria (359 slot). Por esta razón, serán una opción de descarte debido a que para algunos periodos no habría espacio para almacenar materiales. Por lo contrario, la primera y segunda aproximación genera una capacidad superior a la capacidad necesaria, obteniendo un 87 % y 89 % de utilización proyectada para doce periodos. A partir de lo anterior, la configuración seleccionada para el almacén con un slot de altura (nz = 1) es nx = 9 slot, ny = 42 slot , debido a que es la que presenta mejor utilización proyectada. En la Tabla XI se presentan los resultados finales que establecen la configuración seleccionada de almacenamiento para cada nivel nz .
Tabla X: Numero de compuertas para cada configuración de flujo.
En la Tabla XI se puede identificar que la configuración correspondiente a 2 y 3 slot de altura genera el mismo porcentaje de utilización y además el mayor entre todos. Para este caso, la selección se determina finalmente a la configuración que requiera menor inversión o a la mayor compatible con las restricciones de espacio físico que limiten la construcción del almacén.
Tabla XI: Número de compuertas para cada configuración de flujo.

Fase 2: etapa 4 cálculo área de almacenamiento
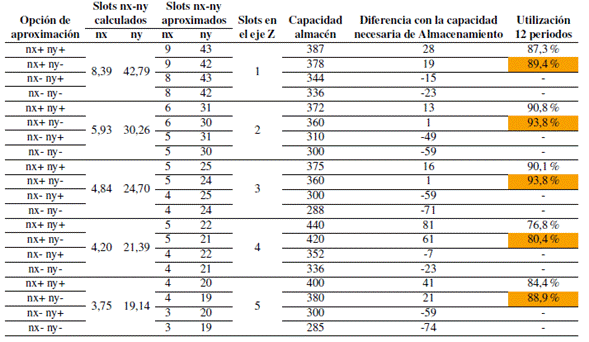
El área del almacén se considera un resultado muy importante para definir cuanto espacio se requiere para su construcción. Este resultado depende de la longitud del almacén en el eje X y Y, para ello se aplican las ecuaciones (5), (6) y (7). Las áreas obtenidas para cada uno de los niveles de altura experimentados se presentan en la Tabla XII.
Tabla XII: Área de almacenamiento por cada nivel de altura
De acuerdo con la Tabla XI, las mejores configuraciones eran las que correspondían a 2 y 3 slot de altura; sin embargo, en la Tabla XII se puede identificar que por área necesaria se escogería la configuración de 3 slot de altura, debido a que requiere menor área proyectando una menor inversión en su infraestructura. El promedio general, teniendo en cuenta todos los posibles niveles de altura, es de 517,9 m2.
Fase 2: etapa 5 dimensionámiento integral del almacén
En la etapa final de la segunda fase, se integran los resultados obtenidos en la segunda, tercera y cuarta etapa; para este caso, el número de compuertas calculadas se integra con el área de almacenamiento que a su vez depende del total de slots definidos. Existen varias opciones de diseño debido a que los resultados pueden combinar cada uno de los modelos de configuración de flujo con cinco niveles de almacenamiento que alternarían su capacidad y área requerida. Para efectos de culminar con el dimensionamiento integral, se toma como referente el mejor nivel de slots obtenidos en la etapa cuatro, para combinarlos con cada una de las configuraciones de flujo, garantizando menor inversión en infraestructura, menor ocupación de espacio y mayor utilización de la zona de almacenamiento. En este orden, se selecciona la asignación de tres slots de altura en el área de almacenamiento cuya área requerida es de 374,8 m2 y una utilización proyectada de 93,8 %. El resultado de la aplicación del método de dimensionamiento integral en el caso de estudio se resume mediante la siguiente ficha técnica.
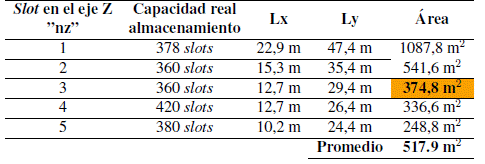
La información presentada en la Tabla XIII se clasifica en tres conjuntos de resultados. El primero de ellos “variables y parámetros”, relaciona las especificaciones de entrada presentadas en la Tabla V. Esta información es identificada en la primera fase del método de dimensionamiento. Por otra parte, se integra los resultados obtenidos a partir del MRP como lo es el movimiento promedio de materiales para carga y descarga, así como la capacidad necesaria de almacenamiento, correspondientes a la segunda fase, primera etapa respectivamente.
Tabla XIII: Ficha técnica para dimensionamiento del almacén
El segundo conjunto de resultados “dimensionamiento” presenta los datos obtenidos en la segunda fase, segunda, tercera y cuarta etapa, en la que se resume el niñero de compuertas para recepción y envío, el niñero de espacios, capacidad, utilización y área necesaria de la zona de almacenamiento
Finalmente, el tercer conjunto “layout” incluye los resultados obtenidos a partir de la aplicación de la quinta etapa “dimensionamiento integral” que parametrizan las opciones de dimensionamiento del almacén. Para este caso se presentan cuatro diseños: I Shapedflow (A), L Shapedflow (B), U Shapedflow con muelles independientes (C) y U shapedflow con muelles compartidos (D), presentando así opciones de implementación que se ajusten a posibles restricciones de espacio o de flujo
4. Discusión
El plan de requerimiento de materiales es una herramienta de planeación de la producción que tiene muchas variaciones en su aplicación, es decir, pueden modificarse sus estrategias de inventario, políticas de abastecimiento, lead time, entre otros. Debido a que estos datos son parámetros iniciales de entrada, su variabilidad genera cambios representativos en el dimensionamiento final del almacén. De acuerdo con las condiciones de la empresa en estudio, no se tiene un nivel de stock de seguridad y se trabaja con la política de abastecimiento por lotes; por ejemplo, experimentos aplicados previamente con el método demostraron que al cambiar la política de dimensionamiento a “lote a lote”, el área requerida para el almacenamiento disminuye comparada con los resultados presentados en la Tabla XIII. Lo anterior se justifica debido a que esta segunda política se enfoca al inventario cero, en la que se abastece técnicamente lo que se requiere para cumplir una orden de pedido.
Otra opción experimentada está relacionada con el tipo de estantería en la que se evaluaron cinco niveles de altura de acuerdo con la infraestructura que dispone la empresa; en los resultados presentados en la Tabla XII se puede identificar que entre mayor sean los niveles de altura (nz), menor será el área necesaria de almacenamiento, demostrando que este parámetro y resultado son inversamente proporcionales. El anterior análisis permite a la compañía evaluar las condiciones de infraestructura que requiere menor inversión en área de almacenamiento, manteniendo las mismas características de flujo de material. Es conveniente experimentar con diversos sistemas de almacenamiento, por ejemplo, sistemas automatizados de auto recuperación (AS/RS), en los que dependiendo de su diseño se puede utilizar mayor espacio en la altura. Si se tomara esta opción, es necesario condicionando la unidad de carga a una diferente de Isopallet .
El método de dimensionamiento de la zona de almacenamiento está restringido a ciertas configuraciones de diseño, su restricción se debe a que inicialmente es aplicable en almacenes de carga unitaria ( unit-load ) ya que involucra las dimensiones de una sola unidad de carga; teniendo en cuenta que también existen condiciones de flujo de material que integran diferentes unidades de carga (multiload), el método debería acondicionarse para este caso a cada una de ellas, es decir, si el almacén maneja Isopallet y Europallet a la vez, se debe calcular espacios y áreas de almacenamiento por separado y al final integrar a un área común que sea flexible para cualquier tipo de material.
Para el caso particular de configuración interna de la zona de almacenamiento, estudios han demostrado que las distribuciones en V y Fishbone (espina de pescado) analizadas por [36] presentan mejores comportamientos en el proceso de alistamiento de pedidos, logrando una disminución de tiempo aproximada al 20 % con respecto a la distribución tradicional de estanterías paralelas. En este sentido, el método de dimensionamiento propuesto se restringe a este tipo de distribuciones, ya que en ellas se utilizan ecuaciones de dimensionamiento diferentes a las utilizadas en el método propuesto; además, se ha validado que estas distribuciones generan buen comportamiento solo en los casos en el que el almacén este sujeto a un pequeño número de elementos en la lista de pedido [37]. En este orden, puede considerarse la adaptación de este tipo de distribuciones como una posible extensión al método de dimensionamiento.
5. Conclusiones
De acuerdo con los resultados del caso de estudio, se puede concluir que el método es funcional en la organización, pues permite evaluar opciones de dimensionamiento que transcienden en decisiones de gran importancia como lo es la capacidad operativa de la empresa. Dicha funcionalidad es argumentada desde el referente teórico, conceptual y matemático de las variables y sus relaciones que previamente fueron explicadas. Es relevante mencionar que en el método presentado se integran dos áreas del conocimiento: la planeación de la producción y el dimensionamiento del almacén, cuya relación permite una mejor sincronización en datos relacionados con recepción, almacenamiento y distribución siendo estas operaciones primarias en este tipo de instalaciones.
La definición de las fases y etapas del método de dimensionamiento de almacenes permite evaluar diferentes políticas de planeación del sistema de producción y almacenamiento. Los resultados obtenidos y las políticas de la organización generan cuatro opciones de configuración de flujo de material, recomendando así la combinación U-Shaped flow con muelles compartidos y con tres slots de altura, logrando un buen indicador de utilización para los periodos proyectados siendo del 93,8 % de la capacidad disponible de almacenamiento como se demuestra en la tercera etapa y un área de 374,8 m2 obtenida en la cuarta etapa, para una capacidad real de almacenamiento de 360 pallet identificada en la primera etapa.
Se identificaron restricciones con el método de dimensionamiento relacionadas con la adaptación en almacenes que manejan múltiples unidades de carga, así como la compatibilidad con distribuciones diferentes a la configuración tradicional de estanterías paralelas. Estas restricciones generan opciones de extensión del método para futuras investigaciones, logrando así diseñar almacenes desde la caracterización de su proceso de abastecimiento hasta la configuración interna que garantice la reducción de tiempos de alistamiento y sus costos respectivos.
Referencias
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










