DOI:
https://doi.org/10.14483/23448393.21108Published:
2024-08-05Issue:
Vol. 29 No. 2 (2024): May-AugustSection:
Industrial EngineeringMethodology for the Selection of Risk Response Actions while Considering Corporate Objectives in the Metalworking Industry
Metodología para la selección de acciones de respuesta a riesgos considerando los objetivos estratégicos en la industria metalmecánica
Keywords:
fuzzy logic, Monte Carlo simulation, project risk management, risk response actions (en).Keywords:
lógica difusa, simulación Monte Carlo, gestión de riesgos de proyectos, acciones de respuesta a riesgos (es).Downloads
References
S. Mittal and N. Gorowara, “Knowledge Integration in engineering, procurement and construction projects: A conceptual study,” Psychol. Educ. J., vol. 58, no. 1, pp. 5733–5738, 2021. https://doi.org/10.17762/PAE.V58I1.2209
H. Erol, I. Dikmen, G. Atasoy, M. Talat Birgonul, and M. T. Birgonul, “An analytic network process model for risk quantification of mega construction projects,” Expert Syst Appl, vol. 191, art. 116215, 2022. https://doi.org/10.1016/J.ESWA.2021.116215
E. Oliveira and C. Santos, “Application of a risk management methodology in industrial projects: A case study in the metalworking sector,” in Educ. Excellence Innov. Manag. Vision 2020 App., 2019, pp. 5647–5662, Online]. Available: https://repositorium.sdum.uminho.pt/bitstream/1822/61217/1/Application%20of%20a%20Risk%20Management%20Methodology%20in%20Industrial%20projects.pdf.
A. Birjandi and S. M. Mousavi, “Fuzzy resource-constrained project scheduling with multiple routes: A heuristic solution,” Autom. Constr., vol. 100, pp. 84–102, Apr. 2019. https://doi.org/10.1016/j.autcon.2018.11.029
J. Silva et al., “Improvement of planning and time control in the project management of a metalworking industry - Case study,” Procedia Comput. Sci., vol. 196, no. 2021, pp. 288–295, 2021. https://doi.org/10.1016/j.procs.2021.12.016
PricewaterhouseCoopers, “En la ruta de la Competitividad. Principales hallazgos de la 1ra Encuesta Nacional de Madurez en Gerencia de Proyectos,” PwC, Bogotá, Colombia, 2011.
S. Changali, A. Mohammad, and M. Van Niewlan, “The construction productivity imperative,” 2015. [Online]. Available: https://www.mckinsey.com/~/media/mckinsey/business functions/operations/our insights/the construction productivity imperative/the construction productivity imperative.pdf
PMI, A guide to the Project Management Body of Knowledge (PMBOK Guide), 6th, 2017.
L. Bai, Q. Xie, J. Lin, S. Liu, C. Wang, and L. Wang, “Dynamic selection of risk response strategies with resource allocation for construction project portfolios,” Comput. Ind. Eng., vol. 191, p. 110116, May 2024. https://doi.org/10.1016/j.cie.2024.110116
Y. Zhang and F. Zuo, “Selection of risk response actions considering risk dependency,” Kybernetes, vol. 45, no. 10, pp. 1652–1667, Nov. 2016. https://doi.org/10.1108/K-05-2016-0096
APM, Association for Project Management Body of Knowledge, 6th., 2012.
OGC, Managing successful projects with PRINCE2, 6th ed., 2017.
M. R. Gleim, H. McCullough, N. Sreen, and L. G. Pant, “Is doing right all that matters in sustainability marketing? The role of fit in sustainable marketing strategies,” J. Retail. Consum. Serv., vol. 70, 2023, art. 103124. https://doi.org/10.1016/j.jretconser.2022.103124
W. Stevenson, Operations Management, 14th ed., New York, NY, USA: McGraw-Hill Education, 2021.
R. F. Jacobs and R. B. Chase, Administracion de operaciones: produccion y cadena de suministros, 15th ed., New York, NY, USA: McGraw-Hill Education, 2019. https://book4you.org/book/11172205/6d75a9
PMI, "The standard for portfolio management," 2017. [Online]. Available: https://www.pmi.org/pmbok-guide-standards/foundational/standard-for-portfolio-management
L. E. Dounavi, E. Dermitzakis, G. Chatzistelios, and K. Kirytopoulos, “Project management for corporate events: A set of tools to manage risk and increase quality outcomes,” Sustainability, vol. 14, no. 4, pp. 1–37, 2022. https://doi.org/10.3390/SU14042009
M. Hamid, A. M. Abdelalim, M. Abdel, H. Hassanen, and A. M. Abdelalim, “Risk identification and assessment of mega industrial projects in Egypt,” Int. J. Manag. Commer. Innov., vol. 10, no. 1, pp. 187–199, 2022. https://doi.org/10.5281/zenodo.6579176
S. Bakri et al., “Identification of factors influencing time and cost risks in highway construction projects,” Int. J. Sustain. Constr. Eng. Technol., vol. 12, no. 3, pp. 280–288, 2021. https://doi.org/10.30880/ijscet.2021.12.03.027
T. Yuan, P. Xiang, H. Li, and L. Zhang, “Identification of the main risks for international rail construction projects based on the effects of cost-estimating risks,” J. Clean. Prod., vol. 274, p. 122904, 2020. https://doi.org/10.1016/j.jclepro.2020.122904
A. Nurdiana, M. Agung Wibowo, Y. Fundra Kurnianto, M. A. Wibowo, and Y. F. Kurnianto, “The identification of risk factors of delay on the road construction project in indonesia,” in Int. Conf. Maritime Archipelago (ICoMA 2018), 2019, pp. 384–387. https://doi.org/10.2991/ICOMA-18.2019.82
M. H. Kotb and M. M. Ghattas, “Risk identification barriers in construction projects in MENA,” PMI World J., 2018. https://doi.org/10.13140/RG.2.2.20614.83525.
S. Maulana and F. D. Ariyanti, “Application of lean project management method in environmental drainage development case study: x area Bekasi City,” IOP Conf. Ser. Mater. Sci. Eng., vol. 1096, no. 1, art. 12085, 2021. https://doi.org/10.1088/1757-899X/1096/1/012085
J. Chilumo et al., “Risk management practices on performance of building construction projects,” J. Entrep. Proj. Manag., vol. 4, no. 6, art. 202, 2020. https://stratfordjournals.org/journals/index.php/journal-of-entrepreneurship-proj/article/view/659
J. Crispim, L. H. Silva, and N. Rego, “Project risk management practices: The organizational maturity influence,” Int. J. Manag. Proj. Bus., vol. 12, no. 1, pp. 187-210, 2018. https://doi.org/10.1108/IJMPB-10-2017-0122
E. Prihartanto and M. D. Bakri, “Identification the highest risk of performance based contract in Bojonegoro-Padangan road projects,” in Reg. Conf. Civil Eng. RCCE, Surabaya, Indonesia, 2017. http://dx.doi.org/10.12962/j23546026.y2017i6.3243
D. K. Sudarsana, “A concept model to scale the impact of safety risk in a construction project using a semi quantitative method,” Civ. Eng. Archit., vol. 9, no. 1, pp. 263–269, 2021. https://doi.org/10.13189/cea.2021.090122
Ayuningtyas, D. and Dita Rarasati, A, “Work acceleration strategy development on design-build project to improve risk based quality performance,” Glob. J. Sci. Eng., vol. 02, pp. 10–15, 2020. https://doi.org/10.37516/global.j.sci.eng.2020.007
L. Wu, H. Bai, C. Yuan, and C. Xu, “FANPCE technique for risk assessment on subway station construction,” J. Civ. Eng. Manag., vol. 25, no. 6, pp. 599–616, 2019. https://doi.org/10.3846/JCEM.2019.10373
B. Barghi, S. S. sikari, and S. Shadrokh sikari, “Qualitative and quantitative project risk assessment using a hybrid PMBOK model developed under uncertainty conditions,” Heliyon, vol. 6, no. 1, art. 3097, Jan. 2020. https://doi.org/10.1016/J.HELIYON.2019.E03097
M. Kaut, H. Vaagen, and S. W. Wallace, “The combined impact of stochastic and correlated activity durations and design uncertainty on project plans,” Int. J. Prod. Econ., vol. 233, art. 108015, 2020. https://doi.org/10.1016/J.IJPE.2020.108015
M. Eckhart, B. Brenner, A. Ekelhart, and E. Weippl, “Quantitative security risk assessment for industrial control systems: Research opportunities and challenges,” J. Internet Serv. Inf. Secur. (JISIS)2, vol. 09, no. 03, pp. 52–73, 2019. https://doi.org/10.22667/JISIS.2019.08.31.052.
N.-T. Nguyen, Q.-T. Huynh, and T.-H.-G. Vu, “A Bayesian critical path method for managing common risks in software project scheduling,” in Ninth Int. Sym. Info. Comm. Tech. - SoICT 2018, 2018, pp. 382–388. https://doi.org/10.1145/3287921.3287962
X. Xu, J. Wang, C. Z. Li, W. Huang, and N. Xia, “Schedule risk analysis of infrastructure projects: A hybrid dynamic approach,” Autom. Constr., vol. 95, pp. 20–34, 2018. https://doi.org/10.1016/j.autcon.2018.07.026
M. Alipour-Bashary, M. Ravanshadnia, H. Abbasianjahromi, and E. Asnaashari, “Building demolition risk assessment by applying a hybrid fuzzy FTA and fuzzy CRITIC-TOPSIS framework,” Int. J. Build. Pathol. Adapt., vol. 40, no. 1, pp. 134–159, 2022. https://doi.org/10.1108/IJBPA-08-2020-0063
A. B. Ashkezari, M. Zokaee, A. Aghsami, F. Jolai, and M. Yazdani, “Selecting an appropriate configuration in a construction project using a hybrid multiple attribute decision making and failure analysis methods,” Buildings, vol. 12, no. 5, art. 0643. 2022. https://doi.org/10.3390/buildings12050643
S. Pehlivan and A. E. Öztemir, "Integrated risk of progress-based costs and schedule delays in construction projects," Eng. Manag. J., vol. 30, no. 2. 2018, pp. 108–116. https://doi.org/10.1080/10429247.2018.1439636
B. Yan, J. Wu, and F. Wang, “CVaR-based risk assessment and control of the agricultural supply chain,” Manag. Decis., vol. 57, no. 7, pp. 1496–1510, Jul. 2018. https://doi.org/10.1108/MD-11-2016-0808/FULL/XML
E. Cheraghi, M. Khalilzadeh, S. Shojaei, and S. Zohrehvandi, “A mathematical model to select the risk response strategies of the construction projects: Case study of Saba Tower,” Procedia Comput. Sci., vol. 121, pp. 609–616, 2017. https://doi.org/10.1016/j.procs.2017.11.080
R. Soofifard and M. Bafruei, “An optimal model for project risk response portfolio selection (P2RPS) (Case study: Research institute of petroleum industry),” Iran. J. Manag. Stud., vol. 9, no. 4, pp. 741–765, 2016. https://doi.org/10.22059/ijms.2017.59374
Y. Zhang, “Selecting risk response strategies considering project risk interdependence,” Int. J. Proj. Manag., vol. 34, no. 5, pp. 819–830, 2016. https://doi.org/10.1016/j.ijproman.2016.03.001
Z.-P. Fan, Y.-H. Li, and Y. Zhang, “Generating project risk response strategies based on CBR: A case study,” Expert Syst. Appl., vol. 42, no. 6, pp. 2870–2883, 2015. https://doi.org/10.1016/j.eswa.2014.11.034
F. Marmier, I. Filipas Deniaud, D. Gourc, I. F. Deniaud, and D. Gourc, “Strategic decision-making in NPD projects according to risk: Application to satellites design projects,” Comput. Ind., vol. 65, no. 8, pp. 1107–1114, Oct. 2014. https://doi.org/10.1016/J.COMPIND.2014.06.001
S. Jordan, L. Jørgensen, and H. Mitterhofer, “Performing risk and the project: Risk maps as mediating instruments,” Manag. Account. Res., vol. 24, no. 2, pp. 156–174, Jun. 2013. https://doi.org/10.1016/J.MAR.2013.04.009
S. Goh and H. Abdul-rahman, “The Identification and management of major risks in the Malaysian construction industry,” J. Constr. Dev. Ctries., vol. 18, no. 1, pp. 19–32, 2013. [Online]. Available: https://core.ac.uk/download/pdf/199244814.pdf
A. Pla, B. López, P. Gay, and C. Pous, “eXiT*CBR.v2: Distributed case-based reasoning tool for medical prognosis,” Decis. Support Syst., vol. 54, no. 3, pp. 1499–1510, Feb. 2013. https://doi.org/10.1016/J.DSS.2012.12.033
L.-C. Ma, “Screening alternatives graphically by an extended case-based distance approach,” Omega, vol. 40, no. 1, pp. 96–103, Jan. 2012. https://doi.org/10.1016/J.OMEGA.2011.03.010
E. Kujawski and D. Angelis, “Monitoring risk response actions for effective project risk management,” Syst. Eng., vol. 13, no. 4, pp. 353–368, 2010. https://doi.org/10.1002/sys.20154
S. M. Seyedhoseini, S. Noori, and M. A. Hatefi, “An integrated methodology for assessment and selection of the project risk response actions,” Risk Anal., vol. 29, no. 5, pp. 752-753, 2009. https://doi.org/10.1111/j.1539-6924.2008.01187.x
A. Öztaş and Ö. Ökmen, “Judgmental risk analysis process development in construction projects,” Build. Environ., vol. 40, no. 9, pp. 1244–1254, 2005. https://doi.org/10.1016/j.buildenv.2004.10.013
M. Vanhoucke, Integrated Project Management Sourcebook, vol. 2, CHam, Germany: Springer International Publishing, 2016. https://doi.org/10.1007/978-3-319-27373-0
I. Wallace, “Schedule risk and contingency using @ RISK and probabilistic analysis,” 2010. [Online]. Available: https://www.palisade.com/downloads/pdf/Wallace_Schedule_Risk.pdf
J. Song, A. Martens, and M. Vanhoucke, “Using schedule risk analysis with resource constraints for project control,” Eur. J. Oper. Res., vol. 288, pp. 736–752, 2020. https://doi.org/10.1016/j.ejor.2020.06.015
A. Öztaş and Ö. Ökmen, “Construction project network evaluation with correlated schedule risk analysis model,” J. Constr. Eng. Manag., no. 1, pp. 49–63, 2008. https://doi.org/10.1061/(ASCE)0733-9364(2008)134:1(49)
A. Grando, V. Beldevere, S. Raffaele, and G. Stabilini, Production, Operations and Supply Chain Management,1st ed., Milan, Italy: Bocconi University Press, 2021.
H. Jafarzadeh, P. Akbari, and B. Abedin, “A methodology for project portfolio selection under criteria prioritisation, uncertainty and projects interdependency – Combination of fuzzy QFD and DEA,” Expert Syst. Appl., vol. 110, pp. 237–249, Nov. 2018. https://doi.org/10.1016/J.ESWA.2018.05.028
J. Osorio, M. Peña, and D. Arias, “Priorización de despachos en empresas de manufactura usando QFD difuso,” Rev. Ing. Univ. Medellín, vol. 17, pp. 173–186, 2018. https://doi.org/10.22395/rium.v17n33a9
J. Osorio, D. Manotas, and J. García, “Operational risk assessment in 3PL for maritime transportation,” Res. Comput. Sci., vol. 132, pp. 63–69, 2017. https://doi.org/10.13053/rcs-132-1-6
S. S. Agarwal and M. L. Kansal, “Risk based initial cost assessment while planning a hydropower project,” Energy Strateg. Rev., vol. 31, art. 100517, 2020. https://doi.org/10.1016/j.esr.2020.100517
León, R,. Scaco, E. and Galiano, N. “Identificación de factores de riesgo operativo en el sector metalmecánico manufacturero,” Rev. Espacios, vol. 40, no. 20, p. 23, 2019. [Online]. Available: https://www.revistaespacios.com/a19v40n20/a19v40n20p23.pdf
J. Liu, F. Jin, Q. Xie, and M. Skitmore, “Improving risk assessment in financial feasibility of international engineering projects: A risk driver perspective,” Int. J. Proj. Manag., vol. 35, no. 2, pp. 204–211, 2017. https://doi.org/10.1016/j.ijproman.2016.11.004
M. J. Naude and N. Chiweshe, “A proposed operational risk management framework for small and medium enterprises,” South African J. Econ. Manag. Sci., vol. 20, no. 1, pp. 1–10, 2017. https://doi.org/10.4102/sajems.v20i1.1621
J. Osorio, D. Manotas, and L. Rivera, “Priorización de riesgos operacionales para un proveedor de tercera parte logística - 3PL,” Inf. Tecnol., vol. 28, no. 4, pp. 135–144, 2017. https://doi.org/10.4067/S0718-07642017000400016
J. R. Ríos, D. Manotas, and J. C. Osorio, “Operational supply chain risk identification and prioritization using the SCOR model,” Ing. Univ., vol. 23, no. 1, pp. 1–20, 2019. https://doi.org/10.11144/Javeriana.iyu23-1.oscr
F. Romero. (2017), "El riesgo operativo y su influencia en el crecimiento empresarial del sector metalmecánica - Puente Piedra (lado sur)" M.S. thesis, Facultad de Ciencias Empresariales, Universidad Cesar Vallejo, Lima, Perú, 2017.
F. Sánchez, S. Steria, E. Bonjour, J.-P. P. J.-P. P. Micaelli, and D. Monticolo, “An approach based on bayesian network for improving project management maturity: An application to reduce cost overrun risks in engineering projects,” Comput. Ind., vol. 119, art. 103227, 2020. https://doi.org/10.1016/j.compind.2020.103227
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 8 de agosto de 2023; Aceptado: 14 de mayo de 2024
Abstract
Context:
Projects in metalworking companies are affected by risk. Proper risk management depends on the responses provided to improve the project plan. However, multiple potential actions may result in constraints due to multiple factors. The purpose of this article is to propose a hybrid approach to solve the problem of selecting risk response actions while considering strategic objectives, fuzzy logic, and simulation.
Method:
First, 334 risks were identified through a literature review and a discussion with experts. These were then filtered, resulting in 70 operational risks. Subsequently, the ten critical risks were prioritized using the risk matrix. Then, using Monte Carlo simulation and correlation analysis, the activities most affected by the risks were identified. Finally, potential response actions were designed for each case, and fuzzy logic and quality function deployment were applied to evaluate them.
Results:
The selected responses were framed within the strategic objectives, i.e., customer satisfaction, business profitability, and implementation of new technologies. This, while considering some corporate attributes that the actions had to meet finishing the project on time, having low costs, and meeting the scope. The selected actions had a better profile than others seeking to minimize time or costs.
Conclusions:
EPCC projects are complex and often suffer from gaps in scope, time, and cost. Risk analysis and the selection of responses in the planning phase help to improve performance. This study developed a risk response plan for a project executed in Brazil. Risks were identified, classified, and mitigated using simulations, resulting in an 11-day reduction in the project’s estimated duration.
Keywords:
fuzzy logic, Monte Carlo simulation, project risk management, risk response actions.Resumen
Contexto:
Los proyectos en empresas metalmecánicas se ven afectados por el riesgo. Una correcta gestión de riesgos depende de las respuestas que se brinden para mejorar el plan del proyecto. Sin embargo, múltiples acciones potenciales pueden resultar en restricciones por múltiples factores. El propósito de este artículo es
proponer un enfoque híbrido para resolver el problema de seleccionar acciones de respuesta a riesgos considerando objetivos estratégicos, lógica difusa y simulación.
Método:
Primero, se identificaron 334 riesgos mediante una revisión de la literatura y una discusión con expertos. Estos fueron filtrados, lo que resultó en 70 riesgos operacionales. Posteriormente, se priorizaron los 10 riesgos críticos utilizando la matriz de riesgos. Luego, mediante simulación Monte Carlo y análisis de correlación, se identificaron las actividades más afectadas por los riesgos. Finalmente, se diseñaron potenciales acciones de respuesta para cada caso, y se aplicó lógica difusa y despliegue de funciones de calidad para evaluarla.
Resultados:
Las respuestas seleccionadas se enmarcaron en los objetivos estratégicos, i.e., satisfacción del cliente, rentabilidad del negocio, e implementación de nuevas tecnologías. Esto, teniendo en cuenta algunos atributos corporativos que las acciones debían cumplir: finalizar a tiempo el proyecto, tener costos bajos y cumplir con el alcance. Las acciones seleccionadas tuvieron un mejor perfil que otras opciones que buscaban minimizar tiempo o costos.
Conclusiones:
Los proyectos EPCC son complejos y a menudo sufren de desfases en alcance, tiempo y costo. El análisis de los riesgos y la selección de las respuestas en la fase de planificación ayudan a un mejor desempeño. Este estudio desarrolló un plan de respuesta a riesgos para un proyecto desarrollado en Brasil. Los riesgos fueron identificados, clasificados y mitigados mediante simulaciones, lo que resultó en una reducción de 11 días en la duración estimada del proyecto.
Palabras clave:
lógica difusa, simulación Monte Carlo, gestión de riesgos de proyectos, acciones de respuesta a riesgos..Introduction
Industrial projects involve several specialties such as construction, metalworking, electricity, hydraulics, environment, and safety. The metalworking discipline is responsible for transforming steel into goods, building machines and structures using raw metal materials. This process includes cutting, burning, welding, machining, forming, and assembly tasks. The products range from laminates, pipes, metal structures, and wires to industrial machinery, such as elevators and boilers.
The lifecycle of these projects follows the generic EPCC process (engineering, procurement, construction, and commissioning). The engineering component includes basic and detailed engineering as well as planning; procurement includes logistics, transportation, receipts, purchases, and invoices; construction includes mechanical, electrical, and civil installations; and commissioning includes testing and delivery, after-sales service, and modernization 1. By nature, these projects are quite complex and plagued by uncertainty 2,3.
This is an industry that generally operates on projects commissioned by external clients. The work is of job shop nature, so the characteristics of the activities are unique. The work is subject to unpredictable factors, such as activity durations, special project requirements, and uncertainty 4. The complexity of this type of project impacts performance, and these projects may even finish with time delays or cost overruns. Project durations may extend up to 25% beyond the planned timeline due to scope changes and unconsidered risks 5. Other estimates consider cost overruns of 30% and delays of 40% 6.
Bodies of knowledge on project management promote several practices to successfully complete projects. One of them, the Project Management Body of Knowledge (PMBOK) proposes several areas to plan and control, i.e., scope, time, cost, communication, quality, resources, and risks 7. Planning and control require decision-making processes to select paths of action in several situations during a project’s lifecycle.
The selection of corrective actions is required at two moments during the project lifecycle. The first moment is the planning phase, when a potential threat to the baseline is identified. To prevent these threats, corrective actions become part of the baseline. The second moment is the execution phase, when an event has occurred. In this case, these actions take place after the event, aiming to correct the progress of the project. Research has typically studied the first of these moments, i.e., the selection of risk response strategies (RRS) 8 or actions (RRA) 9.
This selection process is conducted during the planning phase, after designing a preliminary baseline of scope, time, and costs 7. Risk management is the process involved in this type of decision-making, and its phases include identification, prioritization, evaluation, response design, implementation, and control 7,10,11.
On the other hand, organizations develop projects to implement business strategies and enable the creation of business value 7. They may choose among low-cost, scale-based, specialization, newness, f lexibility, quality, service, and sustainability strategies (12, 13). According to the selected corporate strategy, they define objectives and projects. However, when monitoring and controlling them, they often fail to consider their strategic logic. Corrective actions are usually selected to meet time and cost goals 7.
This paper proposes a hybrid approach to the selection of corrective actions during the planning phase. This approach combines risk management, fuzzy quality function deployment (FQFD), and Monte Carlo simulation (MCS). Response actions are selected through FQFD, and pre-mitigation and post-mitigation analysis is performed via MCS.
The remainder of this document is structured as follows. Section 2 provides an overview of the relevant literature, presenting risk management methods as well as their advantages and disadvantages. Section 3 details the steps involved in constructing the risk response model. In Section 4, the model is applied to a real EPCC project carried out in São Paulo (Brazil). Different response plans were also used to evaluate alternative selection approaches. Section 5 presents the conclusions of this work, states its contributions, and proposes future lines of research.
Literature review
The risk management methodology involves a series of activities that may be conducted through several methods. These are presented below.
Identification of potential risks. The first step in the methodology is to identify the risks that may positively and negatively affect the project. There are different risk categories within the scope of a project, e.g., operational, economic, social, political, financial, regulatory, nature-related, environmental or technological. Operational risks, for instance, are those related to the actual operation of the project. The product of this phase is a list with many potential risks. Table I presents the various methods for identifying potential risks.
Sources: (7,14,15).
Table I: Techniques used for risk identification

Qualitative analysis. After obtaining the list of potential risks, the methodology determines their priority level to identify critical risks for the project. Some qualitative analysis methods are shown in Table II.
Sources: (7,16-18).
Table II: Techniques used for qualitative risk análisis

Quantitative analysis. Once the critical risks have been identified, a numerical evaluation of the impact on project objectives is conducted. This effect is usually oriented to the project’s time or cost objectives 7,19. Some quantitative analysis methods are shown in Table III.
Sources: (7,20,21).
Table III: Techniques used for quantitative risk análisis

Response planning. After evaluating the project’s risk level, response plans must be developed while considering several corrective actions, thereby minimizing the threats to the project objectives and maximizing the opportunities it can offer 7. Those actions are usually classified into four general categories: acceptance, transference, avoidance, and reduction. A decision-making process has to be conducted to evaluate and select the appropriate action. Some response planning methods are shown in Table IV.
Sources: (16-24).
Table IV: Techniques used for response planning

Methodology
This study proposes a model for selecting risk responses while following the risk management methodology. Its first phase identifies the set of potential risks that may arise during the project. The second phase identifies critical risks. Afterwards, the impact of risks on the schedule is assessed (pre-mitigation analysis). The next phase identifies potential responses, which are later evaluated. Subsequently, a post-mitigation analysis is conducted to validate the improvement of the schedule. At the end, a project baseline is designed, which may be executed. This framework is shown in Fig. 1.
Figure 1: Framework for the proposed model
Identification of operational risks
This process generates a list of all the risks that may affect the project. Two strategies were combined to identify risks. A review of scientific literature and a review of historical projects in the studied organization were conducted. The risks obtained were integrated into a single list that was later refined with the support of experts. These experts discarded repeated risks, those that were implicit in others, and those that did not apply to the context. To better understand the risks, they were described in terms of event, impact, and causes 7. Subsequently, the list was categorized using the PMI’s structure of f irst- and second-level categories 7.
Experts are definedaspeoplewitheducation,knowledge,skills, orspecialized training, who provide a judgment based ontheir experience in some area of knowledge, industry, or discipline 7. The experts considered in this study hold decision-making positions in the organization’s projects. Their profession and experience in projects must be considered. These experts also took part in the other steps of the methodology
Prioritization of operational risks
This involved a qualitative analysis to identify critical risks from a potential risks list. These risks were identified through a survey applied to experts in relation to their analysis of the probability and impact of each risk.
Assessment of risks impact
This involved a quantitative analysis that measured the impact of critical risks on the project. To this effect, MCS was used. This analysis was performed in pre-action mode and once again in post-action mode. Thus, the impact of response actions could be evaluated.
MCS generates thousands of possible outcomes or scenarios based on probability distributions. This allows modeling costs and times at the activity level 7. Input values are chosen randomly for each iteration, and the outputs represent the range of possible outcomes, such as the project completion date. Thus, the impact of risks on the objectives of the project can be evaluated 25.
According to 35, MCS replaces the estimated duration of any activity of a project with a randomly generated number extracted from a statistical distribution. In general, MCS operates in three steps. The f irst step is the generation of random numbers in the interval (0,1). In the second step, the probability value is located in the distribution function of the task, in order to determine the value that corresponds to said probability. Finally, the generated value is used as the input number in the iteration, i.e., the value of the duration or cost of the task.
Using MCS to evaluate the impact of risks on projects is not a new approach. Research varies according to how the information is obtained; the relationship between tasks is studied, as well as the impact of risks on tasks and between the risks themselves. An example of research on the topic is the one by 26. Regarding the impact of risks on project scheduling, MCS is regarded as easy to apply and is indeed the most widely applied method 7,27.
That said, the methodological structure that we decided to use in this work is CSRAM 28, as it facilitates data collection- most of the data were obtained qualitatively through expert judgment. In addition, it considers the influence of risk on tasks and the correlation between risks. The required data results from the steps presented below.
Deterministic model design. This step involves the elaboration of a network diagram showing task (most probable time tm) and project duration (critical path method), in addition to minimum (optimistic time to) and maximum task duration (pessimistic time tp).
Influence analysis. This step first defines the risk influence degree of the activities. Influence is categorized as effective (E) and very effective (VE). By default, any other relationship is rated as ineffective (IE) Risks and tasks are related through a matrix specifying how each risk affects each activity. Moreover, potential scenarios regarding the impact of risks on task performance are established. The probability limits are categorized as better than expected if the task is positively affected by the risk; as expected when the risk had no impact on the task; and as worse than expected when the uncertainty of the risk negatively affects the task. For all risks, the better-than-expected limit was set at 0.1, and the worse-than-expected limit was defined as 1.0. The limit for what was expected was between 0.3 and 0.5. The sum of these three values must be equal to 1. Finally, the correlation between risk factors was included. This is typically done through a rating of 1 or 0 given by experts. If the initial risk materializes 1, then the correlated risk also receives that value. However, if the initial risk does not occur (0), there is a random probability that the correlated risk materializes.
Stochastic modeling and simulation. Several computational tools were available for running the model, but we decided to run the deterministic model on MS Project and the stochastic model on Palisade @Risk. First, we defined the inputs, outputs, and number of iterations for the MCS. Task duration wasconsidered asaninputrelated to risk impact andwasincludedusingadurationcoefficient (?). Two types of analysis were conducted: Eqs. (1) and (2) were used if the coefficient was greater or lower than zero, respectively.


where ADi represents the duration of activity i; tm denotes the most probable time; tp is the pessimistic time; to represents the optimistic time; and DCi is the duration coefficient for activity i.
In Eq. (3), activity duration oscillates between the most probable and the maximum value. In Eq. (4), the duration oscillates between the minimum and the most probable duration. The duration coefficient depends on the state of the risks. It is a random number that simulates a scenario within the probability limit imposed on each risk. It also depends on the value associated with the degree of influence of the risk-activity factor. This coefficient aims to combine how risks materialize and how they influence activities, and it is given by Eq. (3).

where rni is a random number; ivij represents the degree of influence of every risk j on activity i; and N represents the total number of risks.
The duration coefficient increases or decreases the task duration based on the most probable time. If the risk turns out to be worse than expected, the value of the degree of influence is positive. If the risk materializes as expected, the value of the degree of influence is zero. If the risk occurs better than expected, the value of the degree of influence is negative. These qualitative analyses are converted to quantitative values, considering that very effective ratings represent 70% of the total impact, as shown in Eq. 4, and that the effective ones account for the remaining 30%, which is indicated in Eq. (5).


where veti represents the number of very effective terms assigned to activity i; and eti denotes the number of effective terms assigned to activity i.
In addition, considering that a risk may or may not materialize, a binomial variable was included. Anewformula to obtain the activity duration coefficient was proposed, replacing Eq. (6).

where Ej is 1 if the risk occurs and 0 if it does not.
Analysis of response actions
This analysis comprised three steps: identification of potential responses, fuzzy analysis to select the response, and simulation to re-evaluate the risk profile.
First, potential response actions were designed to project risks through workshops with a group of experts. Later, the potential actions were prioritized through a fuzzy quality function deployment (QFD) analysis. QFD was designed by Mitsubishi in 1972 for the manufacturing industry 29. It has spread to other applications such as services and product development, but it is rarely employed in project management 30. It is a tool that links customer requirements to technical specifications. It translates ordinary language into technical terms, facilitating cooperation between marketing, engineering, and manufacturing. It ensures that all requirements are considered and not forgotten 29, and it brings the voice of the customer (VOC) to the product’s technical characteristics 29.
This involves the so-called house of quality, a matrix that relates customer needs/attributes, known as whats (left side), to engineering characteristics, i.e., hows (top side). The what-how relationship level is in the center of the matrix. It also includes needs-relative importance (left side) and requirements co-relationships (upper side), and it allows carrying out benchmarking with competitors or with earlier product versions (right side) as well as assigning requirements importance weights (bottom side) 29.
To consider the uncertainty related to real-world problems and decision-making for modeling imprecise data, the researchers expanded it with fuzzy logic, known as fuzzy QFD (FQFD) 30. The FQFDwasapplied as proposed by Osorio 31,32 with the following steps:
Identifying customer needs (whats). A workshop was conducted with the team of experts to define the project’s basic requirements.
Determining the relative importance of the whats. A linguistic scale was defined to allow each member of the group to determine the level of importance or weight of each what. This scale was associated with a fuzzy number (Table V).
Sources: (31).
Table V: Fuzzy linguistic scale

To obtain the weight, the average of each rating given by the experts was calculated using Eq. (7), the result of which was a fuzzy triangular number.

where wi represents the triangular number (wia,wib,wic) for every what; q represents the total number of whats; and n represents the number of experts.
Identifying the company’s strategic objectives (hows). These are the criteria with which all possible alternatives were evaluated. The identification process was carried out through interviews with two of the team’s experts who hold management positions in the organization. They determined the objectives based on their experience in the company and after consulting with the company’s management.
Determining the correlation between the whats and the hows. This correlation was established by using the aforementioned linguistic scale and the following equation:

where Correlation = {rij | i = 1,...,q; j = 1,...,c}; c represents the total number of hows; and rij is the triangular number (rija,rijb,rijc) consolidated between each qi and each cj.
Determining the weight of the hows. The average value of the evaluations provided by the experts in previous steps was calculated according to Eq. (9).

where Wj is the triangular number (Wja,Wjb,Wjc)
Determining the impact of alternatives on the hows. The experts determined the level of importance of each alternative regarding the strategic objectives using the same scale as in Table V and according to Eq. (10).
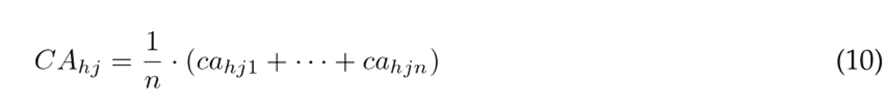
where CA = {CAhj, whereh = 1,...,p; j = 1,...,c}; p represents the number of alternatives; andcahjn represents the fuzzy evaluation of the expert n for the alternative h in relation to the variable j.
Prioritizing the alternatives. The fuzzy affinity index (ID) was calculated for each alternative. The result was a fuzzy triangular number obtained through Eq. (11).


Finally, to obtain a non-fuzzy number, the Facchinetti approach was employed. The triangular fuzzy numbers were defuzzified to get a priority ranking that could be ordered from the highest to the lowest value.

Finally, a post-action analysis was carried out through simulation to re-evaluate the risk profile, which included risks responses, new tasks, changes in project logic, and new task durations (to,tm, and tp). This was done through workshops with experts, who evaluated the new conditions to carry out the project.
Results- a case study in a construction project
Our method was applied in a real construction project executed in São Paulo (Brazil) by a Colombian engineering company. The research project had the support of five experts from the organization: one mechanical engineer, one electrical engineer, and three industrial engineers with more than five years of experience in project management.
Identification of operational risks
This process was carried out in two stages. First, a keyword search was carried out, and, later, a detailed review to identify the papers that should be used in the study. In this literature review, 53 articles were found. They were reviewed in detail, and those that dealt with non-operational risks or were related to sectors other than engineering, construction, metalworking companies, logistics, and hydroelectric projects were discarded. Finally, 11 articles remained, corresponding to studies in Ecuador, Colombia, Spain, Peru, the United Kingdom, South Africa, France, China, Australia, and India 33,34. The literature review allowed identifying 252 operational risks, and the review of projects in the organization and workshops with project managers returned 82 risks.
The final list included a total of 334 operational risks. It was filtered with the experts, resulting in 70 classified risks. Following the PMI categorization approach, the first-level risks were technical, management, commercial, and external in nature. These four categories included 22 second-level categories.
The largest number of potential risks was found in the management category, which consolidated 44%oftherisks identified 31, followed by the technical category with 24% (17 risks). The external and commercial risk categories grouped 19% 13 and 13% 9, respectively.
Prioritization of operational risks
For this analysis, a survey for the expert group was designed. This survey, elaborated in Excel Visual Basic, included the risks list and the qualifications defined by the experts. The critical risks were as follows: failure to deliver plans and manufacturing lists on time (R27); poor management of the communication between those involved in the project (R65); little documentation of activities (R3); loss of intellectual property by sharing design, production, or technology capabilities with other companies (R68); lack of learning techniques to increase knowledge (R2); failure of IT systems (R5); poor project management (R66); reactive risk management (R67); optimistic bias (time, cost) (R63); and pandemics (R55).
Assessment of risks impact
First, the deterministic model was defined, and information from the influence analysis was collected. The next step was to calculate the duration coefficient of each task, in order to model the duration of the tasks that served as input in the simulation. The output of the model was the duration of the project. With the @Risk add-in of Microsoft Excel, the model was elaborated, and several tests were carried out to evaluate the convergence of the results. The simulation was carried out with 2000, 5000, and 10 000 iterations. In the first case, the average duration was 70.68 days, with a standard deviation of 2.2 days. In the second case, this value was 70.68 days, also with standard deviation of 2.2 days. In the third case, the average duration was 70.62 days, with the same standard deviation. With the little variation obtained, we decided to use the model with 5000 iterations for the project. The results are shown in Fig. 2.
Figure 2: Frequency distribution with 5 000 iterations
An important finding was that the original 63 days schedule had a 0the 5000 iterations. On the other hand, a sensitivity analysis was conducted, considering activity duration changes. We elaborated a tornado graph by calculating the duration of the project plus the randomness related to the coefficient of activity duration. This graph highlighted the activities that most affected the duration of the project, with the first four being 1.8.0 Dispatch, 1.3.1 Legalization of the contract, 1.3.3 Validation of PTF, and 1.4.1.1 Modulation through Forline.
Framework for the proposed model
Following the proposed method, the potential response actions were initially designed. The expert group designed responses for the critical risks (step 3.2) and the tasks with the greatest variability (step 3.3). The group designed several actions that could respond to each case. Table VI presents the number of potential actions designed by the project team.
Table VI.: actions

A set of 40 potential actions was used to design the response plan and adjust the project. Each action was thoroughly designed. To decide which action to implement, FQFD was applied. The experts defined the components of the matrix. A set of basic project requirements was established, representing customer needs (whats). The project requirements were as follows: finish the project on time (Q1), have low costs (Q2), and comply with the scope (Q3). A set of company strategic objectives was established to represent the hows.
For the workshop, the expert group also invited the manager of the company. The group defined some strategic objectives while considering the corporate strategy and goals, i.e., satisfy the customer (C1), make the business profitable (C2), and implement new technologies (C3). The correlation between whats and hows was established while considering several values, following fuzzy logic as seen in Table VI.
Table VII. : What-how relation ship

The Q and C weights were also established. The project requirements were assigned the same weight, while the strategic objectives received different weights. Table VIII shows the weight of the hows
Table VIII. : Weight of the hows

The following is the application of the method for the first risk (R27, failure to deliver manufacturing plans and lists on time). This risk impacts 22 tasks and may cause delays in the company's production plant. The proposed response actions were hiring more personnel to speed up the delivery of plans (A) and applying two shifts to the engineering area (B).
The FQFD analysis of each alternative, considering its impact on strategic objectives, resulted in 220 (option A) and 313 points (option B). Option B was selected, and two shifts were defined for the engineering area,entrusted with modeling, design, and blueprint elaboration. Two groups of five individuals were assigned to the shifts from 6 am to 2 pm and from 2 pm to 10 pm. The same method was applied for the remaining risks. The final response plan included 17 possible actions
The last step was to carry out a post-action simulation of the project. Considering the responses to the prioritized risks, the new conditions were included in the model. For the non-prioritized, remaining, and secondary risks, the group decided to apply a contingency reserve from the MCS, and, for the unknown risks, the group used a management reserve defined by the company (1%). The simulation was carried out with 5000 iterations, resulting in a duration between 55 and 64 days, with an average of 60 daysFig 3..
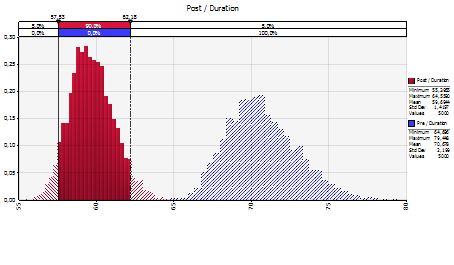
Figure 3: Post-action frequency distribution with 5 000 iterations
Compared to the pre-action simulation, the 63-day project had a 96% probability of completion. In graphical terms, the frequency curve shifted to the left, as indicated in Fig. 4 where the initial simulation is seen in red and the post-action one is seen in blue.
Figure 4: Pre- and post-action frequency distribution
The new project design includes new tasks but was accelerated by 11 days. To achieve this, increased Project budgets were established. The project went from an initially estimated cost of $1 030 772 694 to $1 135 813 141. However, part of the budget reserves may become part of profitability if they are not required.
The development of new response plans aimed to test the behavior of the model. Following the literature, the team developed plans with the lowest cost and shortest duration. Other plans logically and comprehensively integrated actions for the project. Finally, the team conducted simulations using the same parameters as the previous application. Table IX summarizes the information for each plan, including the FQFD-designed base plan.
Table IX: Response plans

The first response plan aimed to minimize costs, resulting in a total cost of $8 463 631. It changed the project network because of the emergence of new tasks and the adjustment of some task durations. The simulation resulted in an average duration of 63 days, which is the maximum term of the project. The simulation also revealed that there was a 50% chance that the project duration would exceed 63 days. As a result, the team decided that this option was not viable.
After exploring different potential actions, a new plan was designed to cost less than the model’s proposed plan. The new plan would cost $19 999 996 and include changes to the project network, such as adding new tasks, removing others, and changing the duration of some. The initial simulation showed that the project would take an average of 70 days to complete, which is longer than the maximum allowable time. Additionally, based on the simulation data, there was a 0% probability of delivering the project within 63 days or less, meaning that the project would not be completed within the required timeframe under any scenario.
By shifting the directive to prioritize minimal time, two combinations of actions were found which involved modifications to the project design. Plans 3 and 4 resulted in an average duration of 59 days and deviations of 3.1 and 3.3 days, respectively. In both cases, the probability of meeting the maximum term of 63 days was high, it i.e., 90 and 89%, respectively. However, these plans cost more than the previously designed, $59 278 522 plan.
Two additional plans proposed by the organization’s engineering team were tested. Plan 5 resulted in an expected duration of 61 days, within the maximum time allowed. Considering the resulting deviation of this simulation, this plan had an 83% probability of completion before 63 days for $64 589 764. This plan was in the middle of the previous plans, which sought to minimize cost and time. However, it was more expensive than the base plan and had a lower probability of success.
Finally, plan 6 turned out to be an inconvenient option. Its average duration was 65 days, longer than required, and it had a 19% chance of being delivered. The cost, $79 463 853, was one of the highest among all the options.
In summary, plans 3, 4, and 5 were convenient, resulting in a >83% probability of meeting the required time. Nevertheless, considering the cost of the proposals, it was convenient to implement the base plan. In order of convenience, plan 5 could follow it, given its cost, despite offering an 83% probability of delivery within the term, which was the lowest among the options.
Discussion
Theoretical implications
This paper proposes a hybrid approach for selecting RRAs in EPCC projects, which combines risk management, mathematical techniques, and business strategy. This broadens the scope of study regarding construction project risk management and offers a new viewpoint for choosing RRAs. The theoretical implications of this research are threefold.
First, this study expands research on the selection of RRAs for EPCC projects by proposing a strategic perspective. Prior studies used selection criteria based on operational factors such as cost, time, or quality, without taking the organization’s strategic direction into account. This study adds strategic criteria to the existing literature on RRA selection research and uses FQFD to evaluate them. By integrating techniques like WBS and mathematics in the selection process, this study also broadens the body of literature.
Second, this study enriches research on project scheduling in risk situations in EPCC projects. Unlike other studies, uncertainty is not applied to task duration, but to the way in which risks can materialize. This development contributes to the theoretical understanding of variability and expands the boundaries of RRA selection research. It can also inspire academics to conduct in-depth research on the relationship between uncertainty and task duration ranges.
Third, this research contributes to the modeling of other approaches for managing uncertainty in EPCCprojects. Our modelconsiders the design of individual actions selected via the strategic approach, whose impact is evaluated with a post-mitigation simulation. This enables a comparative pre- vs. post-mitigation evaluation during project design and the selection of the best strategy to respond to risks. Current research selects the best actions from criteria such as time or cost, using optimization models that do not consider the relationships between actions.
Practical implications
This model provides relevant and necessary information for decision-making by the project team. It is consistently integrated into the project baseline planning process. In addition, it allows for the discussion of decisions by the management (with a strategic focus) and the project team (with an operational focus). It also allows delving deeper into the analysis of risks in EPCC projects, their behavior and impact, and the way to design better responses. Consequently, it offers a way to improve planning and increase the probability of success.
Limitations and discussion of future research
Some limitations suggest avenues for future research. Our model establishes task durations while considering uncertainty as a deviation from the most probable time. Future research could incorporate uncertainty in another way, within optimistic and pessimistic time ranges. Additionally, variability may be considered based on the effect of resource usage, which ultimately affects the task duration. Likewise, new ways of understanding the relationship between the risks themselves can be explored, which can entail additional effects on the project.
Since response actions can generate secondary risks, future research may consider aggregating these impacts into decision-making. This requires understanding whether risk behavior can change during the project’s lifecycle. In this way, models can more accurately assess impacts.
The model relates strategic and project objectives to assess potential responses to risks. More research is needed on how to relate these goal levels in order to validate their usefulness. Future works could study how to relate them to the requirements formulation of the project. Other criteria, such as stakeholder or sustainability considerations, should also be explored.
Our model analyzes and makes decisions regarding potential risks in a project. Future research should relate comprehensive decision-making to both the project and the project portfolio. Another future direction for research is to apply the proposed model to more EPCC projects, aiming to verify its broad applicability.
Conclusions
EPCC projects are complex and often suffer from gaps in basic objectives regarding scope, time, and cost. Analyzing risks and selecting responses in the planning phase helps for a better execution and increases the likelihood of success. Usually, the problem is not studied outside the criteria of time, cost, quality, and optimization, which can affect the selection of responses. This study developed a practical model based on risk management which considers the impact of and relationships between risks and strategic and operational criteria to select RRAs. The validation of said model in a real project carried out in Brazil allowed verifying its applicability. Experimentation with response plans focused on decreasing project times or costs, resulting in cross-effects. The plans that decreased time resulted in the highest costs, while those that decreased cost lengthened the project. The model led to a cost-and-time response plan with the confidence that decisions were framed within the organization’s strategic priorities.
The main contributions of this study are as follows. First, it introduces a new perspective for evaluating RRAs, enriching theoretical research on the selection of RRAs in EPCC projects. Second, it effectively integrates the relationship between risks and incorporates effect variability into the problem, instead of assessing duration. Third, the proposed model can integrate the risk management process with the scope, time, and cost definition process, serving as a guide for planners to enhance project performance
References
License
Copyright (c) 2024 Álvaro Julio Cuadros-López, Alexander Bustos-Useche, Leonardo Bustos-Useche

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.








2.jpg)










