DOI:
https://doi.org/10.14483/udistrital.jour.reving.2013.1.a04Published:
2013-06-30Issue:
Vol. 18 No. 1 (2013): January - JuneSection:
ArticleUbicación y dimensionamiento como parámetros en el diseño de almacenes: revisión del estado de arte
Location and sizing as parameters in the warehouse design: A survey paper
Keywords:
Warehouse design, Location, Sizing. (en).Keywords:
diseño de almacén, ubicación, dimensionamiento. (es).Downloads
References
. A, Shulman. (1991) Algorithm for solving dynamic capacitated plant location problems with discrete expansion sizes. Operations re-search. vol. 39 (3) 423-436.
. A.K. Rao & M.R. Rao. (1998). Solution procedures for sizing of warehouses. European Journal of Operational Research, Vol 108 (1), 16-25.
. Andreas, Klose y A. Drexl. (2000) Lower bounds for the capacitated facility location problem based on column generation, Universidad St. Gallen,1-3.
. Andreas Klose, (1998) A branch and bound algorithm for an uncapacitated facility location problem with a side constraint, International Transactions in Operational Research, Vol 5, 155-168
. B. Rouwenhorst, B. Reuter, V. Stockrahm, G.J. van Houtum, R.J. Mantel, W.H.M. Zijm, (2000) Warehouse design and control: Framework and literature review, European Journal of Operational Research, Vol 122, Pág. 515-533.
. C.H.Y. Lam, K.L. Choy, G.T.S. Ho, S.H. Chung, (2012) A hybrid case-GA-based decision support model for warehouse operation in fulfilling cross-border orders, Expert Systems with Applications, Vol 39, Pág 7015-7028.
. C.T. Ng, T.C.E. Cheng, Vladimir Kotov, Mikhail Y. Kovalyov, (2009) The EOQ problem with decidable warehouse capacity: Analysis, solu-tion approaches and applications, Discrete Applied Mathematics, Vol 157, Pág 1806-1824.
. Charles J. Malmborg, (1996) An integrated storage system evaluation model, Applied Mathematical Modelling, Vol 20, Pág 359-370.
. Charles J. Malmborg, Swaminathan Balachandran, Daniel M. Kyle, (1986) A model based evaluation of a commonly used rule of thumb for warehouse layout, Applied Mathematical Modelling, Vol 10, Pág 133-138.
. Charles J. Malmborg, Krishnakumar Bhaskaran, (1990). A revised proof of optimality for the cube-per-order index rule for stored item lo-cation, Applied Mathematical Modelling, Vol 14, Pág 87-95.
. Charles J. Malmborg, Khalid Al-Tassan, (2000). An integrated performance model for orderpicking systems with randomized storage, Applied Mathematical Modelling, Vol 24, Pág 95-111.
. El-Houssaine Aghezzaf, (2007) Production planning and warehouse management in supply networks with inter-facility mold transfers, European Journal of Operational Research, Vol 182, Pág 1122-1139.
. Emre Cakmak, Noyan Sebla Gunay, Gulsah Aybakan, Mehmet Tanyas, (2012) Determining the Size and Design of Flow Type and U-Type Warehouses, Procedia - Social and Behavioral Sciences, Vol 58, Pág 1425-1433
. F. Saldanha y F., Captivo, (1998) Heuristic approach for the discrete dynamic location problem. Location science, vol. 6, 211-223
. F. Guerriero, R. Musmanno, O. Pisacane, F. Rende, (2012) A mathematical model for the Multi-Levels Product Allocation Problem in a warehouse with compatibility constraints, Applied Mathematical Modelling.
. Farhad Kiya, Hamid Davoudpour, (2012) Stochastic programming approach to re-designing a warehouse network under uncertainty, Transportation Research Part E: Logistics and Transportation Review, Vol 48, Pág. 919-936.
. Felix T.S. Chan, H.K. Chan, (2011) Improving the productivity of order picking of a manual-pick and multi-level rack distribution ware-house through the implementation of class-based storage, Expert Systems with Applications, Vol 38 Pág. 2686-2700.
. Francesco Basile, Pasquale Chiacchio, Domenico Del Grosso, (2012) A control oriented model for manual-pick warehouses, Control Engi-neering Practice, Vol 20, Pág. 1426-1437.
. Galvan, Jose L. (2012). Writing Literature Reviews: A guide for students of the social and behavioral Sciences. Pyrczak Publishing. 5 Ed. 81-96
. G.P. Broulias, E.C. Marcoulaki, G.P. Chondrocoukis and L.G. Laios. Warehouse management for improved order picking performance:an application case study from the wood industry
. Geraldes, Carla, Sameiro, Maria y Pereira Guillerme. (2010) Integrated models for warehouse design and planing. Semana de Enganarhia 2010. Guimaraes
. Géraldine Strack, Yves Pochet, (2010) .An integrated model for warehouse and inventory planning, European Journal of Operational Re-search, Vol 204, Pág. 35-50.
. Gilles Cormier, Eldon A. Gunn. (1992). A review of warehouse models, European Journal of Operational Research, Vol 58, Pág. 3-13
. Gómez M., Rodrigo A.Correa E., Alexander A. (2010). Métodos cuantitativos utilizados en el diseño de la gestión de almacenes y centros de distribución. Revista Avances en Sistemas e Informática, Diciembre Pág. 109-117.
. Günther Zäpfel, Michael Wasner, (2006) Warehouse sequencing in the steel supply chain as a generalized job shop model, International Journal of Production Economics, Vol 104, Pág. 482-501
. Héctor J. Carlo, Germán E. Giraldo, (2012). Toward perpetually organized unit-load warehouses, Computers & Industrial Engineering, Vol 63, Pág. 1003-1012.
. Heung Suk Hwang, Gyu Sung Cho, (2006) A performance evaluation model for order picking warehouse design, Computers & Industrial Engineering, Vol 51, Pág 335-342.
. J.P.van den Berg, W.H.M. Zijm, (1999) Models for warehouse management: Classification and examples, International Journal of Produc-tion Economics, Vol 59, Pág. 519-528.
. Jacek Żak a, Piotr Sawicki. (2011). The multiobjetive ranking of the warehouse infraestructure in the physical distribution system.
. Jean-Philippe Gagliardi, Angel Ruiz, Jacques Renaud. (2008) Space allocation and stock replenishment synchronization in a distribution center, International Journal of Production Economics, Vol 115, Pág. 19-27.
. Jinxiang Gu, Marc Goetschalckx, Leon F. McGinnis, (2007) Research on warehouse operation: A comprehensive review, European Jour-nal of Operational Research, Vol 177, Pág. 1-21.
. Jinxiang Gu, Marc Goetschalckx, Leon F. McGinnis, (2010) Research on warehouse design and performance evaluation: A comprehensive review, European Journal of Operational Research, Vol 203, Pág. 539-549.
. Jukka Korpela, Antti Lehmusvaara, Jukka Nisonen. (2007) Warehouse operator selection by combining AHP and DEA methodologies, In-ternational Journal of Production Economics, Vol 108, Pág. 135-142.
. Kevin R. Gue, Goran Ivanovid, Russell D. Meller. (2012) A unit-load warehouse with multiple pickup and deposit points and non-traditional aisles, Transportation Research Part E: Logistics and Transportation Review, Vol 48, Pág. 795-806.
. Klaus Moeller, (2011) Increasing warehouse order picking performance by sequence optimization, Procedia - Social and Behavioral Sciences, Vol 20, Pág. 177-185.
. Kumar Bhaskaran, Charles J. Malmborg, (1990) Economic tradeoffs in sizing warehouse reserve storage area, Applied Mathematical Modelling, Vol 14, Pág 381-385.
. Larry J. LeBlanc, (1977). A heuristic approach for large scale discrete stochastic transportation-location problems, Computers & Mathe-matics with Applications, Vol 3, Pág. 87-94.
. Letitia M. Pohl, Russell D. Meller, Kevin R. Gue. (2009) An analysis of dual-command operations in common warehouse designs, Trans-portation Research Part E: Logistics and Transportation Review, Vol 45, Pág. 367-379.
. LF, Moreno Velasquez, JD, Velasquez Henao y FJ, Díaz Serna. (2005) Solución al problema combinado de ubicación estratégica de alma-cenes y asignación de inventarios usando técnicas heurísticas. Pág. 7257-66.
. Lu Chen, André Langevin, Diane Riopel, (2011) A tabu search algorithm for the relocation problem in a warehousing system, Interna-tional Journal of Production Economics, Vol 129, Pág. 147-156.
. M.S. Hung, John C. Fisk, (1984) Economic sizing of warehouses: A linear programming approach, Computers & Operations Research, Vol 11, Pág. 13-18.
. Mier, Ortega, y J, Delgado. (2002) Utilización de metaheurísticas para el dimensionamiento y localización de instalaciones industriales. II Conferencia de Ingeniería de Organización. Pág. 623-621.
. O. Hounkonnou, (1990) Modelling and simulation of an automated warehouse in activity, Mathematical and Computer Modelling, Vol 14, Pág. 1100-1102.
. Peter Baker, Marco Canessa, (2009) Warehouse design: A structured approach, European Journal of Operational Research, Vol 193, Pág. 425-436.
. René de Koster, (2007) Tho Le-Duc, Kees Jan Roodbergen, Design and control of warehouse order picking: A literature review, Euro-pean Journal of Operational Research, Vol 182, Pág. 481-501.
. Ria Kalfakakou, Stefanos Katsavounis, Kostas Tsouros, (2003) Minimum number of warehouses for storing simultaneously compatible products, International Journal of Production Economics, Pág. 559-564.
. Ronald H. Ballou, (1975). A multiproduct plant/warehouse location model with nonlinear inventory costs, Journal of Operations Man-agement, Vol 5, Pág. 75-90.
. Roy, t.j. y Erlenkotter, d.(1982). A dual based procedure for dynamic facility location. management science. vol. 28 (10) 1091-1105.
. Sebastian Henn, (2012) Algorithms for on-line order batching in an order picking warehouse, Computers & Operations Research, Vol 39, Pág. 2549-2563.
. Sebastian Henn, Gerhard Wäscher, (2012). Tabu search heuristics for the order batching problem in manual order picking systems, Eu-ropean Journal of Operational Research, Vol 222, Pág. 484-494.
. Semih Önüt, Umut R. Tuzkaya, Bilgehan Doğaç, (2008). A particle swarm optimization algorithm for the multiple-level warehouse layout design problem, Computers & Industrial Engineering, Vol 54, Pág. 783-799
. Stefan Minner, (2009). A comparison of simple heuristics for multi-product dynamic demand lot-sizing with limited warehouse capacity, International Journal of Production Economics, Vol 118, Pág. 305-310
. Steffey, William. (2008). Layout design analysis for the storage area in the distribution center.
. T.C. Poon, K.L. Choy, Harry K.H. Chow, Henry C.W. Lau, Felix T.S. Chan, K.C. Ho, (2009). A RFID case-based logistics resource management system for managing order-picking operations in warehouses, Expert Systems with Applications, Vol 36, Pág. 8277-8301.
. Venkata Reddy Muppani (Muppant), Gajendra Kumar Adil, (2008). A branch and bound algorithm for class based storage location as-signment, European Journal of Operational Research, Vol 189, Pág. 492-507
. Venkata Reddy Muppani (Muppant), Gajendra Kumar Adil, (2007). Efficient formation of storage classes for warehouse storage location assignment: A simulated annealing approach, Omega, Vol 36 Pág. 609-618
. W. Yang, Felix T.S. Chan, V. Kumar, (2012). Optimizing replenishment polices using Genetic Algorithm for single-warehouse multi-retailer system, Expert Systems with Applications, Vol 39, Pág. 3081-3086
. Y., Hinojosa, Y., Puerto, J., Fernández.(2000). Multiperiod two-echelon multicommodity capacitated plant location problem. European Journal of Operational Research, vol. 123, Pág. 271-291.
. Yon-Chun Chou, Yao-Hung Chen, Hui-Min Chen, (2012). Recency-based storage assignment and warehouse configuration for recurrent demands, Computers & Industrial Engineering, Vol 62, Pág. 880-889.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
UBICACIÓN Y DIMENSIONAMIENTO COMO PARÁMETROS EN EL DISEÑO DE ALMACENES: REVISIÓN DEL ESTADO DE ARTE
LOCATION AND SIZING AS PARAMETERS IN THE WAREHOUSE DESIGN: A SURVEY PAPER
Andrés Mauricio Hualpa Zúñiga, Universidad Cooperativa de Colombia. Bogotá, Colombia. andres.hualpa@campusucc.edu.co
Carolina Suárez Roldan, Universidad Cooperativa. Bogotá, Colombia. carolina.suarez@campusucc.edu.co
Recibido: 14/01/2013 - Aceptado: 14/06/2013
RESUMEN
Este artículo presenta una revisión literaria de los parámetros de ubicación y dimensionamiento en el diseño de almacenes, en el cual se identificaron modelos, métodos, algoritmos y herramientas que se han propuesto para abordar este problema. Se aplicó una metodología de exploración, recolección, clasificación, evaluación y selección de los trabajos publicados desde los años 1970 hasta 2012. El estudio concluye identificando posibles rutas de investigación en esta área de interés, a la luz de la revisión realizada.
Palabras clave: Diseño de almacén, Ubicación, Dimensionamiento.
ABSTRACT
This article presents a survey of the literature concerning location and design as parameters in the design of stores. The survey includes identification of models, methods, algorithms and tools that have been proposed to address this problem. The methodology applied was based on exploration, collection, classification, evaluation and selection of the papers published in the period 1970-2012. The study concludes by identifying possible research routes in this area of interest according to the survey.
Key words: Warehouse design, Location, Sizing.
1. INTRODUCCIÓN
El proceso de ubicación y dimensionamiento de almacenes es un factor estratégico al momento de diseñar sistemas logísticos, debido a que se convierte en un componente físico que genera ventajas competitivas de reducción de costos, tiempos de respuesta y servicio al cliente. Este caso específico se aplica para sectores industriales especializados en la producción basada en proyectos, como en el sector de la construcción. En él, el diseño de almacenes tiende a convertirse en una actividad variable y temporal que depende de diferentes condiciones específicas de la obra y que se desarrolla en mayor parte a través de la experiencia, dejando de lado el conocimiento y técnicas que pueden generar resultados con mayor eficiencia. A pesar de los avances realizados en el campo de la Ingeniería Industrial relacionados con el proceso de ubicación y dimensionamiento de instalaciones, se está dejando de lado la oportunidad de generar aplicaciones de innovación y desarrollo que determinen mejores prácticas en el proceso operativo de este tipo de empresas. En este contexto se propone la adaptación de técnicas expresadas mediante algoritmos, que faciliten la interpretación de operaciones secuenciales y que determinen soluciones eficientes al diseñar almacenes temporales. En este artículo se realiza una revisión literaria desde la década de los 70 hasta la década actual, además de identificar herramientas y tendencias en el estado del arte, y finaliza con una discusión sobre posibles rutas de investigaciones en el área de interés.
2. MATERIALES Y MÉTODOS
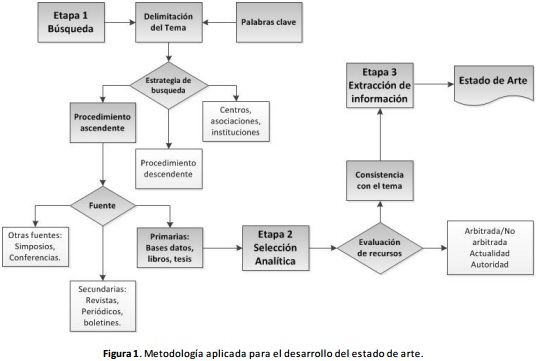
Para la construcción del estado del arte se aplicó un método adaptado del modelo de redacción de reseñas bibliográficas [19], integrado por tres etapas generales: Búsqueda, Selección analítica y Extracción de información para desarrollo de artículos de revisión. A su vez, en cada una de estas etapas se utilizaron variables metodológicas que se describen en la Figura 1.
En la etapa de “Búsqueda”, se definieron dos palabras clave para delimitación del tema: “Ubicación” y “Dimensionamiento” de almacenes. Como estrategia de búsqueda se aplicó el procedimiento ascendente, localizando resultados de estudio a partir de referencias bibliográficas. El porcentaje de consulta de fuentes de información es de un 85% con la base de datos Science Direct y un 15% con otras bases de datos bibliográficas, entre ellas Redalyc y Proquest. Adicionalmente a este último porcentaje se integra la consulta de literatura aplicada al tema de instalaciones de almacenamiento. El objeto de identificar la información principalmente en la base de datos Science Direct obedece a la rigurosidad y acceso de artículos que contiene, específicamente en la sección de Ciencias físicas e Ingeniería. Un criterio adicional de búsqueda fue bajo los tópicos respectivos a: Supply Chain, Journal of Production Economics, Operations Research and Mangement, Computers and Industrial Engineering, dado que muchos resultados tenían relación con las ciencias de la salud y sistemas inteligentes de información. Los resultados obtenidos generaron un total de 164 artículos preseleccionados para la etapa posterior.
En la etapa de “Selección Analítica”, los artículos obtenidos fueron clasificados bajo el criterio de consistencia con el tema de diseño de instalaciones de almacenaje, específicamente con los parámetros de ubicación y dimensionamiento, siendo necesaria una exclusión del 64% del total obtenido inicialmente. En la selección de artículos finales se identificó adicionalmente que algunos de ellos tienen en cuenta la combinación del parámetro de distribución.
En la etapa final de “Extracción de información”, los artículos y documentos finales fueron interpretados y organizados en una matriz por año, autor, y método de solución propuesto, siendo este último el principal aspecto de revisión para determinar parámetros de diseño del algoritmo relacionado con el proyecto de investigación de maestría.
3. ESTADO DEL ARTE
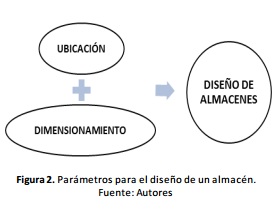
El diseño del almacén consta de cinco grandes decisiones: determinación de la estructura, dimensionamiento, diseño interno, selección de equipos y selección de estrategias operacionales [32] [48], representando cada una de ellas una etapa determinante para la integración de una instalación de almacenamiento. Para el caso específico del “diseño interno”, existen dos parámetros claves que son la ubicación de las instalaciones y el dimensionamiento de las mismas, como se expresa en la Figura 2.
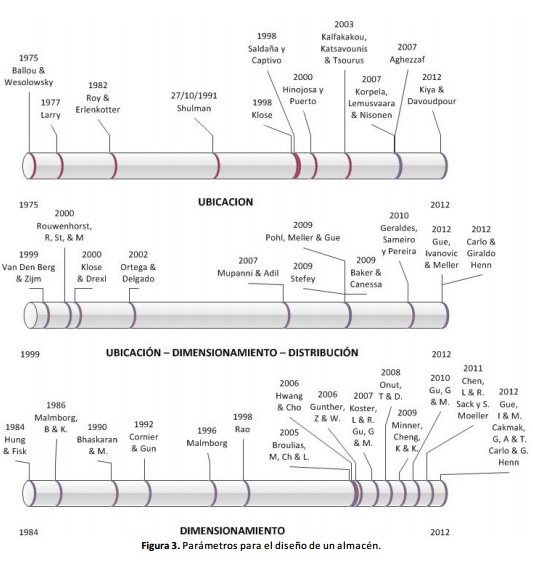
A pesar que se destaca la interrelación de estos dos aspectos, estudios realizados por diferentes autores a lo largo de 40 décadas generalmente los han tomado por separado. A partir de lo anterior se desarrolla la revisión de literatura obtenida de artículos disponibles en bases de datos y teniendo como referencia de búsqueda el termino: “diseño del almacén”.
Entre los estudios desarrollados se tiene registro desde la década de los 70’s, en donde se encuentran modelos de localización, entre ellos el de múltiples periodos presentando soluciones factibles a partir de programación dinámica [47]. Este modelo presenta restricciones de capacidad acondicionando distintas variables, entre ellas el número máximo de instalaciones por periodo, posibilidad de recolocación, entre otras. Dos años más tarde se plantea la heurística STPL (Stochastic Transportation Location Problem) [37], que determina la ubicación de las plantas de acuerdo a la programación de envíos cuyo comportamiento es estocástico. Esta heurística supone que existe un número discreto de posibles ubicaciones y que los costos de envío son lineales.
En la década de los 80’s se plantea un modelo de localización multi-periodo conocido como modelo DUFLP (Dynámic Uncapacitated Facility Location Problem) [48]. Este modelo no tiene restricciones de capacidad, permitiendo abrir o cerrar instalaciones. La solución para este modelo es el algoritmo Dual Ascent Method, descartando así a la programación dinámica como herramienta imprescindible para dar solución a problemas de localización dinámica. En el año 1984 se acondiciona la formulación de programación lineal para el dimensionamiento óptimo del almacén [41]. En este modelo se extiende para el problema dinámico el tamaño, generando flexibilidad en su diseño. En el año 1986 se plantea un modelo de diseño de almacén basado en los costos de inventario y preparación de pedidos [9].
En la década de los 90’s se desarrolla un estudio orientado al dimensionamiento de la zona de almacenaje en donde se establece que su tamaño depende del costo de almacenamiento y el costo de reposición [36]. Este modelo se formula para el caso de almacenes con estanterías convencionales obteniendo soluciones a partir de aproximación estocástica. En el mismo año se propone una ampliación a este modelo mediante la integración del índice cúbico por pedido (COI), como parámetro de asignación de políticas de inventario y preparación de pedidos [10] [11]. Desde este año se visualiza el incremento en la utilización de aplicaciones computacionales para este proceso. Mediante la combinación de modelos matemáticos y computacionales se desarrollan estudios de simulación en actividades de automatización de almacenes [43]. Entre los principales problemas trabajados en este estudio se contempla la baja utilización de espacios disponibles para almacenamiento. Se propone el incremento de la capacidad del almacén mediante la utilización de espacios ubicados en altura y la asignación de rutas de recolección de pedidos mediante teoría de grafos. Un año después se desarrolla el modelo DCPLP (Dynamic Capacitated Facility locatión problema) [1], el cual retoma restricciones de capacidad finita con la posibilidad de aumentar la misma. La solución propuesta fue desarrollada a partir de técnicas lagrangianas aplicadas a límites superiores e inferiores mediante un método basado en programación dinámica.
En el año 1992 se realiza una revisión de los modelos aplicados al diseño de la capacidad de almacenamiento [23]. En dicho estudio se determina que la capacidad de almacenamiento depende de cuatro factores: políticas de alistamiento de pedido, procesamiento de lote, asignación de almacenamiento y modelos de control dinámico. En el año 1996 se retoma el estudio del comportamiento aleatorio de la demanda como un parámetro de alistamiento de materiales y de diseño de la zona de almacenamiento. Mediante el modelo de evaluación de sistemas integrados de almacenamiento [8], se plantea el análisis de costos asociados con el diseño y operación de un sistema de distribución. Para el año 1998 se desarrolla el algoritmo UFLP (Uncapacited Facility Location Problem) [4], para ubicación de instalaciones con restricciones de capacidad a partir del método Branch and Bound. En el mismo año fue desarrollado un modelo de localización discreta mediante la técnica heurística de DROP apoyado de la herramienta CPLEX [14], considerando todas las instalaciones iguales con capacidad ilimitada. En este mismo año se desarrolla un modelo de programación lineal para el dimensionamiento económico de un almacén en el que las demandas presentan comportamiento estacional [2]. Mediante la formulación de este modelo se obtiene el tamaño óptimo de la bodega. Un año después se presenta una clasificación de los problemas de gestión de almacenes [28]. En este trabajo se realiza una revisión frente al diseño del sistema de gestión de inventario teniendo en cuenta restricciones de espacio. Posteriormente se agrega la novedad de considerar la manipulación de múltiples productos ubicados en almacenes intermedios que cumplen restricciones de producción y demanda [58]. Su función objetivo busca minimizar el costo de la instalación. En este mismo año se desarrolló el modelo denominado CFLP (Capacited Facility Location Problem )[3], el cual se caracteriza por trabajar la combinación de localización y capacidad suponiendo que las instalaciones no tienen una capacidad fija ya que existen variables de decisión que integran dimensiones de cada una de las instalaciones. De la misma forma se obtiene un modelo matemático para dimensionamiento basado en el flujo de materiales, el cual integra la configuración del almacenamiento y los parámetros para alistamiento de pedidos. A partir de ello se presenta como resultado ciclos de tiempo para realizar el procesamiento de pedidos. En este mismo año se presenta una revisión frente al proceso de diseño de almacenes [5], en el que se propone un proceso conformado por cinco fases: Concepto y adquisición de datos, especificaciones funcionales, especificaciones técnicas, selección de los equipos y selección de las políticas de planificación y control.
Dos años más tarde se realizó una modificación al modelo CFLP creando el modelo MCLFP (Múltiple Capacitated Facility Location Problem) [42], en donde se incluye restricciones de tiempo para un único periodo y su solución está definida mediante técnicas meta heurísticas y de simulación. En el año 2003 se desarrolla un modelo heurístico que determina el menor número de zonas de almacenamiento necesarios [46]. Este modelo integra múltiples productos y a cada uno un deposito con capacidad limitada. En el año 2005 se presenta un método de dimensionamiento de almacenes basado en políticas de reordenación de materiales [20]. Este se desarrolla en tres etapas de medición. En este mismo año se trabaja el problema combinado de ubicación y asignación óptima de inventarios [39]. La solución propuesta se desarrolla mediante heurística de búsqueda exhaustiva PODA. En el año 2006 se desarrolla un modelo de evaluación de desempeño de la configuración de un almacén [27], el cual está diseñado para mejorar el rendimiento al momento de preparar un pedido. Los parámetros de comparación están determinados por el tamaño del almacén, el tamaño de los estantes y el número de transportadores. En este mismo año se desarrolla un modelo de asignación de materiales solucionado mediante programación dinámica [25]. La aplicación de este modelo fue realizada en una industria de materiales de acero.
En el año 2007 se plantea un modelo de dimensionamiento del almacén a partir del sistema de disposición interna y los métodos de enrutamiento para el procesamiento de pedidos [45]. En el mismo año se plantea un modelo de dimensionamiento del almacén considerando las restricciones de capacidad obtenida a partir de un proceso de planeación de la producción [12]. Este modelo considera la distribución de múltiples productos a lo largo de una cadena de suministro teniendo la posibilidad de activar o desactivar el almacén según se requiera. Su solución está definida a partir de la combinación de métodos de programación lineal, entera mixta y relajación lagrangiana. De la misma manera se realiza una revisión sobre el grado de relación que existe entre las funciones básicas del almacén: recepción, almacenamiento, preparación de pedidos, envíos y el dimensionamiento del mismo [31]. El proceso de ubicación de almacenes vuelve a trabajarse en este año mediante la combinación de las metodologías AHP (Analytic Hierarchy Process) y DEA (Data Envelopment Analysis) [33]. El resultado determina que el orden de aplicación de las metodologías es generar rendimientos de cada ubicación del almacén mediante AHP, como información de entrada para medir la eficiencia de los mismos mediante DEA. En este mismo año se desarrolla un modelo de distribución de zonas de almacenamiento a partir del índice cúbico de ocupación [56]. Esto determina la clasificación de materiales para la asignación de espacios de almacenamiento.
En el año siguiente se desarrolla una configuración de almacenes de varios niveles que minimiza el costo de mantenimiento anual [51]. Este algoritmo PSO (Particle Swarm Optimization) integra problemas de distribución, orientación de bastidores de almacenamiento, asignación de espacios, que ha demostrado ser un modelo matemático NP-duro. En este mismo año se aplica el algoritmo Branch and Bound en el dimensionamiento de un almacén basado en los costos de manejo de materiales [55]. Sus resultados demostraron ser más eficientes que las soluciones mediante programación dinámica o lineal. En este mismo año se propone un modelo de dimensionamiento del almacén a partir del proceso de reposición de materiales [30]. Los resultados obtenidos a partir del modelo Pick to belt demuestran la reducción de esperas en el proceso de abastecimiento.
En el año 2009 se plantea el diseño del almacén a partir de la comparación de tres configuraciones evaluadas con indicadores de distancia de viaje [38]. Los resultados obtenidos demuestran que la designación de un pasillo transversal medio, facilita el proceso de alistamiento y determina las dimensiones mínimas del almacén. En este mismo año se plantea la integración de un modelo sistemático para el diseño de almacenes [44]. En este modelo se tiene en cuenta la integración de herramientas y técnicas resumidas en 11 pasos. De la misma manera la integración del modelo EOQ como parámetro de dimensionamiento [7]. En tal estudio la capacidad de almacenamiento máximo es una variable de decisión. Por otra parte, en ese año se realiza la comparación de tres heurísticas que determinan la temporización de reposición de artículos teniendo en cuenta las restricciones de capacidad en el almacén [52]. Los resultados obtenidos en esta comparación demostraron que aplicando una política de reposición de lote, por lote en horarios definidos, se generan ahorros en los costos asociados. Este método de reposición a su vez define la configuración del almacén. Por otra parte el modelo de distribución física “espina de pescado” también ha sido evaluado [53]. Allí se realiza la comparación con el modelo tradicional de cuadrícula en donde se obtiene mayor rendimiento en términos de distancia de recorrido y utilización de espacio.
En el año 2010 se desarrolla un estudio en donde se analiza la relación cuantitativa que existe entre los límites de capacidad para el dimensionamiento del almacén y las decisiones de inventario [22]. Se identifica a través de este estudio que los costos de inventario se pueden reducir teniendo en cuenta la planificación y restricciones de almacenamiento. En este mismo año se elabora una revisión de los métodos cuantitativos al diseño de almacenes [24]. En sus resultados principales se propone la utilización de técnicas de simulación y diseño experimental. Por otra parte se determina la integración del proceso de planeación con el dimensionamiento del almacén [21]
En el año 2011 se desarrolla una investigación que establece que el diseño del almacén estará asociado a variables de dimensionamiento, sistema de almacenamiento, preparación de pedidos y tendencias de la demanda las cuales fueron previamente trabajadas por otros autores [17]. La principal diferencia es que integra otras variables adicionales relacionadas con las características dimensionales del material y tasas de rotación. Los resultados obtenidos a partir de simulación determinaron que el rendimiento de las operaciones del almacén depende totalmente de estas variables combinadas con la asignación multinivel de estanterías. Para este mismo año se adelantó un estudio que evalúa la relación que existe entre el diseño y configuración del almacén y el proceso de alistamiento de pedidos [35]. Se realizó experimentación con diferentes configuraciones de dimensionamiento y el modelo LSO (Linear Sequence Optimization), obteniendo como resultado una serie de patrones de secuencia asignados para diferentes dimensiones de almacenamiento. En este mismo año se desarrolló un modelo de dimensionamiento solucionado mediante Algoritmo de búsqueda Tabú [40]. De la misma manera se plantea el método MCDA (Multiple Criteria Decision Making) [29], el cual está sujeto a un análisis de decisión multicriterios para la evaluación de la utilidad de un almacén.
Finalmente para el año 2012 se integran varios estudios y aplicaciones de diseño de almacenes. Uno de ellos determina que la configuración “Flying-V” [34], genera resultados numéricos favorables para rendimientos de tiempo y distancia. Esta configuración establece de la misma manera parámetros de dimensionamiento del almacén. En este mismo año se retoma un estudio de localización de almacenes a través de programación estocástica [16]. Este modelo plantea el rediseño de una red de almacenes realizando eliminación de instalaciones. La solución se plantea mediante la aproximación SAA (Sample Average Approximation). Los resultados demuestran que las soluciones estocásticas tienen mayor solidez que las soluciones deterministas. Otro parámetro propuesto para el diseño de almacenes es la inclusión del proceso de asignación de materiales en instalaciones disponibles [15]. Este estudio plantea la comparación de las soluciones obtenidas entre un modelo matemático lineal y una heurística de búsqueda local iterativa. El objetivo planteado es reducir tiempos de entrega, niveles de inventario, costos de almacenamiento e incrementar el nivel de servicio. El resultado demuestra que la heurística genera buenos resultados en menor tiempo y esfuerzo computacional de cálculo. Nuevamente se plantea un modelo de dimensionamiento y configuración del almacén basado en el comportamiento estocástico de la demanda [59]. En este trabajo se determina como factor fundamental de diseño el grado de relación entre el sistema de distribución de materiales y el dimensionamiento del almacén. Los casos que se analizan especialmente son los de flujo de material de almacenamiento con retorno. La solución se plantea en cuatro partes a la que se aplica modelos de programación lineal. También se plantea un modelo de dimensionamiento del almacén a partir de la configuración de la instalación en “U” [13]. De acuerdo con este estudio se determina que este tipo de distribución minimiza la distancia total de recorrido y por ende determina algunas condiciones de longitud del almacén. El modelo de asignación de almacenamiento por carga unitaria [26] [6] se convierte en otro modelo de dimensionamiento dependiente de la configuración de la instalación. Para este caso el indicador a ser evaluado se relaciona con el tiempo de ocupación para movimiento de materiales y tiempos de respuesta. De la misma manera otro estudio que evalúa el indicador de tiempo de respuesta es el algoritmo On-line Order Picking [49] [50]. Este algoritmo evalúa la aplicación de diferentes heurísticas de ruteo combinadas con la asignación de materiales.
4. RESULTADOS
Los artículos obtenidos para la construcción del estado de arte fueron ordenados de acuerdo al año de publicación y su autor respectivo. A partir de esto se identificaron tres parámetros particulares de análisis: ubicación, dimensionamiento y distribución. En la Tabla I se integran los resultados para la interpretación y construcción del algoritmo de asignación de espacios de almacenamiento teniendo en cuenta para cada uno de los parámetros definidos los resultados y el método de solución propuesto por cada autor.
A partir de la consulta realizada se puede identificar que en el desarrollo investigativo que ha tenido el proceso de Diseño de Almacenes a lo largo de cuatro décadas, tiene como punto de partida la aplicación de modelos y técnicas matemáticas de localización de instalaciones inicialmente. Este comportamiento exclusivo se mantiene sólo hasta finales de la década de los 80, periodo en el cual comienza a trabajarse el dimensionamiento mediante algoritmos de programación lineal y programación estocástica, orientados a la minimización de costos de inventario y optimización del proceso de alistamiento de pedidos. Desde la década de los 80 en adelante el dimensionamiento, la ubicación y distribución han sido parámetros de diseño que se han trabajado hasta la fecha, caracterizados especialmente por la utilización de aplicaciones computacionales fundamentadas en modelos matemáticos de programación lineal, estocástica y dinámica, algoritmos de búsqueda y simulación. En la Figura 3 se presenta la ventana de tiempo en la que se caracteriza la evolución de publicaciones relacionadas con el diseño de almacenes, teniendo como parámetros de clasificación la ubicación, dimensionamiento y distribución, en donde en algunos casos se trabajaron de una manera combinada.
5. DISCUSIÓN DE RESULTADOS
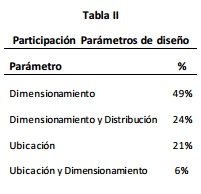
Luego de la revisión del estado de arte sobre el diseño de instalaciones de almacenamiento, se identifica que ubicación y dimensionamiento no son los únicos parámetros que han sido objeto de investigación y desarrollo. Varios expertos agregan el parámetro de distribución al proceso de gestión del almacén, dado que se combina con el dimensionamiento. Según la Tabla II, los resultados demuestran que el 49% de los estudios se enmarcan en su mayoría en el desarrollo de métodos matemáticos, heurísticos y algorítmicos para el dimensionamiento del almacén, seguido por un 24% por la combinación entre este y el parámetro de distribución. De la misma manera el parámetro de ubicación ocupa el tercer lugar con un 21% de participación. Adicionalmente la combinación entre los parámetros de ubicación y dimensionamiento ocupan el nivel más bajo de la tabla, con un 6% de participación.
De acuerdo con la revisión se identifica un bajo desarrollo investigativo en la integración total de los parámetros de diseño de almacenes. Generalmente la ubicación, dimensionamiento y distribución se toman por separado ocasionando incertidumbre en cuanto a la objetividad y globalidad de los resultados. Una de las principales causas está asociada a la parcialidad de los investigadores debido a la complejidad del funcionamiento de los almacenes, representado en la planeación y ubicación de espacios de los procesos de recepción, manejo y custodia de materiales, alistamiento de pedidos, acondicionamiento de unidades de carga, expedición entre otros, así como la relación de variables de tipo de producto, el comportamiento de la demanda, el nivel de servicio al cliente , el flujo de materiales y la flexibilidad del almacén . A lo anterior se agrega una nueva característica que están asumiendo los almacenes, donde las unidades no son enviadas a la zona de almacenamiento sino acondicionadas en un área de expedición para ser distribuidas de la manera más inmediata.
Los modelos de dimensionamiento del almacén resuelven el problema de la capacidad bajo un criterio de costos de construcción y operación, omitiendo factores de importancia como es el manejo de materiales; es decir que es necesario desarrollar modelos más robustos que junto con el desarrollo de hardware, software de optimización y simulación permitan considerar los efectos del dimensionamiento frente a variables y/o parámetros definidos en el diseño integral del almacén y que respondan a problemas que no han recibido ninguna atención, ya que en la revisión no se encontraron estudios que consideren tales parámetros.
El diseño del almacén ha sido un tema de investigación abordado por varios autores, con diferentes propuestas que varían el alcance y las actividades que se definen en cada una de las etapas de diseño. A partir de esto el problema sigue siendo un sistema complejo, de manera que buscar una solución optima frente a la cantidad de posibilidades que se encuentran en cada uno de las etapas del diseño del almacén, es una oportunidad de investigación. Para terminar es importante recalcar que las decisiones que se tomen en el diseño del almacén no pueden estar soportadas solamente en la intuición y experiencia, puesto que los costos de operación y almacenamiento se determinan en gran medida en la fase del diseño y desempeñan un papel vital en el funcionamiento de las cadenas de suministro. De allí la importancia de desarrollar modelos formales que incluyan en su planteamiento tanto reglas de optimización matemática como heurísticas que generen soluciones integrales.
Finalmente se identificó en la revisión que pocos han sido los estudios especializados en el diseño de almacenes en Colombia, pues los resultados se orientan a resolver problemas globales de la cadena de abastecimiento, en las que se integran proveedores, planta de producción, centros de almacenamiento, distribución y clientes; por lo anterior, se consiera esta una área de interés para futuras investigaciones en el país.
6. CONCLUSIONES
Particularmente se identifica que el parámetro de dimensionamiento y distribución son predominantes en relación con la problemática prevista para el proceso de asignación de espacios de almacenamiento, debido a que las variables que se trabajan en los diferentes artículos son relacionadas con modelos geométricos y se desarrollan a través de aplicaciones computacionales. Mediante el análisis de cada uno de los trabajos investigativos de dimensionamiento, se resaltan los resultados obtenidos al aplicar políticas de ubicación de materiales de acuerdo al índice cúbico por pedido. Para este caso la metodología propuesta establece la necesidad de tener una estandarización de las dimensiones de los pedidos con el objeto de determinar la capacidad óptima a lo largo de un periodo de planeación. De la misma manera esta capacidad se convierte en un factor dimensional que dependerá del tamaño de los materiales a almacenar, siendo estos necesariamente compatibles con los diferentes equipos e instalaciones con que cuenta el almacén. Cada uno de estos materiales estará sujeto a una dinámica de flujo en función de la demanda, que para algunos casos tendrán componentes probabilísticos. Esta afirmación se obtiene de aquellos modelos de dimensionamiento en donde los métodos de solución propuestos están apoyados de programación estocástica y lineal. Las aplicaciones computacionales son relevantes, debido a la utilización de herramientas informáticas de simulación de datos y gráfica, como es el caso del software Automod y CAD, en el cual demostraron ser elementos potencialmente eficientes para determinar dimensiones necesarias de almacenamiento, facilitando la medición de rendimientos en distancia de viaje y tiempo de alistamiento de pedidos. Por otra parte se identifica que la configuración interna del almacén es un factor condicional para los casos asociados a restricciones de espacio y/o capacidad. De acuerdo con el análisis teórico, el modelo de reposición de materiales que se utilice se convierte en una solución a esta problemática, ya que puede lograr una compensación en la demanda.
En síntesis se puede confirmar que hay muchos factores que afectan la asignación de espacios de almacenamiento, como es el tamaño, el diseño del sistema de almacenamiento, las características del producto, las tendencias de la demanda, las tasas de rotación, entre otros. Aún más el parámetro de ubicación, a pesar de estar claramente definido entre las primeras etapas de diseño de almacenes, se tiende a descartar su teoría en razón a que no existe una relación directa con la problemática de asignación de espacios de almacenamiento. Esto debido a que los modelos desarrollados se orientan a una macro-localización, siendo esta una aplicación para el diseño de sistemas de abastecimiento y distribución.
7. REFERENCIAS
- A, Shulman. (1991) Algorithm for solving dynamic capacitated plant location problems with discrete expansion sizes. Operations research. vol. 39 (3) 423-436.
- A.K. Rao & M.R. Rao. (1998). Solution procedures for sizing of warehouses. European Journal of Operational Research, Vol 108 (1), 16-25.
- Andreas, Klose y A. Drexl. (2000) Lower bounds for the capacitated facility location problem based on column generation, Universidad St. Gallen,1-3.
- Andreas Klose, (1998) A branch and bound algorithm for an uncapacitated facility location problem with a side constraint, International Transactions in Operational Research, Vol 5, 155-168
- B. Rouwenhorst, B. Reuter, V. Stockrahm, G.J. van Houtum, R.J. Mantel, W.H.M. Zijm, (2000) Warehouse design and control: Framework and literature review, European Journal of Operational Research, Vol 122, Pág. 515-533.
- C.H.Y. Lam, K.L. Choy, G.T.S. Ho, S.H. Chung, (2012) A hybrid case-GA-based decision support model for warehouse operation in fulfilling cross-border orders, Expert Systems with Applications, Vol 39, Pág 7015-7028.
- C.T. Ng, T.C.E. Cheng, Vladimir Kotov, Mikhail Y. Kovalyov, (2009) The EOQ problem with decidable warehouse capacity: Analysis, solution approaches and applications, Discrete Applied Mathematics, Vol 157, Pág 1806-1824.
- Charles J. Malmborg, (1996) An integrated storage system evaluation model, Applied Mathematical Modelling, Vol 20, Pág 359-370.
- Charles J. Malmborg, Swaminathan Balachandran, Daniel M. Kyle, (1986) A model based evaluation of a commonly used rule of thumb for warehouse layout, Applied Mathematical Modelling, Vol 10, Pág 133-138.
- Charles J. Malmborg, Krishnakumar Bhaskaran, (1990). A revised proof of optimality for the cube-per-order index rule for stored item location, Applied Mathematical Modelling, Vol 14, Pág 87-95.
- Charles J. Malmborg, Khalid Al-Tassan, (2000). An integrated performance model for orderpicking systems with randomized storage, Applied Mathematical Modelling, Vol 24, Pág 95-111.
- El-Houssaine Aghezzaf, (2007) Production planning and warehouse management in supply networks with inter-facility mold transfers, European Journal of Operational Research, Vol 182, Pág 1122-1139.
- Emre Cakmak, Noyan Sebla Gunay, Gulsah Aybakan, Mehmet Tanyas, (2012) Determining the Size and Design of Flow Type and U-Type Warehouses, Procedia - Social and Behavioral Sciences, Vol 58, Pág 1425-1433
- F. Saldanha y F., Captivo, (1998) Heuristic approach for the discrete dynamic location problem. Location science, vol. 6, 211-223
- F. Guerriero, R. Musmanno, O. Pisacane, F. Rende, (2012) A mathematical model for the Multi-Levels Product Allocation Problem in a warehouse with compatibility constraints, Applied Mathematical Modelling.
- Farhad Kiya, Hamid Davoudpour, (2012) Stochastic programming approach to re-designing a warehouse network under uncertainty, Transportation Research Part E: Logistics and Transportation Review, Vol 48, Pág. 919-936.
- Felix T.S. Chan, H.K. Chan, (2011) Improving the productivity of order picking of a manual-pick and multi-level rack distribution warehouse through the implementation of class-based storage, Expert Systems with Applications, Vol 38 Pág. 2686-2700.
- Francesco Basile, Pasquale Chiacchio, Domenico Del Grosso, (2012) A control oriented model for manual-pick warehouses, Control Engineering Practice, Vol 20, Pág. 1426-1437.
- Galvan, Jose L. (2012). Writing Literature Reviews: A guide for students of the social and behavioral Sciences. Pyrczak Publishing. 5 Ed. 81-96
- G.P. Broulias, E.C. Marcoulaki, G.P. Chondrocoukis and L.G. Laios. Warehouse management for improved order picking performance: an application case study from the wood industry
- Geraldes, Carla, Sameiro, Maria y Pereira Guillerme. (2010) Integrated models for warehouse design and planing. Semana de Enganarhia 2010. Guimaraes
- Géraldine Strack, Yves Pochet, (2010) .An integrated model for warehouse and inventory planning, European Journal of Operational Research, Vol 204, Pág. 35-50.
- Gilles Cormier, Eldon A. Gunn. (1992). A review of warehouse models, European Journal of Operational Research, Vol 58, Pág. 3-13
- Gómez M., Rodrigo A.Correa E., Alexander A. (2010). Métodos cuantitativos utilizados en el diseño de la gestión de almacenes y centros de distribución. Revista Avances en Sistemas e Informática, Diciembre Pág. 109-117.
- Günther Zäpfel, Michael Wasner, (2006) Warehouse sequencing in the steel supply chain as a generalized job shop model, International Journal of Production Economics, Vol 104, Pág. 482-501
- Héctor J. Carlo, Germán E. Giraldo, (2012). Toward perpetually organized unit-load warehouses, Computers & Industrial Engineering, Vol 63, Pág. 1003-1012.
- Heung Suk Hwang, Gyu Sung Cho, (2006) A performance evaluation model for order picking warehouse design, Computers & Industrial Engineering, Vol 51, Pág 335-342.
- J.P.van den Berg, W.H.M. Zijm, (1999) Models for warehouse management: Classification and examples, International Journal of Production Economics, Vol 59, Pág. 519-528.
- Jacek Żak a, Piotr Sawicki. (2011). The multiobjetive ranking of the warehouse infraestructure in the physical distribution system.
- Jean-Philippe Gagliardi, Angel Ruiz, Jacques Renaud. (2008) Space allocation and stock replenishment synchronization in a distribution center, International Journal of Production Economics, Vol 115, Pág. 19-27.
- Jinxiang Gu, Marc Goetschalckx, Leon F. McGinnis, (2007) Research on warehouse operation: A comprehensive review, European Journal of Operational Research, Vol 177, Pág. 1-21.
- Jinxiang Gu, Marc Goetschalckx, Leon F. McGinnis, (2010) Research on warehouse design and performance evaluation: A comprehensive review, European Journal of Operational Research, Vol 203, Pág. 539-549.
- Jukka Korpela, Antti Lehmusvaara, Jukka Nisonen. (2007) Warehouse operator selection by combining AHP and DEA methodologies, International Journal of Production Economics, Vol 108, Pág. 135-142.
- Kevin R. Gue, Goran Ivanović, Russell D. Meller. (2012) A unit-load warehouse with multiple pickup and deposit points and non-traditional aisles, Transportation Research Part E: Logistics and Transportation Review, Vol 48, Pág. 795-806.
- Klaus Moeller, (2011) Increasing warehouse order picking performance by sequence optimization, Procedia - Social and Behavioral Sciences, Vol 20, Pág. 177-185.
- Kumar Bhaskaran, Charles J. Malmborg, (1990) Economic tradeoffs in sizing warehouse reserve storage area, Applied Mathematical Modelling, Vol 14, Pág 381-385.
- Larry J. LeBlanc, (1977). A heuristic approach for large scale discrete stochastic transportation-location problems, Computers & Mathematics with Applications, Vol 3, Pág. 87-94.
- Letitia M. Pohl, Russell D. Meller, Kevin R. Gue. (2009) An analysis of dual-command operations in common warehouse designs, Transportation Research Part E: Logistics and Transportation Review, Vol 45, Pág. 367-379.
- LF, Moreno Velasquez, JD, Velasquez Henao y FJ, Díaz Serna. (2005) Solución al problema combinado de ubicación estratégica de almacenes y asignación de inventarios usando técnicas heurísticas. Pág. 7257-66.
- Lu Chen, André Langevin, Diane Riopel, (2011) A tabu search algorithm for the relocation problem in a warehousing system, International Journal of Production Economics, Vol 129, Pág. 147-156.
- M.S. Hung, John C. Fisk, (1984) Economic sizing of warehouses: A linear programming approach, Computers & Operations Research, Vol 11, Pág. 13-18.
- Mier, Ortega, y J, Delgado. (2002) Utilización de metaheurísticas para el dimensionamiento y localización de instalaciones industriales. II Conferencia de Ingeniería de Organización. Pág. 623-621.
- O. Hounkonnou, (1990) Modelling and simulation of an automated warehouse in activity, Mathematical and Computer Modelling, Vol 14, Pág. 1100-1102.
- Peter Baker, Marco Canessa, (2009) Warehouse design: A structured approach, European Journal of Operational Research, Vol 193, Pág. 425-436.
- René de Koster, (2007) Tho Le-Duc, Kees Jan Roodbergen, Design and control of warehouse order picking: A literature review, European Journal of Operational Research, Vol 182, Pág. 481-501.
- Ria Kalfakakou, Stefanos Katsavounis, Kostas Tsouros, (2003) Minimum number of warehouses for storing simultaneously compatible products, International Journal of Production Economics, Pág. 559-564.
- Ronald H. Ballou, (1975). A multiproduct plant/warehouse location model with nonlinear inventory costs, Journal of Operations Management, Vol 5, Pág. 75-90.
- Roy, t.j. y Erlenkotter, d.(1982). A dual based procedure for dynamic facility location. management science. vol. 28 (10) 1091-1105.
- Sebastian Henn, (2012) Algorithms for on-line order batching in an order picking warehouse, Computers & Operations Research, Vol 39, Pág. 2549-2563.
- Sebastian Henn, Gerhard Wäscher, (2012). Tabu search heuristics for the order batching problem in manual order picking systems, European Journal of Operational Research, Vol 222, Pág. 484-494.
- Semih Önüt, Umut R. Tuzkaya, Bilgehan Doğaç, (2008). A particle swarm optimization algorithm for the multiple-level warehouse layout design problem, Computers & Industrial Engineering, Vol 54, Pág. 783-799
- Stefan Minner, (2009). A comparison of simple heuristics for multi-product dynamic demand lot-sizing with limited warehouse capacity, International Journal of Production Economics, Vol 118, Pág. 305-310
- Steffey, William. (2008). Layout design analysis for the storage area in the distribution center.
- T.C. Poon, K.L. Choy, Harry K.H. Chow, Henry C.W. Lau, Felix T.S. Chan, K.C. Ho, (2009). A RFID case-based logistics resource management system for managing order-picking operations in warehouses, Expert Systems with Applications, Vol 36, Pág. 8277-8301.
- Venkata Reddy Muppani (Muppant), Gajendra Kumar Adil, (2008). A branch and bound algorithm for class based storage location assignment, European Journal of Operational Research, Vol 189, Pág. 492-507
- Venkata Reddy Muppani (Muppant), Gajendra Kumar Adil, (2007). Efficient formation of storage classes for warehouse storage location assignment: A simulated annealing approach, Omega, Vol 36 Pág. 609-618
- W. Yang, Felix T.S. Chan, V. Kumar, (2012). Optimizing replenishment polices using Genetic Algorithm for single-warehouse multi-retailer system, Expert Systems with Applications, Vol 39, Pág. 3081-3086
- Y., Hinojosa, Y., Puerto, J., Fernández.(2000). Multiperiod two-echelon multicommodity capacitated plant location problem. European Journal of Operational Research, vol. 123, Pág. 271-291.
- Yon-Chun Chou, Yao-Hung Chen, Hui-Min Chen, (2012). Recency-based storage assignment and warehouse configuration for recurrent demands, Computers & Industrial Engineering, Vol 62, Pág. 880-889.
Este trabajo está autorizado por una Licencia Attribution-NonCommercial-NoDerivs CC BY-NC-ND.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.







2.jpg)










