DOI:
https://doi.org/10.14483/23448393.18127Publicado:
2022-01-04Número:
Vol. 27 Núm. 1 (2022): Enero-AbrilSección:
Ingeniería Eléctrica y ElectrónicaEstudio de desempeño de distintos perfiles de álabe de una turbina eólica para aprovechar vientos de baja velocidad
Performance Study of Different Blade Profiles of a Wind Turbine to Harness Low-Speed Winds
Palabras clave:
álabe, baja velocidad, CFD, energía eólica, turbina Savonius (es).Palabras clave:
blade, CFD, low speed, Savonius turbine, wind power (en).Descargas
Referencias
Ali M Abdelsalam, MA Kotb, Khaled Yousef, and IM Sakr. Performance study on a modified hybrid wind turbine with twisted Savonius blades. Energy Conversion and Management, 241, 2021. https://doi.org/10.1016/j.enconman.2021.114317 DOI: https://doi.org/10.1016/j.enconman.2021.114317
JP Abraham, GS Mowry, BP Plourde, EM Sparrow, and WJ Minkowycz. Numerical simulation of fluid flow around a vertical-axis turbine. Journal of Renewable and Sustainable Energy, 3(3), 2011. https://doi.org/10.1063/1.3588037 DOI: https://doi.org/10.1063/1.3588037
Joao Vicente Akwa, Gilmar Alves da Silva Júnior, and Adriane Prisco Petry. Discussion on the verification of the overlap ratio influence on performance coefficients of a Savonius wind rotor using computational fluid dynamics. Renewable Energy, 38(1): 141-149, 2012. https://doi.org/10.1016/j.renene.2011.07.013 DOI: https://doi.org/10.1016/j.renene.2011.07.013
Hussain H Al-Kayiem, Bilawal A Bhayo, and Mohsen Assadi. Comparative critique on the design parameters and their effect on the performance of S-rotors. Renewable Energy, 99:1306-1317, 2016. https://doi.org/10.1016/j.renene.2016.07.015. DOI: https://doi.org/10.1016/j.renene.2016.07.015
Nur Alom. Influence of curtain plates on the aerodynamic performance of an elliptical bladed Savonius rotor (S-rotor). Energy Systems, pages 1-16, 2021. https://doi.org/10.1007/s12667-021-00428-w. DOI: https://doi.org/10.1007/s12667-021-00428-w
Nur Alom, Bastav Borah, and Ujjwal K Saha. An insight into the drag and lift characteristics of modified Bach and Benesh profiles of Savonius rotor. Energy Procedia, 144:50-56, 2018. https://doi.org/10.1016/j.egypro.2018.06.007. DOI: https://doi.org/10.1016/j.egypro.2018.06.007
Nur Alom and Ujjwal K Saha. Arriving at the optimum overlap ratio for an elliptical-bladed Savonius rotor. In Turbo Expo: Power for Land, Sea, and Air, volume 50961, page V009T49A012. American Society of Mechanical Engineers, 2017. https://doi.org/10.1115/GT2017-64137 DOI: https://doi.org/10.1115/GT2017-64137
Nur Alom and Ujjwal K Saha. Influence of blade profiles on Savonius rotor performance: Numerical simulation and experimental validation. Energy Conversion and Management, 186:267-277, 2019. https://doi.org/10.1016/j.enconman.2019.02.058 DOI: https://doi.org/10.1016/j.enconman.2019.02.058
Bengt Andersson, Ronnie Andersson, Love Haakansson, Mikael Mortensen, Rahman Sudiyo, and Berend Van Wachem. Computational Fluid Dynamics for Engineers. Cambridge University Press, 2011. DOI: https://doi.org/10.1017/CBO9781139093590
Alvin H Benesh. Wind turbine with Savonius-type rotor, 1996. US Patent 5,494,407.
Muhammad Mahmood Aslam Bhutta, Nasir Hayat, Ahmed Uzair Farooq, Zain Ali, Sh Rehan Jamil, and Zahid Hussain. Vertical axis wind turbine - A review of various configurations and design techniques. Renewable and Sustainable Energy Reviews, 16(4): 1926-1939, 2012. https://doi.org/10.1016/j.rser.2011.12.004 DOI: https://doi.org/10.1016/j.rser.2011.12.004
YA Cengel and JM Cimbala. Fluid Mechanics: Fundamentals and Applications. McGraw-Hill Education, 2018.
Liu Chen, Jian Chen, and Zhouzhou Zhang. Review of the Savonius rotor’s blade profile and its performance. Journal of Renewable and Sustainable Energy, 10(1), 2018. https://doi.org/10.1063/1.5012024 DOI: https://doi.org/10.1063/1.5012024
Joachim Toftegaard Hansen, Mahak Mahak, and Iakovos Tzanakis. Numerical modelling and optimization of vertical axis wind turbine pairs: A scale up approach. Renewable Energy, 171:1371-1381, 2021. https://doi.org/10.1016/j.renene.2021.03.001 DOI: https://doi.org/10.1016/j.renene.2021.03.001
Pramod Jain. Wind Energy Engineering. McGraw-Hill, 2011.
Emeel Kerikous and Dominique Thévenin. Optimal shape of thick blades for a hydraulic Savonius turbine. Renewable Energy, 134:629-638, 2019. https://doi.org/10.1016/j.renene.2018.11.037 DOI: https://doi.org/10.1016/j.renene.2018.11.037
Anuj Kumar and RP Saini. Performance parameters of Savonius type hydrokinetic turbine - A review. Renewable and Sustainable Energy Reviews, 64:289-310, 2016. https://doi.org/10.1016/j.rser.2016.06.005. DOI: https://doi.org/10.1016/j.rser.2016.06.005
Ivo Marinić-Kragić, Damir Vučina, and Zoran Milas. Numerical workflow for 3D shape optimization and synthesis of vertical-axis wind turbines for specified operating regimes. Renewable Energy, 115:113-127, 2018. https://doi.org/10.1016/j.renene.2017.08.030 DOI: https://doi.org/10.1016/j.renene.2017.08.030
Sathyajith Mathew. Wind Energy: Fundamentals, Resource Analysis and Economics. Springer, 2006.
John W Mitchell. Fox and McDonald’s Introduction to Fluid Mechanics. John Wiley & Sons, 2020.
Amin A Mohammed, Hassen M Ouakad, Ahmet Z Sahin, and Haitham Bahaidarah. Vertical axis wind turbine aerodynamics: Summary and review of momentum models. Journal of Energy Resources Technology, 141(5), 2019. https://doi.org/10.1115/1.4042643 DOI: https://doi.org/10.1115/1.4042643
MH Pranta, MS Rabbi, and MM Roshid. A computational study on the aerodynamic performance of modified Savonius wind turbine. Results in Engineering, 10, 2021. https://doi.org/10.1016/j.rineng.2021.100237 DOI: https://doi.org/10.1016/j.rineng.2021.100237
Hamid R Rahai and H Hefazi. Development of optimum design configuration and performance for vertical axis wind turbine. Feasibility Analysis Report, 2005.
Hamid R Rahai and Hamid Hefazi. Vertical axis wind turbine with optimized blade profile, 2008. US Patent 7,393,177.
AFP Ribeiro, AM Awruch, and HM Gomes. An airfoil optimization technique for wind turbines. Applied Mathematical Modelling, 36(10):4898-4907, 2012. https://doi.org/10.1016/j.apm.2011.12.026 DOI: https://doi.org/10.1016/j.apm.2011.12.026
Sukanta Roy, Prasenjit Mukherjee, and Ujjwal K Saha. Aerodynamic performance evaluation of a novel Savonius-style wind turbine under an oriented jet. In Gas Turbine India Conference. American Society of Mechanical Engineers, 2014. https://doi.org/10.1115/GTINDIA2014- 8152.
Sukanta Roy and Ujjwal K Saha. Numerical investigation to assess an optimal blade profile for the drag based vertical axis wind turbine. In ASME International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, 2013. https://doi.org/10.1115/IMECE2013-64001 DOI: https://doi.org/10.1115/IMECE2013-64001
S. J. Savonius. Vertical axis wind turbine, 1929. US Patent 1,697,574.
Sigard J Savonius. The S-rotor and its applications. Mechanical Engineering, 53(5):333-338, 1931.
Shikha, TS Bhatti, and DP Kothari. Early development of modern vertical and horizontal axis wind turbines: A review. Wind Engineering, 29(3): 287-299, 2005. https://doi.org/10.1260/030952405774354859 DOI: https://doi.org/10.1260/030952405774354859
Henk Kaarle Versteeg and Weeratunge Malalasekera. An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Pearson Education, 2007.
Lu Wang and Ronald W Yeung. On the performance of a micro-scale Bach-type turbine as predicted by discrete-vortex simulations. Applied Energy, 183:823-836, 2016. https://doi.org/10.1016/j.apenergy.2016.08.185 DOI: https://doi.org/10.1016/j.apenergy.2016.08.185
M Niyat Zadeh, M Pourfallah, S Safari Sabet, M Gholinia, S Mouloodi, and A Taheri Ahangar. Performance assessment and optimization of a helical Savonius wind turbine by modifying the Bach’s section. SN Applied Sciences, 3(8), 2021. https://doi.org/10.1007/s42452-021- 04731-0 DOI: https://doi.org/10.1007/s42452-021-04731-0
Baoshou Zhang, Baowei Song, Zhaoyong Mao, and Wenlong Tian. A novel wake energy reuse method to optimize the layout for Savoniustype vertical axis wind turbines. Energy, 121:341-355, 2017. https://doi.org/10.1016/j.energy.2017.01.004 DOI: https://doi.org/10.1016/j.energy.2017.01.004
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 10 de junio de 2021; Aceptado: 17 de septiembre de 2021
Resumen
Contexto:
Las turbinas eólicas de eje vertical, y en particular las turbinas de arrastre tipo Savonius, áventajan a los otros tipos de turbinas en aplicaciones que comprenden vientos erráticos y de baja velocidad. Si bien su eficiencia esta entre las más bajas, esto puede verse compensado con sus bajos costos, lo que las convierte en una alternativa sostenible y atractiva para este tipo de aplicaciones. En esta investigación se busca seleccionar la geometría de mayor rendimiento para el alabe de una turbina eólica tipo Savonius.
Método:
Para ello, se analizan numéricamente diversas configuraciones geométricas empleadas en este tipo de turbinas, las cuales fueron consultadas en la literatura. Todos los modelos de perfil son estudiados bajo los mismos parámetros y modelos de dinámica de fluidos computacional a través del software ANSYS Fluent.
Resultados:
A través de las simulaciones computacionales se estiman las condiciones de optimo rendimiento de cada una de las geometrías. Dichas condiciones permiten comparar, bajo los mismos términos, el desempeño de los perfiles e identificar los de mayor rendimiento. Se determina que el perfil semicircular convencional y el conocido como Bach modificado presentan coeficientes de potencia de 0,287 y 0,395 respectivamente, lo que representa un aumento en su rendimiento del 37,8 %.
Conclusiones:
Este resultado superior motiva a un análisis detallado del perfil Bach modificado qué permita encontrar las proporciones geométricas óptimas para su desempeño aerodinámico.
Palabras clave:
alabe, baja velocidad, CFD, energía eólica, turbina Savonius..Abstract
Context:
Vertical-axis wind turbines, and Savonius-type turbines in particular, outstrip other types of turbines in applications that include erratic and low-speed winds. Although their efficiency is among the lowest, this can be compensated by their low cost, turning them into a sustainable alternative which is also appealing for this type of applications. This research seeks to select the highest-performance geometry for the blade of a Savonius-type wind turbine.
Method:
To this effect, various geometric configurations used in this type of turbines, which were consulted in the literature, are numerically analyzed. All the profile models are studied under the same computational fluid dynamics parameters and models through the ANSYS Fluent software.
Results:
Through computational simulations, the optimal performance conditions of each of the geometries are estimated. These conditions allow comparing the performance of the profiles under the same terms, as well as identifying the ones with the highest performance. It is determined that the conventional semicircular profile and the one known as the modified Bach have power coefficients of 0,287 and 0,395, respectively, which represents a performance increase of 37,8 %.
Conclusions:
These superior results motivate a detailed analysis of the modified Bach profile which allows finding the optimal geometric proportions for its aerodynamic performance.
Keywords:
blade, CFD, low speed, Savonius turbine, wind power..Introducción
Los vientos erráticos y de baja velocidad suelen presentarse con mayor frecuencia, por lo que, a pesar de su menor densidad energética, el desarrollo de dispositivos que aprovechen efectivamente su potencial toma cada vez más valor debido al continuo aumento en la demanda energética y la ausencia de otros recursos energéticos en muchos sitios 1, (2.
Gracias a su funcionamiento omnidireccional, las turbinas eólicas de eje vertical son capaces de aprovechar vientos que varían frecuentemente su dirección sin requerir sistemas adicionales de alineación. Generalmente pueden representar menores costos en construcción, operación y mantenimiento, y de esta manera logran conseguir una mayor relación entre beneficio y costo 1 - (4. Asimismo, en los últimos a no se ha evidenciado que las turbinas eólicas de eje vertical pueden operar a menor distancia entre rotores que las turbinas eólicas de eje horizontal, lo que permite disponer un mayor número de turbinas en una misma área de emplazamiento 1, 5.
Aunque ofrecen múltiples prestaciones, las turbinas eólicas de eje vertical también presentan considerables limitaciones. La más conocida de ellas es la alta variabilidad en el torque según la posición angular del rotor, debido al continuo cambio de alineación entre el alabe y la dirección del flujo durante el movimiento de la turbina 2, 6.
De acuerdo al principio de operación de la turbina, también se presentan algunas particularidades. La turbina de sustentación o tipo Darrieus llama la atención por su eficiencia superior entre las turbinas de eje vertical, logrando actualmente valores cercanos al 75 % de los obtenidos a partir de las turbinas de eje horizontal. Sin embargo, requiere mayor velocidad de flujo para iniciar su movimiento, lo que limita su uso a emplazamientos con vientos de mayor categoría y en muchos casos exige dispositivos de arranque (4, 6 - (8. Por otro lado, la turbina de arrastre o tipo Savonius presenta bondades en el arranque a velocidades bajas de flujo pero su eficiencia apenas alcanza valores cercanos al 50 % del rendimiento de las turbinas de eje horizontal 9 - (12. Pese a ello, los beneficios de la omnidireccionalidad y la capacidad de autoarranque combinados en un mismo dispositivo pueden hacer viable el aprovechamiento de vientos erraticos y aquellos cuyo contenido energ ético no es tan elevado. én esta investigacion se pretende estudiar num éricamente la geometr ía del alabe de una turbina éolica de tipo arrastre que permita aprovechar vientos de baja velocidad, vinculando en la mejor medida la eficiencia energetica con las prestaciones que caracterizan esta turbina. Para ello, se propone evaluar mediante la simulacion de un viento de baja categor ía el desempeno de diversos ˜ modelos de turbinas de este tipo consultados en la literatura, permitiendo así reconocer las geometrías que presentan el mayor rendimiento bajo tales condiciones y seleccionar finalmente la masádecuada. Estudios similares han sido llevados a cabo, uno de los mas representativos es la inves- tigacion realizada por Alom y Saha 13, en la que evaluan la influencia del perfil de los álabes én el rendimiento del rotor Savonius. Sin embargo, los rotores son probados a una velocidad de viento de 6, 2 m/s, la cual corresponde a un viento de mayor categoría. Adicionalmente, aunque los autores manifiestan que las geometrías analizadas son de gran rendimiento, no se consideran todas las configuraciones que son de interes en el presente trabajo.
Materiales y metodos
Detalles geométricos de los perfiles de alabe
En la Figura 1 se muestran las geometrías de diferentes perfiles de alabe que serán objeto de estudio en la presente investigación. Estos modelos son seleccionados ya que reportan altos rendimientos en sus respectivos estudios realizados por otros autores. Se toman algunas parejas que corresponden a la versión básica y la versión mejorada de diversos modelos, con el fin de evidenciar la mejora en su rendimiento luego de su modificación.
Se consideran el perfil semicircular convencional y el perfil semicircular dividido con una relación de traslape de 1/6 14 - 16. También es considerado el perfil tipo Bach básico y un perfil desarrollado a partir de este, denominado perfil de Bach modificado 13, 17 - (19. El perfil elíptico y su versión modificada también son analizados 20, 21. Por último, son considerados los perfiles patentados por Benesh;22, 23 y Rahai 24, (25. Todas las geometrías están acotadas por un diámetro constante de 200 mm (D) y construidas considerando un espesor de pared de 1 mm.
Figura 1: Configuración de los diferentes perfiles de prueba
Especificación del análisis numérico
Los estudios tridimensionales pueden presentar mejores resultados que los estudios bidimensionales al considerar el flujo por encima y por debajo de la turbina. Sin embargo, los estudios bidimensionales pueden capturar las propiedades de flujo con gran precisión si la relación de aspecto de la turbina (altura/diámetro) es mayor o igual a la unidad 26.
En este estudio se analizan las geometrías bajo modelos bidimensionales y en régimen transitorio. Se propone el modelo de turbulencia k − ω SST por su buen desempeño en la predicción de flujos libres y de gradientes de presión adversos 27 - (30. Todas las geometrías son analizadas bajo iguales algoritmos, parámetros y modelos de la dinámica de fluidos computacional (CFD por su sigla en inglés) a través del solucionador de volúmenes finitos ANSYS Fluent 19.2.
Similar al estudio realizado por Alom y Saha del mismo tipo de turbina 20, el dominio del análisis consiste en dos partes divididas por una interfaz deslizante: una región circular rotativa y una región rectangular estacionaria (Figura 2). La región circular contiene el perfil estudiado y gira de manera constante a la velocidad establecida para cada simulación.
Figura 2: Dominio de análisis y condiciones de frontera
Se fija una entrada de aire a una velocidad de 4 m/s (viento de clase 1) 31, correspondiente a un régimen de flujo con un n umero Reynolds de 6 × 104 . De igual manera, se establece una salida a condiciones atmosféricas y el campo lateral se simula bajo condiciones de simetría, ya que allí se presentan gradientes de baja escala 30, 32 (Figura 2).
El desempeño de cada modelo es evaluado en términos de los coeficientes de torque y de potencia en función de la relación de velocidad en la punta del alabe (T SR por su sigla en inglés). El coeficiente de torque (CT) se estima como la relación entre el torque generado por la turbina en su éje (T) y el torque que es posible generar en las condiciones dadas (ecuación (1) 33.

Donde ρ es la densidad del aire, v es la velocidad del viento en flujo libre y A = DH es el área transversal de la turbina, siendo H la altura de la misma (unitaria en análisis bidimensionales).De manera similar, el coeficiente de potencia (CP ) es la relación entre la potencia generada por la turbina y el flujo energético transportado por el fluido (ecuación (2)); donde ω es la velocidad angular de la turbina (33;.

Teniendo en cuenta que la T SR se expresa como se muestra en la ecuación (3), la ecuación (2) puede reescribirse como la ecuación (4) 33.


El extraer la energía cinética del viento en su totalidad implica el estancamiento del aire y por lo tanto la inexistencia de un flujo del cual tomar energía. Esto lleva a la idea de un límite máximo en la energía que puede ser captada. Este valor es conocido como el límite de Betz y es el principal referente para la medición del rendimiento de un dispositivo aerogenerador, ya que representa una base cuantificable de la energía disponible 31. Dicho límite se encuentra descrito en la ecuación (5).

De esta manera, la eficiencia de una turbina eólica puede ser expresada como la proporción entre el CP propio del dispositivo y el valor numérico de dicho límite, tal como se muestra en la ecuación (6).

Cada modelo se hace rotar a diferentes velocidades con el propósito de construir las curvas de desempeño de cada uno de ellos. Estas velocidades se establecen en valores enteros entre ˜ 1 y 10 rps(revoluciones por segundo), con los que se calcula las T SR correspondientes mediante la ecuación (3).
De las simulaciones se toma como resultado el CT generado en el eje del rotor en función de su posición acimutal ( θ). Cada simulación se lleva a cabo para 15 revoluciones completas del rotor buscando conseguir un estado cuasi-estable; sin embargo, solo se tienen en cuenta los valores de las últimas dos revoluciones para estimar el CT promedio, ya que estos corresponden a los resultados con mayor estabilidad temporal (Figura 3).
Figura 3: Resultados obtenidos a través de la simulación del rotor con el perfil semicircular a una velocidad de rotación de 5 rps (T SR = 0, 7854)
De esta manera se obtiene un único valor que representa el CT en todas las posiciones angulares del rotor. Este valor de CT promedio permite determinar el valor promedio del CP a través de la ecuación (4), para cada velocidad de rotación Figura 4 3, 34.
Figura 4: Curvas de desempeño del rotor con el perfil semicircular (los valores corresponden a los coeficientes promedio)
Seguidamente, se ajusta un polinomio interpolador de segundo grado entre los tres puntos consecutivos que describen el pico de mayor rendimiento en la curva de CP de cada rotor (ecuación (7)) y se calcula el valor en que su derivada se hace cero, ya que este punto de pendiente nula corresponde al de máximo desempeño (ecuación (8)) (Figura 5).
Figura 5: Polinomios de interpolación ajustados a los picos de las curvas de rendimiento para cada modelo de rotor


Análisis de independencia de discretización
Para obtener el número de particiones en las que se dividió la geometría de análisis de cada simulación y el periodo que se simulo, fue necesario realizar un análisis de independencia para las discretizaciones espacial y temporal, buscando obtener una convergencia en el resultado de manera eficiente.
El análisis de independencia para la discretización espacial se realiza bajo las mismas condiciones con las que se estudian las geometrías en cuestión. Se establece el rotor semicircular como el modelo de prueba y se hace rotar a una velocidad de 5 revoluciones por segundo. Se analizan cinco discretizaciones espaciales (mallados) con la misma estructura, pero con un crecimiento binomial en el número de particiones de cada borde de acuerdo al grado de refinamiento de cada malla. El cuerpo estático que simula el fluido en campo lejano tiene una malla estructurada con elementos únicamente cuadriláteros, mientras que el cuerpo móvil que simula el campo cercano al rotor posee una malla no estructurada con elementos cuadriláteros predominantes y algunos triangulares para conseguir una mayor adaptabilidad a la geometría (Figura 6 izquierda). El mallado referente a las paredes del rotor esta refinado y posee una estructuración por capas perpendiculares (inflación) que permiten una mejor predicción del flujo en las condiciones de capa límite (Figura 6 derecha).
Figura 6: Estructura general de los mallados (izquierda). Detalle del mallado cerca a las paredes del perfil (derecha)
Los resultados obtenidos en este análisis para cada mallado describen el comportamiento del CT de acuerdo al acimut del rotor (Figura 7). Al estimar el valor promedio del CT para cada malla, se observa que su desviación es mínima al ser comparado con el valor correspondiente de la malla más fina, indicando que existe convergencia en el resultado (Tabla I).
Figura 7: Coeficiente de torque (CT ) según acimut (θ) para cada mallado
Tabla I: Resultados de la prueba de independencia de mallado

Otro parámetro importante para la selección de la malla es el valor de y +, el cual se recomienda inferior a la unidad al utilizar el modelo de turbulencia k − ω SST, así se garantizan predicciones adecuadas en el flujo cercano a las paredes 30. De acuerdo a lo anterior, se selecciona el cuarto mallado y se procede con el análisis de independencia temporal.
El análisis de independencia para la discretización temporal se realiza bajo las mismas condiciones y para la misma geometría que el análisis de independencia de mallado. Se toman cinco discretizaciones de tiempo generadas al dividir el periodo de revolución del rotor en un número de elementos o pasos de tiempo (time step). Similar al análisis de independencia de mallado, los resultados obtenidos en este análisis para cada discretización describen el comportamiento del CT de acuerdo al Angulo de acimut del rotor (Figura 8). Luego de estimar el valor promedio del CT para cada discretización temporal, se observa que su desviación va disminuyendo a medida que la partición se hace m as fina, acercándose cada vez m as a un valor de convergencia (Tabla II). Se determina entonces una discretización de 720 pasos temporales por revolución, que representa una relación adecuada entre el error admisible y el tiempo de simulación.
Figura 8: Coeficiente de torque (CT ) según acimut (θ) para cada paso temporal
Tabla II: Resultados de la prueba de independencia temporal. ts/rev corresponde a time step por revolución

Resultados
Análisis de resultados
Al estimar el punto de optimo desempeño de cada modelo de rotor, se identifican los parámetros que se muestran en la Tabla III. La eficiencia de cada perfil se obtiene al relacionar el CP con el límite de Betz a través de la ecuación (6) (6
Tabla III: Condiciones óptimas de desempeño para las geometrías analizadas

Estos parámetros permiten obtener una comparación más objetiva del desempeño de las geometrías, al ser estimados bajo iguales términos y condiciones. En la Figura 9 se puede apreciar gráficamente la magnitud de cada parámetro de acuerdo a la geometría. Similarmente, en la Figura 10 se detalla la eficiencia obtenida por cada modelo de rotor. Se puede apreciar que las geometrías que presentan un perfil dividido pueden conseguir un mejor rendimiento a mayores velocidades de rotación, lo que puede verse reflejado en el aumento del CP máximo. Los perfiles Bach modificado y el óptico dividido presentan el mayor rendimiento, y lo consiguen en valores de T SR superiores a la unidad. Al comparar el perfil semicircular convencional y el perfil Bach modificado en función de su Angulo acimutal (Figura 11), se puede apreciar que el desempeño del segundo rotor es siempre superior al del primero, consiguiendo la mayor diferencia de rendimiento en la alineación de mayor oposición al flujo, es decir a un ángulo de 0° de acuerdo con el sistema de referencia tomado. Esto indica que la mayor ventaja del segundo perfil sobre el primero se encuentra en la optimización de las fuerzas de arrastre.
Figura 9: Gráfico comparativo de las condiciones óptimas de desempeño para las geometrías analizadas
Figura 10: Eficiencia máxima de cada geometría con respecto al límite de Betz
Figura 11: Diferencia entre el coeficiente de torque (CT) del perfil semicircular convencional y el Bach modificado, a una T SR de 1,0996
Del mismo modo, puede observarse en la misma Figura que la posición acimutal de mayor generación de torque para ambos rotores es cercana a 110°, la cual corresponde a una alineación de baja oposición al flujo y por ende de bajo arrastre. Esto evidencia el significativo aporte de la fuerza de sustentación en el desempeño de estos rotores.
Se evidencia que la menor ventaja en el desempeño entre los dos rotores se presenta en las posiciones cercanas a los 50°, las cuales corresponden a las de mayor solapamiento (sombra) entre los alabes de un mismo rotor.
Contornos de presión y velocidad
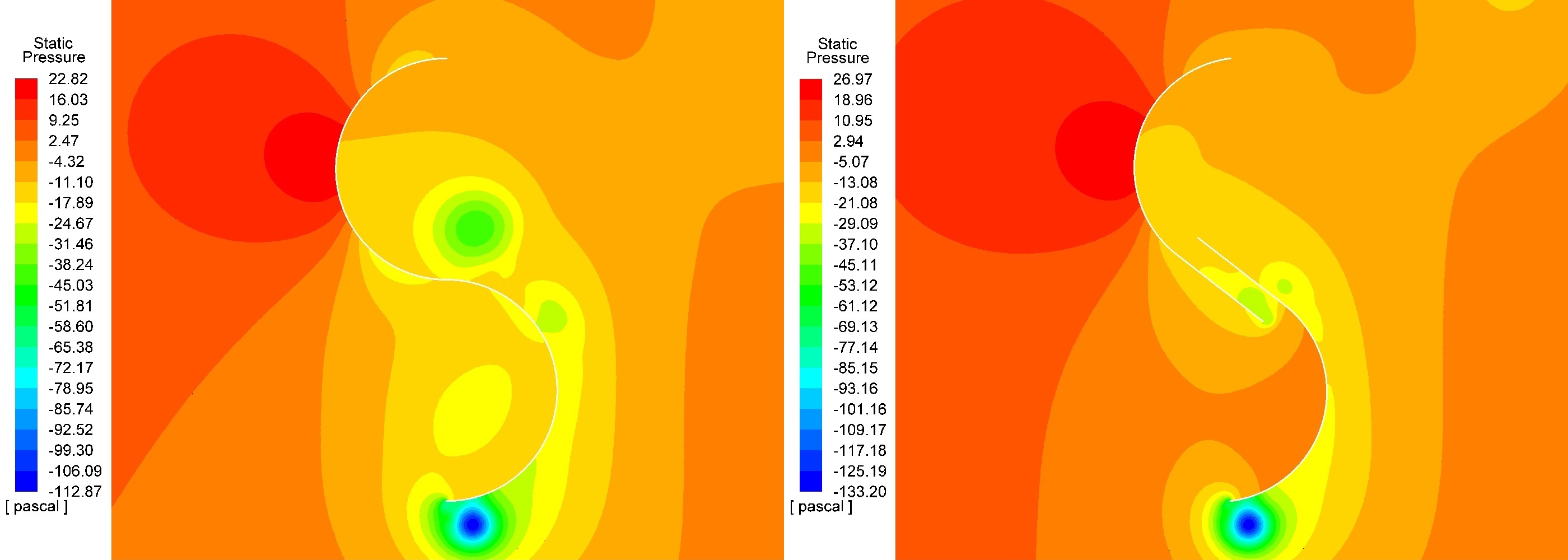
Al comparar los gráficos de contornos de presión de la Figura 12, puede evidenciarse que la presión en el lado cóncavo del alabe que avanza es superior para el perfil dividido (perfil Bach modificado) que para el perfil integral (perfil semicircular convencional). Esto se debe a que el flujo existente a través de la abertura generada por la división del perfil (Figura 13) evita la despresurización temprana de dicha región, y de manera consecuente aumenta el momento producido en el eje del rotor, reflejándose en un rendimiento superior y en la posibilidad de girar a una mayor velocidad. Por otro lado, puede observarse una mayor velocidad y turbulencia en el flujo desprendido de la punta del alabe del perfil dividido (Figura 13), lo que demuestra un mayor contenido energético en el fluido adyacente a la superficie. Esta energía es proveniente en su mayoría del flujo a través de la abertura y evita la separación temprana de la capa límite de fluido, lo que para bajos números de Reynolds puede representar una disminución en la resistencia por arrastre 12, 18.
Figura 12: Contornos de presión para el perfil semicircular convencional (izquierda) y el perfil Bach modificado (derecha) a una T SR de 1,0996
Figura 13: Contornos de velocidad para el perfil semicircular convencional (izquierda) y el perfil Bach modificado (derecha) a una T SR de 1,0996
Conclusiones
En la presente investigación se ha estudiado de forma numérica el efecto de la geometría del alabe en el rendimiento de una turbina eólica de arrastre. Las simulaciones se llevaron a cabo para los perfiles semicircular convencional, semicircular dividido, Bach, Bach modificado, elíptico, elíptico dividido, Benesh y Rahai. El perfil Bach modificado presento el mejor desempeño entre las geometrías evaluadas, con un CP máximo de 0,395 a una T SR de 1,2 y a un régimen de flujo correspondiente a un viento de baja categoría (con un numero Reynolds de 6×104 ), lo que representa una eficiencia de 66,6 % con referencia al límite de Betz y un aumento del 37,8 % con respecto al desempeño del perfil semicircular convencional. Las condiciones de máximo desempeño para el perfil Bach modificado, entre algunos otros perfiles, se encuentran en relaciones de velocidad de punta (T SR) superiores a la unidad, esto permite determinar que algunas geometrías favorecen en mayor medida la existencia de fuerzas distintas al arrastre aerodinámico para la producción del torque, en este caso, la fuerza de sustentación. Esto abre las puertas a un análisis en detalle del perfil Bach modificado, que permita encontrar las proporciones geométricas óptimas para su desempeño, estimar el aporte de los coeficientes aerodinámicos en la obtención del CT y evaluar el efecto que tiene un alabe sobre el otro en un mismo rotor. Si bien el objetivo del estudio es seleccionar un perfil para aprovechar vientos de baja velocidad, es necesario evaluar en futuros trabajos el comportamiento del perfil seleccionado a velocidades de viento superiores, con el fin de predecir su desempeño en tales condiciones y compararlo con las turbinas eólicas convencionales de eje horizontal.
Acknowledgements
Agradecimientos
Los autores agradecen al Programa Colombia científica como fuente de financiación, en el marco de las convocatorias Ecosistema científico [Contrato No. FP44842-218-2018]
Referencias
Licencia
Derechos de autor 2022 Luis Antonio Gallo Jaramillo, Edwin Lenin Chica Arrieta, Elkin Gregorio Flórez Serrano

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.

















2.jpg)