DOI:
https://doi.org/10.14483/23448393.18482Published:
2022-01-04Issue:
Vol. 26 No. 3 (2021): September - DecemberSection:
Sección Especial: Mejores artículos extendidos - WEA 2021Proposal of a Dynamic Algorithm for the Maintenance and Vehicle Routing Problem with Time Windows
Propuesta de un algoritmo dinámico para el problema de mantenimiento y ruteo de vehículos con ventanas de tiempo
Keywords:
mantenimiento, algoritmo dinámico, ruteo de vehículos, eficiencia computacional (es).Keywords:
maintenance, dynamic algorithm, vehicle routing, computational efficiency (en).Downloads
References
O. Mack, A. Khare, A. Krämer, and T. Burgartz, Managing in a VUCA world, New York, NY, USA: Springer, 2015. https://doi.org/10.1007/978-3-319-16889-0 DOI: https://doi.org/10.1007/978-3-319-16889-0
E. López-Santana, R. Akhavan-Tabatabaei, L. Dieulle, N. Labadie, and A. L. Medaglia, “On the combined maintenance and routing optimization problem,” Reliab. Eng. Syst. Saf., vol. 145, pp. 199-214, Jan. 2016. https://doi.org/10.1016/j.ress.2015.09.016 DOI: https://doi.org/10.1016/j.ress.2015.09.016
J. A. Andrawus, J. Watson, and M. Kishk, “Wind Turbine Maintenance Optimisation: Principles of Quantitative Maintenance Optimisation,” Wind Eng., vol. 31, no. 2, pp. 101-110, Mar. 2007, https://doi.org/10.1260/030952407781494467 DOI: https://doi.org/10.1260/030952407781494467
N. M. de Souza and A. T. de Almeida Filho, “A systematic airport runway maintenance and inspection policy based on a delay time modeling approach,” Autom. Constr., vol. 110, 103039, Feb. 2020, https://doi.org/10.1016/j.autcon.2019.103039 DOI: https://doi.org/10.1016/j.autcon.2019.103039
R. Dekker, “Applications of maintenance optimization models: A review and analysis,” Reliab. Eng. Syst. Saf., vol. 51, no. 3, pp. 229-240, Mar. 1996. https://doi.org/10.1016/0951-8320(95)00076-3 DOI: https://doi.org/10.1016/0951-8320(95)00076-3
N. Zhang, M. Fouladirad, and A. Barros, “Maintenance of a two dependent component system: a case study,” IFAC-PapersOnLine, vol. 49, no. 12, pp. 793-798, Jan. 2016. https://doi.org/10.1016/j.ifacol.2016.07.871 DOI: https://doi.org/10.1016/j.ifacol.2016.07.871
R. Baldacci, A. Mingozzi, and R. Roberti, “New route relaxation and pricing strategies for the vehicle routing problem,” Oper. Res., vol. 59, no. 5, pp. 1269-1283, Oct. 2011. https://doi.org/10.1287/opre.1110.0975 DOI: https://doi.org/10.1287/opre.1110.0975
G. Desaulniers, “Branch-and-price-and-cut for the split-delivery vehicle routing problem with time windows,” Oper. Res., vol. 58, no. 1, pp. 179-192, Sep. 2010. https://doi.org/10.1287/opre.1090.0713 DOI: https://doi.org/10.1287/opre.1090.0713
R. Fukasawa et al., “Robust branch-and-cut-and-price for the capacitated vehicle routing problem,” Math. Program., vol 106, pp. 491-506, Oct. 2006. https://doi.org/10.1007/s10107-005-0644-x DOI: https://doi.org/10.1007/s10107-005-0644-x
B. Afshar-Nadjafi and A. Afshar-Nadjafi, “A constructive heuristic for time-dependent multi-depot vehicle routing problem with time-windows and heterogeneous fleet,” J. King Saud Univ. - Eng. Sci., vol 29, no. 1, pp. 29-34, Jan. 2017. https://doi.org/10.1016/j.jksues.2014.04.007 DOI: https://doi.org/10.1016/j.jksues.2014.04.007
T. Vidal, T. G. Crainic, M. Gendreau, and C. Prins, “Heuristics for multi-attribute vehicle routing problems: A survey and synthesis,” Eur. J. Oper. Res., vol. 23, no. 1, pp. 1-21., Nov. 2013. https://doi.org/10.1016/j.ejor.2013.02.053 DOI: https://doi.org/10.1016/j.ejor.2013.02.053
N. Azi, M. Gendreau, and J. Y. Potvin, “An exact algorithm for a vehicle routing problem with time windows and multiple use of vehicles,” Eur. J. Oper. Res., vol. 202, no. 3, 756-763, May 2010. https://doi.org/10.1016/j.ejor.2009.06.034 DOI: https://doi.org/10.1016/j.ejor.2009.06.034
J. E. Fontecha, O. O. Guaje, D. Duque, R. Akhavan-Tabatabaei, J. P. Rodríguez, and A. L. Medaglia, “Combined maintenance and routing optimization for large-scale sewage cleaning,” Ann. Oper. Res., vol. 286, no. 1-2, pp. 441-474, Aug. 2020. https://doi.org/10.1007/s10479-019-03342-8 DOI: https://doi.org/10.1007/s10479-019-03342-8
S. K. Goyal and A. Gunasekaran, “Determining economic maintenance frequency of a transport fleet,” Int. J. Syst. Sci., vol. 23, no. 4, pp. 655-659, Apr. 1992. https://doi.org/10.1080/00207729208949239 DOI: https://doi.org/10.1080/00207729208949239
J. Y. Huang and M. J. Yao, “On the coordination of maintenance scheduling for transportation fleets of many branches of a logistic service provider,” Comput. Math. with Appl., vol. 56, no. 5, pp. 1303 1313, Sept. 2008. https://doi.org/10.1016/j.camwa.2008.01.037 DOI: https://doi.org/10.1016/j.camwa.2008.01.037
F. Blakeley, B. Bozkaya, B. Cao, W. Hall, and J. Knolmajer, “Optimizing periodic maintenance operations for Schindler Elevator Corporation,” Interfaces (Providence)., vol. 33, no. 1, pp. 67-79, Feb. 2003. https://doi.org/10.1287/inte.33.1.67.12722 DOI: https://doi.org/10.1287/inte.33.1.67.12722
K. Bouvard, S. Artus, C. Bérenguer, and V. Cocquempot, “Condition-based dynamic maintenance operations planning & grouping. Application to commercial heavy vehicles,”rel. Eng. Sys. Saf., vol. 96, no. 6, pp. 601-610, Jun. 2011. https://doi.org/10.1016/j.ress.2010.11.009 DOI: https://doi.org/10.1016/j.ress.2010.11.009
C. A. Irawan, D. Ouelhadj, D. Jones, M. Stålhane, and I. B. Sperstad, “Optimisation of maintenance routing and scheduling for offshore wind farms,” Eur. J. Oper. Res., vol. 256, no. 1, pp. 76-89, Jan. 2017. https://doi.org/10.1016/j.ejor.2016.05.059 DOI: https://doi.org/10.1016/j.ejor.2016.05.059
A. Troudi, S. Dellagi, and S. A. Addouche, “An optimal maintenance policy for transport| vehicles in a supply chain under infrastructure/environment constraints,” in 45th Int. Conf. Comp. Ind. Eng., Metz, France, Oct. 28-30, 2015, 207.
J. E. Fontecha, R. Akhavan-Tabatabaei, D. Duque, A. L. Medaglia, M. N. Torres, and J. P. Rodríguez, “On the preventive management of sediment-related sewer blockages: A combined maintenance and routing optimization approach,” Water Sci. Technol., vol. 74, no. 2, pp. 302-308, mar. 2016. https://doi.org/10.2166/wst.2016.160 DOI: https://doi.org/10.2166/wst.2016.160
Y. Chen, P. Cowling, F. Polack, S. Remde, and P. Mourdjis, “Dynamic optimisation of preventative and corrective maintenance schedules for a large scale urban drainage system,” Eur. J. Oper. Res., vol. 257, no. 2, pp 494-510, Mar. 2017. https://doi.org/10.1016/j.ejor.2016.07.027 DOI: https://doi.org/10.1016/j.ejor.2016.07.027
E. Zamorano and R. Stolletz, “Branch-and-price approaches for the Multiperiod Technician Routing and Scheduling Problem,” Eur. J. Oper. Res., vol. 257, no. 1, pp. 55-68, Feb. 2017. https://doi.org/10.1016/j.ejor.2016.06.058 DOI: https://doi.org/10.1016/j.ejor.2016.06.058
M. M. Solomon, “Algorithms for the Vehicle Routing and Scheduling Problems With Time Window Constraints.,” Oper. Res., vol. 35, no. 2, pp. 254-265, Apr. 1987. https://doi.org/10.1287/opre.35.2.254 DOI: https://doi.org/10.1287/opre.35.2.254
B. Meindl and M. Templ, “Analysis of commercial and free and open source solvers for linear optimization problems,” ESSnet commom tools Harmon. Methodol. SDC ESS, vol. 1, no. 1, pp. 1-14, Feb. 2012. http://www.statistik.tuwien.ac.at/forschung/CS/CS-2012-1complete.pdf
J. Jablonský, “Benchmarks for Current Linear and Mixed Integer Optimization Solvers,” Acta Univ. Agric. Silvic. Mendelianae Brun., vol. 63, no. 6, pp. 1923-1928, Dec. 2016. https://doi.org/10.11118/201563061923 DOI: https://doi.org/10.11118/actaun201563061923
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 15 de agosto de 2021; Revisión recibida: 27 de agosto de 2021; Aceptado: 15 de septiembre de 2021
Abstract
Context:
In the context of business organizations, every process in which the product is immersed has a cost and time associated with it. The area of maintenance planning and scheduling is no exception;however, it is an aspect in which few companies specialize, tending to be outsourced. In this sense, the application of combinatorial models is a tool with a high potential to improve the overall performance of the organization through the understanding of the integral maintenance process.
Method:
A two-phase (maintenance and routing) dynamic algorithm is proposed which considers a set of clients distributed in a maintenance network (distance), where each of the technicians start from the same central node (depot), which, in turn, is the endpoint of each assigned route. The objective is to minimize the total cost associated with the development of preventive and corrective maintenance of all machines to be evaluated.With this purpose, the formulation of the mathematical problem for each of the phases and its interrelation method is proposed. Then, performance measures are expressed to evaluate the achieved objectives.
Results:
The results satisfy a consistent alternative for the resolution of problems of the NP-Hard type,which generates a high level of complexity to the model. That is, it proposes a tool for solving problems of these characteristics in low computational response times and with appealing results.
Conclusions:
The combined maintenance and routing model using a dynamic algorithm addresses the maintenance and routing problem satisfactorily. The model shows good results with respect to the comparison optimization model in percentage gaps of performance measures lower than 5 %. As for the computational time required, a reduction of up to 98% was achieved, which makes it an ideal alternative for highly complex scenarios. Finally, achieving a higher level of characterization, employing multiobjective decision criteria and a greater number of constraints to the problem, is proposed in future research.
Keywords:
maintenance, dynamic algorithm, vehicle routing, computational efficiency..Resumen
Contexto:
En el contexto de las organizaciones empresariales, todo proceso en el que está inmerso el producto conlleva un costo y un tiempo asociados. El área de planeación y programación de mantenimiento no es la excepción; sin embargo, es un aspecto en el cual pocas compañías se especializan,tendiendo a la tercerización. En este sentido, la aplicación de modelos combinatorios es una herramienta con un alto potencial de mejorar el desempeño global de la organización a través del entendimiento del proceso integral de mantenimiento.
Método:
Se plantea un algoritmo dinámico de dos fases (mantenimiento y ruteo) que considera un conjunto de clientes distribuidos en una red de mantenimiento (distancia) en el que cada uno de los técnicos parte del mismo nodo central (depósito), que a su vez es el punto final de cada ruta asignada. El objetivo consiste en minimizar el costo total asociado al desarrollo del mantenimiento tanto preventivo como correctivo de todas las máquinas a evaluar. Con esta finalidad se plantea la formulación del problema matemático para cada una de las fases y su método de interrelación. Después se expresan medidas de desempeño para evaluar los objetivos alcanzados.
Resultados:
Los resultados satisfacen una alternativa consistente para la resolución de problemas del tipo NP-Hard que genera un alto nivel de complejidad al modelo. Es decir, plantea una herramienta para resolución de problemas de estas características en tiempos de respuesta computacional reducidos y con resultados atractivos.
Conclusiones:
El modelo de mantenimiento y ruteo combinado usando un algoritmo dinámico permite abordar el problema de mantenimiento y ruteo de manera satisfactoria. El modelo presenta buenos resultados frente al modelo de optimización de comparación en brechas porcentuales de medidas de desempeño inferiores al 5 %. Respecto al tiempo computacional requerido, se logró una reducción de hasta el 98 %, lo cual lo convierte en una alternativa ideal para escenarios de gran complejidad. Finalmente,se propone en futuras investigaciones alcanzar un mayor nivel de caracterización por medio de criterios de decisión multiobjetivo y un mayor número de restricciones al problema.
Palabras clave:
mantenimiento, algoritmo dinámico, ruteo de vehículos, eficiencia computacional..Introduction
In the context of large organizations in the 21st century, market dynamics and the volatility of operating conditions generate such a level of uncertainty that it is pertinent to manage it through solutions that enable agile and consistent decision-making. In this sense, business organizations have begun to use the definition of VUCA (volatility, uncertainty, complexity, ambiguity) environments to respond to the challenges posed by competitiveness in different sectors [1].
Growing market challenges lead industries to turn to mathematical modeling and other tools that enable them to effectively manage organizational resources, as well as to meet customer requirements,in other words, solutions that are relevant from both a cost (financial) and niche market (commercial) capture and conversion perspectives.
From this approach, the proposed solution arises for the vehicle routing problem with soft periodic time windows (VRPSPTW) or vehicle routing problem with soft multiple time Windows (VRPSMTW). This approach responds to a two-phase iterative method for the processes of replacement, maintenance, and scheduling of customer visits. The above, through the use of integer linear programming (MILP) and the presentation of a dynamic algorithm as a research extension to the work proposed by [2], which provides shorter response times and a similar level of efficiency in the comparison between both models.
This paper focuses on the combinatorial model of maintenance and routing with time windows (CMR). The paper is organized as follows: section 2 details the literature review; section 3 proposes the two-phase mathematical model; section 4 shows the comparison results with a literature model;and section 5 presents the conclusions in detail.
Literature review
Within the reviewed works, an extensive compendium of authors detailing models and approaches to maintenance models was found [3] - [6]. The scenario against vehicle routing models (VRP), in a general understanding and through extensions such as time windows (VRPTW), is described repeatedly by different authors [7]-[9]. For more complex cases, some researchers have proposed solutions from constructive heuristics [10], [11], up to hybrid methods that combine modeling to a metaheuristic character [12].
Regardless of the above, it should be clarified that the integration of routing problems with maintenance is limited, and very little work has been done on this line of development [13].
Given this combinatorial scenario, [14] postulates a mathematical model that defines the transportation fleet scheduling problem (TFMSP), which consists of determining the frequency of maintenancefor the vehicles of a specific company. In [15], an extension model of the TFMSP is proposed for a service provider that performs logistics processes by branches, demonstrating that there are significant savings based on the coordination of maintenance between branches. For the first time in the new decade, [16] proposes applicability to the problem of assigning technicians who are responsible for a set of elevators and escalators that are geographically distributed throughout a shopping mall. With [17], an optimal methodology for the maintenance of a heavy vehicle is developed while considering a whole multi-component system.
Recently, [2] conducted a two-phase scheduling model that addresses the scenario of machines that require maintenance planning but are geographically distributed. This model contemplates two mutually recurring phases, which consist of a model of both corrective and preventive maintenance during a given planning horizon, defining maintenance time windows for each visit.
An optimization model for maintenance routing and scheduling is proposed for the applied case of an offshore wind farm. It is determined according to the maintenance operations and the optimal transfer vessel routes in association with the number of technicians who carry out the maintenance [18]. Similarly, a preventive maintenance policy has been generated for the vehicles to be delivered by the client or set of clients according to the distance traveled and other external variables [19].
However, in some sectors of the sewerage systems industry, only a few authors have carried out research on the subject [20]. Among the contributions that should be mentioned is [21], which deals with the problem related to the maintenance of gully pots in the United Kingdom. This solution consists of simulating the schedule generated through routes that minimize the traveled distance, a difference compared to other models that focus on the economic aspect, just like [2] in its process of applicability to the oil and gas industry.
Finally, routing and scheduling models for technicians have been postulated. In this case, it is assumed that they are qualified in various skills to carry out equipment assignments concerning scheduled maintenance operations [22].
In conclusion, significant progress has been made in this type of combinatorial problem, where the need to unify maintenance and routing in a single general problem is perceived. In detail, most of the contributions are based on a set of parameterized input data that allow simplifying the problem down to a VRPTW level only.
Proposed mathematical model
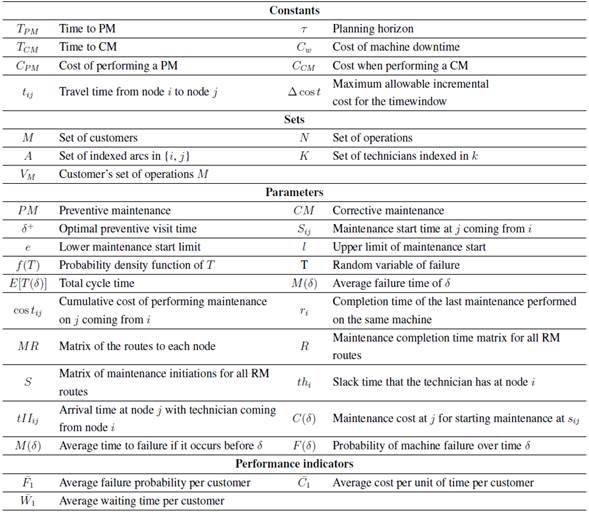
The expected failure time in the maintenance process has a probabilistic behavior, which makes the problem stochastic. This implies an iterative, recurrent, and complex problem when it comes to defining the maintenance routine under feasible time windows. In this research, a two-stage combinatorial algorithm is proposed for its solution: in its first stage, the optimal start time and the cost per unit of maintenance time are mainly obtained, information that is later used in the second stage to perform the routing of the technicians who perform maintenance for the customers within the planning horizon. Once the visits to the customers have been assigned in the second stage, the input information of the first stage is complemented by obtaining the waiting time if the breakdown occurs, so that the maintenance and routing cycle is performed iteratively by defining a stop criterion for its completion. The variables used in the proposed model for the solution of the combinatorial problem are detailed in Table I below.
Table I: Model variables
Phase I
This phase corresponds to the maintenance model, which needs an input information of the failure behavior of the machines and their related costs. The objective is to find the optimal maintenance start time that generates the lowest cost per unit time, as well as the time windows for each of the customers [2]
In this phase, the cumulative probability of failure before _ is found, using the failure probability function that characterizes the customer’s machine, which is expressed in Equation (1). This cumulative probability allows calculating the maintenance cycle, be it preventive or corrective, through Equation (2), as well as the cost per unit of time to perform the maintenance in _ via Equation (3),using the average time to failure in Equation (4) and the average waiting time of a CM in Equation (5). The second phase needs the __ information that minimizes the cost function curve, C(_), and allows finding the time window, fe; lg, which is obtained as the maintenance start times that increase the cost in units, _cos t. Finally, the maintenance model is run in the same way for each of the customers, thus obtaining all the equations of cos t, optimal start time, and time windows.
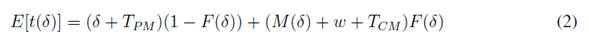
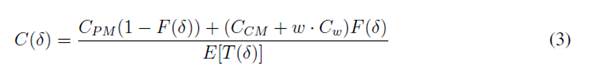


Fig. 1 shows an example of the maintenance cycles and their linkage to cost per unit time. The first cycle shown is preventive maintenance, and it is identified by starting maintenance at time __without a failure in the machine. It then minimizes the maintenance cost curve per unit of time.Preventive maintenance ends at time __ + TPM. The next cycle is corrective maintenance, and it is identified at the occurrence of the failure in time X prior to __, according to the expected failure time. w units of time from failure to the start of maintenance _ are expected. Corrective maintenance ends at time __ +TPM +M(_)+w+TCM. Finally, the last cycle details the time window obtained for the customer with the maximum allowable increase, _cos t.
Figure 1: Example of a machine maintenance cycle
Phase II
This phase corresponds to the routing of technicians to perform maintenance according to the information obtained in phase I and the initial data of the clients. The available technicians are scheduled to attend in the time windows while considering the transport times between customers.The output of this phase provides the average waiting time, the probability of failure, and the total cost per unit of time for each of the customers, as well as the assignment of technicians to the visits and the maintenance start times, sj . The idea of routing is to minimize the total cost per unit time for performing the maintenance assigned to a technician.
The routing problem consists of K technicians andM customers, with 1 or more visits within the planning horizon. For its solution, a dynamic algorithm is proposed, which performs the routing of the technicians jointly, assigning the visit, i, of the customers to the technician, k, and giving the necessary information for the next customer visit within the planning horizon. The dynamic algorithm starts from dispatch to the return of each technician. Stage t consists of the arcs, Aij , where j represents the node with the closest maintenance start that can be performed in its time window by any of the technicians, who are assigned to perform maintenance at nodes i.
For each technician at i, the arrival time, tllij , is calculated through Equation (6) and compared to the optimal start time, __j . If this tllij occurs before the maintenance start, __j , the optimal start time is assigned to sij , which is expressed in Equation (7). Otherwise, the deviation adjustment is performed to generate the lowest cost overrun by finding the one sij that minimizes the cost function at i and j by means of Equation (8). The deviation adjustment obtains the lowest total cost by starting maintenance earlier at i, delaying the start of maintenance by x units of time, bounded by the minimum between the slack time, thi, of node i, which is expressed in Equation (9), and the difference between tllij and __j . If the slack adjustment was made to the technician chosen to perform maintenance at j, it is necessary to update the values of si; ri+n; thi, and cos ti. Once all the sij are obtained, the cos tij are calculated with Equation (10), and the Aij with the lowest cumulative cost is chosen.
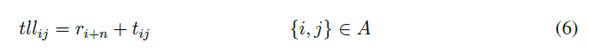
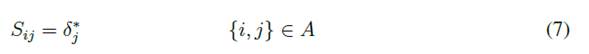



With the information from node j, the maintenance completion time rj+n in Equation (11) and the slack time, thj , are calculated through Equation (9). The next visit of customer j +n is added if the technician can return to the office after performing maintenance within the planning horizon by assigning in __j+n in Equation (12) and its time window [ej+n; lj+n]. To start stage t+1, the unassigned visit with the nearest __ is selected and designated as node j, which represents technicians that can perform maintenance at j without exceeding lj , as expressed by Equation (13). The dynamic algorithm terminates when there are no unassigned visits in the planning horizon and the return to dispatch is added for each of the technicians.
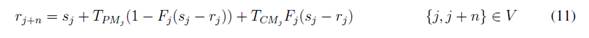

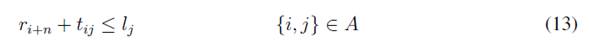
The pseudocode 1 of the two-phase model for the solution of customer maintenance and routing is described below.
Algorithm 1: Maintenance and routing model with time windows
Experimentation
A comparison was made with the model proposed in [2] by using a replica, verifying the performance measures and the computational time required for its solution. In this comparison, the random instances of the model were used, which are an extension of those defined in [23], thus extending the planning horizon to 200 time units.
Comparison of models
For the comparison, a total of 900 tests were performed, which were divided homogeneously among 9 sets of clients, where, for each test, the same initial data were evaluated on the proposed model and on the replica of the comparison model. The evaluation of the two models was performed on a computer provided by the Centro para Computación de Alto Desempeño (Center for High-Performance Computing, CECAD) of Universidad Distrital with 16 CPU processors and 32 GB of RAM, running on the Ubuntu 20.04.1 LTS 64-bit operating system, where a program in the MATLAB language was made, and GUROBI was used for its great performance solving MILPtype problems and its integration with MATLAB [24], [25].
These results were averaged across each of the client sets, where a trend in the behavior of the performance measures and computational time was found. This is shown in Table II.
Table II: Average performance measures of the 100 runs for the clients sets

The results show the same behavior among the sets of customers; the use of the dynamic algorithm for the routing solution in the combinatorial problem of maintenance and routing does not present a considerable decrease in the performance measures, where the cost per unit of time is 0,731% higher, the average waiting time is 4,417% higher, and the probability of failure is 1,087% higher.
Comparison of computational time
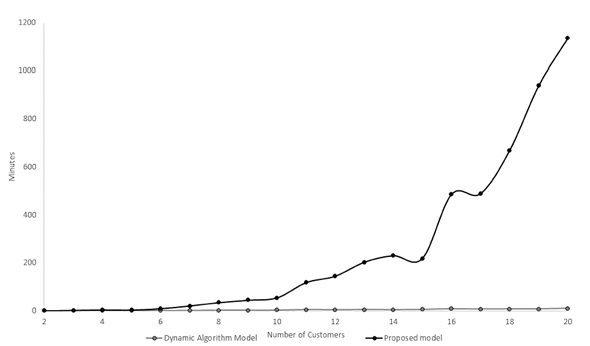
The computational time comparison required 1.700 tests distributed among 19 sets of clients,using the previously specified instances and the MATLAB Profile function. A limit of 20 clients was reached in the comparison model for computational requirements. These results were plotted and are shown in Fig. 2.
The average computational time required by the proposed model shows a linear behavior as the number of clients increases, with the highest average computational time of 10,4 minutes in the set of 20 clients. The highest average computational time of 1.135,5 minutes for the set of 20 clients.
Figure 2: Average computational processing time: time required by the comparison model and the proposed model for the 1.700 results
Proposed model performance
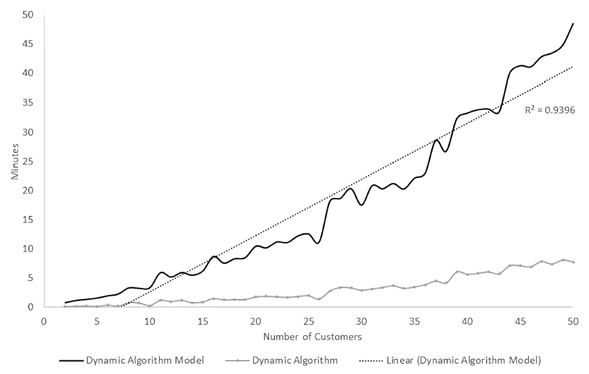
Tests were performed on the proposed model to verify its behavior with sets of up to 50 customers.At least 25 tests were performed on the previously described computer for each set in order to characterize its behavior, the results of which are detailed in Fig. 3.
Figure 3: Average computational processing time of the comparison model and the proposed model for the 1.700 results and up to 50 customers
Fig. 3 shows the average computational time of the model with the full dynamic algorithm and the second phase separately. As it can be seen by its trend line, this model and its second phase present a linear behavior.
Case study
A comparison was made with the case study in the oil and gas industry proposed in [2], where daily operations involve the management of a network of interconnected pumping stations geographically distributed over a region. The stations are subject to unforeseen failures that result in an impact on times. The company has a maintenance department that serves multiple plants (with several pumping stations] scattered over a wide geographical area covering several cities.
The data provided in the case study correspond to the travel time between nodes, the costs and times for performing preventive or corrective maintenance, the _cos t parameter, and the probability of failure function associated with the node. The results obtained from the comparison between the proposed model and the one for comparison are shown in Table III.
Table III: Results of the case study with the comparison between the models

The computational time consumed by the models shows the same behavior previously described for the set of 10 clients. The proposed model obtained a time of 6,814 seconds against 169,41 seconds for the solution of the comparison model.
Conclusions
The combined maintenance and routing model using the dynamic algorithm helped address the CMR problem, where, during first phase, the maintenance model provides information about customer visits, and, in its second phase, it performs the assignment of those visits to the available technicians.
The proposed model shows good results compared to the optimization model presented in [2]; the total costs per unit time and waiting time do not exceed 1 and 5 %, respectively, and the probability of failure only increases by 1% in total. These results demonstrate the feasibility of the proposed model.
The comparison of the computational time between the models demonstrates the resource and time requirements of the optimization model when using a linear MILP approach. The proposed model showed a decrease from 53,56% with few customers to 98,08% with 20 customers, in addition to the few computational resources required for its solution. These results evidence decrease in the complexity of the problem with good results in terms of performance indicators.
Running the proposed two-phase model characterizes the linearity in terms of computational times,even with instances of large number of clients. The model is feasible for the execution of complex problems with a large number of customers, visits, or a long planning horizon. The case study demonstrates its feasibility in real systems, finding similar performance measures, but a computational time of only 4 %.
Future research could apply a multi-objective function in the second phase of the model, different decision-making to choose the best technician assigned to a visit and extensions of the problem with working days, and multiple dispatches of technicians, among others.
Acknowledgements
Acknowledgments: To the High-Performance Computing Center (CECAD - Centro de computación de Alto Desempeño) of Universidad Distrital Francisco José de Caldas for their support, as well as for providing us with a virtual machine to run the proposed mathematical model, which was an essential element in the results obtained.
References
License
Copyright (c) 2022 Carlos Andrés López Ayala, Wilson Jurado Valbuena, Eduyn Ramiro Lopez Santana

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.






2.jpg)










