DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.2.a09Published:
2016-05-26Issue:
Vol. 21 No. 2 (2016): May - AugustSection:
Special Section: Best Extended Articles - WEA 2015A Hybrid Mixed-Integer Optimization and Clustering Approach to Selective Collection Services Problem of Domestic Solid Waste
Un Enfoque Híbrido de Agrupamiento y Optimización Entera Mixta para el Problema de Servicios de Recolección Selectiva de Residuos Sólidos Domésticos
Keywords:
clustering, optimization model, routing, scheduling, waste collection (en).Keywords:
clúster, modelo de optimización, ruteo, programación de tareas, recolección de residuos (es).Downloads
References
T. P. B. Brandão Vecchi, L. M. de Matos Jorge, M. A. da Silva Sá Ravagnani, and P. R. Paraíso, “Optimization of planning routes in solid waste collection,” Journal of Chemistry and Chemical Engineering, vol. 8, no. 6, pp. 596–601, Jun. 2014.
R. S. Xavier, A. C. Lisboa, D. A. G. Vieira, and R. R. Saldanha, “Heuristica para modelagem e minimização do consumo de combustível para rotas de coleta de lixo,” Bento Gonçalves, 2010, p. 12.
B.-I. Kim, S. Kim, and S. Sahoo, “Waste collection vehicle routing problem with time windows,” Computers & Operations Research, vol. 33, no. 12, pp. 3624–3642, Dec. 2006.
T. Y. Afonso LLorente, “Optimización de rutas de recogida de residuos en zonas mixtas urbana-rurales y orografía singular,” Trabajo de Fin de Grado, Universidad de la laguna, La Laguna, 2014.
R. K. Pati, P. Vrat, and P. Kumar, “A goal programming model for paper recycling system,” Omega, vol. 36, no. 3, pp. 405–417, Jun. 2008.
F. Beijoco, V. Semiao, and Z. Zsidgraiová, “Optimization of a municipal solid waste collection and transportation system,” Lisboa, Portugal, 2011.
S. Simón, J. Demaldé, J. Hernández, and M. Carnero, “Optimización de Recorridos para la Recolección de Residuos Infeccio-sos,” Información tecnológica, vol. 23, no. 4, pp. 125–132, 2012.
A. Méndez, S. Simón, D. Palumbo, E. Chiachera, and M. Carnero, “Dos Enfoques para la Solución del Problema de Ruteo De Vehículos (CVRP): Aplicación a un Caso Real de Recolección de Residuos,” Mecánica Computacional, vol. XXIX, pp. 9367–9377, Nov. 2010.
Y. T. Chen, F. T. S. Chan, S. H. Chung, and B. Niu, “Closed-Loop Supply Chain Network Optimization For Hong Kong Cartridge Recycling Industry,” Hong Kong Polytechnic University, Department of Industrial and Systems Engineering, Hong Kong, 2013.
D. Aksen, O. Kaya, F. S. Salman, and Y. Akça, “Selective and periodic inventory routing problem for waste vegetable oil collection,” Optim Lett, vol. 6, no. 6, pp. 1063–1080, Jan. 2012.
J. Beliën, L. De Boeck, and J. Van Ackere, “Municipal Solid Waste Collection and Management Problems: A Literature Re-view,” Transportation Science, vol. 48, no. 1, pp. 78–102, Nov. 2012.
K. Buhrkal, A. Larsen, and S. Ropke, “The Waste Collection Vehicle Routing Problem with Time Windows in a City Logistics Context,” Procedia - Social and Behavioral Sciences, vol. 39, pp. 241–254, 2012.
T. Bianchi-Aguiar, M. A. Carravilla, and J. F. Oliveira, “Vehicle routing for mixed solid waste collection - comparing alterna-tive hierarchical formulations,” Strathprints Institutional Repository, p. 137, 2011.
R. J. A. Fortunato, “Problema de determinação de circuitos de recolha de resíduos sólidos urbanos da Câmara Municipal de Oeiras,” Maestria, Universidade de Lisboa. Instituto Superior de Economia e Gestão., Lisboa, Portugal, 2014.
L. Bardales, “Heurística para la colecta de residuos domiciliarios en la ciudad de Trujillo basado en el ruteo de vehículos con ventana de tiempo,” Universidad Nacional de Trujillo, Trujillo, Perú, Informe de Trabajo de Graduación 3, Dec. 2013.
A. M. Benjamin and J. E. Beasley, “Metaheuristics for the waste collection vehicle routing problem with time windows, driver rest period and multiple disposal facilities,” Computers & Operations Research, vol. 37, no. 12, pp. 2270–2280, Dec. 2010.
I. Markov, S. Varone, and M. Bierlaire, “Vehicle routing for a complex waste collection problem,” presented at the 14th Swiss Transport Research Conference (STRC), 2014.
E. A. V. Toso and D. Alem, “Effective location models for sorting recyclables in public management,” European Journal of Operational Research, vol. 234, no. 3, pp. 839–860, May 2014.
S. Fooladi, H. Fazlollahtabar, and I. Mahdavi, “Waste Collection Vehicle Routing Problem Considering Similarity Pattern of Trashcan,” International Journal of Applied Operational Research - An Open Access Journal, vol. 3, no. 3, pp. 0–0, Jun. 2013.
F. Samanlioglu, “A multi-objective mathematical model for the industrial hazardous waste location-routing problem,” Euro-pean Journal of Operational Research, vol. 226, no. 2, pp. 332–340, Apr. 2013.
C. S. Fatih Rahim, “A location-routing problem in glass recycling,” Annals of Operations Research, vol. 223, no. 1, pp. 329–353, 2014.
E. D. Antmann, X. Shi, N. Celik, and Y. Dai, “Continuous-discrete simulation-based decision making framework for solid waste management and recycling programs,” Computers & Industrial Engineering, vol. 65, no. 3, pp. 438–454, Jul. 2013.
L. B. R. Medina, E. C. G. L. Rotta, and J. A. O. Castro, “Una Revisión al Estado del Arte del Problema de Ruteo de Vehículos: Evolución Histórica Y Métodos De Solución,” Ingeniería, vol. 16, no. 2, pp. 35–55, Dec. 2011.
S. Pirkwieser and G. R. Raidl, “A column generation approach for the periodic vehicle routing problem with time windows,” in International network optimization conference, Pisa, Italia, 2009, vol. 2009.
F. Baniel, “Prise en compte d’objectifs de stabilité pour l’organisation de collectes de déchets,” Doctorat, Université de Toulouse, 2009.
R. A. J. Pirabán, “Métodos Aproximados para la Solución del Problema de Enrutamiento de Vehículos (Dic 2008).” Univer-sidad Nacional de Colombia, Dec-2018.
Y. X. Daza Cruz, J. A. Patiño Chirva, and E. R. López-Santana, “A mixed integer optimization model to design a selective collection routing problem for domestic solid waste,” in 2015 Workshop on Engineering Applications - International Con-gress on Engineering (WEA), 2015, pp. 1–5.
JICA and UAESP, “Proyecto de Estudio del Plan Maestro para el manejo Integral de Residuos sólidos en Bogotá, D.C.,” Uni-dad Administrativa Especial de Servicios Públicos, Bogotá, Colombia, 3, Nov. 2013.
Corte Constitucional, Auto 275 de 2011. 2011, p. 190.
UAESP, “Esquema de Metas a Cumplir para la Inclusión de la Población Recicladora en la gestión pública de los residuos sólidos en la ciudad de Bogotá D.C.,” Secretaría del Hábitat, Bogotá, Colombia, 2011.
K. Shin and S. Han, “A Centroid-based Heuristic Algorithm for the Capacitated Vehicle Routing Problem,” Computing and Informatics, vol. 30, no. 4, pp. 721–732, Jan. 2012.
E. R. López-Santana and J. de J. Romero Carvajal, “A hybrid column generation and clustering approach to the school bus routing problem with time windows,” Ingeniería, vol. 20, no. 1, pp. 111–127, Mar. 2015.
A. Olivera, “Heurísticas para Problemas de Ruteo de vehículos,” Universidad de la República de Montevideo, Uruguay, Reporte técnico serie 04 - 08, Aug. 2004.
S. Ropke, “Heuristic and exact algorithms for vehicle routing problems,” Doctorate, University of Copenhagen, Copenhagen, 2005.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
A Hybrid Mixed-Integer Optimization and Clustering Approach to Selective Collection Services Problem of Domestic SolidWaste
Un Enfoque Híbrido de Agrupamiento y Optimización Entera Mixta para el Problema de Servicios de Recoleccion Selectiva de Residuos Sólidos Domésticos
Johana Andrea Patiño Chirva
Universidad Distrital Francisco José de Caldas- Facultad de Ingeniería. japatinoc@correo.udistrital.edu.co
Yesica Xiomara Daza Cruz
Universidad Distrital Francisco José de Caldas- Facultad de Ingeniería. yxdazac@correo.udistrital.edu.co
Eduyn Ramiro López-Santana
Universidad Distrital Francisco José de Caldas- Facultad de Ingeniería. erlopezs@udistrital.edu.co
Received: 06-11-2015. Modified:01-03-2016. Accepted: 05-04-2016.
Abstract
Context: Waste generation is causing profound negative impacts on our natural environment. Because of that, processes related to waste collection, transportation, transformation and final disposal have increased its importance and major efficiencies are is desirable. We propose a Mixed Integer Programming model and clustering approach for waste collection and transportation process.
Method: An optimization model, inspired on Bogotá context is proposed, to maximize the amount of waste collected, considering real-life aspects of this activity in the city. For large instances in which there is a big computational cost, we proposed an alternative solution of two stages, firstly a clustering step and then a routing step.
Results: In small instances of up to 1453 collection sites grouped in 13 blocks and 51 corners, the model result in an overall collection covering of 100%. For large instances, there are variations between the results of each clustering method. The results suggests that the sweep algorithm is better to clustering the collection sites.
Conclusions: Our proposed model is able to find a solution the waste collection problem in Bogota case considering the vehicle capacity, maximum workday duration and the planning horizon of two days according with the collection process in Bogota. We test three clustering methods in order to group the collection sites and to reduce the complexity of the problem, and then we solve the model using a commercial solver. For the small instances, our model run very fast but in the large in-stances the computational time was increased. Future work will focus in the validation and search of solution methods improving the performance with the proposed model.
Keywords: clustering, optimization model, routing, scheduling, waste collection services.
Acknowledgements: We thank Fair Isaac Corporation (FICO) for providing us with Xpress-MP licenses under the Academic Partner Program and Centro de Investigaciones y Desarrollo Científico at Universidad Distrital Francisco José de Caldas (Colombia) by supporting partially under Grant No. 2-602-468-14. Last, but not least, the authors would like to thank the comments of the anonymous referees that significantly improved our paper. Language: English.
Resumen
Contexto: La generación de residuos está causando profundos y negativos impactos en nuestro ambiente. Por esto, procesos relacionados con la recolección, el transporte, la transformación y la disposición final de residuos han ganado importancia y se propende a su eficiencia. Un modelo de programación entera mixta y de agrupación es propuesto para los procesos de recolección y transporte de residuos.
Método: Se propone un modelo de optimización, inspirado en el contexto de Bogotá, cuyo objetivo es maximizar la cantidad de residuos recolectados teniendo en cuenta las características reales de esta actividad en la ciudad. Para instancias grandes en las que el costo computacional es muy alto, se proponen una alternativa de solución de dos etapas, clusterizar primero y rutear después.
Resultados: En pequeñas instancias de hasta 1453 puntos de recolección agrupados en 13 bloques y 51 esquinas, nuestro modelo logró el cubrimiento total de la recolección. Para grandes instancias, existen variaciones entre los resultados de cada método de agrupación.
Conclusiones: Nuestro modelo propuesto es capaz de encontrar una solución al problema de recolección de residuos en caso de Bogotá considerando la capacidad de los vehículos, la duración máxima de una jornada de trabajo y el horizonte de planificación de dos días de acuerdo con el proceso de recolección de Bogotá. Probamos tres métodos de agrupación para agrupar los sitios de recolecci ón y para reducir la complejidad del problema, y luego se resuelve el modelo usando un paquete comercial. Para instancias pequeñas, nuestro modelo es rápido, pero en grandes instancias se aumenta el tiempo de cálculo. Los trabajos futuros se centrarán en la búsqueda y validación de métodos con el propósito de encontrar aquel que tenga un mejor desempeño con el modelo propuesto.
Palabras clave: clúster, modelo de optimización, ruteo, programación de tareas, recolección de residuos.
Agradecimientos: A Fair Isaac Corporation (FICO) por proveernos la licencia de Xpress-MP y al Centro de Investigaciones y Desarrollo Científico de la Universidad Distrital Francisco José de Caldas (Colombia) por soportar este trabajo parcialmente bajo el proyecto No. 2-602-468-14. Por último, pero no menos importante, damos las gracias a los comentarios de los evaluadores anónimos que han ayudado a mejorar significativamente nuestro documento
1. Introduction
The transformation of cities and the increased of urban population have had several environmental impacts, one of them concern directly with consumption habits, talking about the waste generation and the practices around its last disposition. In this context, the government of Bogotá has done some programs in order to give better destination for waste. These programs not only involve environmental aspects but also there is a social point which is taking into account, the roll of waste pickers. The purpose is to have better practices for waste final disposal by its separation at source and also the participation of recyclers in its returning into the productive cycle. To make this possible waste pickers are being organized into legal organization with better conditions than they had before.
In the progress of recycler inclusion, there is a concern that has been considered, the fact that they have not any technical criterion in the selection of the route that they usually do, so it cannot be guaranteed 100% of recyclable solid waste return which is one of the principal objectives of Bogotá management programs. For this reason, we propose an optimization model inspired on Bogotá context to maximize the amount of waste recollected, considering the real features of this activity in the city.
Waste management includes the process of collection, transport, processing, recycling and final disposition. Within this process there have been taking into consideration several factors like environment, society, legislation, economic, technology and politic in order to have a framework to make decisions such as the opening of recycling centers, final disposition, acquisition of trucks and the development of efficient routes, among others.
Problems of waste collection have been studied for general materials as solid waste [1], urban solid waste [2], commercial waste [3], rural solid waste cite4, and specific materials such as paper [5], glass [6], industrial waste [7], hazardous materials [8], cartridge [9] and vegetal oil [10]. The first publication about waste collection context was made in 1974 by Beltrami and Bodin who explored techniques to solve this kind of problem [11], since then numerous papers and investigations have been published. In the literature, there are different types of models that can be applied to solve this type of problem. In essence the collection of waste is a Vehicle Routing Problem (VRP) that consists in the assignment of routes to a set of vehicles to collect waste of the clients under certain constraints [12].
Among the type of models, there are: TSP (Travelling Salesman Problem) [13], CPP (Chinese Postman Problem) [14], CARP (Capacitated Arc Routing Problem) [14], PVRP (Periodic Vehicle Routing Problem) [13], VRPTW (Vehicle Routing Problem with Time Windows) [15], CVRP (Capacitated Vehicle Routing Problem) [7] [8], Day Assignment Problem, Vehicle Assignment Problem, Day and Vehicle Assignment Problem [13], Location - Routing [16], Closed-Loop Supply Chain [9], Multi-Depot Vehicle Routing Problem with Intermediate Facilities [17].
In terms of objective functions, the most common in the literature is the minimization of costs [7], minimize the total cost of shipping recyclables from zones to centers [18], minimizes the travel cost [19], minimize the operation costs [13], minimize the time and the distance [17], minimize the costs of the routes and the cost of the use of a vehicle [15], but there are also objectives such as: maximize the recuperation of waste at source [5], minimize the number of vehicles or resources to use [3], minimize distance [1],minimize the risk of materials transportation [20], minimize the time of the routes [14], maximize the waste collection [21], maximize social and environmental profits [22] and maximize the compactness of the route [3].
Although there are numerous types of models for routing in waste management systems, most of them are NPHard which implies that its solution cannot be reached in a polynomial time. Around combinatorial models like those mentioned before there have been done several works on methods that could reduce the computational time with acceptable solution [23].
Those methods can be classified as exact methods, heuristics and metaheuristics. For exact methods, there are application of Branch and Bound, Dynamic programming and Column generation [24]. The principal limitation of these methods is its non-polynomial computational times to find solution.
Heuristics and Metaheuristics have less computational time for solving the problem. Heuristics are specific algorithm for a problem; those try to find good solutions, not necessary the optimal one. The principal types of heuristics are: Construction heuristic, that sequentially or parallel inserts new customers into the solution; two phases heuristics, these can be Cluster first-Route second or Route first- Cluster second; and local search heuristics that from an initial solution try to improve it looking in a neighborhood of solutions [23]. The principal limitation of heuristic procedures is that the solution could be a local optimum instead of a solution close to the optimal one.
Metaheuristics have the capacity of avoid local optimums as they have better exploration in solutions space. These are generic procedures, based on analogies of nature and human process. Some of the most common types of metaheuristics are: simulated annealing, tabu search, variable neighborhood search, large neighborhood search, evolutionary algorithms and ant colonies [25], [26].
We propose a hybrid approach of mixed integer programming model and clustering to solve the selective collection service scheduling and routing problem of domestic and recyclable solid waste in the Bogotá"™s context. We remark that this is an extended version of a short paper recently published in the Workshop on Engineering Applications - WEA2015- that was held in Bogotá, September 2015 (see [27]). This paper is organized as follows: Section 2 shows the problem statement. In section 3, a MIP approach is stated. Section 4 presents the methods of solution of the model. Section 5 presents examples based on the in-formation of a work zone of two organizations in an area of Bogotá, one of them is solve by the implementation of three different cluster methods. Finally, section 6 establish some conclusions and future work lines.
2. Problem statement
The current solid waste management in Bogotá has into account three different programs: The Master Plan for Solid Waste Integral Management (PMIRS), Bogotá Zero Waste and the Inclusion Plan for informal recyclers [28]. The first one is the PMIRS, which was established in 2006 in order to have a global view of general waste management where territorial-environmental, social-productive and economic-financial aspects have been considered. From PMIRS there was made a pilot program in which macro-routes were implemented in order to pick recyclable waste. Those routes were the same as ordinary collection routes of the principal waste operators in the city. With this strategy, 37% of the population was covered. Despite having had this cover and having influenced the segregation waste habit of this population, there was no evidence of social inclusion [29] which was a constitutional mandate. With this premise, in 2012 the program Bogotá Zero Waste and the Inclusion Plan for informal recyclers were presented.
Bogotá Zero Waste has six principal subjects: sustainable production strategy, culture of reduction and separa-tion at source, recyclable model for Bogotá, final use and minimization of waste disposition in Doña Juana Landfill, zero debris and integral management of special and hazardous waste.
In the Inclusion Plan for informal recyclers, they have been organized into legal organizations called ORA (Organization of Authorized Recyclers), regulated by the Administrative Special Unit of Public Services (UAESP). The principal objective is to bring them better conditions so fundamental rights could be assure in order to reduce their level of vulnerability [30].
Each ORA has a number of partners who have the recycling labor in Bogotá. They make the collection following historical routes but they do not have any technical criterion in their normal itineraries so it cannot be guaranteed the maximization of recyclable waste collection.
In this context it is proposed an optimization model for de design of selective routes, based on some assumptions which are listed below:
• Based on the program Bogotá Zero Waste, people in the city made separation at source. In this separation, ordinary waste is disposed in black bag and the recyclable one in white bag.
• Collection is made just for recyclable solid waste generated by residential users.
• The waste volume will not exceed the vehicle volume capacity. The constraint is the weight capacity.
• Users dispose their waste just one time per day.
• Ordinary waste operators make their route every two days, when this happens they collect every kind of waste so selective collection will be limited by this situation in two days. There are two consequences causes by this event; first, if recyclers do not recollect waste they will not be able to do so, as the total amount is collected by waste operators. Second, as all residues are collected the next day there is not accumulation and blocks have not waste at the beginning of the day.
• The ORA has eight-hour workday according to national legislation.
• When vehicles enter the area of collection have full capacity is available.
3. MIP Approach
We propose a mixed integer programming model for the collection services of recyclable waste in the Bogotá's context. This is based on the Vehicle Routing Problem (VRP) which is a generalization of TSP proposed by Dantzig and Ramser in 1959 [23]. In addition, there were made some modifications according to the real features of waste collection system in a city. In the next four sections, we describe the index sets, parameters, decision variables and mathematical formulation of the model.
3.1. Index sets
The index set are described as follows:
• I : {I1; I2; I3; :::; Iα} Set of blocks indexed by i.
• J : {J0; J1; J2; J3; :::; JDeposit} Set of corners indexed by j.
• J' : {J1; J2; J3; :::; Jn} Set of corners indexed by j from users of the service.
• K : {K1;K2;K3; :::;Kσ} Set of vehicles indexed by k.
• T : {T1; T2} Set of days indexed by t.
• S : {S1; S2} Set of accumulation states indexed by s.
3.2. Parameters
The parameters are described as follows:
• Rjts: Potential recyclable waste, dispose at corner j in the day t, with an accumulation state s, js ∈ S.
• Ck: Capacity of the vehicle k, k ∈ K.
• vk: Speed of the vehicle k, k ∈ K.
• Tjs: Service time in corner j with an accumulation state s, j∈ J', s∈ S.
• dpq: Distance of the arc(p; q),(p; q) ∈ J.
• G: Hours of working day.
• N: Number of blocks including origin and depot.
• aij : 1 when the corner j belongs to the block i, 0 otherwise, i∈ I, j∈ J.
3.3. Decision variables
The decision variables are described as follows:
• Xpqkt: Take the value of 1 if an arc(p; q) is visit by the vehicle k in the day t and the value of 0 otherwise, p; q ∈ {p 6≠ q; k ∈ K; t ∈ T.
• wqkts: Take the value of 1 if waste in the corner q are recollected by the vehicle k, the day t with an accumulation state s and the value of 0 otherwise, q ∈ J; k ∈ K; t ∈ T; s ∈ S.
• ujkt: Auxiliary variable associated to the corner j visited by the vehicle k in the day t; j ∈ J; k ∈ K; t ∈ T.
3.4. Model
The mathematical formulation of our MIP model is described as follows:

The objective function (1) maximizes the amount of waste recollected. Constraints (2) establish that Blocks must be visited at least one time in two days. Constraints (3) limit visits per day to one. Constraints (4) are the balance flow. Constraints (5) and (6) force vehicles must start at origin, along one unique route, and finish at depot. Constrains (7) limit the workday hours according to national legislation. Constraints (8) put the maximum capacity of each vehicle. Constrains (9) eliminate sub tours. Constraints (10) ensure that when an arc is activated there is waste recollection in day one. Constraints (11), as well as equation (10), ensure recollection and also these do not allow double accumulation state in day two. Constraints (12) control the state of day one and day two to prevent accumulation in day two when collection have been done in day one. Constraints (13) show the relation between the Xpqkt arc variable and the recollection variable wqkts. Constraints (14) and (15) determine the nature of variables Xpqkt and wqkts as binary. Constraints (16) establish the non-negativity of variable ujkt.
4. Solution methods
To solve the model proposed in section 3.4, we proposed a method of cluster-first route-second in which capacity constraint of each vehicle assigned to a cluster must be respected. The strategy is to create clusters grouping blocks and then solve the proposed model. Moreover, there are applied three different methods of cluster. Its purpose is to evaluate which one brings better solutions.
4.1. A Centroid-based heuristic algorithm
This algorithm is based on the geometry of geometrical centers, around which the clusters are generated. This method is divided into two phases. In the first phase, clusters are constructed by selecting the farthest node from the origin, among the nodes that have not been assigned, and it is generated a first cluster; then the geometrical center of the cluster (17), in order to add the nodes closer to the GC, considering the defined capacity of each cluster [31], [32].
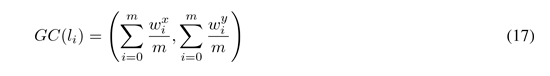
Where wxi and wyi are the coordinates in x, y of the nodes that belong to the cluster. Table I shows the pseudocode of the first phase. After of generating clusters, it is necessary to adjust them in a second phase, in Table II the process is shown.
4.2. Sweep algorithm
This heuristic gives shape to the cluster based on the geometry of polar coordinates. From an origin point, there is displayed a straight that rotates on the zone where nodes must be assigned. The area cover by this straight is a cluster only while capacity constraints are respected [33]. Table III
shows the pseudocode.
4.3. Proposed localization model
Another way to establish cluster is the application of localization models. Fisher and Jaikumar proposed a Gen-eralized Assignment Problem (GAP) for which initial seeds must be selected [34]. Another approach was proposed by Bramel and Simchi-Levi in which some nodes are previously selected to be possible locations for concentrators [33]. Around these concentrators other nodes are assigned as terminals and then, cluster are determined; for this model seeds are found from the solution of the problem, but there must be previous selection of possible locations [33]. We propose a modified approach in which concentrators of cluster can be selected from the entire set of nodes.
4.3.1. Index sets
The index set are described as follows:
• I : {I1; I2; I3; :::; Im} Set of blocks indexed by i.
• J : {J0; J1; J2;J3 :::; Jn} Set of corners indexed by j.
• K : {K1;K2;K3; :::;Kσ} Set of vehicles indexed by k.
4.3.2. Parameters
The parameters are described as follows:
• fi: Distance between the origin and a concentrator j.
• cij : Distance between a concentrator j and a block i.
• Ri: Amount of waste generated by the block i.
• Cjk: Capacity of the concentrator j for the assigned vehicle k.
4.3.3. Decision variables
The decision variables are described as follows:
• xij : Take the value of 1 if block i is assigned to the concentrator j, 0 otherwise.
• yjk: Take the value of 1 if the vehicle k is assigned to the concentrator y, 0 otherwise.
4.3.4. Model
The mathematical formulation of our MIP model is described as follows:
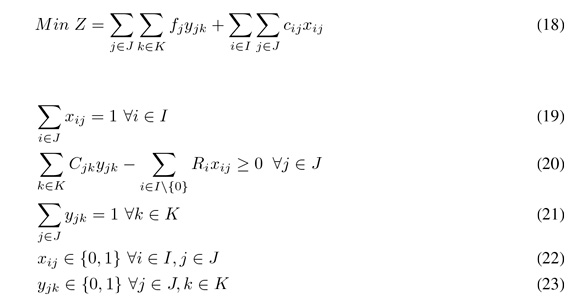
The objective function (18) minimizes the distance between the origin and each block that could be a concentrator and the distance between concentrators and the blocks associated with a concentrator. Constraints (19) force each block to belong only to one concentrator. Constraints (20) ensure that cluster capacity is respected. Constraints (21) limit to one the number of concentrators assigned to each vehicle. Constraints (22) and (23) define the nature of variables xij and yjk as binaries.
5. Results
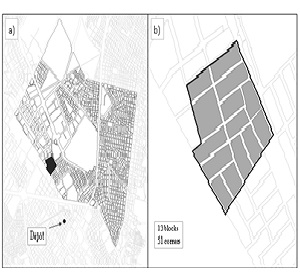
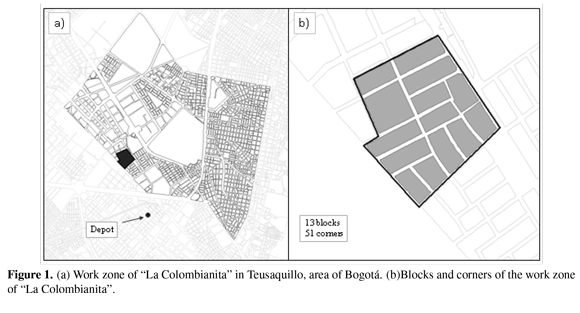
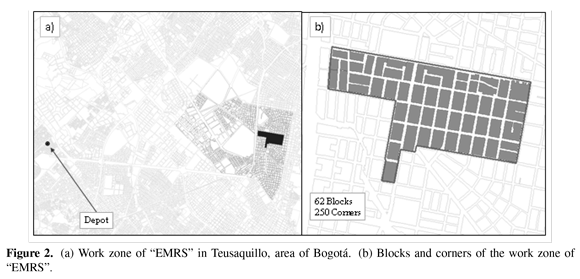
We run some experiments in the context of waste collection system in Bogotá. We selected two ORAs that do collection in the area of Teusaquillo, where there are eight organizations that have a delimited zone of work according to their historical routes. The ORAs selected are "La Colombianita" (see Figure 1) whose area has less users and it is possible to design a route with the proposed model in an acceptable computational time. In addition, we selected the ORA called "EMRS" (see Figure 2) that has more blocks in order to apply cluster methods and generate a comparison.
5.1. Case 1: La Colombianita
Table IV and Table V presents the information about "La Colombianita" case.
Trucks were codified as K1 and K2, and the wheelbarrow was codified as K3. Corners were organized by a number from 1 to 51. The distances of combination among corners were calculated applying Floyd-Warshall Algorithm, considering the real direction of the streets. The legal workday is eight hours. In the solution (see Table VI) J0 corresponds at origin and J52 is the depot. Each corner belongs to a different block and every constraint is satisfied.
5.2. Case 2: EMRS
In Table VII and Table VIII is presented the information about "EMRS".
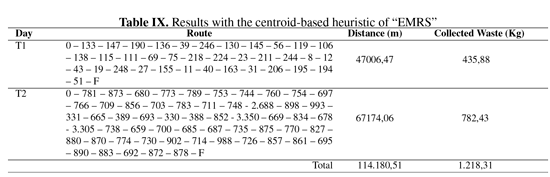
For each clustering method, we have joined the results of every cluster in order to obtain just one route. The connections were made having into account the distance between the origin, the first and last nodes of the clusters. Table IX shows the results with the centroid-based heuristic, where 0 corresponds at origin and F is the depot. Each corner belongs to a different block and every constraint is satisfied.
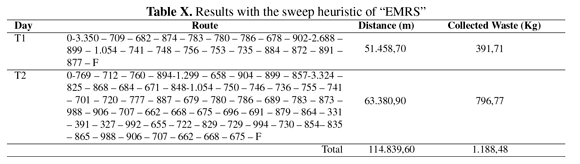
Table X presents the results with the sweep algorithm, where 0 corresponds at origin and F is the depot. Each corner belongs to a different block and every constraint is satisfied.
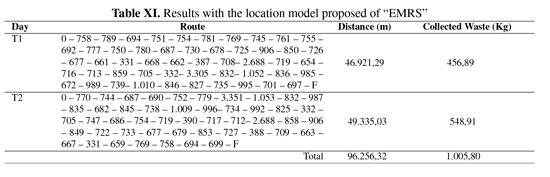
Table XI shows the results with the sweep algorithm, where 0 corresponds at origin and F is the depot. Each corner belongs to a different block and every constraint is satisfied.
For EMRS, the potential amount of waste to be collected was 1.303,64 Kg in both days. With the centroid-base heuristic were collected 91%, with sweep algorithm 93% and with localization model 77%. In a first view of the results, we could infer that the best solution method is the sweep algorithm. Nevertheless, there must be accomplished several tests to have a strong validation of the performance of each method.
6. Conclusions
We present a MIP approach model for selective waste collection as a variant of a VRP model. The problem was applied in real world case in an area of Bogotá, Colombia. From literature review, in selective waste collection there are several models and solution approach. In general, models depend on waste collection necessities and its environment. The selected MIP approach was VRP that takes into account additional aspects such as corners which are the nodes that must belong to specific blocks. Waste is generated by each block and its accumulation is allowed just until ordinary collection occurs.
In the solution with the ORA "La Colombianita", all recyclable waste are collected so it can be ensured 100% of its return to the productive cycle. The model proposed can be applied in contexts where separation at source is a regular activity, and also where there are fixed points so that users could dispose their waste.
We analyzed zones with more number of blocks that are served by other organizations. However, it could not be found an optimal solution in a reasonable computational time. So we perform some test with three clustering methods. These methods could have influenced the solution when the MIP approach was applied, since all off them look for the minimization of distance within the cluster. For these reasons, initial parameters have some improvement in the reduction of distances which could mean more efficiency but not necessarily higher coverage. Future work will concentrate on validation of results in order select the most appropriate method.
References
[1] T. P. B. Brandão Vecchi, L. M. de Matos Jorge, M. A. da Silva Sá Ravagnani, and P. R. Paraíso, "Optimization of planning routes in solid waste collection," Journal of Chemistry and Chemical Engineering, vol. 8, no. 6, pp.596-601, Jun. 2014.
[2] R. S. Xavier, A. C. Lisboa, D. A. G. Vieira, and R. R. Saldanha, "Heuristica para modelagem e minimização do consumo de combustível para rotas de coleta de lixo," Bento Gonçalves, 2010, p. 12.
[3] B.-I. Kim, S. Kim, and S. Sahoo, "Waste collection vehicle routing problem with time windows," Computers & Operations Research, vol. 33, no. 12, pp. 3624-3642, Dec. 2006.
[4] T. Y. Afonso LLorente, "Optimización de rutas de recogida de residuos en zonas mixtas urbana-rurales y orografía singular," Trabajo de Fin de Grado, Universidad de la laguna, La Laguna, 2014.
[5] R. K. Pati, P. Vrat, and P. Kumar, "A goal programming model for paper recycling system," Omega, vol. 36, no. 3, pp. 405-417, Jun. 2008.
[6] F. Beijoco, V. Semiao, and Z. Zsidgraiová, "Optimization of a municipal solid waste collection and transportation system," Lisboa, Portugal, 2011.
[7] S. Simón, J. Demaldé, J. Hernández, and M. Carnero, "Optimización de Recorridos para la Recolección de Residuos Infecciosos," Información tecnológica, vol. 23, no. 4, pp. 125-132, 2012.
[8] A. Méndez, S. Simón, D. Palumbo, E. Chiachera, and M. Carnero, "Dos Enfoques para la Solución del Problema de Ruteo De Vehículos (CVRP): Aplicación a un Caso Real de Recolección de Residuos," Mecánica Computacional, vol. XXIX, pp. 9367-9377, Nov. 2010.
[9] Y. T. Chen, F. T. S. Chan, S. H. Chung, and B. Niu, "Closed-Loop Supply Chain Network Optimization For Hong Kong Cartridge Recycling Industry," Hong Kong Polytechnic University, Department of Industrial and Systems Engineering, Hong Kong, 2013.
[10] . Aksen, O. Kaya, F. S. Salman, and Y. Akça, "Selective and periodic inventory routing problem for waste vegetable oil collection," Optim Lett, vol. 6, no. 6, pp. 1063-1080, Jan. 2012.
[11] J. Beliën, L. De Boeck, and J. Van Ackere, "Municipal Solid Waste Collection and Management Problems: A Literature Review," Transportation Science, vol. 48, no. 1, pp. 78-102, Nov. 2012.
[12] K. Buhrkal, A. Larsen, and S. Ropke, "The Waste Collection Vehicle Routing Problem with Time Windows in a City Logistics Context," Procedia - Social and Behavioral Sciences, vol. 39, pp. 241-254, 2012.
[13] T. Bianchi-Aguiar, M. A. Carravilla, and J. F. Oliveira, "Vehicle routing for mixed solid waste collection - comparing alternative hierarchical formulations," Strathprints Institutional Repository, p. 137, 2011.
[14] R. J. A. Fortunato, "Problema de determinação de circuitos de recolha de resíduos sólidos urbanos da Câmara Municipal de Oeiras," Maestria, Universidade de Lisboa. Instituto Superior de Economia e Gestão., Lisboa, Portugal, 2014.
[15] L. Bardales, "Heurística para la colecta de residuos domiciliarios en la ciudad de Trujillo basado en el ruteo de vehículos con ventana de tiempo," Universidad Nacional de Trujillo, Trujillo, Perú, Informe de Trabajo de Graduación 3, Dec. 2013.
[16] A. M. Benjamin and J. E. Beasley, "Metaheuristics for the waste collection vehicle routing problem with time windows, driver rest period and multiple disposal facilities," Computers & Operations Research, vol. 37, no. 12, pp. 2270-2280, Dec. 2010.
[17] I. Markov, S. Varone, and M. Bierlaire, "Vehicle routing for a complex waste collection problem," presented at the 14th Swiss Transport Research Conference (STRC), 2014.
[18] E. A. V. Toso and D. Alem, "Effective location models for sorting recyclables in public management," European Journal of Operational Research, vol. 234, no. 3, pp. 839-860, May 2014.
[19] S. Fooladi, H. Fazlollahtabar, and I. Mahdavi, "Waste Collection Vehicle Routing Problem Considering Similarity Pattern of Trashcan," International Journal of Applied Operational Research - An Open Access Journal, vol. 3, no. 3, pp. 0-0, Jun. 2013.
[20] F. Samanlioglu, "A multi-objective mathematical model for the industrial hazardous waste location-routing problem," European Journal of Operational Research, vol. 226, no. 2, pp. 332-340, Apr. 2013.
[21] C. S. Fatih Rahim, "A location-routing problem in glass recycling," Annals of Operations Research, vol. 223, no. 1, pp. 329-353, 2014.
[22] E. D. Antmann, X. Shi, N. Celik, and Y. Dai, "Continuous-discrete simulation-based decision making framework for solid waste management and recycling programs," Computers & Industrial Engineering, vol. 65, no. 3, pp. 438-454, Jul. 2013.
[23] L. B. R. Medina, E. C. G. L. Rotta, and J. A. O. Castro, "Una Revisión al Estado del Arte del Problema de Ruteo de Vehículos: Evolución Histórica Y Métodos De Solución," Ingeniería, vol. 16, no. 2, pp. 35-55, Dec. 2011.
[24] S. Pirkwieser and G. R. Raidl, "A column generation approach for the periodic vehicle routing problem with time windows," in International network optimization conference, Pisa, Italia, 2009, vol. 2009.
[25] F. Baniel, "Prise en compte d'objectifs de stabilité pour l'organisation de collectes de déchets," Doctorat, Universit é de Toulouse, 2009.
[26] R. A. J. Pirabán, "Métodos Aproximados para la Solución del Problema de Enrutamiento de Vehículos (Dic 2008)." Universidad Nacional de Colombia, Dec-2018.
[27] Y. X. Daza Cruz, J. A. Patiño Chirva, and E. R. López-Santana, "A mixed integer optimization model to design a selective collection routing problem for domestic solid waste," in 2015 Workshop on Engineering Applications - International Congress on Engineering (WEA), 2015, pp. 1-5.
[28] JICA and UAESP, "Proyecto de Estudio del Plan Maestro para el manejo Integral de Residuos sólidos en Bogotá, D.C.," Unidad Administrativa Especial de Servicios Públicos, Bogotá, Colombia, 3, Nov. 2013.
[29] Corte Constitucional, Auto 275 de 2011. 2011, p. 190.
[30] UAESP, "Esquema de Metas a Cumplir para la Inclusión de la Población Recicladora en la gestión pública de los residuos sólidos en la ciudad de Bogotá D.C.," Secretaría del Hábitat, Bogotá, Colombia, 2011.
[31] K. Shin and S. Han, "A Centroid-based Heuristic Algorithm for the Capacitated Vehicle Routing Problem," Computing and Informatics, vol. 30, no. 4, pp. 721-732, Jan. 2012.
[32] E. R. López-Santana and J. de J. Romero Carvajal, "A hybrid column generation and clustering approach to the school bus routing problem with time windows," Ingeniería, vol. 20, no. 1, pp. 111-127, Mar. 2015.
[33] A. Olivera, "Heurísticas para Problemas de Ruteo de vehículos,"Universidad de la República de Montevideo, Uruguay, Reporte técnico serie 04 - 08, Aug. 2004.
[34] S. Ropke, "Heuristic and exact algorithms for vehicle routing problems," Doctorate, University of Copenhagen, Copenhagen, 2005.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.











2.jpg)










