DOI:
https://doi.org/10.14483/udistrital.jour.reving.2015.1.a07Published:
2015-03-04Issue:
Vol. 20 No. 1 (2015): January - JuneSection:
Special Section: Best Works "VII Symposium on Optimization"A Hybrid Column Generation and Clustering Approach to the School Bus Routing Problem with Time Windows
Un Aproximación Híbrida de Generación de Columnas y Agrupación para Resolver el Problema de Ruteo de Buses Escolares conVentanas de Tiempo
Keywords:
clustering, column generation, optimization, school bus routing (en).Downloads
References
J. Park y B.-I. Kim, “ The school bus routing problem: A review” , Eur. J. Oper. Res., vol. 202, n.o 2, pp. 311-319, abr. 2010.
G. K. Rand, “ The life and times of the Savings Method for Vehicle Routing Problems” , ORiON, vol. 25, n.o 2, dic. 2009.
A. Olivera, “ Heurísticas para problemas de Ruteos de Vehículos”. Universidad de la Republica, Montevideo, Uruguay, 2004.
G. B. Dantzig y J. H. Ramser, “ The truck dispatching problem” , Manag. Sci., vol. 6, n.o 1, pp. 80–91, 1959.
G. Laporte y Y. Nobert, “ Exact algorithms for the vehicle routing problem” , Surv. Comb. Optim., vol. 31, pp.147–184, 1987.
G. Laporte, “ The vehicle routing problem: An overview of exact and approximate algorithms” , Eur. J. Oper.Res., vol. 59, n.o 3, pp. 345–358, 1992.
P. Toth y D. Vigo, The vehicle routing problem. Philadelphia: Society for Industrial and Applied Mathematics,2002.
J. S. Arias-Rojas, J. F. Jimenez, y J. R. Montoya-Torres, “ Solving of school bus routing problem by ant colony optimization.” , Rev. EIA, n.o 17, 2012.
M. Spada, M. Bierlaire, y T. M. Liebling, “ Decision-aiding methodology for the school bus routing and scheduling problem” , Transp. Sci., vol. 39, n.o 4, pp. 477–490, 2005.
T. Bektas y S. Elmastas, “ Solving school bus routing problems through integer programming” , J. Oper. Res. Soc., vol. 58, n.o 12, pp. 1599–1604, 2006.
G. Desaulniers, J. Desrosiers, y M. M. Solomon, Column generation, vol. 5. Springer, 2005.
K. Shin y S. Han, “ A Centroid-based Heuristic Algorithm for the Capacitated Vehicle Routing Problem” ,Comput. Inform., vol. 30, n.o 4, pp. 721-732, ene. 2012.
D. Simchi-Levi, X. Chen, y J. Bramel, “ A case study: School bus routing” , Log. Logist. Theory Algorithms Appl. Logist. Supply Chain Manag., pp. 319–335, 2005.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
A hybrid column generation and clustering approach to the school bus routing problem with time windows
Una aproximación híbrida de generación de columnas y agrupación para resolver el problema de ruteo de buses escolares con ventanas de tiempo
Eduyn Ramiro López Santana; Universidad Distrital Francisco José de Caldas, Facultad de Ingeniería. , erlopezs@udistrital.edu.co
José de Jesús Romero Carvajal; Universidad Distrital Francisco José de Caldas, Facultad de Ingeniería. , jjmisoromero@gmail.com
Recibido: 12-02-2015. Modificado: 01-03-2015. Aceptado: 04-03-2015
Abstract
This paper attempts to solve the School Bus Routing Problem with Time Windows that consists of finding the best set of routes to pick up students distributed geographically with constraints as capacity, time windows and maximum travel time. We formulated the problem as a classic Vehicle Routing Problem with Time Windows and solved it using an approach based on a clustering algorithm and column generation method. A real world case from a school in Bogotá, Colombia is presented including 600 students to pick up in near 400 nodes located in urban and rural areas. The obtained results demonstrate a reduction as the problem’s complexity and an improvement on the performance measures of the proposed method.
Keywords: clustering, column generation, optimization, school bus routing.
Resumen
Este artículo intenta resolver el problema de ruteo de buses escolares con ventanas de tiempo el cual consiste en encontrar el mejor conjunto de rutas para recoger estudiantes geográficamente distribuidos con restricciones de ventanas de tiempo. El problema es formulado como un clásico problema de ruteo de vehículos con ventanas de tiempo y resuelto una aproximación basada en agrupación y generación de columnas. Se presenta un casode aplicación real en un colegio de Bogotá, Colombia con 600 estudiantes y 400 nodos localizados en área urbana y rural. Los resultados obtenidos muestran como la complejidad del problema es reducida y se mejoran las medidas de desempeño.
Palabras claves: agrupación, generación de columnas, optimización, ruteo de buses escolares.
1. Introduction
The School Bus Routing Problem (SBRP) described by [1] as a set of five smaller subproblems: Data preparation, bus stop selection (student assignment to stops), bus route generation, school bell time adjustment and route scheduling. This paper focuses in the bus route generation step,assuming in our case that students are picked up at their homes, buses belong to a single school, so steps two and four are skipped.
The bus route generation step can be formulated and solved as a Vehicle Routing Problem (VRP), which is stated by [2] as a set of costumers with known location and demand to be supplied from a depot by vehicles of known capacity subject to all customer demand to be satisfied. This problem is key in logistics systems and its correct planning could drive into meaningful savings [3].
Since 1959, when Dantzing and Ramser [4] proposed the first VRP formulation it has been widely studied; on one hand formulating models which include more real world characteristics each time and on the other hand developing methods to efficiently solve it [3].The interest in the VRP is not just practical but also academic, since VRP is a combinatorial optimization problem cosidered as an NP-Hard [3], aproaches for solving it are constantly proposed and improved.
Solution methods include heuristic, which perform a limited search in the solutions space and obtain acceptable quality solutions in reasonably calculation times; metaheuristic, which perform a more exhaustive search in the solution space than heuristic methods and generally obtain better results [3], and exact methods in which optimal solution is the goal.
Among exact methods the main approaches are branch and bound, branch and cut, lagrangian relaxation, column generation, dynamic programming, and linear and integer programming. Further information about exact methods can be found in [5], [6] and [7] like wise further information for heuristic methods can be found in [3].
School Bus Routing Problem solution methods have already been studied, for instance an Ant Colony Optimization algorithm is proposed by [8] to solve it, whereas [9] propose a decision aiding methodology for the same purpose. Exact solution methods are also found, in this case [10] solve it through integer programming.
Column generation method have been studied successfully and vastly to solve Vehicle Routing Problem with Time Windows (VRPTW). Desaulniers, Desrosiers and Solomon [11] dedicate a whole chapter to deeply study this application.
In this paper, we study the School Bus Routing Problem with Time Windows. This is a variant of SBRP taking in account that the buses must arrive to pick up students before at specific time (lower bound of time window) and they can arrive before another specific time (upper bound of time window), but the students did not pick up before the beginning of the time window. We consider a case study of school bus routing problem for the Jose Max León school bus system.This school is located at the north west sub urban area in Bogota, Colombia, with near 600 students who use the school bus system, located in 440 nodes approximately.
This problem differs from the classical VRP in some characteristics. For instance, the service is intended to pick up and deliver people (school pupils or workers) rather than products, so that demand is the number of people to be picked up in each location.In SBRP students are delivered to their homes at afternoon, this delivery could be formulated as another problem or be assumed to be done in the inverse path in which they are picked up. Finally, SBRP buses generally departure (parking) and arrive (school) to different locations being similar to Open Vehicle Routing Problem OVRP.
Since the SBRPTW is a NP-hard problem because this is a generalization of the SBRP that is NP-hard [8], we propose a hybrid column generation and clustering method to solve it. Firstly, the clustering phase is executed in two steps then the routing phase is performed. The first clustering step aims to generate large groups of nodes, and then the algorithm is executed again to cluster nearest nodes. Subsequently, with this information, routes between clusters in the group are generated using the Column Generation method. Finally, using the inter-cluster routes previously generated, intra-cluster routes are created by solving a Travelling Salesman Problem.
This paper is organized as follows. Section 2 introduces the problem statement, in which the problem definition, notation and mathematical formulation are presented. Section 3 explains the proposed solution approach. Section 4 provides some numerical results on the real-world case. Finally, Section 5 concludes this work and provides directions for possible future research.
2. Problem statement
We consider the bus system, in which a set of customers C = {1,2,...,n}geographically distributed are meant to be picked up and took to the school (depot) indexed as 0, depot is considered the departure and final location for all vehicles. To do so the school counts on a set of identical vehicles K = {1,2,...,m} with known transportation capacity Q. Students travel time could be maximum as twice as the time they would travel directly from home to school, so time windows are defined for each student as ei as the earliest picking up hour, defined as the travel time of going directly from home to school and li the latest picking up hour,defined as twice ei. Asseveral students may be picked up at the same customer location, pi is defined as the demand of each customer location.
Thus, this problem can be defined in a directed Graph G = (V,A), V = C ∪{0}, A = {(i,j) : i,j ∈ V,i 6= j}.Foreacharc (i,j) anon-negativevalue tij is associated representing the travel time from i to j. So the problem consists of finding a set of routes that pick up all students minimizing the total travelled time, satisfying maximum travelled time and demand satisfaction.
Assumptions and conditions to solve this problem are the following:
-
Arcs are supposed symmetrical, that means tij = tji.
-
Vehicle fleet is homogeneous.
-
Travel times are deterministic and comply with the triangle inequality.
-
The time window [ej,lj] is met, i.e., the vehicles must arrive on customer before time lj and can arrive before ej, but the customer will not be serviced before the beginning of the time window.
Notation used throughout the paper is defined in Table I.
The mathematical formulation is the typical VRPTW formulation; it is presented in equations (1) to (10).
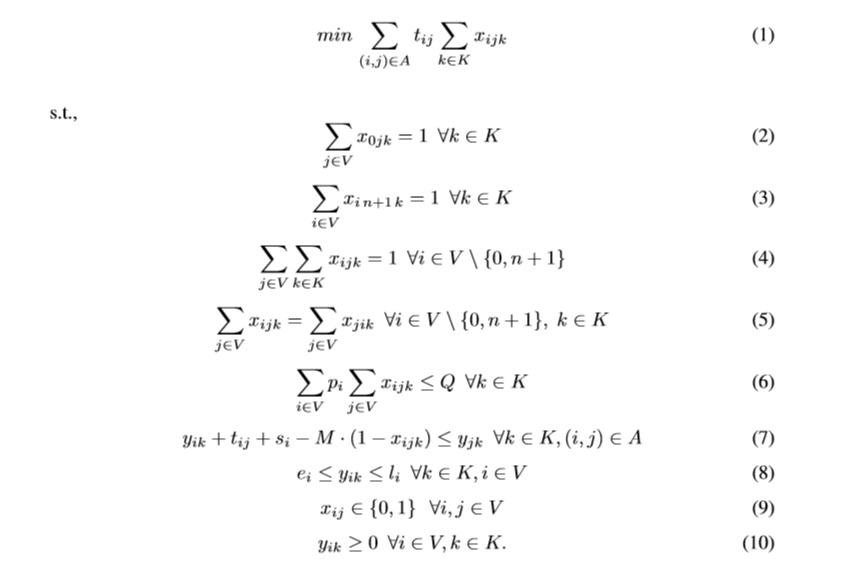
The objective function (1) minimizes the total travel time. Constraints (2) and (3) ensure that all vehicles departure and arrive to depot. Constrains (4) forces that all customers are served exactly once. The flow constraints for each node are presented in (5). Constraints (6) ensures the vehicle’s capacity are observed. Constraints (7) and (8) ensures the service starts between the time windows for each customer. Finally, constraints (9) are integrality conditions and (10) are nonnegative variable conditions.
The problem described and formulated is a combinatorial optimization problem sorted ad NP-Hard, due to its amount of variables and solutions space, so that alternative methods to the classical have been widely studied and successfully applied such as langrangian relaxation, column generation, and Clarke and Wright savings method, among others. Here we propose an alternative hybrid approach that combines column generation and clustering techniques.
3. Description of the solution approach
The solution approach uses the clustering algorithm and a column generation technique in order to find the best set of routes to pick up all students with a minimum routing cost, consisting of two phases:
-
The clustering phase: This phase uses as input the nodes where the bus pick up the students and the number of students that are picked up. This phase executes two steps. In the first step, the clusters are computed with the Shin & Han’s algorithm [12]. The output is a small fixed number of clusters that it is an independent routing problem. In the second step, for each of the clusters from step 1 the Shin & Han’s algorithm is executed again to obtain a number of clusters that are visited for the bus in its path.
-
The routing phase: this phase also consists in two steps. The first step solves a vehicle routing problem with time windows, taking as nodes, the clusters obtained in step 2 of phase 1. With the set of routes in the second step, for each cluster a traveling salesman problem is solved in order to determine the sequence of locations the bus must to visit to pick up students in their respective clusters.
In the next two sections, we describe these phases in detail.
3.1. The clustering phase
We use the algorithm proposed by Shin & Han [12]. This algorithm consists of two parts: cluster construction and cluster adjustment.
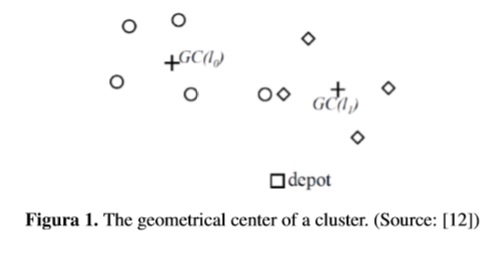
The method use the Geometrical Centre (GC) of a cluster defined as follows: Let qi = {v0,v1,...,vk}be cluster i, where vi is a member of cluster i.
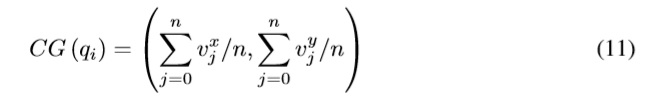
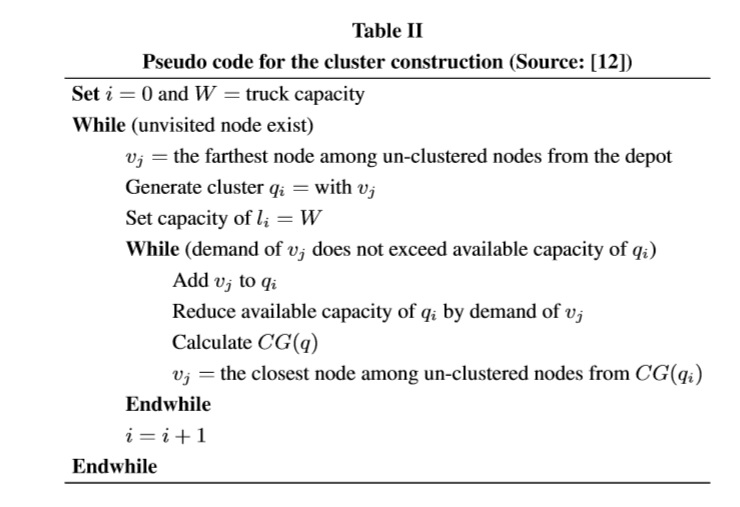
where vxj and vyj are x and y coordinates of vj. Table II shows the pseudo-code of cluster construction. The process starts by selecting the farthest node from the depot as a cluster seed. Then the CG is calculated according with (11) and is illustrated in Fig. 1. Now, to add nodes, we find the un-clustered node, which is located closest from GC, and include the node into the cluster only if the demand does not exceed the available bus capacity of the cluster.If the node is added to cluster, its bus capacity is reduced by the demand of node and GC is recalculated again. The process is repeated until the capacity is feasible to add the new node, if not a new cluster is created and the process is conducted until all nodes are clustered.
Once clusters are constructed, they are optimized using cluster adjustment algorithm proposed by [12] and presented in Table III. This procedure ensure that if node vk, which belongs to cluster qi, is closer to GC(qj) than GC(q li), and the demand vk of does not exceed the available capacity of lj, then move vk from qi to cluster qj. The GC(qj) and GC(qi) are recalculated again.
When running the clustering phase, the first step is aimed at distributing the demand as uniformly as possible in each cluster. This is desirable since each cluster is a vehicle routing problem to be solved. In the second step, we divide each cluster into smaller clusters in order to make them easier to solve using the column generation method. The time complexity of both steps is O(n2) as it was shown in [12]. In the same way as this technique has been used to generate initial solutions as input to a metaheuristic algorithm [12], here we use as input to the column generation method.
3.2. The routing phase
This phase is developed in two steps. The first step use a VRPTW formulation and solved with a column generation method in order to get a set of routes such that the operational constraints are respected. The second step use a TSP formulation in order to set a route such all nodes in each clusters are meet. In both steps, the objective function minimize the total travel time.
3.2.1. Step1: A column generation method to VRPTW
We use a set partitioning formulation problem proposed by Desaulniers, Desrosiers, & Solomon [11]. The constraints (4) in VRPTW formulation relate all vehicles, while the other constraints are for each vehicle k. With the assumption that the vehicle are homogenous, is possible to use the decomposition principle to generate a subproblem for each vehicle and the master problem that related them.
In reference [11] it is stated that to formulate the subproblem as a shortest path problem is so far the most successful decomposition scheme for VRPTW. In this way the problem is solved without enumerating all possible paths [13].
3.2.1.1. The master problem
Let Rk be the set of feasible paths for vehicle k ∈ K. Hence, r ∈ Rk corresponds to an elementary path which can also be described by using the binary values xkijr,where xkijr = 1, if vehicle k goes directly from vertex i to vertex j on path r, and, xkijr = 0 otherwise. Any solution xkijr to the master problem can be written as a non-negative convex combination of a finite number of elementary paths, i.e.
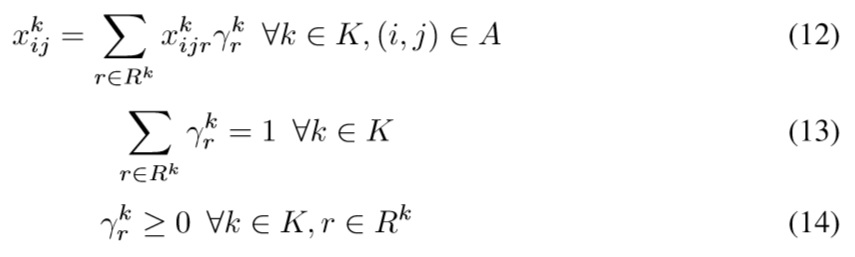
Where γkr is the number of times path r is used by one vehicle k. Using xkijr we can define the cost of a path, tkr, and the number of times a customer i is visited by vehicle k, aki , as:
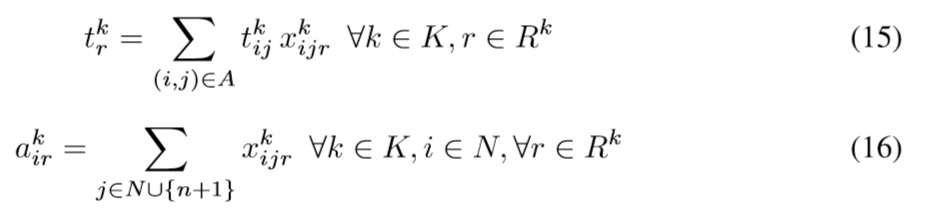

Now we can substitute these values in (1) and (4) and arrive at the revised formulation of the master problem:
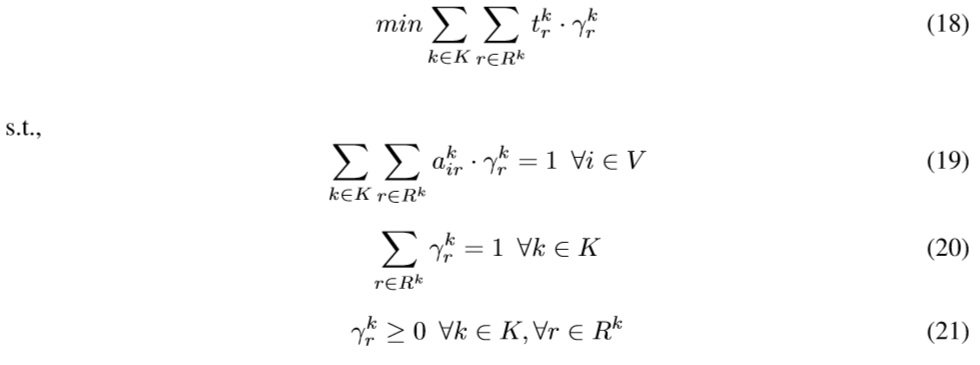
The objective function (18) minimizes the total travel time. Constraints (19) ensure that a node is visited exactly once. Constraints (20) represents that each vehicle use only one route. Constraints (21) ensures nonnegative variables.
In the usual case of a single depot and a homogeneous fleet of vehicles with thesame initial conditions for all vehicles, all are identical, that is, R = Rk, k ∈ K.
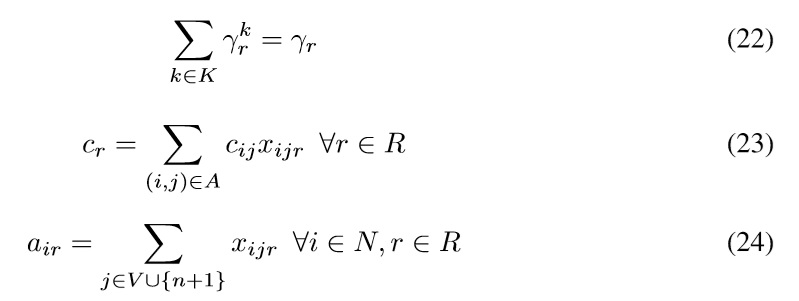
where γr is number of times path r is used. The resulting model given below is the classical linear relaxation of the set partitioning formulation given by equations (25) to (29).
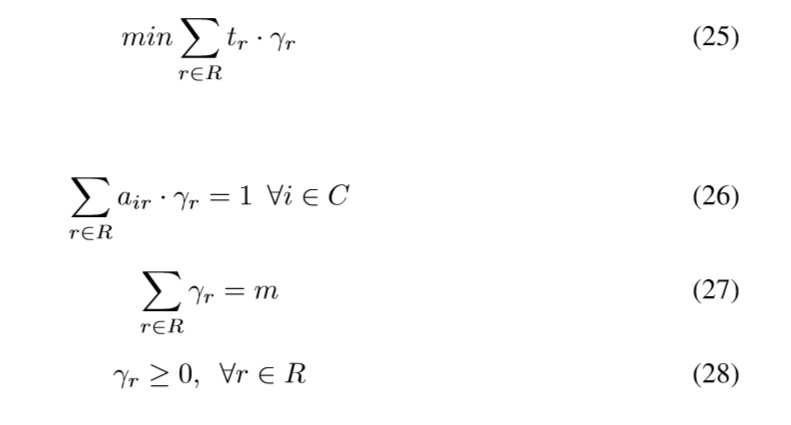
The objective function (25) minimizes the total travel time. Constraints (26) ensure that a node is visited exactly once. Constraints (27) represents that the number of active paths is equal to the number of vehicles. Constraints (28) ensures nonnegative variables.
In the column generation method, the set of paths R is restricted, so this problem is called the Restricted Master Problem (RMP). To find an optimal solution to the master problem, a new variable (column) is requested with negative reduced cost. This variable is obtained to solve the subproblem, sometimes called pricing subproblem, i.e., the subproblem search a path with the least possible reduced cost. This process is repeated until the variable from subproblems has a nonnegative reduce cost (it will actually be 0). It is the stopping criterion. Solving the master problem, we can obtain an integer solution but it is not guaranteed to be so. In the event that a solution is whole, will be a basic solution to the VRPTW, but not necessarily optimal [11].
3.2.1.2. The subproblem
In the column generation approach for the VRPTW proposed by [11], the subproblem de- composes into |K| identical problems, each one being an Elementary Shortest Path Problem with Time Windows and Capacity Constraints (ESPPTWCC), where elementary means that each customer can appear at most once in the shortest path. The resource constraints are the time windows, vehicle capacity and maximum duration travel time of a path. It can be formulated as:
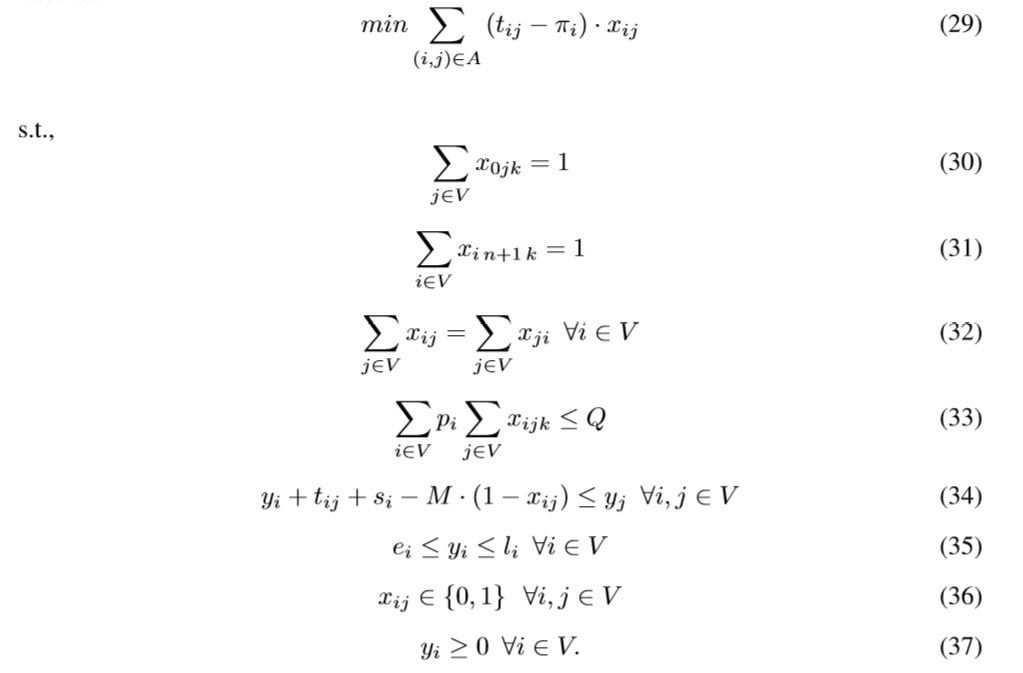
The objective function (29) finds the shortest time path. Constraints (30) and (31) are the re- sulting in a path from the depot to the depot . Constraints (32) are flow constraints. Constraint (33) is the capacity constraint, constraints (34) and (35) are time constraints, while constraint (36) ensures integrality and (37) nonnegative variables.
Since the ESPPTWCC is NP-hard in the strong sense (see [11]), this problem is solved by relaxing some of the constraints or using the special algorithms developed for it, as dynamic programming approach or label algorithms.
To the initial solution of RMP we use the combination of two phase simplex´s method and column generation method. We assume that all tij = 0 and add many artificial variables as constraints there have been as basic solution initial. Then, the column generation is running until all artificial variables leaves the basic solution or all cost are non-negative. Once the basic feasible solution is found, all tij take its original values.
3.2.2. Step 2: A TSP model
After solving the problem as described above, we obtain the path of each vehicle to visit all the clusters. In the second step of routing phase, the visiting sequence of nodes in each cluster is generated.
We propose a variant of TSP formulation in order to find the shortest path to visit all nodes in each cluster observing the obtained sequence in step 1. The proposed variant consists that the vehicle does not return to the origin node. It can be formulated as follows:

The objective function (38) finds the shortest time path. The constraints (39) and (40) ensure the starting from the node 0 and arrive at node n (different start node to the end node of the route), respectively. All other nodes must be visited once time is stated in constraints (41). The flow balance constraints are stated in (42). Finally, constraints (43) remove the sub-tours and constraints (44) ensures nonnegative variables.
After the second stage, the detailed scheduling of each vehicle by setting the check nodes and when the time will. Table IV summarizes the proposed approach.
4. Numerical results
In this section, we apply the proposed method to a real world case. The reported results were obtained using Xpress-MP 7.4 on a Windows 8 64-bit machine, with an Intel Core i5 3337 processor (2×1.8 GHz) and 6GB of RAM.
4.1. Case study
The Jose Max Leon Schools is located in Bogota, Colombia. The school counts on 600 users for its buses system, located in 400 different locations (nodes). Although the bus fleet is currently heterogeneous, with an average 18 passengers capacity, it is provided by a third-party transport company, and so we reason it would be feasible to be changed to an homogenous fleet with no additional costs to the school. Thus, we assume the homogeneous fleet of vehicles with transportation capacity of 18 and 25 passengers. In addition, it was assumed that the vehicles departure and arrive to the school (depot). Finally, the return path to deliver students is supposed to be inverse to picking them up.
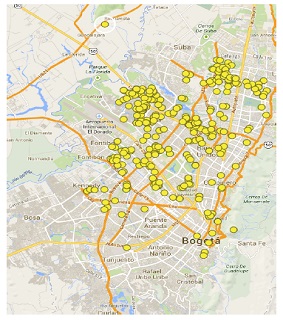
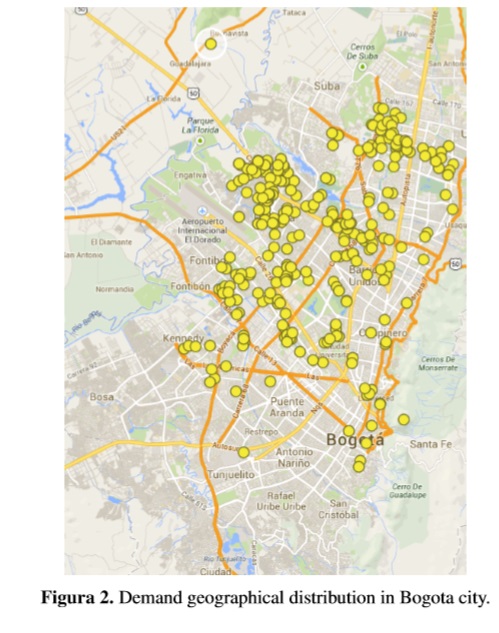
Shortest travel time/distance between each pair of points in the network was computed using the “Euclidian distance” method. We use the free service www.mapas.com.co for geocoding addresses turn into latitude and longitude coordinates. Nodes’ distribution after geocoding the address is shown in Fig. 2.
4.2. Results
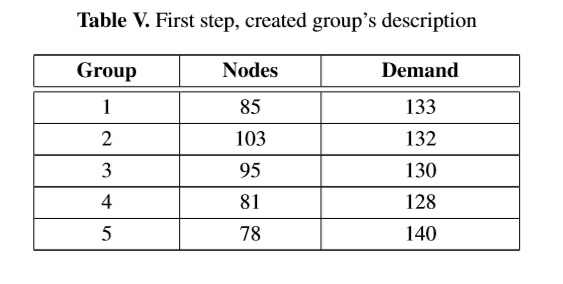
In first step, big groups were formed. The clustering algorithm was run for urban locations, rural locations established fifth group. Groups’ description is presented in Table V. First column shows the number of groups created, second column shows the amount of nodes assigned to each groups and third column the final demand of each group.
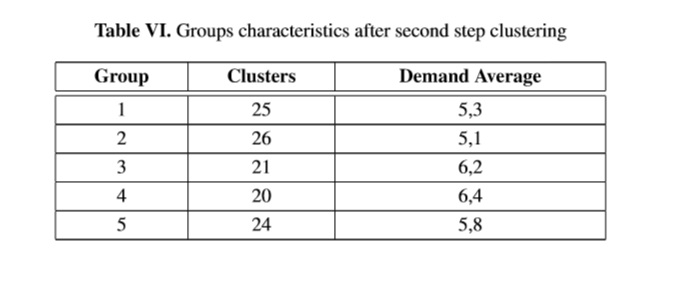
Then, the clustering algorithm was executed once again for each group so to be divided into more or less 25 clusters. Group characteristics are shown in Table VI where first columns identifies each group, second column represent the amount of clusters generated for each group and finally in third column the clusters’ demand average is presented.
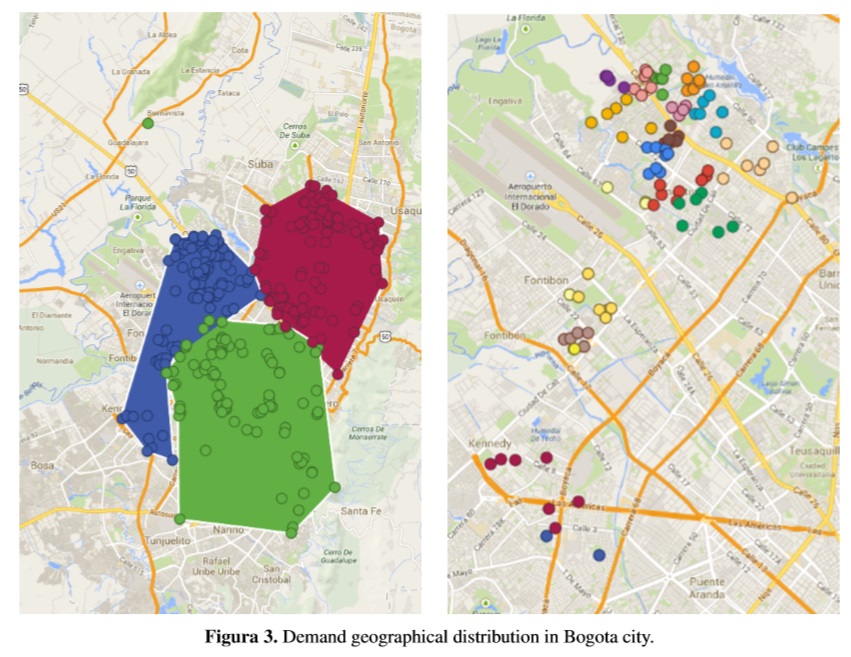
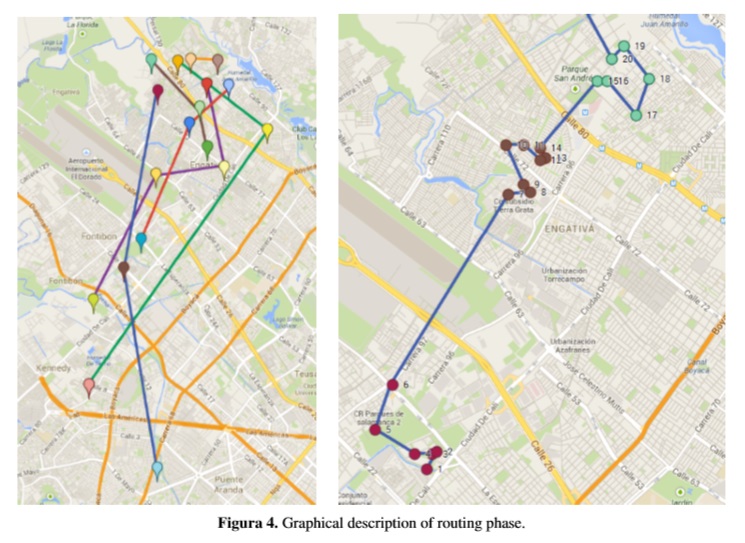
The previous phase intended to reduce the solutions space so that the column generation method could be executed successfully. Results of the clustering phase are shown in Fig. 3, left side shows the big groups’ creation and right side shows clustering inside a group were same-color points represent a cluster.
Routing phase was executed twice, all solution steps took about three minutes of execution. First of all, with the vehicles’ capacity parameter set to 18 passengers and finally increasing this parameter to 25 passenger so as to evaluate the convenience of using one or another kind of vehicles.
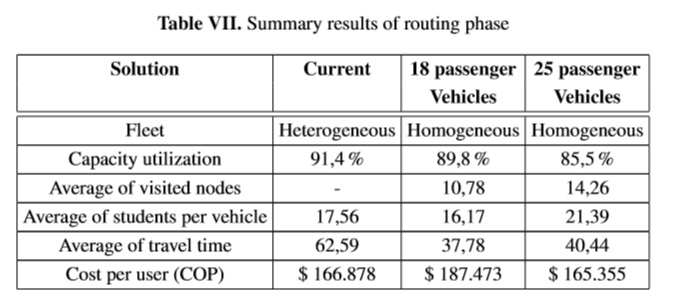
Results of this phase are summarized in Table VII. First column presents the performance measures. Second column shows the current information for Jose Max Leon’s school bus system. Third column shows the solution with homogeneous fleet of vehicles with 18 passenger capacity and finally, fourth column shows the solution with 25 passenger vehicles.
As shown in Table VII, the capacity utilization decreases in both cases (18 and 25 passenger- vehicles) compared to the current solution. In the case of 18 passenger -vehicles, the cost per user is increasing, since more vehicles has to be used in order to serve the same demand. In the case of 25 passenger -vehicles, the capacity utilization decreases, besides that cost per user is also slightly decreased because less vehicles are used and fixed costs are reduced. Lower capacity utilization at a same level of cost per user could drive to have some room to face a marginal demand increase.
The travel times are also improved, the main goal was to reduce students’ travel time and that is achieved in both scenarios. In 18 passenger vehicles, a 39% decrease in travel time whereas in 25 passenger vehicles the reduction goes to a 35% decrease compared to current solution.
A graphical description of routing phase is shown in Fig. 4, left side represents the routing phase performed in every group in which the column generation algorithm was executed and right side shows the routing step for each cluster in which a TSP was solved.
5. Concluding remarks
In this work is studied a variant of the school bus routing problem including time windows. The problem was modeled as a classical vehicle routing problem with time windows. It was solved using a hybrid column generation and clustering method. This is a two-phase method. The first phase uses clustering in order to reduce the number of nodes in the VRPTW formulation.The second phase is aimed at finding the best set of route to pick up all students. This phase was solved in two steps, the first step with a column generation method, while the second step with a modified TSP formulation.
The proposed approach found a reduction of 39% and 35% of the students travel time for the 18 and 25 passenger per vehicle scenarios, respectively. Although the fleet cost is increased in case of, 18 passenger per vehicle since more vehicles has to be used in order to serve the same demand, our approach allows reducing the number of visited students, which implies that the vehicle does less stops, and hence the travel time is reduced. In addition, a student does not take more than 88 minutes on the road and an average travel time of 37 minutes, in case of 18 passenger per vehicle.
Future work should focus in the other clustering method to reduce the complexity of the problem in terms of required computational time to obtain a cluster or explore another classification for instance the importance or priorities and improve the decision-aid tool to allow speeding up the method. Another real world constraints and characteristics can be explored as heterogeneous fleet of buses, stochastic travel times, other objective functions, among others.
6. Acknowledgment
We thank Fair Isaac Corporation (FICO) for providing us with Xpress-MP licenses under the Academic Partner Program subscribed with Universidad Distrital Francisco Jose de Caldas (Colombia). In addition, our special thanks to José Max León School for providing us the information for this research.
References
-
J. Park y B.-I. Kim, “The school bus routing problem: A review”, Eur. J. Oper. Res., vol. 202, n.o 2, pp. 311-319, abr. 2010.
-
G. K. Rand, “The life and times of the Savings Method for Vehicle Routing Problems”, ORiON, vol. 25, n.o 2, dic. 2009.
-
A. Olivera, “Heurísticas para problemas de Ruteos de Vehículos”. Universidad de la República, Montevideo, Uruguay, 2004.
-
G. B. Dantzig y J. H. Ramser, “The truck dispatching problem”, Manag. Sci., vol. 6, n.o 1, pp. 80–91, 1959.
-
G. Laporte y Y. Nobert, “Exact algorithms for the vehicle routing problem”, Surv. Comb. Optim., vol. 31, pp. 147–184, 1987.
-
G. Laporte, “The vehicle routing problem: An overview of exact and approximate algorithms”, Eur. J. Oper. Res., vol. 59, n.o 3, pp. 345–358, 1992.
-
P. Toth y D. Vigo, The vehicle routing problem. Philadelphia: Society for Industrial and Applied Mathematics, 2002.
-
J. S. Arias-Rojas, J. F. Jiménez, y J. R. Montoya-Torres, “Solving of school bus routing problem by ant colony optimization.”, Rev. EIA, n.o 17, 2012.
-
M. Spada, M. Bierlaire, y T. M. Liebling, “Decision-aiding methodology for the school bus routing and scheduling problem”, Transp. Sci., vol. 39, n.o 4, pp. 477–490, 2005.
-
T. Bektas y S. Elmastas, “Solving school bus routing problems through integer programming”, J. Oper. Res. Soc., vol. 58, n.o 12, pp. 1599–1604, 2006.
-
G. Desaulniers, J. Desrosiers, y M. M. Solomon, Column generation, vol. 5. Springer, 2005.
-
K. Shin y S. Han, “A Centroid-based Heuristic Algorithm for the Capacitated Vehicle Routing Problem”, Comput. Inform., vol. 30, n.o 4, pp. 721-732, ene. 2012.
-
D. Simchi-Levi, X. Chen, y J. Bramel, “A case study: School bus routing”, Log. Logist. Theory Algorithms Appl. Logist. Supply Chain Manag., pp. 319–335, 2005.
Eduyn Ramiro López Santana
He is an Assistant Professor at the Engineering Faculty of the Universidad Distrital Francisco José de Caldas - Bogotá, Colombia. He obtained his bachelor degree on Industrial Engineering at the same university in 2009, a Master degree on Industrial Engineering at the Universidad de los Andes – Bogotá, Colombia in 2013, and currently he is performing Doctoral studies on engineering at the Universidad Distrital Francisco José de Caldas. His main interests are: combinatorial optimization, expert systems and applications in production and logistics.
e-mail: erlopezs@udistrital.edu.co
José de Jesús Romero Carvajal
He is a professional engineer at Private Corporation. He obtained his bachelor degree on Industrial Engineering at the Universidad Distrital Francisco José de Caldas – Bogotá, Colombia in 2014.
e-mail: jjmisoromero@gmail.com

This work is authorized by an Attribution-NonCommercial-NoDerivs CC BY-NC-ND license.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.







2.jpg)