DOI:
https://doi.org/10.14483/23448393.12691Published:
2018-05-31Issue:
Vol. 23 No. 2 (2018): May - AugustSection:
Industrial EngineeringEl Problema de Ruteo e Inventarios en Cadenas de Suministro de Perecederos: Revisión de Literatura
Inventory Routing Problem in Perishable Supply Chains: A Literature Review
Keywords:
Supply chain management, optimization, perishables, inventory routing problem, IRP. (en).Keywords:
Gestión de la cadena de suministro, IRP, optimización, perecederos, problema de ruteo e inventarios. (es).Downloads
References
P. Amorim and B. Almada-Lobo, "The Impact of Food Perishability Issues in the Vehicle Routing Problem", Comput. Ind. Eng., Vol. 67, No. 1, pp. 223–233, 2014.
https://doi.org/10.1016/j.cie.2013.11.006
R. F. Roldán, R. Basagoiti, and L. C. Coelho, "A Survey on the Inventory-Routing Problem with Stochastic Lead Times and Demands", J. Appl. Log., Vol. 24, Part A, pp. 15–24, 2017.
M. Soysal, J. M. Bloemhof-Ruwaard, R. Haijema, and J. G. A. J. Van Der Vorst, "Modeling an Inventory Routing Problem for Perishable Products with Environmental Considerations and Demand Uncertainty", Int. J. Prod. Econ., Vol. 164, pp. 118–133, 2015.
https://doi.org/10.1016/j.ijpe.2015.03.008
H. Aguinis and A. Glavas, "What We Know and Don't Know About Corporate Social Responsibility: A Review and Research Agenda", J. Manage., Vol. 38, No. 4, pp. 932–968, 2012.
https://doi.org/10.1177/0149206311436079
D. L. Rincón, J. E. Fonseca, and J. A. Orjuela, "Towards a Common Reference Framework for Traceability in the Food Supply Chain", Ingeniería, Vol. 22, No. 2, pp. 161–189, 2017.
S. Mirzaei and A. Seifi, "Considering Lost Sale in Inventory Routing Problems for Perishable Goods", Comput. Ind. Eng., Vol. 87, pp. 213–227, 2015.
https://doi.org/10.1016/j.cie.2015.05.010
A. Al Shamsi, A. Al Raisi, and M. Afta, "Pollution Inventory Routing Problem with Perishable Goods", In Logistics Operations, Supply Chain Management and Sustainability, pp. 585–596, 2014.
P. C. Nolz, N. Absi, and D. Feillet, "A Stochastic Inventory Routing Problem for Infectious Medical Waste Collection", Networks, Vol. 63, No. 1, pp. 82–95, 2014.
https://doi.org/10.1002/net.21523
V. Hemmelmayr, K. F. Doerner, R. F. Hartl, and M. W. P. Savelsbergh, "Delivery Strategies for Blood Products Supplies", Or Spectr., Vol. 31, No. 4, pp. 707–725, 2009.
M. Soysal, J. M. Bloemhof-Ruwaard, R. Haijema, and J. G. A. J. Van Der Vorst, "Modeling a Green Inventory Routing Problem for Perishable Products with Horizontal Collaboration", Comput. Oper. Res., pp. 1–15, 2016.
J. A. Orjuela-Castro, G. L. Diaz Gamez, and M. P. Bernal Celemín, "Model for Logistics Capacity in the Perishable Food Supply Chain", In Applied Computer Sciences In Engineering, pp. 225–237, 2017.
S. Nahmias, Perishable Inventory Systems, Springer: Us, 2011.
J. A. O. Castro and W. A. Jaimes, "Dynamic Impact of the Structure of the Supply Chain of Perishable Foods onLogistics Performance and Food Security", J. Ind. Eng. Manag., Vol. 10, No. 4, pp. 687–710, 2017.
R. Bai and G. Kendall, "A Model for Fresh Produce Shelf Space Allocation and Inventory Management with Freshness Condition Dependent Demand", Informs J. Comput., Vol. 20, No. 1, pp. 78–85, 2008.
https://doi.org/10.1287/ijoc.1070.0219
F. Andrés Pérez Mantilla and F. Torres, "Modelos de Inventarios con Productos Perecederos: Revisión de Literatura", Ingeniería, Vol. 19, No. 2, pp. 9–40, 2014.
B. Sivakumar, "A Perishable Inventory System with Retrial Demands and a Finite Population", J. Comput. Appl. Math., Vol. 224, pp. 29–38, 2009.
https://doi.org/10.1016/j.cam.2008.03.041
K. Van Donselaar, T. Van Woensel, R. Broekmeulen, and J. Fransoo, "Inventory Control of Perishables inSupermarkets", Int. J. Prod. Econ., Vol. 104, No. 2, pp. 462–472, 2006.
https://doi.org/10.1016/j.ijpe.2004.10.019
J. Pahl and S. Voß, "Integrating Deterioration and Lifetime Constraints inProduction and Supply Chain Planning: a Survey", Eur. J. Oper. Res., Vol. 238, pp. 654–674, 2014.
https://doi.org/10.1016/j.ejor.2014.01.060
A. Mahmoodi, A. Haji, and R. Haji, "One for One Period Policy for Perishable Inventory", Comput. Ind. Eng., Vol. 79, pp. 10–17, 2015.
https://doi.org/10.1016/j.cie.2014.10.012
J. A. Orjuela-Castro, A. L. Caicedo-Otavo, A. F. Ruiz-Moreno, and W. Adarme-Jaimes, "External Integration Mechanisms Effect on the Logistics Performance of Fruit Supply Chains. A Dynamic System Approach", Rev. Colomb. Ciencias Hortícolas, Vol. 10, pp. 311–322, 2016.
D. Cattaruzza, N. Absi, D. Feillet, and T. Vidal, "A Memetic Algorithm for the Multi Trip Vehicle Routing Problem", Eur. J. Oper. Res., Vol. 236, pp. 833–848, 2014.
https://doi.org/10.1016/j.ejor.2013.06.012
J. Jiang, K. M. Ng, K. L. Poh, and K. M. Teo, "Vehicle Routing Problem with a Heterogeneous Fleet and Time Windows", Expert Syst. Appl., Vol. 41, pp. 3748–3760, 2014.
https://doi.org/10.1016/j.eswa.2013.11.029
V. F. Yu, P. Jewpanya, and A. A. N. P. Redi, "Open Vehicle Routing Problem with Cross-Docking", Comput. Ind. Eng., Vol. 94, pp. 6–17, 2016.
https://doi.org/10.1016/j.cie.2016.01.018
L. B. Rocha Medina, E. C. González La Rota, and J. A. Orjuela Castro, "Una Revisión al Estado del Arte del Problema de Ruteo de Vehículos: Evolución Histórica y Métodos de Solución", Ingeniería, Vol. 16, No. 2, pp. 35–55, 2011.
L. C. Coelho, J. F. Cordeau, and G. Laporte, "Heuristics for Dynamic and Stochastic Inventory-Routing", Comput. Oper. Res., Vol. 52, No. Part A, pp. 55–67, 2014.
K. Braekers, K. Ramaekers, and I. Nieuwenhuyse, "The Vehicle Routing Problem: State of the Art Classification and Review", Comput. Ind. Eng., Vol. 99, pp. 300–313, 2015.
https://doi.org/10.1016/j.cie.2015.12.007
J. A. Orjuela-Castro, D. A. Sepulveda-García, and I. D. Ospina-Contreras, "Effects of Using Multimodal Transport Over the Logistics Performance of the Food Chain of Uchuva", In Applied Computer Sciences In Engineering, pp. 165–177, 2016.
E. C. Gonzalez-L., W. Adarme-Jaimes, and J. A. Orjuela-Castro, "Stochastic Mathematical Model for Vehicle Routing Problem in Collecting Perishable Products", Dyna, Vol. 82, No. 189, pp. 199–206, 2015.
https://doi.org/10.15446/dyna.v82n189.48549
R. Lahyani, M. Khemakhem, and F. Semet, "Rich Vehicle Routing Problems: from a Taxonomy to a Definition", Eur. J. Oper. Res., Vol. 241, No. 1, pp. 1–14, 2015.
https://doi.org/10.1016/j.ejor.2014.07.048
Y. Zhang and X. D. Chen, "An Optimization Model for the Vehicle Routing Problem in Multi-Product Frozen Food Delivery", J. Appl. Res. Technol., Vol. 12, No. 2, pp. 239–250, 2014.
https://doi.org/10.1016/S1665-6423(14)72340-5
P. Amorim and B. Almada-Lobo, "The Impact of Food Perishability Issues in the Vehicle Routing Problem", Comput. Ind. Eng., Vol. 67, pp. 223–233, 2014.
https://doi.org/10.1016/j.cie.2013.11.006
U. Emeç, B. Çatay, and B. Bozkaya, "An Adaptive Large Neighborhood Search for An E-Grocery Delivery Routing Problem", Comput. Oper. Res., Vol. 69, pp. 109–125, 2016.
https://doi.org/10.1016/j.cor.2015.11.008
A. F. Ruiz, A. L. Caicedo, and J. A. Orjuela, "Integración Externa en las Cadenas de Suministro Agroindustriales: una Revisión al Estado del Arte", Ingeniería, Vol. 20, No. 2, pp. 167–188, 2015.
M. A. Darwish and O. M. Odah, "Vendor Managed Inventory Model for Single-Vendor Multi-Retailer Supply Chains", Eur. J. Oper. Res., Vol. 204, pp. 473–484, 2010.
https://doi.org/10.1016/j.ejor.2009.11.023
M. Hariga, M. Gumus, A. Daghfous, and S. K. Goyal, "A Vendor Managed Inventory Model Under Contractual Storage Agreement", Comput. Oper. Res., Vol. 40, pp. 2138–2144, 2013.
https://doi.org/10.1016/j.cor.2013.03.005
S. Yanik, B. Bozkaya, and R. Dekervenoael, "A New Vrppd Model and a Hybrid Heuristic Solution Approach for E-Tailing", Eur. J. Oper. Res., Vol. 236, pp. 879–890, 2014.
https://doi.org/10.1016/j.ejor.2013.05.023
L. C. Coelho and G. Laporte, "Optimal Joint Replenishment, Delivery and Inventory Management Policies for Perishable Products", Comput. Oper. Res., Vol. 47, pp. 42–52, 2014.
https://doi.org/10.1016/j.cor.2014.01.013
F. Baita and W. Ukovich, "Dynamic Routing-And-Inventory Problems: a Review", Transp. Res. Part a Policy Pract., Vol. 32, No. 8, pp. 585–598, 1998.
W. J. Bell, L. M. Dalberto, M. L. Fisher, A. J. Greenfield, R. Jaikumar, P. Kedia, R. G. Mack, and P. J. Prutzman, "Improving the Distribution of Industrial Gases with An On-Line Computerized Routing and Scheduling", Interfaces (Providence)., Vol. 13, No. 6, pp. 4–23, 1983.
https://doi.org/10.1287/inte.13.6.4
H. K. Chen, C. F. Hsueh, and M. S. Chang, "Production Scheduling and Vehicle Routing with Time Windows for Perishable Food Products", Comput. Oper. Res., Vol. 36, pp. 2311–2319, 2009.
https://doi.org/10.1016/j.cor.2008.09.010
C. Fu and Z. Fu, "Optimization on Stochastic Inventory-Routing Problem in Multi-Cycle Two-Echelon System", Comput. Eng. Appl., Vol. 46, pp. 198–201, 2010.
L. Bertazzi, A. Bosco, and D. Laganà, "Managing Stochastic Demand in an Inventory Routing Problem with Transportation Procurement", Omega, Vol. 56, pp. 112–121, 2015.
https://doi.org/10.1016/j.omega.2014.09.010
A. Federgruen and P. Zipkin, "A Combined Vehicle Routing and Inventory Allocation Problem", Oper. Res., Vol. 32, No. 5, pp. 1019–1037, 1985.
https://doi.org/10.1287/opre.32.5.1019
L. C. Coelho, J. F. Cordeau, and G. Laporte, "Consistency in Multi-Vehicle Inventory-Routing", Transp. Res. Part C Emerg. Technol., Vol. 24, pp. 270–287, 2012.
https://doi.org/10.1016/j.trc.2012.03.007
R. Cuda, G. Guastaroba, and M. G. Speranza, "A Survey on Two-Echelon Routing Problems", Comput. Oper. Res., Vol. 55, pp. 185–199, 2015.
https://doi.org/10.1016/j.cor.2014.06.008
H. Zhang, Y. Liang, Q. Liao, X. Yan, Y. Shen, and Y. Zhao, "A Three-Stage Stochastic Programming Method for Lng Supply System Infrastructure Development and Inventory Routing in Demanding Countries", Energy, Vol. 133, pp. 424–442, 2017.
https://doi.org/10.1016/j.energy.2017.05.090
S. M. J. M. Al-E-Hashem, Y. Rekik, and E. M. Hoseinhajlou, "A Hybrid L-Shaped Method To Solve a Bi-Objective Stochastic Transshipment-Enabled Inventory Routing Problem", Int. J. Prod. Econ., 2017. https://doi.org/10.1016/j.ijpe.2017.06.020
https://doi.org/10.1016/j.ijpe.2017.06.020
L. C. Coelho, J.-F. Cordeau, and G. Laporte, "Thirty Years of Inventory-Routing", Transp. Sci., Vol. 48, No. 1, pp. 1–19, 2012.
https://doi.org/10.1287/trsc.2013.0472
M. Vidović, D. Popović, and B. Ratković, "Mixed Integer and Heuristics Model for the Inventory Routing Problem in Fuel Delivery", Int. J. Prod. Econ., Vol. 147, pp. 593–604, 2014.
https://doi.org/10.1016/j.ijpe.2013.04.034
Y. Shao, K. C. Furman, V. Goel, and S. Hoda, "A Hybrid Heuristic Strategy for Liquefied Natural Gas Inventory Routing", Transp. Res. Part C Emerg. Technol., Vol. 53, pp. 151–171, 2015.
https://doi.org/10.1016/j.trc.2015.02.001
A. Agra, M. Christiansen, A. Delgado, and L. M. Hvattum, "A Maritime Inventory Routing Problem with Stochastic Sailing and Port Times", Comput. Oper. Res., Vol. 61, pp. 18–30, 2015.
https://doi.org/10.1016/j.cor.2015.01.008
J. Cáceres-Cruz, A. A. Juan, S. E. Grasman, T. Bektas, and J. Faulin, "Combining Monte Carlo Simulation with Heuristics for Solving the Inventory Routing Problem with Stochastic Demands", In Proceedings of the 2012 Winter Simulation Conference (Wsc), pp. 1–9, 2012.
https://doi.org/10.1109/WSC.2012.6464999
A. J. Kleywegt, V. S. Nori, and M. W. P. Savelsbergh, "Dynamic Programming Approximations for a Stochastic Inventory Routing Problem", Source Transp. Sci., Vol. 38, No. 1, pp. 42–70, 2004.
https://doi.org/10.1287/trsc.1030.0041
B. Raa and E.-H. Aghezzaf, "A Practical Solution Approach for the Cyclic Inventory Routing Problem", Eur. J. Oper. Res., Vol. 192, No. 2, pp. 429–441, 2009.
https://doi.org/10.1016/j.ejor.2007.09.032
A. Mjirda, B. Jarboui, R. Macedo, S. Hanafi, and N. Mladenović, "A Two Phase Variable Neighborhood Search for the Multi-Product Inventory Routing Problem", Comput. Oper. Res., Vol. 52, pp. 291–299, 2014.
https://doi.org/10.1016/j.cor.2013.06.006
F. Niakan and M. Rahimi, "A Multi-Objective Healthcare Inventory Routing Problem; a Fuzzy Possibilistic Approach", Transp. Res. Part E Logist. Transp. Rev., Vol. 80, pp. 74–94, 2015.
L. C. Coelho, J. F. Cordeau, and G. Laporte, "Heuristics for Dynamic and Stochastic Inventory-Routing", Comput. Oper. Res., Vol. 52, pp. 55–67, 2014.
https://doi.org/10.1016/j.cor.2014.07.001
G.-S. Liu, K.-P. Lin, H.-W. Lee, and C.-Y. Wang, "A Study of Inventory-Routing Problem for the Distribution System By Applying Genetic Algorithm", In Business Innovation and Technology Management (Apbitm), 2011 Ieee International Summer Conference of Asia Pacific, pp. 104–108, 2011.
T. Singh, J. E. Arbogast, and N. Neagu, "An Incremental Approach Using Local-Search Heuristic for Inventory Routing Problem in Industrial Gases", Comput. Chem. Eng., Vol. 80, pp. 199–210, 2015.
https://doi.org/10.1016/j.compchemeng.2015.05.023
L. Qin, L. Miao, Q. Ruan, and Y. Zhang, "A Local Search Method for Periodic Inventory Routing Problem", Expert Syst. Appl., Vol. 41, pp. 765–778, 2014.
https://doi.org/10.1016/j.eswa.2013.07.100
L. Wong and N. H. Moin, "Ant Colony Optimization for One-To-Many Network Inventory Routing Problem", In 2014 Ieee International Conference on Industrial Engineering and Engineering Management, 2014, pp. 877–881, 2014.
https://doi.org/10.1109/IEEM.2014.7058764
L. C. Coelho and G. Laporte, "The Exact Solution of Several Classes of Inventory-Routing Problems", Comput. Oper. Res., Vol. 40, pp. 558–565, 2013.
https://doi.org/10.1016/j.cor.2012.08.012
M. Hewitt, G. Nemhauser, M. Savelsbergh, and J. H. Song, "A Branch-And-Price Guided Search Approach To Maritime Inventory Routing", Comput. Oper. Res., Vol. 40, pp. 1410–1419, 2013.
https://doi.org/10.1016/j.cor.2012.09.010
L. Bertazzi, A. Bosco, F. Guerriero, and D. Laganà, "A Stochastic Inventory Routing Problem with Stock-Out", Transp. Res. Part C Emerg. Technol., Vol. 27, pp. 89–107, 2013.
https://doi.org/10.1016/j.trc.2011.06.003
L. Bertazzi and M. G. Speranza, "Inventory Routing Problems with Multiple Customers", Euro J. Transp. Logist., Vol. 2, No. 3, pp. 255–275, 2013.
https://doi.org/10.1007/s13676-013-0027-z
S. M. J. Mirzapour Al-E-Hashem and Y. Rekik, "Multi-Product Multi-Period Inventory Routing Problem with a Transshipment Option: a Green Approach", Int. J. Prod. Econ., Vol. 157, pp. 80–88, 2014.
https://doi.org/10.1016/j.ijpe.2013.09.005
D. J. Papageorgiou, G. L. Nemhauser, J. Sokol, M. S. Cheon, and A. B. Keha, "Mirplib - a Library of Maritime Inventory Routing Problem Instances: Survey, Core Model, and Benchmark Results", Eur. J. Oper. Res., Vol. 235, pp. 350–366, 2014.
https://doi.org/10.1016/j.ejor.2013.12.013
L. C. Coelho and G. Laporte, "Improved Solutions for Inventory-Routing Problems Through Valid Inequalities and Input Ordering", Int. J. Prod. Econ., Vol. 155, pp. 391–397, 2014.
https://doi.org/10.1016/j.ijpe.2013.11.019
K. Li, B. Chen, A. I. Sivakumar, and Y. Wu, "An Inventory-Routing Problem with the Objective of Travel Time Minimization", Eur. J. Oper. Res., Vol. 236, pp. 936–945, 2014.
https://doi.org/10.1016/j.ejor.2013.07.034
A. A. Juan, S. E. Grasman, J. Cáceres-Cruz, and T. Bektaş, "A Simheuristic Algorithm for the Single-Period Stochastic Inventory-Routing Problem with Stock-Outs", Simul. Model. Pract. Theory, Vol. 46, pp. 40–52, 2014.
https://doi.org/10.1016/j.simpat.2013.11.008
P. Vansteenwegen and M. Mateo, "An Iterated Local Search Algorithm for the Single-Vehicle Cyclic Inventory Routing Problem", Eur. J. Oper. Res., Vol. 237, pp. 802–813, 2014.
https://doi.org/10.1016/j.ejor.2014.02.020
B. Raa, "Cyclic Versus Reactive Planning for Inventory Routing", Procedia - Soc. Behav. Sci., Vol. 111, pp. 909–917, 2014.
https://doi.org/10.1016/j.sbspro.2014.01.125
Y. Zhang, M. Qi, L. Miao, and E. Liu, "Hybrid Metaheuristic Solutions To Inventory Location Routing Problem", Transp. Res. Part E, Vol. 70, pp. 305–323, 2014.
https://doi.org/10.1016/j.tre.2014.07.010
T. Jia, X. Li, N. Wang, and R. Li, "Integrated Inventory Routing Problem with Quality Time Windows and Loading Cost for Deteriorating Items Under Discrete Time", Math. Probl. Eng., Vol. 2014, pp. 1–14, 2014.
https://doi.org/10.1155/2014/537409
M. Mes, M. Schutten, and A. P. Rivera, "Inventory Routing for Dynamic Waste Collection", Waste Manag., Vol. 34, No. 9, pp. 1564–1576, 2014.
https://doi.org/10.1016/j.wasman.2014.05.011
N. Nekooghadirli, R. Tavakkoli-Moghaddam, V. R. Ghezavati, and S. Javanmard, "Solving a New Bi-Objective Location-Routing-Inventory Problem in a Distribution Network By Meta-Heuristics", Comput. Ind. Eng., Vol. 76, pp. 204–221, 2014.
https://doi.org/10.1016/j.cie.2014.08.004
H. Z. A. Halim and N. H. Moin, "Solving Inventory Routing Problem with Backordering Using Artificial Bee Colony", In Ieee International Conference on Industrial Engineering and Engineering Management, 2014, pp. 913–917.
https://doi.org/10.1109/IEEM.2014.7058771
B. Raa, "Fleet Optimization for Cyclic Inventory Routing Problems", Int. J. Prod. Econ., Vol. 160, pp. 172–181, 2015.
https://doi.org/10.1016/j.ijpe.2014.10.006
J.-F. Cordeau, D. Laganà, R. Musmanno, and F. Vocaturo, "A Decomposition-Based Heuristic for the Multiple-Product Inventory-Routing Problem", Comput. Oper. Res., Vol. 55, pp. 153–166, 2015.
https://doi.org/10.1016/j.cor.2014.06.007
Y. Jiang and I. E. Grossmann, "Alternative Mixed-Integer Linear Programming Models of a Maritime Inventory Routing Problem", Comput. Chem. Eng., Vol. 77, pp. 147–161, 2015.
https://doi.org/10.1016/j.compchemeng.2015.03.005
A. Hemmati, M. Stålhane, L. M. Hvattum, and H. Andersson, "An Effective Heuristic for Solving a Combined Cargo and Inventory Routing Problem in Tramp Shipping", Comput. Oper. Res., Vol. 64, pp. 274–282, 2015.
https://doi.org/10.1016/j.cor.2015.06.011
S. Nurminarsih, A. Rusdiansyah, N. Siswanto, and A. Z. Gani, "Dynamic-Inventory Ship Routing Problem (D-Isrp) Model Considering Port Dwelling Time Information", Procedia Manuf. Serv. Sci. Procedia Manuf., Vol. 4, No. 4, pp. 344–351, 2015.
https://doi.org/10.1016/j.promfg.2015.11.050
J. Brinkmann, M. W. Ulmer, and D. C. Mattfeld, "Short-Term Strategies for Stochastic Inventory Routing in Bike Sharing Systems", Transp. Res. Procedia, Vol. 10, pp. 364–373, 2015.
https://doi.org/10.1016/j.trpro.2015.09.086
M. Zenker, S. Emde, and N. Boysen, "Cyclic Inventory Routing in a Line-Shaped Network", Eur. J. Oper. Res., Vol. 250, pp. 164–178, 2016.
https://doi.org/10.1016/j.ejor.2015.10.067
W. Lefever, E.-H. Aghezzaf, and K. Hadj-Hamou, "A Convex Optimization Approach for Solving the Single-Vehicle Cyclic Inventory Routing Problem", Comput. Oper. Res., Vol. 72, pp. 97–106, 2016.
https://doi.org/10.1016/j.cor.2016.02.010
Y. B. Park, J. S. Yoo, and H. S. Park, "A Genetic Algorithm for the Vendor-Managed Inventory Routing Problem with Lost Sales", Expert Syst. Appl., Vol. 53, pp. 149–159, 2016.
https://doi.org/10.1016/j.eswa.2016.01.041
A. Hemmati, L. M. Hvattum, M. Christiansen, and G. Laporte, "An Iterative Two-Phase Hybrid Matheuristic for a Multi-Product Short Sea Inventory-Routing Problem", Eur. J. Oper. Res., Vol. 252, pp. 775–788, 2016.
https://doi.org/10.1016/j.ejor.2016.01.060
F. Etebari and N. Dabiri, "A Hybrid Heuristic for the Inventory Routing Problem Under Dynamic Regional Pricing", Comput. Chem. Eng., Vol. 95, pp. 231–239, 2016.
https://doi.org/10.1016/j.compchemeng.2016.09.018
C. Cheng, M. Qi, X. Wang, and Y. Zhang, "Multi-Period Inventory Routing Problem Under Carbon Emission Regulations", Int. J. Prod. Econ., Vol. 182, pp. 263–275, 2016.
https://doi.org/10.1016/j.ijpe.2016.09.001
J. Y. J. Chow, "Dynamic Uav-Based Traffic Monitoring Under Uncertainty As a Stochastic Arc-Inventory Routing Policy", Int. J. Transp. Sci. Technol., Vol. 5, No. 3, pp. 167–185, 2016.
https://doi.org/10.1016/j.ijtst.2016.11.002
R. F. Roldán, R. Basagoiti, and L. C. Coelho, "Robustness of Inventory Replenishment and Customer Selection Policies for the Dynamic and Stochastic Inventory-Routing Problem", Comput. Oper. Res., Vol. 74, pp. 14–20, 2016.
https://doi.org/10.1016/j.cor.2016.04.004
M. Chitsaz, A. Divsalar, and P. Vansteenwegen, "A Two-Phase Algorithm for the Cyclic Inventory Routing Problem", Eur. J. Oper. Res., Vol. 254, No. 2, pp. 410–426, 2016.
https://doi.org/10.1016/j.ejor.2016.03.056
M. Soysal, "Closed-Loop Inventory Routing Problem for Returnable Transport Items", Transp. Res. Part D Transp. Environ., Vol. 48, pp. 31–45, 2016.
https://doi.org/10.1016/j.trd.2016.07.001
M. Li, Z. Wang, and F. T. S. Chan, "A Robust Inventory Routing Policy Under Inventory Inaccuracy and Replenishment Lead-Time", Transp. Res. Part E Logist. Transp. Rev., Vol. 91, pp. 290–305, 2016.
R. Nambirajan, A. Mendoza, S. Pazhani, T. T. Narendran, and K. Ganesh, "Care: Heuristics for Two-Stage Multi-Product Inventory Routing Problems with Replenishments", Comput. Ind. Eng., Vol. 97, pp. 41–57, 2016.
https://doi.org/10.1016/j.cie.2016.04.004
E. Santos, L. S. Ochi, L. Simonetti, and P. H. González, "A Hybrid Heuristic Based on Iterated Local Search for Multivehicle Inventory Routing Problem", Electron. Notes Discret. Math., Vol. 52, pp. 197–204, 2016.
https://doi.org/10.1016/j.endm.2016.03.026
M. Zhalechian, R. Tavakkoli-Moghaddam, B. Zahiri, and M. Mohammadi, "Sustainable Design of a Closed-Loop Location-Routing-Inventory Supply Chain Network Under Mixed Uncertainty", Transp. Res. Part E Logist. Transp. Rev., Vol. 89, pp. 182–214, 2016.
A. Ghorbani and M. R. Akbari Jokar, "A Hybrid Imperialist Competitive-Simulated Annealing Algorithm for a Multisource Multi-Product Location-Routing-Inventory Problem", Comput. Ind. Eng., Vol. 101, pp. 116-127, 2016.
https://doi.org/10.1016/j.cie.2016.08.027
I. T. Peres, H. M. Repolho, R. Martinelli, and N. J. Monteiro, "Optimization in Inventory-Routing Problem with Planned Transshipment: a Case Study in the Retail Industry", Int. J. Prod. Econ., Vol. 193, pp. 748–756, 2017.
https://doi.org/10.1016/j.ijpe.2017.09.002
F. Rayat, M. Musavi, and A. Bozorgi-Amiri, "Bi-Objective Reliable Location-Inventory-Routing Problem with Partial Backordering Under Disruption Risks: a Modified {Amosa} Approach", Appl. Soft Comput., Vol. 59, pp. 622–643, 2017.
https://doi.org/10.1016/j.asoc.2017.06.036
N. Dabiri, M. J. Tarokh, and M. Alinaghian, "New Mathematical Model for the Bi-Objective Inventory Routing Problem with a Step Cost Function: a Multi-Objective Particle Swarm Optimization Solution Approach", Appl. Math. Model., Vol. 49, pp. 302–318, 2017.
https://doi.org/10.1016/j.apm.2017.03.022
A. De, S. K. Kumar, A. Gunasekaran, and M. K. Tiwari, "Sustainable Maritime Inventory Routing Problem with Time Window Constraints", Eng. Appl. Artif. Intell., Vol. 61, pp. 77–95, 2017.
https://doi.org/10.1016/j.engappai.2017.02.012
M. Rahimi, A. Baboli, and Y. Rekik, "Multi-Objective Inventory Routing Problem: a Stochastic Model To Consider Profit, Service Level and Green Criteria", Transp. Res. Part E Logist. Transp. Rev., Vol. 101, pp. 59–83, 2017.
S. Hasni, S. Toumi, B. Jarboui, and A. Mjirda, "{Gvns} Based Heuristic for Solving the Multi-Product Multi-Vehicle Inventory Routing Problem", Electron. Notes Discret. Math., Vol. 58, pp. 71–78, 2017.
https://doi.org/10.1016/j.endm.2017.03.010
C. Cheng, P. Yang, M. Qi, and L.-M. Rousseau, "Modeling a Green Inventory Routing Problem with a Heterogeneous Fleet", Transp. Res. Part E Logist. Transp. Rev., Vol. 97, pp. 97–112, 2017.
B. Raa and W. Dullaert, "Route and Fleet Design for Cyclic Inventory Routing", Eur. J. Oper. Res., Vol. 256, No. 2, pp. 404–411, 2017.
https://doi.org/10.1016/j.ejor.2016.06.009
G. Iassinovskaia, S. Limbourg, and F. Riane, "The Inventory-Routing Problem of Returnable Transport Items with Time Windows and Simultaneous Pickup and Delivery in Closed-Loop Supply Chains", Int. J. Prod. Econ., Vol. 183, Part, pp. 570–582, 2017.
S. K. Goyal and B. C. Giri, "Recent Trends in Modeling of Deteriorating Inventory", Eur. J. Oper. Res., Vol. 134, No. 1, pp. 1–16, 2001.
https://doi.org/10.1016/S0377-2217(00)00248-4
R. Li, H. Lan, and J. R. Mawhinney, "A Review on Deteriorating Inventory Study", J. Serv. Sci. Manag., Vol. 3, No. 1, pp. 117–129, 2010.
https://doi.org/10.4236/jssm.2010.31015
J. A. Orjuela-Castro, F. S. Morales-Aguilar, and L. F. Mejía-Flórez, "Which is the Best Supply Chain for Perishable Fruits, Lean Or Agile?", Rev. Colomb. Ciencias Hortícolas, Vol. 11, pp. 294–305, 2017.
https://doi.org/10.17584/rcch.2017v11i2.5950
A. Federgruen, G. Prastacos, and P. H. Zipkin, "An Allocation and Distribution Model for Perishable Products", Oper. Res., Vol. 34, No. 1, pp. 75–82, 1986.
https://doi.org/10.1287/opre.34.1.75
T. Le, A. Diabat, J. P. Richard, and Y. Yih, "A Column Generation-Based Heuristic Algorithm for An Inventory Routing Problem with Perishable Goods", Optim. Lett., Vol. 7, No. 7, pp. 1481–1502, 2013.
https://doi.org/10.1007/s11590-012-0540-2
J. A. Orjuela-Castro, L. A. Sanabria-Coronado, and A. M. Peralta-Lozano, "Coupling Facility Location Models in the Supply Chain of Perishable Fruits", Res. Transp. Bus. Manag., Vol. 24, pp. 73–80, 2017.
https://doi.org/10.1016/j.rtbm.2017.08.002
B. Notarnicola, S. Sala, A. Anton, S. J. Mclaren, E. Saouter, and U. Sonesson, "The Role of Life Cycle Assessment in Supporting Sustainable Agri-Food Systems: a Review of the Challenges", J. Clean. Prod., pp. 1–11, 2016.
H. Shaabani and I. N. Kamalabadi, "An Efficient Population-Based Simulated Annealing Algorithm for the Multi-Product Multi-Retailer Perishable Inventory Routing Problem", Comput. Ind. Eng., Vol. 99, pp. 189–201, 2016.
https://doi.org/10.1016/j.cie.2016.07.022
Y. Li, F. Chu, Z. Yang, and R. W. Calvo, "A Production Inventory Routing Planning for Perishable Food with Quality Consideration", Ifac-Papersonline, Vol. 49, No. 3, pp. 407–412, 2016.
https://doi.org/10.1016/j.ifacol.2016.07.068
M. Rahimi, A. Baboli, and Y. Rekik, "Sustainable Inventory Routing Problem for Perishable Products By Considering Reverse Logistic", Ifac-Papersonline, Vol. 49, No. 12, pp. 949–954, 2016.
https://doi.org/10.1016/j.ifacol.2016.07.898
J. Lmariouh, L. C. Coelho, N. Elhachemi, G. Laporte, A. Jamali, and D. Bouami, "Solving a Vendor-Managed Inventory Routing Problem Arising in the Distribution of Bottled Water in Morocco", Eur. J. Ind. Eng., Vol. 11, No. 2, pp. 168–184, 2017.
https://doi.org/10.1504/EJIE.2017.083249
M. Rahimi, A. Baboli, and Y. Rekik, "Inventory Routing Problem for Perishable Products By Considering Customer Satisfaction and Green Criteria", In Dynamics in Logistics: Proceedings of the 5th International Conference Ldic, 2016 Bremen, Germany, M. Freitag, H. Kotzab, and J. Pannek, Eds. Cham: Springer International Publishing, pp. 445–455, 2017.
https://doi.org/10.1007/978-3-319-45117-6_39
A. Hiassat, A. Diabat, and I. Rahwan, "A Genetic Algorithm Approach for Location-Inventory-Routing Problem with Perishable Products", J. Manuf. Syst., Vol. 42, pp. 93–103, 2017.
https://doi.org/10.1016/j.jmsy.2016.10.004
A. Azadeh, S. Elahi, M. H. Farahani, and B. Nasirian, "A Genetic Algorithm-Taguchi Based Approach To Inventory Routing Problem of a Single Perishable Product with Transshipment", Comput. Ind. Eng., Vol. 104, pp. 124–133, 2017.
https://doi.org/10.1016/j.cie.2016.12.019
B. Vahdani, S. T. A. Niaki, and S. Aslanzade, "Production-Inventory-Routing Coordination with Capacity and Time Window Constraints for Perishable Products: Heuristic and Meta-Heuristic Algorithms", J. Clean. Prod., Vol. 161, No. Supplement C, pp. 598–618, 2017.
C. Chao, T. Zhihui, and Y. Baozhen, "Optimization of Two-Stage Location- Routing-Inventory Problem with Time-Windows in Food Distribution Network", Ann. Oper. Res., pp. 1–24, May 2017.
https://doi.org/10.1007/s10479-017-2514-3
Y. Crama, M. Rezaei, M. Savelsbergh, and T. Van Woensel, "Stochastic Inventory Routing for Perishable Products", Transp. Sci., pp. 1–41, 2017.
M. Tavana, A.-R. Abtahi, D. Di Caprio, R. Hashemi, and R. Yousefi-Zenouz, "An Integrated Location-Inventory-Routing Humanitarian Supply Chain Network with Pre- and Post-Disaster Management Considerations", Socioecon. Plann. Sci., P. , 2017. https://doi.org/10.1016/j.seps.2017.12.004
https://doi.org/10.1016/j.seps.2017.12.004
Y. Li, F. Chu, and K. Chen, "Coordinated Production Inventory Routing Planning for Perishable Food", Ifac-Papersonline, Vol. 50, No. 1, pp. 4246–4251, 2017.
https://doi.org/10.1016/j.ifacol.2017.08.829
E. Morganti and J. González-Feliu, "City Logistics for Perishable Products. The Case of the Parma's Food Hub", Case Stud. Transp. Policy, Vol. 3, No. 2, pp. 120–128, 2015.
https://doi.org/10.1016/j.cstp.2014.08.003
M. Jedliński, "The Position of Green Logistics in Sustainable Development of a Smart Green City", Procedia - Soc. Behav. Sci., Vol. 151, pp. 102–111, 2014.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 16 de noviembre de 2017; Revisión recibida: 12 de marzo de 2018; Aceptado: 21 de marzo de 2018
Resumen
Contexto:
Revisión de literatura del problema de ruteo e inventarios (IRP) aplicado a las cadenas de suministro de productos perecederos. Se identifican y describen los diferentes enfoques en cuanto a estructuras, modelos y métodos de solución.
Método:
Se realiza una revisión sistemática de la literatura en diferentes bases de datos bibliográficas y se plantea una taxonomía que clasifica las características de los estudios, lo anterior durante el periodo comprendido entre 2004 y 2017
Resultados:
Se encuentra que la mayoría de algoritmos propuestos son de carácter heurístico. Debido a complejidad computacional inherente al problema, se usan metaheurísticas y mateheurísticas combinadas con métodos exactos. Se aplican principalmente en alimentos, medicamentos y sangre humana. Las restricciones que diferencian de otros tipos de IRP son las de periodo de vida útil y deterioro.
Conclusiones:
Las condiciones y particularidades de la cadena de suministro de perecederos hace necesario que se planteen nuevas variables, parámetros, restricciones y funciones objetivo; por otro lado, en los estudios revisados no se establecen diferencias claras al involucrar la perfectibilidad de los productos en los modelos. Las futuras investigaciones deberán tener en cuenta las múltiples maneras en las cuales se lleva a cabo el deterioro con factores como la temperatura, la luz, el oxígeno, la humedad y en algunos casos los microorganismos; asimismo, incluir en los modelos la cadena de frío, normas de higiene, contaminación del aire, emisiones de gases de efecto invernadero, generación de residuos, ocupación de vías y demás aspectos relacionados con city logistics y green logistics.
Palabras clave:
Gestión de la cadena de suministro, IRP, optimización, perecederos, problema de ruteo e inventarios, Idioma: Español.Abstract
Context:
This paper presents a literature review of the Inventories Routing Problem (IRP) applied to supply chains of perishable products. Different approaches to solve this problem are identified and described in terms of structures, models and solution methods.
Method:
A systematic literature review is conducted searching in different bibliographic databases and selecting the most relevant studies within the period 2004 to 2017. The results are analyzed so as to propose a taxonomy to classify and compare the different approaches proposed to address this problem.
Results:
We identified that the majority of studies consider heuristic-based algorithms to solve the pro- blem. Because of its computational complexity the methods resort to metaheuristics and mateheuristics combined with exact methods. Regarding the application to specific supply chains of perishable products, they refer mostly to processed foods, medicines, and human blood. The constraints that differentiate this problem from other types of IRP are useful life and deterioration.
Conclusions:
The conditions and particularities of the supply chain of perishables products imply the need to consider new variables, parameters, constraints and objective functions; in the reviewed studies it is not clearly defined the differences involved when considering the perishability of the products in the supply chain. Future research should take into account the multiple ways in which deterioration is carried out with factors such as temperature, light, oxygen, humidity and in some cases microorganisms. Also include in the models the cold chain, hygiene standards, air pollution, emissions of greenhouse gases, generation of waste, occupation of roads and other aspects related to City Logistics and Green Logistics.
Keywords:
Supply chain management, optimization, perishables, inventory routing problem, IRP, Languag: Spanish.1. Introducción
El problema conjunto de ruteo e inventarios (IRP, por sus siglas en inglés, Inventory Routing Problem) tiene importancia en la gestión operativa de la cadena de suministro (CS) [1]. El estudio simultáneo de ruteo e inventarios es complejo, sin embargo, se ha demostrado que tiene un impacto mayor en el rendimiento global de la CS [2]. En la actualidad los modelos IRP consideran objetivos como la minimización de desperdicios de alimentos, uso de energía y emisiones [3].
Se realiza una revisión sistemática de la literatura del IRP para productos perecederos y, con base en su evolución histórica, se propone una taxonomía con respecto a la formulación matemática, los métodos y técnicas de solución propuestos. Se describen los modelos más importantes respecto a los problemas de aplicación.
En la segunda sección se presenta la metodología, en la tercera y la cuarta se analizan los modelos de inventarios y el problema de ruteo de vehículos (VRP, por sus siglas en inglés, Vehicle Routing Problem) para perecederos de forma independiente. La descripción del IRP y la taxonomía de modelos conforman la quinta sección, la cual está conformada por las subsecciones que describen los tipos de modelos y métodos de solución, la clasificación de variables de decisión, restricciones y los parámetros. Las conclusiones y los trabajos futuros se presentan en la sexta y séptima sección respectivamente.
2. Metodología
Para la elaboración de este artículo se realizó una revisión sistemática de la literatura, basado en la metodología propuesta por Aguinis y Glavas [4], según los pasos propuestos empleados por [5] que son buscar los artículos, revisarlos y clasificarlos, generar una taxonomía y establecer los tipos de modelos y sus características. Teniendo en cuenta lo anterior, se consultaron seis bases de datos: Scopus, IEEE ProQuest, MasterFILE Elite, Springer Link, ISI Web of Knowledge y JSTOR, así como el buscador de bibliografía Google Académico. En los artículos publicados en el periodo 2004 a 2017 se presenta una tendencia creciente de publicaciones sobre los problemas de ruteo e inventario de productos perecederos.
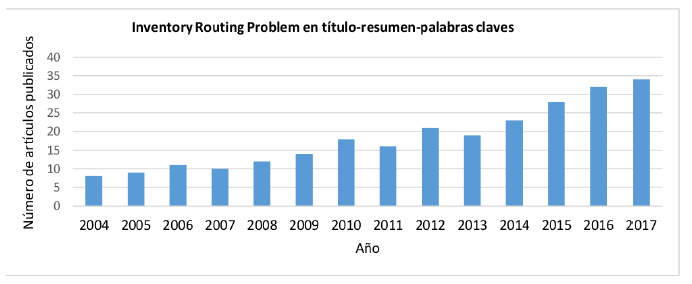
La primera revisión bibliográfica del IRP, se realizó con base en los artículos más relevantes, teniendo en cuenta los antecedentes y número de citaciones. El procedimiento consistió en identificar en el título, resumen y palabras claves las siguientes fórmulas de búsqueda: Food Supply Chain, IRP y VMI. La tendencia histórica de los artículos se presenta en la Figura 1.
Figura 1: Número de artículos publicados en IRP en el periodo comprendido entre 2004 y 2017.
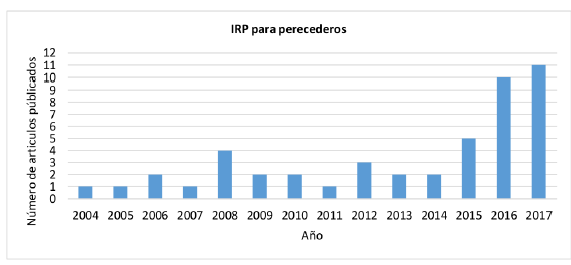
En una segunda búsqueda se incluyó la palabra “perishable” en las fórmulas de búsqueda, los artículos se redujeron a 47 (18,43 %) de un total de 255 obtenidos en la primera búsqueda, se presenta un incremento mayor en 2016-2017 (Figura 2).
Figura 2: Gráfica de artículos publicados de IRP en perecederos 2004 y octubre de 2017.
Se realizó una tercera búsqueda que incluyó el término “food”, se referencian tres artículos en Scopus: [3], [6] y [7]. Respecto al IRP para sangre humana, se identifican dos artículos: [8], [9]. Con la palabra “frutas” o “fruta” un solo artículo lo aplica a higos y cerezas [10].
El objetivo de este documento es determinar el estado de la literatura en los estudios que han trabajado el IRP como marco de referencia para su aplicación a la logística de las CS de perecederos. Las preguntas planteadas fueron ¿cuáles son los modelos matemáticos y métodos de solución más representativos en problemas IRP?, ¿qué estructuras a nivel de variables, parámetros, restricciones y funciones objetivo existen en las aplicaciones de IRP?, y ¿qué medidas de desempeño logístico son usadas en el IRP para productos alimenticios perecederos?
3. Análisis de modelos de inventarios para perecederos
La gestión de inventarios ha generado modelos que toman como referencia el modelo de cantidad económica de pedido (EOQ, por sus siglas en inglés, Economic Order Quantity), el cual asume que los productos tienen vida ´útil ilimitada. Supuesto que no aplica en los productos perecederos [11],[12].
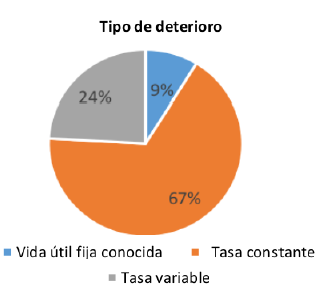
El 67% de los artículos analizados por [15] consideran que el deterioro de los productos es a una tasa constante, como se observa en la Figura 3, lo cual aplica a algunos productos perecederos. Sin embargo, para los alimentos, y en especial las frutas, dicho supuesto no es completamente apropiado, pues en estos productos la condición de frescura, que disminuye gradualmente con el tiempo, influye en la demanda del producto [13], [14].
Figura 3.: Gráfica que muestra el tipo de deterioro en perecederos.
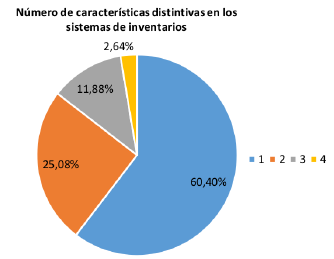
En [15] se clasifican ocho características distintivas en los sistemas de inventario: permiten periodos de desabastecimiento, consideran políticas de pago a proveedores, determinan una política de precios óptima, consideran sistemas multiniveles, tienen en cuenta el valor del dinero en el tiempo, consideran dos o más almacenes, estudian múltiples productos e introducen parámetros inciertos o difusos. El 60,40% de los 303 artículos que analizan incluye solamente una, siendo la más frecuente que los modelos permiten periodos de desabastecimiento; no obstante, la mayoría los modelos revisados tienen como una de sus restricciones evitar el desabastecimiento. La menor parte de los artículos (2,64 %) incluye cuatro de las características listadas. Los resultados porcentuales de la cantidad incluida de características distintivas en los modelos, se muestran en la Figura 4.
Figura 4: Gráfica consolidada de las características distintivas de los modelos de demanda conocida.
En [16] se asume que la demanda se genera en fuentes finitas y el tiempo de vida de cada producto se supone como una función exponencial, como es el caso del modelo de revisión continua de inventario para perecederos, aplicado por [17]. El contexto son las tiendas y supermercados, se busca disminuir costos al minimizar la canti- dad de residuos que se derivan de las pérdidas por fecha de vencimiento. Los resultados incluyen: reducción de los plazos de entrega, sustitución de la demanda y surtidos limitados. En [15] se resalta que solo un artículo hasta el 2013 considera una política óptima de inventario para varios eslabones de la CS, múltiple productos sujetos a deterioro y un adecuado sistema de información para un sistema multinivel.
El trabajo de [18] proporciona estrategias de planificación de la CS con limitaciones de vida para productos sujetos a deterioro. Encuentran vacíos de investigación con respecto a tiempos de preparación y alistamiento en la secuencia de costos y las estructuras de múltiples niveles que facilitan el deterioro de los productos en el procesamiento interno, clasifican de forma extensiva los modelos que se usan. En su mayoría se desprenden del modelo EOQ para la CS, incluso analizan la producción mediante el modelo EPQ.
Para demanda con comportamiento estocástico se han desarrollado modelos como [19]. Se propone que la política de inventario (1, T) se aplique a productos perecederos, así, el intervalo de tiempo entre dos órdenes consecutivas y el valor del tamaño del pedido son constantes. Se asume el problema de inventario como un sistema de líneas de espera M/M/1. Si el tiempo de permanencia de un cliente supera un valor constante predeterminado, este abandona el sistema.
Los estudios anteriores proponen asumir el deterioro y la demanda desde una perspectiva más real. Se separan de la mayoría de estudios de inventarios para productos perecederos que consideran el deterioro como un parámetro de vida útil fija, el cual no depende de las características del producto y la demanda como conocida. Sin embargo, tampoco tienen en cuenta la cooperación e integración de varios eslabones de la CS [20], factores clave que se puede generar en el contexto de modelos IRP.
4.Análisis de VRP en productos perecederos
El VRP es un problema de optimización combinatoria donde un conjunto de clientes, geográficamente dispersos, deben ser servidos por una flota de vehículos. Uno de los supuestos principales es que cada vehículo puede realizar solo una ruta en el horizonte de planeación [21], una ruta implica un recorrido que inicia en un nodo determinado, pasando por un subconjunto de nodos en una secuencia dada y, por lo general, el recorrido termina en el nodo inicial [22]. Los nodos pueden representar clientes que deben ser visitados en alguna ruta. El tamaño total de las entregas no debe exceder la capacidad de los vehículos y al mismo tiempo satisfacer la demanda [23]. Los objetivos al obtener las rutas apropiadas, son minimizar el costo total del viaje o la distancia recorrida.
Varios estudios han hecho revisión de la literatura de VRP. En [24] se analizan 28 variaciones del problema de ruteo de vehículos que podrían ser adaptados al IRP, que incluso se considera una extensión del VRP [25]. La revisión realizada en [26], muestra un crecimiento en las últimas décadas del número de métodos de solución, ya que la posibilidad de implementar instancias más grandes hace que el CVRP o VRP capacitado, una flota de vehículos homogénea y con la misma capacidad, sea la variante más usada -88,89%- en los artículos revisados. Lo anterior también sucede en la mayoría de los modelos IRP, ya que pocos autores han planteado el uso de flota heterogénea y transporte multimodal [27].
En cuanto al VRP aplicado a perecederos, resalta el VRP con nodos estocásticos (SVRP, por sus siglas en inglés, Vehicle Routing Problem Stochastic Nodes) para el caso de flores estudiado en [28]. En la literatura se proponen diferentes problemas que implican la distribución de productos alimenticios de carácter perecedero [29], [30], aunque la mayoría de los modelos no tiene en cuenta de forma explícita la degradación de calidad (pérdida de frescura) de los alimentos durante el transporte y podrían ser aplicados a productos no perecederos [31]. En la actualidad, modelos VRP han sido usados en el comercio electrónico y las compras en línea. Los alimentos son distribuidos mediante un modelo denominado el E-Problema de ruteo y entrega de comestibles (EDRP, por sus siglas en inglés, E-grocery Delivery Routing Problem) [32].
El VRP, al ser un problema enfocado al ruteo de vehículos, no considera la gestión de inventarios en el tiempo, los modelos revisados no tienen en cuenta las condiciones de perecibilidad de los productos, aunque ha tenido una evolución importante de los métodos de solución que permite disminuir la complejidad computacional e incluir más nodos. El desempeño global de la CS puede ser mejor aplicando modelos IRP.
5.Inventory Routing Problem (IRP)
Quizá el primer modelo que propende por la integración entre agentes de la CS es el inventario administrado por el vendedor (VMI, por sus siglas en inglés, Vendor Managed Inventory) [33]. El VMI considera la colaboración directa entre un proveedor y comprador, el vendedor asume la responsabilidad sobre la gestión del inventario de sus clientes, decide la cantidad, el tiempo de los envíos y garantiza que no se presente desabastecimiento por la disponibilidad de información precisa y oportuna para los agentes de la CS [34]. La política VMI es considerada como un acuerdo gana-gana [35], no obstante, su implementación implica decisiones de ruteo e inventarios para los clientes [31], [36], [37], por lo cual se hace necesario integrar estos dos aspectos (IRP) [29], [38].
El estudio del problema conjunto de ruteo e inventarios data de 1983 con el artículo seminal de [39]; en este trabajo los autores proponen un modelo de programación entera, aplicado a la distribución de gases industriales. Se obtienen rutas, asignación de vehículos, costos de transporte y volúmenes de entrega. La demanda se supone estocástica y se tiene en cuenta una política de cumplimiento para los niveles de inventario [39]. Algunas versiones IRP consideran multiproducto, con minoristas que tienen demandas de producto variable en un horizonte de planeación dado [40].
En el problema estocástico de ruteo e inventarios (SIRP, por sus siglas en inglés, Stochastic Inventory Routing Problem). Un objetivo es que el proveedor determine una política de distribución que minimice su valor descontado esperado (ingresos menos costos) en el horizonte de planeación que puede ser finito o infinito [41]. La estocasticidad corresponde a la demanda y se puede producir escasez [42].
El IRP considera en simultáneo dos problemas: enrutamiento de vehículos y gestión de inventario. Uno o varios proveedores ofertan productos a un número de clientes geográficamente dispersos, dado un conjunto de restricciones. El propósito central es brindar soluciones de logística integrada, se pretende la coordinación de políticas para el reabastecimiento de inventarios y planes de distribución que minimicen los costos totales [43]. El proveedor toma decisiones de cuánto y cuándo entregar a cada cliente, y en qué rutas [44], así como el tipo y capacidad de vehículo a utilizar [45].
La demanda de los clientes puede ser estocástica con distribución normal y tiempos de viaje promedios [6]. En los modelos IRP también se ha utilizado optimización con demanda bajo incertidumbre, mediante programación entera mixta no lineal. Se determina un plan de distribución factible con parámetros de tiempo de ciclo de reposición y nivel de inventario de seguridad, aplicando simulación de Monte Carlo [3].
Se ha propuesto un método de programación estocástica de tres etapas para el sistema de suministro de gas natural licuado a lo largo del río Yangtzé en China, el modelo empleado es de programación lineal entera mixta, minimiza los costos de entrega, licuefacción, compra y construcción [46].
En la actualidad, los modelos SIRP tienen como reto contrarrestar las fluctuaciones de la demanda, así como el impacto ambiental que generan los procesos de distribución e inventario y no solamente minimizar costos; por ejemplo, se emplea transbordo como una forma de mejorar el desempeño económico y ambiental [47].
5.1. Taxonomía de modelos IRP
A través del tiempo se han propuesto modelos IRP específicos para diferentes situaciones, sin embargo, la complejidad del problema es un reto para su formulación. Para más detalles sobre los modelos generales de IRP, Coelho, Cordeau y Laporte realizan una clasificación a partir de una revisión de la literatura en el periodo 1982- 2012 [48]. En esta parte se realiza una revisión para los artículos IRP del 2013 al 2017, se propone una taxonomía que clasifica los artículos por tipos de modelos y métodos de solución, se clasifican las variables de decisión, los tipos de restricciones y parámetros.
5.1.1. Tipos de modelos y métodos de solución
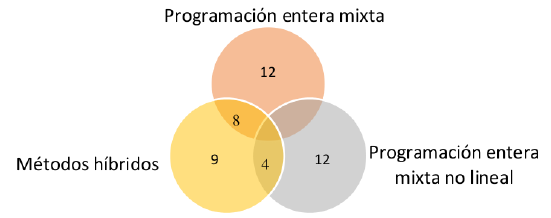
Siguiendo la Tabla I, el modelo matemático empleado con mayor frecuencia es la programación entera mixta (44,4 %), le siguen la programación entera mixta no lineal (35,6 %) y la programación dinámica (11,1 %). La programación lineal y la programación entera (4,4 %) son las menos utilizadas. Las intersecciones hacen referencia al modelo y método aplicado simultáneamente y se muestran en la Figura 5.
Figura 5: Frecuencia según modelo matemático empleado en IRP.
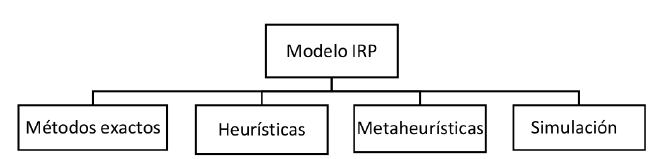
El IRP se deriva del VRP clásico y se clasifica como un problema NP-Hard, debido a esta situación la mayoría de trabajos proponen heurísticas, metaheurísticas y mateheurísticas para su solución, aunque algunos autores han abordado el problema con algoritmos exactos. Para el análisis de los modelos se establecieron cuatro categorías: métodos exactos, heurísticas meta-heurísticas y simulación como se observa en la Figura 6.
Figura 6: Esquema de los métodos de solución IRP más usados en la literatura.
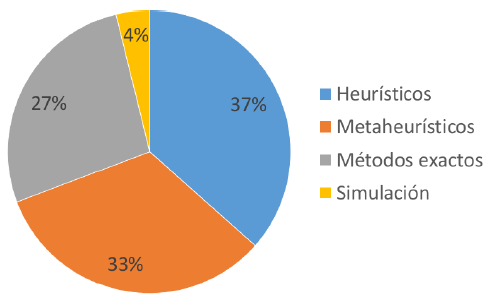
Según la Tabla I, la mayor parte de trabajos IRP han aplicado heurísticas que exploran el espacio de solución mediante el uso de estructuras simples que descomponen el IRP en subproblemas jerárquicos. Los métodos de simulación representan la menor proporción. Los porcentajes por categoría se muestran en la Figura 7.
Figura 7: Gráfica porcentajes según método de solución IRP.
En [49] se plantea una heurística constructiva para resolver una versión multiproducto y multiperiodo para la distribución de combustible; por otro lado, en [50] proponen una heurística de dos fases: la primera considera un algoritmo de búsqueda adaptativa aleatorizada y la segunda fase mejora la solución con programación entera mixta y nuevas técnicas de búsqueda de vecindad variable.
Para el problema estocástico se propone un método de solución de ramificación y corte. La matriz de costo de transporte es simétrica y contempla arcos no dirigidos con el fin de reducir el número de variables [51]. Sin embargo, una solución económica óptima a veces puede dar lugar a inconvenientes tanto para el proveedor como para los clientes, es el caso de entregas muy pequeñas durante días consecutivos, seguidas de una entrega muy grande. Después el cliente no es visitado durante un largo periodo [30], [46] y [47].
El IRP también ha sido estudiado aplicando programación dinámica. Se formula una decisión de Markov con un método propuesto de aproximación, se divide el problema general en subproblemas, eligiendo subconjuntos de clientes en una sola etapa [53], incluso los vehículos puedan realizar más de una ruta por periodo y se puede resolver mediante heurísticas, como la de generación de columnas [54]. Se han propuesto algoritmos de búsqueda local rápida para el caso de un solo vehículo; asimismo, se aplican políticas de inventario cíclico que restringen el conjunto de posibles soluciones al problema [55].
En [56] se propone una heurística con enfoque de dos fases. En la primera se combinan dos métodos para transformar el modelo en uno de programación lineal entera; en la segunda fase se aplica un método multiobjetivo difuso que resuelve el modelo de programación obteniendo la solución óptima. En [57] se desarrolla una metaheurística adaptativa de búsqueda por vecindad, asumen el IRP como un caso especial de un problema más amplio que incluye transbordos. El algoritmo lo desarrollan en dos fases, una definición de rutas de vehículos a través de la búsqueda por vecindad y la determinación de cantidades a entregar con un algoritmo exacto que minimiza el costo total de la red.
Entre los métodos híbridos, la simulación (52 %) y los algoritmos genéticos (11,5 %), así como la gran búsqueda local adaptativa (6 %) son los más usados; estos métodos tienen en cuenta el horizonte de planeación, la cantidad de eslabones, la variedad de producto y la cantidad de nodos en la red. Los criterios presentados que se han estudiado en algún momento incluyen versiones específicas del IRP. Con un solo cliente [53], con múltiples clientes [58], con entregas directas [59], multiproducto [60], con varios proveedores y clientes [61], con flota heterogénea [40], entre otros. Los modelos matemáticos se pueden clasificar en cuatro tipos como se muestra en la Tabla I, donde se resumen los modelos y métodos de solución que se obtuvieron de la evaluación bibliográfica del periodo 2013 a 2017. Dado que se dispone de una revisión hasta 2012 [48].
Tabla I: Modelos y métodos de solución para el IRP.
Las principales variaciones del IRP que se han publicado en los últimos cuatro años son: IRP with maritime transportation (MIRP), single-vehicle cyclic IRP (SV-CIRP), multi-product multivehicle IRP (MMIRP), vendormanaged IRP with lost sales (VMIRPL), IRP with time windows (IRPTW), stochastic IRP (SIRP), dynamic and stochastic IRP (DSIRP), stochastic programming IRP (SMIRP), healthcare IRP (HIRP), single-period stochastic IRP (SSIRP), infinite-horizon deterministic IRP (IHIRP), cyclic IRP (CIRP), IRP with transshipments (IRPT), inventory routing and pricing problem (IRPP), multi-product and multi-period Location-IRP (LIRP), perishable IRP (PIRP).
5.1.2. Clasificación por variables de decisión
Se han definido tres conjuntos para agrupar las variables de decisión, estos son costo, tiempo y cantidad, los cuales son descritos en la Tabla II. La clasificación depende de las variables de asignación, por ejemplo, se usan variables binarias para determinar los nodos a visitar en las rutas y variables continuas para las cantidades a entregar. Se identifican diez tipos de costos en las funciones objetivo, el costo total es la principal variable de decisión y el costo de mantener el inventario es fundamental en la estructura de los modelos analizados.
Costos C: CTE: total por envió, CTV: total por viaje, CTA: total de almacenamiento, CTT: total del transporte, C TI: total inventario, CIV: incurridos por el vendedor, CT: total, CA: alistamiento, CMP: manipulación del producto, CMI mantener inventario. Tiempo T: TTV: total por viaje, TVV: viaje por vehículo, TR: por ruta, TEE: envió entre vehículos, TTE: total de espera, TCD: total de cargue y descargue. Cantidad C: CPS: producto sobrante, CPE: del producto entregado, CEE: entrega por estación, CPV: producto por vehículo, CAR: transportada a través del arco, CAD: a descargar, CIC: inventario por cliente, CVR: vehículos requeridos, CEA: espacio de almacenamiento requerido. Inventario I: IRA: reposición por almacén, IRV: reposición por vendedor, NI: nivel de inventario. LR: longitud de la ruta, RV: ruta por vehículo
Tabla II: Variables de decisión IRP.
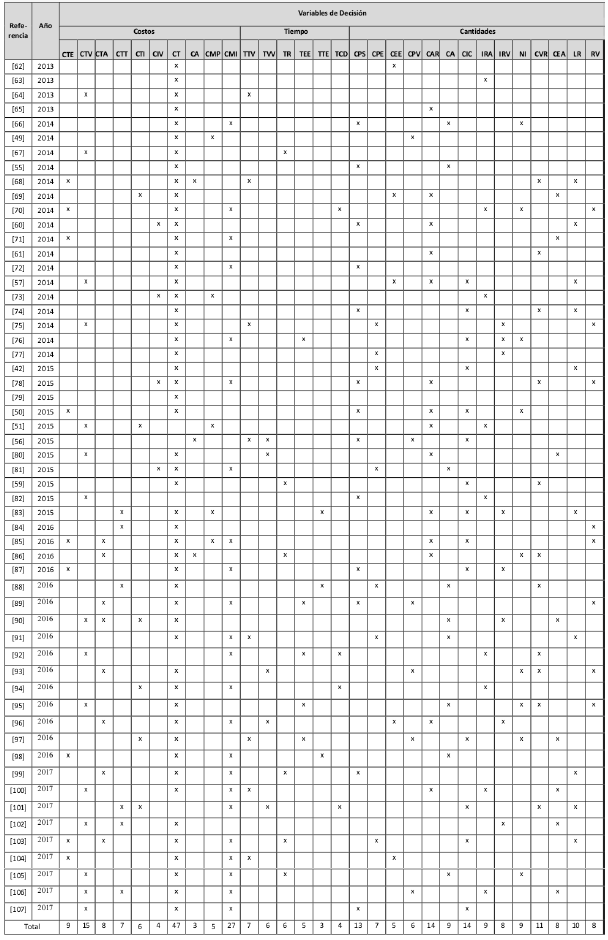
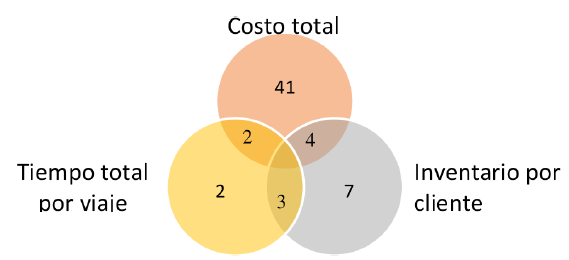
En la Figura 8 se muestra la relación de las variables de decisión más empleadas por categoría; las áreas de intersección revelan que son pocos los modelos que plantean una función multiobjetivo
Figura 8: Frecuencia de las variables de decisión IRP.
El análisis de costos muestra los resultados en el siguiente orden: costo total (90 %), costo de mantener inventario (44 %), costo total por viaje (26 %) y costo total por envío (15 %). Lo anterior corresponde con el 82,69% de los artículos analizados cuya función objetivo es minimizar costos. El tiempo total por viaje (13 %), el tiempo por ruta (11 %), el tiempo de viaje por vehículo (9 %) y el tiempo total de espera (9 %) son los más representativos. Prevalece como aspecto crítico de la gestión de inventario los modelos con horizonte de tiempo largo para la generación de rutas.; asimismo, la cantidad de inventario por cliente (27 %), la cantidad transportada a través del arco (25 %) y la cantidad de vehículos requeridos (21 %) son las variables más empleadas en esta categoría.
5.1.3. Clasificación por tipo de restricciones
Se clasifican las restricciones en dos categorías: ruteo e inventarios, como se observa en la Tabla III.
Ruteo: PR: programación de rutas, PV: programación de viajes, CD: cumplimiento de demanda, VC: visitar al cliente una sola vez, RR: realizar todas las rutas , CE: control de entregas, AV: asignación de vehículos, CF: conservación de flujo en la red, ES: eliminación de subtours, LF: limitaciones de la frecuencia de entrega, RN: ruta comienza y termina en el mismo nodo, EC: evitar congestión de vehículos, VT: ventanas de tiempo, UE: unificación de entregas, DD: demanda diaria por ruta. Inventario: NIT: nivel de inventario de la tienda, BFP: balance de flujo de producto, CCD: cantidad de cargue y descargue, AIA: actualización del inventario a bordo diario, AIM: actualización inventario mayorista , NIC: nivel de inventario de clientes, MNI: máximo nivel de inventario, BIM: balance de inventario minoristas, EI: equilibrio de inventario, NIP: nivel de inventario de cada producto, NIV: nivel de inventario antes y después de la visita al depósito, CDA: capacidad de los depósitos de almacenamiento, NIP: nivel de inventario entre periodos, NIA: nivel de inventario del almacén, CI: capacidad de inventario, DMI: demanda máxima de inventario.
Tabla III: Tipos de restricciones IRP.
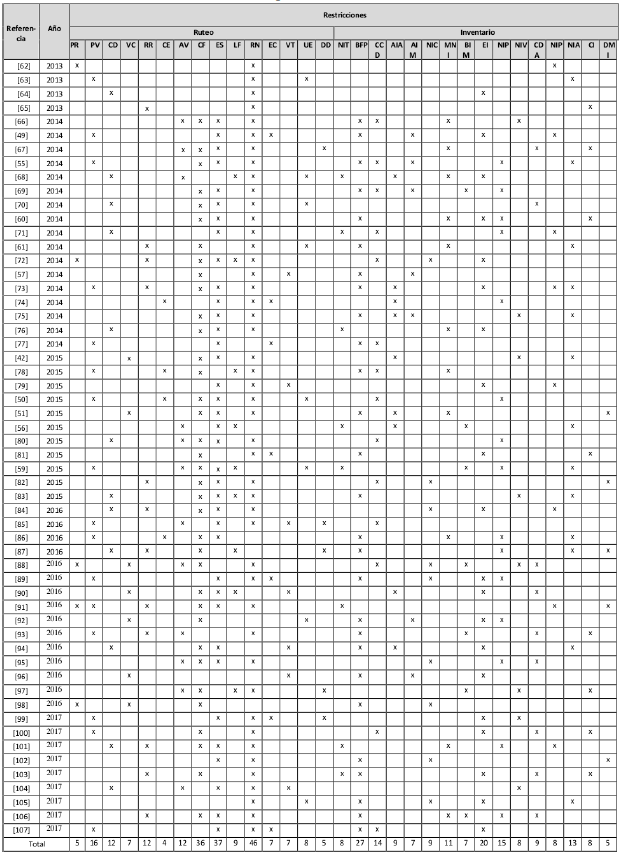
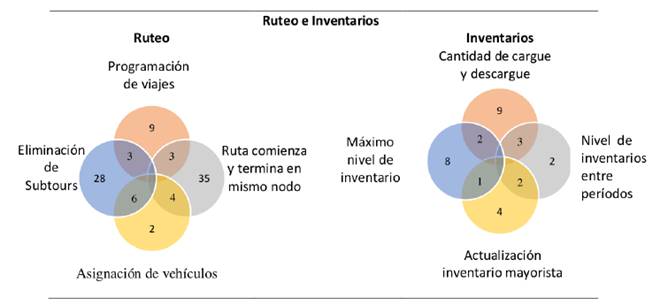
Las áreas de intersección hacen referencia al número de artículos que comparten tipos de restricciones; por ejemplo, tres artículos tienen restricción de programación de viajes y, al mismo tiempo, de eliminación de subtours. Las restricciones de ruteo según su frecuencia son: la ruta comienza y termina en el mismo nodo (80,7 %), eliminación de subtours (71,1 %), programación de viajes (28,8 %), asignación de vehículos (23,0 %) y realizar todas las rutas (21,1 %), los demás tipos tienen una baja utilización en estos modelos.
Para las restricciones de inventario se obtuvo que balance de flujo de producto (50 %), equilibrio de inventario (36,5 %), nivel de inventario entre periodos (28,8 %) y la cantidad de cargue y descargue (26,9 %) son las más representativas, como se muestra en la Figura 9.
Figura 9: Frecuencia por tipo de restricciones IRP.
5.1.4. Clasificación por parámetros
El análisis de los parámetros se agrupó en cuatro categorías: tiempo, inventario, demanda y costo. Los parámetros más frecuentes son el tiempo de entrega, el tiempo de recorrido por ruta, la demanda de producto, el inventario de los clientes y el costo de mantenimiento del inventario, como se muestra en la Tabla IV.
Tiempo T: TV: de viaje promedio TM: de mantenimiento TE: de entrega TD: de descargue TIF: al inicio y al final de cada turno parada TR: recorrido por rutas TP: preparaci´on cargue y descargue TLL: esperado de llegada TED: entre despacho de vehículos H: horarios de cargue y descargue. Inventario y Demanda VP: volúmenes de producción DM: demanda mayorista DP: demanda de producto IS: inventario de seguridad GC: grupo de Clientes TDE: tasa de demanda TPR: tasa de producción CP: cantidad de proveedores CD: conjunto de depósitos IC: inventario Clientes TN: tasa neta de producto DMI: demanda del minorista. Costo: fijo por vehículo, variable vehículo, por unidad de distancia, de mantenimiento del inventario, de espera, costo de escasez.
Tabla IV: Parámetros IRP.
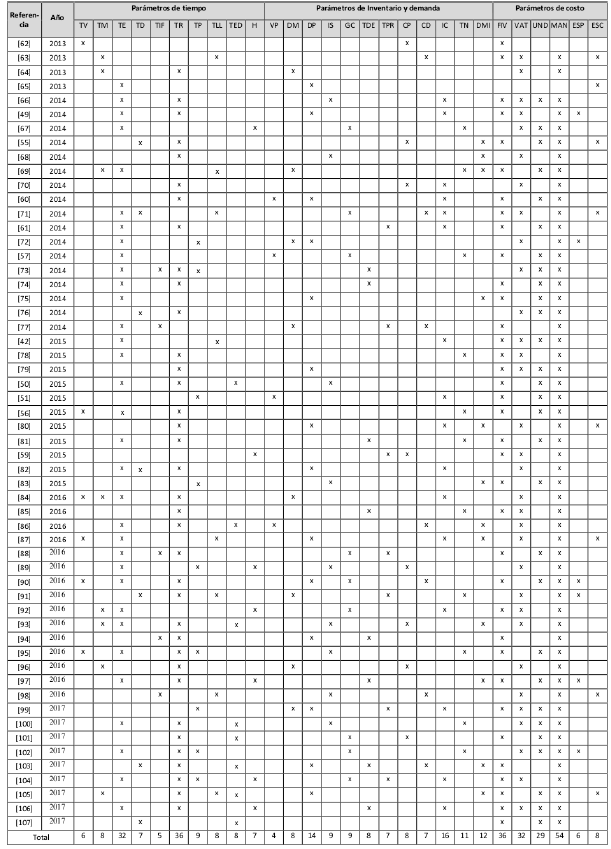
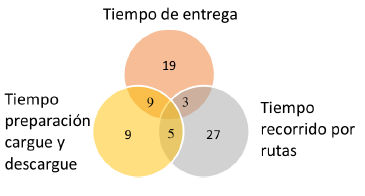
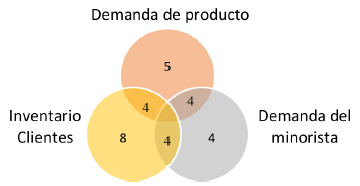
Los parámetros se han agrupado según el tiempo, inventario y demanda. Las áreas de intersección muestran los parámetros simultáneos que incluyen los modelos analizados como se ilustra en la Figura 10 y la Figura 11.
Figura 10: Frecuencia por tipo de restricciones de tiempo.
Figura 11: parámetros de demanda e inventario..
Los parámetros más representativos asociados al tiempo según su frecuencia son: recorrido por rutas (67,3 %), entrega (59,6 %), preparación cargue y descargue (17,3 %). En cuanto al inventario y demanda: clientes (30,7 %) demanda de producto (25 %), la demanda minorista (23 %). En los parámetros de costo resalta que el 100% de los artículos incluyen el costo de mantenimiento del inventario. El 65,38% tienen costos fijos vinculados a los vehículos y 57,6% costos variables
Los artículos IRP clasificados y analizados presentan casos de aplicación para los modelos formulados, ya que los modelos clásicos solo permiten un análisis teórico del problema. Se emplean variaciones y combinaciones tanto del modelo propuesto como del método de solución, no obstante, aunque se conserva una estructura fundamental orientada a las condiciones de inventarios y ruteo, se observa que la construcción de los modelos y su solución son específicas para cada situación de la CS que involucra.
5.2. IRP de perecederos
En general, un producto perecedero es aquel que se descompone, daña, evapora, expira, invalida o devalúa a través del tiempo [108]. La literatura ha planteado que los perecederos forman parte de un conjunto de productos sujetos a deterioro, que clasifican en tres tipos: los primeros son productos en descomposición como el alcohol y la gasolina, caracterizados por tener una vida útil ilimitada y disminuyen en cantidad por vaporización; los segundos son productos que pierden valor parcial o total a través del tiempo por nueva tecnología o cambios como los chips de computadora, teléfonos móviles y moda; por su parte, los terceros son productos perecederos como frutas, vegetales, carnes, sangre humana, medicinas y flores, tienen una vida útil máxima en el tiempo [109]. Su estudio debe contemplar características biofísicas y organolépticas, el tiempo de producción, condiciones de transporte y almacenamiento, su vida útil [110]. Solo se consideran productos perecederos en esta sección.
A continuación, se presentan las investigaciones que han aplicado el IRP a los productos perecederos. Se hace una revisión de los propósitos fundamentales de dichos estudios, de sus metodologías y las técnicas empleadas. El primer artículo que se identificó de IRP para perecederos distribuye el producto desde un centro de acopio regional a un conjunto de minoristas con demandas aleatorias, considera el problema simultáneo de gestión del inventario para cada locación y la forma en que debe realizarse la asignación de la flota de vehículos para las entregas. Los productos tienen un tiempo de vida fijo durante el cual se pueden usar y luego deben ser desechados. Es el caso de la sangre humana y los medicamentos [111].
En [112] se propone una formulación con vida útil máxima de productos perecederos, utilizan un algoritmo de generación de columnas y una restricción para garantizar que el minorista no tenga un inventario mayor que la demanda total en horizontes de tiempo consecutivos. La demanda de los clientes es determinística, pero pueden variar de un periodo al siguiente. Las entregas llegan a los clientes al inicio del periodo. La red incluye el almacén, conjunto de clientes y una flota homogénea de vehículos.
En [74] se estudia un problema IRP integrado. El proveedor tiene capacidad de producción limitada y distribuye un único producto a un conjunto de minoristas que utilizan vehículos homogéneos. El deterioro de los productos es fijo. Proponen un modelo de programación entera mixta en tiempo discreto y desarrollan un algoritmo de dos fases, en la primera fase se utiliza búsqueda tabú para obtener la matriz de pedidos de los minoristas, mientras que en la segunda se genera la programación de la producción y se definen las rutas de distribución.
Algunos supuestos tradicionales en la literatura del IRP restringen el uso de los modelos propuestos en los sistemas de logística para perecederos [3]. En primera instancia, los costos de distribución entre los nodos son conocidos de antemano y son constantes. Sin embargo, el consumo de combustible y los costos asociados pueden cambiar en función de la carga del vehículo, la cual depende de la asignación de visitas a los clientes, entre otros aspectos. En segundo lugar, el supuesto de una vida ilimitada de los productos perecederos en los modelos IRP no permite que se considere la decadencia de su calidad, estos son obstáculos principales para la aplicación de los modelos básicos del IRP en perecederos [29]. Las anteriores consideraciones han traído nuevos objetivos logísticos, tales como la capacidad de controlar la calidad del producto, la capacidad de colaborar en la red de la CS para reducir el desperdicio de alimentos, la capacidad de reducir los impactos ambientales y sociales de las operaciones [3].
No son muchos los estudios que han abordado el IRP para perecederos y prescinden de los supuestos y restricciones iniciales de la técnica. Es relevante aclarar que en las últimas dos décadas la gestión de la CS de perecederos ha evolucionado, entre otras razones por la demanda de productos alimenticios seguros y de alta calidad, el aumento de la conciencia de la salud de los consumidores [113], el crecimiento de la población mundial, el cambio climático, recursos naturales limitados y la escalada de la conciencia de sostenibilidad [114], lo anterior muestra la necesidad de analizar el estado actual de la logística para perecederos.
En cuanto a los artículos específicos de modelos IRP de perecederos, se presentan los artículos en la Tabla V. Se incluye la clasificación con respecto al tiempo, la estructura, ruteo, inventario y flota de vehículo.
Tabla V: Artículos IRP de Productos Perecederos
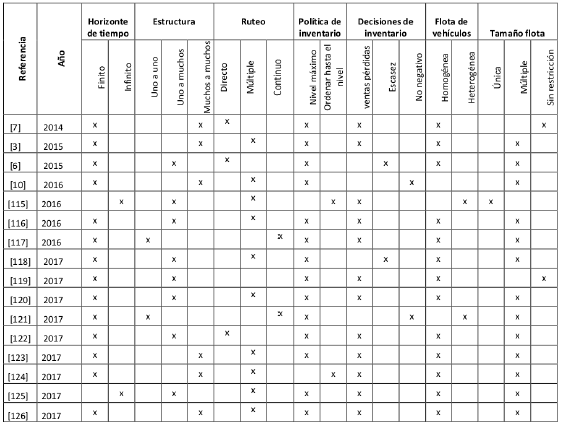
En [7] se consideran dos eslabones de la CS, varios proveedores envían a clientes minoristas los productos que tienen una vida útil y tiempo de almacenamiento fijo antes de que se consideren como pérdidas; incorpora parámetros de emisiones de dióxido de carbono estimando el consumo de combustible de las operaciones de transporte. En [3] se presenta un modelo multiperiodo IRP que tiene en cuenta la generación de CO2 y el consumo de combustible de los vehículos, el modelo lo aplican a la distribución de tomate fresco en una cadena de supermercados. El objetivo del problema es determinar las rutas y la cantidad de los envíos en cada periodo de manera que el costo total sea el mínimo. En el ámbito de las de restricciones, se considera el nivel de servicio para satisfacer una demanda incierta, se tiene en cuenta para el producto una restricción de tiempo de vida útil de tres y cuatro semanas. Las demás condiciones del modelo no incluyen otros aspectos críticos para perecederos.
En [6] se propone una CS de dos eslabones, un proveedor que sirve a un conjunto de minoristas geográficamente dispersos y con demanda determinística. Supone que la demanda del cliente final es una función decreciente lineal o exponencial de la vida útil de los productos perecederos. Cualquier unidad de producto que quede en inventario en el momento de la próxima entrega se considera en el modelo como una pérdida. En [10] se plantea un modelo con dos proveedores que producen higos y cerezas, emplean estimaciones detalladas de consumo de combustible en función de factores como el tipo de vehículo, la distancia recorrida, la carga del vehículo y la velocidad del vehículo. La consideración explícita de consumo de combustible asegura estimar el costo de transporte y las emisiones con mayor precisión para reducir el costo total de distribución. El objetivo del problema es determinar las rutas y la cantidad de los envíos en cada periodo, de tal manera que costo total previsto sea el mínimo. Consideran la vida útil como un parámetro fijo de tres semanas y no contempla otros factores que la afectan.
En [115] se presenta un modelo IRP multiproducto para perecederos con vida útil fija. La CS es de dos niveles, los productos se producen por un fabricante y se entregan a varios minoristas a través de una flota de vehículos heterogénea con capacidad fija. El objetivo es minimizar el costo total. Encuentran que un algoritmo de recocido simulado es superior que los algoritmos genéticos. Emplean el método de ramificación y corte y diferentes métodos de relajación. En [116] se formula un modelo integrado de programación lineal entera mixta. El nivel de calidad de los alimentos se verifica en toda la CS. El objetivo es maximizar la ganancia total, ingresos de venta menos la suma de los costos de producción, inventario y transporte. Las restricciones de perecibilidad implican vida útil fija.
En [117] se propone un modelo biobjetivo con medidas de desempeño adicionales a las económicas para la distribución de productos perecederos con fecha de vencimiento fija. El primer objetivo se centra en la minimización de costos de inventario y distribución, el segundo objetivo considera aspectos sociales como la tasa de accidentes vehiculares y la cantidad de productos caducados, que a su vez tienen un impacto directo en el medioambiente y deben reciclarse; por ello, se aplica el concepto de logística de reversa para reunir los productos caducados de los minoristas y devolverlos al proveedor. En [118] se considera un modelo IRP aplicado a una empresa marroquí productora de agua potable embotellada que toma decisiones de inventario y ruteo para sus diferentes tipos de presentaciones. La distribución implica a un proveedor, un conjunto de depósitos regionales y mayoristas, para la solución se emplean algoritmos de ramificación y corte. La demanda se asume determinística en el horizonte de planeación.
En [119] se presenta un modelo IRP multiobjetivo de tres partes: la primera función es económica asociada a los costos, la segunda corresponde al nivel de satisfacción del cliente y la tercera a los aspectos ambientales. Los productos son alimentos perecederos con fecha de vencimiento fija. Se propone para trabajos futuros el uso de vehículos diésel y eléctricos en la distribución urbana. Emplean un algoritmo genético de clasificación no dominada-II (por sus siglas en inglés, Non-dominated Sorting Genetic Algorithm-II, NSGA-II). En [120] se propone un modelo de localización, inventario y ruteo para productos alimenticios perecederos, el cual determina el número y la ubicación de los depósitos requeridos, el nivel de inventario para cada minorista y las rutas recorridas por cada vehículo. El modelo propuesto añade las decisiones de localización al IRP tradicional, aplicando el concepto de integración en el ámbito de las decisiones estratégicas, tácticas y operativas que producen mejores resultados para la CS. Utilizan un algoritmo genético y una heurística de búsqueda local, para resolver el problema.
En [121] se propone un modelo IRP con transbordo para un solo producto perecedero. El propósito es satisfacer la demanda del cliente bajo la política de nivel máximo durante el horizonte de planificación. Asumen una tasa de deterioro exponencial durante el tiempo que se almacenan el producto en el depósito del cliente. Para la solución, proponen un algoritmo genético y los parámetros se determinan utilizando el enfoque de diseño Taguchi.
En [122] se plantea un modelo de programación matemática IRP que maximiza los beneficios del sistema de producción multietapa, con restricciones de capacidad de producción. Toman en cuenta el inventario en cada etapa para calcular los costos. Incluyen restricciones de ventanas de tiempo con flota heterogénea y proponen dos algoritmos heurísticos para resolver el problema. En [123] se propone un IRP de dos etapas para productos alimenticios, la primera etapa corresponde al problema de inventario con ventanas de tiempo y la segunda es el problema de transporte con restricciones de capacidad del vehículo. El problema se formula como un modelo de programación entera mixta, para la solución se propone una heurística híbrida, que usa el enfoque de agrupamiento para las distancias.
En [124] se desarrollan diferentes métodos de solución para resolver un IRP para productos perecederos con demandas estocásticas. Los métodos de solución se comparan empíricamente en términos de beneficio promedio, nivel de servicio y frescura real. Cuantifican los beneficios de considerar explícitamente la incertidumbre de la demanda.
En [125] se estudia, mediante un modelo de programación lineal entera mixta, una red de logística humanitaria de varios niveles que considera la ubicación de los almacenes centrales, para la gestión del inventario de productos perecederos en la fase previa a un desastre y el ruteo para los vehículos de socorro en la fase posterior al desastre. Para su solución empelan un algoritmo genético de ordenación no dominado y un algoritmo genético de clasificación no dominado. En [126] se plantea un modelo IRP de producción extendido para alimentos perecederos, donde la calidad está formulada explícitamente. Se adapta un enfoque iterativo de dos fases para resolver el modelo propuesto. Lo descomponen en dos subproblemas y lo resuelven secuencialmente. Los resultados muestran que con hasta 50 minoristas se obtienen soluciones de buena calidad dentro de un tiempo aceptable.
Como se puede observar, las industrias involucradas en la producción y distribución de productos perecederos, enfrentan grandes retos debido al corto ciclo de vida de los productos, así que los temas relacionados con la planificación de la CS, la gestión del inventario y el transporte, deben ser diferentes en comparación con industrias de productos no perecederos. La gestión de las fechas de vencimiento de los productos, la recolección de los productos caducados, la contaminación y el costo del reciclaje de los productos caducados son algunos aspectos que aumentan la complejidad de considerar productos perecederos en el IRP [122]
El alto costo de transporte y la baja calidad del servicio son debilidades comunes en las diferentes redes de logística, especialmente en la entrega de alimentos. Debido a sus características perecederas, la calidad de los alimentos se deteriorará durante el proceso de entrega, por ende, se evidencia una necesidad de coordinación en las actividades de ruteo e inventarios, con un enfoque de integración. Por ejemplo, uno de los problemas de coordinación es cómo integrar decisiones operativas importantes, incluida la programación de producción y el problema de enrutamiento de vehículos, que en sí, son los problemas más importantes para la satisfacción de los clientes [123].
6. Conclusiones
El IRP tiene su origen hace más de 33 años y aunque se deriva del VRP, se ha consolidado como un importante campo de investigación que ha generado varias formas de plantear el problema en términos de supuestos, restricciones y métodos de solución que parten de la programación lineal.
Para su clasificación se pueden tener en cuenta dos aspectos: el primero tiene que ver con la estructura del problema que está relacionada con la aplicación, el producto y la configuración de la CS. El segundo es el modelo y método de solución que hace al IRP difícil de resolver en la mayoría de los casos dada su condición NP-Hard. Así, la mayoría de algoritmos construidos son de carácter heurístico. Inclusive algunos métodos usan metaheurísticas y mateheurísticas más complejas combinadas con métodos exactos.
En cuanto a sus aplicaciones se verifica una amplia gama, sin embargo, sobresalen los artículos de transporte marítimo y distribución de gas. Las principales variaciones del IRP incluyen: el problema de ruteo e inventarios en la producción (PIRP), el IRP con un solo cliente y múltiples clientes, el IRP estocástico (SIRP), el IRP con entregas directas, el IRP multiproducto, IRP con flota heterogénea, IRP con transbordo (IRPT), IRP dinámico y estocástico (DSIRP), IRP con multivehículo (MIRP), el IRP con entregas directas y trasbordo, el IRP consistente, el IRP sostenible y el IRP para perecederos.
La aplicación en productos perecederos tiene pocos estudios, incluye alimentos procesados, medicamentos y sangre humana. La diferencia más importante con respecto a otros tipos de IRP es la restricción de vida útil, que en la mayoría de los casos se asume fija. Muy pocos autores han abordado funciones de deterioro en el tiempo para los productos perecederos, en esa medida, es necesario estudiar el impacto de esta consideración en los modelos propuestos. Tampoco se evidencia que los estudios definan claramente las diferencias que involucra en sus modelos la perecibilidad de los productos, lo que está relacionado con el bajo uso de modelos de inventarios específicos para perecederos.
Por último, se tiene que las extensiones del IRP se han empezado a plantear para situaciones específicas y particulares de la vida real, por lo tanto, la tendencia es aumentar el conjunto de extensiones y derivados, más que la formulación de problemas generales. Con respecto a las variables, restricciones y parámetros del IRP, se identifica que no es posible aplicarlas directamente dadas las condiciones y particularidades de las CS de perecederos, es necesario proponer su adaptabilidad con base en lo descrito en esta revisión.
7. Trabajo futuro
Los trabajos futuros en IRP para perecederos deberán tener en cuenta aspectos relacionados con las características de estos productos con base en sus respectivas CS, por ejemplo, aún no se tiene en cuenta las múltiples maneras que se lleva a cabo el deterioro con factores como la temperatura, la luz, el oxígeno, la humedad y en algunos casos los microorganismos; asimismo, los procesos asociados a la manipulación y el almacenamiento.
Los futuros modelos serán específicos para el problema a resolver. Los métodos de solución tenderán a hacer más eficiente los procesos heurísticos y metaheurísticos requeridos, dado que para instancias grandes y horizontes de tiempo largos el tiempo computacional es una barrera importante. El IRP para perecederos es un campo incipiente y con potencial para futuras investigaciones, tanto en los modelos y métodos de solución, deberán tener en cuenta condiciones como: la cadena de frío, normas de higiene, contaminación del aire, emisiones de gases de efecto invernadero, generación de residuos, ocupación de vías y demás aspectos relacionados con city logistics [127] y green logistics [128].
Referencias
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










