DOI:
https://doi.org/10.14483/23448393.2284Published:
1998-11-30Issue:
No 1 (1999)Section:
Science, research, academia and developmentAnálisis estadístico de las fuentes de video digitales comprimidas
Statistics Analysis of Compressed Digital Video Sources
Keywords:
estadística, video digital comprimido, procesamiento de señales. (es).Downloads
References
Shanmugan, K. Sam y Breipohl; A. M., Random Signals: Detection, Estimation and Data Analysis; New York; John Wiley & Sons; 1988.
ISO/IEC 11172; Coding of Moving Pictures and Associated Audio for Digital Storage Media at up to About 1.5 Mbit/s, Part 2 : Video; Organization of International Standards; 1990.
Watkinson, John; Compression in Video & Audio; Rochester, GB; Focal Press, 1995; pp. 128-169.
Jack, Keith; Video Demystified: A Handbook for the Digital Engineer; Segunda Edición; San Diego, USA; High Text Interactive, Inc.; 1996; pp. 426-502.
Rodríguez, Adolfo, et al; MPEG-2 Fundamentals for Broadcast and Post-Production Engineers; Video and Networking Division White Paper; Tektronix; July, 1996.
Poularikas, Alexander D.; The Transforms and Applications Handbook; Boca Ratón, Florida, USA; CRC Press Inc. en cooperación con IEEE Press; 1996; pp. 227-280.
Onvural, Raif O.; Asynchronous Transfer Mode Networks: Performance Issues; Segunda Edición; Norwood, Massachusets,USA; Artech House, Inc.; 1995; pp. 77-138.
Papoulis, Athanasios; Probability, Random Variables, and Stochastic Processes; Tokio, Japan; McGraw-Hill Kogakusha, Ltd.; International Student Edition; 1965; pp. 83-115.
Scheaffer, Richard L. y McClave, James T.; Probabilidad y Estadística para Ingeneiría; México D.F.; Grupo Editorial Iberoamérica, S.A.; 1993; pp. 289-298.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Investigación y Ciencia
Ingeniería, 1999-00-00 vol: nro:1 pág:29-35
Análisis estadístico de las fuentes de video digitales comprimidas
Statistics Analysis of Compressed Digital Video Sources
Rodrigo Javier Herrera García
Resumen
En este artículo se estudia el comportamiento del tráfico generado por una fuente de video digital comprimido con la intención de obtener un modelo estadístico. El análisis se realizó sobre la señal de una película de 87 minutos de duración. La generación de información de una fuente de video digital es, en general, de tasa de bits variable. Para el análisis se tuvo en cuenta que los servicios de comunicaciones de video requieren sistemas en tiempo real y que cada imagen debe ser presentada en instantes específicos. El modelo planteado se basó en la variación de la tasa de bits en intervalos iguales a la tasa de cuadros/segundo. Tener un modelo que permita simular la generación de una fuente de video digital sirve para simular y analizar el tráfico en las redes digitales de telecomunicaciones. Por consiguiente, un algoritmo puede ser implementado en un computador.
Palabras clave:
estadística, video digital comprimido, procesamiento de señales.
Abstract
This paper treats the behavior features of traffic obtained from a compressed digital video source to getting out a statistics model. Analysis over a 87 minutes duration movie was made. The information generated by a digital video source is generally variable bit rate data. To analize data, it should be considered that video systems services need to be real time processes and each picture must be presented in fixed times. The proposed model was based on the variation of bit rate over the interval of time each picture must be presente (i.e., picture rate). If we have a model that we can use to simulate a digital video source, we can simulate and analize the behavioral traffic in telecommunication digital networks. Nevertheless, a computer algorithm can be implemented.
Key words:
statistics, compressed digital video, signal processing.
INTRODUCCIÓN
En el análisis de las redes de datos, la incorporación de nuevas fuentes hace necesario que se tengan herramientas nuevas. Dado el avance en la capacidad de transporte de información que se ha obtenido de las redes digitales, la posibilidad de distribuir señales de video digital comprimido a través de estas redes es una realidad. Sin embargo, la presencia de congestiones es inevitable por la heterogeneidad de los medios de comunicación, los sistemas de enrrutamiento y protocolos utilizados, la cantidad de tráfico del momento, entre otros. Por esto, la posibilidad de manejar modelos que representen las nuevas fuentes permite al diseñador o administrador de la red hacer una evaluación del comportamiento del tráfico previo a la instalación de la red o durante su operación para hacer las modificaciones que haya lugar.
Los modelos le permiten al ingeniero o al investigador realizar construcciones abstractas de los fenómenos que quiere estudiar. Con los modelos analíticos los resultados pueden ser de forma cerrada y hasta es posible obtener formas generalizadas que permiten encontrar soluciones rápidas. No obstante, los modelos de forma cerrada son difíciles de obtener cuando en el fenómeno que se estudia existen muchos elementos en juego. Más aún, cuando la naturaleza del fenómeno es aleatoria o no se conoce una regla que la rige. Para estos casos se recurre a crear modelos alternativos que se basan en las mediciones que se puedan lograr[1]. Este es precisamente el caso de las señales de video comprimido. Los elementos incorporados en el proceso de compresión de las señales de video digital son varias y diversas y, además, a la señal original misma no se le conoce un comportamiento explícito.
En este artículo se pretende encontrar un modelo de una fuente de video digital comprimido basado en la estadística de la cantidad de bits que se genera. Se estudia una señal de video digital comprimido producido por un codificador que cumple con el estándar de la Organización de Estándares Internacionales (o ISO, Organization of International Standards) ISO/ IEC 11172 [2] también conocida como MPEG- 1 (Moving Pictures Expert Group). El modelo tiene el propósito primario de servir como herramienta básica de análisis en el tráfico de redes de comunicaciones.
COMPRESIÓN DE LAS SEÑALES DE VIDEO
El proceso de compresión de las señales de video está basado en la eliminación de la redundancia espacial y temporal [3][4]. La primera se debe al hecho que existen altas correlaciones entre pixeles adyacentes. La segunda, a que hay una alta probabilidad de que un pixel, cuando cambia, se mantenga así por un tiempo relativamente largo (algunos segundos). El estándar ISO/IEC 11172 tiene en cuenta estos dos tipos de redundancia y procesa la señal de video de manera que trata de reconocerlas y, luego de eliminarlas, codificar la información resultante de la mejor forma posible.
La señal de video digital comprimida está constituida por tres tipos de cuadros: Intracodificados (I), Predichos (P) y Bidireccionales (B). Los cuadros I se comprimen teniendo en cuenta la información de ellos mismos. Por eliminar únicamente la redundancia espacial, el nivel de compresión es relativamente bajo. Los cuadros P tienen en cuenta la información del cuadro I o P anterior. Con la predicción se trata de eliminar también la redundancia temporal. El nivel de compresión de los cuadros P es bastante mayor que los cuadros I. Los cuadros B se comprimen teniendo en cuenta la información de los cuadros I o P anterior y posterior. Con estos cuadros se obtiene el mayor nivel de compresión. En la Figura 1 se puede apreciar la estructura de los cuadros en el algoritmo de compresión MPEG-1.
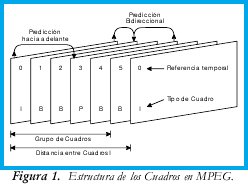
A la señal de video se le somete a una serie de procesos que permiten reconocer y eliminar las redundancias y la información resultante se cuantifica y codifica aplicando métodos que requieran el menor número de bits [5]. El proceso que se aplica a la señal se muestra en la Figura 2. Los formatos de video posibles son 4:4:4, 4:2:2 o 4:2:0. La señal de video digital comprimido no transporta la imagen propiamente dicha sino su espectro. La Transformada Discreta de Coseno o DCT (Discrete Cosine Transform) produce este cambio de dominio [6]. La cuantificación permite, además de adaptar los valores a niveles más apropiados para codificar, eliminar aquellos que tampoco aportan mucho a la semántica de la imagen sin deteriorar los niveles de calidad exigidos. La codificación de entropía involucra dos procesos: codificación de secuencias largas o RLC (Run-Length Coding) y la codificación de longitud variable o VLC (Variable Length Coding). Por último, para calcular la predicción de los cuadros es necesario mantener cuadros anteriores almacenados en memoria. La estimación de movimiento requiere comparar cuadros presentes con cuadros anteriores y obtener los vectores de desplazamiento de los objetos de la imagen.
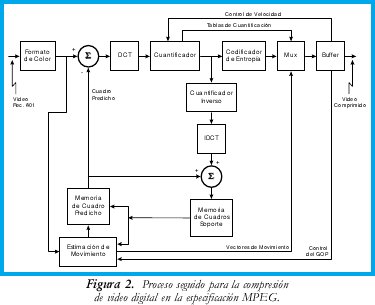
ANÁLISIS ESTADÍSTICO DE LA TRAMA DE VIDEO DIGITAL COMPRIMIDO
En el caso de video en tiempo real, la señal se va codificando basada en la cantidad de información que tiene cada cuadro. Pero cada uno contiene una cantidad de bits que depende de la información de la imagen misma, la información de los cuadros adyacentes y del tipo de operaciones que se utilicen para su compresión y codificación. El número de bits que se produce en cada cuadro es variable[7]. Por esta razón se ha considerado el estudio de la generación de bits de una fuente de video como una trama de tasa de bits variable o VBR (Variable Bit Rate).
Por otro lado, la base de tiempo del análisis se basó en la tasa de cuadros puesto que ellos deben ser presentados en intervalos de tiempo bien definidos. Aunque la codificación podría cambiar ligeramente estos intervalos, es de anotar que mientras no se tenga cada cuadro completo no es posible obtener la codificación del cuadro actual. Entonces, para el análisis estadístico se tomó como base la cantidad de bits (o bytes puesto que la trama MPEG tiene elementos que la alinean a múltiplos de 8 bits) que se produce en cada cuadro.
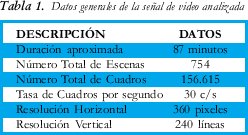
Para el estudio se tomó el archivo de video digital comprimido MPEG de la película The Woman in Red de 87 minutos de duración. En la tabla 1 se tienen algunos datos generales de la película. La película tiene 754 escenas cuya longitud en número de cuadros se puede ver en la Figura 3. En promedio, se tienen 208 cuadros/ escena aproximadamente. Aunque se buscó algún tipo de correlación del número de cuadros por escena no se encontró relación alguna entre ellos.
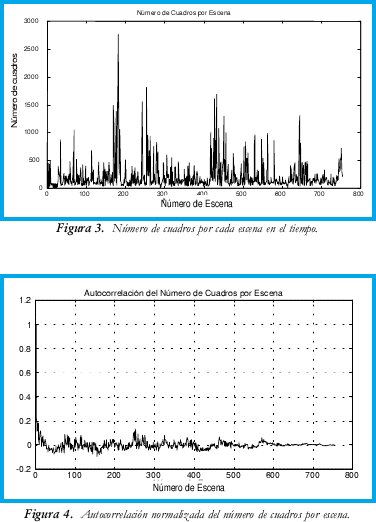
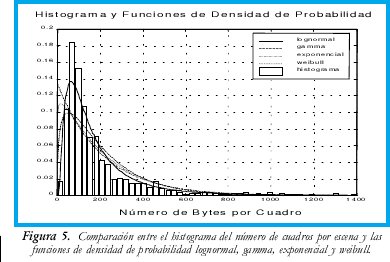
La Figura 4 muestra la autocorrelación normalizada del número de cuadros por escena. Para obtener un modelo que represente la cantidad de cuadros por escena de una película se realizaron unas medidas estadísticas para encontrar parámetros de la población. En la Figura 5 se puede observar la aproximación a las funciones de densidad de probabilidad o pdfs (probability density function) de las distribuciones exponencial, gamma, lognormal y weibull [8] frente al histograma obtenido del número de cuadros/escena de la película. La Tabla 2 muestra el error cuadrático medio o MSE (Mean Squared Error) entre los datos del histograma y las pdf, obteniéndose el menor error en la distribución lognormal.
Para el estudio de los cuadros primero se analizó las relaciones que existen entre los diferentes tipos de cuadros y se encontró que existe una alta correlación dependiendo del tipo. En la Figura 6 se puede observar la autocorrelación normalizada del número de bytes por cuadro de la señal de video. Es claro que se diferencian los tipos de cuadro por su tamaño. Los cuadros de mayor cantidad de bytes son los cuadros I, los siguientes son los cuadros P y los cuadros que menos bytes/cuadro tienen son los B. La Estructura del Grupo de Cuadros definida para esta señal es I0, B1, B2, P3, B4, B5, P6, B7, B8, P9, B10, B11, P12, B13, B14, I0, B1, ..., donde I, P o B es el tipo de cuadro y el subíndice representa la secuencia temporal relativa al GOP. De este resultado se consideró importante hacer el estudio de la distribución del tamaño de los cuadros agrupándolos de acuerdo con el tipo.
Una observación más detallada de los tamaños de los cuadros para la señal de video nos muestra una distribución multimodal (ver Figura 7). El modelamiento de una distribución de este tipo requiere del reconocimiento de las reglas que rigen estos modos. Con el resultado obtenido del análisis de la autocorrelación y del histograma se trabajó separando los tipos de cuadros dentro de la señal. Por ejemplo, al separarse y encontrarse el promedio del número de bytes por tipo de cuadro se encontró que están representados en el histograma por los modos (i.e. promedios de: cuadros I 11.575, cuadros P 5.358, cuadros B 3.287). Esto permitió reconocer las distribuciones que rigen el comportamiento del tamaño de cada cuadro.
Para tener un modelo estadístico del tamaño de cada uno de los tipos de cuadros se parte de considerar algunos aspectos que debe cumplir. En primer lugar, la distribución no puede tener valores negativos en la variable. En la generación de la cantidad de bits por cuadro se puede llegar a tener cantidades bastante pequeñas pero nunca negativas. En segundo lugar, la cantidad máxima de bits que se pueden generar por cuadro es desconocida. Por esta razón se considerará aquí que el número puede llegar a ser infinito. Además, el tamaño de cada cuadro tiene tendencia a estar cerca de un promedio y la probabilidad de que sea una cantidad extremadamente grande se reduce casi a cero. Esto permite involucrar distribuciones que sin la última aproximación no podrían involucrarse en el estudio.
El método que se utilizó para determinar la distribución más cercana consistió en buscar los parámetros de las funciones de densidad de probabilidad (pdf) a través de la estimación de máxima posibilidad o MLE (Maximum Likelihood Estimators) [9]. Las funciones que se consideraron fueron las distribuciones lognormal, gamma y weibull quienes cumplen con las condiciones mencionadas. Estas están definidas todas para x>0 como
distribución normal:
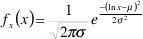
distribución gamma:
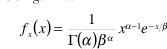
distribución weibull:
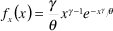
en donde x representa el tamaño de los cuadros (en bytes), µ y σ representan los parámetros de forma de la distribución lognormal, α y β, los parámetros de forma de la distribución gamma y γ y θ, los parámetros de la distribución weibull. Para la estimación de estos parámetros se consideraron como muestras los tamaños de los cuadros medidos del video para cada tipo de cuadro (I, P y B). La estimación se obtuvo con la ayuda del programa MATLAB®, cuyos valores se muestran en la Tabla 3. La cantidad de datos suministrados para la estimación fue de 5.544 para los cuadros I, 22.176 para los cuadros P y 55.440 para los cuadros B.
Posteriormente, con los parámetros se generaron distribuciones que cumplan con las funciones mostradas. Luego se compararon cada una de las distribuciones con el histograma encontrando el error cuadrático medio (MSE) o la suma de la diferencia entre cada uno de los valores del histograma y los valores equivalentes calculados para cada pdf, al cuadrado, así,
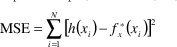
donde h(xi) son los valores del histograma de los datos, fx* (xi) son los datos obtenidos de cada pdf normalizada y N es el número de barras del histograma. Se optó por la función que presente el menor error. Todas las comparaciones se hicieron sobre distribuciones normalizadas, es decir ∑xi=1, para garantizar la equidad en los resultados junto con la normalización del histograma para todos los tipos de cuadros.
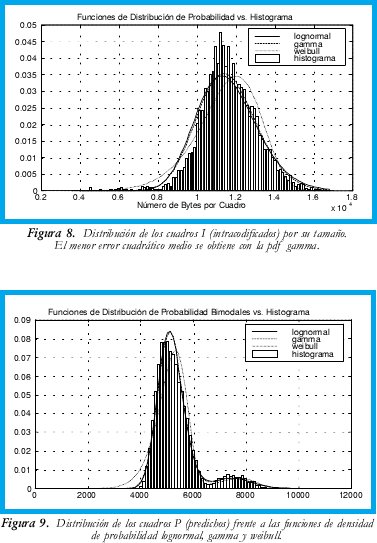
Con los tamaños de los cuadros I de la trama de video medida, se buscó la pdf que más se aproximara a la distribución obtenida. En la Figura 8 se pueden encontrar las comparaciones entre las pdf lognormal, gamma y weibull y el histograma del tamaño de los cuadros I. Calculado el error cuadrático medio (MSE) (Tabla 4) se obtuvo una mejor aproximación de la función de densidad de probabilidad de la distribución Gamma.
Con los cuadros P y B se presentaron distribuciones bimodales. Para lograr las comparaciones fue necesario estudiar la manera de separar las muestras. Al observar la secuencia se encontró que esporádicamente aparecen muestras que tienen tamaños significativamente superiores. En consecuencia, se utilizó un algoritmo que permitió separar las muestras teniendo en cuenta una variación abrupta en la secuencia. El algoritmo consiste en verificar cuánto difiere cada muestra del promedio de las muestras cercanas. Se determinó también un umbral de decisión. Es decir, las muestras se separaron considerando el siguiente criterio,
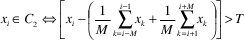
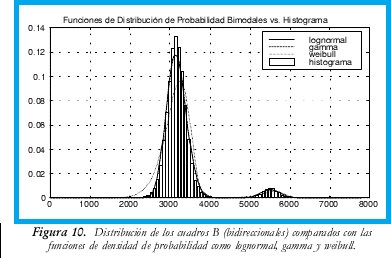
donde xi son todas las muestras, C2 es el conjunto de muestras del segundo modo, 2M es el intervalo de muestras alrededor de la muestra de prueba y T es el umbral. Considerados los subconjuntos, se realizó la aproximación de las funciones de densidad de probabilidad cuyos resultados se muestran en las Figuras 9 y 10 para los cuadros P y B, respectivamente. Los errores cuadráticos medios se muestran en la Tabla 3 donde se observa que ambos responden a distribuciones gamma.

Con la distribución de cada uno de los tipos de cuadros entonces se puede determinar el comportamiento de una fuente de video digital. El tipo de distribución para los tres tipos de cuadros es el mismo. Los resultados permiten entonces modelar un tráfico con el mismo tipo de distribución probabilística donde cambian los parámetros de la función de densidad de probabilidad. La medición del error cuadrado medio permite cuantificar de forma algo burda la similitud de la distribución obtenida para cada uno de los tipos de cuadros con las distribuciones que se usan para comparar.
CONCLUSIONES
En este artículo se plantearon los resultados de modelar la generación de video digital comprimido basado en una señal de video real. Aunque se pueden definir diferentes niveles de abstracción de la trama de video, se observó que la opción más aproximada del comportamiento de una fuente de video digital comprimido se obtiene cuando se estudia a nivel de cuadro. La cantidad de bits que se producen depende del tipo de cuadro que se está codificando. La autocorrelación de la señal muestra claramente la diferencia de tamaño entre ellos. De hecho, este resultado se utilizó como argumento principal en el modelamiento de la generación de tráfico en la fuente.
Por otro lado, se encontró que las distribuciones de la cantidad de bits que se genera por cuadro son las mismas. El resultado mostró que cada cuadro tiene un tamaño (en bits) que responde a una distribución gamma. Esto facilita la implementación de un modelo de simulación puesto que no es necesario recurrir a diferentes algoritmos sino que con las modificaciones en los parámetros se obtiene el tráfico de cada cuadro. Afortunadamente, por el hecho de que la señal de video comprimido se compone de una estructura de tipos de cuadros definida, la generación simulada de tráfico sólo implicaría cambiar los parámetros de la función generadora.
Sin embargo, es conveniente reconocer que si existe una correlación entre cuadros adyacentes, estos pueden modificar su tamaño cuando hay cambios de escena. El programa que genera el tráfico de un fuente de video puede estar regido por una generación de ajuste a los parámetros que responda a la distribución lognormal que se obtuvo en el número de cuadros por escena.
El modelo es bastante sencillo y su implementación en simulación requiere de la generación de números aleatorios con distribuciones lognormal y gamma. Dentro de los programas de simulación ya existen algoritmos optimizados que permiten obtener estas secuencias. Con el modelo, lo que se espera para el futuro es analizar el comportamiento de las redes de comunicaciones frente a diversos tipos de tráfico incluidos los de video digital con diferentes aplicaciones.
BIBLIOGRAFÍA
[1] Shanmugan, K. Sam y Breipohl; A. M., Random Signals:Detection, Estimation and Data Analysis; New York; John Wiley & Sons; 1988.
[2] ISO/IEC 11172; Coding of Moving Pictures and Associated Audio for Digital Storage Media at up to About 1.5 Mbit/s, Part 2 : Video; Organization of International Standards; 1990.
[3] Watkinson, John; Compression in Video & Audio; Rochester, GB; Focal Press, 1995; pp. 128-169.
[4] Jack, Keith; Video Demystified: A Handbook for the Digital Engineer; Segunda Edición; San Diego, USA; High Text Interactive, Inc.; 1996; pp. 426-502.
[5] Rodríguez, Adolfo, et al; MPEG-2 Fundamentals for Broadcast and Post-Production Engineers; Video and Networking Division White Paper; Tektronix; July, 1996.
[6] Poularikas, Alexander D.; The Transforms and Applications Handbook; Boca Ratón, Florida, USA; CRC Press Inc. en cooperación con IEEE Press; 1996; pp. 227-280.
[7] Onvural, Raif O.; Asynchronous Transfer Mode Networks: Performance Issues; Segunda Edición; Norwood, Massachusets,USA; Artech House, Inc.; 1995; pp. 77-138.
[8] Papoulis, Athanasios; Probability, Random Variables, and Stochastic Processes; Tokio, Japan; McGraw-Hill Kogakusha, Ltd.; International Student Edition; 1965; pp. 83-115.
[9] Scheaffer, Richard L. y McClave, James T.; Probabilidad y Estadística para Ingeneiría; México D.F.; Grupo Editorial Iberoamérica, S.A.; 1993; pp. 289-298.
Rodrigo Javier Herrera García
Ingeniero Electrónico, Universidad Distrital. Magister en Teleinformática, Universidad Distrital Profesor Facultad de Ingeniería, Universidad Distrital
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










