Investigación y Ciencia

Ingeniería, 1999-00-00 nro:1 pág:52-56

Comunicaciones ópticas de alta velocidad

HIGH-SPEED OPTICAL COMMUNICATIONS

Walter Montes
Alexánder Vargas

Resumen

Este artículo describe el uso de solitones en comunicaciones ópticas de alta velocidad. Los solitones son un tipo de ondas que se caracterizan fundamentalmente por la compensación de la dispersión lineal del pulso con la compresión no lineal del mismo. Los solitones son muy apropiados para comunicaciones digitales a gran velocidad o con un considerable ancho de banda.

La propagación de la envolvente de los solitones en fibras exentas de pérdidas puede ser descrita por la ya bien conocida Ecuación no lineal de Schrödinger. Para resolverla se han desarrollado diversos métodos, uno de ellos consiste en dividir la ecuación en dos partes, una lineal y otra no-lineal; la primera se soluciona mediante transformada de Fourier y la otra analíticamente.

Palabras claves:
Solitones, Ancho de Banda, Comunicaciones ópticas, Dispersión, Compresión no-lineal, Fibra ópticas

Abstract

This paper describes the employment of solitons in high-speed optical communications. The solitons are a type of waves characterized fundamentally by the compensation of the linear dispersion of the pulse with its own non-linear compression. The solitons are very appropriate for digital communications at great speed or with a large bandwidth.

The propagation of wave-envelope of solitons in optical fibres with no losses can be described by the very well-known non-linear Equation of Schrödinger. Several methods have been developed to solve it, one way is splitting the equation in two parts, one linear and another non-linear; the first one is solved using Fourier transfor m and the other one is solved analytically.

Keywords:
Solitons, Bandwidth, Optical Communications, Dispersion, non-linear Compression, Optical Fibre.

INTRODUCCIÓN

Este artículo básicamente considera como problema la difusión de los conocimientos existentes sobre solitones aplicados en comunicaciones ópticas de alta velocidad [1] que se pueden conseguir en una versión en español. Actualmente los investigadores buscan mejorar la velocidad y las distancias a las cuales se puede transmitir información sin necesidad de regenerar la señal y para esto han escogido el uso de solitones en fibras ópticas. La principal dificultad para ellos ha sido conocer la física del solitón con el fin de obtener el máximo provecho en aplicaciones prácticas.

Hoy en día la información encontrada es dispersa y confusa, cada investigador realiza pruebas y sus publicaciones son específicas, aunque existen algunos desarrollos en el ámbito práctico, en países en vía de desarrollo como Colombia no se le ha dado la importancia necesaria. La gran ventaja que tenemos es el montaje de redes de fibra óptica que se está llevando a cabo en este momento en el país; lo cual nos permitiría aprovechar la experiencia de otros países para implementar tecnologías de punta sin el alto costo que conlleva la experimentación.

Los sistemas de comunicaciones tienen un ancho de banda (BW) cada vez más limitado desde el punto de vista de la cantidad de información que se requiere transportar, es entonces cuando se ve la necesidad de desarrollar diferentes métodos para incrementar dicha capacidad.

Uno de estos métodos es la implementación de solitones en las comunicaciones ópticas; dado que el ancho de banda es un parámetro fijo en sistemas de transmisión, los solitones teniendo características peculiares resultan una buena alternativa; dichas características refieren aspectos tales como: poca dispersión, baja atenuación e interferencia nula. Lo que les da una gran ventaja con respecto a los fotones.

HISTORIA

Las ondas usadas en comunicaciones ópticas presentan una atenuación y una deformación mientras se desplazan en algún medio y a lo largo del tiempo. Sin embargo, existen ondas que se caracterizan por mantener su forma mientras viajan, a éstas se les llama solitones. Su origen se remonta al siglo pasado [2], sin embargo, su aplicación en comunicaciones no fue propuesta sino hasta 1973 cuando Hagesawa y Tappert vislumbraron el potencial del solitón. No obstante habría que esperar hasta 1980 cuando Mollenauer y Gordon demostraron experimentalmente la existencia del solitón en la fibra óptica.

En 1988 se demuestra la amplificación de solitones mediante el amplificador de fibra dopada con erbio, con el cual, se compensan las pérdidas producidas por la fibra. Con este avance tecnológico se abre la posibilidad de enviar solitones a grandes distancias sin necesidad de usar repetidores regenerativos (elementos electro-ópticos encargados de amplificar y dar forma a la señal).

Los solitones son considerados los pulsos luminosos ideales para las comunicaciones ópticas. Son muy apropiados para comunicaciones digitales a gran velocidad o con un considerable ancho de banda, ya que son estables a muy grandes distancias y permiten la multiplexación por división de longitud de onda (transmisión simultánea de dos o más longitudes de onda), con lo cual el ancho de banda disponible crece de manera importante.

En la actualidad, muchos investigadores han reportado avances considerables en el alcance y en la velocidad de transmisión de solitones. Por ejemplo, el equipo de Aubin [4] montó un sistema de solitones con un alcance superior a 30.000 Km, a una rata de 20Gb/s y repetidores cada 200Km.

¿QUÉ SON LOS SOLITONES?

Un solitón es un tipo especial de onda que se caracteriza por compensar la dispersión que sufre en su recorrido con una compresión no lineal provocada por la alta intensidad del pulso. El origen físico del solitón es el efecto Kerr, el cual se manifiesta mediante una constante dieléctrica no lineal, que puede compensar la dispersión de grupo en el medio óptico de propagación.

El fenómeno del solitón puede ser usado para generar un láser solitón con el fin de tener un dispositivo capaz de funcionar para compresión de señales y propósitos de conmutación (switching). La naturaleza del solitón es muy parecida a la del fotón con lo cual se intuye que comparten algunas propiedades.

Mas que tratar de decir qué es un solitón los investigadores han centrado sus esfuerzos en comprender las características que lo hacen especial. Estas características se presentan a continuación.

FISICA DEL SOLITÓN

La característica fundamental del solitón, es la compensación de la dispersión lineal del pulso con la compresión no lineal del mismo, lo cual puede ser explicado en términos físicos. Para hacer esto es necesario comprender dos fenómenos presentes: la dispersión y la modulación de autofase (no-linealidad):

Dispersión

Hace referencia al fenómeno por el cual la señal se deforma por ensanchamiento a medida que se desplaza debido a que sus componentes de frecuencia no se mantienen constantes.

Modulación de autofase (efecto Kerr)
Se refiere a la deformación del pulso por compresión (aplastamiento) ocasionado por un exceso de potencia en la fuente.

ANÁLISIS MATEMÁTICO

La transformada de Fourier multidimensional es generalmente utilizada para resolver problemas gobernados por ecuaciones diferenciales lineales, de coeficientes constantes y de derivadas parciales donde las variables dependientes son funciones del tiempo y de tres coordenadas espaciales.[5]

En fibras ópticas la transmisión de solitones generalmente se estudia mediante la envolvente de los mismos. Su propagación en fibras exentas de pérdidas puede ser descrita por la ya bien conocida Ecuación no lineal de Schrödinger [6]. Las pérdidas en la fibra y la dispersión cromática son los principales obstáculos que afectan la propagación de pulsos solitones.

Para modelar dicha propagación se usan las soluciones de la ecuación de Schrödinger, para obtenerlas se recurre a diferentes técnicas (algoritmos) [7]. Una de ellas, la usada generalmente es la SSFM (Split-Step Fourier Method) [8], la cual consta básicamente de dos partes:

1. Hallar la solución analítica de la parte no lineal en el dominio del tiempo.
2. Resolver la parte lineal en el dominio de la frecuencia usando transformada de Fourier.

Para utilizar la SSFM la ecuación diferencial parcial no lineal se reemplaza por dos ecuaciones, las cuales se resuelven para un mismo paso de longitud x. Se requiere una condición inicial para empezar los cálculos y se emplea la transformada rápida de Fourier (FFT) para convertir la señal del dominio del tiempo al de la frecuencia.

Luego de haber sido propagada una distancia Δx en ambas partes, se puede obtener el resultado, el cual será usado como condición inicial para el siguiente paso y así sucesivamente hasta obtener la distancia requerida. El uso de la SSFM se muestra a continuación:

La ecuación general del solitón (Ecuación no lineal de Schrödinger) viene dada por:

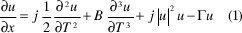
donde

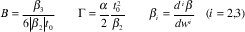
Además:

U (x, t) es la amplitud normalizada del pulso solitón

X es la distancia normalizada

T es el tiempo

β es la constante de propagación

B es el coeficiente de dispersión de tercer orden

Γ es el factor de pérdidas normalizado

α son las pérdidas en la fibra

t₀ es el ancho del pulso inicial

Para resolver la ecuación (1) se puede dividir en 2 ecuaciones como se presenta a continuación:

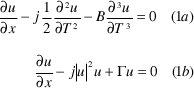
Para resolver la parte lineal (1 a) se aplica la transformada de Fourier a ambos lados, con lo cual se tiene:

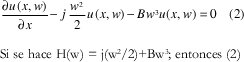
se convierte en:

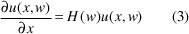
De la condición inicial de u(x,w) con x= 0, la ecuación (3) se resuelve como:

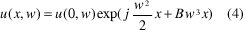
Para resolver la parte no lineal (1 b).
Esta parte puede ser resuelta analíticamente en el dominio del tiempo.

Para empezar considérese la siguiente ecuación:

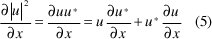
Tomando el conjugado a ambos lados de (1 b) se obtiene:

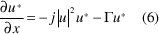
Aplicando (6) y (1 b) a (5) se llega a:

De la condición inicial u(0, T) la ecuación (7) se puede resolver como:

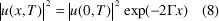
Remplazando (8) en (1 b) y usando la condición inicial de u(0, T) se obtiene la solución general dada por:

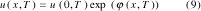
donde

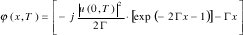
Para la solución general de la ecuación (1) se aplica la condición inicial a la ecuación (9) con un desplazamiento Δx, este resultado se lleva al dominio de la frecuencia aplicando transformada de Fourier y remplazándola con la ecuación (4). Finalmente se halla la solución en el dominio del tiempo usando transformada inversa de Fourier.

CONCLUSIONES

Como se puede apreciar de la ecuación (1) los dos primeros términos al lado derecho de la igualdad representan la dispersión, el tercero, los efectos nolineales en la fibra y el último las pérdidas propias de ésta. Ahora bien, si podemos lograr que los dos primeros términos tengan la misma magnitud (para un caso ideal) que el tercero entonces sus efectos se cancelarán mutuamente. El último término se ha logrado disminuir con la tecnología actual de construcción de fibras ópticas obteniendo valores muy próximos a cero, con lo cual se puede ver que prácticamente el término de la derecha se hace nulo. Esto implica que la solución de la ecuación sea una constante, es decir, en la practica la onda se propaga sin sufrir deformación alguna.

El método usado en este artículo presenta una solución aproximada de la propagación del solitón. Su manejo resulta fácil de entender aunque restringido para algunos casos particulares o modelos más reales.

Como se puede apreciar el hecho que los solitones presenten una dispersión nula los ubica como la mejor alternativa para las comunicaciones ópticas de alta velocidad y de considerable ancho de banda, aún más en nuestro país donde las superautopistas están siendo actualmente implementadas y se requiere el uso de tecnologías acordes a nuestras necesidades.

BIBLIOGRAFÍA

[1] Desurvire, "Comunicaciones ópticas: la quinta generación", Investigación y ciencia. pp 74-82, 1992.

[2] Arnold, J. "Solitons in communications", Journal Electronics And communication engineering, pp 88-96, 1996.

[3] Nakazawa, Y. Kimura, et al. "Field demostration of soliton transmission at 10Gb/s over 2000 Km in Tokyo Metropolitan Opticalal Loop Network",Electronics Letters, Vol. 31, No. 12, pp 992-993,Junio 1995.

[4] Aubin, T. Montalant, et al. "Record 20-Gigabitper-second-200 Km repeater span transoceanic soliton transmission using in-line remote pumping", IEEE Photonics and Technology Letters, Vol. 8, No. 9, pp 1267-1269, Septiembre 1996

[5] Shum, P. And S. F. Yu, "Improvement of Fourier Series Analysis Technique by Time-Domain Window Function", IEEE Photonics Tecnology Letters, Vol 8, No 10, pp1364-1367, Octubre 1996.

[6] Min Du, A. K. Chan, and C. K. Chui, "A novel approach to solving the nonlinear Schrödinger Equation by the coupled amplitude-phase for mulation", IEEE Journal Quantum Electronics. Vol. 31, No 1, pp 177-182, Enero 1995.

[7] Schrader, D., "Explicit Calculation of N-Soliton Solutions of the Nonlinear Schrodinger Equation", IEEE Journal of Quantum Electronics,Vol 31, No 12, pp 2221-2225, Diciembre 1995

[8] Ghafouri-Shiraz, H., Shum, P. And M. Nagata, "A novel method for analysis of soliton propagation in opticalal fibres", IEEE Journal of Quantum Electronics., Vol 31, No 1, pp 190-200, Enero 1995.

Walter Montes Dávila.
Estudiante de Ingeniería Electrónica, Universidad Distrital Actualmente realiza su proyecto de grado sobre solitones aplicados a las comunicaciones por fibra óptica. montesdvila@excite.com

Alexánder Vargas Cuellar
Estudiante de Ingeniería Electrónica, Universidad Distrital Actualmente realiza su proyecto de grado sobre comunicaciones ópticas empleando solitones. alexvar@excite.com