DOI:
https://doi.org/10.14483/23448393.2820Published:
2001-11-30Issue:
Vol. 7 No. 2 (2002): July - DecemberSection:
Science, research, academia and developmentSegmentación de imágenes de microanatomía de madera mediante una clasificación multiescala basada en operaciones morfológicas
Keywords:
Microanatomía de madera, granulometría, segmentación, multiescala, fuzzy c-means. (es).Downloads
References
R. Gonzalez and R. Woods, Digital Image Processing. Prentice Hall, Inc. Second Edition. New Jersey. 2002.
Russ, Jhon C. The Image Processing Handbook. Second Edition. CRC Press. 1995.
Acton S. and Mukherjee D. Scale Space Classification Using Area Morphology. IEEE Trans. Image Processing, vol. 9, no. 4, pp. 623-636, April. 2000.
M. Unser, "Texture Classification and Segmentation Using Wavelet Frames," IEEE Trans. Image Processing, vol. 4, no.11, pp. 1549-1560, Nov. 1995.
Randen T. and Håkon J. "Filtering for Texture Classification: A Comparative Study". IEEE Transactions On Pattern Analysis And Machine Intelligence, Vol. 21, No. 4, April 1999. pp 291-310.
H. Choi and R. Baraniuk. "Multiescale Image Segmentation Using Wavelet-Domain Hidden Markov Models". IEEE Trans. Image Processing, vol. 10, no. 9. September 2001. pp. 1309-1321.
Pollak I. Segmentation and Restoration via Nonlinear Multiscale Filtering. IEEE Signal Processing Magazine. Sept. 2002. pp. 26-37.
X. Zhang and M. Desai. "Segmentation of Bright Target Using Wavelet and Adaptive Thresholding," IEEE Trans. Image Processing, vol. 10, no. 7. July 2001. pp. 1020-1030.
I. Pollak, "Nonlinear scale-space análisis in image processing," Ph. D. Disertation, LIDS, MIT, Cambridge, MA, Aug. 1999.
Zana F. and Klein J.C. Segmentation of Vessel-Like Patterns Using Mathematical Morphology and Curvature Evaluation. IEEE Trans. Image Processing, vol. 10, no. 7. July 2001. pp. 1010-1028.
M.R. Rezaee et al. A multiresolution Image Segmentation Technique Based on Pyramidal Segmentation and Fuzzy Clustering. IEEE Trans. Image Processing, vol. 9, no. 7. July 2000. pp. 1239-1249.
Wang, Li-Xing. A Course in Fuzzy Systems and control. The fuzzy c-means Algorithm. Ed Prentice Hall. 1997, pp. 342-353.
Image Processing Toolbox User's Guide, 1993 - 2001 by The MathWorks, Inc.
E. Montseny, P. Sobrevilla. "An Approach to Computational Microtexture Perceptual Detection with Management of Uncertainty". Technologies for Constructing Intelligent Systems 1 (tasks). Editores Bernardette Bouchon-Meunier, Julio Gutierrez Rios, Luis Magdalena y Ronald Yager, 2002, pp281-294, ISBN 3-7908-1454-7.
The Handbook of Pattern Recognition and Computer Vision (2nd Edition), by C. H. Chen, L. F. Pau, P. S. P. Wang (eds.), pp. 207248, Texture Analysis. World Scientific Publishing Co., 1998.
H. Guevara, Y. Ayala y C. Merlano. Caracterización y diferenciación anatómica de algunas maderas comercializadas en SantaFe de Bogotá con los nombres de Cedro y Guayacán. Trabajo de grado. Ingeniería Forestal. Universidad Distrital Francisco José de Caldas. Bogotá. 1997.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:2 pág:64-72
Segmentación de imágenes de microanatomía de madera mediante una clasificación multiescala basada en operaciones morfológicas
Resumen
El propósito de este trabajo pretende estudiar la madera con más detalle para un mejor entendimiento de su naturaleza, debido a que es un material orgánico con un amplio rango de aplicaciones. Existen algunos métodos y herramientas utilizados en los laboratorios de tecnología de maderas, encaminados a estudiar las propiedades y usos potenciales de las especies. En este documento se propone un método basado en procesamiento digital de imágenes, soportado sobre una herramienta computacional, que busca mejorar el análisis de estas características. En esta propuesta inicial, se muestra una segmentación de imágenes de microanatomía, encaminada a la identificación de las estructuras microanatómicas con el fin de cuantificar su concentración dentro de una muestra. El método utilizado consiste en la creación de un espacio multiescala basado en operaciones morfológicas y una técnica de clustering usando el algoritmo fuzzy c-means. El espacio multiescala se crea aplicando operaciones morfológicas de cierre-apertura y apertura-cierre sobre la imagen. La operación morfológica depende de un elemento estructurante, el cual cambia de tamaño para variar la escala. Las escalas son determinadas por un estudio de granulometría de la imagen usando FFT. Se muestra cómo el método puede ser útil para segmentar texturas de microanatomía de maderas.
Palabras Clave:
Microanatomía de madera, granulometría, segmentación, multiescala, fuzzy c-means.
Abstract
In this work we seek to study wood in more detail to understand better its nature, due to is an organic material with a wide range of applications. There are some methods and tools used in the wood technology laboratories to study properties and potential uses of the species. In this paper we propose a method based on digital image processing, supported on a computational tool, for improving the analysis of these characteristics. In this initial proposal, we show a segmentation of wood microanatomy, directed to identify microanatomies structures for quantifying its concentration into the sample. The used method consists on the creation of a scale space based on morphologic operations and a technique of clustering using the fuzzy c-means algorithm. The multiscale space is created by applying open-close and close-open morphologic operations over images. The morphologic operations are based on a structuring element, which change its size in order to vary scale. Scales are determined by image granulometry study using FFT. We show how the method can be useful for wood microanatomy textures segmentation.
Key words:
Wood microanatomy, segmentation, granulometry, multiscale, fuzzy c-means.
I. INTRODUCCIÓN
Muchos de los métodos de investigación en el área forestal, especialmente los relacionados con el estudio de la madera, involucran el análisis de muestras de microanatomía de diferentes especies. Algunos centros de investigación como el Laboratorio de Tecnología de Maderas de la Universidad Distrital ha contemplado dentro de su labor, el estudio de estas muestras, con el fin de determinar los usos potenciales y ventajas de los diferentes tipos de madera. Buscando mejorar los métodos de estudio existentes, este trabajo incursiona en la utilización de procesamiento digital de imágenes para el estudio de estas muestras microanatómicas. Se ha dedicado parte de este trabajo a la segmentación de la imagen y al estudio de sus texturas, las cuales caracterizan los elementos y estructuras que diferencian una especie de otra.
Dentro del área del tratamiento digital de imágenes, González y Woods [1] han considerado que el interés de los métodos de tratamiento digital de imágenes deriva de dos áreas principales de aplicación: la mejora de la información pictórica para la interpretación humana y el procesamiento de los datos de la escena para la percepción autónoma de una máquina. En este sentido, y buscando complementar los métodos de estudio existentes en el área forestal, basados en la percepción visual humana, se espera contribuir con una mejora de la información pictórica que se obtiene. Así, se contribuye a estas investigaciones y al avance en las herramientas de investigación involucradas en esta área.
Como parte del proceso de percepción, por el cual un especialista logra determinar las diferentes estructuras y elementos dentro de la imagen, distinguiéndolos de los demás, se ha determinado que la segmentación es uno de los primeros pasos a seguir en el análisis de estas imágenes. Desde el punto de vista del tratamiento digital de imágenes, la segmentación de imágenes busca asignar a cada píxel de la imagen una etiqueta, basado en sus propiedades y su relación con sus vecinos. El objetivo final está en separar la imagen en regiones, caracterizadas por algunas propiedades, y las cuales contienen una textura diferente[1][2].
Algunos métodos para segmentar la imagen recurren al estudio de las propiedades espaciales de la imagen, tales como la discontinuidad o similitud de los niveles de intensidades. Se utilizan métodos de umbralización, detección de discontinuidades, detección de límites, métodos orientados a regiones, entre otros[1]. Sin embargo, estos métodos tienen ciertas desventajas que los hacen ineficientes en el momento de la segmentación. Algunos se ven afectados por la iluminación no uniforme dentro de la imagen, el ruido y las discontinuidades en las intensidades. Por otro lado, comúnmente se realiza la segmentación a una escala específica, lo que algunas veces provoca errores en la segmentación. Los errores en la segmentación consisten básicamente en asignar etiquetas diferentes a píxeles de la misma región u objeto[3]. En general muchos de estos métodos fallan en la forma de clasificación del píxel y en la representación de la imagen para su análisis. La utilización de una sola escala implica estudiar la imagen con muchos detalles o estudiar la imagen con pocos detalles, en este último caso, sólo se logran apreciar los objetos de mayor tamaño y se pierden los detalles. En los dos casos se tienen pérdidas de información, ya que en realidad se han omitido algunas características, por analizar otras. De este problema, principalmente, surge la motivación de utilizar en vez de una sola escala, varias escalas, derivando así en un modelo multiescala para analizar la imagen.
Algunos modelos multiescala o multiresolución se implementan mediante transformaciones lineales, como es el caso de la transformada wavelet [4][5]. Adicionalmente, algunos utilizan sobre un dominio wavelet modelos ocultos de Markov, realizando una segmentación multiescala como resultado de la clasificación de ventanas de distinto tamaño, que son combinadas para obtener una segmentación más precisa en escalas finas [6]. Algunos métodos lineales presentan el problema de degradar la información de los bordes con un efecto de borrosidad, debido a la forma como se genera el espacio multiescala [7]. De esta forma, han aparecido ciertas modificaciones a estos modelos. Zhang y Desai[8] usaron wavelets y una umbralización adaptiva; otros, como el presentado por Pollak [9] convergen a filtros no lineales para la generación de espacios multiescala. Los modelos no lineales tienen la ventaja de conservar los bordes que limitan cada región de la imagen que se quiere segmentar. Algunos están basados en filtros modificados [7], otros utilizan operaciones morfológicas para generar los filtros no lineales. Los filtros morfológicos realizan un filtrado considerando la forma de los objetos que se quieran segmentar; Zana y Klein [10] utilizan morfología matemática, además de una evaluación de curvatura, para la segmentación de patrones dentro de la imagen, el cual está apoyado en algunas propiedades morfológicas de los patrones. Aprovechando las ventajas de estos filtros, Acton y Mukherjee [3] generaron un espacio multiescala a partir de un tipo de filtros morfológicos, los cuales crean versiones cada vez más toscas de la imagen, pero conservando los bordes. Además, en este caso, la clasificación se puede realizar teniendo en cuenta la morfología del área.
En la segmentación de una imagen con el espacio multiescala, se debe incurrir en el proceso de clasificación. Es aquí donde se le asigna a cada píxel de la imagen su etiqueta. La asignación de etiquetas se puede efectuar con algoritmos de clustering. Este es el caso del clasificador k-means, que es un clasificador rígido; o un clasificador Bayesiano, el cual realiza una partición de la imagen a través de la agrupación de regiones con intensidad uniforme o de variación leve[3][6][8]. Además, otro tipo de clasificadores como el fuzzy c-means se ha implementado con buenos resultados [3][11]. En un proceso de clustering, los datos se han asociado en grupos mediante alguna regla (a cada grupo de datos se le denomina un cluster). El que un dato pertenezca a un cluster puede hacerse de forma rígida, sin embargo, los datos usualmente no están tan bien distribuidos como para realizar este tipo de clasificación; así, en vez de asignar un dato directamente a un cluster, se determina un grado de pertenencia del dato a cada cluster, lo cual se acomoda de mejor forma al mundo real. Este tipo de planteamiento desemboca en la conveniencia de utilizar un modelo difuso en el problema de reconocimiento de patrones [12].
En este mismo orden, el documento se presenta de la siguiente forma: Inicialmente, se describirán el modelo multiescala utilizado y las operaciones morfológicas implicadas, esto corresponde a la Sección II. En la Sección III, se darán algunas características de las estructuras o elementos de las imágenes de microanatomía; además, se mostrará por qué el modelo multiescala basado en operaciones morfológicas (filtrado no lineal), se acomoda al problema en estudio. En la Sección IV un estudio de granulometría de la imagen es mostrado; se propone un método eficiente basado en transformada wavelet y transformada de Fourier. En la Sección V se muestra cómo se utiliza el clasificador fuzzy c-means. En la Sección VI, se mostrarán algunos resultados del método utilizado sobre las imágenes de microanatomía de madera. Se presentan algunas conclusiones en la Sección VII.
II. MODELO
A. Operaciones morfológicas sobre imágenes
Las operaciones morfológicas (en este caso matemáticas) se pueden utilizar como un filtrado morfológico [1]. Estas operaciones son útiles para eliminar o reducir en la imagen algunos objetos o regiones que tengan alguna forma y tamaño particular, la cual está determinada por las intensidades de la imagen. Estas operaciones dependen de un elemento estructurante (EE), que se encarga de limitar el área en el cual se realiza la operación morfológica. Este EE realiza el filtrado morfológico y puede tener cualquier forma.
Cuando una imagen se representa en escala de grises, los operadores manipulan las intensidades de los píxeles en la imagen basándose en las intensidades de los píxeles vecinos; en conclusión, se realiza una manipulación en relación con los niveles de intensidad de la imagen [13].
Las operaciones morfológicas que se consideran en este trabajo son dilatación, erosión, apertura y cierre de la imagen. En el caso de la dilatación, el valor de salida de un píxel es el máximo valor de todos los píxeles en la vecindad del píxel en la imagen de entrada, donde la vecindad está definida por el EE utilizado en la operación. En la figura 1(a), se muestra el proceso de dilatación por un EE en forma de línea de longitud tres, para una imagen con intensidades de gris. Para la erosión el procedimiento es similar, sin embargo, en este caso, el valor de salida no es el máximo, sino el mínimo de todos los píxeles dentro de la vecindad [13].
Teniendo en cuenta lo anterior, se pueden definir las operaciones de apertura (1) y cierre (2) de una imagen, como:
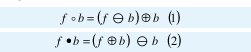
Donde, las operaciones erosión y dilatación se representan como:

f corresponde a los datos de entrada y b corresponde al EE.
De esta forma, la apertura-cierre de la imagen es la aplicación consecutiva de los procedimientos de erosión-dilatación-dilatación-erosión. En general, en la dilatación, la imagen de salida tiende a ser más brillante y se disminuye el efecto de los detalles oscuros. En la erosión, la imagen de salida tiende a ser más oscura y se disminuye el efecto de los detalles brillantes. En la apertura se eliminan pequeños detalles claros, dejando sin modificar los niveles de gris globales y los detalles brillantes más grandes. El cierre elimina detalles oscuros de una imagen mientras deja casi sin modificar los detalles brillantes[1].
Para la generación del espacio multiescala, el EE es variado en tamaño, desde uno muy pequeño, que permite tener detalles, hasta un EE grande en el que se han filtrado detalles y sólo se observan los objetos grandes. Existe un límite para el tamaño del EE, que depende del tamaño de los objetos y regiones sobre la imagen y sobre todo del tamaño de la imagen estudiada.
El EE se define de acuerdo con los parámetros de vecindad y forma. Por ejemplo, la figura 1(b) muestra un EE en forma de disco con una vecindad de tres. Para cambiar el tamaño del EE, se aumenta o disminuye la vecindad. Así, cuando se define una vecindad grande se cubre una región mayor sobre la imagen.
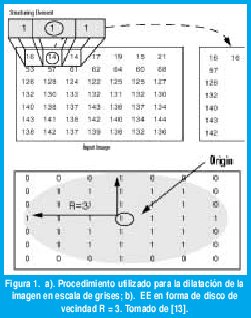
Lo que se busca con este filtrado morfológico es remover componentes de acuerdo con una condición de máximo o mínimo, la cual depende totalmente de la vecindad definida por el EE. Esto conlleva también a eliminar componentes que no cumplan con la condición de intensidades impuesta por la vecindad definida. Además, esta condición también depende de la forma como están distribuidas las intensidades dentro de la imagen.
Una de las ventajas en la utilización de un procedimiento de apertura-cierre de la imagen, está en la capacidad de incrementar el área de regiones con intensidad constante. Con esto también, se reduce el número de regiones dentro de la imagen. Cuando se tienen objetos, regiones o elementos, que no tienen una intensidad constante por la cual se puedan identificar o segmentar con precisión, pero que tienen una intensidad dominante, las operaciones morfológicas contribuyen a encontrarlas. Al aumentar el tamaño de las zonas que tienen una intensidad dominante debido a que se han convertido en zonas con intensidad constante por el proceso de apertura-cierre, se incrementa la homogeneidad de la imagen, permitiendo así, separar fácilmente un objeto o región de otra.
B. El modelo multiescala sobre la imagen
Para aumentar la comprensión sobre la aplicación de un modelo multiescala sobre una imagen, este modelo se puede describir de la siguiente forma: si se tiene una imagen donde se desconocen los objetos que en ella se encuentran, y la forma de estos objetos dentro de la misma, la primera forma de identificarlos es mediante una apreciación visual de la imagen a una escala determinada. Sí esta escala es fina, se puede apreciar una mayor cantidad de detalles; sin embargo, esta apreciación puede que no ayude a determinar los objetos grandes que se encuentran dentro de la imagen. Este proceso que realiza una persona, en el cual intenta distinguir algunos objetos de otros, ya sea por sus características de intensidad, textura o color, es análogo a un proceso de segmentación que se realiza mediante un método de procesamiento digital.
La apreciación a una fina o pequeña escala se puede relacionar con la acción de una persona al observar una imagen a una distancia muy corta de la misma. Si alguna persona realiza este ejercicio observará muchos detalles sobre la imagen y sin embargo, no logrará diferenciar con exactitud las regiones u objetos grandes que se encuentran. Si la persona se colocara a una distancia mayor de la imagen, tendría una apreciación un poco más general sobre ésta, y se podrían observar otras características que a otras escalas no se observarían. Si la persona se aleja un poco más de la imagen podría diferenciar de mejor forma los objetos más grandes. Sin embargo, ya no se observarán detalles, sino una versión más tosca de la imagen original. En general, si la persona se desplazara desde una distancia muy cercana a una distancia mayor, podría tener una apreciación más completa y general de los objetos y las regiones de diferente tamaño (a diferentes escalas) que se encuentran sobre la imagen.
De esta forma, la apreciación que realiza una persona a una distancia se toma como una escala. Todas las escalas (apreciaciones que se realizan a escalas diferentes), permite una descripción multiescala de la imagen. En la misma forma el procesamiento digital de imágenes ha generado modelos que permiten tener una descripción multiescala de la imagen. En resumen, lo que se busca es obtener una descripción de cómo varía la intensidad de cada píxel a través de una evolución de la imagen, que se da por la observación multiescala de la muestra. Así, no se podría inferir sobre cómo están distribuidas las intensidades dentro de toda la imagen basado en el estudio de las intensidades en algunas regiones, pero por el contrario, es posible saber qué intensidad predomina en un píxel o en una vecindad de píxeles, sabiendo qué intensidades hay en una escala más fina y qué valores toman en las siguientes escalas de estudio. Esto se debe a que se pueden saber las intensidades de toda una imagen a una escala más tosca, si se conocen sus intensidades en escalas más finas.
C.Modelo multiescala basado en operaciones morfológicas
El modelo multiescala utilizado se basa en las operaciones morfológicas presentadas anteriormente. Básicamente, dentro de la generación del espacio, se obtienen tantas imágenes como número de escalas que se desean para representar la imagen. Así, se obtiene un espacio multiescala, el cual se puede denotar por {I}, donde Is es la imagen a una escala s. La escala s varía con el tamaño del EE. A medida que aumenta s se realiza un filtrado morfológico y se obtiene una versión más general o menos fina de la imagen original.

III. IMÁGENES MICROESTRUCTURALES
A.Características de las estructuras de imágenes de microanatomía
Algunas características que se utilizan para describir las texturas y regiones de las microestructuras están basadas en la percepción humana. Estas se han agrupado bajo los siguientes conceptos: Granularidad, linealidad, tosquedad, homogeneidad, continuidad, contraste, y cambios abruptos [14]. Así, algunas texturas se componen por primitivas con una forma particular [15], que se pueden describir con las características que se han enunciado anteriormente.
Analizando las características de una textura, se puede concluir que algunas de las estructuras y elementos dentro de la microanatomía se caracterizan por su textura dentro de la imagen, esto se muestra en la figura 2. Este es el caso del parénquima el cual está compuesto de primitivas con forma de disco. Igualmente dentro de todo el contraste de la imagen, los vasos también se caracterizan por una forma, que es predominante en toda la muestra. Otros elementos, como los radios, se caracterizan por ser líneas verticalmente orientadas. Teniendo en cuenta esto, un análisis morfológico matemático es muy útil para el estudio de estas imágenes, ya que debido a la manipulación que se hace sobre la imagen, los EEs pueden resaltar o suprimir formas.
B. Modelo Multiescala sobre las imágenes de microanatomía
Debido a que existen dentro de la imagen, estructuras o elementos de diferente tamaño, como es el caso de las primitivas del parénquima y los vasos, es conveniente utilizar un modelo multiescala que permita segmentar estas regiones considerando todos los posibles tamaños de los elementos. Además, como más adelante se muestra, cuando se quiere clasificar cada píxel, es mejor tener varias escalas para la representación de la imagen.
Se observa en las imágenes del espacio multiescala, figura 3, que los bordes se intentan conservar a medida que se va aumentando la escala. También se puede observar que el modelo multiescala aumenta el contraste de la imagen y la homogeneidad de algunas regiones con intensidades dominantes.
IV. ESTUDIO DE GRANULOMETRÍA DE LA IMAGEN
La segmentación implementada inicialmente consideraba un número fijo de escalas para realizar el estudio. Para mejorar el tiempo de procesamiento se ha realizado un estudio de granulometría previo para determinar las escalas más representativas. El procedimiento evita la ejecución de una operación innecesaria en una escala donde los cambios no son significativos, es decir, que su aporte al modelo multiescala es poco.
Para estudiar la granulometría de una imagen, comúnmente se utilizan operaciones de apertura con EEs en forma de disco [1]. Estos métodos se basan en el cálculo del área de objetos abiertos luego de la apertura de la imagen con un disco (EE) a una escala determinada. Cuando se obtiene la apertura de la imagen se calcula el área de los objetos que permanecen abiertos. El área de objetos abiertos disminuye a medida que aumenta la escala. La variación de la escala se realiza a través de la variación del radio del EE con forma de disco.
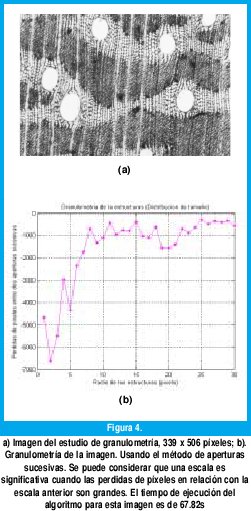
Para determinar las escalas más significativas, se obtiene la derivada de la curva de la variación del área de los objetos abiertos (píxeles), en función de la escala. El resultado es una gráfica que muestra las perdidas de píxeles en función de la escala definida por el EE; para la imagen de la figura 4(a) esta gráfica se muestra en la figura 4(b), el tiempo de procesamiento es de 67.82s. Una escala significativa se encuentra allí donde la variación del área de objetos abiertos y la pérdida de píxeles es alta. De la figura 4(b) se pueden tomar como posibles escalas significativa s= [ 2 5 9 12 14 17 19 23 26 28 ].

Sin embargo, este método recurre a una operación morfológica que implica un mayor tiempo de procesamiento. El tiempo de procesamiento con una operación morfológica depende del tamaño de la imagen y de la escala de estudio. Por lo tanto, aunque el método presentado es útil para caracterizar las imágenes, igualmente ejecutaría las operaciones morfológicas innecesarias que se quieren evitar.
Se propone una forma más eficiente de determinar las escalas representativas dentro de la imagen, la cual se basa en la relación entre las escalas de una imagen y las frecuencias espaciales que la caracterizan. Una forma eficiente de determinar las frecuencias espaciales de una imagen es mediante la Trasformada Discreta de Fourier.
Adicionalmente, un estudio multiescala es útil para observar de forma más precisa qué escalas se encuentran en la imagen. Una forma de obtener los detalles de la imagen a diferentes escalas es mediante la Transformada Wavelet [4]. Además, esta transformada entrega coeficientes que representan los detalles verticales, horizontales y diagonales de la imagen a diferentes niveles de descomposición. Estos coeficientes consideran las orientaciones más importantes que presentan los objetos dentro de la imagen.
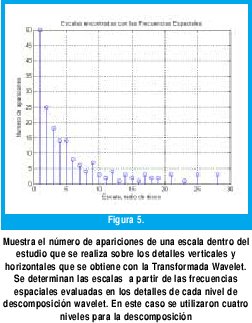
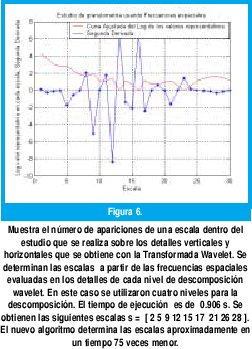
El método propuesto realiza una descomposición mediante la DWT (Discrete Wavelet Transform), usando una wavelet madre Haar. Los coeficientes que se obtienen son estudiados en frecuencia a través de una FFT (se implementó para 512 muestras; también, dependiendo de las características de la imagen puede ser necesaria más resolución). A partir de las frecuencias espaciales se determinan las escalas. Se realiza un conteo de las escalas más repetidas, encontradas en todos los niveles de descomposición (escalas) y sobre cada uno de los detalles (verticales y horizontales). Así, se obtiene una gráfica (figura 5) que muestra el número de apariciones de una escala dentro de todo el estudio. Sin embargo, debido a la forma como se obtienen estos datos, las escalas significativas no son las que presentan más apariciones, ya que las escalas más pequeñas aparecen en la mayoría de los niveles de descomposición. Para determinar las escalas útiles se ajustaron los puntos a una curva (fitting con interpolación shape preserving). El logaritmo de los valores de la figura 6 es implementado para compensar los valores pequeños en las escalas mayores. Se obtienen de la segunda derivada de la curva los valores picos negativos, que representan los puntos en que la curva tiene concavidad hacia abajo. Estos puntos son las escalas significativas tal como lo muestran los resultados de la figura 6. En este caso se utilizaron cuatro niveles para la descomposición; el tiempo de ejecución del algoritmo para la misma imagen es de 0.906 s. El método determinó las siguientes escalas s = [ 2 5 9 12 15 17 21 26 28 ]. El algoritmo propuesto determina las escalas aproximadamente en un tiempo 75 veces menor.
Para realizar la segmentación se determinan previamente las escalas representativas con el método anteriormente expuesto; luego, estas escalas son utilizadas para dar un tamaño al EE que crea el espacio multiescala de la imagen. Necesariamente algunos filtros morfológicos se deben implementar, aunque sea en sólo algunas escalas, ya que son los que eliminan o incrementan el contraste de las formas dentro de la imagen.
V. CLASIFICACIÓN
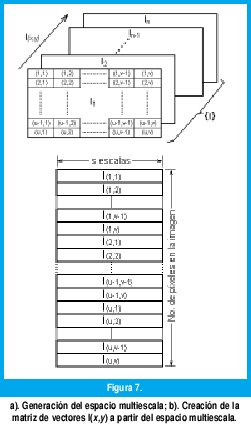
El algoritmo implementado construye una matriz tridimensional que contiene los valores de las intensidades del espacio multiescala, es decir, las imágenes Is. Las dimensiones de la matriz están determinadas por el tamaño de la imagen y el número de escalas utilizadas para generar el espacio multiescala, esto se muestra en la figura 7(a).
Para utilizar el clasificador fuzzy c-means, se ha obtenido del modelo multiescala una matriz con tantos vectores como píxeles dentro de la imagen, como se muestra en la figura 7(b). Cada posición espacial de un píxel de la imagen original tiene asociado un vector I(x,y), que muestra la evolución de la intensidad de cada píxel desde una escala muy fina hasta una escala tosca. Para clasificar cada píxel, se tiene en cuenta la evolución de cada una de las intensidades de un píxel en relación con la evolución de las intensidades de píxeles en la imagen. La ecuación (3) [3][12] muestra el criterio de error cuadrático mínimo utilizado por el algoritmo de clustering para asignar un vector a un cluster. U es la partición fuzzy en C clusters del espacio multiescala. Dado un vector I(x,y) en la posición (x,y), la medida di( x, y ) = I( x, y ) - µ i es la distancia entre el vector obtenido del espacio multiescala y el centro µi del cluster i. La distancia es ponderada por el valor de la función de pertenencia de cada vector µi(x,y) correspondiente al cluster i. Aquí, representa la cuantificación de la imagen en el dominio (x,y). En la ecuación m es una constante.
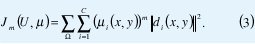
Se realiza un proceso denominado defuzzification, en el cual se convierten los valores difusos a valores que representen intensidades en la imagen de salida. Para asignarle una etiqueta a cada píxel, se evalúa la función de pertenencia de cada píxel con respecto a cada uno de los clusters, entonces, el píxel se asigna al cluster que tenga la mayor función de pertenencia.
VI. RESULTADOS DE LA SEGMENTACIÓN
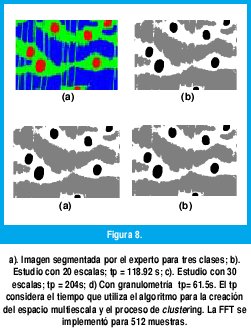
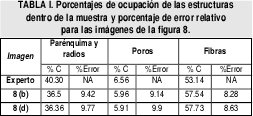
Usar un estudio de granulometría permite automatizar el proceso de segmentación con un tiempo menor de cómputo. Esto se puede comparar con una segmentación en la cual se utilizan todas las escalas desde la imagen original (s=1) a una lo suficientemente mayor para la descripción. La figura 8 muestra las imágenes obtenidas para varias escalas junto a los tiempos de cómputo necesarios. Se observa que utilizando un estudio de granulometría previo, el tiempo de cómputo se puede reducir a la mitad. Además, se obtienen resultados similares en la segmentación.
El algoritmo que genera el espacio multiescala y que realiza el agrupamiento se implementó sobre software especializado en matemática. Se utilizó un PC con procesador 1.7GHz, con 512M RAM. Para el estudio con 20 escalas; tp = 118.92 s, figura 8(b); estudio con 30 escalas, tp = 204 s, figura 8(c); estudio con granulometría, tp = 61.5 s, figura 8(d). El tp considera el tiempo que utiliza el algoritmo para la creación del espacio multiescala y el proceso de clustering.
La Tabla I muestra los porcentajes de ocupación de las estructuras dentro de la muestra. Para los métodos basados en computador los valores son menores para parénquima y radios, y poros en comparación con la segmentación del experto. Esto se debe a que el experto segmenta inicialmente estas dos regiones por separado (lo restante se considera como fibras). El experto coloca los bordes de tal forma que: para el caso de los poros es donde termina la pared de éste, y para el caso del parénquima y radios es donde la región está totalmente difuminada.
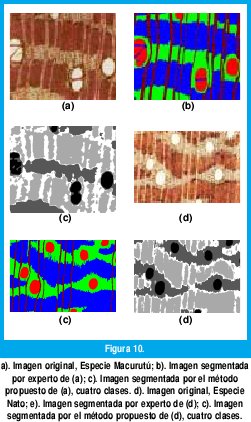
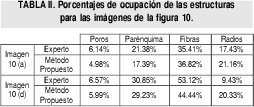
La figura 9 muestra el resultado de la segmentación de algunas muestras mediante el método pro- puesto, usando un clasificador para tres clases. La figura 10 muestra una imagen segmentada por un experto y la segmentación que se obtiene por el método, para cuatro clases. En la Tabla II se muestran los valores de la concentración de cada estructura dentro de la muestra, considerando ambas segmentaciones. El error más grande se observa en la segmentación de las fibras cuando se usan cuatro clases. Esto se debe a que el EE utilizado en la segmentación no se acomoda tan bien a la morfología de estas estructuras.

VII. CONCLUSIONES
Se ha presentado un método para el estudio de la microanatomía de la madera, utilizando una herramienta computacional y técnicas de procesamiento digital de imágenes. Se ha comprobado que un modelo multiescala basado en operaciones morfológicas es útil para la segmentación de estas imágenes.
Los métodos existentes que identifican estas estructuras por su textura considerando las primitivas que caracterizan cada una de ellas, pueden ser implementados mediante un proceso computacional encaminado al reconocimiento de patrones y de formas. Así, para este tipo de microestructuras, un análisis morfológico apoyado de un método de clasificación, es ventajoso tanto para la segmentación como para la descripción de estas estructuras. Adicionalmente, el modelo multiescala utilizado también es muy útil porque permite una clasificación considerando un rango amplio de tamaños dentro de las diferentes estructuras.
Debido a la gran cantidad de texturas que presentan las estructuras de las imágenes microanatómicas, un sistema experto que necesite ser entrenado para identificarlas demandaría un gran costo computacional. El método utilizado no requiere un entrenamiento previo, por lo cual tiene un costo computacional menor.
Con este trabajo se logra inicialmente diferenciar las regiones (estructuras) dentro de la muestra. Esta segmentación cuenta con cierta exactitud en las fronteras. Así, es posible cuantificar la concentración de los diferentes elementos sobre la muestra, de una forma aproximada. Esto mejora la calidad de la información sobre estas estructuras, ya que antes sólo se consideraban los aspectos cualitativos [16]. También, se contribuye al estudio de estas muestras, ya que un especialista puede realizar estudios que se pueden apoyar sobre datos cuantitativos. Esto es útil para estandarizar las dimensiones de las estructuras dentro de la muestra..
También se ha propuesto un estudio de granulometría para estas imágenes, basado en un método computacional eficiente y con alto grado de confiabilidad. Esto también permite automatizar, en cierta manera, la segmentación de imágenes.
AGRADECIMIENTOS
Agradecemos al Ing. Sergio Barato por su ayuda en el tema de técnicas de clustering..
REFERENCIAS
[1] R. Gonzalez and R. Woods, Digital Image Processing. Prentice Hall, Inc. Second Edition. New Jersey. 2002.
[2] Russ, Jhon C. The Image Processing Handbook. Second Edition. CRC Press. 1995.
[3] Acton S. and Mukherjee D. Scale Space Classification Using Area Morphology. IEEE Trans. Image Processing, vol. 9, no. 4, pp. 623-636, April. 2000.
[4] M. Unser, "Texture Classification and Segmentation Using Wavelet Frames," IEEE Trans. Image Processing, vol. 4, no.11, pp. 1549-1560, Nov. 1995.
[5] Randen T. and Håkon J. "Filtering for Texture Classification: A Comparative Study". IEEE Transactions On Pattern Analysis And Machine Intelligence, Vol. 21, No. 4, April 1999. pp 291-310.
[6] H. Choi and R. Baraniuk. "Multiescale Image Segmentation Using Wavelet-Domain Hidden Markov Models". IEEE Trans. Image Processing, vol. 10, no. 9. September 2001. pp. 1309-1321.
[7] Pollak I. Segmentation and Restoration via Nonlinear Multiscale Filtering. IEEE Signal Processing Magazine. Sept. 2002. pp. 26-37.
[8] X. Zhang and M. Desai. "Segmentation of Bright Target Using Wavelet and Adaptive Thresholding," IEEE Trans. Image Processing, vol. 10, no. 7. July 2001. pp. 1020-1030.
[9] I. Pollak, "Nonlinear scale-space análisis in image processing," Ph. D. Disertation, LIDS, MIT, Cambridge, MA, Aug. 1999.
[10] Zana F. and Klein J.C. Segmentation of Vessel-Like Patterns Using Mathematical Morphology and Curvature Evaluation. IEEE Trans. Image Processing, vol. 10, no. 7. July 2001. pp. 1010-1028.
[11] M.R. Rezaee et al. A multiresolution Image Segmentation Technique Based on Pyramidal Segmentation and Fuzzy Clustering. IEEE Trans. Image Processing, vol. 9, no. 7. July 2000. pp. 1239-1249.
[12] Wang, Li-Xing. A Course in Fuzzy Systems and control. The fuzzy c-means Algorithm. Ed Prentice Hall. 1997, pp. 342-353.
[13] Image Processing Toolbox User's Guide, 1993 - 2001 by The MathWorks, Inc.
[14] E. Montseny, P. Sobrevilla. "An Approach to Computational Microtexture Perceptual Detection with Management of Uncertainty". Technologies for Constructing Intelligent Systems 1 (tasks). Editores Bernardette Bouchon-Meunier, Julio Gutierrez Rios, Luis Magdalena y Ronald Yager, 2002, pp281-294, ISBN 3-7908-1454-7.
[15] The Handbook of Pattern Recognition and Computer Vision (2nd Edition), by C. H. Chen, L. F. Pau, P. S. P. Wang (eds.), pp. 207- 248, Texture Analysis. World Scientific Publishing Co., 1998.
[16] H. Guevara, Y. Ayala y C. Merlano. Caracterización y diferenciación anatómica de algunas maderas comercializadas en SantaFe de Bogotá con los nombres de Cedro y Guayacán. Trabajo de grado. Ingeniería Forestal. Universidad Distrital Francisco José de Caldas. Bogotá. 1997.
Rodrigo Javier Herrera
Director del Grupo de Investigación en Procesamiento Digital de Señales. UD Ingeniero Electrónico. Universidad Distrital. Profesor del Proyecto Curricular de Ingeniería Electrónica.
Henry A. Roncancio. Hugo F. Velasco
Laboratorio de Automática, Microelectrónica en Inteligencia Computacional. Universidad Distrital. Estudiantes de X semestre de Ingeniería Electrónica. Universidad Distrital.
César A. Polanco
Productos y Procesos del Bosque. Ingeniero Forestal. Universidad Distrital. Profesor de la Facultad de Medio Ambiente.
Jenny Rosado
Productos y Procesos del Bosque. Facultad de Medio Ambiente. UD. Estudiante de X semestre de Ingeniería Forestal.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










