DOI:
https://doi.org/10.14483/23448393.2668Published:
2007-11-30Issue:
Vol. 13 No. 2 (2008): July - DecemberSection:
Science, research, academia and developmentModelo para la Localización de un Plataforma de Cross Docking en el Contexto de Logística Focalizada
Downloads
References
Kent John L Jr y Flint Daniel J. Perspectives on the evolution of logistics thought. Journal of Business logistics. Vol.18.1997
Sachan Amit y Datta Subhash. Review of supply Chain management and logistics research. Journal of physical distribution & logistics management. Vol 35 No 9, 2005.
Posada Eduardo, La logística Militar y sus aplicaciones en la logística empresarial, Revista "Pensamiento y Gestión" Universidad del Norte. Barranquilla. nº 6 , 2000
Huston James A, The sinews of war: Army Logistics 1775-1953
Paulus Robert, Logistics in the Forgotten war.
Pagonis William G, Moving Mountains: Lessons in leadership and logistics from the gulf war, Harvard Business School Press, 1992.
Mc Grath John J, The Other End of the Spear: The Tooth to- Tail Ratio (T3R) in Modern Military Operations, The Long War Series Occasional Paper 23, Combat Studies Institute Press, 2007
Hess Earl J, Retreat from Gettysburg: Lee, Logistics, and the Pennsylvania Campaign, The Journal of American History; 92, 4; 2006.
Paulus Robert. D, Implementing focused logistics, Army Logistician, No 35, vol6, 2003.
Department of Defense, Joint Vision 2020, publicado en http://www.dtic.mil/jointvision/jvpub2.htm Fecha de consulta 10 de septiembre de 2007
Joint Chiefs of state, Focused Logistics campaign plan, 2004, disponible en https://acc.dau.mil/ CommunityBrowser.aspx?id=32577
Simchi Levi D, Kaminsky P y Simchi Levi E, Designing and managing the supply chain concepts, strategies and cases. Mc Graw Hill
Department of defense, Focused logistics Roadmap, 2005, disponible en, https://acc.dau.mil/ CommunityBrowser.aspx?id=22548&lang=en-US
C S Sung and S H Song. Integrated service network design for a cross-docking supply chain network.The Journal of the Operational Research Society 54, no. 12 (December 1, 2003):
Thompson Brockmann y Patty Godin.. Flexibility for the future in warehouse design. IIE Solutions. Jul 1997, 97,7; ABI/INFORM Global Pg.22
Moskovich, D. Investigación de operaciones. Editorial, Mc graw hill. Mexico, 1995.
Kalenatic D, Lopez C, Gonzalez L, Modelo Integral de Producción de Empresas Manufactureras, 1ª Ed, Kimpres, Bogotá, Colombia, 2006.
Charnes A & Cooper W. Management Models ans Industrial Applications of linear Programming. New York, USA, 1961
Dantzig G.B., Linear Programming and Extensions. Princeton University Press. 1951.
López, C., González, L., Estimación de los parámetros de un modelo de pronóstico con componente cíclico con programación lineal. Revista Ingeniería (Bogotá). UDFJC: , n.2, p.12 - 20, 2002
Rios Insua S, Programación Lineal y Aplicaciones. RAMA, Madrid, España, 1998.
Mehmet Gümüs; James H Bookbinder. Cross-Docking and its implications in locations-distribution systems. Journal of Business Logistics . Vol 25, Nº2, 2004.
Vidal C and Goetschalckx M, Strategic productiondistribution models: a critical review with emphasis on global supply chain models. European Journal of Operational Research 1997
Love RF, Morris JG and Wesolowsky GO Facilities Location. North- Holland, Amsterdam, 1988
Laporte G Location-routing problems. In Vehicle Routing: Methods and Studies (ed. Golden BL and Assad AA). NorthHolland, Amsterdam, 1988.
Basheer M. Khumawala. An Efficient Branch and Bound Algorithm for the Warehouse Location Problem. Management Science, Application Series Vol. 18, No. 12, 1972)
Klose A, A Branch and Bound Algorithm for An Uncapacitated Facility Location Problem with a Side Constraint, International Transactions in Operational Research, Volume 5, Number 2, 1998
Jean-François Cordeau, Federico Pasin, Marius M. Solomon. 2006. An integrated model for logistics network design. Annals of Operations Research 144, no. 1 (April 1): 59-82. http://www.proquest.com/ (accessed April 3, 2008).
M T Ramos, J Sáez. 2005. Solving capacitated facility location problems by Fenchel cutting planes. The Journal of the Operational Research Society 56, no. 3 (March 1): 297-306. http://www.proquest.com/ (accessed April 3, 2008).
Samir Elhedhli, Jean-Louis Goffin. 2004. The integration of an interior-point cutting plane method within a branch-andprice algorithm. Mathematical Programming 100, no. 2 (June 1): 267-294. http://www.proquest.com/ (accessed April 3, 2008).
L Muyldermans and D Cattrysse and D Van Oudheusden 2003. District design for arc-routing applications. The Journal of the Operational Research Society 54, no. 11 (November 1): 1209-1221. http://www.proquest.com/(accessed April 3, 2008).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2008-00-00 vol:13 nro:2 pág:36-43
Modelo para la localización de un plataforma de cross docking en el contexto de logística focalizada
Dusko Kalenatic
Director de los Grupos de Investigación GIP Universidad Católica de Colombia, Investigador, Grupo de Investigación en Sistemas Logísticos, Universidad de la Sabana.
Cesar Amilcar López Bello
Investigador del Grupo MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia, Investigador Grupo de Investigación en Sistemas Logísticos, Universidad de la Sabana.
Leonardo José González Rodríguez
Director Grupo de Investigación en Sistemas Logísticos, Universidad de la Sabana, Investigador grupo de investigación MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia.
Feizar Javier Rueda Velasco
Investigador de los Grupos de investigación GIP y MECUAC Universidad Católica de Colombia, y Grupo de Investigación MMAI Universidad Distrital.
Resumen
El actual contexto de los escenarios globales de defensa ha impulsado el desarrollo de conceptos cómo el de logística focalizada, creada para brindar soporte logístico en ambientes de alta volatilidad e incertidumbre Dentro de ese marco la logística focalizada requiere de herramientas que permitan agilizar los procesos de toma de decisiones.
Atendiendo dicha necesidad se presenta un modelo que pretende soportar la decisión de localización de una plataforma de crossdocking y asignación de medios de transporte que permita garantizar una distribución ágil desde orígenes de suministro hasta los orígenes de demanda siendo especialmente novedosa la estratégica de solución del mismo
Abstract
The current context of global defence scenarios has enhanced development of new concepts like focused logistics concept. Focused logistics is a concept created to support logistics operations in uncertainty environments. In this framework focused logistics needs tools to enable an agile, reliable and accurate decision processes.
In order of these requirements, this paper shows a mathematical model as a support tool to find a good location of a cross-docking facility and allocate workloads of different kinds of vehicles from suppliers to demand centres being especially innovative to the strategy used for the solution of the present model.
Key words: Focused logistics, cross-docking, decisions support tools, location, Distribution Systems.
1. INTRODUCCIÓN
A lo largo de la historia, los desarrollos militares se han caracterizado por cambiar la perspectiva del desarrollo global, la logística no ha sido la excepción. La logística militar aparece incluida dentro de la categoría de Ingeniería y Modelación matemática logística (una de las 4 categorías académicas del pensamiento logístico propuestas por Kent & Flint en 1997) [1], la cual combina los desarrollos mas relevantes en ingeniería con las fortalezas del modelamiento matemático para atender las necesidades logísticas de las fuerzas armadas. De igual manera dicha categoría se encuentra incluida dentro de los dos enfoques de investigación en logística; el económico y el comportamental, evidenciados en [2].
La logística militar se ha definido cómo la ciencia que tiene como objetivo proporcionar a las fuerzas armadas los medios necesarios para la guerra a través de ciclo logístico [3] es decir, los medios de apoyo para el combate. Su papel determinante en la historia ha sido evidenciado entre otros por [4], [5], [6], [7], [8], sin embargo el contexto clásico de los escenarios de conflicto ha sufrido cambios significativos.
El actual contexto de los escenarios de conflicto esta caracterizado por las amenazas asimétricas, las significativas alteraciones políticas, económicas y por los rápidos cambios tecnológicos en donde no es fácil prever el surgimiento de conflictos que, sin embargo, requieren de una respuesta contundente en periodos cortos de tiempo. En este marco surge el concepto de logística focalizada, planteado como la integración de las TICs y tecnologías logísticas para proveer rápida respuesta a las necesidades de las fuerzas armadas. [9]
La logística focalizada requiere la utilización de herramientas que permitan tomar decisiones oportunas bajo condiciones de incertidumbre. Por lo tanto se plantea en este artículo un modelo que permita tomar una decisión táctica de localización de una plataforma de crossdocking cómo concepto organizativo para su preposicionamiento de tal manera que dicha plataforma pueda abasrecer unidades militares localizadas en diferentes puntos del teatro de operaciones. Adicionalmente el modelo permite realizar una asignación adecuada de los medios de transporte disponibles.
A partir de la formulación del modelo se observa que presenta complejidad algorítmica, por lo cual se plantea una estrategia de solución por etapas., la cual consiste en primera instancia en tomar la decisión de localización de la plataforma de cross-docking, para posterior mente asignar los medios de transporte y efectuar la programación de los viajes a realizar por los vehículos.
2. MARCO CONTEXTUAL
La logística Focalizada se describe como la habilidad de proveer a las fuerzas armadas con el adecuado personal, equipamiento y provisiones en el lugar adecuado, en el momento adecuado, en la cantidad adecuada en todo el espectro de las operaciones militares a través de un sistema de información en tiempo real y basado en redes, que provee una visibilidad total de los recursos vinculando efectivamente al personal operativo y logístico en todos los servicios y agencias de apoyo, a través de innovaciones transformativas a las organizaciones y los procesos ,es decir, con apoyo para todas las funciones. [10]
Siendo especialmente innovador en este concepto el uso intensivo de los sistemas de información en tiempo real como herramienta para la toma de decisiones en todos los niveles. Atendiendo a lo anterior, la logística focalizada se enfoca en brindar el soporte exacto y oportuno al combatiente en todo el espectro de operaciones, para lo cual es necesario generar habilidades y capacidades logísticas que permitan una eficaz toma de decisiones. Dicha agilidad en el proceso de toma de decisiones solo es posible si se crea un concepto del soporte logístico basado en conocimiento y centrado en redes lo cual depende de: una fuente de datos relacionada con el comportamiento de la demanda y la visibilidad de los recursos; comunicaciones que permitan compartir datos en tiempo real; estándares que hagan interoperativos los datos , los procesos y los sistemas así como herramientas que permitan convertir el compartir datos en compartir información y estos a su vez transformados en conocimiento compartido, que finalmente, se reflejen en decisiones superiores.[11]
Estas decisiones en el contexto clásico de los sistemas logísticos empresariales se tornan importantes, en el contexto de logística focalizada se convierten en críticas. En los primeros el objetivo generalmente esta relacionado con minimizar el costo del sistema, mientras que se satisfacen los requerimientos de nivel de servicio [12] y sus agentes son en su mayoría organizaciones empresariales y en una menor proporción empresas públicas. Sin embargo, en los segundos, además de estar sujetos a restricciones de presupuestales relacionados con objetivos de minimización de costo se encuentran inmersos en un entorno donde los propósitos se enfocan sobre el mantenimiento y aseguramiento de intereses regionales, nacionales o internacionales, donde el nivel de servicio al consumidor final (en este caso unidades militares) más que el fin se convierte en un medio para el logro de los objetivos. Dichas decisiones "superiores" deben contar con herramientas que permitan soportarlas oportunamente tanto a nivel estratégico, operacional, táctico como operativo
Dentro de las decisiones de tipo táctico, una decisión de interés es aquella relacionada con la localización de plataformas que permitan el aprovisionamiento y distribución de paquetes personalizados a las unidades militares, de tal manera que permitan soportar sus necesidades con precisión en el lugar y tiempo correctos [13] para obtener de esta manera una ventaja operativa.
Una práctica difundida para obtener dicha ventaja operativa es el cross-docking, en donde el principio general radica en recibir productos de uno o varios centros de producción o proveedores, consolidarlos y embarcarlos a los centros de consumo tan rápido como sea posible [14], lo cual se ajusta a las necesidades de los escenarios de conflicto. Adicionalmente el uso de esta práctica atiende, entre otros, a algunos de los principios de logística militar propuestos en [4] cómo lo son la flexibilidad, la dispersión y "timing"(precisión en tiempo y espacio) , entre otros.
Coherentemente con lo anterior, la práctica del cross-docking fue presentada por [15] cómo uno de las prácticas que responden al requerimiento de flexibilidad para el diseño de los sistemas de almacenamiento del futuro, donde se destaca como principal razón para la flexibilidad la habilidad para responder oportunamente a la demanda. De acuerdo con este marco se presenta en los apartados siguientes, un modelo que permita localizar una plataforma de cross-docking con el objetivo de realizar el acopio y consolidación de suministros de los proveedores y fabricantes para distribuirlos ágilmente a los orígenes de la demanda que en el contexto de logística focalizada pueden estar relacionados con diferentes áreas de operaciones o puntos de soporte a las mismas.
3. MODELO DE LOCALIZACIÓN
De acuerdo con el marco contextual se formula un modelo matemático que permite tomar la decisión de la localización de la plataforma de cross-docking teniendo en cuenta entre otros parámetros: la localización de los orígenes de demanda a distribuir; la localización de los orígenes de suministros (proveedores, fabricantes , otras plataformas, etc.); los medios de transporte y sus capacidades; los costos de transporte, de tal manera que se minimizaran los costos de transporte y distribución.
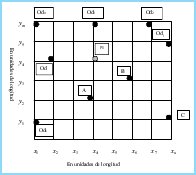
En esa medida la situación inicial, tal como se muestra en el ejemplo de la Figura 1, parte tres orígenes de suministro A, B y C que buscan entregar suministros a los orígenes de la demanda Od 1, Od2, ..., Od 6, realizando el cross-docking en la plataforma P1. Tanto los Orígenes de suministros, los orígenes de demanda, como la plataforma se representan a través de coordenadas cartesianas bidimensionales.
La decisión de la localización de la plataforma se toma con base en las distancias desde los orígenes de suministro hacia la plataforma y desde los orígenes de la demanda hacia la misma, no obstante no se hace uso de las distancias euclidianas ya que en las situaciones dentro del contexto de logística focalizada son menos probables las posibilidades de desplazamiento a través de rutas rectas debido a que generalmente pueden no estar disponibles, lo que obliga predominantemente a los medios de transporte a realizar recorridos no lineales. Con base en este supuesto se resuelve el problema representando las distancias entre el origen y el destino, por medio de la suma de los cuadrantes recorridos exclusivamente a través de las abscisas y las ordenadas, es decir, distancias rectilíneas mostradas en [16] donde los recorridos diagonales no son contemplados.
De acuerdo con lo anterior se definen las variables de decisión las cuales incluyen las distancias rectilíneas desde la plataforma de cross-docking (plataforma central) desde los orígenes de suministro y hacia los orígenes de la demanda donde;
dxi : Diferencia entre la abscisa del origen de suministro "i", y la abscisa de la plataforma de cross-docking donde, dxi ∈ ℜ ∀ i= 1,2,..., m
Distancia sobre las abscisas entre el origen de suministro "i",
y la plataforma de cross- docking, donde, |dxi|≥ 0
dyi: Diferencia entre la ordenada del origen de suministro "i", y la ordenada de la plataforma de cross- docking donde, dyi ∈ ℜ
∀i = 1,2,..., m
Distancia sobre las ordenadas entre el origen de suministro "i",
y la plataforma de cross- docking, donde, |dyi| ≥ 0
dx j : Diferencia entre la abscisa del origen de demanda "j", y la abscisa de la plataforma de cross- docking, donde, dxj ∈ ℜ ∀ j = 1,2,..., n
Distancia sobre las abscisas entre el origen de suministro"j", y la plataforma de cross- docking, donde, |dxj| ≥ 0
dyj : Diferencia entre la ordenada del origen de demanda "j", y la ordenada de la plataforma de cross- docking, donde, dyj ∈ ℜ ∀ j = 1,2,..., n
Distancia sobre las ordenadas entre el origen de suministro "j", y la plataforma de cross- docking, donde, |dyj| ≥ 0
Como dxi , dyi , dxj , dyj , son variables no restringidas y reales su valor absoluto representa la distancia. En ese orden de ideas se plantea una primera aproximación a un modelo de localización con el objetivo de minimizar las distancias rectilíneas entra la plataforma central y los orígenes de suministro y demanda así:
Cómo se puede observar en (1), el valor absoluto incrementa la función objetivo. Por otra parte los dxi , dyi , dxj, dyj , generan un
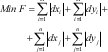
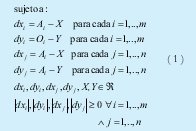
problema no convexo, es decir, un problema de programación no lineal.
Análogamente se puede observar, como se dijo anterior mente que las variables dxi, dyi , dxj, dyj , son no restringidas por lo que es necesario aplicar el principio de programación lineal en donde una variable de este tipo se expresa como la diferenta de dos variables positivas, es decir:
|X| = X '- X ' ' donde X ∈ ℜ ∧ X' , X' ' ≥ 0
Con la siguiente implicación:
X 'X ' ' = 0
Lo que quiere decir que una de las dos variables es cero y por lo tanto el valor absoluto se carga a la variable diferente de cero, tal que:
|X| = X' + X''
Lo que para el problema específico implica:
|dxi| = dxi(+) - dxi(-) ∀i = 1,.., m
|dxi| = dxi(+) + dxi(-) ∀i = 1,.., m
|dyi|= dyi(+) - dyi(-) ∀i = 1,.., m
|dyi| = dyi(+) + dyi(-) ∀i = 1,.., m
|dxj| = dxj(+) - dxj(-) ∀j = 1,.., n
|dxj| = dxj(+) + dxj(-) ∀j = 1,.., n
|dyi| = dyj(+) - dyi(-) ∀j = 1,.., n
|dyi| = dyj(+) + dyj(-) ∀j = 1,.., n
Teniendo en cuenta lo anterior se definen las variables de decisión así:
Variables de decisión:
dxi(+) : Distancia desde la abscisa de la plataform a de cross-docking hasta la abscisa del origen de suministro "i", donde i = 1,2 ,L , m cuando la pla taforma está a la izquierda del origen de suministro
dxi(-) : Distancia desde la abscisa del origen de suministro "i", hasta la abscisa de la plataforma de cross-docking , donde i = 1,2,L ,m cuando la plataforma está a la derecha del origen de suministro
dyi(+) : Distancia desde la ordenada de la plataform a de cross-docking hasta la orde nada del origen de sum inistro "i", donde i = 1,2,..., m cuando la plataforma está por de bajo del origen de suministro
dyi(-): Distancia desde la ordenada del origen de suministro "i", hasta la ordenada de la plataforma de cross-docking, donde i = 1,2,...,m cuando la plataforma está arriba del origen de suministro
dxj (+) : Distancia desde la abscisa de la plataform a de cross-docking hasta la abscisa del orige n de la demanda "j", donde j = 1, 2,..., n cuando la plataforma está a la izquierda del origen de la demanda
dxj(-): Distancia desde la abscisa del origen de la demanda "j", hasta la abscisa de la plataforma de cross-docking donde j = 1, 2,..., n
dyj(+) : Distancia desde la ordenada de la plataform a de cross-docking hasta la ordenada del origen de la dem anda "j", donde j = 1, 2,..., n
dyj(-) : Distancia desde la ordenada del origen de la demanda "j", hasta la ordenada de la plataforma de cross-docking, donde j = 1, 2,.., n
X: Abscisa de la plataforma de cross-docking
Y : Ordenada de la plataforma de cross-docking
Xi,k : Número de viajes a programar del origen de suministro "i" a l plataforma de cross-docking en el medio de transporte tipo "k", donde i = 1,2,..., m ∧ k = 1,2,... , l
Yj,k : Número de viajes a programar de la plataforma de cross-docking al origen de la demanda "j" en el medio de transporte tipo "k ", donde j = 1,2,..., n ∧ k = 1,2,..., l
Zi,k : Cantidad a transportar del origen "i" a la plataforma de crossdocking en el medio de transporte "k", donde i = 1,2 ,..., m ∧ k = 1,2,..., l
Wj,k : Cantidad a transportar de la plataforma de crossdocking al destino "j" en el medio de transporte "k", donde j = 1,2,...,n k = 1,2,...,l
Parámetros:
Cdi : Capacidad de oferta del origen de suministro "i", donde i = 1,2 ,..., m
Drj : Demanda requerida en origen de la demanda "j", donde j = 1,2,... , n
fr : Fa ctor de retorno me dio vacío
cudk : Costo por unidad de distancia de un m edio de transporte tipo "k", donde k = 1,2 ,..., l
Sk : Costo de carga y descarga y de operación fija de un me dio de transporte tipo "k", donde k = 1,2 ,... ,l
Ai : Abscisa del orige n "i", donde i = 1,2 ,..., m
Oi : Ordenada del orige n "i", donde i = 1,2 ,..., m
Aj : Abscisa del de stino "j", donde j = 1,2,..., n
Oj : Ordenada del destino "j" , donde j = 1,2,...,n
N k : Número de v ehículos disponibles del tipo "k", donde k = 1,2 ,... ,l
NVVk : Número de viajes permitidos por ve hículo de l tipo "k", donde k = 1,2 ,...,l
CCk : Capacidad de carga del medio de transporte tipo "k", donde k = 1,2 ,..., l
Es importante resaltar que la obtención de los parámetros en ambientes de alta incertidumbre como lo son los asociados a la logística focalizada depende en gran medida del concepto de fusión de información [11] que comprende una red total fin a fin que permita obtener información en tiempo real entre otras acerca del despliegue, la distribución, el sostenimiento de los canales de distribución, la demanda y necesidades de las unidades operativas que a su vez permitan alimentar herramientas de soporte que permitan tomar decisiones tales como la presentada en este modelo.
Función Objetivo
El modelo pretende buscar una alternativa de localización adecuada para la plataforma dado el conocimiento previo de la localización de los orígenes del suministro, orígenes de la demanda, costos asociados al transporte y la capacidad de los medios de transporte.
Con base en lo anterior el modelo tiene el objetivo de determinar la ubicación de una locación y la asignación de medios de transporte de tal manera que se minimice los costos de transporte y distribución en función de las coordenadas de la localización de la plataforma central, las distancias de los orígenes de suministro y demanda hacia la misma, y el número de viajes realizado por medio de transporte, tal como se muestra en (2)

Dónde:
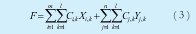
Se pretende minimizar la función objetivo presentada en (3) la cual representa una minimización de los costos de transporte y distribución.
Es importante anotar que la estimación de los costos está en función de las distancias, las cuales son variables de decisión y que al estar multiplicadas por las variables número de viajes, Nk , hace que el modelo se enmarque en un problema de programación no lineal mixta con variable enteras y reales, haciendo que el tratamiento algoritmo sea complejo.
Restricciones
El modelo presenta diferentes tipos de restricciones: restricciones de oferta de los orígenes de suministro (4) y (5); restricciones de demanda (6), (7) y (8); y finalmente restricciones de localización (9), (10), (11) y (12).

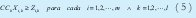
La restricción (4) indica que la cantidad transportada desde cada origen de suministro debe ser menor o igual a la capacidad del mismo origen, esto garantiza que las cantidades transportadas desde los diferentes orígenes están disponibles para su consumo.
La restricción (5) indica que la capacidad total de los medios de transporte por le numero de viajes realizados desde cada origen de suministro hacia la plataforma central debe ser al menos igual a la capacidad de los orígenes de suministro.
La restricción (6) garantiza que las cantidades transportadas de los orígenes de suministro hacia la plataformansean suficientes con respecto a las transportadas desde la plataforma hasta los orígenes de la demanda. A su vez (7) aseguran la capacidad de los medios de transporte para transportar desde los orígenes de los suministros hacia los orígenes de la demanda.
Por otra parte (8) implica el cumplimiento de la demanda en cada origen de la misma.

Las restricciones (9), (10), (11) y (12) plantea el uso de distancias rectilíneas como concepto de programación meta mostradas, entre otros por [16][17],[18],[19],[20] y [21]. Modelos con distancias euclidianas son muy comunes y pueden verse entre otros [22], [23] ,[24] y [25]
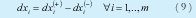
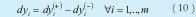
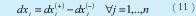
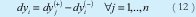
Por último las restricciones lógicas estan dadas por (13)

4. ESTRATEGIA DE SOLUCIÓN
Tal como se observo anteriormente, la dificultad de solución del problema de localización de la plataforma se disminuye haciendo uso de una estrategia de solución multietapas comúnmente utilizada en otras técnicas de programación matemática, de tal manera que la complejidad computacional es menor y por lo tanto la eficiencia algorítmica es mayor al subdividir el problema inicial en dos problemas de baja de complejidad, como lo son: un problema de localización exclusivamente, y un problema de distribución y transporte, exclusivamente.
De acuerdo con lo anterior se plantea la solución del problema en dos fases: la primera tiene como objetivo determinar la ubicación de la plataforma central, de tal manera que los datos obtenidos se convierte en información paramétrica para alimentar la segunda fase, que a su vez tiene como objetivo seleccionar los medios de transporte y el número de viajes que deben realizar Primera fase.
Modelo de localización.
El modelo de localización presentado en (14) pretende obtener las coordenadas de la plataforma central que minimicen las distancias ponderadas entre los orígenes de suministro y los orígenes de la demanda
El problema presentado es un problema de programación lineal entera de baja complejidad que puede ser resuelto, entre otros, por el algoritmo de ramificación y acotamiento o por el algoritmo de plano de corte.
Algunas aplicaciones del algoritmo de ramificación y acotamiento a problemas de localización son presentadas por [26], [27], [28] entre otros. De igual manera trabajos relacionados con el algoritmo de plano de corte aplicado al problema de localización son presentados por: [29], [30], [31]

Una vez conocidas las coordenadas de la plataforma de cross-docking es necesario resolver el problema asociado de selección de medios de transporte y número de viajes por tipo de medio, tal como se muestra en la segunda fase.
Segunda fase. Selección de Medios de Transporte
En esta fase se resuelve el problema de transporte asociado, las coordenadas de la plataforma central se convierten en parámetros de tal manera que se pueden determinar los costos unitarios por viaje tal como se muestra en (15).
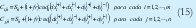
Una vez calculados los costos unitarios de transporte, se plantea el modelo que permite asignar los medios de transporte a utilizar y el número de viajes a realizar con base en una función objetivo que busca minimizar el costo de transporte, como se observa en (16).
La solución a este modelo junto con la de la primera fase trae consigo una solución apropiada para el modelo general, brindando una alternativa de localización de la plataforma central priorizada por el flujo entre los orígenes de suministro y los orígenes de la demanda permitiendo de la misma forma seleccionar los medios de transporte y asignación de cargas a los mismos.

CONCLUSIONES
El concepto de logística focalizada surge como respuesta al actual contexto de los escenarios de conflicto los cuales se encuentran sujetos a altas dosis de incertidumbre de tal manera que se pueda brindar un soporte logístico basado en un sistema de información en tiempo real y basado en redes. Dicho sistema de información debe incluir herramientas que permitan asesorar el proceso de toma de decisiones tanto a nivel estratégico, operacional o táctico.
Se destacó la importancia del uso de plataformas de cross-docking como una práctica que además de reducir costos logísticos permite conectar orígenes de suministro con áreas de operaciones de una manera precisa, dispersa, flexible y oportuna.
En respuesta a lo anterior se presentó un modelo matemático que permite encontrar una alternativa de localización de una plataforma de cross-docking y adicionalmente la selección de medios de transporte y su asignación de cargas. El modelo involucra complejidad en su solución la cual se incrementará en la medida que se aumenten los nodos de suministro y de demanda, además de involucrar restricciones de limitaciones de ubicación que implican el uso de variables de carácter binario para resolver restricciones disyuntivas.
Por ende se optó por una estrategia multietapa que permitiera dividir el problema en dos fases de baja complejidad. La primera, un modelo de localización basado en distancias rectilíneas que per mite encontrar las coordenadas de la plataforma central bajo un criterio de minimización de distancias ponderadas, lo que posibilita ubicar la plataforma de tal manera que se favorezcan los flujos de suministro más grandes. Lo anterior responde a los principios citados de logística militar como lo son la flexibilidad, la dispersión así como la precisión en tiempo y espacio.
En la segunda etapa se usan las coordenadas de la plataforma central, halladas en la etapa uno, como dato de entrada en un modelo de transporte que genera la selección de los medios de transporte y la asignación de las cargas de los mismos. Por consiguiente, y una vez finalizadas las dos etapas se obtiene una solución apropiada al modelo original. Dicha estrategia de solución presenta una ventaja significativa frente al modelo original al mejorar la eficiencia algorítmica, la facilidad de análisis y cálculo lo cual redunda en una solución ágil del mismo.
Por otra parte, el modelo presentado involucra un objetivo de minimización de costo lo cual, tal como se presento en el marco contextual, no es el único objetivo contemplable dentro del enfoque de logística focalizada, en donde también tienen importancia criterios como la del minimización tiempo de respuesta, la minimización del riesgo, entre otros.
Debido a las condiciones del modelo actual y a su posibilidad de complementación, se presentará en futuras publicaciones modelos relacionados con el cumplimiento de los objetivos alternativos mencionados, así como el abordaje del problema en un enfoque multicriterio. Adicionalmente es importante destacar que los modelos presentados presentan una solución estática para un instante o periodo de tiempo, la cual tiene validez mientras que las condiciones se mantengan.
Por último el modelo presentado se planteó dentro de un enfoque de logística focalizada el cual fue creado como respuesta primordial ante ambientes de defensa, sin embargo sus alcances pueden ser extendidos a contextos sujetos a condiciones de volatilidad e incertidumbre.
Referencias bibliográficas
[1] Kent John L Jr y Flint Daniel J. Perspectives on the evolution of logistics thought. Journal of Business logistics. Vol.18.1997
[2] Sachan Amit y Datta Subhash. Review of supply Chain management and logistics research. Journal of physical distribution & logistics management. Vol 35 No 9, 2005.
[3] Posada Eduardo, La logística Militar y sus aplicaciones en la logística empresarial, Revista "Pensamiento y Gestión" Universidad del Norte. Barranquilla. nº 6 , 2000
[4] Huston James A, The sinews of war: Army Logistics 1775-1953
[5] Paulus Robert, Logistics in the Forgotten war.
[6] Pagonis William G, Moving Mountains: Lessons in leadership and logistics from the gulf war, Harvard Business School Press, 1992.
[7] Mc Grath John J, The Other End of the Spear: The Tooth to- Tail Ratio (T3R) in Modern Military Operations, The Long War Series Occasional Paper 23, Combat Studies Institute Press, 2007
[8] Hess Earl J, Retreat from Gettysburg: Lee, Logistics, and the Pennsylvania Campaign, The Journal of American History; 92, 4; 2006.
[9] Paulus Robert. D, Implementing focused logistics, Army Logistician, No 35, vol6, 2003.
[10] Department of Defense, Joint Vision 2020, publicado en http://www.dtic.mil/jointvision/jvpub2.htm Fecha de consulta 10 de septiembre de 2007
[11] Joint Chiefs of state, Focused Logistics campaign plan, 2004, disponible en https://acc.dau.mil/ CommunityBrowser.aspx?id=32577
[12] Simchi Levi D, Kaminsky P y Simchi Levi E, Designing and managing the supply chain concepts, strategies and cases. Mc Graw Hill
[13] Department of defense, Focused logistics Roadmap, 2005, disponible en, https://acc.dau.mil/ CommunityBrowser.aspx?id=22548&lang=en-US
[14] C S Sung and S H Song. Integrated service network design for a cross-docking supply chain network.The Journal of the Operational Research Society 54, no. 12 (December 1, 2003):
[15] Thompson Brockmann y Patty Godin.. Flexibility for the future in warehouse design. IIE Solutions. Jul 1997, 97,7; ABI/INFORM Global Pg.22
[16] Moskovich, D. Investigación de operaciones. Editorial, Mc graw hill. Mexico, 1995.
[17] Kalenatic D, Lopez C, Gonzalez L, Modelo Integral de Producción de Empresas Manufactureras, 1ª Ed, Kimpres, Bogotá, Colombia, 2006.
[18] Charnes A & Cooper W. Management Models ans Industrial Applications of linear Programming. New York, USA, 1961
[19] Dantzig G.B., Linear Programming and Extensions. Princeton University Press. 1951.
[20] López, C., González, L., Estimación de los parámetros de un modelo de pronóstico con componente cíclico con programación lineal. Revista Ingeniería (Bogotá). UDFJC: , n.2, p.12 - 20, 2002
[21] Rios Insua S, Programación Lineal y Aplicaciones. RAMA, Madrid, España, 1998.
[22] Mehmet Gümüs; James H Bookbinder. Cross-Docking and its implications in locations-distribution systems. Journal of Business Logistics . Vol 25, Nº2, 2004.
[23] Vidal C and Goetschalckx M, Strategic productiondistribution models: a critical review with emphasis on global supply chain models. European Journal of Operational Research 1997
[24] Love RF, Morris JG and Wesolowsky GO Facilities Location. North- Holland, Amsterdam, 1988
[25] Laporte G Location-routing problems. In Vehicle Routing: Methods and Studies (ed. Golden BL and Assad AA). NorthHolland, Amsterdam, 1988.
[26] Basheer M. Khumawala. An Efficient Branch and Bound Algorithm for the Warehouse Location Problem. Management Science, Application Series Vol. 18, No. 12, 1972)
[27] Klose A, A Branch and Bound Algorithm for An Uncapacitated Facility Location Problem with a Side Constraint, International Transactions in Operational Research, Volume 5, Number 2, 1998
[28] Jean-François Cordeau, Federico Pasin, Marius M. Solomon. 2006. An integrated model for logistics network design. Annals of Operations Research 144, no. 1 (April 1): 59-82. http://www.proquest.com/ (accessed April 3, 2008).
[29] M T Ramos, J Sáez. 2005. Solving capacitated facility location problems by Fenchel cutting planes. The Journal of the Operational Research Society 56, no. 3 (March 1): 297-306. http://www.proquest.com/ (accessed April 3, 2008).
[30] Samir Elhedhli, Jean-Louis Goffin. 2004. The integration of an interior-point cutting plane method within a branch-andprice algorithm. Mathematical Programming 100, no. 2 (June 1): 267-294. http://www.proquest.com/ (accessed April 3, 2008).
[31] L Muyldermans and D Cattrysse and D Van Oudheusden 2003. District design for arc-routing applications. The Journal of the Operational Research Society 54, no. 11 (November 1): 1209-1221. http://www.proquest.com/ (accessed April 3, 2008).
Dusko Kalenatic
Doctor en Ciencias Técnicas, Universidad de Las Villas "Marta Abreu", Santa Clara, Especialista en Ingeniería de Producción Universidad Distrital Francisco José de Caldas, Especialista "Instituto de Periodismo Yugoslavo", Economista, Escuela Superior de Economía, Belgrado, Ingeniero Diplomado en Organización del Trabajo, Universidad de Belgrado, Profesor Titular, Director del Grupos de Investigación GIP de la Universidad Católica de Colombia, Investigador Grupo de Investigación en Sistemas Logísticos, Universidad de la Sabana. dusko.kalenatic@unisabana.edu.co
César Amílcar López Bello
Magíster en Ingeniería Industrial, Universidad de los Andes. Especialista en Ingeniería de Producción, Universidad Distrital Francisco José de Caldas. Ingeniero Industrial Universidad Distrital Francisco. Investigador Grupo de Investigación en Sistemas Logísticos Universidad de la Sabana. Profesor Asociado, Facultad de Ingeniería Universidad Distrital.Director de la Maestría en Ingeniería Industrial, Universidad Distrital Francisco José de Caldas.clopezb@udistrital.edu.co, cesar.lopez@unisabana.edu.co
Leonardo José González Rodríguez
Magíster en Ingeniería Industrial, Universidad de los Andes. Especialista en Ingeniería de Producción, Universidad Distrital. Ingeniero Industrial, Universidad Distrital. Profesor Asistente, Facultad de Ingeniería. Universidad Distrital Francisco José de Caldas. Director de las Especializaciones en Ingeniería de Producción e Informática Industrial de la Universidad Distrital, Director Grupo de Investigación en Sistemas Logísticos, Universidad de la Sabana, Investigador grupo de investigación MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia. lejogorod@yahoo.com
Feizar Javier Rueda Velasco
Ingeniero Industrial, Escuela Colombiana de Ingeniería "Julio Garavito". Investigador Grupo de investigación en Producción "GIP", Universidad Católica de Colombia, Investigador Grupo MMAI Universidad Distrital.fjrueda@ucatolica.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










