DOI:
https://doi.org/10.14483/23448393.2813Published:
2001-11-30Issue:
Vol. 7 No. 2 (2002): July - DecemberSection:
Science, research, academia and developmentEstimación de los parámetros de un modelo de pronóstico con componente cíclico con programación lineal
Keywords:
Técnicas de pronóstico, Ciclicidad, Series de Fourier, Regresión lineal, Estimación de parámetros, Error absoluto, Programación lineal. (es).Downloads
References
Adam E.,Ebert R. Jr. Administración de la producción y las Operaciones. Prentice Hall. Mexico. 1991
Schroeder R. G., Administración de Operaciones, Mexico : Mc GRAW-HILL, Tercera Edición,1992
Sneddon I.N., Fourier Series,The Free Press,Glencoe, III.,1961. Bowman E. H., "Production Scheduling by the Transportation Method of Linear Programming" Operations Research, 3, no. 1, 1956.
Walpole R. E., et al. "Probability and Statistics for Engineers and Scientists". Prentice Hall, Inc. 1998.
Bedworth D. D.,Bailey J. E., Integred Production Control Systems, John Wiley & sons, Inc. 1995.
Buffa E., and Miller J. G., Production Inventory Systems : Planning and Control. Homewood, IL : Richard d. Irwin, 1979.
Johnson, L.A., and Montgomery D.C., Operations Research in Production Planning, Scheduling and Inventory Control. New York: John Wiley & Sons.,1974.
Silver E., Decision Sistems for Inventory Management and Production Planning. New York: John Wiley & Sons. Second Edition, 1985
Rios Insua S., et al. Programación lineal y aplicaciones. Editorial RA-MA, Madrid España, 1998.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:2 pág:12-20
Estimación de los parámetros de un modelo de pronóstico con componente cíclico con programación lineal
César Amílcar López Bello y Leonardo José González Rodríguez
Resumen
Los modelos de pronóstico con componente cí- clico son poco estudiados, y la estimación de los parámetros de esta clase de modelos usualmente se realiza con el método de los mínimos cuadrados. Se propone en este artículo el uso de la programación lineal para la estimación de parámetros en un modelo de pronóstico con componente cíclico basado en series de Fourier, usando como criterio la minimización de la suma absoluta del error, posteriormente se realiza un análisis comparativo de esta técnica y la de mínimos cuadrados usando simulación.
Palabras clave:
Técnicas de pronóstico, Ciclicidad, Series de Fourier, Regresión lineal, Estimación de parámetros, Error absoluto, Programación lineal.
Abstract
The forecasting models with cyclic component are few treated, and the parameters estimations of those kind of models usually can be made with minims squares method. In this article is proposed the use of linear programming for made parameter estimation, in a forecasting model with cyclic component based in Fourier series, using as criteria the minimization of sum of absolute error. Finally, is make a comparative analysis of this technique, with, the minims squares method using simulating.
Key words:
Forecasting technique, Cycling , Fourier series, Linear regression, Parameter estimation, Absolute error, Linear programming.
I. INTRODUCCIÓN
Los pronósticos de la demanda de bienes y/o servicios son vitales como insumo de información para realizar los procesos de planeación, programación y control de la función de operaciones en las organizaciones productivas, por esto de su adecuada estimación depende la formulación de planes que se puedan ajustar más a los hechos reales y que por lo tanto conlleven a que las empresas sean más productivas y competitivas.
Los procesos de pronóstico en el ámbito empresarial se soportan en herramientas, técnicas y métodos sistemáticos estructurados de naturaleza cuantitativa y cualitativa. Entre los de carácter cualitativo, se pueden mencionar los estudios de mercado, el método Delfi, el análisis de ciclo de vida del producto y el juicio de expertos entre otros; por otra parte las técnicas de carácter cuantitativo se agrupan en dos grandes clases, los modelos del orden causa efecto (como modelos de regresión, modelos econométricos, etc.) y las técnicas de pronóstico de serie de tiempos, de las que trata el presente artículo. Estas herramientas y su aplicación individual y combinada constituyen el marco de referencia de la ciencia de la predicción.
El tratamiento de la predicción de eventos con modelos de series de tiempo requiere de la identificación y el análisis de componentes tales como: la tendencia, la estacionalidad y la ciclicidad [1],[2], para lo cual existen diferentes metodologías, siendo una, la formulación de modelos de regresión con estructuras semejantes a las series de Fourier [3], para lo cual es necesario la estimación de los parámetros del modelo representativo del fenómeno presente en el sistema real.
La estimación de los parámetros de una función de predicción se realiza normalmente con el método de los mínimos cuadrados, cuyo propósito es minimizar la suma de los errores cuadráticos, es decir la suma de los cuadrados de las diferencias entre el valor estimado por la función de regresión y el valor observado en el sistema real [4] . Es así como este artículo presenta otra metodología de regresión fundamentada en el criterio de minimización de la suma de los valores absolutos de las desviaciones, lo cual se logra utilizando un modelo de programación lineal.
La novedad radica en la posibilidad de construir modelos con características cíclicas de una manera rápida y con un nivel de representabilidad alto, para ilustrar el proceso de construcción del modelo se efectúa una simulación y se compara la estimación por el método de optimización lineal y la obtenida utilizando el método de los mínimos cuadrados.
II. MODELO DE PRONÓSTICO
El pronóstico es una verdadera herramienta de "sistemas". Los conceptos subyacentes del análisis de series de tiempo provienen de la teoría del control automático y del análisis estadístico[5]. Ciertas técnicas para determinar las frecuencias predominantes en la teoría de la información también son aplicables para encontrar las relaciones cíclicas en los datos de las ventas. Los procedimientos matemáticos para determinar las relaciones polinómicas se pueden aplicar ciertamente para determinar las tendencias de crecimiento en datos de venta [6].
Para realizar el análisis cíclico se tiene un modelo basado en una serie de análisis de Fourier. El análisis cíclico se usa para obtener los valores aproximados de las características estacionales.
El modelo de predicción cíclico se ajusta a la expresión (1)
Donde p1 y p2 representan los periodos más significativos y se determinan por un análisis espectral,
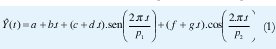
es posible que se requiera de varios ajustes para eliminar ruido.
El propósito es encontrar los valores de los parámetros a,b,c,d,f, y g por un procedimiento de regresión, de tal manera que se obtenga un modelo que estime los valores lo más cercano posible a la realidad en función del tiempo.
III. ESTIMACIÓN POR EL MÉTODO DE MÍNIMOS CUADRADOS
El procedimiento de estimación de un modelo de regresión es el método de los mínimos cuadrados. El objetivo es encontrar los valores de los parámetros [7], [8], de una función que minimiza la suma de los cuadrados de los errores (desviaciones) como se muestra en la expresión (2)
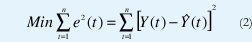
Utilizando la optimización clásica se deriva parcialmente con respecto a los parámetros a,b,c,d,f,g de tal manera que se obtienen las expresiones (3),(4),(5),(6),(7),(8)
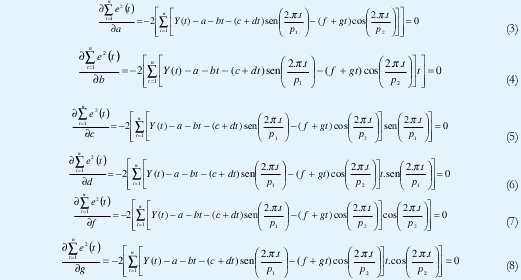
Para resolver el sistema de ecuaciones se realizan las siguientes sustituciones:

Debido a que el modelo es lineal en los parámetros se tiene un modelo de regresión múltiple, de tal manera que el problema consiste en resolver el siguiente sistema de ecuaciones :

IV. MODELO DE ESTIMACIÓN PARAMÉTRICA POR PROGRAMACIÓN LINEAL
Otra alternativa de estimación es la utilización de la programación matemática, en donde se pueden determinar los parámetros en función de la suma de los valores absolutos de las desviaciones [9] y que con algunas transformaciones se puede expresar como un modelo de programación lineal. La función de estimación general de un pronóstico de serie de tiempo se muestra en la expresión (9).
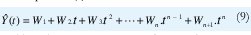
Ahora bien, visto como una función de regresión múltiple se expresa como (10)
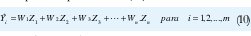
Siendo el problema escoger los parámetros W1,W2,...,Wn, donde, Y(t) es la variable dependiente y Zj j=1,2,...,n son las variables independientes. Para caracterizar el problema se supone que existen m observaciones como se muestra el la matriz[Yi|Zi,j] así:
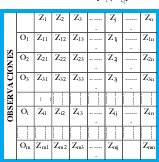
El problema consiste en determinar los valores Wj, que minimice la suma del valor absoluto de las desviaciones entre Yi y Yi , i=1,2,...,m.
Se podría formular un modelo con otro criterio por ejemplo encontrar los parámetros de la función de pronóstico que minimicen la máxima desviación absoluta. La formulación del modelo es la siguiente:
Objetivo: Determinar el vector de coeficientes de peso en una función de regresión que minimice la suma de las desviaciones absolutas
Variables de decisión:
Wj: Vector de pesos de la función de pronóstico,
donde j=1,2,...,n
Di: Vector de desviaciones de la observación i diferencia (Yi- Y i ).
Donde i=1,2,...,m
Si+: Vector de desviaciones positivas, (Yi- Y i>0).
Donde i=1,2,...,m
Si-: Vector de desviaciones negativas, (Yi- Y i>0).
Donde i=1,2,...,m
Parámetros:
Zi,j: Matriz de observaciones de los valores de las variables independientes j, del modelo de regresión en la observación i para i=1,2,...,m y j=1,2,...,n
Yi: Valor real de la variable dependiente en la observación i para i=1,2,...,m
j: Índice que identifica la variable independiente, (causa), j=1,2,...,n
i: Índice que identifica el número de la observación,i=1,2,...,m
m: Número de observaciones
n: Número de variables independientes o términos en la función de pronóstico
Entonces el modelo se muestra en la expresión

Como Di (i=1,2,...,m) son no restringidas entonces se expresa en términos de la diferencia entre dos variables positivas así:
Di= Si+ - Si- para i = 1,2,..., m
Si+ , Si- ≥0 para cada i = 1,2,..., m
Esto significa que puede existir una desviación por encima o por debajo pero no las dos simultáneamente de tal manera que el modelo se puede escribir como (12):

V. ESTIMACIÓN DEL MODELO POR PROGRAMACIÓN LINEAL
Para el modelo de estimación que se está considerando para el análisis cíclico en particular se tiene la siguiente formulación:
Objetivo: Determinar los coeficientes paramétricos de una función de pronósticos que contempla tendencia, estacionalidad y ciclicidad con el objeto de minimizar la suma de las desviaciones absolutas.
Función Objetivo: F= f(Dt, t=1,2,..,n) =Función de la suma de desviaciones absolutas.
Variables de decisión:
Dt: Desviación de la observación t con respecto al valor estimado para ese período,
donde t=1,2,..,n
St+ : Desviación positiva de la observación t, donde t=1,2,..,n
St-: Desviación positiva de la observación t, donde t=1,2,..,n
a,b,c.d,f.g: Parámetros de la función de regresión.
Parámetros:
P1,P2: Período del ciclicidad
t: Indice que identifica el número de la observación,
donde t=1,2,..,n
Yt: Valor real de la variable dependiente en la observación t, donde t=1,2,..,n
Función de pronóstico:
P1,P2: Período del ciclicidad
t: Indice que identifica el número de la observación, donde t=1,2,..,n
Yt: Valor real de la variable dependiente en la observación t, donde t=1,2,..,n
Función de pronóstico:
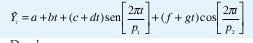
Donde:
Yˆt: Valor estimado en la observación "t", donde
t=1,2,..,n
(a +bt): Componente de tendencia
[(c+dt)sen(2πt/p1)]: Componente de ciclicidad
[(f+gt)cos(2πt/p2)]: Componente de estacionalidad.
Por lo tanto, el modelo de programación matemática se resume de acuerdo a la expresión (13)
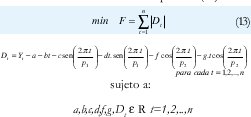
Para poder resolver el problema dado que la función objetivo es no lineal entonces se sustituyen las variables de decisión Dt por la suma de dos variables positivas St+ y St- para cada t=1,2,..,n de tal manera, que de cada par de variables, una sola variable asuma valor ( donde una represente una desviación por encima y la otra una desviación por debajo del valor estimado con respecto al valor real ) basado en la relación St+ . St-= 0 para cada t=1,2,..,n de tal manera, que el modelo transformado se muestra según la expresión (14)

VI. EVALUACIÓN DE LA CONSTRUCCIÓN DE LA FUNCIÓN POR LASTÉCNICAS MÍNIMOS CUADRADOS Y PROGRAMACIÓN LINEAL
Para comparar las técnicas de estimación del modelo de pronóstico propuesto, se diseño un proceso experimental de diez replicas de simulación con ruido aleatorio en hoja electrónica en donde se obtuvieron los siguientes resultados:
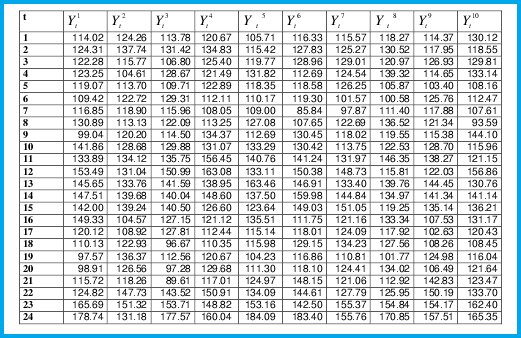
Posteriormente se calcularon los parámetros por el método de los mínimos cuadrados como se muestra en la tabla I
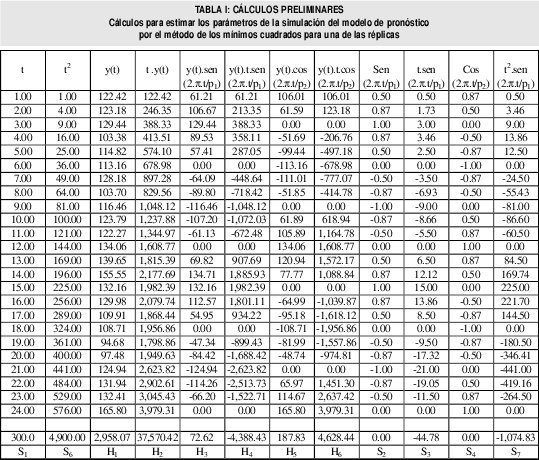
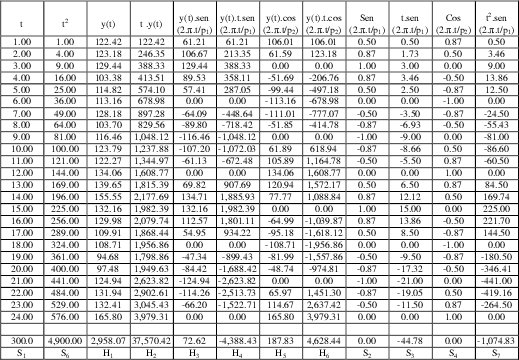
De tal manera que el sistema de ecuaciones a resolver es:

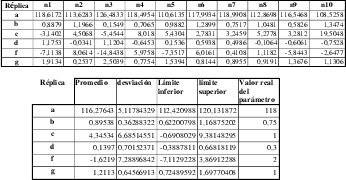
Se resolvió el sistema de ecuaciones para cada réplica, (se utilizó Derive) dando como resultado las siguientes estimaciones para los parámetros:

Así se puede apreciar que los parámetros estimados conforman un intervalo de confianza de 95 % de confianza que contiene el valor real de los parámetros, la función con el promedio de los parametros estimados por regresion se puede apreciar en la expresión (15)

De otra parte se estimaron los valores de los parámetros por programación lineal, (se utilizó el método simplex del paquete (QSBWIN) la formulación se muestra en el tabla II y los resultados en la tabla III

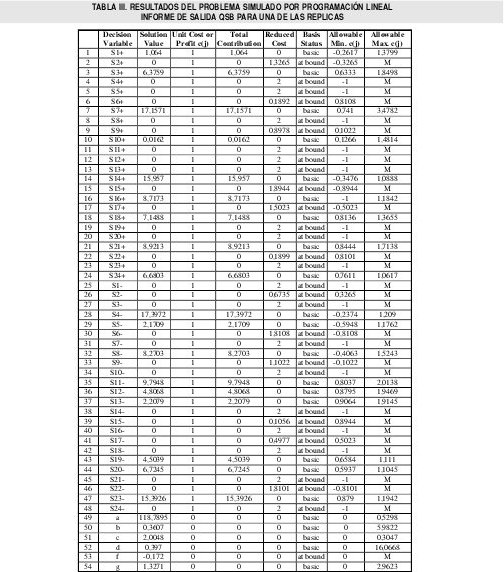
Los valores de los parámetros estimados por el método de la mínima distancia calculado con el modelo de programación lineal son:
Es así como la función de pronóstico estimada por programación lineal es la expresión (16)

Para comparar las dos técnicas se utilizó los siguientes criterios:

Inicialmente se ilustra el proceso mostrando el modelo gráfico, en donde observan la curva simulada y las curvas estimadas por los dos métodos de estimación, como se observa en la figura 1, para tal efecto se utilizaron las funciones estimadas para ampliar el número de observaciones a 48, con el fin de verificar la utilidad de dichas funciones para la obtencion de pronósticos.
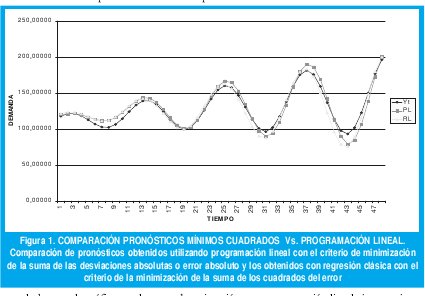
Parece que al observar la gráfica que la curva de estimación por programación lineal ajusta mejor que la estimada por el método de mínimos cuadrados, pero la diferencia entre los dos métodos no es muy significativa.
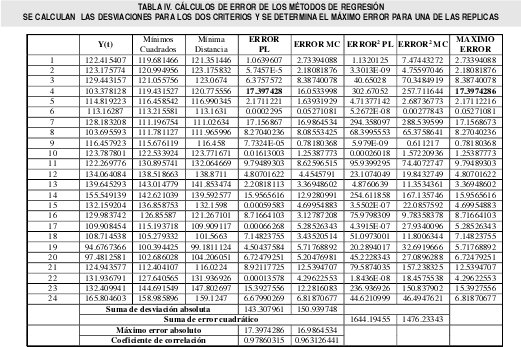
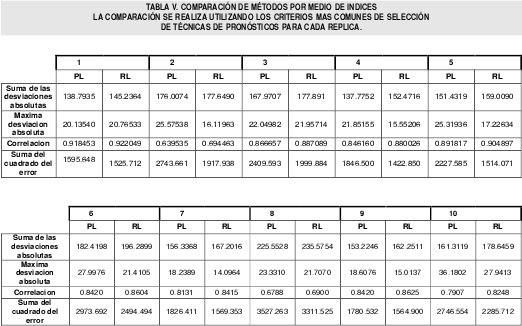
Para el experimento de simulación se calcularon los criterios de comparación expuestos anteriormente para cada una de las replicas como se muestra en la tabla IV. El resumen de los resultados para el experimento de simulación se muestra en la tabla V
VII. CONCLUSIONES
Se puede concluir que la programación lineal es utilizable como una técnica de estimación de parámetros para modelos de pronostico con componente cíclico desarrollados por regresión usando el criterio de la minimización de la suma absoluta del error. La técnica es de fácil y rápida implementación, dadas las herramientas computacionales con que se cuenta en l actualidad.
La diferencia en el ajuste de los modelos obtenidos por ambas técnicas no es significativa, ya que el grado de representación del modelo cíclico basado en series de Fourier es muy similar, para los criterios correspondientes a la suma de desviaciones absolutas, la suma de error cuadrático, la máxima desviación absoluta y el coeficiente de correlación, por esto, para determinar la superioridad de una técnica sobre la otra se requiere de un proceso experimental y de un análisis muy completo.
Para el modelo simulado al realizar una proyección más grande se observa que la función de regresión obtenida por programación lineal parece que ajustara mejor a la luz de los resultados. Se puede lograr otras formulaciones, si se toman otros criterios de decisión como por ejemplo buscar la mínima desviación absoluta.
REFERENCIAS
[1] Adam E.,Ebert R. Jr. Administración de la producción y las Operaciones. Prentice Hall. Mexico. 1991
[2] Schroeder R. G., Administración de Operaciones, Mexico : Mc GRAW-HILL, Tercera Edición,1992
[3] Sneddon I.N., Fourier Series,The Free Press,Glencoe, III.,1961. Bowman E. H., "Production Scheduling by the Transportation Method of Linear Programming" Operations Research, 3, no. 1, 1956.
[4] Walpole R. E., et al. "Probability and Statistics for Engineers and Scientists". Prentice Hall, Inc. 1998.
[5] Bedworth D. D.,Bailey J. E., Integred Production Control Systems,John Wiley & sons, Inc. 1995.
[6] Buffa E., and Miller J. G., Production Inventory Systems : Planning and Control. Homewood, IL : Richard d. Irwin, 1979.
[7] Johnson, L.A., and Montgomery D.C., Operations Research in Production Planning, Scheduling and Inventory Control. New York: John Wiley & Sons.,1974.
[8] Silver E., Decision Sistems for Inventory Management and Production Planning. New York: John Wiley & Sons. Second Edition, 1985
[9] Rios Insua S., et al. Programación lineal y aplicaciones. Editorial RA-MA, Madrid España, 1998.
Cesar Amilcar López Bello
Ingeniero Industrial, Universidad Distrital. Especialista en Ingeniería de Producción, Universidad Distrital. Magíster en Ingeniería Industrial, Universidad de los Andes. Candidato a Doctor en Ciencias Técnicas, Universidad de Las Villas (Cuba). Docente Tiempo completo, Facultad de Ingeniería Universidad Distrital. Director de la Maestría en Ingeniería Industrial, Universidad Distrital. Correo electrónico: cesaralopez@latinmail.com
Leonardo José González Rodríguez
Ingeniero Industrial, Universidad Distrital. Candidato a Magíster en Ingeniería Industrial, Universidad de los Andes. Docente Tiempo completo, Facultad de Ingeniería Universidad Distrital. Correo electrónico: le-gonza@uniandes.edu.co
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










