DOI:
https://doi.org/10.14483/23448393.2679Published:
2005-11-30Issue:
Vol. 11 No. 2 (2006): July - DecemberSection:
Science, research, academia and developmentModelo de planeación de capacidades utilizando programación fraccional lineal en un contexto de múltiples criterios de decisión
Keywords:
Gestión de capacidades, Programación lineal, Programación fraccional, Programación multi-objetivo (es).Downloads
References
Hamid Noori y Russell Radford. Administración de Operaciones y Producción. Mc Graw Hill. 1997
David J. Sumanth. Ingeniería y Administración de la productividad. Mc Graw Hill .1990
J. A. Domínguez Machuca et al. Dirección de Operaciones, Aspectos Tácticos y Operativos en la Producción y los Servicios. Editorial Mc Graw Hill Interamericana de España. 1995
Keith Lockyer. Production and Operation Management. Prentice Hall 1991.
Narashimhan, L. et al. Planeación de la Producción y Control de Inventarios. Prentice Hall. 1996
Kalenatic D. Modelo Integral y dinámico para el análisis, planeación, programación y control de las capacidades productivas en empresas manufactureras. Universidad Distrital «Francisco José de Caldas»Centro de Investigaciones y desarrollo científico 2001.
Chiavenato I. Iniciación a la planeación y control de la producción 1994
Krajewski & Ritzman Operation Management. Prentice Hall 1996
Frederick Hiller and Gerald J. Lieberman, Investigación de Operaciones, Séptima Edición. Mc Graw Hill. 2002
Lewis H. et al, Master scheduling in assemble-to-order environments: a capacitated multi-objective lot-sizing model, Decision sciences, Jan/Feb 1992; 23, 1 Pg. 21
Sixto Rios Insua et al. Programación lineal y aplicaciones. RA-MA. Madrid 1998.
Karabuk S. & Wu D., Coordinating strategy capacity planning in the semiconductor industry, Operation Research Nov/ Dec 2003, 51,6 Pg.839
Bermon S. & Hood S., Capacity optimisation planning system CAPS, Interfaces, Sep/Oct 1999, 29, 5 Pg.31
Eppen G. et al, A Scenario approach to capacity planning, Operations research, Jul/Ag 1989; 37,4; Pg. 517
Sherali H., Stachus K., Huacuz J., An integer programming approach and implementation for an electric utility capacity planning problem with renewable energy sources, Management science, Jul 1987, 3, 7 Pg. 831
Kalenatic D. &Blanco E., Aplicaciones computacionales en producción, Biblioteca de catedráticos, UDFJC, Bogota, 1993
Balachandran B. et al, On the efficiency of cost-based decision rules for capacity planning, The Accounting revew; Oct 1997, 72,4; Pg. 599
Leachman R. & Carmon T., On capacity modelling for production planning with alternative machine types, IIE transactions September 1992, Vol 24, No 4
Hung Y. & Cheng G., Hybrid capacity modelling for alternative machine types in linear programming production planning, IIE Transactions, Feb 2002, 34,2 Pg. 157
Paraskevopoulos D. Et al, Robust capacity planning under uncertainty management science, Jul 1991, 37,7 Pg. 787
McClain J. et al, Efficient solutions to a linear programming model for production scheduling with capacity constraints and no initial stock, IIE Transactions Jul 1989, 21,2 Pg.144
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2006-00-00 vol:11 nro:2 pág:48-60
Modelo de planeación de capacidades utilizando programación fraccional lineal en un contexto de múltiples criterios de decisión
Dusko Kalenatic
Investigador del CITAD, Universidad de la Sabana.
César Amilcar López Bello
Director grupo de investigación MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia, Investigador CITAD, Universidad de la Sabana.
Leonardo José González Rodríguez
Director Grupo de Investigación en Sistemas Logísticos, CITAD Universidad de la Sabana, Investigador grupo de investigación MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia.
Resumen
El presente artículo propone un modelo de planeación de capacidades para las empresas manufactureras con un enfoque multi-criterio utilizando programación fraccional. Con él, se pretende enriquecer el proceso de toma decisiones para evaluar el comportamiento del sistema productivo bajo relaciones de productividad parcial y total de los recursos críticos que intervienen en las actividades productivas.
Este modelo es resultado de la investigación desarrollada en el marco del proyecto Modelos Integrales de Planeación de Capacidades. El modelo combina técnicas de programación matemática fraccional lineal con técnicas de programación meta con un enfoque propuesto por los autores. El modelo se formula bajo el supuesto de fuerza laboral de carácter polivalente, conforme a las tendencias actuales en la formación de personal, y considera la disponibilidad del recurso máquina en el contexto de un proceso de producción por etapas.
Con él se pretende generar un soporte teórico que se adecue a diferentes situaciones en las cuales una organización puede estar orientando su actividad para el aprovechamiento racional de sus recursos, además de fijar una metodología para abordar el problema de gestión de la capacidad en un entorno de múltiples criterios fraccionales.
La información obtenida con el modelo de criterios múltiples fraccionales, permite la identificación de cuellos de botella además de facilitar el proceso de análisis, programación y planeación de la actividad productiva, la medición y evaluación de la eficiencia, y la formulación de estrategias para el mejoramiento de la productividad y rentabilidad de las organizaciones.
Palabras clave: Gestión de capacidades, Programación lineal, Programación fraccional, Programación multi-objetivo.
Abstract
This paper presents a model of capacity planning for the manufacturing companies with an approach on fractional multi-criterion. This model tries to enrich decisions making process to evaluate the behavior of the productive system through relations of partial and whole productivity of the critical resources that intervene in the productive activities.
The model combine linear fractional mathematical programming techniques whit goal programming techniques by the way to give original treatment proposed by the authors. The model is formulated whit the assumption of polyvalent labor force, in conformity with the current trends in the personnel training, furthermore consider the availability of the machine resource in the context of production process multi-stages.
With the related model its tried to give a theoretical support to different situations in which an organization can be orientating its activity for the rational utilization of its resources, besides fixing a methodology to approach the problem of management of the capacity in an environment of fractional criteria multiple.
With the fractional criteria multiple model, the generated information determine the respective bottle necks, and facilitating the process of analysis, programming and planning of the productive activity, measurements and evaluation of the efficiency, and also the formulation of strategies for the improvement of the productivity and profitability of the organizations.
Key words: Capacity management, linear programming, fractional programming, multiobjective programming
1. INTRODUCCIÓN
Cotidianamente en la actividad gerencial a mediano y largo plazo es importante evaluar el desempeño de la función de operaciones y proyectar el crecimiento y desarrollo de las organizaciones, de esta actividad surgen interrogantes como: ¿Que tan eficiente es la organización? ¿Como se deben usar los recursos para que la empresa sea más productiva?, ¿Como hacer que los recursos que intervienen en la producción sean más rentables?, ¿Como hacer que el dinero invertido en la producción produzca el mayor beneficio?, ¿será necesario ampliar la capacidad de la organización? , ¿Es necesario comprar nuevas instalaciones?, ¿Es preponderante aumentar las operaciones?, ¿comprar nuevas máquinas?, ¿apropiarse de nuevas tecnologías? ¿Se deben construir o habilitar varias instalaciones pequeñas o es mejor construir una instalación grande?, todos estos cuestionamientos los deben abordar los administradores a medida que se concibe una estrategia para desarrollar la capacidad y mejorar la productividad de la empresa.
La actividad productiva se ve afectada por las limitaciones impuestas por la capacidad disponible de los recursos máquina y por la mano de obra, es así como la formulación de la estrategia de ampliación de la capacidad, y los procesos de planeación y programación de las capacidades productivas se muestran como una de las temáticas más atractivas para la gestión de las operaciones, de otra parte la gama de objetivos que se presentan en los diferentes escenarios, dependiendo de la situación particular del sistema bajo estudio, e inclusive los propósitos particulares que presentan los subsistemas, orientados por diferentes planes, conllevan al desarrollo y formulación de un modelo fraccional integral de planeación de capacidades.
La estrategia para desarrollar la capacidad es un plan de amplio alcance para satisfacer la demanda potencial de los productos y servicios que ofrece una organización. [1]
La inversión en la adecuación y adquisición de instalaciones, la formulación de alternativas para el mejoramiento de la productividad, desarrollo de nuevos procesos de operación, aumento en el nivel de la fuerza laboral, compra de maquinaria y equipo son estrategias que por su importancia tienden a decidirse en los niveles jerárquicos más altos de las empresas. La adquisición de nuevas instalaciones y equipos son factores que afectan significativamente la competitividad de la empresa, si se tiene insuficiencia de capacidad no se puede responder rápidamente a las fluctuaciones de la demanda y por tanto la perdida de su nicho de mercado, esto se debe a que la ampliación de la capacidad es una decisión costosa e implica un tiempo considerable para habilitar los nuevos equipos a la producción.
De otra parte, la planeación de la producción a nivel táctico requiere de la planeación e identificación de la disponibilidad de la capacidad a mediano plazo, además de la estimación de los requerimientos de capacidad para realizar la provisión de los recursos necesarios para la actividad productiva.
La factibilidad técnica que tienen las máquinas y equipos para realizar determinados productos, así como el ordenamiento secuencial, los tiempos de alistamiento y el grado tecnológico de las operaciones de producción afectan y reducen significativamente la disponibilidad de la capacidad a corto plazo, en otras palabras en el intento de materializar los planes de producción a largo y mediano plazo, en la programación al detalle, existe una diferencia importante que se debe tomar en cuenta para la planeación global de la capacidad.
2. ASPECTOS CONCEPTUALES SOBRE PRODUCTIVIDAD Y CAPACIDADES PRODUCTIVAS
La importancia que tiene la productividad como indicador de rendimiento en las organizaciones, ha generado que las empresas fijen estrategias para su mejoramiento.
La productividad se puede definir como la producción de bienes o servicios con el uso racional de los recursos que intervienen en la actividad productiva. Autores como Sumath [2] indican que el término productividad tiene tres formas básicas de definición.
Productividad parcial, es la razón entre la cantidad producida y un solo tipo de insumo.
Productividad de factor total, es la razón de la producción neta con la suma asociada con los insumos de mano de obra y capital. Por producción neta se entiende producción total menos servicios y bienes intermedios comprados.
Productividad total, es la razón entre la producción total y la suma de todos los factores de insumo.
Normalmente el nivel de producción se traduce en cifras monetarias, que al ser evaluada frente a los recursos o insumos que intervienen en la producción originan el concepto de rentabilidad, de igual manera los insumos se traducen en términos monetarios lo que facilita el proceso de medición.
La capacidad productiva, su análisis, planeación, programación y control, constituyen actividades críticas para el mejoramiento de la productividad, que se desarrollan paralelamente con las actividades de programación y planeación de materiales, siendo la capacidad la cantidad de productos o servicios destinados a satisfacer las necesidades del cliente o de la sociedad que puede ser obtenida por una unidad productiva en un determinado periodo de tiempo. [3]
Otros autores [4] la definen como el volumen de producción que se puede alcanzar en un tiempo determinado o como [5] la velocidad máxima que un sistema puede realizar un trabajo.
Por otra parte, el concepto de capacidad puede ser definido también a diferentes niveles jerárquicos de la organización, de acuerdo a los objetivos que en cada caso se persigan, es decir, a nivel global de todo el sistema productivo y de sus unidades estructurales, así como de las instalaciones, máquinas, equipos y puestos de trabajo.
Capacidad es el potencial de un trabajador, una máquina, un centro de trabajo, un proceso, una planta o una organización para fabricar productos por unidad de tiempo.(1)
La capacidad de un proceso que genera una amplia variedad de productos por lo general se expresa como tasa de producción por unidad de tiempo.
Es complicado expresar la capacidad como tasa de producción cuando se produce diversidad de productos que requieren diferentes niveles de recursos; para tal situación la tasa de producción depende de la mezcla de productos y del tamaño de los lotes, para tal efecto, la capacidad puede medirse en unidades de recurso disponible.
Cuando un proceso requiere de una serie de operaciones, su capacidad se determina por la operación que ocupa el nivel más bajo en la secuencia. La operación que limita la capacidad se denomina operación cuello de botella.
Una forma de expresar la capacidad cuando se refiere a la disponibilidad de un recurso requerido para la producción de una mezcla de productos en un espacio de tiempo, como la capacidad del recurso máquina en horasmáquina al año.
El término capacidad se relaciona a la potencialidad técnica y económica que posee un sistema u organización productiva, sus unidades estructurales, las componentes y elementos que lo componen para participar en la elaboración de productos y/o prestación de servicios de una forma técnica, racional y económicamente eficiente, en un tiempo determinado. De esta manera se puede diferenciar:
Capacidad Técnica, Aquella determinada por la potencialidad que tiene un sistema, unidad estructural, elemento, máquina o persona para realizar una determinada producción y/ o servicio en un lapso de tiempo dado, es decir el máximo rendimiento posible que se puede obtener en su desempeño.
Capacidad Económica, definida en relación a los costos asociados a la producción en un horizonte temporal definido; en otras palabras, cuando la organización en su conjunto obtiene los menores costos por unidad de producción y/o servicio realizado, garantizándose así, el denominado "optimum" técnico-económico. [6]
La capacidad de los medios de producción, en general, puede también diferenciarse, en función de la disponibilidad, requerimiento y utilización temporal en:
Capacidad Instalada, es aquella que está potencial y totalmente disponible para alcanzar los resultados productivos máximos especificados por un productor. La magnitud de esta capacidad se ve solo disminuida por razones de mantenimiento de los medios de producción, requeridos para garantizar su propia disponibilidad y utilización en la actividad productiva. [6].
La capacidad instalada es la cantidad de máquinas y equipo que una organización productiva posee y el potencial de producción que estos permiten alcanzar. La capacidad instalada representa la producción posible, si todas las máquinas y equipos estuvieran trabajando al 100 % del tiempo ininterrumpido [7]. A su vez, la capacidad instalada puede ser sostenida por muy cortos periodos de tiempo, así como pocas horas al día o pocos días al mes [8]
Es habitual denominar la capacidad de espacio físico como capacidad instalada para el almacenamiento de productos terminados, productos en proceso y materiales, así como para la instalación de nuevos equipos y puestos de trabajo.
Capacidad Disponible, su magnitud es inferior a la de la capacidad instalada y depende de las condiciones de producción, administración y organización, se calcula en función de los días hábiles, el número de turnos programados y su longitud, considera las pérdidas de tiempo originadas por el ausentismo de los trabajadores, las originadas por factores organizacionales y por aquellos otros factores externos que de una u otra forma hacen que se disminuya la capacidad. Las máquinas no se pueden usar a toda capacidad a lo largo del periodo de producción. Hay varias razones para que esto ocurra.
La necesidad de instalación, mantenimiento preventivo, afilado de herramientas, fallas y reparaciones imprevistas reduce el tiempo disponible para la producción. Las máquinas con tecnología más antigua son susceptibles de averiarse que las nuevas, ocasionando así una menor productividad.
Factores relacionados con la fuerza laboral, como el ausentismo, los tiempos de para, las necesidades personales, el tiempo de valoración de lo producido, los ajustes de las máquinas y preparación y alistamiento de las máquinas y del material reducen la disponibilidad del recurso máquina.
Debido a los requerimientos de calidad en los procesos de producción, tienen asociados cierta perdida de capacidad inclusive cuando el equipo este adecuadamente instalado y se opere correctamente. Además se pierde alguna producción al desechar algunas unidades defectuosas cuando la máquina esta operando mal o se produce incorrectamente produciéndose piezas con la calidad no deseada.
En ciertas situaciones se les asigna más de una máquina a un solo operario, lo cual se conoce como acoplamiento de máquina. Esto se determina dividiendo el tiempo de ciclo total en dos partes, a saber el tiempo de la máquina y el tiempo del trabajador. El tiempo de máquina es aquel en que la máquina está funcionando sin asistencia del operario, y el tiempo del operario es aquel en donde el trabajador está con la máquina inactiva, realizando por ejemplo actividades de alimentación y carga de las máquinas. Cuando el tiempo de máquina es relativamente más grande que el tiempo del trabajador es usual que en este tiempo de operación de la máquina el trabajador realice actividades de carga de otras máquinas. Por lo tanto es posible que a un operario se la asigne varias máquinas en su actividad productiva.
En el sistema de conversión, un problema de desperfecto en una máquina o una producción defectuosa puede afectar la producción de otras máquinas del proceso productivo. Así mismo, un operario ocupado en tratar de solucionar un problema, o corregir una producción defectuosa pude descuidar las demás máquinas que requieren de la manipulación del operario para su funcionamiento.
El tiempo disponible para la producción no se incrementa en la misma proporción que el número de turnos; la programación de otro turno de producción no añade otras 8 horas de producción. La perdida de tiempo de producción aumenta por que el tiempo libre disponible para reparaciones disminuye. Por ejemplo si en algún momento una máquina se avería, usualmente su reparación se realizaría en el segundo turno de trabajo, lo cual haría que se disminuyera el tiempo destinado para la producción de ese segundo turno. De otra parte factores como la falta de material, la falta de ayuda técnica, el ausentismo de los trabajadores afectan el rendimiento y la capacidad en mayor grado en el segundo turno que en el primero. En general el grado de ausentismo es mayor en el segundo turno y aún más en el tercero.
3. ASPECTOS CONCEPTUALES SOBRE PROGRAMACIÓN FRACCIONAL LINEAL Y PROGRAMACIÓN META
La presencia de modelos con estructuras de relación para medir eficiencia conduce a la formulación y solución de problemas mediante la programación fraccional lineal.
Los modelos de programación fraccional lineal, en general, tienen la estructura dada por (1)
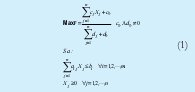
Donde:
F: Es la función objetivo, compuesta por la relación de dos funciones una cóncava y la otra convexa
Xj: Vector de variables de decisión.
Cj:Vector paramétrico que acompaña a las variables de decisión en el numerador de la función objetivo.
dj:Vector paramétrico que acompaña a las variables de decisión en el denominador de la función objetivo.
ai,j:Matriz de coeficientes tecnológicos
bi :Vector del lado derecho.
c0:Termino independiente en el numerador de la función objetivo.
d0:Termino independiente en el denominador de la función objetivo.
 Son las restricciones del sistema
Son las restricciones del sistema
Xj≥ 0 para cada j = 1,2,... n Son las restricciones lógicas de no negatividad.
Para resolver los problemas de programación fraccional lineal es necesario realizar un proceso retransformaciones lineales definiendo (2) y (3) así:
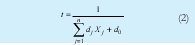
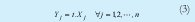
Y luego sustituyendo se obtiene (4)
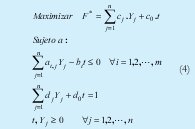
Por otra parte, una metodología de programación de múltiples criterios es la programación meta, en donde el conjunto de criterios de decisión al que se enfrenta una problemática se puede transformar en un conjunto de restricciones, fijándose metas o logros deseables, adicionando variables de desviación por exceso y por defecto sobre la meta deseada. De tal manera que el objetivo integral consiste en tratar de minimizar la suma de desviaciones no deseadas sobre las metas contempladas en el modelo.
El formato general de un modelo de programación por metas se podría representar con la expresión (5)
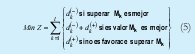
Sujeto a restricciones del sistema (6)
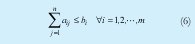
A las restricciones meta (7) que se estructuran agregando variables de desviación sobre la meta establecida.
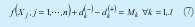
Y las restricciones lógicas de no negatividad (8)
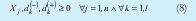
4. MODELO INTEGRAL FRACCIONAL DE PLANEACIÓN DE CAPACIDADES
Para abordar el problema de planeación y programación de capacidades productivas en un contexto de criterios múltiples fraccionales se propone un modelo metodológico integral que contribuye a la obtención de una significativa variedad de información para la gestión de la función de operaciones.
Se plantea un conjunto de criterios de decisión, los cuales deben ser resueltos individualmente, utilizando programación fraccional lineal [9] con el objeto de identificar soluciones alternativas, e información relevante para la toma de decisiones.
4.1 Función(es) Objetivo(s)
El modelo integral fraccional lineal de análisis y planeación de capacidades se desarrollo a partir de criterios de decisión que miden eficiencia como la productividad parcial del recurso máquina (9),(10), y del recurso mano de obra (11),(12), la maximización de la rentabilidad de los recursos máquina(13), (14) y mano de obra (15), (16) y de la maximización de la relación beneficio costo (17)y (18). Adicionalmente se podrían tomar otros criterios de decisión como lo plantean otros autores [10] amplían la gama de criterios y objetivos, considerando en contextos distintos criterios como Maximización del índice de rotación inventarios de producto en proceso y terminado, así como reducción de faltantes, entre otros. En general el objetivo del modelo esta dado por:
Objetivo(s): Determinar un plan de producción orientado al logro del criterio "g", donde g = 1,2,... h
Permitiendo integrar los diferentes criterios a la función objetivo que lo representa. El primer criterio considerado es el de maximización de la productividad parcial del recurso máquina (9),(10), el cual es utilizado para evaluar la eficiencia de la capacidad en términos de la obtención del mayor volumen de producción con el uso racional del fondo de tiempo máquina, así:

Donde:
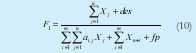
El criterio de maximización de la productividad parcial del recurso mano de obra (11),(12) es considerada para fijar un plan de producción orientado a la obtención de un mayor volumen de producción con el uso racional del recurso mano de obra.

Donde:
La función de productividad parcial del recurso mano de obra(11) y (12) maximiza los volúmenes de producción en función del fondo de tiempo disponible de mano de obra para realizar la producción.
La función rentabilidad del recurso máquina (13) es otra forma para evaluar la eficiencia y mide como el uso racional del recurso máquina puede rentar más por unidad de tiempo de recurso.
El numerador indica la contribución total originada por la producción relativa al fondo de tiempo disponible del recurso máquina (14)

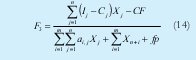
La función rentabilidad del recurso mano de obra (15) evaluar la eficiencia del recurso mano de obra en la actividad productiva y mide como el uso racional del recurso máquina puede rentar más por unidad de tiempo.
La razón indica (16) como contribuye el recurso mano de obra expresado como el tiempo disponible para la producción en la generación de utilidad neta por la actividad productiva
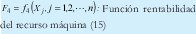
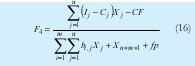
La función relación beneficio costo (17) expresa como renta la inversión total en la producción.
En la relación (18) el denominador esta constituido por el costo total invertido en la producción y el numerador se expresa la utilidad neta percibida por la producción y venta de lo producido lo que expresa el margen de utilidad percibida por unidad de dinero invertido en la producción.
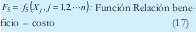
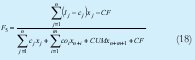
Variables de decisión
Xj:Cantidad a elaborar de producto tipo "j", donde j=1,2,...,n
Xn+i: Ocio productivo de la maquinaria tipo "i", donde i=1,2,...,m
Xn+m+1: Ocio productivo del recurso mano de obra.
Xn+m+1+j: Unidades demandadas pero no producidas del producto tipo "j", j=1,2,...,n
Yj:Vector de variables de decisión que representa a las variables Xj en el modelo lineal donde j=1,2,...,n
Yn+i: Ocio productivo de la maquinaria tipo en el modelo lineal "i", donde i=1,2,...,m
Yn+m+1: Ocio productivo del recurso mano de obra en el modelo lineal.
Yn+m+1+j: Unidades demandadas pero no producidas del producto tipo "j" en el modelo lineal, j=1,2,...,n
Parámetros
Cj : Costo unitario de producción del artículo tipo "j", donde j=1,2,...,n
Ij: Precio de venta por unidad de producto tipo "j", donde j=1,2,...,n
C F: Costo Fijo
dmaxj: Demanda potencial del producto tipo "j", donde j=1,2,...,n
d minj : Demanda requerida del producto tipo "j", donde j=1,2,...,n
Cdi: Capacidad disponible de la maquinaria en la etapa de proceso"i", donde i=1,2,...,m
K D: Capacidad disponible del recurso mano de obra.
aij: Tiempo de elaboración estándar de un producto tipo "j" en una máquina de la etapa de proceso "i", donde i = 1,2,...m Λ j= 1,2,... n
bij: Tiempo de ejecución requerido de mano de obra por unidad de producto tipo "j" en la etapa de proceso "i", donde
des: Desperdicio expresado en unidades defectuosas
fp: Factor de pérdida de capacidad
4.2 Restricciones del modelo
En el modelo fraccional integral de capacidades se toma como mas representativas cuatro tipos de restricciones: de capacidad disponible por grupo de sitios de trabajo (19),(20), restricciones de mano de obra (bajo el supuesto de polivalencia) (21),(22), restricciones de aseguramiento de punto de equilibrio (23) y restricciones de demanda (24),(25), y las emplea en la construcción de diferentes modelos alternativos, asociados a la planeación de la producción.
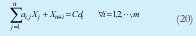
Las restricciones de capacidad disponible por grupo de sitios de trabajo (19) y (20), al igual que las restricciones de capacidad de mano de obra (21) y (22) se diferencian en la inclusión de las variables de holgura que representan en el primer caso (20) el ocio productivo de los medios de trabajo, y en el segundo (22) el ocio productivo del recurso mano de obra, esto con el fin de satisfacer diferentes objetivos en los modelos propuestos en este articulo. Diferen tes autores [11] [12] realizan modificaciones a esta restricción con el fin de incluir la capacidad perdida en actividades de alistamiento, otros autores [13] desagregan el lado derecho de la restricción por grupos de herramientas y/o centros de trabajo, así mismo analizan el impacto de cambios tecnológicos en la capacidad [5] [14] [15].
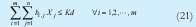
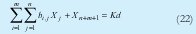
La restricción de beneficio nulo (23) expresa la condición de generar los suficientes ingresos netos para cubrir los costos fijos, para los modelos en donde las funciones de productividad son objetivo no es relevante la restricción y no se toma en cuenta, pero en los modelos en los cuales se requiere obtener rentabilidad, así como la función relación beneficio costo son consideradas.
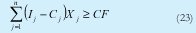
La restricción de demanda con cota superior e inferior (24) es valida para todos los criterios propuestos en el articulo sin embargo podrían no tener significado para otro criterio de decisión en donde es necesario considerar solamente una cota o la superior o la inferior según la situación. Otros autores [16] [17] [18] utilizan la demanda como cota superior, bajo los supuestos de perdida de la demanda insatisfecha y de no producción para inventario.
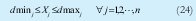
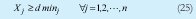
La combinación de los criterios y restricciones expresadas, generan los modelos fraccionales propuestos en el artículo aplicables a diversas situaciones, objetivos y estrategias, los modelos mas representativos (26),(27),(28), (29),(30),(32), bicriteriales y multicriterial se presentan a continuación.
4.3 Productividad Parcial de Recurso Máquina
En este modelo se pretende generar un plan de producción orientado a la maximización de la productividad parcial del recurso máquina, en donde la función expresa la contribución en la producción por el uso del fondo de tiempo máquina utilizado en la producción. El esta constituido por la función objetivo (10), las restricciones (20),(22) ,(24) y las restricciones lógicas de no negatividad.
La formulación del modelo de productividad parcial del recurso máquina se observa en la relación (26)

Realizando la transformación de un programa fraccional a un programa lineal, se tiene la expresión (27):

Al resolver el programa es necesario realizar los cálculos de conversión (28) entre variables para encontrar los valores originales
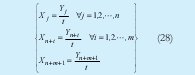
4.4 Productividad Parcial del Recurso Mano de Obra
El modelo (29) esta constituido por la función objetivo (12), las restricciones (20),(22) ,(24) y las restricciones lógicas de no negatividad.

Realizando la transformación lineal se tiene el modelo lineal (30):
La función expresa como con el fondo de tiempo de recurso mano de obra que puede expresarse como horas hombre empleadas en la actividad productiva es posible producir un nivel máximo de producción agregada.

De igual manera es necesario calcular los valores originales de las variables empleando la expresión (28)
4.5 Rentabilidad del Recurso Máquina
Este modelo (30) esta constituido por la función objetivo (14), las restricciones (20), (22), (23), (24) y las restricciones lógicas de no negatividad.

Con esta función se expresa la rentabilidad que se produce al utilizar el recurso máquina en la producción, como las horas máquina utilizadas para un periodo de planeación determinado. Realizando la transformación lineal se tiene la expresión (31).
Como en los modelos anteriores es necesario realizar las conversiones de las variables utilizando las expresiones (28)

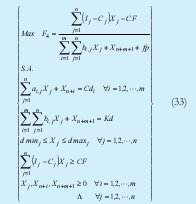
4.6 Rentabilidad del Recurso Mano de Obra.
Este modelo (32) esta constituido por la función objetivo (16), las restricciones (20), (22), (23), (24) y las restricciones lógicas de no negatividad.
Realizando la transformación lineal se tiene la expresión (34). En ella se indica como el recurso mano de obra aporta al beneficio neto de la actividad productiva.

Para efectos de cálculo de las variables originales es necesario como en los modelos anteriores utilizar las expresiones (28), mencionando que el optimo de la función original es igual a la de la transformada.
4.7 Relación Beneficio - Costo
Este modelo (33) esta constituido por la función objetivo (18), las restricciones (20), (22), (23), (24) y las restricciones lógicas de no negatividad.
El modelo expresa como la inversión total en la producción, dinero invertido en recurso máquina, recurso material y mano de obra más los costos por improductividades posiblemente por desbalanceo de las líneas de producción genera el máximo beneficio, restringido principalmente a la disponibilidad de los recursos máquina y mano de obra, así mismo de la demanda y la condición de beneficio nulo.
Realizando la transformación lineal se tiene a partir de (35) la expresión (36)
No sobra indicar que de igual manera que en los modelos anteriores es necesario encontrar los valores de las variables originales empleando las expresiones (28)
4.8 Función multicriterio
Posteriormente con el método de programación meta sin prioridades [11] se formula un modelo de programación por objetivos [9] ajustado a funciones de carácter bicriterial cuya función objetivo (38) integra los criterios y funciones anteriormente tratados.
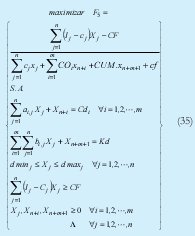

El procedimiento empleado consiste en fijar metas para cada uno de los índices generados por cada una de las funciones objetivo como se muestra en la expresión (37)
Posteriormente cada función se expresa como una restricción agregando dos variables de desviación para cada criterio de decisión como se observa en la expresión (38), es importante observar que al ser los criterios individuales funciones de maximización, las variables de desviación por debajo se convierten en las variables objeto a ser minimizadas, pero para otra situación en donde el objeto es minimizar como por ejemplo un riesgo o donde el valor nomina es el mejor, entonces la función objetivo meta se constituiría como se indico en (5), de otra parte el efecto que puede existir por los pesos de importancia entre criterios y las prioridades generarían modificaciones en la modelación y en los resultados obtenidos.


Donde:
d(-)k: Variable de desviación por debajo del valor meta del criterio "k" donde k=1,2,...,l
d(+)k: Variable de desviación por encima del valor meta del criterio "k" donde k=1,2,...,l
Mk: Meta o logro del criterio de decisión "k" donde k=1,2,...,l
3.10 Modelo con Función de Criterios Múltiples
La eficiencia de los sistemas de producción se encuentra restringida por el uso racional de los recursos y la actividad productiva se encuentra restringida por la capacidad de la mano de obra, de los medios de trabajo, así como por la disponibilidad de recursos y las condiciones del mercado; dichos sistemas son diseñados y modificados para lograr los objetivos de la organización, por esta razón es deseable utilizar criterios múltiples (39) para soportar las decisiones en función de las necesidades de la empresa, evaluada en varios indicadores de gestión, esto se alcanza con la aplicación conjunta, ya sea parcial o total, de los criterios propuestos, en la cual la ponderación de los mismos depende la importancia de cada uno de ellos en el cumplimiento de los objetivos y estrategias organizacionales.

Enfoques complementarios en donde se utiliza programación meta para modelos lineales desarrollados hasta ahora incluyen la partición del problema [19], el uso de variables no controlables [20], y el impacto de los inventarios [21], entre otros.
5. CONCLUSIONES
La integración de modelos fraccionales por medio de la programación meta representa una novedad para el análisis de problemas en el contexto de múltiples criterios de decisión.
La utilización de programación fraccional para abordar problemas de planeación y programación de capacidades productivas con múltiples criterios de decisión, permite calcular indicadores de gestión compuestos, tales como productividad parcial de los recursos, rentabilidad parcial y relación beneficio costo, entre otros.
La aplicación conjunta de la programación fraccional y meta en el contexto de la programación de capacidades productivas, brinda la información necesaria para entender el impacto de la utilización de la mano de obra, la maquinaria y los recursos financieros, entre otros, en el logro de cada uno de los objetivos de las empresas manufactureras.
La utilización del modelo propuesto permite el análisis de la productividad de los recursos en relación al cumplimiento de cada una de las metas propuestas, lo que facilita los procesos de establecimiento de prioridades, tanto en el uso de los recursos, como en la determinación de metas, propiciando la viabilidad del sistema en entornos competitivos.
La posibilidad de calcular indicadores de productividad parcial simultáneamente con el análisis de capacidades facilita y enriquece el proceso de toma de decisiones asociadas a la asignación de recursos en los procesos de manufactura, al permitir cuantificar impacto de las prioridades del tomador de decisión en la utilización de las capacidades, la rentabilidad y la productividad.
REFERENCIAS BIBLIOGRÁFICAS
[1] Hamid Noori y Russell Radford. Administración de Operaciones y Producción. Mc Graw Hill. 1997
[2] David J. Sumanth. Ingeniería y Administración de la productividad. Mc Graw Hill .1990
[3] J. A. Domínguez Machuca et al. Dirección de Operaciones, Aspectos Tácticos y Operativos en la Producción y los Servicios. Editorial Mc Graw Hill Interamericana de España. 1995
[4] Keith Lockyer. Production and Operation Management. Prentice Hall 1991.
[5] Narashimhan, L. et al. Planeación de la Producción y Control de Inventarios. Prentice Hall. 1996
[6] Kalenatic D. Modelo Integral y dinámico para el análisis, planeación, programación y control de las capacidades productivas en empresas manufactureras. Universidad Distrital «Francisco José de Caldas»Centro de Investigaciones y desarrollo científico 2001.
[7] Chiavenato I. Iniciación a la planeación y control de la producción 1994
[8] Krajewski & Ritzman Operation Management. Prentice Hall 1996
[9] Frederick Hiller and Gerald J. Lieberman, Investigación de Operaciones, Séptima Edición. Mc Graw Hill. 2002
[10] Lewis H. et al, Master scheduling in assemble-to-order environments: a capacitated multi-objective lot-sizing model, Decision sciences, Jan/Feb 1992; 23, 1 Pg. 21
[11] Sixto Rios Insua et al. Programación lineal y aplicaciones. RA-MA. Madrid 1998.
[12] Karabuk S. & Wu D., Coordinating strategy capacity planning in the semiconductor industry, Operation Research Nov/ Dec 2003, 51,6 Pg.839
[13] Bermon S. & Hood S., Capacity optimisation planning system CAPS, Interfaces, Sep/Oct 1999, 29, 5 Pg.31
[14] Eppen G. et al, A Scenario approach to capacity planning, Operations research, Jul/Ag 1989; 37,4; Pg. 517
[15] Sherali H., Stachus K., Huacuz J., An integer programming approach and implementation for an electric utility capacity planning problem with renewable energy sources, Management science, Jul 1987, 3, 7 Pg. 831
[16] Kalenatic D. &Blanco E., Aplicaciones computacionales en producción, Biblioteca de catedráticos, UDFJC, Bogota, 1993
[17] Balachandran B. et al, On the efficiency of cost-based decision rules for capacity planning, The Accounting revew; Oct 1997, 72,4; Pg. 599
[18] Leachman R. & Carmon T., On capacity modelling for production planning with alternative machine types, IIE transactions September 1992, Vol 24, No 4
[19] Hung Y. & Cheng G., Hybrid capacity modelling for alternative machine types in linear programming production planning, IIE Transactions, Feb 2002, 34,2 Pg. 157
[20] Paraskevopoulos D. Et al, Robust capacity planning under uncertainty management science, Jul 1991, 37,7 Pg. 787
[21] McClain J. et al, Efficient solutions to a linear programming model for production scheduling with capacity constraints and no initial stock, IIE Transactions Jul 1989, 21,2 Pg.144
Dusko Kalenatic, PhD.
Doctor en Ciencias Técnicas, Universidad de Las Villas "Marta Abreu", Santa Clara, Especialista en Ingeniería de Producción Universidad Distrital Francisco José de Caldas. Especialista "Instituto de Periodismo Yugoslavo", Economista, Escuela Superior de Economía, Belgrado, Ingeniero en Organización de Trabajo, Universidad de Belgrado, Investigador CITAD, Centro de investigaciones en tecnologías avanzadas de decisión "Carlos Jordana" Universidad de la Sabana. dusko.kalenatic@unisabana.edu.co
MsC. César Amilcar López Bello
Magíster en Ingeniería Industrial, Universidad de los Andes. Especialista en Ingeniería de Producción, Universidad Distrital. Francisco José de Caldas. Profesor Asociado, Facultad de Ingeniería Universidad Distrital. Director de la Maestría en Ingeniería Industrial, Universidad Distrital Francisco José de Caldas. Director grupo de investigación MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia, Investigador CITAD, Centro de investigaciones en tecnologías avanzadas de decisión "Carlos Jordana" Universidad de la Sabana. clopezb@udistrital.edu.co
MsC. Leonardo José González Rodríguez
Magíster en Ingeniería Industrial, Universidad de los Andes. Especialista en Ingeniería de Producción, Universidad Distrital. Ingeniero Industrial, Universidad Distrital. Profesor Asistente, Facultad de Ingeniería. Universidad Distrital Francisco José de Caldas. Profesor, Facultad de Ingeniería Universidad de la Sabana, Director Grupo de Investigación en Sistemas Logísticos, CITAD- Centro de investigaciones en tecnologías avanzadas de decisión "Carlos Jordana" Universidad de la Sabana, Investigador grupo de investigación MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia. lejogorod@yahoo.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










