DOI:
https://doi.org/10.14483/23448393.2114Published:
2008-11-30Issue:
Vol. 14 No. 1 (2009): January - JuneSection:
Science, research, academia and developmentDiseño de un Metodo Heurístico para Secuenciación en Sistemas Flow Shop Estrictos con Buffers Ilimitados
Designing a heuristic method for Sequencing Systems Strong Flow Shop with Buffers Unlimited
Keywords:
Buffer Ilimitado, Eficacia, Flow Shop Estricto, Indicadores de desempeño, Método heurístico, Secuenciación. (es).Downloads
References
Alemán González. Estudio y aplicación del algoritmo Lomnicki Pendular al problema de Flow Shop sin pulmones intermáquina. Laboratorio de Organización industrial. Universidad Politécnica de Cataluña. España 2004.
Conway R. W., W.L. Mazwell, L.W. Miller. Theory of Scheduling. Adison-Wesley, Reading, MA, 1967.
José Domínguez Machuca. Dirección de operaciones. Aspectos tácticos y operativos en la producción y los servicios. Ed. Mc Graw Hill, Madrid, 1998.
Ruben Ruiz. Evaluación de heurísticas para el problema del taller de Flujo. XXVII Congreso Nacional de stadística e Investigación Operativa. Universidad Politécnica de Valencia. España. 2003. Disponible en www.upv.es/gio/rruiz/files/SEIO2003_heu.pdf
Michael Pinedo. Scheduling: theory, algorithms and system. Ed. Prentice Hall, 2002
Agustín Alemán. Estudio y Aplicación del algoritmo Lomnicki Pendular al problema Fm/Block/Fmax. Laboratorio de Organización industrial. 2005. Disponible en https://upcommons.upc.edu/pfc/bitstream/2099.1/2645/1/34561-1.pdf
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2009-00-00 vol:14 nro:1 pág:4-12
Diseño de un Metodo Heurístico para Secuenciación en Sistemas Flow Shop Estrictos con Buffers Ilimitados
Designing a heuristic method for Sequencing Systems Strong Flow Shop with Buffers Unlimited
Diana Catherine Salamanca Leguizamón
Ingeniera Industrial de la Universidad Distrital Francisco José de Caldas.
Harry Andrés Ortiz Cabuya
Ingeniero Industrial de la Universidad Distrital Francisco José de Caldas.
César Amilcar López Bello
Investigador principal de grupo de investigación MMAI de la Universidad Distrital, Investigador grupo GIP Universidad Católica de Colombia, Investigador CITAD, Universidad de la Sábana.
Resumen
Este artículo propone un método heurístico para resolver el problema de secuenciación para sistemas Flow Shop Estrictos con Buffer Ilimitados, con una función objetivo que consiste en la minimización del tiempo de procesamiento de la última orden en el sistema, es decir, el makespan.
La solución del problema se basó en la creación de un método de aproximación que presenta dos fases: la primera, donde se obtiene una secuencia inicial a través de una heurística constructiva y la segunda fase, donde se aplica una heurística de mejora, que toma como base la respuesta encontrada en la fase anterior, y a través de una serie de iteraciones se generan respuestas alternas dentro de las cuales se escoge la mejor secuencia.
Con la utilización del método propuesto, se obtuvieron mejores respuestas respecto a las reglas FIFO, LPT, SPT y el método heurístico de Palmer para el objetivo trazado, en los indicadores Makespan, tiempo de flujo, tiempo promedio de flujo, porcentaje de utilización de máquina, porcentaje de ocio de máquina, tiempo total de espera y tiempo promedio de espera.
Palabras clave: Buffer Ilimitado, Eficacia, Flow Shop Estricto, Indicadores de desempeño, Método heurístico, Secuenciación.
Abstract
This article proposes a heuristic method for solve the problem of sequencing for systems with Strong Flow Shop Buffer Unlimited, with an objective function that is the minimization the processing time of the last order in the system, the makespan.
The solution to the problem was based on the creation of an approximation method or procedure heuristic, which has two phases: the first where he gets an initial sequence through a heuristic constructive, and the second phase which applies a Heuristic improvement taking as a basis the response found in the earlier stage, and through a series of iterations, generated responses alternate, within which they choose the best sequence.
By using the proposed method, we obtained better answers regarding the rules FIFO LPT, SPT and the Palmer Heuristic Method route to the goal, in the indicators Makespan, flow time, average flow time, rate of use of machine, percentage dead-time machine, total waiting time and average waiting time.
Key words: Key words: Buffer unlimited, effectiveness, Strong Flow Shop, performance indicators, heuristic method, sequencing.
1. INTRODUCCIÓN
El proceso de planificación y control de la producción consta de tres etapas, enmarcadas en los siguientes espacios de tiempo, largo plazo, mediano plazo y corto plazo. Respectivamente, el resultado obtenido es, la elaboración de la Planeación Estratégica, el Plan Táctico y, la Programación Operativa [3].
El trabajo realizado presenta un aporte en una de las actividades que se realiza para efectuar esa Programación, la secuenciación de operaciones. Consiste exactamente, en diseñar y probar un método heurístico de dos etapas, la obtención de una respuesta inicial y un algoritmo de mejoramiento de esa respuesta, a partir de operaciones sobre una matriz de trabajo, que sugiere un orden para procesar el grupo de trabajos requerido en una estructura productiva dada.
El análisis hecho en la literatura para abordar el problema de la secuenciación de operaciones, fue sobre sistemas de producción basados en una configuración por lotes, que se procesan bajo un ordenamiento del tipo Flow Shop Estricto con Buffers Ilimitados, esto es, que todas las órdenes son procesadas siguiendo una misma ruta a través de todas las etapas del proceso, disponiendo de un solo tipo de máquina para cada proceso, con una capacidad ilimitada de almacenamiento del producto al final de cada operación y antes de pasar a la siguiente.
Respecto al tema, se encuentra que los estudios realizados por el profesor Michael Pinedo [5] de la Universidad de Nueva York en los últimos 25 años han sido de gran reconocimiento, ya que ha sido uno de los investigadores con mayor especialización en el tema de la secuenciación, más conocido en la literatura como Scheduling, Adicionalmente, se tiene en cuenta los aportes de otros autores como Johnson [1954], Ignall y Schrage [1965] con su algoritmo de Bifurcación y Acotamiento, Campbell, Dudeck y Smith [1970], heurísticas como la de Palmer [1965], Ho y Chang [1991] y métodos como las Reglas de Prioridad. Algunos son muy simples y cubren parcialmente todas las restricciones del sistema productivo y otros, en cambio, son complejos algorítmicamente a medida que el número de órdenes de trabajo y de máquinas crece, siendo dispendiosa su utilización.
Como resultado del trabajo que se presenta en este artículo, se generó una herramienta heurística con el propósito de facilitar el proceso de secuenciación de tareas en sistemas de producción tipo Flow Shop Estrictos con Buffer Ilimitados, para n órdenes de trabajo y m máquinas, y así lograr un nivel mínimo esperado de eficacia en términos de los criterios de desempeño definidos.
Esta herramienta consta de dos etapas. En la primera, una heurística constructiva, en la cual se genera una secuencia inicial y, una segunda etapa, en la que se propone una heurística de mejora, donde con base en la respuesta inicial, se obtiene un conjunto de 20 respuestas alternas, para finalizar con la selección de la mejor de ellas, dado el mejor valor del criterio objetivo dado.
Para soportar el desarrollo teórico, se desarrolló una herramienta informática que facilita la utilización del método propuesto. El nombre de este aporte es Planifier. Este aplicativo sirvió para ejecutar las pruebas diseñadas. En general, se ejecutaron 545 pruebas para la combinación de 11 diferentes valores de m y n. Los valores obtenidos con Planifier fueron comparados con seis métodos, tres reglas de prioridad: FIFO, SPT y LPT; y tres heurísticas: Palmer, CDS y Enumeración Completa.
2. MÉTODO DE SECUENCIACIÓN
2.1 Supuestos del Método
Utilizando algunas acotaciones aceptadas para el problema de secuenciación propuestas por Conway, Maxwell y Miller [Conway 1967] [2], se formalizaron las siguientes restricciones al funcionamiento del método propuesto [1], [4], [7]:
- La estructura de producción es tipo flow shop estricta. Todas las órdenes tienen la misma ruta por las máquinas y, el orden de procesamiento de los trabajos en todas las máquinas es el mismo.
- Para cada operación i existe una sola precedente inmediata i-1, exceptuando la primera operación de cada pieza, que no dispone de precedente.
- Para cada operación i existe una sola siguiente inmediata i+1, exceptuando la última operación de cada pieza, que no tiene siguiente.
- No existen montajes de piezas (convergencias) ni particiones en lotes (divergencias); el número de órdenes entrantes es igual al número de órdenes saliente.
- No pueden solaparse dos operaciones de la misma pieza en la misma máquina o en máquinas distintas; cada máquina elabora un solo proceso a la vez y a cada orden se le realiza un solo proceso a la vez.
- Cada máquina tiene asociada una única operación.
- Sólo hay una máquina de cada tipo en el taller.
- El número de piezas es finito y, tanto las órdenes como las máquinas se encuentran disponibles desde el instante inicial 0 hasta T, con T arbitrariamente grande.
- Cuando una operación ha comenzado, debe terminarse antes de empezar otra en la misma máquina y no se admiten interrupciones en la misma; máquina sin mantenimiento ni daños.
- La única restricción activa en el taller es la relativa a las máquinas. No existen problemas de disponibilidad de mano de obra, materiales o de cualquier otra índole.
- El tiempo de duración de la operación de la máquina i procesando la orden j es conocido con anticipación (determinístico). Este tiempo incluye tiempos de preparación, conclusión, colocación de piezas, retiro de piezas, tiempos suplementarios, etc.
- El sistema productivo funciona con Buffers ilimitados. Al finalizar cualquier operación en una de las máquinas esta queda disponible aún si la siguiente máquina de la ruta no esta disponible, almacenando este producto en proceso en los buffers que se encuentran entre las máquinas (Número de buffers = m-1).
- La programación de operaciones es hacia adelate, sin fechas de entrega establecidas. Producción para disponer.
- No se tienen en cuenta los costos asociados a la operación.
- La naturaleza del sistema es estática, conservando constantes los valores de las variables durante el período de programación.
3. FORMULACIÓN
3.1 Objetivo
Como se mencionó anteriormente, el objetivo del problema es minimizar el Makespan: Mín Cmáx, siendo Cmáx el instante en el que termina el procesamiento de la n-ésima orden en la m-ésima máquina.
3.2 Referentes
i: Subíndice de referencia para las máquinas del sistema productivo; i = 1, 2,.., m
j: Subíndice de referencia para las órdenes de trabajo; j = 1, 2,.., n
j': Subíndice de referencia para las órdenes de trabajo; j' = 1, 2,.., n
Es utilizado para indicar la segunda orden de una pareja de órdenes, separadas con una (_) [ej. orden j_orden j']. Se diferencia de una combinación de máquina-orden, porque en general no utiliza separador y cuando lo requiere, se coloca (,) [ej. Máquina i, orden j].
3.3 Parámetros
m: Número de máquinas definidas para el sistema productivo.
n: Número de órdenes de trabajo definidas a procesar en el sistema productivo.
Tij: Duración de la operación a realizar en la máquina i sobre el trabajo j.
R: Ruta de trabajo u ordenamiento de las máquinas para el procesamiento de las órdenes.
O: Orden en que son recibidas en el sistema los trabajos por parte del cliente. (Necesario para la comparación con la regla de prioridad FIFO).
3.4 Variables
S: Secuencia de procesamiento de las órdenes de trabajo, representada en un vector de n elementos ordenados por el criterio de iniciación.
Iij: Momento o instante del tiempo en el que inicia el procesamiento de la orden de trabajo j en la máquina i.
S: Secuencia de procesamiento de las órdenes de
3.5 Ecuaciones de equilibrio
1. Iij: Instante en el que inicia el procesamiento en la máquina i de la orden j (1).
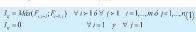
Fij: Instante en el que finaliza el procesamiento de la orden j en la máquina i.
Tij:: Duración de la operación a realizar en la máquina i sobre la orden j.
2. Fij Instante en el que finaliza el procesamiento de la orden j en la máquina i (2).
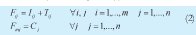
Iij: Instante en el que inicia el procesamiento en la máquina i de la orden j.
Tij: Duración de la operación a realizar en la máquina i sobre la orden j.
Cj: Tiempo de terminación de la orden j en la m-ésima máquina.
3. Ti Tiempo total efectivo de operación de la máquina i procesando las n órdenes (3).
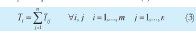
Tij: Duración de la operación a realizar en la máquina i sobre la orden j.
n: Número de órdenes configuradas.
4. Tj Tiempo total efectivo de operación de la orden j en su procesamiento por las m máquinas (4).
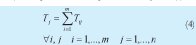
Tij: Duración de la operación a realizar en la máquina i sobre la orden j.
m: Número de máquinas configuradas.
3.6 Indicadores de Desempeño
1. Cmax, Tiempo de Completamiento ó Makespan: Tiempo en el que termina de ser procesada la última orden en el sistema ó, tiempo máximo de terminación de todas las órdenes (5).
Objetivo: Minimizar.
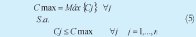
Cj: Tiempo de terminación de la orden j en la m-ésima máquina.
2. Tt, Tiempo de Flujo: Suma de la finalización en la m-ésima máquina de las n órdenes (6).
Objetivo: Minimizar.

Cj: Tiempo de terminación de la orden j en la m-ésima máquina.
3. Tp, Tiempo Promedio de Flujo: Promedio de la finalización en la m-ésima máquina de las n órdenes (7).
Objetivo: Minimizar.

TF: Tiempo de flujo.
n: Número de órdenes configuradas.
4. MU, % Utilización de Máquina: Es el porcentaje del tiempo de operación que las máquinas se encuentran procesando las n órdenes (8).
Objetivo: Maximizar.
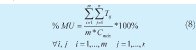
Tij: Duración de la operación a realizar en la máquina i sobre la orden j.
n: Número de órdenes configuradas. Cmáx: Makespan.
5. MO, % Ocio de Máquina: Es el porcentaje del tiempo de operación que las máquinas no se encuentran procesando las órdenes (9).
Objetivo: Minimizar.
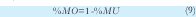
% MU: Porcentaje de utilización de máquina.
6. Wt, Tiempo Total de Espera: Suma del inicio en la primera máquina de la operación de las n órdenes más, la suma del tiempo de diferencia entre la finalización en cualquiera de las máquinas y el inicio en la inmediatamente siguiente para todas las órdenes (10).
Objetivo: Minimizar.
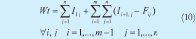
Iij: Instante en el que inicia el procesamiento en la máquina i de la orden j.
Fij: Instante en el que finaliza el procesamiento de la orden j en la máquina i.
7. Wp, Tiempo Promedio de Espera: Promedio del inicio en la primera máquina de la operación de las n órdenes (11).
Objetivo: Minimizar.

Wt: Tiempo total de espera.
n: Número de órdenes configuradas.
4. HEURÍSTICA CONSTRUCTIVA
4.1 Paso 0: Información de entrada
Los primeros parámetros a definir deben ser: m, n, R y O, para luego relacionar el tiempo que permanece cada orden de trabajo j en cada una de las máquinas i: Tij (12). Esto se hace en una matriz llamada T, de tamaño m filas (máquinas) y n columnas (órdenes) cuyos elementos son Tij.
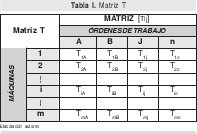

4.2 Paso 1: Tiempo total en máquina de cada orden
A partir de los datos anteriores, se calcula el tiempo total de operación para cada una de las órdenes en su paso por las máquinas (13).
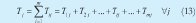
4.3 Paso 2: Matriz Cmáx {j_j`}
Este paso es el origen del trabajo de investigación. Para recrear la metodología diseñada, supóngase un rompecabezas de n piezas lineales, donde el objetivo más allá de lograr una figura preestablecida, está en lograr que las piezas con sus diversas formas encajen una a otra, minimizando el espacio que quede entre las puntas de una pieza y el espacio de otra.
Si un problema macro es abordado aisladamente por cada uno de sus componentes y, para cada uno de ellos se obtiene un óptimo, que sería el "óptimo local", la implementación de ellos en conjunto no necesariamente corresponde al óptimo del ejercicio, aún así, es una buena solución factible.
Eso mismo sucede con esta metodología, ya que se busca encontrar la pareja de piezas del rompecabezas que mejor encaja y, a este nuevo componente, compuesto por dos piezas, identificar la tercera pieza que mejor encaja. A este componente de tres piezas, se busca la pieza que mejor encaje, y así sucesivamente hasta que el componente complete sus n piezas.
En el problema planteado en la investigación no hay piezas de rompecabezas si no órdenes de trabajo, con las cuales se desea hacer exactamente lo mismo, ordenarlas de tal forma que se minimice el tiempo (en el ejemplo era el espacio) que se inutiliza en las máquinas.
Para determinar el ordenamiento, se efectúa el cálculo de máxima finalización para todas y cada una de las posibles permutaciones de parejas, registrando los resultados en una Matriz cuadrada C de tamaño n, cuyos elementos de la diagonal principal están penalizados con un valor muy grande M; esta penalización se debe a que no es posible la existencia de una pareja de órdenes cuyos elementos son la misma orden.
El cálculo se realiza utilizando la siguiente metodología, planteada por los autores para facilitar el desarrollo. Supóngase que se tienen dos órdenes de trabajo, A y B:
a. Para la primera orden de la pareja, en este caso la A, se tiene que el tiempo de inicio en la primera máquina es 0 y, en las siguientes máquinas es igual al de finalización en la máquina inmediatamente anterior (14). De la misma manera, el instante de finalización en la i-ésima máquina es igual a la suma de los tiempos de operación desde la primera máquina hasta la i (15).

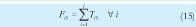
b. Para el caso de la segunda orden de la pareja, en este caso B, se tiene que el instante de inicio en la i-ésima máquina, es igual al máximo valor entre el instante de finalización de la orden en la máquina inmediatamente anterior y, el de finalización de la anterior orden, A, en la máquina en la cual se desea iniciar la operación, i. Por su parte, el instante de finalización en cualquiera de las máquinas, al igual que con la orden A, es igual al instante de inicio en esa máquina más, el tiempo de operación correspondiente de la orden. En las relaciones (16) y (17), se muestra el caso para orden j' en la primera máquina.
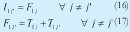
Para visualizar lo descrito, la Tabla II muestra ordenadamente el análisis permitiendo entender la metodología propuesta, a través de la Matriz denominada X.

4.4 Paso 3: Mínimo Cj,j` en matriz C.
Se debe buscar el elemento de la matriz C con menor valor. En caso de que haya más de un elemento con valor igual al mínimo Cj_j` se recurre al siguiente criterio de desempate:
Entre los elementos Cj_j` empatados, calcular el indicador de tiempo total en máquina para la pareja (j_j`) de la forma Tj_ j `= Tj + Tj ` , seleccionando el elemento correspondiente al mayor Tj_j`. Este criterio se basa en el índice % MU, porcentaje de utilización de máquina (18); entre las combinaciones (j_j`) empatadas, los valores de m y Cj_j` son constantes, por tanto para maximizar el valor de % MU, se debe buscar el mayor Tj_j` que haga más grande la expresión.
De persistir el empate entre algunos elementos, se asocia un número aleatorio con distribución uniforme (mayor o igual a 0 y menor que 1) a cada mínimo Tj_j`, seleccionando la pareja (j_j`) con mayor aleatorio asociado. Los valores de la pareja (j_j`) representan el primer elemento del vector S.
4.5 Paso 4: Agregar elementos a vector S
Una vez identificada la pareja a ingresar al vector S, se debe validar si esta es la primera en ingresar o no. Para el primer caso, simplemente esta combinación de elementos (j, j´) es adicionada. Para el segundo caso, se debe determinar si la pareja de elementos ingresa al comienzo o al final del vector. Esto se hace con el siguiente criterio:
Sea el valor del primer elemento del vector S y Ω el último elemento. Si j´ = α => j va al comienzo de S precediendo al elemento j´; de lo contrario, es decir, j = Ω => j´ va al final de S posterior al elemento j.
4.6 Paso 5: Actualización de la matriz C
Una vez ingresado el elemento (j, j´) al vector S, se debe actualizar la matriz C de modo que al iterar el procedimiento no se generen incoherencias. Se propone lo siguiente:
- Eliminar ó penalizar la fila j de la matriz C: con ello se evita obtener un nuevo elemento (j, y), que al ingresar al vector S generaría un conjunto de elementos repetitivos, rompiendo con la naturaleza de la secuencia objetivo. j e y son valores de órdenes entre 1 y n.
- Eliminar ó penalizar la columna j´ de la matriz C: se busca la no obtención de un nuevo elemento (x, j´) que al ingresar al vector S generaría un conjunto de elementos repetitivos, rompiendo con la naturaleza de la secuencia objetivo. j` y x son valores de órdenes entre 1 y n.
- Eliminar ó penalizar el elemento (j´,j) de la matriz C: al haber ingresado al vector S el elemento (j,j´), la pareja (j´,j) causaría una incongruencia de forma en la secuencia objetivo.
4.7 Paso 6: Mínimo Cj,j` en matriz C
Manteniendo la consistencia en la búsqueda de la secuencia, la siguiente pareja a ingresar debe ser una que contenga entre sus elementos el primero ó el último valor del vector S. Por ello la búsqueda se efectuará solamente en la fila j=Ω y la columna j´= α de la matriz C modificada, que llamaremos C '. De los valores de los elementos de esta fila y esta columna se selecciona el menor, siguiendo con el paso 4; de haber empates se emplea la metodología expuesta en el paso 3.
4.8 Paso 7: Criterio de parada
La iteración termina cuando la cantidad de elementos en el vector S es igual a n. A la vez esto se refleja, en que al concluir el paso 5 en la k-ésima etapa del proceso, la matriz C tiene todos sus n x n elementos penalizados. En este momento se tiene que el vector corresponde a la respuesta (secuencia) inicial.
5. HEURÍSTICA DE MEJORA
5.1 Paso 8: Algoritmo de respuestas alternas
En la ejecución de pruebas preliminares se detectó que esta respuesta estaba distante del objetivo en una cantidad importante de veces, por tal motivo se diseñó un algoritmo que permite la obtención de respuestas alternas, para compararlas entre sí por el valor del criterio objetivo y seleccionar entre ellas la mejor.
Parte de un análisis de sensibilidad sobre la respuesta inicial, y dos iteraciones. En cada iteración se obtienen cuatro secuencias alternas por cada secuencia principal. Es decir, que al finalizar la iteración 1 se obtienen 5 secuencias, la inicial y cuatro alternas, y, al finalizar la iteración 2 se obtienen 21 secuencias, las ya descritas y 16 alternas de las cuatro obtenidas en la iteración anterior.
Recordemos que en la Primera Etapa ingresaron al vector S, n-1 parejas de valores, de modo que el "análisis de sensibilidad" que se propone consiste en determinar esa n-ésima pareja de valores que debería entrar a la secuencia. Siguiendo la metodología propuesta en esa etapa, debe ingresar una pareja que su primer elemento sea el último de S ó, que su segundo elemento sea el primero de S.
Sea α el valor del primer elemento del vector S y Ω el último elemento. Para una secuencia cualquiera S_0, se encuentra cual es el elemento (j, j´) con j = Ω y el elemento (j, j´) con j´ = α con menor valor, de modo que cada uno de ellos es un candidato a ingresar a la secuencia.
Para el primer caso, j = Ω, se obtienen dos secuencias alternas así:
S_1: En la secuencia S "pivotear" el elemento j´ a la última posición.
S_2: En la secuencia S "pivotear" el elemento j a la posición inmediatamente anterior donde se encuentra j´.
En el segundo caso, j´ = α, se obtienen otras dos secuencias alternas así:
S_3: En la secuencia S "pivotear" el elemento j a la primera posición.
S_4: En la secuencia S "pivotear" el elemento j´ a la posición inmediatamente siguiente donde se encuentra j.
Esta es la primera iteración. En la segunda, se repite el procedimiento señalado a S_0, pero para S_1, S_2, S_3 y S_4, obteniendo como respuestas alternas de S_5 a S_20. Las 21 secuencias se enlistan, detectando cuales de ellas están repetidas para solo tener en cuenta en el siguiente paso las únicas.
Ejemplo:
S_0: D-E-C-A-B En este caso α= D, Ω = B
En la matriz C se busca el elemento (j, j`) de menor valor en la fila B y el de menor valor en la columna D.
j = Ω; menor valor encontrado (j, j`) = (Ω, j`) = (B, E)
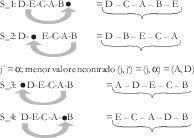
Con cada una de estas cuatro respuestas alternas, S_1 a S_4, se efectúa el mismo proceso que el realizado con S_0, de modo que se obtengan otras 16 respuestas alternas, de S_5 a S_20.
Para S_1: DCABE, se encuentra α= D, Ω= E
En la matriz C se busca el elemento (j, j`) de menor valor en la fila E y el de menor valor en la columna D.
j =Ω ; menor valor encontrado (j, j`) = (Ω, j`) = (E, C)
j´ = ; menor valor encontrado (j, j`) = (j,α) = (A, D)
5.2 Paso 9: Selección de la mejor Solución
Del conjunto obtenido en el paso anterior, se hace el cálculo del indicador objetivo, mínimo makespan, para cada una de ellas, seleccionado la secuencia que mejor indicador obtenga. El cálculo se obtiene aplicando las ecuaciones de equilibrio de iniciación y finalización descritas.
Si el makespan de más de una de las 21 respuestas es igual, se calcula a ellas el indicador Tiempo de Flujo y se selecciona la respuesta con menor valor en este segundo indicador. Si persiste el empate en dos ó más respuestas, se les calcula el Porcentaje de Utilización de Máquina, escogiendo entre las secuencias que persiste la igualdad la secuencia con mayor porcentaje. Por último y de darse como caso excepcional un equilibrio en los tres indicadores, se calcula el Tiempo Total de Espera para las secuencias cuyas respuestas han estado empatadas; se selecciona la que tenga menor este indicador ó de lo contrario se asigna un número aleatorio (0,1] a cada una y se escoge la que mayor valor se le haya asignado.
6. RESULTADOS
Después de analizar individualmente el grado de eficacia de Planifier para cada indicador con respecto a los diferentes métodos de solución, se procedió a realizar un análisis conjunto de la eficacia involucrando todos los indicadores de desempeño y al mismo tiempo los métodos de comparación, con el fin de observar el rendimiento del método heurístico propuesto. Como se mencionó anteriormente, para el Tiempo de Espera sólo se tuvo en cuenta las heurísticas. También se escogieron los resultados de Tiempo Promedio de Flujo y Tiempo Promedio de Espera, ya que su comporta-miento es equivalente al Tiempo de Flujo y Tiempo de Espera respectivamente. Los resultados pueden observarse en la Figura 1.
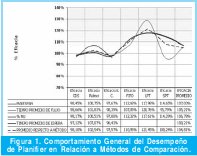
Para analizar el comportamiento del método respecto a variaciones en los valores de m y de n, se presentan las Figuras 2 y 3. Allí se muestra como se ve afectado el desempeño del método propuesto respecto al comporta-miento de los valores de m y n definidos para el indicador Makespan, que es el indicador que se quiere minimizar.


5.3 Análisis Estadístico de Resultados
Para calcular los intervalos de confianza de la eficacia esperada de Planifier respecto a los métodos de comparación seleccionados, con un 98% de confianza, se elabora una regresión para cada método comparando, las eficacias observadas en cada una de las pruebas realizadas con el valor de las variables exógenas m y n.
5.3.1 Eficacia respecto a heurística CDS
- De acuerdo a la prueba con el estadístico Fisher, al menos un parámetro es diferente de 0.
- El coeficiente de intercepción es significativo individualmente en el modelo.
- El coeficiente de la variable m no es significativo individualmente en el modelo.
- El coeficiente de intercepción n no es significativo individualmente en el modelo.
- La eficacia de Planifier respecto a la heurística CDS esta entre el 98.42% y el 99.65% con un 98% de confianza.
5.3.2 Eficacia respecto a heurística de Palmer
- De acuerdo a la prueba con el estadístico Fisher, al menos un parámetro es diferente de 0.
- El coeficiente de intercepción es significativo individualmente en el modelo.
- El coeficiente de la variable m no es significativo individualmente en el modelo.
- El coeficiente de intercepción n no es significativo individualmente en el modelo.
- La eficacia de Planifier respecto a la heurística de Palmer esta entre el 101.29% y el 102.77% con un 98% de confianza.
5.3.3 Eficacia respecto al método de Enumeración Completa
- De acuerdo a la prueba con el estadístico Fisher, al menos un parámetro es diferente de 0.
- El coeficiente de intercepción es significativo individualmente en el modelo.
- El coeficiente de la variable m es significativo individualmente en el modelo, impactando la eficacia esperada entre el -0.01% y el 0.02% por cada máquina que tenga el sistema.
- El coeficiente de intercepción n no es significativo individualmente en el modelo.
- Dado que m afecta la eficacia esperada, se tomó ésta como el promedio de las observadas, que es del 97.67%.
5.3.4 Eficacia respecto a la regla de prioridad FIFO
- De acuerdo a la prueba con el estadístico Fisher, al menos un parámetro es diferente de 0.
- El coeficiente de intercepción es significativo individualmente en el modelo.
- El coeficiente de la variable m no es significativo individualmente en el modelo.
- El coeficiente de intercepción n no es significativo individualmente en el modelo.
- La eficacia de Planifier respecto a la heurística de Palmer esta entre el 114.04% y el 119.88% con un 98% de confianza.
5.3.5 Eficacia respecto a la regla de prioridad LPT
- De acuerdo a la prueba con el estadístico Fisher, al menos un parámetro es diferente de 0.
- El coeficiente de intercepción es significativo individualmente en el modelo.
- El coeficiente de la variable m no es significativo individualmente en el modelo.
- El coeficiente de intercepción n no es significativo individualmente en el modelo.
- La eficacia de Planifier respecto a la regla LPT está entre el 117.57% y el 124.38% con un 98% de confianza.
5.3.6 Eficacia respecto a la regla de prioridad SPT
De acuerdo a la prueba con el estadístico Fisher, todos los parámetros son iguales a 0. Las conclusiones se desvirtúan, ya que la variable endógena no es explicada las variables exógenas. Sin embargo se visualiza que:
- El coeficiente de intercepción es significativo individualmente en el modelo.
- El coeficiente de la variable m no es significativo individualmente en el modelo.
- El coeficiente de intercepción n no es significativo individualmente en el modelo.
- La eficacia de Planifier respecto a la regla SPT esta entre el 112.61% y el 119% con un 98% de confianza.
7. CONCLUSIONES
- El método propuesto facilita el proceso de secuenciación en sistemas tipo Flow Shop Estrictos con Buffers Ilimitados, ya que funciona con un algoritmo simple y sencillo en su estructura, que es fácilmente soportado por una aplicación informática y, con un nivel de eficacia esperado superior al 97% respecto a cualquier método y, superior al 110% respecto a cualquier regla de prioridad, con un 98% de confianza.
- Con la utilización del método propuesto Planifier en problemas de secuenciación de operaciones para Sistemas del tipo Flow Shop Estrictos con Buffers Ilimitados, se obtienen mejores respuestas respecto a las reglas FIFO, LPT, SPT y el método heurístico de Palmer para el objetivo trazado, minimización ó maximización según corresponda, con un 98% de confianza, en los indicadores Makespan (Cmáx), tiempo de flujo (Tt), tiempo promedio de flujo (Tp), porcentaje de utilización de máquina (MU), porcentaje de ocio de máquina (MO), tiempo total de espera (Wt) y tiempo promedio de espera (Wp).
- La herramienta informática que soporta la aplicación de el método heurístico Planifier, tiene capacidad de procesamiento para valores de m entre 2 y 150, y para valores de n entre 3 y 150, en una máquina con sistema Microsoft® Windows XP, Profesional versión 2002, Service Pack 2 con procesador Intel® Pentium® 4, CPU 2.39 GHz, 496 MB de RAM.
- Con ese mismo equipo se pueden procesar mediante el método de Enumeración Completa, que es el detalle de todas las posibles combinaciones de secuencia, hasta ejercicios con valores de m no mayores a 10 y n no mayores a 15.
- El algoritmo del método de Planifier solo es eficiente algorítmicamente para valores de n mayores a 4, ya que el selecciona la respuesta entre un conjunto de 21 secuencias y, por ejemplo, para n = 4 las posibles secuencias son apenas 16.
- Para valores mayores o iguales a 5, el algoritmo es muy eficiente, ya que sin importar el número de n, que es quien determina la cantidad de posibles secuencias, solo hay selección entre un número fijo equivalente a 21.
- El desempeño observado del método Planifier, medido en términos de las respuesta obtenida para los indicadores Cmáx, Tt, Tp, MU, MO, Wt y Wp, es muy similar al de la heurística CDS de Campbell, Dudeck y Smith, distando la eficacia en tan solo un -1.9% en promedio, con un máximo de -1.58% y mínimo de -0.35%, con el 98% de confianza.
- El rendimiento comparativo de Planifier tiene a primera vista (gráficamente) un comportamiento escalonado de un peldaño decreciente, respecto a los valores de las variables m y n; Para valores de n menores a 25, la respuesta de Planifier es en promedio mejor respecto de 5 a 10%; para valores mayores a 25, la respuesta promedio decae en eficacia y tiende a ubicarse en un 98% para valores cercanos a 100, donde se presenta la convergencia; Para valores de m menores a 15, la respuesta de Planifier es en promedio mejor respecto de 5 a 10%; para valores mayores a 15, la respuesta promedio decae en eficacia y tiende a ubicarse en un 98% para valores cercanos a 25, donde se presenta la convergencia.
- La evidencia estadística que se deriva de este estudio, muestra que el comportamiento de la eficacia esperada, con un 98% de confianza, no es explicada por los valores de m y de n, ya que esos parámetros son no significativos en las pruebas realizadas. Aún así se presentó el análisis gráfico, porque se consideró que esos parámetros si determinan la calidad de la respuesta cuando su valor es alto.
- Respecto al método de Enumeración Completa, que es el detalle de todas las posibles combinaciones de secuencia, con Planifier se obtiene una respuesta desmejorada del 1.9% en promedio. Lo que significa, que los resultados con Planifier distan del óptimo el 1.9% en promedio.
- Solo en comparación con este método, se obtuvo significancia en el parámetro m, como variable explicativa de la eficacia esperada, validando lo expuesto en el punto anterior respecto a la influencia de m y n en la calidad de la respuesta que se obtiene con Planifier.
REFERENCIAS BIBLIOGRÁFICAS
[1] Alemán González. Estudio y aplicación del algoritmo Lomnicki Pendular al problema de Flow Shop sin pulmones intermáquina. Laboratorio de Organización industrial. Universidad Politécnica de Cataluña. España 2004.
[2] Conway R. W., W.L. Mazwell, L.W. Miller. Theory of Scheduling. Adison-Wesley, Reading, MA, 1967.
[3] José Domínguez Machuca. Dirección de operaciones. Aspectos tácticos y operativos en la producción y los servicios. Ed. Mc Graw Hill, Madrid, 1998.
[4] Ruben Ruiz. Evaluación de heurísticas para el problema del taller de Flujo. XXVII Congreso Nacional de stadística e Investigación Operativa. Universidad Politécnica de Valencia. España. 2003. Disponible en www.upv.es/gio/rruiz/files/SEIO2003_heu.pdf
[5] Michael Pinedo. Scheduling: theory, algorithms and system. Ed. Prentice Hall, 2002
[7] Agustín Alemán. Estudio y Aplicación del algoritmo Lomnicki Pendular al problema Fm/Block/Fmax. Laboratorio de Organización industrial. 2005. Disponible en https://upcommons.upc.edu/pfc/bitstream/2099.1/2645/1/34561-1.pdf
Diana Catherine Salamanca L.
Ingeniera Industrial Universidad Distrital Francisco José de Caldas, 2007. Proyecto de grado meritorio por el Diseño de un Método Heurístico de Secuenciación en Sistemas Flow Shop Estrictos con Buffers Ilimitados, bajo la dirección del docente MsC. Cesar A. López Bello. Actualmente cursando la Especialización de Gestión de Proyectos de Ingeniería en la Universidad Distrital, y ejerciendo como Ingeniera Investigadora del Centro de Investigación y Desarrollo Tecnológico de la Industria Electro Electrónica e Informática. dianitasale@gmail.com
Harry Andrés Ortiz Cabuya
Ingeniero Industrial Universidad Distrital Francisco José de Caldas, 2007. Proyecto de grado meritorio por el Diseño de un Método Heurístico de Secuenciación en Sistemas Flow Shop Estrictos con Buffers Ilimitados, bajo la dirección del docente MsC. Cesar A. López Bello. Actualmente se desempeña como Auxiliar de informática vinculado al proyecto CIMA en Alpina S.A. harryortiz@gmail.com
César Amilcar López Bello
Magister en Ingeniería Industrial, Universidad de los Andes. Especialista en Ingeniería de Producción, Universidad Distrital Francisco José de Caldas. Ingeniero Industrial Universidad Distrital Francisco José de Caldas. Profesor Asociado, Facultad de Ingeniería Universidad Distrital. Director de la Maestría en Ingeniería Industrial, Universidad Distrital. Investigador principal del grupo de Investigación MMAI de la Universidad Distrital, Investigador Grupo GIP, Investigador CITAD, Centro de Investigaciones en tecnologías avanzadas de decisión, Universidad de la Sábana. clopezb@udistrital.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










