DOI:
https://doi.org/10.14483/23448393.2681Published:
2005-11-30Issue:
Vol. 11 No. 2 (2006): July - DecemberSection:
Science, research, academia and developmentControl del Empuje de una Barra usando dos Robots Móviles y Visión Artificial
Bar-Pushing Control using two Mobile Robots and Machine Vision
Keywords:
Robótica móvil, visión artificial, robótica cooperativa, empuje de una barra (es).Downloads
References
Ioan Doré Landau, Identification et Commande des Systémes, Editions HERMES, Deuxiéme Édition Revue et Augmentée, 1993.
Roderich Grob, Marco Dorigo. Evolving a Cooperative Transport Behavior for Two Simple Robots, Springer Verlag, Berlin, P.P. 305-316, 2004.
Guilherme Pereira, Vijay Kumar. Decentraliced Algorithms for Multi-Robot Manipulation Via Caging. 2003.
Peng Song, Vijay Kumar. A Potential Field Based Approach to Multi Robot Manipulation, 2003.
Tang, C. P., and Krovi, V., "Manipulability-Based Configuration Evaluation of Cooperative Payload Transport by Mobile Robot Collectives," Proceedings of the 2004 ASME Design Engineering Technical Conferences and Computer and Information in Engineering Conference, Salt Lake City Utah, September 28 - October 2, 2004.
Bruce Randall Donald, James Jennings and Daniela Rus, Analyzing Teams of Cooperating Mobile Robots, in Proceedings ICRA 1994, San Diego.
Jhon J. Craig, Introduction to Robotics Mechanics and Control, Second Edition, Silma Inc., Addison-Wesley Publishing Company, 1989, Chapter 7(Trajectory Generation).
José Santos-Victor, Vision-based remote control of cellular robots, Robotics and Autonomous Systems 23 (1998) 221234.
João Jorge Torcato, José Xavier Rodrigues, Teleoperated Cellular Robot, Trabalho final de curso, July 1999.
Helder Fernandes, Alexandre Cunha, Sjoerd van der Zwaan, Controlo de Robot em Posição, Trabalho de Projecto da Disciplina de PSPCD.
Ollero Anibal, "Robótica, Manipuladores y Robots Móviles", Marcombo S.A. 2001.
C. Canudas de Wit, H. Khennouf, C. Samson and O. J. Sordalen, Recent Trends in Mobile Robots, Chapter 5 (Nonlinear Control Design for Mobile Robots), Edited by Yuan F. Zhang, January 1994.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigació, Academia y Desarrollo
Ingeniería, 2006-00-00 vol:11 nro:2 pág:70-79
Control del Empuje de una Barra usando dos Robots Móviles y Visión Artificial
Bar-Pushing Control using two Mobile Robots and Machine Vision
Eval Bladimir Bacca Cortés
Profesor Escuela de Ingeniería Eléctrica y Electrónica, Universidad del Valle.
Eduardo F. Caicedo Bravo
Profesor Escuela de Ingeniería Eléctrica y Electrónica y Director del Grupo de Investigación Percepción y Sistemas Inteligentes (P.S.I.), Universidad del Valle.
Resumen
En este artículo se describe la solución del control del empuje de una barra usando dos robots móviles y una cámara de visión artificial como sensor global, cuyas aplicaciones directas son el transporte y manejo cooperativo de grandes objetos. La solución propuesta involucra a dos robots móviles cuya posición, orientación y velocidad son obtenidas a través de una cámara ubicada en la parte superior de la escena; cada robot posee un controlador de orientación independiente, cuyo objeto de control es el seguimiento de una trayectoria previamente definida; usando la cinemática de un robot móvil diferencial se modela y controla la orientación de la barra que los dos robots móviles empujan, la trayectoria descrita debe ser perpendicular a la barra. La solución descrita emplea un control digital tipo RST [1] para los controles de orientación de los robots, con TS=0.2s, ξ=0.707, ωN = 3.5 rd/s y un error de estado estacionario promedio de aproximadamente 15%. El control de orientación de la barra manipula la velocidad de desplazamiento de los robots, el controlador usado fue un PD con: KP = 2.7, KD = 0.2, ξ= 2.807 y ωN = 3.539 rad/s y error de estado estacionario promedio de aproximadamente el 5.1%.
Palabras clave: Robótica móvil, visión artificial, robótica cooperativa, empuje de una barra.
Abstract
This paper describes a solution to the visionbased bar pushing control using two robots, which direct applications are the cooperative transport and handle of big objects. The solution proposed involves two mobile robots which position, heading and velocity are gathering through a video camera placed on scene top; each robot has an independent heading controller, which control objective is the path following previously defined; using the kinematics' differential mobile robot the bar's model and its control is obtained, the bar is pushed with help of the two robots and its trajectory is perpendicular to it. The solution described use a RST [1] digital controller for the mobile robots' heading control, with TS=0.2s, x=0.707, wN = 3.5 rd/s and a stable state error mean of 15% approximately. The bar's heading control modifies the mobile robots' lineal velocity, a PD controller was used with: KP = 2.7, KD = 0.2, x = 2.807 y wN = 3.539 rad/s and a stable state error mean of 5.1% approximately.
Key words: Mobile robotics, artificial vision, cooperative robotics, bar pushing.
1. INTRODUCCIÓN
La robótica cooperativa es un área de investigación que posee una buena cantidad de aplicaciones, enfocándose en la disminución de tiempo invertido en la realización de una tarea, aumento en la robustez de la aplicación a través de la redundancia, aumento del área de acción, distribución adecuada de recursos dependiendo de las restricciones de la tarea, manipulación de grandes cargas, entre otras. Sin embargo, la robótica cooperativa no solo plantea una posible solución, sino, grandes retos en la interacción de los robots a todos los niveles de control.
Una de las líneas de especial interés es la manipulación de grandes cargas, la cual trata de la movilización, transporte o vigilancia de un objeto de interés usando varios robots. Este problema posee varios retos: la dependencia con la forma geométrica del objeto, la estabilidad del sistema, el tipo de estrategia de control empleada (centralizada o descentralizada), el tipo de cooperación empleado, la respuesta del sistema ante el mal funcionamiento de alguno de sus miembros, entre otros.
Los esquemas de trabajo propuestos son variados, en [2] se muestra una estrategia en la cual el objeto a mover se llama presa y un solo robot no es capaz de hacerlo, por tanto se usan dos, sin comunicación explícita, un robot no puede percibir al otro, excepto por sus acciones sobre la presa; usan controladores neuronales producto de un algoritmo genético. Debido a que la tarea de empujar, llevar o transportar un objeto grande requiere la participación de más de un robot. En [3] se muestra una estrategia de control descentralizada para el transporte de objetos usando la técnica llamada "Object Closure", de tal manera que se determinan unas condiciones geométricas, dependientes del objeto a trasladar, con el fin de determinar si esta tarea es posible de realizar. En [4] se muestra un sistema descentralizado para la manipulación de objetos usando varios robots móviles. Se plantea una estrategia de control basada en campos de potencial, tanto de cada una de los robots como a nivel de grupo. En [4] se plantea el mantenimiento de una formación, a la cual se asocian ciertas características producto de un análisis de estabilidad de la formación misma.
Finalmente, otra alternativa en la manipulación cooperativa de objetos es el transporte de éstos empleando plataformas móviles. En [5] se muestra una estrategia que responde a las restricciones cinemáticas de los actuadotes (robot móvil más brazo articulado lineal), más que a la forma del objeto. En este caso se usa un control centralizado en el comportamiento del equipo para luego convertir estos planes de movimiento en planes individuales de movimiento para cada robot.
Las estrategias descritas muestran la tendencia en la solución del problema, el cual no es fácil. El trabajo que se presenta a continuación usa dos robots para empujar una barra desde una posición inicial hasta una final a través de una trayectoria definida. Se usa un esquema de control lineal tipo RST, cuyo único sensor global es una cámara de vídeo a través de la cual se realizan las estimaciones de posición y velocidad de los dos robots involucrados en empujar una barra; la cooperación es implícita [6] ya que un robot no es capaz de percibir al otro de forma directa, solo a través de los cambios de orientación de la barra.
La primera parte del documento muestra la descripción del sistema; luego las bases teóricas aplicadas al sistema para la generación de trayectorias y control de movimiento; finalmente se presentan las pruebas y resultados, mostrando el adecuado funcionamiento del sistema desde el empleo de un robot en la escena, luego los dos robots y finalmente los dos robots y la barra.
2. DESCRIPCIÓN DEL SISTEMA
La Figura No. 1 muestra la descripción del sistema de experimentación, el cual está conformado por: un espacio en el cual se mueven los robots libre de obstáculos, dos robots que empujan una barra, un transmisor RF para comunicar las sentencias de control a los robots, una cámara de vídeo que identifica a los robots, su posición, orientación, velocidad y a la barra también y un PC con Matlab para procesar las imágenes e implementar las estrategias de control.
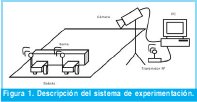
Los robots por sí solos no pueden desplazar adecuadamente la barra desde una posición inicial a una posición final, siguiendo una trayectoria específica y teniendo en cuenta que ésta debe estar alineada perpendicularmente a la trayectoria. Los robots poseen dos colores de fondo distintos y de alto contraste con el piso, uno es rojo y el otro es azul (esta diferencia será mantenida a pesar que las figuras no sean a color); el robot rojo posee una banda verde en la parte de atrás y una azul en la parte de adelante y el robot azul posee a diferencia del rojo una banda roja en la parte de adelante, estas bandas son usadas para capturar la orientación del robot en la escena y el color de fondo para obtener su posición. La barra es de color blanco, su centroide y el de los robots son usados para seguir una trayectoria previamente definida entre un punto inicial y uno final.
Los robots móviles usados son de tipo diferencial, por tanto teniendo en cuenta [1 7] [5 8] [6 9] [12 10], el modelo cinemático y dinámico de la planta obtenido es mostrado en la Ecuación No. 1
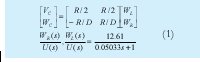
Donde R es el radio de las ruedas; D es el radio del robot; VC y WC son las velocidades lineal y angular del robot; WL y WR son las velocidades angulares de las ruedas.
3. METODOLOGÍA
El control del empuje de la barra usando los dos robots y la cámara de vídeo como sensor global, requiere la implementación y ejecución de:
Primero, la identificación y seguimiento de los robots en la escena - Los robots son identificados manualmente ubicando el ratón en un punto cercano a cada robot y una ventana de dimensiones predefinidas es creada y mantenida a lo largo de la prueba para capturar la posición, orientación y velocidad del robot.
Segundo, la generación de la trayectoria - La trayectoria es generada automáticamente empleando los puntos iniciales y finales de los robots y la barra. Esta trayectoria se genera usando polinomios de grado 3 [11], lo cual asegura una trayectoria curva con el fin de probar el control de orientación de la barra.
Tercero, el seguimiento de trayectoria del Robot - Cada robot posee una trayectoria que seguir pero a una velocidad lineal constante, cambiando solamente su velocidad angular.
Cuarto, el control de orientación de la Barra -La orientación de la barra depende de la velocidad lineal de los robots y esta orientación es el mecanismo de cooperación implícita entre los dos robots.
3.1. Generación de Trayectorias
Las trayectorias para ambos robots son generadas usando la metodología expuesta en [11], donde para cada robot se define una trayectoria paramétrica en términos del tiempo para la coordenada X y Y. Esta trayectoria es de la forma mostrada en la ecuación No. 2.
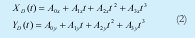
A Donde A0X a A3X y A0Y a A3Y son los coeficientes que deben ser encontrados dadas las restricciones mostradas en la ecuación No. 3.
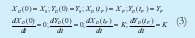
Donde [X0, Y0] y [XF, YF] conforman la posición inicial y final del robot; tF es el tiempo final estimado de la prueba y K es la velocidad final deseada. Resolviendo el sistema de ecuaciones, se pueden expresar los coeficientes de la trayectoria en términos de las restricciones de la ecuación No. 3, como se muestra en la ecuación No. 4.
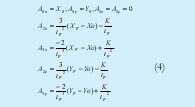
Por lo tanto con estas restricciones es posible generar un camino que conecta la posición inicial y final del robot en la escena.
3.2. Estrategia para el Seguimiento de Trayectorias
La Figura No. 2 muestra la estrategia implementada para el seguimiento de la trayectoria, en ella se distinguen: la posición actual de robot [XP, YP], el punto de la trayectoria más cercano al robot [XM, YM], la orientación deseada del robot θR, la orientación actual del robot θA y la distancia entre el robot y la trayectoria L. Ya que en un robot móvil diferencial, la velocidad lineal y la velocidad angular están desacopladas [7] [8] [9] el objetivo de control es seguir la trayectoria a una velocidad lineal constante pero variando la orientación del robot según la trayectoria lo diga. En términos generales el algoritmo de control es el siguiente:
Primero, empleando las ecuaciones (2), (3) y (4) se obtiene y traza una trayectoria deseada. Segundo, se mide el error de orientación entre el robot y la recta tangente en el punto más cercano a la trayectoria deseada, ver Ecuación (5).
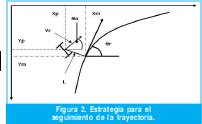
Donde [XM+1, YM+1], [XM-1, Y M-1] son los próximos y anteriores puntos sobre la trayectoria; y →R son los vectores tangente y perpendicular a la trayectoria en el punto M. El error de orientación está dado por la Ecuación (6).
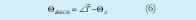
Tercero, con el fin de incluir el aporte entre la distancia de separación del robot y la trayectoria al error de orientación, se debe definir de que lado se encuentra el robot, para lo cual se emplea el producto punto así [12]: si →T • →R < 0 el robot se encuentra a la derecha de la trayectoria y si se encuentra a la izquierda.
Entonces:
Donde K es un número mayor que cero que permite incrementar el error de orientación con el fin tener en cuenta la distancia de separación del robot a la trayectoria (L).
4. CONTROL DE ORIENTACIÓN DE LOS ROBOTS
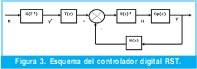
El control de orientación de cada uno de los robots se implementó a través de un controlador digital tipo RST [1], su estructura es mostrada en la Figura No. 3, en la cual: G(Z-1) es la dinámica del sistema deseado, el cual tiene la forma de la Ecuación (8).
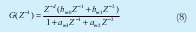
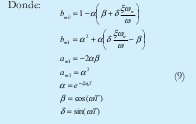
Nótese que dadas ξ y ωN correspondientes a la dinámica deseada, se obtienen los coeficientes de (9) que definen a (8).
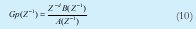
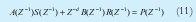
GP(z) es el modelo digital de la planta, cuya forma se muestra en la Ecuación (10). T(z), R(z) y S(z)-1 son los polinomios del controlador a calcular, lo cual se hace empleando el polinomio característico del modelo completo del sistema, mostrado en la Ecuación (11). De acuerdo a [1] es posible definir un controlador digital tipo PID a partir de un controlador RST, cuya forma lo muestra la Ecuación (12).
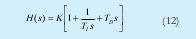
Donde TI es la constante integral, TD es la derivativa y K la ganancia. Con el fin de encontrar la relación entre las constantes de la Ecuación (11) y los coeficientes del polinomio característico, definimos la forma de los polinomios P, A, B, S y R, ver Ecuación (13).
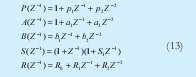
Empleando la Ecuación (11) tenemos un sistema de ecuaciones a resolver y cuya solución analítica se muestra en la Ecuación (14).
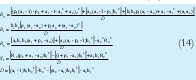
Finalmente, de acuerdo a [1], TI, TD y K en términos de los polinomios S(Z-1) y R(Z-1) se expresan como lo muestra la Ecuación No. 15.
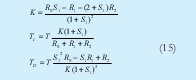
5. CONTROL DE ORIENTACIÓN DE LA BARRA
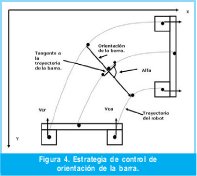
La Figura No. 4 muestra la estrategia para el control de orientación de la barra, la cual consiste en aplicar el mismo modelo cinemática de un robot móvil diferencial a la barra misma. Las velocidades VCR y VCA corresponden a las velocidades lineales del robot Rojo y Azul, tal que su modelo cinemática es expresado en la ecuación No. 16.
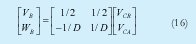
Donde D es la distancia entre el centro de masa de la barra y cada robot. Teniendo en cuenta a [10] para el modelo cinemática inverso de un robot móvil obtenemos el valor de la velocidad lineal necesaria para cada robot con el fin de lograr una velocidad lineal y angular de la barra, entonces, de la velocidad angular de la barra definida usando las velocidades lineales de los robots obtenemos el modelo de inclinación continuo y discreto de la barra, ver ecuación No. 17.
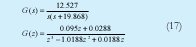
El modelo discreto de la planta tiene en cuenta el retardo de la cámara de vídeo (z-1). El modelo de orientación posee los siguientes parámetros: ξ = 2.807 y ωN = 3.539 rad/s. Se desean los siguientes parámetros: ξ= 0.6, TEST = 2s, y wN = 3.333 rad/s, para lo cual se diseñó un controlador PD empleando la técnica de localización de polos, cuya función de transferencia se muestra en la Ecuación No. 18.
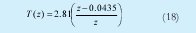
Desde el punto de vista de implementación, las constantes KP = 2.688 y KD = 0.1222. Por tanto, empleando este controlador podemos variar las velocidades lineales de los robots e influir en la orientación de la barra, tal que el ángulo a entre la longitud de la barra y la pendiente de la trayectoria, sea lo más perpendicular posible.
6. PRUEBAS Y RESULTADOS
Las pruebas y resultados mostrados en este documento son llevados a cabo en tres etapas: el seguimiento de la trayectoria de un solo robot, lo cual permite identificar las limitaciones de esta estrategia a este nivel de aplicación; el seguimiento de trayectoria con los dos robots, con el fin de validar si el tiempo de muestreo es suficiente para interactuar con el sistema o de lo contrario realizar los ajustes necesarios en el modelo; y finalmente el empuje de la barra usando los dos robots.
6.1 Seguimiento de Trayectorias para un Robot
En esta prueba el modelo cinemática y dinámico del robot mostrado en la ecuación (1) se digitalizó usando TS=0.2s, la trayectoria se calculó usando los coeficientes mostrados en la ecuación (3) y el controlador de orientación RST se calculó usando las restricciones 0.8 < ξ < 0.9, ωn = 3.5 y las ecuaciones (7) (11) (14). Se incluyen resultados en los cuales los robots se desplazan en línea recta, en una curva, alejándose y acercándose a la cámara; para cada uno de estos resultados se pueden apreciar la evolución de la posición en la imagen real, la posición en el plano XY y la orientación del robot.
La Figura No. 5 y 6 muestran dos experimentos de dos robots siguiendo una trayectoria recta en gran parte de su recorrido. Estos dos experimentos fueron realizados con los dos robots con el fin de mostrar que su comportamiento es distinto, pero que el controlador seleccionado realiza adecuadamente su trabajo, esto es controlar la orientación del vehículo y mantenerlo lo más cercano posible a la trayectoria deseada. En aplicaciones de control de movimiento para robótica móvil que usan una cámara como único sensor global, la perspectiva es un aspecto de especial interés y las pruebas aquí realizadas tratan de trabajar en la zona de la imagen que menos se afecta por este factor, sin embargo, debe anotarse que no se tiene ninguna información acerca de la posición relativa a.
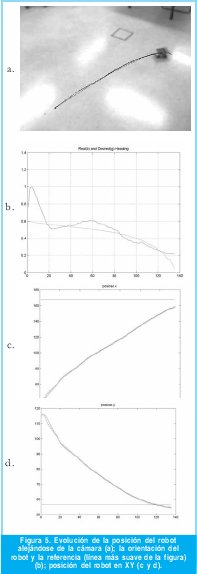
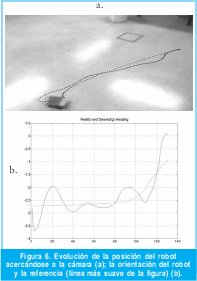
La Figura No. 5 (b) y 6 (b) muestran la evolución de la orientación del robot a lo largo de la trayectoria (azul) y la orientación deseada (verde), en ambas figuras se puede apreciar el trabajo de control realizado después de producirse un sobre - impulso en la orientación; en la Figura No. 5(b) paulatinamente se compensa el error de orientación hasta llegar a la posición deseada; en la Figura No. 6(b) la trayectoria posee una variación de orientación más exigente en su tramo final, lo cual el controlador trata de compensar. Ubicar al robot con la orientación deseada es difícil, más aún si el usuario es quién selecciona la posición final, lo cual exige más al controlador de orientación. Además, se verá más adelante que debido a las características de color del piso donde los robots mueven, el robot azul presenta mejores respuestas en el control de orientación que el robot rojo, ya que presenta mejor contraste.
En la Figura No. 5 (c y d) muestran la evolución de la posición del robot a lo largo de la trayectoria, en rojo se muestra la posición final deseada, en azul la posición actual del robot y en verde la trayectoria deseada. Estas figuras solo son mostradas para la primera prueba, ya que como se observa de la Figura 5 (c y d) la posición [X, Y] es seguida con buena precisión como consecuencia del adecuado control de orientación.
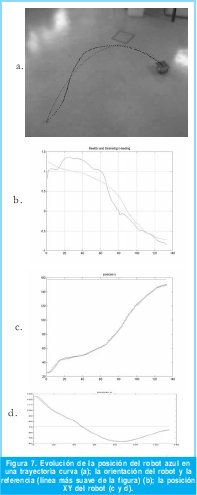
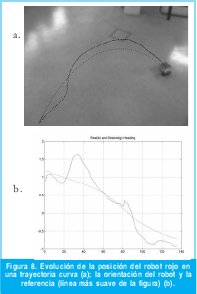
El próximo paso es complicar aún más la trayectoria aumentando su curvatura, las Figuras No. 7 y 8 muestran los mismos datos que la anterior prueba, pero correspondientes a una trayectoria curva. Las Figuras No. 7 (b) y 8 (b) muestran la evolución de la orientación, en las cuales es notoria la acción de control, sin embargo se observa que el sistema en lazo cerrado para el robot rojo posee una tendencia a presentar unas pequeñas oscilaciones decrecientes alrededor de la referencia, lo cual es una consecuencia de la aproximación inicial que se tuvo en el modelo dinámico de sus actuadotes, esto es, ajustar los parámetros del modelo de los motores de DC para cada rueda (K y t) al promedio geométrico de los modelos individuales. Este efecto es más notorio en el robot rojo que en el azul.
Con una trayectoria curva es más acentuado el efecto de la descompensación inicial de orientación, en ambos casos el robot tenía una orientación completamente diferente a la que debía seguir, sin embargo, el control de orientación compensa tanto este error inicial como el cambio de curvatura en la trayectoria. Las Figuras No. 7 (c y d) muestran de nuevo que el seguimiento de la posición tiene características deseables: adecuada precisión y movimientos suaves.
Entre trayectorias rectas y curvas se realizaron 10 pruebas, 5 para el robot azul y 5 para el robot rojo, teniendo en cuenta el comportamiento en bucla cerrada del sistema, cuyo tiempo de establecimiento es de aproximadamente 2s se obtuvo un promedio de error de estado estacionario igual a 13.4%.
6.2. Seguimiento de Trayectorias para dos Robots
Una vez probado el comportamiento del controlador para un solo robot usando trayectorias rectas y curvas, la próxima etapa es verificar el comportamiento del controlador de orientación con dos robots en la misma escena.
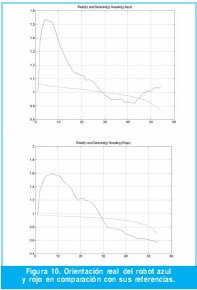
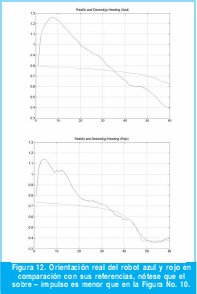
Las Figuras No. 9, 10, 11 y 12 muestran la representación real de dos experimentos y las curvas de orientación de cada uno de los robots. Una vez a.b. se seleccionan gráficamente las posiciones iniciales de los robots, se definen las posiciones finales y un par de trayectorias es generada automáticamente, lo cual, como se mencionó anteriormente impide que los robots estén inicialmente alineados con la trayectoria deseada generándose el sobre impulso inicial para ambos robots. Este sobre - impulso es gradualmente compensado por el controlador de orientación de cada uno de los robots, esto se puede observar comparando las gráficas de orientación (Figuras 10a, 10b, 12a y 12b) y las imágenes reales del sistema (Figuras 9 y 11).

En las gráficas de orientación del robot rojo, Figuras 10b y 12b, se observa que su comportamiento es más ruidoso que las gráficas de orientación del robot azul, Figuras 10a y 12ª, esto tiene como consecuencia que la variación de orientación en el tiempo es menos suave. Como se puede observar, al igual que en las anteriores pruebas, las características del suelo hacen que el contraste sea más alto para el robot azul que para el rojo; aunque se ensayaron filtros mediana de varios tamaños después de la binarización para filtrar el ruido, éste no desaparecía por completo afectando la estimación de su posición y orientación.
Se realizaron 5 pruebas, teniendo en cuenta las especificaciones de los controladores se obtuvo un promedio del error de estado estacionario aproximadamente igual a 16%.

6.3. Seguimiento de Trayectoria para dos Robots Empujando una Barra
Finalmente, se tienen los resultados del control de orientación de una barra usando dos robots móviles. Las especificaciones de los controladores son mantenidas, sin embargo, debe anotarse que no existen sensores adicionales a la cámara, lo cual no permite garantizar que el robot realmente esté en contacto con la barra. De acuerdo a (16) y (17) se definen dos parámetros globales para el experimento: la velocidad de desplazamiento deseada de la barra y su velocidad angular, obteniéndose la velocidad lineal de desplazamiento de cada uno de los robots, dejando al controlador de orientación la modificación de las velocidades lineales de las ruedas de cada uno de los robots.
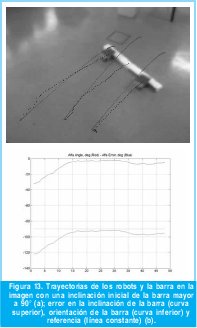
La Figura No. 13 muestra un experimento en el cual la inclinación inicial de la barra es superior a 90°, esto con el fin de verificar la estrategia de control planteada. La Figura No. 13 (b) muestra la evolución de la orientación de la barra en rojo, el error de orientación en azul y la referencia (90°) en verde. Se puede observar que el comportamiento de los controladores genera un pequeño error de estado estacionario. Nótese que la posición inicial del robot rojo está adelantada en relación con la posición del robot azul, observando la Figura 13a se nota que la trayectoria inicial del robot azul tiene unos puntos más separados que la trayectoria inicial del robot rojo, lo cual se produce debido a que los controladores intentan compensar el error de inclinación de la barra.
La Figura No. 14 muestra un experimento contrario al anterior, la inclinación inicial es menor a 90°, la Figura No. 14 (b) muestra la evolución de la orientación de la barra con un error de estado estable pequeño. En ambos experimentos el centroide de la barra no alcanza su posición final, lo cual es intencional, es decir, los primeros que alcanzan su posición final son los robots y una vez esto ocurre el experimento termina.

7. CONCLUSIONES
Este trabajo presenta una solución al problema del empuje de una barra usando dos robots móviles. La solución planteada incluye un control de orientación para los robots móviles usando un control digital tipo RST, el cual permitió que el sistema trabajara con las siguientes características: 0.8 < ξ < 0.9, ωn = 3.5. Los resultados obtenidos para el seguimiento de trayectorias empleando un solo robot y dos robots, muestran que se alcanza un error promedio de estado estacionario de 13.4% y 16% en el control de orientación; desde el punto de vista del seguimiento de trayectorias, las pruebas mostraron que esta tarea es llevada a cabo con una buena precisión. El control de orientación de la barra fue llevado a cabo modificando las velocidades lineales de los robots con el fin de obtener un efecto en la orientación, las velocidades lineales son modificadas usando un control PD cuyas características en bucla cerrada son: KP = 2.7, KD = 0.2, ξ = 2.807 y ωN = 3.539 rad/s. Las pruebas mostraron un adecuado comportamiento del controlador, tanto para orientaciones iniciales mayores de 90° como para orientaciones iniciales menores a 90°, observándose un error de estado estacionario promedio de 5.1%. En todas las pruebas se observaron oscilaciones iniciales debidas en su mayoría a que el robot o los robots no poseían una orientación alineada con la orientación de la trayectoria trazada.
8. AGRADECIMIENTOS
Este trabajo fue producto de una pasantía realizada en el laboratorio de visión artificial VISLAB, en el Instituto Superior Técnico, Lisboa, Portugal y gracias al apoyo económico del proyecto CYTED-SISPER.
REFERENCIAS BIBLIOGRÁFICAS
[1] Ioan Doré Landau, Identification et Commande des Systémes, Editions HERMES, Deuxiéme Édition Revue et Augmentée, 1993.
[2] Roderich Grob, Marco Dorigo. Evolving a Cooperative Transport Behavior for Two Simple Robots, Springer Verlag, Berlin, P.P. 305-316, 2004.
[3] Guilherme Pereira, Vijay Kumar. Decentraliced Algorithms for Multi-Robot Manipulation Via Caging. 2003.
[4] Peng Song, Vijay Kumar. A Potential Field Based Approach to Multi Robot Manipulation, 2003.
[5] Tang, C. P., and Krovi, V., "Manipulability-Based Configuration Evaluation of Cooperative Payload Transport by Mobile Robot Collectives," Proceedings of the 2004 ASME Design Engineering Technical Conferences and Computer and Information in Engineering Conference, Salt Lake City Utah, September 28 - October 2, 2004.
[6] Bruce Randall Donald, James Jennings and Daniela Rus, Analyzing Teams of Cooperating Mobile Robots, in Proceedings ICRA 1994, San Diego.
[7] Jhon J. Craig, Introduction to Robotics Mechanics and Control, Second Edition, Silma Inc., Addison-Wesley Publishing Company, 1989, Chapter 7(Trajectory Generation).
[8] José Santos-Victor, Vision-based remote control of cellular robots, Robotics and Autonomous Systems 23 (1998) 221- 234.
[9] João Jorge Torcato, José Xavier Rodrigues, Teleoperated Cellular Robot, Trabalho final de curso, July 1999.
[10] Helder Fernandes, Alexandre Cunha, Sjoerd van der Zwaan, Controlo de Robot em Posição, Trabalho de Projecto da Disciplina de PSPCD.
[11] Ollero Anibal, "Robótica, Manipuladores y Robots Móviles", Marcombo S.A. 2001.
[12] C. Canudas de Wit, H. Khennouf, C. Samson and O. J. Sordalen, Recent Trends in Mobile Robots, Chapter 5 (Nonlinear Control Design for Mobile Robots), Edited by Yuan F. Zhang, January 1994.
Eval Bladimir Bacca Cortes, M.Sc.
Nació en Pasto, Nariño, Colombia. Es Ingeniero Electrónico de la Universidad del Valle, Cali, Colombia. Obtuvo su título de Maestría en Automática en la Universidad del Valle, Cali, Valle. Ha desempeñado cargos en ingeniería de desarrollo de sistemas de información en empresas como: El Diario el País y el Centro Nacional de Productividad.
Actualmente se desempeña como profesor en el área de Robótica Móvil e Interfaces en la Universidad del Valle, Cali, Colombia, y pertenece como investigador al grupo de Percepción y Sistemas Inteligentes donde realiza estudios sobre Robótica Móvil (terrestre y aérea), Visión Artificial, Laboratorios Virtuales y desarrollo de sistemas embebidos. evbacca@univalle.edu.co
Eduardo F. Caicedo Bravo, Ph.D.
Nació en Pasto, Nariño, Colombia. Es Ingeniero Electricista de la Universidad del Valle, Cali, Colombia. Obtuvo su título de Maestría en Informática Industrial en la Universidad Complutense, Madrid, España. Obtuvo su PhD en la Universidad Complutense, Madrid, España.
Actualmente se desempeña como profesor en el área de Inteligencia Computacional en la Universidad del Valle, Cali, Colombia, y es director del grupo de investigación Percepción y Sistemas Inteligentes donde realiza estudios sobre Robótica Móvil, Parametrización de Redes Neuronales Artificiales, Redes Neuronales por Imitación y Controladores Neuronales para Prótesis de Rodilla. ecaicedo@univalle.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










