DOI:
https://doi.org/10.14483/udistrital.jour.reving.2013.2.a07Published:
2013-11-05Issue:
Vol. 18 No. 2 (2013): July - DecemberSection:
Special Section: Best Papers "VI Symposium on Optimization".Algunos problemas provenientes de la Teoría de Rayos Aplicada a las Ecuaciones de Onda Sísmica
Some open problems from Ray Theory Applied to Seismic Wave Equations
Keywords:
Ray theory, Eikonal Equation, Transport Equation. (en).Keywords:
Teoría de Rayos, Ecuacional Iconal, Ecuación de Transporte (es).Downloads
References
Azmy S. Ackleh, E.J. Allen, R.B. Hearfott, and P. Seshaiyer. Classical and Modern Numerical Analysis. Chapman & Hall/CRC, Boca Raton, FL USA, 2010.
K. Aki and P Richards. Quantitative Seismology. Theory and Methods, Volume I. W.H. Freeman and Company, New York, 1980.
V.I. Arnold. Mathematical methods of Classical Mechanics. Springer-Verlag, Nueva York,1978.
V.M. Babic and V.S. Buldyrev. Short-wavelenght diffraction theory (Asymptotic methods). Springer, Berlin, 1991.
N. Blestein. Mathematical Methods for Wave Phenomena. Academic Press, New York, 1984.
N. Blestein, J.K. Cohen, and J.W.H. Stockwell Jr. Mathematics of Multidimensional Seismic Imaging. Springer, Berlin, 2001.
A. Bona and M. Slawinski. Wavefronts and Rays: As Characteristics and Asymptotics. World Scientifi c Publisher Company, Pte. Ltd, Hackensack, NJ, USA, 2011.
J.E. Dennis and R.B. Schnabel. Numerical Methods for Unconstrained Optimization. Prentice Hall, Engle- wood Cliffs, New Jersey, 1983.
P. Docherty. A Fast Ray Tracing Routine for laterally Inhomogeneous Medsi, CWP-018. PhD thesis, Colorado School of Mines, Golden, Colorado, EUA, 1985.
P. Docherty. Ray theoretical modeling, migration and inversion in two-and-one-halfdimensional layered acoustic media, Research Report number CWP-051. Center for Wave Phenomena, Colorado school of Mines, Golden, 1987.
Lawrence C. Evans. Partial Differential Equations: Second Edition. AMS, Providence, Rhode Island, USA, 2010.
S. Gray. Effi cient traveltime calculations for kirchhoff migration. Geophysics, 51:1685–1688, 1986.
V. Cˆ erveny. Seismic Ray Theory. Cambridge University Press, Cambridge, 2001.
V. Cˆ erveny, I.A. Molotkov, and Psencik. Ray Method in Seismology. Universita Karlova, Praha, 1977.
H.B. Keller and D.J. Perozzi. Fast seismic ray tracing. SIAM J. APPL. MATH., 43(4):981–992, 1983.
Y. Kravtsov and Y.I. Orlov. Geometrical Optics of Inhomogeneous Media. Springer Verlag, Berlin, 1990.
Carlos César Piedrahita. Generalização do Método de Continuação no Traçãmento de Raios utilizando o Conceito dos Autômatos Finitos. PhD thesis, Universidad Estadual de Campinas, Campinas, SP, Brasil, 2002.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
ALGUNOS PROBLEMAS PROVENIENTES DE LA TEORÍA DE RAYOS APLICADA A LAS ECUACIONES DE ONDA SÍSMICA
SOME OPEN PROBLEMS FROM RAY THEORY APPLIED TO SEISMIC WAVE EQUATIONS
Carlos César Piedrahita Escobar
Departamento de Ciencias Básicas, Universidad de Medellín cpiedrahita@udem.edu.co
Recibido: 15/10/2013 Aceptado: 13/12/2013
RESUMEN
La parte inicial de este artículo revisa la aplicación de la teoría de rayos en las ecuaciones de onda sísmicas, en particular, la propagación de ondas P. La parte final del artículo se centra en un par de problemas que se generan a partir del análisis utilizando teoría de rayos. Estos problemas posee un interés académico en su formulación matemática, además tienen un interés práctico para el área de la Geofísica de Exploración y/o Producción.
Palabras clave: Teoría de Rayos, Ecuacional Iconal, Ecuación de Transporte
ABSTRACT
This paper gives an overview of the application of ray theory in the seismic wave equations, in particular, to P wave propagation. In addition, a couple of open problems that are obtained from the analysis using ray theory are stated. These problems have an academic interest in their mathematical formulation, and also have a practical application in Exploration and /or Production Geophysics.
Key words: Ray theory, Eikonal Equation, Transport Equation.
1. INTRODUCCIÓN
En el presente artículo presentamos los elementos básicos de la teoría de rayos aplicada a la aproximación asintótica de la Ecuación Elastodinámica, que se presenta en la sísmica de Exploración .
Esta aproximación es utilizada ampliamente para diversos asuntos en la sísmica de exploración y/o explotación, en particular, en los temas del modelado y la inversión sísmica (ver [6], [13] y [14]. Dichas técnicas son empleadas desde los mismos comienzos de la sismología, a principios del siglo XX, y han sido traídas de la Óptica y la Propagación de las ondas electromagnéticas en general. También han sido utilizadas en aplicaciones diversas, como por ejemplo, el radar, las microondas, etc. Además es posible aplicar estas ideas a temas como el modelado y los problemas inversos en las técnicas de ensayos no-destructivos y las imágenes médicas, en las cuales se utilizan ondas de tipo elástico y/o electromagnéticos en medios continuos.
La propagación de ondas mecánicas en un medio continuo, está caracterizada por la Ecuación Acústica para el caso que el medio sea un fluido y la Ecuación de Onda Elastodinámica para el caso general de un sólido[13]. Estas ecuaciones son ecuaciones en derivadas parciales de tipo hiperbólico, de segundo orden. En general, resolver estas ecuaciones para una un dominio complejo es difícil, solamente para casos simples se puede dar una solución analítica, utilizando, por ejemplo, funciones de Green. La teoría de rayos realiza una aproximación al problema para aquellos casos en que las escalas lo permitan, es decir, que la longitud de onda de la señal sea muy pequeña comparado respecto a las dimensiones del objeto analizado, tal como está justificado en [4] y [16]. La Ecuación de Propagación de la Onda P en un medio isótropo está dada por (ver [2]):
donde φ (x, t), es la divergencia del desplazamiento de una partícula, φ = ∇ • u, donde u (x, t), representa el desplazamiento de una partícula en el medio, desde su posición de equilibrio, en la posición x, en el tiempo t, y v (x), representa la velocidad de propagación de la onda en el medio.
Para deducir las ecuaciones que caracterizan un rayo, consideramos la ecuación de onda en el dominio de la frecuencia, y asúmase que se busca una aproximación a la ecuación de onda, en las altas frecuencias (o en forma equivalente, longitudes de onda pequeñas respecto a las dimensiones del modelo). El problema se transforma en la solución de las llamadas Ecuaciones Iconal y de Transporte. La solución se aproxima por una serie asintótica (ver [13],[6]):
ωβ ≡ Transformada de Fourier de un pulso
τ(x) ≡ Tiempo de tránsito
Aj (x) ≡ Amplitudes independientes de la frecuencia, j = 0, 1, 2, . . .
donde ω es la frecuencia angular.
En el apéndice A, se daráuna justificación de la aproximación asintótica, nos basaremos en [6] y [5] para dar soporte a los argumentos.
2. APROXIMACIÓN ASINTÓTICA
Al substituir la aproximación, Ecuación (2), en la Ecuación (1), obtenemos una expresión en potencias de (iω). En general, no podemos garantizar que los términos de la serie se cancelen entre ellos, por tanto necesitamos que los coeficientes de la serie se anulen independientemente. Como se explica en el apéndice A, se obtiene la Ecuación (15). Para que esto se cumpla en las altas frecuencias, se iguala a cero cada potencia de (iω), comenzando con la máxima potencia, β + 2, que aparece solo en la primera serie de la ecuación, cuando j = 0. Al igualar a cero el coeficiente de la primera serie, obtenemos la llamada Ecuación Iconal
Se observa que no hemos tomado la posibilidad alterna A0 = 0, es decir, se asume que la serie comienza con un primer término no-nulo. Con el resultado ( 3 ), toda la primera serie se anula.
Analizando el resto de términos de la serie, se tiene que para la segunda serie, la potencia mayor no-nula de ω es β + 1, la cual surge cuando j = 0, y se obtiene la llamada Ecuación de Transporte de orden cero.
Para el resto de la serie, sí se analiza j = 1, 2, 3 . . ., se obtienen las llamadas Ecuaciones de Transporte de orden superior
La Ecuación Iconal (3) y de Transporte de orden cero (4), son las ecuaciones usualmente empleadas en sísmica de exploración (ver [6]). Las Ecuaciones de Transporte de orden superior, en general, no son utilizadas en el modelado e inversión sísmica, puesto que representan perturbaciones de orden superior que no aportan mucho a la solución, si el problema estáenmarcado en las altas frecuencias.
3. CARACTERíSTICAS PARA LA ECUACIÓN ICONAL
Una forma de resolver la Ecuación Iconal es utilizando el Método de las Características (ver [5],[6],[11], [7]), como se explica en el Apéndice B, se puede considerar a σ como una variable de integración. Este tipo de curvas, es lo que en Ó ptica Geométrica se denominamos un rayo. Este problema queda enmarcado como un problema de valores iniciales en el cual las variables dependen del parámetro σ. Considerando la notación del Apéndice B, si se analiza la Ecuación Iconal:
se puede identificar a τ con u y las componentes de ∇τ con las componentes de p, donde c(x) es un parámetro del modelo, que representa la velocidad, y es una función escalar de posición .
Además τ no aparece explícito en esta ecuación, o sea que la derivada con respecto a u = τ, representadas por el término Fu en las ecuaciones características, es nula. Por todo lo anterior, al aplicar el método de las características a la Ecuación Iconal es más simple que el caso general.
La magnitud del vector p está dado por
y se puede escribir la Ecuación Iconal como:
Las ecuaciones características se convierten en:
Se obtienen entonces siete ecuaciones y ocho incógnitas, incluyendo a λ como incógnita, cada una en términos del parámetro σ. Para poder resolver el sistema se escoge λ a nuestra conveniencia, se discutirá varias opciones más adelante. Si hacemos λ independiente de τ, las primeras seis ecuaciones son independientes de τ y forman un sistema cerrado de ecuaciones para las seis variables: las componentes de x y p. Para la Ecuación Iconal se pueden encontrar los rayos sin determinar el tiempo de propagación a lo largo de los rayos.
Una formula más compacta de las ecuaciones características, usando notación vectorial, es asumir que λ = 1/2 y σ como el parámetro. Esta selección está motivada con el fin de eliminar el factor 2 que aparece en varias de las ecuaciones, entonces se simplifican:
Realizando un análisis dimensional de σ en este caso, λ = 1/2, σ es un parámetro con unidades de [L2 /T ]. En la propagación en modelos 2.5D, la selección de σ surge naturalmente como el parámetro que describe los efectos fuera del plano.
Las ecuaciones características son entonces un sistema de ecuaciones diferenciales ordinarias que puede ser resuelto utilizando, en algunos casos, métodos analíticos, por ejemplo, para medios homogéneos, donde la solución es una segmento de recta o para medios con un gradiente constante de velocidad, por ejemplo, cuya solución da un arco de círculo. Para el caso general (medios heterogeneos y/o anisótropos), se requiere de métodos numéricos, el método de Runge Kutta es una metodología estándar en estos casos, entre otros (ver [10] y [12]). La solución a dicho sistema es llamado en la literatura como trazado de rayos. Seguidamente, se analiza un tipo de caso simplificado y generalizaciones que nos permiten abordar algunos problemas que surgen en la exploración de hidrocarburos.
4. EL TRAZADO DE RAYOS COMO LA SOLUCIÓN A UN SISTEMA DE ECUACIONES NO-LINEALES
Se va a describir en esta sección una posible representación de un modelo del subsuelo, el cual consiste en un dominio en dos dimensiones R, o por un dominio tridimensional, con simetría cilíndrica en relación a un eje perpendicular al plano de interés (llamado en la literatura geofísica como modelo 2.5D). Por tanto, el modelo matemático es un conjunto cerrado en dos dimensiones, subdividido en una partición de subconjuntos o sub-regiones para los cuales los parámetros físicos del modelo (en particular la velocidad v (x) o la densidad ρ (x), donde x es un punto arbitrario en la subregión) son constantes.
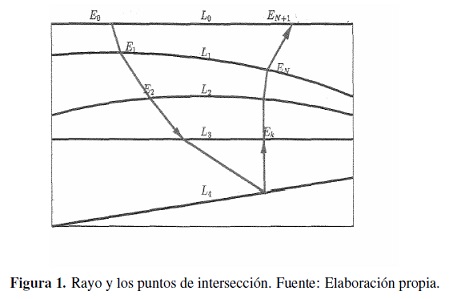
Se asume que el modelo de la Tierra está contenido dentro de una caja cerrada, figura 1, definida por, , además las interfaces entre las subregiones y la superficie de la Tierra son curvas de clase C 2, es decir, con continuidad en la segunda derivada en intervalos cerrados Di = [ai, bi ] ε [a, b],, representadas como
donde NI es el total de interfaces, es decir,
todo el dominio se dividió en NR subconjuntos disjuntos, como se muestra en la Figura 1,
de esta forma construyendo una partición del dominio R. Llamaremos a estos subconjuntos
como subregiones o capas sedimentarias, en el léxico de la geociencia.
En términos formales, tenemos una colección de subconjuntos cerrados Rj, que satisfacen las siguientes condiciones
El ´índice i = 0 denota la interface que representa la superficie de la Tierra y el dominio de interés serápara z ≥ 0, en Geofísica el eje Z está orientado positivamente en dirección al subsuelo de la Tierra.
Se define al conjunto Int como la colección de ´índices {1, 2, • • •, NI }, que representan todas las interfaces. Similarmente, se define Reg., como la colección de ´índices {1, 2, • • •, NR } que representa las subregiones. Se utilizaran estas ideas para definir el concepto de signatura más adelante.
4.1. Trazado de un Rayo dados dos puntos
Para la solución cinemática del problema, es decir, para encontrar los tiempos de tránsito de un rayo de un punto a otro, tenemos en cuenta:
- Un rayo que une dos puntos que están localizados en una región donde la velocidad es suave1 satisface la Ecuación Iconal, particularmente, para el caso de la velocidad constante, la solución de la Ecuación Iconal, es un segmento de línea, dentro de cada subregiÓ n.
- Cuando ocurre una discontinuidad en la velocidad de propagación de una subregión Ri a otra Rj2 , el rayo satisface la Ley de Snell en las intersecciones con las interfaces.
1 Usualmente funciones con segundas derivadas continuas en la subregión
Formalmente, el problema puede ser escrito como: dados dos puntos E0 (localización de la fuente) y EN+1 (localización del receptor), ambos localizados en interfaces fijas3
, no necesariamente en la superficie de la Tierra, L0 . Además se define una secuencia finita de enteros positivos i1, i2, • • •, iN que representan los índices de las N interfaces interceptadas
por la trayectoria del rayo. Entonces el objetivo es encontrar puntos
Ek ε para k =
1, 2, • • •, N . En otras palabras, el problema es equivalente a encontrar la abscisa de cada
uno de los puntos de intercepción, de la k-ésima interface encontrada por el rayo (en total N
abcisas). En estos puntos de intersección, la Ley de Snell es satisfecha.
Un rayo puede ser descrito entre dos puntos consecutivos de intercepción como un segmento de línea de recta [Ek−1, Ek ] para k = 1, 2, • • •, N + 1, como se muestra en la Figura 1, para un modelo sísmico 2D. Observemos que el rayo posee N puntos de intercepción con las interfaces, además de los puntos en los extremos (fuente y receptor). Esto nos da un total de N + 2 puntos, que generan + 1 segmentos (estas cantidades son importantes en la implementación computacional de los algoritmos para realizar el trazado de rayos).
4.2. Signatura de un Rayo
En Sismología o en Sísmica de exploración, la signatura de un rayo es una forma de representar la naturaleza de rayo, es decir, el tipo de onda y las interfaces interceptadas. Para un medio elástico isótropo, dos tipos de ondas se generan, una denominada Onda P, con polarización longitudinal, o sea que la partícula vibra en la dirección de la onda y otra onda denominada Onda S, con polarización transversal, o sea, que las partículas del medio son perpendiculares al desplazamiento de la onda. Estas dos ondas viajan a velocidades diferentes VP, velocidad de la Onda P y VS, velocidad de la Onda S, donde se cumple que Vp > VS .
Otra de las caracterizaciones del rayo está dado por las interfaces que el rayo intercepta, es decir, donde hay discontinuidades en las velocidades. Cada vez que el rayo intercepta una interface se produce el denominado fenÓ meno de la conversiÓ n. Es decir, el rayo puede cambiar su naturaleza de un tipo a otra (de P a S o viceversa) o permanecer del mismo tipo.
En este trabajo solo se considera el caso de la onda P sin conversiÓ n, es decir, solo se considera ondas de tipo P en cada segmento del rayo. Sin embargo, el caso más general multi-componente, o sea el de las ondas convertidas, se puede considerar sin problema con estas técnicas. Para el caso considerado, la signatura identifica las interfaces que el rayo intercepta en un modelo dado (ver [15] ).
Fijada una signatura, se puede definir una relación de equivalencia en el conjunto de rayos del modelo sísmico. Por ejemplo, dos rayos están en la misma relación de equivalencia, si para ambos rayos las fuentes y los receptores de cada uno están en las mismas interfaces, respectivamente. Además ambos rayos interceptan las mismas interfaces y atraviesan las mismas regiones. La idea, como se explica más adelante, obteniendo un rayo de la clase podemos obtener los otros rayos por el llamado método de continuación en las fuentes o en los receptores.
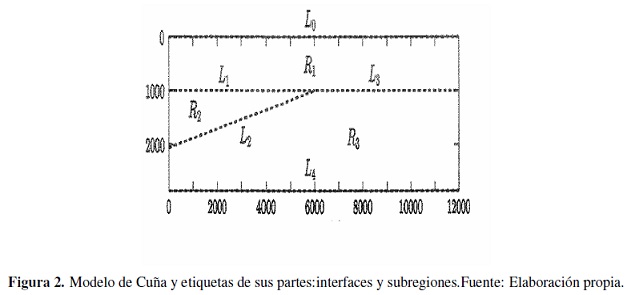
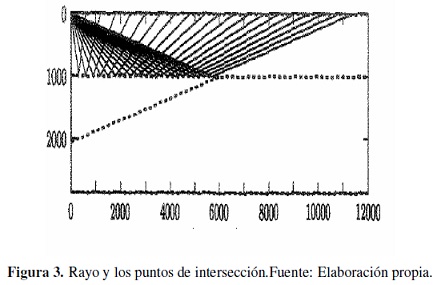
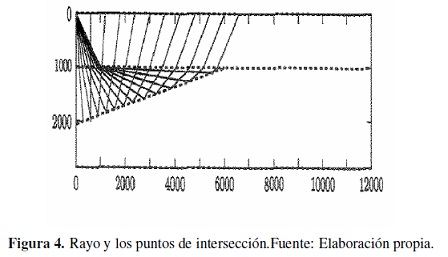
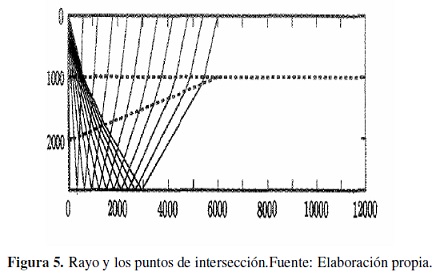
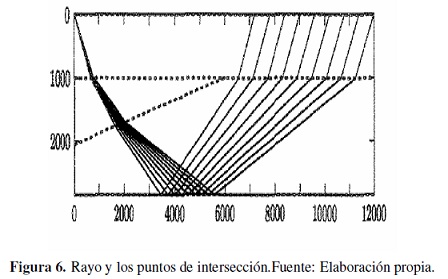
Por ejemplo, en las Figuras 3, 4,5 y 6, se observan cuatro clases de rayos diferentes para un modelo sísmico de una estructura geológica, tipo cuña, donde las interfaces del modelo están cauterizadas por el conjunto {L0, L1, L2, L3}. En cada caso la fuente está localizada en las coordenadas (0, 0), en la interface que representa la superficie, L0, también los receptores están localizados en L0 . La figura 3 representa unos rayos pertenecientes a la clase de equivalencia dada por la signatura [L0, L1, L0 ], la figura 4 representa unos rayos pertenecientes a la clase de equivalencia dada por [L0, L1, L2, L1, L0 ], la figura 5 representa unos rayos pertenecientes a la clase de equivalencia dada por la signatura [L0, L1, L2, L3, L2, L1, L0 ], y la figura 6 representa unos rayos pertenecientes a la clase de equivalencia dada por [L0, L1, L2, L3, L1, L0 ].
4.3. El Método de Continuación en el Trazado de Rayos
El problema de construir un rayo, la solución en las altas frecuencias, entre una fuente y un receptor, en un modelo por bloques, se puede plantear en forma equivalente como la solución de un sistema no-lineal ([9],[15]). Dado que el interés es encontrar múltiples rayos, cambiando fuentes y receptores, se puede utilizar el llamado método de Continuación para volver el problema computacionalmente eficiente .
El sistema no-lineal que surge de este problema depende de unos parámetros, en este caso las velocidades de los bloques por donde viaja el rayo, la posición de la fuente y del receptor, respectivamente. El método clásico de resolución de estos problemas, es el Método de Newton, el cual posee convergencia cuadrática [1]. El inconveniente que posee dicho método está en la dependencia del método en la aproximación inicial al problema. En el caso del modelado sísmico, esto implica resolver múltiples sistemas no-lineales, donde cada sistema proviene de una perturbación de los parámetros, por ejemplo la ubicación de los receptores. El método de continuación permite a partir de la solución de un sistema, encontrar una mejor aproximación uncial para el sistema perturbado, es decir, modificando la ubicación en los receptores [8].
La solución al sistema planteado, es entonces los puntos coordenados que describen el rayo. En este caso tenemos un problema de tipo determinístico, puesto que se supone que las velocidades son conocidas, lo cual en la práctica no se tiene sino una estimación n, a veces con niveles apreciables de incertidumbre.
5. PROBLEMAS NUEVOS
Vamos a finalizar planteando unos futuros trabajos posibles para investigadores y/o estudiantes interesados.
5.1. Uso de aritmética Intervalar
Se propone un trabajo donde el sistema que surge de la construcción de un rayo, dado un modelo, la posición de una fuente y de los receptores, los parámetros del modelo, las velocidades de las subregiones, están dadas por intervalos, no por números[1]. Esto estáenmarcado dentro de la llamada computación intervalar y daría múltiples soluciones al problema, en el sentido de la incertidumbre.
Esto es conveniente en los problemas de Geofísica de Exploración o Producción n, pues se podría dar una interpretación a la solución del mismo, ya no como un camino dado, sino como múltiples caminos posibles. Lo cual a su vez implica múltiples soluciones o imágenes sísmicas correspondientes al problema. Este punto de vista es más realista pues el usuario de este tipo de experimentos ya puede considerar diferentes escenarios donde la realidad del subsuelo puede encontrarse. En la práctica solo información adicional puede ir acotando la solución al problema y las soluciones del modelo de incertidumbre le darán al usuario posibilidades para la toma de decisiones.
5.2. Uso de teoría de Sistemas diná micos
Este posible trabajo parte del hecho de que el trazado de rayos es un proceso muy sensitivo a la posición de fuentes y receptores, motivada en el uso de herramientas de la Teoría de Sistemas Dinámicos Finitos ([17]) para estudiar la sensibilidad de las ecuaciones a las perturbaciones de los parámetros de las mismas. Esto puede ser crítico en ciertos tipos de geometrías del subsuelo, como la geología del subsuelo en el piedemonte Llanero colombiano, donde fácilmente se puede perder las iluminación de determinadas estructuras por una posición perturbada de las fuentes o receptores.
El objetivo de este tipo de investigación entonces es cuantificar la sensibilidad del sistema no-lineal a las perturbaciones de los parámetros, por ejemplo, cambios en la geometría del modelo o cambios en las velocidades o posiciones de fuentes o receptores. En la literatura científica se ha mostrado que los sistemas no-lineales que provienen de la teoría de rayos son altamente inestables a cualquier cambio en los parámetros. La teoría de los sistemas dinámicos puede darnos una aclaración de la estabilidad del problema [3].
6. CONCLUSIONES
A partir de la Sísmica de Exploración o producción n, utilizando la Ecuación Elastodinámica, se obtiene un sistemas de ecuaciones diferenciales ordinarias (EDO) denominadas Ecuaciones Características, que representan las trayectorias donde la energía fluye en un medio continuo. Dichas trayectorias se pueden obtener, dados los parámetros del modelo, utilizando métodos numéricos. En particular, para el caso de un modelo compuesto por bloques de velocidad constante, este sistema de EDO se transforma en un problema de resolver un sistema de ecuaciones no-lineales.
Este sistema es altamente sensitivo a los valores de los parámetros, en particular, a las posiciones de fuentes y receptores. Esto tiene bastante impacto en los programas de adquisición sísmica, puesto que unos cambios en las posiciones de estos datos pueden implicar la falta de iluminación de un reflector de interés. Esto motiva la aplicación de la Teoría de los sistemas dinámicos al estudio de los mismos y el analizar la estabilidad de los mismos para diferentes valores de los parámetros. Además, el parámetro representado por las velocidades de propagación en cada subregiÓ n, incide en las trayectorias del modelo. Puesto que dichos parámetros no son conocidos, a diferencia de la posición de fuentes y receptores, que son controlados en el experimento, se asumen unos valores. Estos datos son usualmente estimados, basados en la experiencia o en técnicas de procesamiento sísmico. Esto nos lleva a sugerir el uso de la aritmética intervalar combinada con elementos de Métodos Numéricos, lo cual permitiría realizar nuevas interpretaciones de la modelación sísmica y obtener escenarios posibles de la respuesta sísmica de los modelos, más realista que considerar modelos con parámetros determinísticos.
A MOTIVACIÓN PARA LOS MÉTODOS ASINTÓTICOS
Este apéndice se apoya en [6] y [5] y considera el asunto de las altas frecuencias y las escalas. Considerando la transformada de Fourier inversa dada por:
donde la expresión a la derecha representa una onda progresiva en el dominio del tiempo, es decir, F (t), es la transformada inversa de ωβ, y esta se propaga en la dirección de incremento de τ(x). Al dividir por potencias superiores de (iω), en el dominio de la frecuencia, esto representa integraciones sucesivas en el dominio temporal, que pueden ser interpretadas como elementos de una sucesión cada vez más suaves
donde la flecha representa integración en el dominio del tiempo y δ (t) es la función Delta de Dirac, H (t) es la función de Heaviside y r (t) es la función rampa. En otras palabras, el primer término de la serie (2), representa la transformada de Fourier de la parte más singular de la solución n, asociada a las altas frecuencias, mientras que los términos posteriores, representan contribuciones más suaves, o sea, asociadas a las bajas frecuencias, a la solución de la ecuación de la Onda P
Utilizando la versión en el dominio de la frecuencia de la Ecuación de Onda, es decir, la Ecuación de Helmholtz (12), se substituye la aproximación asintótica, con coeficientes desconocidos, en la ecuación . A partir de esta substitución n, se obtienen ecuaciones diferenciales para el tiempo de tránsito y para los coeficientes de amplitud. Realmente no es una serie convergente, por el contrario, se tiene una serie asintÓ tica, la cual, en general, al colocar mayor número de términos diverge del valor al cual se quiere aproximar.
A.1 Una definición formal de esta idea
Definición La serie es una aproximación de F (ω), en el punto singular, ω = ω0 ,
(ver [5])y escribimos
si para todo N ε Z+0 y para todo ε > 0, existe un δ > 0 tal que si ω ε Bδ (ω0 ), entonces
Es decir en una vecindad de un valor frecuencial, ω0, la suma parcial está cerca al valor de la función aproximada. En la Ó ptica geométrica, ω0, representa un valor infinito, es decir, para altas frecuencias podemos aproximar la función con unos pocos términos.
Al substituir la serie asintótica en la Ecuación de Helmholtz, obtenemos:
igualando a cero cada factor de (iω), obtenemos la Ecuación Iconal (3) y las Ecuaciones de Transporte (4 y 5).
B EL MÉTODO DE LAS CARACTERíSTICAS
Se quiere resolver una ecuación de la forma
Donde x, y y z son variables independientes y u, ux, uy y uz son la solución y sus respectivas derivadas parciales con respecto a x, y, y z. En nuestro caso la variable independiente u corresponde al tiempo de transito τ de la ecuación Iconal, y ux, uy y uz corresponden a las componentes del gradiente de τ Se puede interpretar la ecuación
como una función en el espacio de , y considerar como una función que define una familia de superficies de nivel en el espacio, una superficie para cada valor de u. El gradiente de u describe vectores normales a las superficies de nivel. Para la ecuación Iconal las superficies de nivel son superficies de igual tiempo de tránsito (frentes de onda) con el gradiente de u (dirección del rayo) en la dirección normal a las superficies de tiempo de tránsito.
Seguidamente, se deriva un sistema de EDO (Ecuaciones Diferenciales Ordinarias) que nos dice como moverse de una superficie de nivel u a otra. La solución a las coordenadas espaciales describe curvas en el espacio físico. Estas curvas son llamadas curvas características. La solución a los componentes del gradiente se interpretan como la forma en el que el vector cambia a lo largo de cada curva, mientras que la solución de u representan como cambia la variable u a lo largo de las características.
Las características se describen en términos de un conjunto auxiliar de variables: dos para etiquetar cada curva característica y una tercera que actúa como variable a lo largo de la curva (puede ser longitud de arco o tiempo ). Usando una notación más general se describen las variables espaciales como x = x1, y = x2 y z = x3, respectivamente, y las componentes del gradiente de u como:
respectivamente.
Reescribiendo la expresión general de F, en términos de las nuevas variabas, se tiene:
Para el anterior sistema de EDO de primer orden, la ecuación F = 0 puede ser interpretada como describiendo una superficie embebida en un espacio de siete dimensiones. A partir de esto se va a deducir el sistema de las siete ecuaciones EDO.
Se considera una pequeña perturbación a lo largo de la superficie, F = 0, es decir, a partir de un punto x de la superficie se obtiene una perturbación al punto en la superficie, x + δx. Por tanto, se produce una variación en u y p, y además se cumple que
Como F = 0 en el punto inicial, si se aplica una aproximación de Taylor de primer orden en las perturbaciones, se obtiene:
donde las derivadas parciales son evaluadas en (x, u, p)
Además como u y p dependen de x, se pueden escribir las perturbaciones de estas cantidades, en términos de la perturbación en x
Substituyendo los resultados de ( 22) en ( 21), se obtienen:
y como los diferenciales son arbitrarios, la Ecuación (23) se cumple para cualesquier variación, en particular, si x = (dx1, 0, 0) x = (0, dx2, 0) x = (0, 0, dx3 ), por tanto se debe cumplir que
La ecuación anterior se puede reescribir como
la cual es del llamado tipo cuasi-lineal [11] Finalmente resolviendo por un método estándar: se define un vector
donde λ es el factor de escala entre las longitudes de los dos vectores. Se reescribe el producto punto como
y la Ecuación (25) como
En total se tienen seis (6) ecuaciones entre (26) y (28), las primeras tres definen una dirección en el espacio y las uúltimas tres definen la razón de cambio de p en esa dirección n. Se puede visualizar que existen unas curvas que llenan el espacio y asociado a ellas existen vectores tangentes, estas curvas son llamadas curvas características. En cada punto de una curva característica, el vector p, define una dirección normal a la superficie de nivel de u. Finalmente, se requiere una ecuación que nos describa la razón de cambio de u a lo largo de las características.
Utilizando la regla de la cadena se obtiene:
En cada punto de una curva característica, el vector p, define una dirección normal a la superficie de nivel de u.
Reescribiendo todas las EDO explícitamente, se tiene que
RECONOCIMIENTOS
Agradezco a los organizadores del VI Simposio de Optimización en Septiembre del 2013, por su apoyo para participar en el evento y al profesor JoséAlberto Rua, director del Departamento de Ciencias Básicas de la Universidad de Medellín por el apoyo y los tiempos que el autor dispuso para la realización del documento.
REFERENCIAS
- Azmy S. Ackleh, E.J. Allen, R.B. Hearfott, and P. Seshaiyer. Classical and Modern Numerical Analysis. Chapman & Hall/CRC, Boca Raton, FL USA, 2010.
- K. Aki and P Richards. Quantitative Seismology. Theory and Methods, Volume I. W.H. Freeman and Company, New York, 1980.
- V.I. Arnold. Mathematical methods of Classical Mechanics. Springer-Verlag, Nueva York, 1978.
- V.M. Babic and V.S. Buldyrev. Short-wavelenght diffraction theory (Asymptotic methods). Springer, Berlin, 1991.
- N. Blestein. Mathematical Methods for Wave Phenomena. Academic Press, New York, 1984.
- N. Blestein, J.K. Cohen, and J.W.H. Stockwell Jr. Mathematics of Multidimensional Seismic Imaging. Springer, Berlin, 2001.
- A. Bona and M. Slawinski. Wavefronts and Rays: As Characteristics and Asymptotics. World Scientific Publisher Company, Pte. Ltd, Hackensack, NJ, USA, 2011.
- J.E. Dennis and R.B. Schnabel. Numerical Methods for Unconstrained Optimization. Prentice Hall, Englewood Cliffs, New Jersey, 1983.
- P. Docherty. A Fast Ray Tracing Routine for laterally Inhomogeneous Medsi, CWP-018. PhD thesis, Colorado School of Mines, Golden, Colorado, EUA, 1985.
- P. Docherty. Ray theoretical modeling, migration and inversion in two-and-one-half-dimensional layered acoustic media, Research Report number CWP-051. Center for Wave Phenomena, Colorado school of Mines, Golden, 1987.
- Lawrence C. Evans. Partial Differential Equations: Second Edition. AMS, Providence, Rhode Island, USA, 2010.
- S. Gray. Efficient traveltime calculations for kirchhoff migration. Geophysics, 51:1685–1688, 1986. [13] V. Cˆ erveny. Seismic Ray Theory. Cambridge University Press, Cambridge, 2001.
- V. Cˆ erveny, I.A. Molotkov, and Psencik. Ray Method in Seismology. Universita Karlova, Praha, 1977. [15] H.B. Keller and D.J. Perozzi. Fast seismic ray tracing. SIAM J. APPL. MATH., 43(4):981–992, 1983.
- Y. Kravtsov and Y.I. Orlov. Geometrical Optics of Inhomogeneous Media. Springer Verlag, Berlin, 1990.
- Carlos César Piedrahita. Generalização do Mé todo de Continuação no Traçamento de Raios utilizando o Conceito dos Autoˆ matos Finitos. PhD thesis, Universidad Estadual de Campinas, Campinas, SP, Brasil, 2002.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.


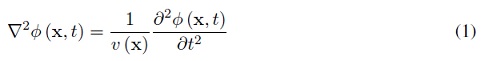
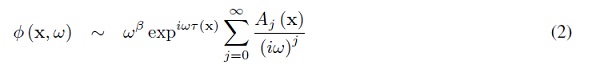

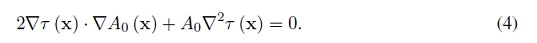
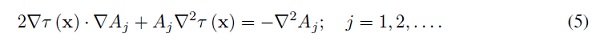

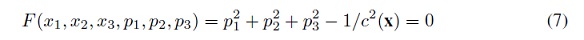
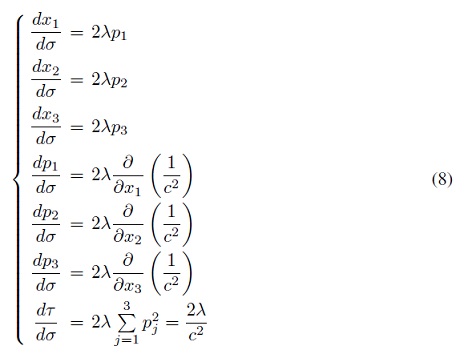
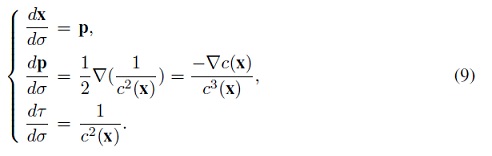
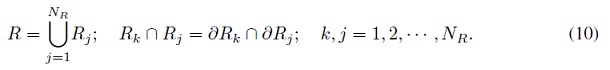
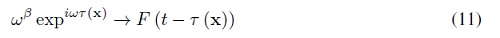
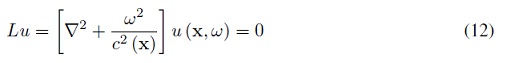


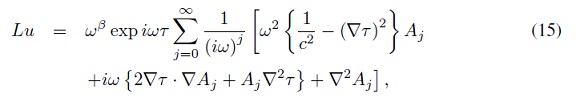

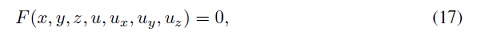

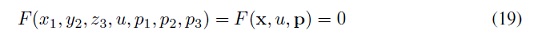
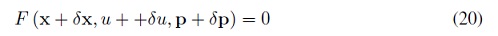
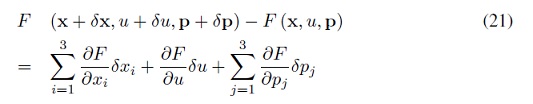
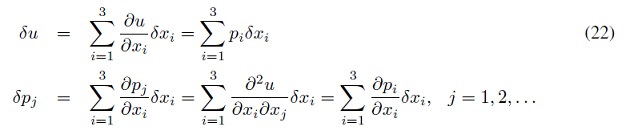
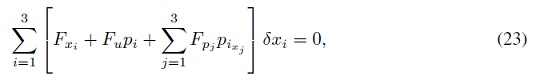
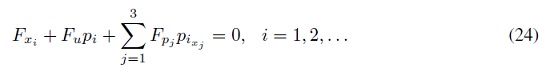
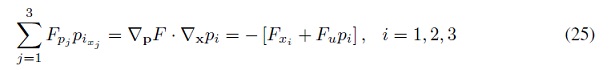

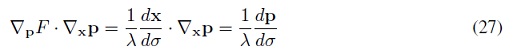

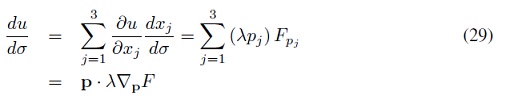
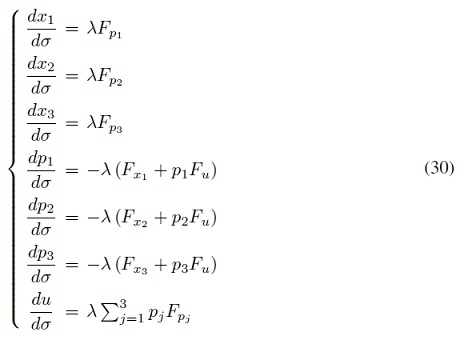




2.jpg)










