DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.3.a06Published:
2016-10-09Issue:
Vol. 21 No. 3 (2016): September - DecemberSection:
Computational IntelligenceMétrica de Hausdorff en el ambiente difuso
Hausdorff metric in the fuzzy environment
Keywords:
Compact sets, fuzzy sets, Hausdorff metric (en).Keywords:
Conjuntos compactos, conjuntos difusos, métrica de Hausdorff (es).Downloads
References
T. M. Apostol. Mathematical Analysis. Addison-Wesley Publishing Company. Massachusetts. 1981.
M. Barnsley. Fractals Everywhere. Academic Press. San Diego. 1988.
P. Diamond y P. Kloeden. Metric Spaces of Fuzzy Sets. World Scientific. Singapore. 1994.
D. Dubois y H. Prade. Fuzzy Sets and Systems: Theory and Applications. Academic Press. 1980.
W. Gonz´alez. Una aproximaci´on a los conjuntos alcanzables de una inclusi´on diferencial difusa.
Revista Integraci´on, vol. 30, n´um. 1, 2012, pp. 57-74.
C. Castaing y M. Valadier. Convex Analysis and Measurable Multifunctions. Springer-Verlag. 1932.
E. Kreyszig Introductory Functional Analysis with Applications. John Wiley & Sons. Canada 1978.
V. Lakshmikanthan y R.N. Mohapatra. Theory of Fuzzy Differential Equantions and Inclusions. Taylor
y Francis. 2003.
J. Rodr´ıguez-Lpeza y S. Romaguera. On completion of fuzzy metric spaces. Fuzzy Sets and Systems.
Vol.130, 2002, pp.399-404283.
J. Rodr´ıguez-Lpeza y S. Romaguera. The Hausdorff fuzzy metric on compact sets. Fuzzy Sets and
Systems. Vol.147, 2004, pp.273283.
S. S. Silva. Modelo Basado en L´ogica difusa para la comparaci´on de objetos con atributos imprecisos.
Universidad Centro Occidental Lisandro Alvarado. 2013.
L. A. Zadeh. Fuzzy Sets. Inf. Control 8. 1965.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.3.a06
Métrica de Hausdorff en el ambiente difuso
Hauddsorf Metric in the Fuzzy Environment
Carlos Orlando Ochoa Castillo
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. oochoac@udistrital.edu.co
Laura Victoria Forero Vega
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. lau_forero85@hotmail.com
Recibido: 28-04-2015. Modificado: 01-09-2015. Aceptado: 26-07-2016
Resumen
Contexto: De manera intuitiva, se ha establecido el concepto de conjunto como una colección distinta de elementos, esto es, un conjunto se determina vía la relación de pertenencia de un elemento de un universo al conjunto. La situación, por supuesto, es si pertenece o no pertenece; en un subconjunto difuso a cada elemento del universo se le asocia con un grado de pertenencia, que es un número entre 0 y 1. Los subconjuntos difusos se establecen como una correspondencia entre cada elemento del universo y un grado de pertenencia.
Método: El estudio fue basado en trabajos anteriores como artículos o libros, en donde autores exponen ideas sobre la importancia de los subconjuntos difusos y la necesidad de crear con ellos nuevas teorías y espacios.
Resultados: Al combinar dos teorías, se genera un nuevo ambiente de estudio que permite afirmar que
la distancia de Hausdorff corresponde, extiende y ajusta la noción de distancia entre subconjuntos no
vacíos compactos en el ambiente de los espacios métricos, mas exactamente en 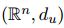 .
.
Conclusiones: La construcción realizada permite obtener un espacio métrico con varias cualidades, en donde se puede afirmar que son consequencia del objeto de estudio inicial.
Palabras claves: Conjuntos compactos, conjuntos difusos, métrica de Hausdorff.
Idioma: Español.
Abstract
Context: Intuitively, the concept the set has been established as a collection of different elements, that is, a set is determined via the relationship of membership of an element of a universe as a whole. The situation, of course, is whether or does not belong; in a diffuse to each element subset of the universe it is associated with a degree of membership, which is a number between 0 and 1. The fuzzy subsets are established as a correspondence between each element of the universe and a degree of membership.
Method: The study was based on previous work as articles or books, where authors present ideas about the importance of fuzzy subsets and the need to create with them new theories and spaces.
Results: By combining two theories, a new study environment that allows state that corresponds Hausdorff
distance, extends and adjusts the notion of distance between nonempty compact subsets in the
environment of metrics spaces, more accurately generated in 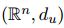 .
.
Conclusions: The construction carried out allows a metric space with several qualities, where we can say that are the object consequence initial study.
Keywords: Compact sets, fuzzy sets, Hausdorff metric.
1. Introduction
En 1965 Zadeh introdujo la noción de conjunto difuso (ver [12]) debido a que la mayoria de la veces, las clases de cosas encontradas en el mundo fisico real no tienen precisamente un criterio de pertenencia. Esta observación pone en conexión la existencia de las representaciones mentales de la realidad y representaciones matematicas habituales de los mismos y fue el punto de partida hacia el desarrollo de los conjuntos difusos.
En 1980 Dubois y Prade definieron las distancia entre dos conjuntos difusos (ver [4]); luego Puri
y Ralescu en 1983 expusieron una introducción de utilizar la distancia de Hausdorff entre conjuntos
difusos; aunque la mayor referencia fue expuesta por Diamond y Kloeden [3] en 1994. Lo anterior
condujo a que más adelante y mientras se investigaba problemas de sistemas dinamicos sin solución,
Laksmikanthan y R.N Mohapatra [8] en 2003 publicaron lo hecho por Diamond y Kloeden
para  como medio de resolver dichos problemas.
como medio de resolver dichos problemas.
Este artículo tiene como finalidad el estudio de la métrica de Hausdorff, construída inicialmente
en el ambiente  y luego extendida a una clase particular de subconjuntos difusos de
y luego extendida a una clase particular de subconjuntos difusos de
 , obteniendo
un nuevo espacio métrico. Se parte de una definición de distancia entre un punto y un
conjunto, con ello se edifica paso a paso la métrica de Hausdorff, igualmente se exhibe para el ambiente difuso.
, obteniendo
un nuevo espacio métrico. Se parte de una definición de distancia entre un punto y un
conjunto, con ello se edifica paso a paso la métrica de Hausdorff, igualmente se exhibe para el ambiente difuso.
En la primera sección, Métrica de Hausdorff, se muestra la construcción del espacio métrico
(Kn, dH), de los subconjuntos compactos de  con la métrica de Hausdorff y se exponen algunas de sus propiedades; en la sección. El espacio En,
se describe un espacio particular de conjuntos difusos de
con la métrica de Hausdorff y se exponen algunas de sus propiedades; en la sección. El espacio En,
se describe un espacio particular de conjuntos difusos de  y algunas características; en la tercera sección. El espacio métrico ( En, d ) , se muestra
el espacio resultante al relacionar la teoría de las dos secciones anteriores; en la ultima sección,
Comparación con otros espacios métricos, se exponen otras distancias definidas en subconjuntos
difusos y se realiza una comparación con el trabajo realizado anteriormente.
y algunas características; en la tercera sección. El espacio métrico ( En, d ) , se muestra
el espacio resultante al relacionar la teoría de las dos secciones anteriores; en la ultima sección,
Comparación con otros espacios métricos, se exponen otras distancias definidas en subconjuntos
difusos y se realiza una comparación con el trabajo realizado anteriormente.
2. Métrica de Hausdorff
A partir del espacio métrico 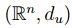 , es decir para
, es decir para 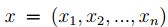 y
y 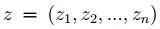 elementos de
elementos de 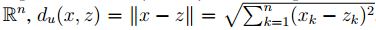 ,[7], [8]; se inicia
la construcción de la métrica de Hausdorff.
,[7], [8]; se inicia
la construcción de la métrica de Hausdorff.
Definición 2.1 Sea x un punto de  y A un subconjunto no vacío de
y A un subconjunto no vacío de
 , la distancia d(x, A) del punto x a A es
, la distancia d(x, A) del punto x a A es
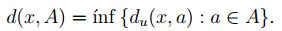
En los espacios métricos, se tienen diferentes tipos de colecciones de sus elementos de acuerdo a unas condiciones, estos son, entre otros, los conceptos de vecindad, bola abierta, bola cerrada y adherencia, que son como en [1].
Proposición 2.1 Sea x un punto en  y A
un subconjunto no vacío de
y A
un subconjunto no vacío de  entonces:
entonces:
1. d ( x , A ) ≤ 0,
2. d ( x , A ) = 0 si y solo si x ∈ Ā
Prueba.
1. Por ser 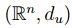 , un espacio métrico
, un espacio métrico 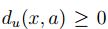 para todo
para todo 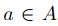 , luego por propiedades del ínfinito, ínf
, luego por propiedades del ínfinito, ínf 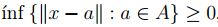 ,así
,así 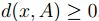 .
.
2. Sea 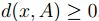 y se supone que
y se supone que 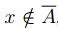 , esto es,
existe
, esto es,
existe 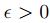 tal que
tal que 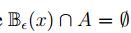 lo que indica que
lo que indica que
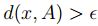 , lo cuál es una contradicción.
, lo cuál es una contradicción.
Recíprocamente 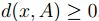 , esto es , para todo
, esto es , para todo 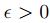 se tiene
se tiene 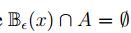 , en particular, para todo
, en particular, para todo 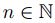 se tiene
se tiene 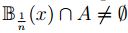 . Lo que indica que,
. Lo que indica que, 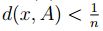 y
y
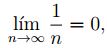
entonces 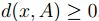 .
.
Definició 2.2 Sean A y B dos subconjuntos acotados y no vacíos de  ,
la separación de Hassdorff de B a A es:
,
la separación de Hassdorff de B a A es:
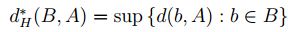 .
.
Este concepto tiene una definición equivalente, 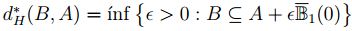 , aparece [2]
su demostración donde
, aparece [2]
su demostración donde 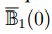 es la bola cerrada de centro 0 y radio 1 de
es la bola cerrada de centro 0 y radio 1 de  .
.
Proposición 2.2 Sean 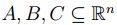 no vacíos y acotados,entonces
no vacíos y acotados,entonces
1. 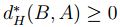
2. 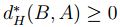 si y solo si
si y solo si 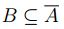
3. 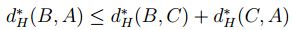
Prueba.
1. Como 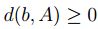 para todo
para todo 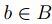 , por propiedades del supremo ([1]),
, por propiedades del supremo ([1]),
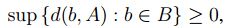 .
.
en consecuencia 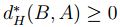 .
.
2. Se supone que 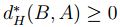 , esto es ,
, esto es , 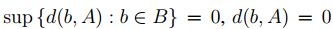 para todo
para todo
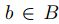 ; por la proposición 2.1
; por la proposición 2.1 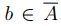 y como es para
todo elemento de B, se obtiene quue
y como es para
todo elemento de B, se obtiene quue 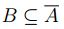 .
.
Recíprocamente , si 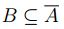 , por la proposició 2.1,
, por la proposició 2.1,
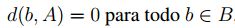 .
.
en general, 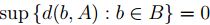 , luego
, luego 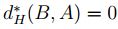 .
.
3. Sean 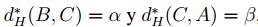 , entonces
, entonces 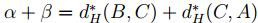 , esto es,
, esto es,
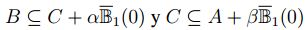 .
.
así
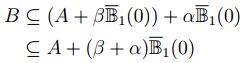
con lo cual,
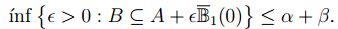 .
.
En consecuencia,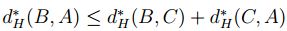 .
.
La separación de Hausdorff se constituye en un instrumento eficaz en la consecución de una métrica, claro está con algunas propiedades adicionales en el contexto.
Definición 2.3 Sean A y B dos subconjuntos no vacíos y acotados de  , la distancia de Hausdorff entre A y B es
, la distancia de Hausdorff entre A y B es
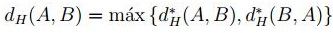 .
.
Con esta definición, la distancia Hausdorff satisface la simetría, pero aun falta agregar condiciones
adicionales al ambiente para obtener la estructura de espacio métrico; así, se restringe, aun más,
la naturaleza de los subconjuntos de  en consideración. El resultado que sigue, se aplica a un universo específico con alguna incidencia en los demás.
en consideración. El resultado que sigue, se aplica a un universo específico con alguna incidencia en los demás.
Proposición 2.3: 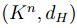 , la colección de subconjuntos compactos de
, la colección de subconjuntos compactos de
 con la distancia de Hausdorff, es un espacio métrico.
con la distancia de Hausdorff, es un espacio métrico.
Prueba. Sean 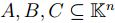 no vacíos.
no vacíos.
- Se afirma que
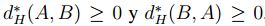 , entonces máx
, entonces máx 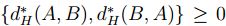 ,
luego
,
luego 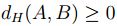
Sea
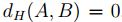 , por propiedades de máximo
, por propiedades de máximo 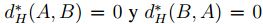 , se tiene,
, se tiene,
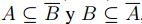 , dado que A y B son cerrados de
, dado que A y B son cerrados de  entonces
entonces
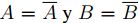 , es decir, A = B.
, es decir, A = B.Recíprocamente, sea A = B, dado que A , B son subconjuntos cerrados de
 ,
,
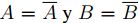 , de modo que
, de modo que 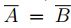 , esto es,
, esto es, 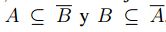 , se tiene
, se tiene 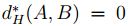 y
y 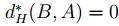 , luego
, luego  .
. - Se tiene que
- Como
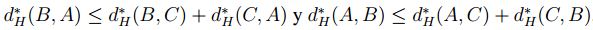 , entonces
, entonces
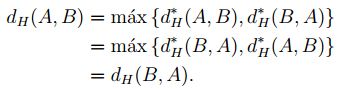 .
.
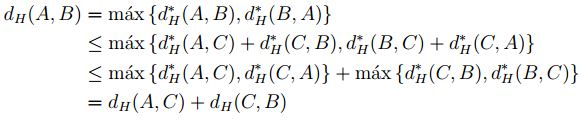 .
.
De modo que la distancia de Hausdorff mide cuan lejos están uno de otro dos subconjuntos compactos de  . Además, ( Kn , dH ) cuenta con las propiedades de la completitud y
. Además, ( Kn , dH ) cuenta con las propiedades de la completitud y 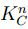 , la colección
de subconjuntos compactos y convexos de
, la colección
de subconjuntos compactos y convexos de  , es un subconjunto cerrado en él; para ver esto, es necesario el resultado que sigue,
, es un subconjunto cerrado en él; para ver esto, es necesario el resultado que sigue,
Proposición 2.4. Sean A , B subconjuntos no vacios de K n , si 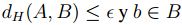 , existe
, existe 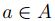 tal que
tal que 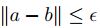
Prueba. Sean 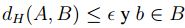 , supongamos que para todo
, supongamos que para todo 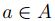 se tiene
se tiene 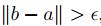 , en consecuencia ínf
, en consecuencia ínf 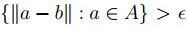 , es decir,
, es decir,
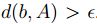 . Por otro lado,
. Por otro lado, 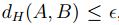 , con lo cual
, con lo cual
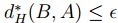 , por tanto,
, por tanto, 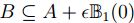 . Así, para todo
. Así, para todo
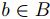 , se tiene que
, se tiene que 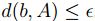 , lo que contradice el supuesto.
, lo que contradice el supuesto.
La prueba del siguiente teorema aparece en [2]
Teorema 2.1 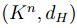 es un espacio métrico completo1, además si
es un espacio métrico completo1, además si 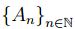 es una sucesión de Cauchy en K n , su límite es
es una sucesión de Cauchy en K n , su límite es
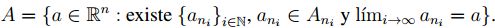
Teorema 2.2 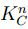 , la colección de todos los conjuntos convexos compactos de
, la colección de todos los conjuntos convexos compactos de  , es un subconjunto cerrado del espacio métrico ( K n , dH ).
, es un subconjunto cerrado del espacio métrico ( K n , dH ).
Prueba. Sea 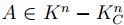 , así A es compacto no convexo, luego existen
, así A es compacto no convexo, luego existen 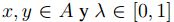 tales que
tales que
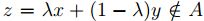 . Como es A compacto, es cerrado, con lo cual existe
. Como es A compacto, es cerrado, con lo cual existe 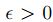 tal que
tal que 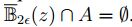
Sea 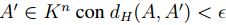 , entonces,
, entonces, 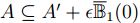 y como
y como  , existen
, existen 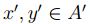 con
con 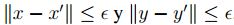 . Luego:
. Luego:
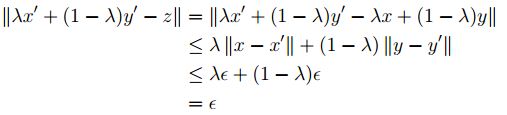
Ahora sea 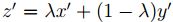 y se supone que
y se supone que 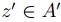 , como
, como 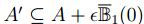 , existe
, existe 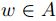 tal que
tal que 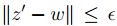 . Entonces
. Entonces 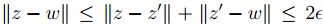 . Lo que contradice que
. Lo que contradice que
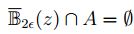 . Luego A' es no convexo y por tanto A es un conjunto abierto de
. Luego A' es no convexo y por tanto A es un conjunto abierto de 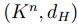 .
.
Con esto 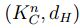 es también un espacio métrico completo [1]. El siguiente resultado aparece en [8], está dado para elementos de
es también un espacio métrico completo [1]. El siguiente resultado aparece en [8], está dado para elementos de
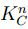 , sin embargo en [6], se observa que para elementos de K n funciona igualmente.
, sin embargo en [6], se observa que para elementos de K n funciona igualmente.
Proposición 2.5. Sea 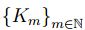 una sucesión en
una sucesión en 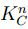 que converge a K, además, sea
que converge a K, además, sea
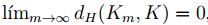 ,
,
entonces,
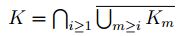
Prueba. Sea 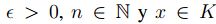 , entonces existe
, entonces existe 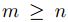 tal que
tal que 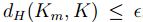 , por
la proposición 2.4, existe un punto
, por
la proposición 2.4, existe un punto 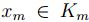 tal que
tal que 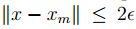 .Por consiguiente
.Por consiguiente
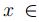
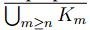 para cada
para cada 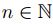 .
.
Sea 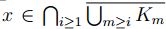 entonces para cada
entonces para cada 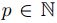 existe
existe 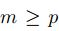 tal que
tal que
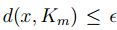 . Así si
. Así si 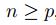 , se tiene que:
, se tiene que:
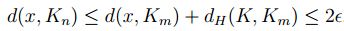 ,
,
entonces 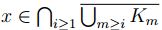 para n, esto prueba que
para n, esto prueba que 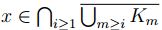
Sea 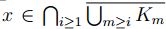 , de que la sucesión
, de que la sucesión 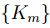 converge a K , se tiene que
converge a K , se tiene que
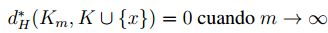 ,
,
además sea p tal que para 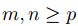 implique
implique 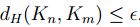 .
Del hecho que
.
Del hecho que 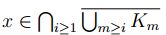 se sigue que existe
se sigue que existe 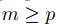 tal que
tal que 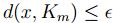 ,
luego si
,
luego si 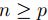
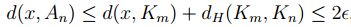 ,
,
con lo cual 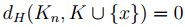 y luego
y luego 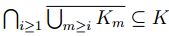 .
.
3. El espacio En
Definición 3.1. Un subconjunto difuso u de X, está determinado por una función 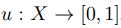 ,
que indica el grado de pertenencia o membresía de un elemento x en el conjunto u.
,
que indica el grado de pertenencia o membresía de un elemento x en el conjunto u.
Es de aclarar, que en la teoría difusa se utilizan diferentes tipos de notaciones, en este caso, se siguen las ideas de [12], pero dado a las modificaciones que con el tiempo se han venido utilizando, se sigue la notación de [5].
Observése que u generaliza la noción de función característica de un conjunto. Además, de acuerdo con [5],
si 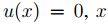 no pertenece al conjunto; si
no pertenece al conjunto; si 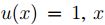 pertenece al conjunto y si
pertenece al conjunto y si
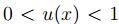 , se tiene que x pertenece de manera parcial, su grado de membresíaes justamente
, se tiene que x pertenece de manera parcial, su grado de membresíaes justamente 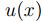 .
.
Un subconjunto de A de B, se caracteriza, por tanto, por la función de pertenencia A : B → [0 , 1] , es preciso
fijar el conjunto B para definir la función A,que a su vez define A. Por eso se habla de subconjunto difuso y no de conjunto difuso, (otros detalles en [12 ]);
Ahora se presta atención a una colección particular de subconjuntos difusos de 
Sea En la colección de todos los subconjuntos difusos de  que satisfacen:
que satisfacen:
- El soporte y los α- cortes de u son conjuntos compactos de
 , para todo
, para todo 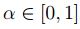 .
. - u es convexo difuso,esto es, para x, y , ∈

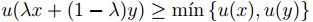 ,
,
para todo 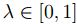 .
.
Lema 3.1. Si u ∈ E n , entonces se satisface
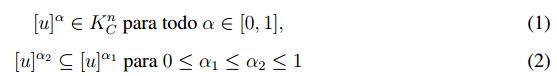 ,
,
y si 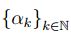 es una sucesión creciente que converge
es una sucesión creciente que converge 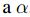 , entonces
, entonces
 ,
,
Recíprocamente, si 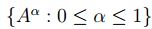 es la colección de subconjuntos de
es la colección de subconjuntos de  que satisface (1)
(2) y (3), entonces existe un
que satisface (1)
(2) y (3), entonces existe un 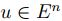 tal que
tal que
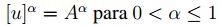
y
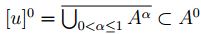
Prueba. Sea 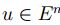 , por la definició de
, por la definició de 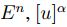 es compacto para
es compacto para 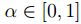 ,
resta entonces ver
,
resta entonces ver 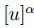 es convexo. Para
es convexo. Para 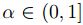 , sean
, sean 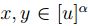 , esto es,
, esto es,
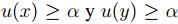 , entonces al ser u convexo difuso se tiene
, entonces al ser u convexo difuso se tiene
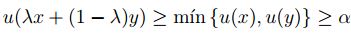 ,
,
luego 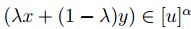 . Con lo cual satisface (1).
. Con lo cual satisface (1).
Sean 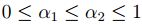 , se sabe que
, se sabe que
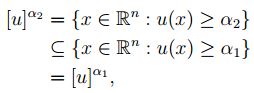
con lo que satisface (2).
Ahora sea 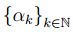 ,una sucesión creciente que converge a
,una sucesión creciente que converge a 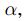 ,luego por (2) se tiene que
,luego por (2) se tiene que
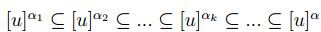 ,
,
por otro lado 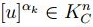 ,ahora aplicando la proposición 2,9 , se tiene que esta sucesión converge a
,ahora aplicando la proposición 2,9 , se tiene que esta sucesión converge a
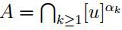 , con lo cual
, con lo cual 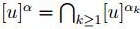 , y (3) se sigue.
, y (3) se sigue.
Recíprocamente, sea 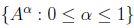 la colección de subconjuntos de
la colección de subconjuntos de  que satisface (1),(2)
y (3); dado
que satisface (1),(2)
y (3); dado 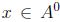 , se define
, se define 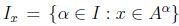 , y sea
, y sea 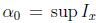 , de donde se obtiene que
, de donde se obtiene que
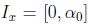 . En efecto, si
. En efecto, si 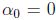 , de inmediato
, de inmediato 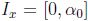 , entonces se supone que
, entonces se supone que
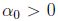 y sea
y sea 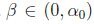 ; luego existe
; luego existe 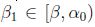 , tal que
, tal que 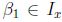 así, dado que
así, dado que 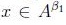 implica por (2)
implica por (2) 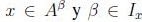 por definición
por definición 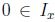 y se obtiene que
y se obtiene que
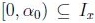 ; ahora sea
; ahora sea 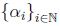 una sucesión monotona en I x que converge a
una sucesión monotona en I x que converge a
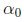 , entonces
, entonces 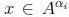 para cada
para cada 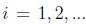 y por (3)
y por (3) 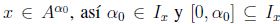 .Igualmente,dado
.Igualmente,dado 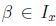 , implica que
, implica que 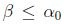 ,luego
,luego 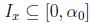 .
.
Se define 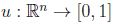 como
como 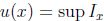 para todo
para todo 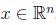 , por consiguiente, sea
, por consiguiente, sea 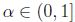 ,
si
,
si 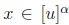 entonces
entonces 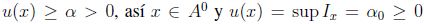 ; por consiguiente,
; por consiguiente, 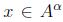 y por 2,
y por 2, 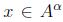 , esto es ,
, esto es ,
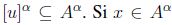 .Si
.Si 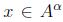 ,entonces
,entonces 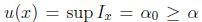 y
y 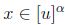 . Por tanto
. Por tanto 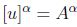 .
.
Construido lo anterior, se verifica que 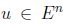 , en efecto, u es un conjunto difuso de
, en efecto, u es un conjunto difuso de  , por su definición, ahora
, por su definición, ahora 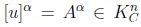 ,
entonces
,
entonces 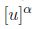 es compacto para todo
es compacto para todo 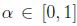 . Finalmente, sean
. Finalmente, sean 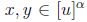 con
con 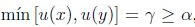 , entonces
, entonces 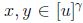 , que es convexo y así
, que es convexo y así 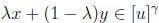 para cualquier
para cualquier 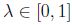 . Por consiguiente
. Por consiguiente
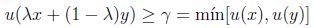 ,
,
lo que prueba que u es convexo difuso.
Al espacio E n se le puede dotar una estructura para sus α-cortes, es expuesto con el siguiente concepto, cabe resaltar que los dos anteriores resultados son tomados de [8].:
Lema 3.2 Sean 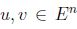 entonces la adición
entonces la adición 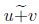 y multiplicación por un escalar
y multiplicación por un escalar 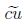 difusa pertenece a E n donde los α-cortes son definidos como:
difusa pertenece a E n donde los α-cortes son definidos como:
 ,
,
y
 ,
,
para 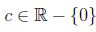 .
.
Prueba. Dado que 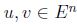 , se satisface (1) ,(2) y (3), entonces
, se satisface (1) ,(2) y (3), entonces 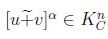 ; sean
; sean
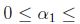
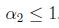 , entonces
, entonces
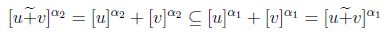 ;
;
sea 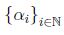 una sucesión creciente que converge a
una sucesión creciente que converge a 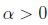 entonces
entonces

de donde 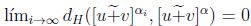 , luego, por la proposición 2.5,
, luego, por la proposición 2.5, 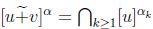 .
De modo que
.
De modo que 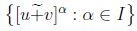 satisface (1) , (2) y (3) por el teorema 3.1,
satisface (1) , (2) y (3) por el teorema 3.1, 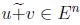
Similarmente 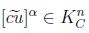 ; sean
; sean 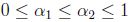 , entonces
, entonces
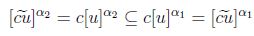 ;
;
sean 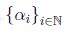 una sucesión creciente que converge a
una sucesión creciente que converge a 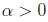 entonces
entonces
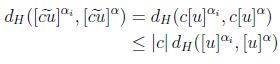 ;
;
de donde 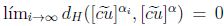 , luego por la proposición 2.5,
, luego por la proposición 2.5, 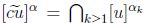 . De modo que
. De modo que 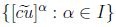 satisface (1), (2) y (3), por el teorema 3.1,
satisface (1), (2) y (3), por el teorema 3.1, 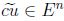 .
.
4. El espacio métrico ( E n , d )
Se procede al intersectar las dos teorías expuestas, se tiene el siguiente resultado, que ha sido difundido por variados autores, entre ellos V. Lakshmikantham em [8].
Lema 4.1. El par ( E n , d ) con la métrica del supremo d en E n definida como
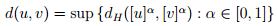 ;
;
donde u , v ∈ E n , es un espacio métrico.
Prueba. Sean u , v , w ∈ E n , entonces
- Para cada α ∈ [ 0 , 1 ], dado que
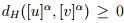 , luego por propiedades del supremo se obtiene que:
, luego por propiedades del supremo se obtiene que: - Sea
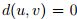 , entonces
, entonces 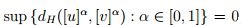 , por propiedades del supremo,
, por propiedades del supremo, - La simetría se satisface, en efecto,
- Ahora se verifica la desigualdad triangular,
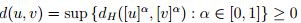
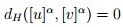
para todo α ∈ [ 0 , 1 ], luego 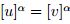 , entonces
, entonces 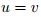
Recíprocamente si 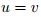 entonces
entonces 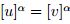 , luego
, luego
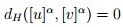
así por propiedades del supremo, 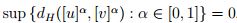 , luego
, luego 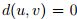 .
.
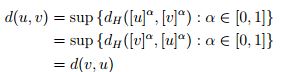
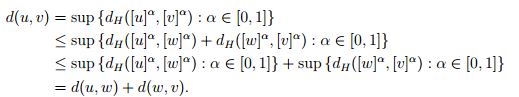
Finalmente, se prueba:
Teorema 4.1. ( E n , d ) es un espacio métrico completo
Sea. 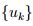 una sucesión de Cauchy en ( E n , d ) entonces
una sucesión de Cauchy en ( E n , d ) entonces 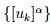 para cada α ∈ [ 0 , 1 ], es una sucesión de Cuachy in
para cada α ∈ [ 0 , 1 ], es una sucesión de Cuachy in 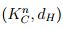 , que es un espacio métrico completo, así existe un
, que es un espacio métrico completo, así existe un
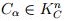 para cada α ∈ [ 0 , 1 ] tal que
para cada α ∈ [ 0 , 1 ] tal que
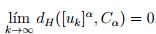
Se considera la colección 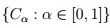 , y cada
, y cada 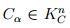 lo que satisface (1); sea
lo que satisface (1); sea 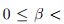
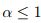 , entonces
, entonces
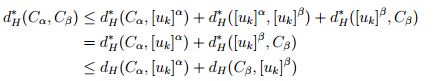
con lo cual
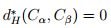
y esto indica, segun la proposición 2.2, que 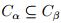 , liego se satisface (2); sea
, liego se satisface (2); sea 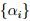 una sucesión decreciente en [ 0 , 1 ]
que converge a
una sucesión decreciente en [ 0 , 1 ]
que converge a 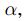 con lo cual
con lo cual 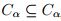 para
para 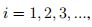 luego,
luego,
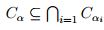
ahora sea 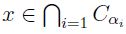 , así
, así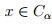 para todo
para todo 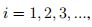 , entonces
, entonces
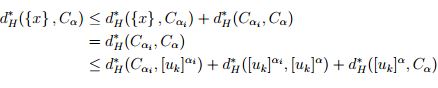
de modo que 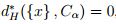 por la proposición 2.2
por la proposición 2.2 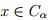 y por consiguiente
y por consiguiente
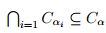 .
.
Por tanto, se satisface la condición (3) de que
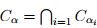 .
.
Entonces al satisfacer (1), (2) y (3), se aplica el teorema 3.1, con lo cual, existe un 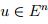 tal que
tal que 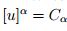 para todo
para todo 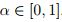 . Además,
. Además,
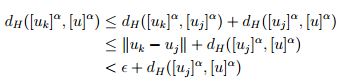 .
.
para todo 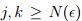 , debido a que
, debido a que 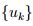 es una suceción de Cauchy en ( E n , d ). Tomando el límnite cuando
es una suceción de Cauchy en ( E n , d ). Tomando el límnite cuando
 , se obtiene
, se obtiene
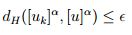 .
.
para todo 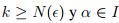 , por tanto
, por tanto 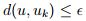 para todo
para todo 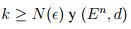 es un espacio métrico completo .
es un espacio métrico completo .
Los conceptos arriba expuestos, se extienden y profundizan en [ 8 ], [9] y [ 10] en donde el horizonte se amplía y abre lejanas perspectivas.
5. Comparación con otros espacios métricos
De las secciones anterior resulto un nuevo espacio métrico, la idea ahora es realizar una comparación con otros espacios métricos [11] relacionados con subconjuntos difusos.
Sean A, B subconjuntos difusos del universo X cualquiera, la distancia de Hamming se define como
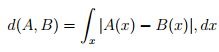 ,
,
la distancia euclídea como
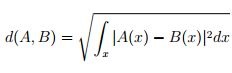 ,
,
y la distancia de Tchebyschev como
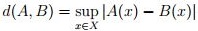 .
.
Se resaltar que dichas distancias se encuentran entre dos subconjuntos difusos con el mismo universo X y se puede afirmar que cuanto mayor sea la similitud de los subconjuntos difusos, la distancia es menor.
En el espacio ( E n , d ) solo intervienen subconjuntos difusos de  con restricciones particulares ya expuestas, para estas tres distancias, no hay restricción alguna, así que se obtiene una bifurcación
de los subconjuntos difusos, y por consiguiente no estan muy relacionadas. Además la información
obtenida de las tres distancias es muy débil, mostrando una cualidad muy general, que es grado
de similaridad de dos subconjuntos dados. Mientras que en el espacio ( E n , d ) , se comparan los
α-cortes con la métrica de Hausdorff, es decir, se le está dando analisis a cada
con restricciones particulares ya expuestas, para estas tres distancias, no hay restricción alguna, así que se obtiene una bifurcación
de los subconjuntos difusos, y por consiguiente no estan muy relacionadas. Además la información
obtenida de las tres distancias es muy débil, mostrando una cualidad muy general, que es grado
de similaridad de dos subconjuntos dados. Mientras que en el espacio ( E n , d ) , se comparan los
α-cortes con la métrica de Hausdorff, es decir, se le está dando analisis a cada 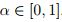 .
.
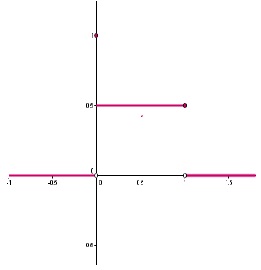
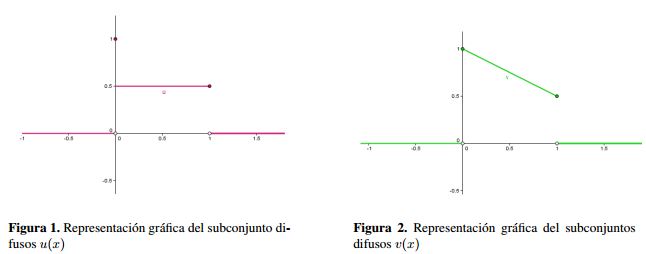
Se presenta una situación en donde se calculan las cuatro distancias. Sean u , v ∈ E1, como las Figuras 1 y 2, y matemáticamente definidos de la siguiente forma:
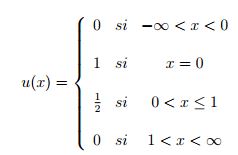 .
.
y
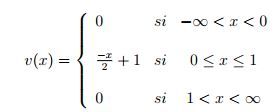 .
.
De esta forma podemos decir que los α - cortes son
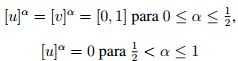 .
.
y
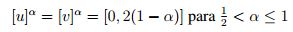 .
.
Luego se tiene que  para
para 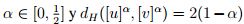 para
para 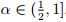 .
Por tanto
.
Por tanto 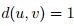
Para las otras disposiciones se tienen los siguientes cálculos, para la distancia de Hamming
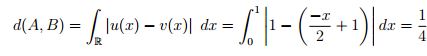 ,
,
para la distancia euclídea
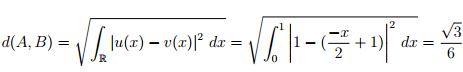 ,
,
y para la distancia de Tchebyschev
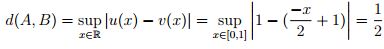 .
.
Por los gráficos se observa que los subconjuntos difusos son similares y esto se ve representado en las tres distancias, ya que se acercan a 0. Mientras que con la métrica del espacio E1, no tienen relación, al realizar los cálculos, es necesario el análisis de los α-cortes, osea que, en casos de aplicaciones, se tendrá que analizar parte por parte del subconjunto difuso, proporcionando más información de su significado.
Conclusiones
La construcción de la métrica de Hausdorff en  es una edificación desde la definición de distancia entre un punto y un conjunto acotado no vacío, con ella se produce un nuevo espacio métrico
completo
es una edificación desde la definición de distancia entre un punto y un conjunto acotado no vacío, con ella se produce un nuevo espacio métrico
completo 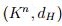 con los subconjuntos compactos de
con los subconjuntos compactos de  , que además se obtiene
, que además se obtiene 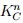 , el conjunto de compactos y convexos
, el conjunto de compactos y convexos  ,
es un conjunto cerrado par este espacio métrico.
,
es un conjunto cerrado par este espacio métrico.
El espacio En tiene dos operaciones cerradas de adición y multiplicación por un escalar entre sus elementos, dado por el principio de extensión de Zadeh y las propiedades del espacio.
Al relacionar el espacio En y la métrica de Hausdorff, se enriquece la noción de la métrica de Hausdorff, obteniendo un espacio completo. Esta propiedad permite la utilidad en ambientes diferentes, lo que conlleva a otros rumbos de investigación.
Comparando con otras distancias entre subconjuntos difusos, se puede afirmar que en ( En , d ) se necesita analizar cada elemento del espacio para poder obtener su distancia con otro, luego es necesario un mayor detalle y con eso conocer mejor su naturaleza.
Referencias
[1] T. M. Apostol. Mathematical Analysis. Addison-Wesley Publishing Company. Massachusetts. 1981.
[2] M. Barnsley. Fractals Everywhere. Academic Press. San Diego. 1988.
[3] P. Diamond y P. Kloeden. Metric Spaces of Fuzzy Sets. World Scientific. Singapore. 1994.
[4] D. Dubois y H. Prade. Fuzzy Sets and Systems: Theory and Applications. Academic Press. 1980.
[5] W. González . Una aproximación a los conjuntos alcanzables de una inclusión diferencial difusa. Revista Integración, vol. 30, núm. 1, 2012, pp. 57-74.
[6] C. Castaing y M. Valadier. Convex Analysis and Measurable Multifunctions. Springer-Verlag. 1932.
[7] E. Kreyszig Introductory Functional Analysis with Applications. John Wiley & Sons. Canada 1978.
[8] V. Lakshmikanthan y R.N. Mohapatra. Theory of Fuzzy Differential Equantions and Inclusions. Taylor y Francis. 2003.
[9] J. Rodríguez-Lópeza y S. Romaguera. On completion of fuzzy metric spaces. Fuzzy Sets and Systems. Vol.130, 2002, pp.399-404-283.
[10] J. Rodríguez-Lópeza y S. Romaguera. The Hausdorff fuzzy metric on compact sets. Fuzzy Sets and Systems. Vol.147, 2004, pp.273-283.
[11] S. S. Silva. Modelo Basado en Logica difusa para la comparación de objetos con atributos imprecisos. Universidad Centro Occidental Lisandro Alvarado. 2013.
[12] L. A. Zadeh. Fuzzy Sets. Inf. Control 8. 1965.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

 .
.


2.jpg)










