DOI:
https://doi.org/10.14483/23448393.2713Published:
2004-11-30Issue:
Vol. 10 No. 2 (2005): July - DecemberSection:
Science, research, academia and developmentMecánica de la Fractura Aplicada a Ejes de Molinos de Caña de Azúcar
Keywords:
mecánica de fractura, eje, guijo, tenacidad de fractura, fisura (es).Downloads
References
Reid, M. J. «Possible causes of recent roll shaft failures in South African sugar mill», Proceeding of the XX ISSCT Congress, 12-21 Oct. 1989, Sao Paulo. Brazil.
Arzola, N. «Esquema de análisis para los árboles de los molino de caña de azúcar y aplicación de la Mecánica de la Fractura en la evaluación de la falla por fatiga». Nelson Arzola de la Peña. Tesis de Doctorado. Universidad de Cienfuegos: CEDON, 2003. 118p.
Stress Intensity Factors Handbook, Y. Murakami, editor-inchief, Pergamon Press. Oxford, Vols. 1 y 2, 1987; Vol.3, 1992. 215 p.
Dowling, N. E. «Mechanical behavior of materials: engineering methods for deformation, fracture, and fatigue». Upper Saddle River (NJ): Prentice Hall, cop. 1999. p. 239-550.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2005-00-00 vol:10 nro:2 pág:23-29
Mecánica de la fractura aplicada a ejes de molinos de caña de azúcar
Sara Rodríguez Pulecio
Miembro Grupo de Investigación en Mejoramiento Industrial. Escuela de Ingeniería Mecánica. Universidad del Valle.
John Jairo Coronado Marín
Miembro Grupo de Investigación en Mejoramiento Industrial. Escuela de Ingeniería Mecánica. Universidad del Valle.
Nelson Arzola de la Peña
Ph.D. Profesor de la Universidad Nacional de Colombia. Sede Bogotá. Departamento de Ingeniería Mecánica y Mecatrónica.
Resumen
En este artículo se presenta un método basado en la Mecánica de la Fractura para el cálculo del tamaño crítico de fisuras y la vida remanente del eje superior de los molinos de caña de azúcar, con fisuras semielípticas y circunferenciales. Los cálculos fueron realizados en el eje superior del primer molino de un Ingenio Azucarero, pero puede ser aplicado a cualquier otro caso en particular. Debido a la presencia de un campo de esfuerzos multiaxiales es necesario usar en la ecuación de París un factor de intensidad de tensiones equivalente. Se obtuvo el intervalo entre inspección requerido para evitar una falla por fatiga de estos elementos. El cálculo de vida residual y tamaño de fisura máxima se realizó en la zona del cambio de diámetro del guijo más próximo al acoplamiento cuadrado, donde se encontraron el 25% de las fallas.
Palabras clave:
mecánica de fractura, eje, guijo, tenacidad de fractura, fisura.
Abstract
In this article a method based on the Fracture Mechanics is presented for the calculation of the critical crack size and the life prediction of the mill top shafts of the sugar mills, with semielliptic and circumferential cracks. The calculations were carried out to the top shaft of the first mill in a Sugar Mill, but it can be applied in particular to any other case. Due to the presence of a multiaxial stress field it is necessary to use an equivalent stress intensity factor in the equation of Paris. The inspection interval required to avoid a fatigue failure of these elements was obtained. The calculation of residual life and maximum crack size was carried out in the area of the journal diameter change nearest to the square coupling. In this location the 25% of the failures were reported.
Key words:
fracture mechanics, shaft, journal, fracture toughness, crack.
1. INTRODUCCIÓN
Los ejes de los molinos de caña de azúcar son elementos críticos, altamente esforzados y por tanto propensos a la falla por fatiga. Los ingenios azucareros realizan grandes esfuerzos para evitar la ruptura imprevista de los ejes de los molinos de caña de azúcar y con ello evitar las grandes pérdidas económicas que esto conlleva. Estos elementos se ven sometidos a cargas considerables, que provocan su falla en un número de ciclos de trabajo no muy grande en dependencia de la posición que ocupen en el molino y en el Tandem respectivamente. Por ejemplo, los ejes superiores tienen condiciones de carga más severas. Las grietas surgen a partir de microdefectos localizados en la superficie o muy cercanos a ella y se propagan en un plano próximo a la sección transversal del eje.
La potencia ingresa al molino por medio de un eje cuadrado llamado entre dos. Este acople conecta el eje de salida de la última etapa de reducción de velocidad con la espiga cuadrado del eje superior. El eje del reductor de baja es unido al entre dos por medio de un acople cuadrado y el entre dos es unido a cuadrante del eje superior por medio de otro acople cuadrado. La potencia es distribuida a las mazas cañera y bagacera por medio de engranes, llamados en el argot azucarero coronas, y a la cuarta maza por medio de cadenas a través de la maza cañera o en ocasiones a través de la maza superior empleando coronas.
Fueron analizados los reportes de fisuras detectadas en los ejes para encontrar los sectores del eje en donde con mayor frecuencia aparecen. Los resultados para el Ingenio Manuelita S.A. se muestran en la Figura 1, en donde aparece el porcentaje de ejes que presentaron grie-tas y sus ubicaciones. Se observa que la zona del eje con mayor porcentaje de fallas es el cambio de sección chumacera asiento de la maza del lado de la espiga cuadrada, con un 25% de la frecuencia observada. Otros investigadores han encontrado frecuencias de ubicación de las fallas algo diferentes, pero en general se mantiene el mismo comportamiento en cuanto a su distribución, según cita Reid, 1989 [1].
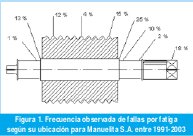
Para analizar el fenómeno de fisuración progresiva se requiere del empleo de la Mecánica de la Fractura, debido a que la utilización del método brindado por la fatiga clásica no aportaría información sobre el tamaño y la razón de propagación de la grieta. Por otro lado, la presencia de un estado tensional triaxial genera la aparición de un modo mixto de carga en el vértice de la grieta, lo cual obliga a emplear un factor de intensidad de esfuerzos equivalente si se requiere de exactitud en el modelo de propagación. Con anterioridad al trabajo de Arzola, 2003 [2] no había sido presentado el enfoque que aparece en este trabajo para la determinación de la razón de propagación de la grieta y el establecimiento del periodo de tiempo entre inspecciones para los ejes de molinos de caña de azúcar.
En la actualidad no se emplea en la Industria Azucarera Colombiana un procedimiento para establecer el periodo de tiempo máximo entre inspecciones, ni para conocer tamaños críticos de grietas en los ejes de los molinos, de modo que este trabajo presenta un instrumento de gran utilidad para evitar las paradas forzosas de los ingenios por fallas imprevistas de estos elementos.
2. ESTADO DE CARGA DEL EJE SUPERIOR
Con el objetivo de definir el estado tensional en las diferentes secciones del eje se construyeron los diagramas de cargas distribuidas, fuerzas de cortante y momentos flectores para dos planos mutuamente perpendiculares. Las Figuras 2, 3 y 4 muestran estos diagramas para el plano YZ. Como puede observarse la reacción del colchón de caña no es homogénea a lo largo de la maza y por tanto no está sujeta a un mismo grado de compresión, esto es causado por la flotación desigual del eje y es analizado por Arzola, 2003 [2].
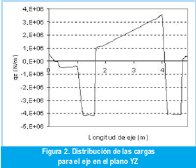
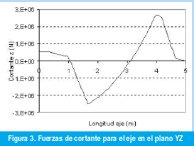
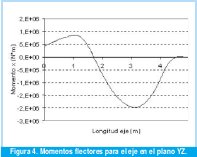
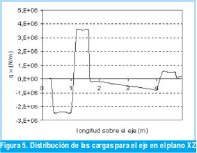
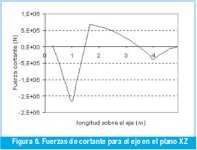
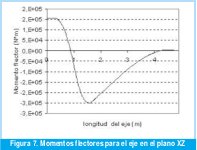
En el plano XZ se tienen como incógnitas las reacciones normales sobre la cureña, las cuales son obtenidas de las ecuaciones de equilibrio en el eje X (eje horizontal). Posteriormente se determinaron los valores de carga distribuida, fuerza de cortante y momento flector para dicho plano como se observa en las Figuras 5, 6 y 7.
3. ESFUERZOS EN LA SECCIÓN TRANSVERSAL BAJO ANÁLISIS
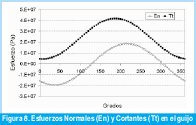
En la Tabla I se muestran las fuerzas de cortante y los momentos flectores en los planos YZ y XZ respectivamente, y el momento torsor que actúa en la sección bajo análisis, para cinco niveles de carga obtenidos durante el funcionamiento normal del molino. En la Figura 8 se muestra la variación del esfuerzo cortante y normal en la superficie del eje para una vuelta completa del mismo.
La Figura 9 muestra como varía el esfuerzo equivalente Von Mises a lo largo del eje para cuatro posiciones angulares del punto donde se determina el estado tensional (esfuerzo Von Mises). Como puede observarse el punto de esfuerzo máximo se encuentra en el cambio de sección guijo maza. Por tanto, se establece este punto como el punto de interés.


4. TAMAÑOS DE GRIETA CRÍTICOS Y PERMISIBLES
Existen dos modelos de grieta que concuerdan con las grietas detectadas en la práctica: la grieta semielíptica superficial y la grieta circunferencial. En una sección dada del eje pueden surgir una o varias grietas semielípticas superficiales, las cuales al crecer dan lugar al surgimiento de una grieta circunferencial cuando sus bordes hacen contacto. Además, puede surgir y propagarse una grieta circunferencial de existir un defecto periférico en la superficie del eje. Por ejemplo, el rayado provocado por defectos de maquinado o el ocasionado por un cuerpo extraño que se introduzca en la chumacera del eje.
4.1 Modelo para una grieta semielíptica superficial
El factor de intensidad de esfuerzos (KI) para el caso de un eje con grieta semielíptica superficial sometida a flexión fue hallado por Murakami, 1992 [3].
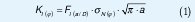
Donde «F1» es el factor geométrico para el modo I de carga y «a» es la profundidad de la grieta. El esfuerzo cortante radial propicia el deslizamiento de las superficies creadas por la grieta en dirección transversal a su vértice, por lo que provoca el modo de carga II. El factor de intensidad de esfuerzos para este modo de carga es encontrado por la expresión.
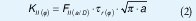
Mientras que el esfuerzo cortante circunferencial induce deslizamiento en la dirección del vértice de la grieta, provocando el modo III de carga, cuyo factor de intensidad de esfuerzos es obtenido a través de la siguiente expresión:
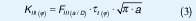
Se calculó el factor de intensidad de esfuerzo equivalente, empleando el criterio de la energía de deformación liberada para el estado de deformación plana:
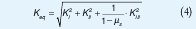
Donde µs es el coeficiente de Poisson para el material del eje.
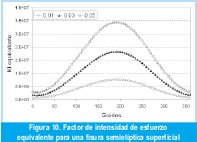
La gráfica de K equivalente se muestra en la Figura 10 para tres profundidades distintas de la grieta.
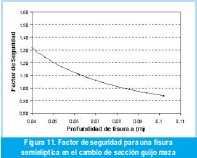
Haciendo uso de la ecuación de Keq e igualándola a la tenacidad de fractura del acero SAE 1045 (Kic= 88 MPam1/2) fue determinada la profundidad crítica de una fisura semielíptica. Para el caso del eje superior del molino 1, del tandem II del Ingenio Manuelita S.A. fue de 80 mm. En la Figura 11 puede observarse el comportamiento del factor de seguridad para un eje con fisura semielíptica.
4.2 Modelo para una grieta circunferencial
Otro tipo de grieta encontrada en ejes de molino de caña es la grieta circunferencial. Los modos de carga presentes en el vértice de este tipo de grieta, para el estado de esfuerzos planteado, son el I y el III. Para el caso del eje, estos factores de intensidad de esfuerzos se expresan según las ecuaciones.
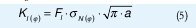
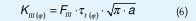
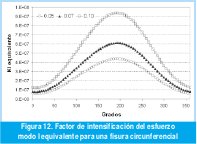
La gráfica del K equivalente es mostrada en la Figura 12, donde se grafica el factor de concentración del esfuerzo equivalente para diferentes profundidades de fisura.
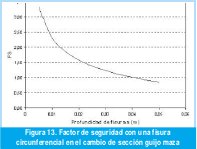
Para el eje superior del molino 1, en el tandem II, la profundidad crítica de una fisura circunferencial fue de 40mm. En la Figura 13 puede observarse el comportamiento del factor de seguridad de un eje con fisura circunferencial.
5. MODELO DE CRECIMIENTO DE LAS GRIETAS CIRCUNFERENCIALES
El crecimiento subcrítico de la grieta puede ser modelado satisfactoriamente por la expresión propuesta por Paris, según Dowling, 1999 [4] se expresa como:

Donde da/dN es la proporción de crecimiento de grietas, y C y n son constantes del material. Para este caso se empleará el rango de variación del factor de intensidad de tensiones equivalente (ΔKeq) por presentarse un modo mixto de cargas.
Utilizando el criterio de la energía de deformación liberada puede obtenerse la relación que existe entre cada uno de los factores de intensidad de esfuerzos actuando de forma combinada y el factor de intensidad de esfuerzos equivalente. El cálculo de la razón de crecimiento de la grieta tuvo que ser repetido tantas veces como niveles de carga existen, es decir, desde j =1 hasta 5, y la expresión de Paris reescrita como:
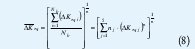
Donde:
ΔKeq: Rango del factor de intensidad de esfuerzos equivalente que causa la misma razón de crecimiento de la grieta que la historia de esfuerzos variables para el mismo número de ciclos (MPa m1/2).
ΔKeq:j Rango del factor de intensidad de esfuerzos equivalente para la historia de esfuerzos variables j (MPa m1/2).
nj: Fracción de tiempo respecto a la unidad en que está presente el estado de carga j.
El factor de intensidad de esfuerzos equivalente alcanza valores máximos y mínimos en este caso para las posiciones angulares del eje, de 0° y 195° para el estado de carga estudiado.
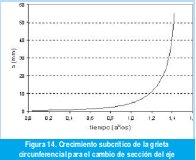
En la Figura 14 se muestra el crecimiento subcrítico de la grieta circunferencial para el eje superior del molino 1. El tamaño inicial de la grieta elegido es igual a 0,001 mm, sin embargo el crecimiento es muy poco sensible al valor inicial del defecto.
6. INTERVALO DE TIEMPO ENTRE INSPECCIONES
Debe garantizarse que la grieta sea detectada antes de que alcance el tamaño máximo permisible. Si se designa al período de tiempo desde que surge la grieta hasta que esta alcanza un tamaño detectable, por las técnicas de ultrasonido, como td, y como tp el tiempo para el cual la grieta alcanza un tamaño máximo permisible; entonces, se deberá realizar al menos una inspección en el intervalo td<t<tp si se quiere evitar una falla imprevista por fatiga. Afortunadamente el tiempo requerido para el crecimiento de la grieta desde su tamaño detectabl hasta el tamaño máximo permisible es independiente del tamaño inicial de la grieta ao, el cual en la práctica es desconocido. Para evitar realizar inspecciones de manera muy frecuente se diseñó un programa basado en un intervalo de tiempo máximo permisible entre inspecciones, dadas las limitaciones que genera tener que desarmar parte del molino para realizar la inspección ultrasónica.
La determinación del período de tiempo entre inspecciones requiere no solamente del establecimiento de un tamaño de grieta máximo permisible, sino también de un tamaño mínimo detectable de grieta. Este último está definido por la tecnología de detección utilizada, la facilidad de acceso al lugar que se necesita inspeccionar, y la calificación y experiencia del personal a cargo de la operación. Es importante aclarar que se entiende por profundidad mínima detectable a la profundidad de grieta que sería detectada con una probabilidad alta (95% o mayor) durante un procedimiento rutinario de inspección. El periodo de tiempo entre inspecciones depende de este valor como puede apreciarse en la Figura 15.
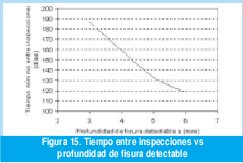
Como ΔK aumenta con la profundidad de la grieta y como da/dN depende de ella, la razón de crecimiento de la grieta se acelera con el incremento de la dimensión del defecto. Esta situación obliga a utilizar un procedimiento de integración numérica para poder conocer cuanto tarda el crecimiento de la grieta. Para obtener dicho intervalo, la ecuación de Paris para el estado de carga equivalente es reescrita como:
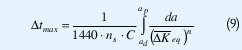
Donde:
ad: Tamaño mínimo detectable de la grieta (m).
ap: Tamaño máximo permisible de la grieta (m).
Δtmax: Intervalo entre inspección máximo permisible (días).
Para el eje superior, el periodo de tiempo entre inspecciones fue establecido en 159 días de operación, usando como profundidad mínima detectable 4mm. La ecuación anterior puede además ser empleada para el cálculo de la vida remanente de los ejes de los molinos. Si una grieta de tamaño aw es detectada en el eje durante una inspección, la vida remanente podrá conocerse cambiando el límite inferior de integración por este tamaño. Esto resulta muy útil, ya que se puede reemplazar estos elementos en el momento más ventajoso desde el punto de vista productivo, evitando paradas innecesarias y costosas.
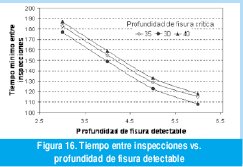
Conocer la vida remanente de un eje puede ser de gran utilidad, porque puede utilizarse el criterio de «elemento con grieta en operación» cuando no se cuenta con un eje de repuesto en ese momento o su reemplazo inmediato puede perjudicar el proceso de producción. Además, la presencia de grietas no significa categóricamente la condición de no apto para explotación o la de falla instantánea. De hecho un eje agrietado bajo condiciones de cargas controladas puede emplearse satisfactoriamente durante cierto tiempo. Cuando ac es sustancialmente mayor que ad y n tiene valor alrededor de tres o mayor, el tamaño inicial de la grieta es el que domina el resultado de la ecuación, siendo insensible este último al valor de ac. Este comportamiento puede ser observado en la Figura 16, donde se grafica el tiempo entre inspecciones calculado para diferente profundidades criticas de fisura. Este hecho se explica debido a que gran parte del tiempo que consume la grieta para su crecimiento es cuando posee dimensiones pequeñas. Por ejemplo, al tomar como tamaño mínimo detectable de grieta un valor de ad= 3 mm, y realizar los cálculos en (9), se obtiene como resultado un aumento del intervalo de tiempo entre inspecciones del 18%.
7. CONCLUSIONES
1. Se encontró que el estado tensional más crítico ocurre en el cambio de sección de la chumacera, que se encuentra más cercana al acoplamiento cuadrado, coincidiendo con la posición para la cual se reportan el 25% de la fallas.
2. Para las condiciones actuales de operación del molino 1, del tandem II, se encontró que el eje superior posee un tamaño crítico de grieta semielíptica superficial en el cambio de sección guijo maza de 80mm, mientras que el tamaño crítico para una grieta circunferencial es de 40mm, por lo que no se deben permitir grietas de estos tipos con magnitudes próximas a las señaladas.
3. Con el objetivo de asegurar la integridad estructural del eje superior del molino 1, del tandem II, el mismo deberá ser inspeccionado cada 159 días de operación.
4. El tiempo entre inspecciones es fuertemente dependiente del tamaño de fisura mínima detectable, por lo que deberá emplearse una técnica ultrasónica de detección de grietas más precisa si se quiere contar con un mayor intervalo de tiempo entre inspecciones. Por ejemplo, este periodo puede ser aumentado en un 18% si se garantiza un tamaño mínimo detectable de grieta de 3 mm.
8. AGRADECIMIENTOS
El Grupo de Investigación en Mejoramiento Industrial de la Escuela de Ingeniería Mecánica (Universidad del Valle), en el marco del «Proyecto Cooperativo Agroindustrial para Reducir el Desgaste en Equipos de Preparación y Molienda» que se lleva a cabo en el Ingenio Manuelita S.A., con la participación de CENICAÑA, agradece los aportes del personal de estas organizaciones y el apoyo financiero de COLCIENCIAS, que con dinero del BID, ha posibilitado este trabajo.
9. REFERENCIAS BIBLIOGRÁFICAS
[1] Reid, M. J. «Possible causes of recent roll shaft failures in South African sugar mill», Proceeding of the XX ISSCT Congress, 12-21 Oct. 1989, Sao Paulo. Brazil.
[2] Arzola, N. «Esquema de análisis para los árboles de los molino de caña de azúcar y aplicación de la Mecánica de la Fractura en la evaluación de la falla por fatiga». Nelson Arzola de la Peña. Tesis de Doctorado. Universidad de Cienfuegos: CEDON, 2003. 118p.
[3] Stress Intensity Factors Handbook, Y. Murakami, editor-inchief, Pergamon Press. Oxford, Vols. 1 y 2, 1987; Vol.3, 1992. 215 p.
[4] Dowling, N. E. «Mechanical behavior of materials: engineering methods for deformation, fracture, and fatigue». Upper Saddle River (NJ): Prentice Hall, cop. 1999. p. 239-550.
Sara Rodríguez Pulecio
Ingeniera Mecánica. Grupo de Investigación en Mejoramiento Industrial. Escuela de Ingeniería Mecánica. Universidad del Valle. sararopu@hotmail.com
John Jairo Coronado Marín
M.Sc. Profesor de la Escuela de Ingeniería Mecánica. Universidad del Valle. Grupo de Investigación en Mejoramiento Industrial. johncoro@univalle.edu.co o johnjairocoronado@yahoo.com
Nelson Arzola de la Peña
Ph.D. Profesor de la Universidad Nacional de Colombia. Sede Bogotá. Departamento de Ingeniería Mecánica y Mecatrónica. narzola@unal.edu.co
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










