DOI:
https://doi.org/10.14483/23448393.2712Published:
2004-11-30Issue:
Vol. 10 No. 2 (2005): July - DecemberSection:
Science, research, academia and developmentAplicación de Teorías de Color en Imágenes Digitales
Keywords:
Estandarización de color, Espacio de Hering, espacio de color, segmentación de color (es).Downloads
References
W. Skarbek y A. Koschan, «Colour Image Segmentation - A Survey-», Techniser Berich 94-32, (1994).
J. Liu, «Multiresolution Colour Image Segmentation», Department of Computational Science University of Saskatchewan, (1993).
S. Fischer, P. Schmid and J. Guillod, «Analysis of skin lesions with pigmented networks», Proceedings of the International Conference on Image Processing, (1996).
A. Drimbaream and P. F. Whelan, «Colour texture analysis: A comparative study» . Vision System Laboratory, School of Electronic Engineering, Dublin City University, (2000).
A. Hanbury y J. Serra. «Mathematical Morphology in the HLS Colour Space», (2001).
Z. Garzon Z, A. Restrepo P. Avances en estandarización de color en imágenes digitales bajo condiciones de iluminación cambiante. Memorias VIII Simposio de Tratamiento de Señales, Imágenes y Visión Artificial, Universidad Industrial de Santander, Bucaramanga, Colombia (2002).
Alfredo Restrepo Palacios, Jesús A. Vega. Localized color contrast enhancement. IX Simposio de Tratamiento de Señales, Imágenes y Visión Artificial, Universidad Nacional sede Manizales, Manizales, Colombia (2004).
Alfredo Restrepo, Alejandra Nieto, Sandra Ardila, and Jesús Vega. An Aproximation to Color standardization. 4th IASTED International Conference on Signal and Image Processing, Kauai, Hawaii, USA (2002).
U. Nehmzow and H. V. Neto, «Locating Objects Visually Using Opposing-Colour-Channel Coding», Proc. Towards Intelligent Mobile Robots, TIMR (2003).
Bai Hangliang and Lin Changping. «An hybrid license plate extraction method based on edge statistics and morphology». Proceedings of the 17th International Conference on Pattern Recognition, (2004).
S. J. Sangwine, R. E. N. Horner. The Colour Image Processing Handbook, Chapman & Hall, (1998).
R. C. Gonzalez, R. E. Woods. Digital Image Processing, Prentice Hall, Inc., (2001).
J. C. Russ. The Image Processing Handbook, CRC Press, (2002).
R. L. Burden, J. D. Faires. Análisis Numérico, International Thomson Editores, S. A., (2002).
J. H. Mathews, K. D. Fink. Métodos Numéricos con Matlab, Prentice Hall, Inc., (2000).
S. C. Chapra, R. P. Canale. Métodos Numéricos para Ingenieros, Mc Graw-Hill, (1999).
W. K. Pratt. Digital Image Processing/3E, John Wiley, (2001).
Varsha Kamat and Subramaniam Ganesan. «An Efficient implementation of the Hough transform for detecting vehicle license plates using DSP's». Real-Time Technology and Applications Symposium, (1995).
T. Naito, K. Yamada, T. Tsukada, K. Kozuda and S. Yamamoto. «License plate recognition method for inclined plates outdoors». International Conference on Information Intelligence and Systems, 1999.
Jun-Wei Hsieh, Shih-Hao Yu and Ling-Shang Chen. «Morphology-based license plate detection from complex scenes». Proceedings. 16th International Conference on Pattern Recognition, (2002).
Muhammad Sarfraz, Mohammed Jamael Ahmed and Syed A. Ghazi. «Saudi Arabian license plate recognition system». Proceedings of the 2003 International Conference on Geometric Modeling and Graphics, (2003).
M. Shridhar, J. W. V. Miller, G. Houle, Leendert Bijnagte. «Recognition of license plate images: issues and perspectives». Fifth International Conference on Document Analysis and Recognition, (1999).
Image Processing Toolbox for use with Matlab, user's guide version 5. The Mathworks, Inc., (2004).
I. Pitas. Digital Image Processing and Applications, John Wiley, (2000).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2005-00-00 vol:10 nro:2 pág:14-22
Aplicación de teorías de color en imágenes digitales
Jesús Antonio Vega Uribe
Director del Grupo de Investigación en Tratamiento de Señales y Microelectrónica. Dirección General de Investigaciones. Universidad Pontificia Bolivariana seccional Bucaramanga.
Marlon Alfonso Reyes Figueroa
Miembro del Grupo de Investigación en Tratamiento de Señales y Microelectrónica. Universidad Pontificia Bolivariana seccional Bucaramanga.
Alfredo Restrepo Palacios
Director del Laboratorio de Señales. Universidad de los Andes.
Resumen
Los trabajos recientes realizados con espacios de color en procesamiento digital de imágenes se relacionan con segmentación de imágenes a color, análisis de textura, morfología matemática, estandarización de imágenes a color y localización de objetos. Los sistemas no lineales son frecuentes en Espacios de Color no tradicionales (Espacio de Hering), pues estos buscan realzar ciertas particularidades de una imagen. Este documento presenta el trabajo realizado con las teorías de Colores Oponentes y Tricromaticidad (RGB), como representaciones tridimensionales, utilizando transformaciones lineales y no lineales entre estos espacios de color. Además se presentan dos soluciones numéricas para el sistema de ecuaciones no lineales planteado. Con base en los resultados positivos obtenidos con los algoritmos diseñados, estos fueron utilizados para la implementación de un sistema de ubicación de placas vehiculares para el cual se involucran los efectos de la iluminación.
Palabras clave:
Estandarización de color, Espacio de Hering, espacio de color, segmentación de color.
Abstract
Recent works with colour spaces in digital imagen processing are related to colour image segmentation, texture analysis, image morphology, colour image standardization, and object localization. Non-linear systems are frequently present in non-traditional colour spaces (Hering Space) since they help to enhance some specific image characteristics. The present work is related with the study and application of two colour theories: Opponent Colours and Tricromaticity (RGB) as tridimensional representations, using linear and non-linear transformations among these colour spaces. In addition, this paper presents two numeric solutions to solve the implicit non-linear equation system. Due to the positive results obtained with the proposed algorithms, they were implemented to develop a computerized license plate identification system with the introduction of illumination effects.
Key words:
color standardization, Hering space, color spaces, color segmentation.
1. INTRODUCCIÓN
Existen dos teorías importantes que explican y dirigen la investigación sobre la visión del color: la teoría de la tricromáticidad, también conocida como la teoría de Young-Helmholtz y la teoría de procesos-oponentes. Estas teorías son complementarias y explican los procesos que intervienen en diversos niveles en el sistema visual humano[10]. Por otra parte encontramos los espacios de color o modelos de color, los cuales provienen de modelos de sistemas visuales (RGB, espacio de colores oponentes, IHS), también provienen de adaptaciones del domino técnico (colorimetría: XYZ, televisión: YUV, etc.) o desarrollados especialmente para el procesamiento de imágenes[4] (por ejemplo, espacio Otha, espacio Kodak Photo YCC, etc.)[11].
Los Espacios de Color convencionales, en el procesamiento digital de imágenes a color, como por ejemplo el espacio RGB, con el cual trabajan las cámaras digitales, son arreglos tridimensionales de las sensaciones del color.
Para llevar a cabo el análisis de ciertas imágenes se requiere transformar estas imágenes de su espacio original (Espacio RGB) a otros espacios convencionales tales como: Espacio de Colores Oponentes, Espacio CMY, Espacio CMYK o el Espacio HSI [11], [12], [13]. Para estos espacios de color en ciertas aplicaciones como por ejemplo la segmentación con base en color [1], [2], [3] ó estandarización de imágenes [6], [7], [8], es necesario realizar algunas modificaciones en busca de un mejor aprovechamiento de las características de las imágenes [5], [9]. Estos nuevos espacios de color en su mayoría se representan matemáticamente por sistemas No Lineales, lo cual hace compleja su apreciación en el espacio de color original.
La solución de un sistema de ecuaciones no lineales consiste en un conjunto de valores que simultáneamente deben ser el resultado de todas las ecuaciones igualadas a cero. La mayoría de los enfoques para determinar tales soluciones son extensiones de los métodos abiertos para resolver simples ecuaciones, como por ejemplo: el método de iteración de punto fijo, el método de Newton-Raphson y método de cuasi-Newton o método Broyden. Después de varias pruebas realizadas a los métodos mencionados anteriormente, se obtuvo un excelente resultado mediante el desarrollo de dos algoritmos de análisis numérico, mas concretamente relacionados con el método de Newton para sistemas de ecuaciones no lineales. Estos algoritmos se implementaron utilizando el software de desarrollo Matlab1, obteniendo muy buenos resultados.
2. CONCEPTUALIZACIÓN Y METODOLOGÍA
2.1. Espacios de color
En el espacio RGB (Figura 1) cada color se representa por sus componentes espectrales primarios; rojo, verde y azul [11]. Este modelo está basado sobre un Sistema de coordenadas cartesianas [R G B].

El modelo RGB concuerda con el hecho de que el ojo humano percibe fuertemente el rojo, el verde y el azul. Sin embargo cuando los humanos vemos el color de un objeto, lo describimos por su tono, el cual es un atributo que describe la pureza del color; su saturación, que nos da una medida del grado al cual un color puro es diluido por la luz blanca; y brillantez o valor, que corresponden a una descripción de la intensidad o brillo del color. El modelo de color que se define en términos de estas tres componentes es el Espacio HSV del inglés (Hue) Tono; (Saturation), Saturación; y (Value) Valor.
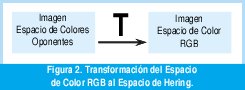
El Espacio de Hering o también llamado Espacio de Colores Oponentes (figura 3) está inspirado por la fisiología del sistema visual humano (Proceso de Colores Oponentes) propuesto por Ewald Hering (1905), quien planteó la existencia de tres canales(procesos) oponentes en el sistema visual humano: rojo-verde denominado proceso RG, amarillo-azul denominado proceso YB y acromático (blanco-negro) denominado proceso WBk. La teoría de procesos oponentes de Hering fue uno de los primeros acercamientos para separar la luminancia de la cromaticidad. La transformación del espacio RGB al espacio de Hering genera un sistema de ecuaciones lineales (figura 4).
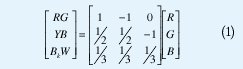

2.2. Espacio de color del nuevo modelo de Hering
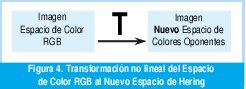
Recientes investigaciones realizadas en estandarización de imágenes [6] concluyeron que «el rojo puro en RGB tiene valor en las tres componentes en Hering», por lo que desarrollaron una nueva transformación no lineal (Ecuación 2) en la que el rojo puro no contenga valores en la componente YB de Hering, figura 5.
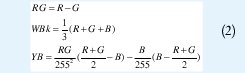
En un sistema de ubicación de placas vehiculares desarrollado con base en segmentación en color se comprobó que el espacio de color para el nuevo modelo de Hering (Figura 5), permite que los conjuntos de convergencia para la segmentación con base en color, se encuentren establecidos por rangos de menor tamaño (Tabla 1) con el problema de visualizar la imagen luego de que esta se ha transformado al nuevo modelo de Hering.
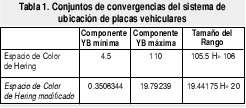

Para lograr realizar esta transformación inversa no lineal se efectuaron dos pruebas, las cuales se describen a continuación:
•Se emplearon programas matemáticos por computador que trabajan desde el punto de vista simbólico, entre ellos Maple 7.0 y Mathematica 4.0 para hallar los sistemas de ecuación para la transformación inversa, pero los resultados fueron tres diferentes soluciones por cada componente de RGB, es decir, R1, G1, B1; R2, G2, B2; y R3, G3, B3. Donde cada trío de solución generaba un número complejo para algunos colores de la imagen. Luego se desarrolló en Matlab un algoritmo en el que los tres tríos estuvieran presentes y con base en una comparación con el valor original (imagen original) se determinó cual de los tres tríos era el adecuado para cada uno de los píxeles. Este procedimiento arrojó buenos resultados para lograr visualizar en el modelo RGB una imagen que se ha transformado al nuevo espacio de Hering, pero presentó la desventaja de depender de una comparación de la imagen original, lo cual no es muy conveniente ya que en este proyecto la imagen original se pierde y lo que interesa es solo el área de la placa vehicular, debido a que las dimensiones de la imagen varían. Por tal motivo se descartó este procedimiento.
•El segundo procedimiento consistió en darle solución a esta transformación no lineal (Ecua ción 2), por medio de análisis numérico. El pri mer método escogido es el método de Newton- Raphson [14], [15], [16] para un sistema no lineal de tres variables (Ecuación 2), el cual permite solucionar numéricamente un sistema no lineal F(x) = 0, dada una aproximación inicial P0, se genera una secuencia {Pk} que converja a la solución P, es decir F(P) = 0, para ello, el método de Newton-Raphson para sistemas de ecuaciones no lineales sigue la estrategia de: linealizar y resolver, repitiendo los pasos con la frecuencia que sea necesaria.
Se considera el sistema no lineal,
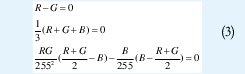
Se utiliza el método de Newton-Raphson iniciando con (R0,G0,B0) y se calcula (R1,G1,B1), (R2,G2,B2), hasta (Rn,Gn,Bn) teniendo en cuenta que el error cumpla con el criterio de parada de 1x10-3. El Algoritmo de Newton-Raphson (N-R) implementado se muestra a continuación:
Punto inicial (número aleatorio) P1 = (R1, G1, B1)
Paso 1N-R. Se Establece la Tolerancia, el cual establece el criterio de parada.
Tol = Error máximo permitido (3)
Paso 2N-R. Mientras el error sea mayor que la tolerancia se ejecutan los pasos de 3 al 6.
Paso 3N-R. Se evalúan las funciones
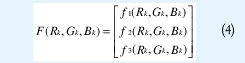

Paso 4N-R. Se calcula el vector corrección P resolviendo el sistema lineal de la ecuación 6, para poder determinar el siguiente punto de la iteración.
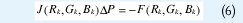
Paso 5N-R. Se calcula el siguiente punto
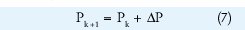
Paso 6N-R. Se calcula el Error

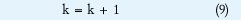
Paso 7N-R. Salida

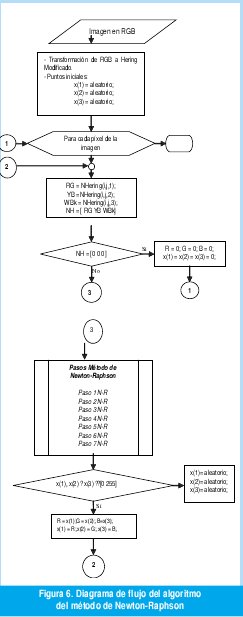
En la figura 6 se muestra el algoritmo implementado para el método de Newton-Raphson.
El segundo método numérico escogido pertenece a la técnica de actualizaciones de secante con cambio mínimo, también denominada Método cuasi-Newton o Método de Broyden14. El método de Broyden aventaja al método de Newton ya que este último requiere en cada iteración evaluar una matriz jacobiana, en cambio el método de Broyden reemplaza la matriz jacobiana con una matriz de aproximación que se actualiza en cada iteración. La principal desventaja del método de Broyden sobre el método de Newton es que se pierde la convergencia cuadrática obtenida en el método de Newton. El algoritmo para el método de Broyden (B) se muestra a continuación:
Paso 1B. Se establecemos la Tolerancia
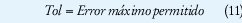

Paso 2B. Se evalúan las funciones
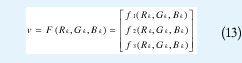
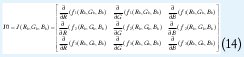
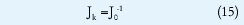
Paso 3B. Se calcula P resolviendo el sistema lineal
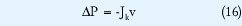
Paso 5B. Se calcula el siguiente punto
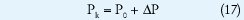
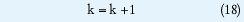
Paso 6B. Mientras el error sea mayor que la tolerancia, realice los paso del 7 al 12.
Paso 7B. Se establece

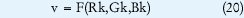

Paso 8B. Se evalúa



Paso 9B. Se aplica la fórmula de ShermanMorrison, la cual permite calcular Jk-1 directamente de Jk-1-1, con lo cual se prescinde de una inversión matricial en cada iteración.
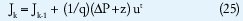
Paso 10B. Se evalua

Paso 11B. Se calcula el siguiente punto

Paso 12B. Se calcula el Error


Paso 13B. Salida

De los algoritmos implementados de Newton-Raphson y Broyden, se toman algunos aspectos importantes:
•Como estos son procedimientos iterativos, conlleva un gasto de tiempo considerable, por tal motivo y tomando en cuenta que el color negro posee las mismas componentes en RGB y en Colores Oponentes, es decir, para cada componente su valor es cero; si el píxel en el modelo de Hering tiene valores (0,0,0) automáticamente a dicho píxel se le adjudica el valor de (0,0,0) en RGB.
•Los puntos iniciales del primer píxel evaluado de la imagen son puntos aleatorios, es decir, las componentes de P0 son números enteros aleatorios dentro del rango [0 255]. Y los puntos iniciales del siguiente píxel y de los demás píxeles evaluados son los resultados del procedimiento para el píxel anterior.
•Si el determinante del Jacobiano es igual a cero o menor que 1*10-16, se interrumpe el proceso y se reanuda con otros valores iniciales, determinados aleatoriamente, ya que, si esto ocurre se presentarían matrices singulares.
En los ejemplos siguientes se muestra que el método de Newton ofrece una mayor aproximación a la imagen original.
3. RESULTADOS EXPERIMENTALES
Para dar validez a los algoritmos implementados, se generaron varios ejemplos con imágenes tomadas principalmente en el parqueadero de la Universidad en el transcurso de un día, con el fin de obtener diferentes grados de iluminación. La principal aplicación de los algoritmos diseñados es la segmentación de placas vehiculares de servicio particular en Colombia. La base de datos fue construida utilizando una cámara digital Sony referencia DSC-P51 con una resolución de 640x480.
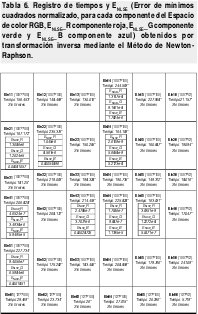
Para realizar el cálculo de error entre la imagen original y la imagen obtenida después de la transformación inversa se utilizó el concepto de Error de mínimos cuadrados normalizado17.
3.1. Pruebas realizadas
Para cualquiera de las imágenes de la base de datos, se tiene un diagrama de bloques que muestra las transformaciones realizadas con el fin de segmentar la placa vehicular (figura 7).
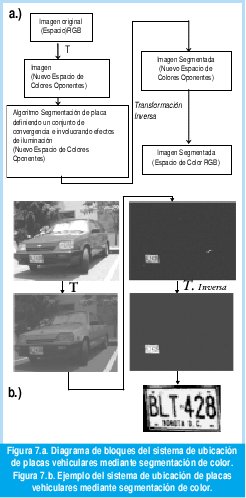
A partir de un píxel de prueba tomado de la imagen de la figura 8 se realizó un estu dio comparativo con los métodos de Newton-Raphson y Broyden. En las tablas 2 y 3 se muestra la rapidez de convergencia entre estos métodos.
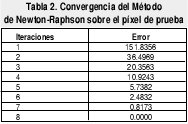

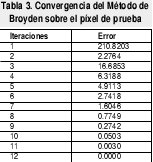
Esta comparación fue realizada para un mismo valor de píxel en una imagen. En las anteriores tablas se puede apreciar fácilmente como el método de Newton converge con mayor rapidez, debido a su característica de convergencia cuadrática.



4. CONCLUSIONES
•Durante el desarrollo de las pruebas de los algoritmos, se determinó que el método de Newton-Raphson ofrece una mayor rapidez de ejecución y un porcentaje de error mucho menor que el método de Broyden. Ver anexo 1.
• Los porcentajes de error que aparecen en la ejecución de los programas se debe a que para ciertos tríos de entrada existen varias posibles raíces. Como se aprecia los resultados son prácticamente exactos por lo que su aplicación es totalmente recomendada en el área de procesamiento de imágenes. La única desventaja de la implementación de estos métodos numéricos esta en que no podemos trabajar las imágenes como matrices, sino, que debemos implementar el procedimiento píxel por píxel lo que hace que el tiempo de ejecución de los métodos sea extenso.
•Gracias a los excelentes resultados obtenidos, estos algoritmos se emplearon en un sistema de ubicación de placas vehiculares (Figura 7) logrando resultados satisfactorios.
5. REFERENCIAS BIBLIOGRÁFICAS
[1] W. Skarbek y A. Koschan, «Colour Image Segmentation - A Survey-», Techniser Berich 94-32, (1994).
[2] J. Liu, «Multiresolution Colour Image Segmentation», Department of Computational Science University of Saskatchewan, (1993).
[3] S. Fischer, P. Schmid and J. Guillod, «Analysis of skin lesions with pigmented networks», Proceedings of the International Conference on Image Processing, (1996).
[4] A. Drimbaream and P. F. Whelan, «Colour texture analysis: A comparative study» . Vision System Laboratory, School of Electronic Engineering, Dublin City University, (2000).
[5] A. Hanbury y J. Serra. «Mathematical Morphology in the HLS Colour Space», (2001).
[6] Z. Garzon Z, A. Restrepo P. Avances en estandarización de color en imágenes digitales bajo condiciones de iluminación cambiante. Memorias VIII Simposio de Tratamiento de Señales, Imágenes y Visión Artificial, Universidad Industrial de Santander, Bucaramanga, Colombia (2002).
[7] Alfredo Restrepo Palacios, Jesús A. Vega. Localized color contrast enhancement. IX Simposio de Tratamiento de Señales, Imágenes y Visión Artificial, Universidad Nacional sede Manizales, Manizales, Colombia (2004).
[8] Alfredo Restrepo, Alejandra Nieto, Sandra Ardila, and Jesús Vega. An Aproximation to Color standardization. 4th IASTED International Conference on Signal and Image Processing, Kauai, Hawaii, USA (2002).
[9] U. Nehmzow and H. V. Neto, «Locating Objects Visually Using Opposing-Colour-Channel Coding», Proc. Towards Intelligent Mobile Robots, TIMR (2003).
[10] Bai Hangliang and Lin Changping. «An hybrid license plate extraction method based on edge statistics and morphology». Proceedings of the 17th International Conference on Pattern Recognition, (2004).
[11] S. J. Sangwine, R. E. N. Horner. The Colour Image Processing Handbook, Chapman & Hall, (1998).
[12] R. C. Gonzalez, R. E. Woods. Digital Image Processing, Prentice Hall, Inc., (2001).
[13] J. C. Russ. The Image Processing Handbook, CRC Press, (2002).
[14] R. L. Burden, J. D. Faires. Análisis Numérico, International Thomson Editores, S. A., (2002).
[15] J. H. Mathews, K. D. Fink. Métodos Numéricos con Matlab, Prentice Hall, Inc., (2000).
[16] S. C. Chapra, R. P. Canale. Métodos Numéricos para Ingenieros, Mc Graw-Hill, (1999).
[17] W. K. Pratt. Digital Image Processing/3E, John Wiley, (2001).
[18] Varsha Kamat and Subramaniam Ganesan. «An Efficient implementation of the Hough transform for detecting vehicle license plates using DSP's». Real-Time Technology and Applications Symposium, (1995).
[19] T. Naito, K. Yamada, T. Tsukada, K. Kozuda and S. Yamamoto. «License plate recognition method for inclined plates outdoors». International Conference on Information Intelligence and Systems, 1999.
[20] Jun-Wei Hsieh, Shih-Hao Yu and Ling-Shang Chen. «Morphology-based license plate detection from complex scenes». Proceedings. 16th International Conference on Pattern Recognition, (2002).
[21] Muhammad Sarfraz, Mohammed Jamael Ahmed and Syed A. Ghazi. «Saudi Arabian license plate recognition system». Proceedings of the 2003 International Conference on Geometric Modeling and Graphics, (2003).
[22] M. Shridhar, J. W. V. Miller, G. Houle, Leendert Bijnagte. «Recognition of license plate images: issues and perspectives». Fifth International Conference on Document Analysis and Recognition, (1999).
[23] Image Processing Toolbox for use with Matlab, user's guide version 5. The Mathworks, Inc., (2004).
[24] I. Pitas. Digital Image Processing and Applications, John Wiley, (2000).
Jesús Antonio Vega Uribe
Ingeniero Electricista, M.Sc. Profesor Asistente Facultad de Ingeniería Electrónica. Universidad Pontificia Bolivariana seccional Bucaramanga. Dirección General de Investigaciones - Director del Grupo de Tratamiento de Señales y Microelectrónica. jvega@upbbga.edu.co
Marlon Alfonso Reyes Figueroa
Ingeniero Electrónico. Universidad Pontificia Bolivariana seccional Bucaramanga. Miembro del Grupo de Tratamiento de Señales y Microelectrónica. marlon.alfonso.reyes.figueroa@gmail.com
Alfredo Restrepo Palacios
Ingeniero Electrónico, Ph.D. Universidad de los Andes, Bogotá. Director del Laboratorio de Señales. arestrep@uniandes.edu.co
ANEXOS



Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










