DOI:
https://doi.org/10.14483/23448393.2828Published:
2001-11-30Issue:
Vol. 7 No. 2 (2002): July - DecemberSection:
Science, research, academia and developmentMedición del grosor de materiales usando microondas
Keywords:
materiales, microondas, técnicas de medición. (es).Downloads
References
S. Ramon and J.R. Whinnery, Fields and Waves in Modern Radio, John Wiley, New York, 1953.
R.E. Collin, Foundations for Microwave Engineering Mc. Graw - Hill Book Co, New York, 1966.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:2 pág:109-112
Medición del grosor de materiales usando microondas1
Ramón Flórez Torres
Resumen
La medición o el monitoreo de materiales delgado en movimiento se debe hacer en forma continua, no debe haber contacto físico con el material y éste no se debe alterar. Por las anteriores razones no resulta práctico el uso de un micrómetro. Las técnicas de medición de grosores usando radioisótopos poseen las características mencionadas.
Igualmente la energía electromagnética en frecuencias de microondas, también posee las características mencionadas y la técnica de medición es la que se sugiere en este artículo. En particular se usa la banda X (8.2 Ghz-12.4), el principio de la medición se basa en medir la onda reflejada.
El método se expone en el apartado dedicado a la teoría y en el apéndice. El método de medición, los resultados, la discusión y las conclusiones se presentan para materiales como el papel y el acetato; se aplica el método sólo para materiales en reposo.
Palabras clave:
materiales, microondas, técnicas de medición.
Abstract
The monitoring and measurement of thin materials in movement has to be done in a continuous way, there must be un physical contact with the material and it should not suffer any alterations.
Thus, because of the reason previously exposed, the use of a micrometer should be avoided. The techniques of width measurement using radiosotops comprohend the mentioned caractheristic.
Key words:
Materials, microwaves, techniques of measurement.
I. LA TEORÍA
Para comprender el método empleado en la medición de grosores de materiales usando microondas se exponen algunos conceptos básicos concernientes a la teoría de propagación y reflexión de ondas electromagnéticas en medios dieléctricos.[1]
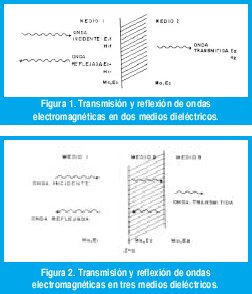
Considere la situación física mostrada en la figura 1, donde una onda electromagnética plana TEM se propaga a través del medio uno, cuyas constantes eléctricas son µ0 y 0 su impedancia intrínseca es 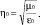
La onda incide en el medio dos de constantes µ0 y ε2 = εr2 e impedancia intrínseca de 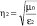
Parte de la que incide sobre el medio dos se transmite en él y parte se refleja. Así, en el medio dos existe sólo la onda transmitida, lo cual implica que ese medio se extiende indefinidamente hacia la derecha.
Se define ρ, el coeficiente de reflexión, a la relación entre el campo eléctrico reflejado (E-) y el campo eléctrico incidente (E+), es decir:
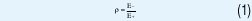
Similarmente, se define τ, el coeficiente de transmisión, a la relación entre el campo eléctrico transmitido en el medio dos (E2) y el campo eléctrico incidente en el medio como (E1+).
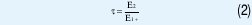
Los dos coeficientes ρ y τ cumplen la relación (3)
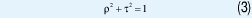
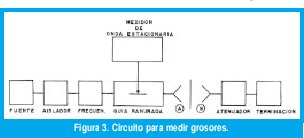
Si se supone que la propagación se hace a través de tres dieléctricos en vez de dos, se tiene, entonces, la situación mostrada en la figura 2, donde el medio tres se extiende indefinidamente hacia la derecha.
En este caso, existe una onda incidente y una onda reflejada, tanto en el medio uno como en el medio dos; mientras que en el medio tres sólo existe la onda transmitida. El coeficiente de reflexión en el medio uno depende de las características eléctricas de los medios dos y tres, de la longitud del medio dos y de la frecuencia de operación. Para hallar el coeficiente de reflexión en el medio uno, es necesario hallar los componentes de los campos eléctricos y magnéticos en cada uno de los medios, para lo cual se resuelven las ecuaciones de Maxwell y se aplican las condiciones de frontera para evaluar las constantes indeterminadas. Sin embargo, es mucho más sencillo tratar los diferentes medios como secciones de líneas de transmisión y usar la teoría de líneas. Usando este último método se puede demostrar (ver apéndice) que el coeficiente de reflexión en el medio uno esta dado por:
Sin el dieléctrico cuyo grosor se desea medir, se colocan los cuernos A y B a una distancia tal que el valor de la onda estacionaria sea 1; es decir, que la onda reflejada sea nula en ausencia del material dieléctrico. El medidor de onda estacionaria permite hacer la medición del coeficiente de reflexión mediante la relación:
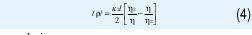
Donde S es el valor de la onda estacionaria.
En la realización del experiemento se usó un equipo de microondas que opera en la banda X.
IV. RESULTADOS
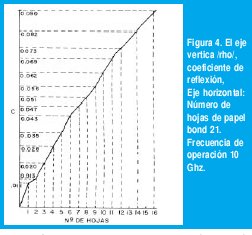
Como medios dieléctricos por medir se usaron hojas de papel bond 21 y láminas de acetato. La figura 4 muestra la curva experiemental del coeficiente de reflexión en función del número de hojas de papel, prefiriéndose así la abscisa por comodidad, aunque hay que anotar que el grosor de las hojas puede variar entre 0.085 y 0.87 mm. Como se puede apreciar en la figura la magnitud del coeficiente de reflexión es casi lineal con el número de hojas. El efecto de espacio entre hojas de papel es difícil de predecir, así que se procuró en el experiento, que las hojas quedaran bien pegadas y evitar de esta manera esos espacios.
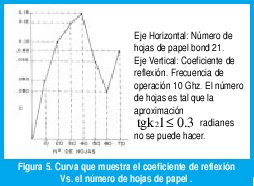
En la figura 5 se muestra la limitación del método a aquellos grosores para los cuales se cumple la desigualdad kl<0.3 radianes.
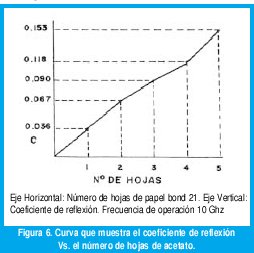
Finalmente, la figura 6 presenta el coeficiente de reflexión vs el número de láminas de acetato; otra vez se observa la linealidad del coeficiente de reflexión con el grosor.
V. DISCUSIÓN
Aunque los resultados son satisfactorios vale la pena discutir varios aspectos de importancia:
5.1 En la deducción de la fórmula del coeficiente de reflexión se implica que la onda incidente so bre el dieléctrico que se va a medir ha de ser una onda plana TEM pura; sin embargo, en el experimento, no es una onda plana TEM la que incide sobre el acetato o el papel. La guía de onda sostie ne el modo TE10, el cual tiene una componente del campo magnético en la dirección de propagación. El modo TE, en la guía, pasa a modo TEM en el espacio cuando ha viajado una distancia considerable. La figura 7 ilustra la transición del modo TE10 al modo TEM en el espacio.
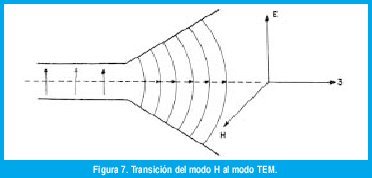
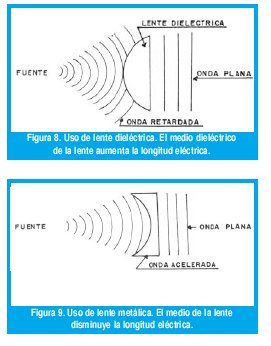
Se dice que sobre el dieléctricono incide una onda plana TEM pura porque el dieléctrico está a una distancia de 2 longitudes de onda, aproximadamente. Una solución a este problema sería la de usar lentes en la boca del cuerno con el fin de conseguir una onda plana. La figura 8 ilustra el uso de una lente de dieléctrico y la figura 9 el uso de una lente metálica, llamada también lente de dieléctrico artificial.
5.2 La guía sostiene el modo TE10 el cual pasa a ser modo TEM en el espacio y a una distancia considerable; el cuerno ayuda a hacer esta transición, no obstante, por ser finito presenta una discontinuidad la cual da lugar a la generación de modos diversos. Estos modos, obviamente representan energía que no va a estar incluida en la onda que se refleja.
5.3 En la teoría se supone que el material de la izquierda y el material de la derecha del dieléctrico dos son idénticos y por lo tanto son iguales sus impedancias intrínsecas. En el experimento estas dos impedancias están representadas por el cuerno A y un pequeño espacio de aire y el cuerno B y un pequeño espacio de aire. Dadas la idéntica construcción de los cuernos y su posición simétrica respecto del dieléctrico dos, se puede suponer que ambos lados del material dos tienen igual impedancia.
5.4 La medición del coeficiente de reflexión , no se hace justamente en el límite izquierdo del material dos sino que se hace de 22 a 32 cms. hacia la izquierda; obviamente, esto afecta tanto la fase como la magnitud del coeficiente de reflexión. Como se expuso en la teoría, lo importante es la magnitud del coeficiente de reflexión, así que las pérdidas en la transmisión (atenuación, generación de modos diversos) y descontinuidad en la guía (como la prueba para medir el coeficiente de reflexión) altera la magnitud de y por consiguiente la medición o control del grosor del material en prueba.
VI. CONCLUSIONES
•El método para medición de grosores funciona bien para dieléctricos de bajas pérdidas y cuya longitud dieléctrica sea inferior a 0.3 radianes.
•El método está restringido a materiales que sean isotrópicos, lineales y homogéneos, ya que el coeficiente de reflexión depende de las características eléctricas del material.
•El empleo de un equipo que opere a una frecuencia inferior a las de la banda X permitirán la medición o control de grosores mayores.
•El uso de lentes, ya sean dieléctricas o metálicas, permitirán realizar un experimento más ceñido a las condiciones que exige la teoría.
APÉNDICE
La demostración de la fórmula (4) es como sigue:
Los tres medios dieléctricos de la figura 2 se puede representar mediante el circuito de la figura 10.
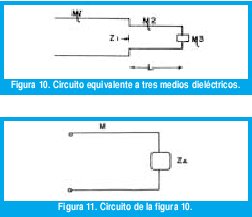
Si los medios dieléctricos uno y tres son iguales, es decir, η1= η3= η , entonces, la impedancia vista desde el punto 1 hacia la derecha esta dada por [2]:
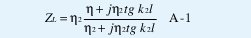
Donde k2 es la constante de propagación en el medio dieléctrico 2:
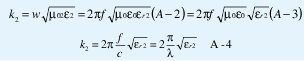
Donde λ es la longitud de onda en el espacio libre y r 2 es la permitividad relativa del medio ε2. Puesto que la permeabilidad magnética de materiales dieléctricos y metales no ferromagnéticos es igual a la permeabilidad del vacio se tiene que µ2 = µ0.
Para longitudes eléctricas pequeñas, donde k21≤ 0.3, se tiene que:

Y ZL en la ecuación (A - 1) se puede escribir así:
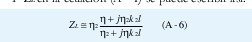
Expandiendo el denominador en una serie y efectuando el producto con el numerador se obtiene:
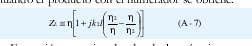
Expresión aproximada, donde los términos con (k2l)2 y potencias superiores se han despreciado.
El coeficiente de reflexión es
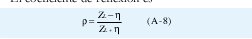
Si se sustituye ZL, que está dado por la ecuación (A-7), en la expresión del coeficiente de reflexión dado por (A-8) se obtiene:
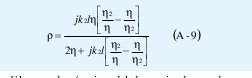
El segundo término del denominador es despreciable en comparación con η2 , así que:
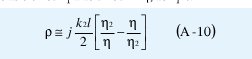
Si la ecuación (A-10) se toman las magnitudes y se despeja l, se obtiene:
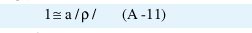
Donde
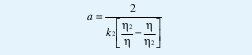
BIBLIOGRAFÍA
[1] S. Ramon and J.R. Whinnery, Fields and Waves in Modern Radio, John Wiley, New York, 1953.
[2] R.E. Collin, Foundations for Microwave Engineering Mc. Graw- Hill Book Co, New York, 1966.
NOTAS
1.Artículo publicado como Homenaje Póstumo a la memoria del Profesor Ramón Flórez Torres, quien se destacó por su labor docente e investigativa contribuyendo al fortalecimiento académico de la Facultad de Ingeniería de la Universidad Distrital Francisco José de Caldas.
Ramón G. Flórez Torres
B.S.E (E.E) y MS, Universidad de Michigan, USA, Fue profesor del programa de Ingeniería Electrónica de la Universidad Distrital Francisco José de Caldas. Fue director del programa de Ingeniería de Sistemas de la Universidad Distrital Francisco José de Caldas.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)