DOI:
https://doi.org/10.14483/23448393.2857Publicado:
2008-11-30Número:
Vol. 8 Núm. 1 (2003): Enero - JunioSección:
Ciencia, investigación, academia y desarrolloMétodo para linealizar la salida de un sensor
Method for Linealizar the Exit of a Sensor
Palabras clave:
Linealizacion, Sensor, Resistencia de linealizacion, Regresión Lineal (es).Descargas
Referencias
DAVID E. JONSON , JOHNNY R JONSON Y METER D SCOTT, Análisis Básico de Circuitos Eléctricos Prentice may, Quinta Edición .
SCHEAFFER MCCLAVE, Probabilidad y Estadística para Ingeniería, Grupo Editorial Iberoamérica Segunda Edición.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2003-00-00 vol:8 nro:1 pág:82-85
Método para linealizar la salida de un sensor
Method for Linealizar the Exit of a Sensor
Rigoberto Quintero Camacho
Miembro Grupo de Investigación Informática Educativa (GIIE) de la Universidad Distrial Francisco José de Caldas.
Resumen
En este artículo se presenta un método sencillo para linealizar un sensor. El método consiste en encontrar un valor fijo para una resistencia que se coloca en paralelo con la resistencia variable, además para probar el método se muestra un ejemplo en el que se linealiza un termistor (resistencia que varia con los cambios de temperatura), el cual es utilizado para el diseño de un circuito de medición de voltaje, en donde se requiere que la salida sea lineal.
Palabras clave: Linealizacion, Sensor, Resistencia de linealizacion, Regresión Lineal
Abstract
In this paper a simple method for lining a sensor is presented. The method consists in finding a fixed value for a resistance put parallel together with the variable resistance, an example, in which a termistor is lined, is shown as well, in order to test the method. This method is used for designing a voltage measuring circuit, where the output is required to be lineal.
INTRODUCCIÓN
Comprender el funcionamiento de los seres vivos no solamente desde el punto de vista de la fisiología si no también desde la ingeniería; este es uno de los principales objetivos de la bioingeniería, por cuanto de esta comprensión depende el éxito en la solución de problemas en el campo de la medicina como: El transplante de órganos, reconstrucción total o parcial de las extremidades, corrección de problemas de visión entre otros.
El diseño de aparatos de medición de alta precisión para sensar el comportamiento de los sistemas vivos, es de suma importancia para el logro de los objetivos anteriormente expuestos, uno de los requisitos cuando se diseñan estos aparatos de medición es la linealidad de su salida (por ejemplo en un medidor de voltaje que depende de la temperatura, la variación del voltaje por unidad de temperatura debe ser constante), es así como en este articulo se presenta un modelo muy sencillo para linealizar la salida de un sensor y este método se prueba linealizando un resistor.
Este trabajo es un aporte en el diseño de sistemas de medición, por cuanto permite calcular el valor de la resistencia constante, que debe colocarse en paralelo con la resistencia variable, de tal manera que la salida de un censor resistivo resulte lineal; investigación que nació como un aporte propio en un trabajo como estudiante de la cátedra de Instrumentación, en la especialización en Bioingeniería.
LINEALIZACIÓN DE UN SENSOR
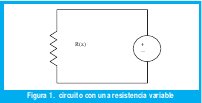
Supongamos que el sistema (sensor) que se esta diseñando tiene una resistencia variable R(x), la cual varia no linealmente de acuerdo con una variable independiente x (por ejemplo la temperatura) que pertenece al intervalo [a , b], esta situación la representamos mediante el circuito de la figura 1, linealizar el sistema consiste en establecer una metodología para diseñar el sistema de tal manera que la salida sea lineal
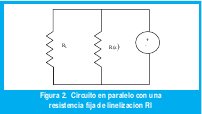
El método consiste en encontrar una resistencia fija en paralelo, la cual llamaremos resistencia de linealización RL, esta situación la mostramos en la figura 2
CÁLCULO DE RL
Supongamos que tomamos n valores de la variable x en el intervalo [a, b], y se toman n valores de la resistencia R(x) sean dichos valores; (x0, R0), (x1,R1) , (x2,R2), ..., (xn-1 ,Rn-1), además, podemos suponer que los xk están ordenados de menor a mayor, esto es: a=x0<x1<x2<x3<.xn-1=b, con lo cual Rk = R(xk), para k= 0,1,2,3,,,,,,n-1, como las resistencias están en paralelo, entonces la resistencia equivalente [1]esta dada por:
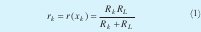
como lo que se busca es que la respuesta rk sea lineal, entonces tenemos que:
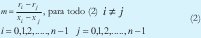
donde m es una constante real (pendiente de la recta), en particular podemos encontrar m así: si definimos rmax = r (x max ) y rmin = r (x min ) , entonces:
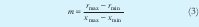
de otra parte reemplazando a cada rk definido en (1) en (2) tenemos:
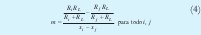
luego:
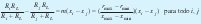
remplazando tenemos:

factorizando RL tenemos que:

como RL es distinto de cero tenemos
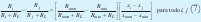
como Rmax = R(xmax) = R(b) = Rb y Rmin = R(xmin) = R(a) = Ra remplazando en (7), y además como la igualdad es cierta para todo i,j entonces se puede tomar i=n:
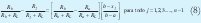
si definimos: p=b-xj/b-a,tenemos que:
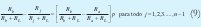
despejando RL en 9 se tiene:
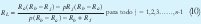
Dado que la salida de los termistores es no lineal, a continuación se presenta un ejemplo en el se linealiza un termistor
LINEALIZACIÓN DE UN TERMISTOR
Los termistores son resistencias sensibles a la temperatura, estos se fabrican de materiales semiconductores tales como los óxidos de níquel, cobalto o manganeso y sulfuros de hierro, aluminio o cobre. Los óxidos semiconductores, al contrario de los metales, muestran un decremento en la resistencia con un incremento en la temperatura. La relación entre la resistencia R(x) como función de la temperatura x del termistor se muestra a continuación:
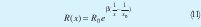
donde Ro es la resistencia del termistor a la temperatura x0 y β es una constante del material, llamada la temperatura característica del material, claramente la ecuación anterior nos indica que la salida de un termistor es no lineal, en la tabla1 y la Fig. 3 se muestra la salida de un termistor (con una constante de auto calentamiento de 2mV/oC) para diseñar un termómetro el cual se quiere que opere en un rango entre 20 y 42 grados centígrados
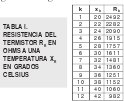

como se observa la salida es no lineal, por lo tanto para linealizar la salida se debe calculara RL en la ecuación (10 ), para lo cual se requiere el valor de p, el cual se calcula mediante la ecuación 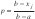 donde j es cualquier valor entre 1 y 12, en este caso elegimos j = 7 es decir el valor central de la temperatura xj = 32, así que
donde j es cualquier valor entre 1 y 12, en este caso elegimos j = 7 es decir el valor central de la temperatura xj = 32, así que 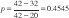 , y para calcular RL, utilizamos la formula 10, esto es:
, y para calcular RL, utilizamos la formula 10, esto es:
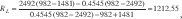 con este valor aplicamos la ecuación (1) a los valores de la tabla 1 y obtenemos la tabla 2 y la Fig 4,
con este valor aplicamos la ecuación (1) a los valores de la tabla 1 y obtenemos la tabla 2 y la Fig 4,

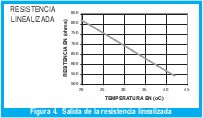
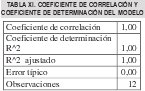
Una forma de probar que efectivamente la salida es lineal es utilizar del método de los mínimos cuadrados [2] para ajustar los datos (xk , rk) a una recta y verificar mediante el coeficiente de determinación del modelo, la tabla de análisis de varianza y las pruebas sobre los parámetros de modelo que los datos se ajustan a un modelo lineal [2], lo cual se puede realizar con cualquier paquete estadístico. Las tablas 3, 4, 5 de salida de computadora, sobre la idoneidad del modelo se muestran a continuación:



como se puede verificar en las tablas tanto el coeficiente de correlación como el de determinación son aproximadamente iguales 1 lo que indica que los datos se ajustan a un modelo lineal, además la prueba F del modelo, la que se muestra en la tabla de análisis de varianza, demuestra también que el modelo es lineal y este hecho se refuerza con la prueba t , para los parámetros del modelo que indica que la pendiente de la recta no es cero, así podemos afirmar que el modelo es : r (x)=-12,52x+1067,05. Que la salida de un sistema de medición sea lineal, es una característica importante del sistema por cuanto el cambio en la respuesta por unidad de la variable independiente es constante.
SENSIBILIDAD
La sensibilidad en un punto a de un sistema f(x), se define como la derivada en ese punto, en el caso del termistor al sensibilidad mide la variación de la resistencia por unidad de temperatura, por lo tanto la sensibilidad de la resistencia linealizada es la pendiente de la recta (-12,52), o también se puede tomar la medida aproximada de la sensibilidad en cada punto mediante la aproximación:
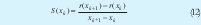
ESTIMACIÓN DEL ERROR
Además del error de estimación del modelo de mínimos cuadrados, el cual se define como ek=rkr(xk), se debe calcular el error que se comente en la medición y se define como la razón entre el error de estimación del modelo y la sensibilidad esto es: Ek = ek/s(xk)aplicando la relación (12 ) y la formula del Ek = error en los datos de la tabla 2 se obtiene la tabla 6, notamos que el error de medición para el termistor da en unidades de temperatura
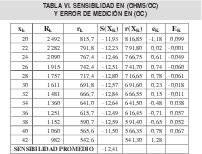
Es de anotar que la sensibilidad promedio como es de esperarse es parecida a la pendiente de la recta estimada.
DISEÑO DEL CIRCUITO DE MEDICIÓN
Usando un montaje potenciometrico de pendiente negativa se diseña un circuito de medición, dicho circuito se presenta en el siguiente gráfico:
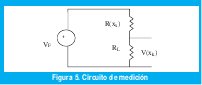
Para calcular el voltaje de alimentación VF , es necesario tener en cuenta que para el termistor que se esta diseñando, la potencia que se disipa dentro de él, no calienta mas 0.05oC, con lo cual como el termistor tiene la característica de que el autocalentamiento es de 2mV/oC, luego La potencia de disipación es (0.05).2=0.1mV = 0.0001V , además utilizando un divisor de voltaje [1]se obtiene la siguiente relación:
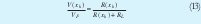
donde RL es la resistencia de linealizacion calculada anteriormente, si tomamos R(xk) = |Rb - Ra| = Rc y para este valor de la resistencia encontramos un valor Vc, mediante la formula para el calculo de la potencia 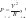 , en particular Vc = √PRc y remplazando la ecuación (13) tenemos:
, en particular Vc = √PRc y remplazando la ecuación (13) tenemos: 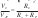 que despejando VF tenemos:
que despejando VF tenemos:
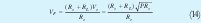
para el caso particular de este resistor Rc = 1510 , RL = 1212,55 , P = 0.0001, y remplazando estos valores en (14) tenemos:
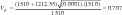
este valor se remplaza en (13), para obtener la salida de voltaje la cual se muestra en la tabla 7 que contiene también los valores de la sensibilidad y el error de medición, la Fig 6 muestra la salida de voltaje en función de la temperatura, donde se observa que efectivamente es lineal, esto se corrobora ajustando los datos, de la temperatura contra voltaje, a un modelo lineal[2] como se puede verificar mediante las tablas 7, 8 y 9, por lo tanto el modelo V(x)=-0,007x+0,617 , ajusta perfectamente la salida de voltaje
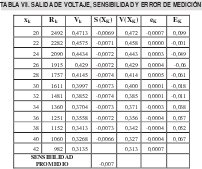



Se observa que los errores de medición de la temperatura en el caso del voltaje (que se calculan utilizando las formulas que se usaron para el calculo de los errores para la resistencia) son los mismos en el caso de resistencia, como era de esperarse.
CONCLUSIONES
- El uso adecuado de los conceptos matemáticos como el de derivada, linealidad nos conducen a resultados de mucha utilidad en la ingeniería.
- Es posible utilizar esta metodología en el caso de sensores capacitivos solamente que la capacitancia variable y la capacitancia fija van en serie.
- La linealizacion de un sensor es importante por cuanto la sensibilidad del sistema de medición es constante.
REFERENCIAS BIBLIOGRÁFICAS
[1] DAVID E. JONSON , JOHNNY R JONSON Y METER D S<COTT, Análisis Básico de Circuitos Eléctricos Prentice may, Quinta Edición .
[2] SCHEAFFER MCCLAVE, Probabilidad y Estadística para Ingeniería, Grupo Editorial Iberoamérica Segunda Edición.
Rigoberto Quintero Camacho
Profesor de Matemáticas de la Facultad de Ingeniería, Licenciado en Matemáticas Universidad Pedagógica Nacional, Especialista en Estadística Universidad Nacional, Especialista en Bioingeniería Universidad Distrital.
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)