DOI:
https://doi.org/10.14483/23448350.12506Published:
01/01/2018Issue:
Vol. 31 No. 1 (2018): January-April 2018Section:
Science and EngineeringSimilarity solution and Runge Kutta method to a thermal boundary layer model at the entrance region of a circular tube: The Lévêque Approximation
Keywords:
Thermal entrance region, Thermal boundary layer, Dimensionless variables, Temperature, Nusselt number, Runge-Kutta method (en).Keywords:
Región de entrada térmica, capa límite térmica, variables sin dimensión, temperatura, número de Nusselt, método de Runge-Kutta (es).Downloads
References
Abramowitz, M. and Stegun, I. (1965). Handbook of Mathematical Functions. New York: Dover.
Asako, Y., Nakamura, H. and Faghri, M. (1988). Developing Laminar Flow and Heat Transfer in the Entrance Region of Regular Polygonal Ducts. Int. J.Heat Mass Transfer, 31, 2590-2593. https://doi.org/10.1016/0017-9310(88)90186-X
Baehr, H. and Stephan, K. (1998). Heat Transfer. Berlin: Springer-Verlag.
Belhocine, A. (2016). Numerical study of heat transfer in fully developed laminar flow inside a circular tube. Int J AdvManuf Tech, 85(9), 2681-2692. https://doi.org/10.1007/s00170-015-8104-0
Belhocine, A. and Wan Omar, W.Z. (2015). Numerical study of heat convective mass transfer in a fully developed laminar flow with constant wall temperature. Case Studies in Thermal Engineering, 6, 116-127. https://doi.org/10.1016/j.csite.2015.08.003
Belhocine, A. and Wan Omar, W.Z. (2017). An analytical method for solving exact solutions of the convective heat transfer in fully developed laminar flow through a circular tube. Heat Transfer-Asian Research, 1-12. https://doi.org/10.1002/htj.21277
Bird, R.B., Stewart, W.E. and Lightfoot, E.N. (1960). Transport Phenomena. New York: John Wiley and Sons.
Churchill, S.W. and Ozoe, H. (1973a). Correlations for Laminar Forced Convection with Uniform Heating in Flow Over a Plate and in Developing and Fully Developed Flow in a Tube. ASME J. Heat Transfer,95, 78-84. https://doi.org/10.1115/1.3450009
Churchill, S.W. and Ozoe, H. (1973b). Correlations for Laminar Forced Convection in Flow Over an Isothermal Flat Plate and in Developing and Fully Developed Flow in an Isothermal Tube. ASME J. Heat Transfer, 95, 416-419. https://doi.org/10.1115/1.3450078
Ebadian, M.A. and Dong, Z.F. (1998). Forced convection internal flows in ducts. In: Rohsenov, W.M., Hartnett, J.P., and Cho, Y.I. (eds.), Handbook of heat transfer,3rd edition (pp.5.1-5.137). New York: McGrawHill.
Garimella, S., Dowling, W.J., Van derVeen, M. and Killion, J. (2000). Heat Transfer Coefficients for Simultaneously Developing Flow in Rectangular Tubes. Proceedings of the 2000 International Mechanical Engineering Congress and Exposition, vol. 2, pp. 3-11.
Hausen, H. (1943). Darstellung des Wärmeübergangs in Rohren durch verallgemeinerte Potenzbezie-hungen. VDI-Zeitung, Suppl. Verfahrenstechnik, 4, 91-98.
Kakac, S. and Yener, Y. (1983). Laminar Forced Convection in the Combined Entrance Region of Ducts. In: Kakac, S., Shah, R.K. and Bergles, A.E. (eds.), Low Reynolds Number Heat Exchangers (pp. 165-204). Washington: Hemisphere Publishing.
Kakac, S., Shah, R.K. and Aung, W. (1987). Handbook of Single Phase Convective Heat Transfer. New York: Wiley.
Lévêque, M.A. (1969). Les lois de la transmission de chaleur par convection. Annales des Mines, Memoires, Series 12, 13, 201-299, 305-362, 381-415 (1928). In Newman, J., Trans. ASME J. Heat Transfer, 91, 177.
Shah, R.K., and London, A.L. (1978). Laminar Flow Forced Convection in Ducts. New York: Academic Press.
Stephan, K. (1959). Warmeubergang und Druckabfall bei Nicht Ausgebildeter Laminar Stromung in Rohren und in Ebenen Spalten. Chem-Ing-Tech,31, 773-778. https://doi.org/10.1002/cite.330311204
Yilmaz., T. and Cihan, E. (1993). General equation for heat transfer for laminar flow in ducts of arbitrary cross-sections. International Journal of Heat and Mass Transfer, 36(13), 3265-3270. https://doi.org/10.1016/0017-9310(93)90009-U
Yilmaz., T. and Cihan, E. (1995). An Equation for Laminar Flow Heat Transfer for Constant Heat Flux Boundary Condition in Ducts of Arbitrary Cross-Sectional Area. J. Heat Transfer, 117(3), 765-766. https://doi.org/10.1115/1.2822644
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de septiembre de 2017; Aceptado: de noviembre de 2017
Abstract
In the thermal entrance region, a thermal boundary layer develops and also reaches the circular tube center. The fully developed region is the zone in which the flow is both hydrodynamically and thermally developed. The heat flux will be higher near the inlet because the heat transfer coefficient is highest at the tube inlet where the thickness of the thermal boundary layer is zero, and decreases gradually to the fully developed value. In this paper, the assumptions implicit in Leveque's approximation are re-examined, and the analytical solution of the problem with additional boundary conditions, for the temperature field and the boundary layer thickness through the long tube is presented. By defining a similarity variable, the governing equations are reduced to a dimensionless equation with an analytic solution in the entrance region. This report gives justification for the similarity variable via scaling analysis, details the process of converting to a similarity form, and presents a similarity solution. The analytical solutions are then checked against numerical solution programming by Fortran code obtained via using Runge-Kutta fourth order (RK4) method. Finally, others important thermal results obtained from this analysis, such as; approximate Nusselt number in the thermal entrance region was discussed in detail.
Keywords:
Thermal entrance region, Thermal boundary layer, Dimensionless variables, Temperature, Nusselt number, Runge-Kutta method.Resumen
En la región de entrada térmica, se desarrolla una capa límite térmica y también alcanza el centro del tubo circular. La región completamente desarrollada es la zona en la que el flujo se desarrolla tanto hidrodinámica como térmicamente. El flujo de calor será mayor cerca de la entrada porque el coeficiente de transferencia de calor es más alto en la entrada del tubo donde el espesor de la capa límite térmica es cero y disminuye gradualmente hasta el valor completamente desarrollado. En este trabajo, se vuelven a examinar las suposiciones implícitas en la aproximación de Leveque, y se presenta la solución analítica del problema con condiciones de contorno adicionales, para el campo de temperatura y el espesor de la capa límite a través del tubo largo. Al definir una variable de similitud, las ecuaciones gobernantes se reducen a una ecuación adimensional con una solución analítica en la región de entrada. Este informe proporciona una justificación para la variable de similitud a través del análisis de escalamiento, detalla el proceso de conversión a una forma de similitud y presenta una solución de similitud. Las soluciones analíticas se verifican luego contra la programación de soluciones numéricas mediante el código de Fortran obtenido mediante el método de cuarto orden (RK4) de Runge-Kutta. Finalmente, otros resultados térmicos importantes obtenidos de este análisis, como; el número aproximado de Nusselt en la región de entrada térmica se discutió en detalle.
Palabras clave:
Región de entrada térmica, capa límite térmica, variables sin dimensión, temperatura, número de Nusselt, método de Runge-Kutta.Resumo
Na região da entrada térmica, desenvolve-se uma camada limite térmica e também alcança o centro do tubo circular. A região totalmente desenvolvida é a zona em que o fluxo é hidrodinâmico e termicamente desenvolvido. O fluxo de calor será maior perto da entrada porque o coeficiente de transferência de calor é mais alto na entrada do tubo onde a espessura da camada limite térmica é zero e diminui gradualmente para o valor totalmente desenvolvido. Neste artigo, os pressupostos implícitos na aproximação de Leveque são reexaminados e a solução analítica do problema com condições de contorno adicionais, para o campo de temperatura e a espessura da camada limite através do tubo longo é apresentada. Ao definir uma variável de similaridade, as equações governantes são reduzidas a uma equação sem dimensão com uma solução analítica na região de entrada. Este relatório fornece justificativa para a variável de similaridade através da análise de escala, detalha o processo de conversão para uma forma de similaridade e apresenta uma solução de similaridade. As soluções analíticas são então verificadas em relação à programação de solução numérica pelo código Fortran obtido através do método Runge-Kutta de quarta ordem (RK4). Finalmente, outros resultados térmicos importantes obtidos a partir desta análise, tais como; O número aproximado de Nusselt na região de entrada térmica foi discutido em detalhes.
Palavras-chaves:
Região de entrada térmica, camada limite térmica, variáveis sem dimensões, temperatura, número Nusselt, método Runge-Kutta.Introduction
In most of heat transfer investigations and in practically convective heat transfer experimental works, heat transfer in a thermally developing laminar flow in circular tubes and channels has been addressed by several authors. The literature research shows that the particular models for predicting heat in the combined inlet region are in the case of a circular tube by Baehr and Stephan (1998) and Stephan (1959) in the case of a parallel plate channel. For the rectangular channel, empirical formulas have been developed by Garimella et al. (2000) while numerical data for the polygonal conduits were obtained by Asako et al. (1988). Shah and London (1978), Kakac et al. (1987) , Ebadian and Dong (1998) and Kakac and Yener (1983) carried out complementary work on a rectangular, circular, triangular and parallel plate channel. Hausen (1943) developed a model to study the Graetz problem inside a circular tube. Churchill and Ozoe (1973 a and 1973b) proposed simple models to develop flux in a circular duct. With the fully developed asymptote, and for the thermal input region. The Leveque solution was combined by Churchill and Ozoe (1973a and 1973b). For the Graetz problem, and in order to predict the thermal characteristics in an arbitrary form of the tube, models have been developed by Yilmaz and Cihan (1993 and 1995). These two authors developed models for uniform wall flow conditions (H) and a uniform wall temperature (T) to predict the fully developed Nusselt number. These models have been combined with these models with the generalized Leveque solution so that the input offers an approved model along the length of the tube. Two different problems must be taken into consideration in the input region near the tube inlet. The first assumes the presence of a fully developed hydrodynamic boundary layer, while the other considers the more general problem containing hydrodynamic and thermal boundary layers that have developed. By using the Leveque approximation for the input region, approximate solutions are revealed useful. We can join that the velocity gradient is linear in the thermal entrance region of non-circular tubes in which the thermal boundary layer is thin and presumed to be evolving. Belhocine and Wan Omar (2015), Belhocine (2016) investigated the convective heat transfer and flow fluid inside a horizontal circular tube in the fully-developed laminar flow regime under the constant wall temperature boundary condition, is commonly called the Graetz Problem that our goal is to get the steady temperature distribution in the fluid. Belhocine and Wan Omar (2017) developed an exact solution to the classical Graetz problem in terms of an infinite hypergeometric series represented by a nonlinear partial differential equation considering two space variables, two boundary conditions, and one initial condition.
The purpose of this paper is to present an analytical solution to the Leveque approximation problem (boundary layer approach) which is based on a few assumptions for a fully developed laminar fluid flow inside a circular tube. The methodology for the resolution of the problem is based on the use of the self similar technique. This technique is based on the observation that a lot of problems admit solutions with a shape which looks like always the same. Our main objective is to find the dimensionless temperature field and the thickness of the thermal boundary layer in the vicinity of the entrance region of the tube. Several steps have been discussed here on the governing equation of the temperature field to reach the solution such that; the non-dimensionalization and the use similarity variables, the transform the partial differential equation to an ordinary differential equation. Summarization of the boundary conditions and the integration of the equation. We then compare the exact approximate solution of the leveque problem with the numerical results using a Runge-Kutta fourth order (RK4) algorithm implemented by the Fortran code. The profiles of the solutions are provided from which we infer that the numerical and exact solutions agreed very well. Another result that we obtained from this study is the number of Nusselt in the thermal entrance region to which a parametric study was carried out and discussed well for the impact of the scientific contribution.
The heat equation in cylindrical coordinates
The general equation for heat transfer in cylindrical coordinates developed by Bird, Stewart, and Lightfoot (1960) is as follows;
The Graetz-Poiseuille flow problem
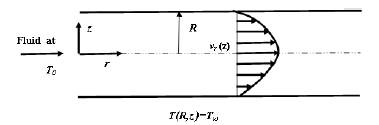
The Graetz problem is the problem of determining the steady-state temperature field in a fluid flowing in a circular tube when the wall of the tube is held at a uniform temperature and the fluid enters the tube at a different uniform temperature. The fluid enters the tube at a temperature T0 and encounters a wall temperature at Tω, which can be larger or smaller than T0. The Graetz problem considers the thermal entry of an incompressible fluid in a circular tube with a fixed velocity profile. The situation is illustrated in figure 1.
Figure 1: Illustration of Graetz problem.
After some hydrodynamic entry length, the velocity profile approaches a steady profile; that is, it ceases to change the downstream position. A fully developed parabolic velocity profile is established in a circular duct and remains unchanged over the length of the duct. There is a sudden jump in the wall temperature, and the fluid temperature is initially uniform at the upstream wall temperature. The thermal entry problem is to determine the behavior temperature profile as it changes to be uniform at the downstream wall temperature. Because the flow is incompressible, the velocity distribution does not depend on the varying temperatures.
-
The flow is steady, laminar and fully developed flow (Re < 2400)
-
Constant physical properties would also be and would not vary with temperature such as ρ, µ, Cp , k. This assumption also implies incompressible Newtonian flow.
-
Axisymmetric temperature field
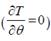 ,
, -
Negligible viscous dissipation
-
For a fully developed hydrodynamic boundary layer, namely Hagen Poiseuille flow, the velocity profile is:
Where 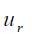 is the maximum velocity existing at the centerline,
is the maximum velocity existing at the centerline, 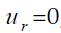 , and
, and 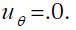 .
.
The energy equation is subject to the assumptions mentioned above, Eq. (1) can be written as follows:
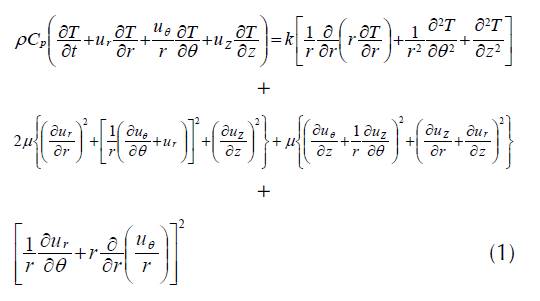

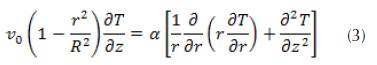
where 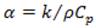 is the thermal diffusivity of the fluid and, our problem is subjected to the following boundary conditions: at the inlet of the tube
is the thermal diffusivity of the fluid and, our problem is subjected to the following boundary conditions: at the inlet of the tube 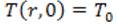 ; at the wall of the tube
; at the wall of the tube 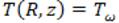 and at the centerline
and at the centerline 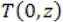 is finite or
is finite or 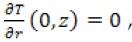
A suitable set of nondimentional variables is given as:
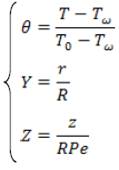
where the Péclet Number 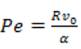
After replacement of these variables, the nondimentional energy equation and the boundary conditions applied to the system will take the following form:
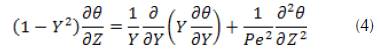
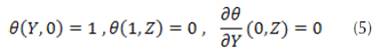
It is apparent that as the Péclet number (Pe) increases, the effect of the axial diffusion is significantly diminished. The boundary layer assumptions call for neglecting the axial diffusion altogether, yielding the following governing equation:
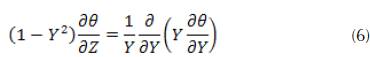
This is a linear equation whose solution can be determined by the method of separation of variables. This method yields an infinite hypergeometric series solution for the scaled temperature field:
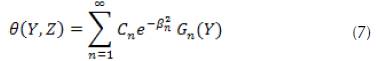
Where , are the eigenvalues and , are the eigenfunctions of a proper Sturm-Liouville system. The coefficients can be obtained by using the orthogonality property of the eigenfunctions defined as follows:
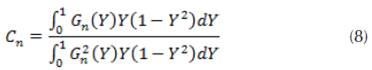
The Lévêque Approximation
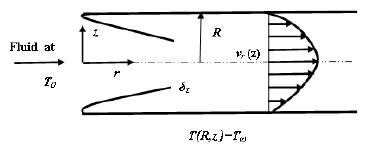
For all values of the axial position, the orthogonal function expansion solution obtained in the resolution of the classical Graetz problem is quite convergent, but the convergence is very slow as soon as one approaches the input tube. Indeed, for very long values of Z, the factor 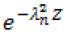 has become converged. Lévêque (1969) observed the thermal input region in a circular tube and developed a periodic solution, which is useful precisely where the expansion of the orthogonal function converges too slowly (figure 2).
has become converged. Lévêque (1969) observed the thermal input region in a circular tube and developed a periodic solution, which is useful precisely where the expansion of the orthogonal function converges too slowly (figure 2).
Figure 2: Schematics of the Lévêque problem and the coordinate system.
We will presently develop the Lévêque solution based on the hypothesis that the thickness of the thermal boundary layer 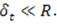 This assumption leads to the following reductions:
This assumption leads to the following reductions:
-
In the radial conduction term, the curvature effects can be neglected. Thus, derivative
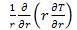 is approximated by
is approximated by 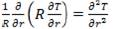
-
Since we have been captivated that by the velocity distribution in the thermal boundary layer, the velocity field is developed in a Taylor series in the distance measured from the tube wall and if we keep the first non-zero term
If we set x=R-r, the speed distribution will take the following form:
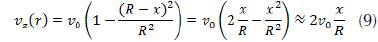
We know that the boundary conditions outside the thermal boundary layer are those of the fluid entering the tube, we will use the boundary condition instead of the centerline boundary condition 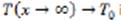 used to arrive at the Graetz solution.
used to arrive at the Graetz solution.
Governing Lévêque’s Equation
Starting from the reduced energy equation whose axial conduction has been neglected yet, and considering the said hypotheses, for the temperature field, we obtain the following governing equation

We have used the chain rule in order to transform the second derivative in r into a secondary derivative of x.

Boundary Conditions
The temperature field T(x, z),is subject to the following boundary conditions.
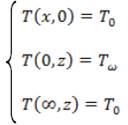
Non-Dimensionalization
Now, we will use dimensionless variables for the simplification of the equation. For this, we introduce the temperature and the axial coordinate of the following forms
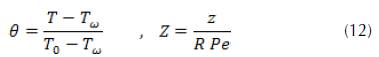
The scaled governing equation from the wall via X=x/R and the boundary conditions are given as follows
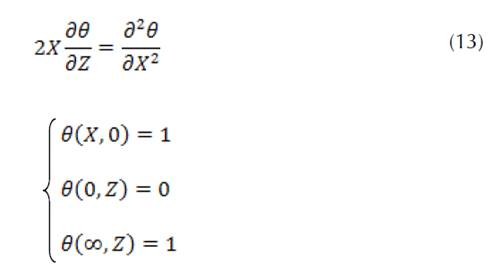
Analytical Methodology for Problem Solving: Temperature Field and Thermal Boundary Layer
At the current problem, we are looking for a similarity solution for the temperature field, we assume, 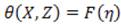 , where
, where 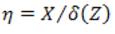 is the similarity variable and
is the similarity variable and 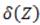 is an unknown variable that draws the thickness of the scaled thermal boundary layer. Using the chain rule, we will perform the following necessary transformations.
is an unknown variable that draws the thickness of the scaled thermal boundary layer. Using the chain rule, we will perform the following necessary transformations.
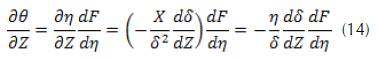
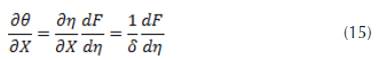
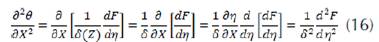
When we use these results, the partial differential equation for θ (X, Z), is converted to an ordinary differential equation for F(n)
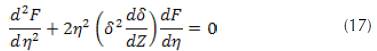
We put the term in parentheses (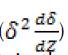 ) a constant is equal to 3/2 because it is certain that the similarity hypothesis will fail unless this quantity is required to be independent of Z. Finally, we obtain an ordinary differential equation for
) a constant is equal to 3/2 because it is certain that the similarity hypothesis will fail unless this quantity is required to be independent of Z. Finally, we obtain an ordinary differential equation for 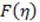 and another for
and another for 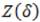 .
.


In order to derive the boundary conditions of these functions, it is enough to go to the limiting conditions on 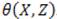 We notice that
We notice that 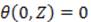 which implies F(0)=0 and
which implies F(0)=0 and 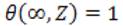 which leads to
which leads to 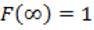 The residual condition (input) gives us
The residual condition (input) gives us

By favoring 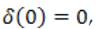 this condition collapses into the condition
this condition collapses into the condition 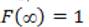 obtained already from the boundary condition on the scaled temperature field as X → ∞. By synthesizing the boundary conditions on / we obtain:
obtained already from the boundary condition on the scaled temperature field as X → ∞. By synthesizing the boundary conditions on / we obtain:
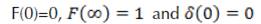
From the equation, we can write

By integrating the two terms of the obtained equation
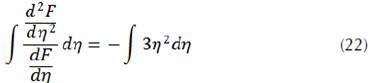
We arrive at the following expression
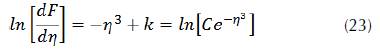
Where k and C are constants of the integral. By analogy, the following is drawn

Finally, the solution of the equation will take the following expression:
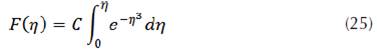
The function 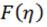 checks the initial condition for
checks the initial condition for 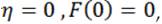 , and also considers the boundary condition for
, and also considers the boundary condition for 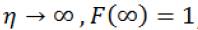 ; which implies
; which implies
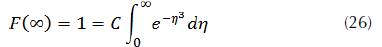
From where

So
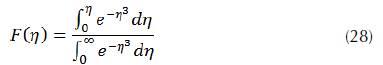
The scaled boundary layer thickness is calculated by the integration, which gives the following solution

Finally, the solution of our differential equation takes the following form
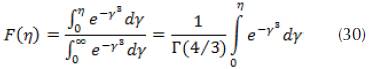
Where 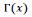 is the Gamma function (Abramowitz and Stegun, 1965), a Matlab code was used to approximate the values of the integral and the function F(η) for each abscissa η.
is the Gamma function (Abramowitz and Stegun, 1965), a Matlab code was used to approximate the values of the integral and the function F(η) for each abscissa η.
Resolution of the problem using the Runge-Kutta 4th order method
The original ODE of our problem is defined as follows:

With η=
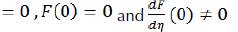
However, we wish to use the 4th order Runge-Kutta method, so I have the system:
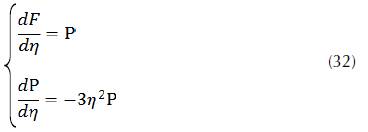
With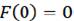 and
and 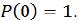 Now, we know that for two general 1st order ODE’s
Now, we know that for two general 1st order ODE’s
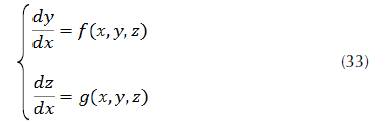
The 4th order Runge-Kutta formula’s for a system of 2 ODE’s are:
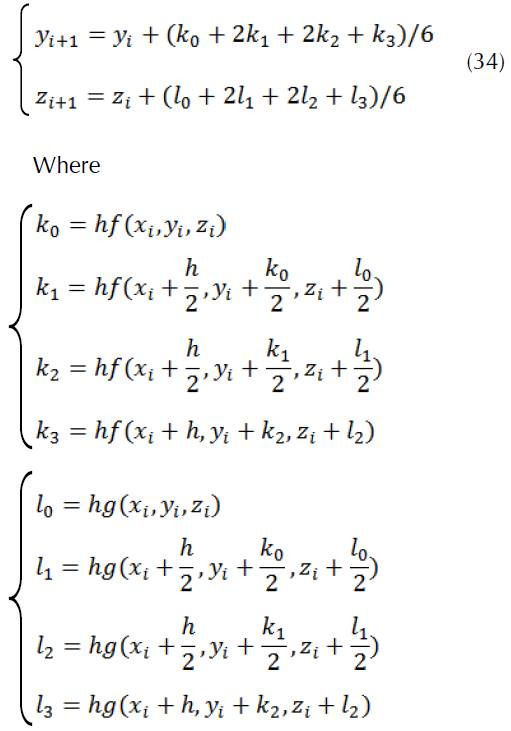
Where
We typically need some inputs for the algorithm:
-
A range that we want to do the calculations over: a≤t≤b, let’s use a=0, b=1
-
The number of steps N, say N=10
-
The step size h=(b−a)/N=1/10=0.1
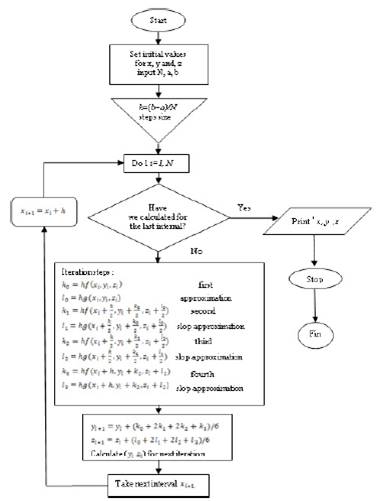
The flowchart for the above process is shown in figure 3.
Figure 3: Flowchart of the RK-4 method for resolving the second ODE’s systems.
The main program is written in Fortran language to solve the Levèque approximation containing a system of two differential equations of order 1 using the fourth-order Runge Kutta method RK04. This program relies on a definition of two functions whose subroutine RK04 is called at each repetition of the loop that intervenes in the calculations. The code edited in the machine that was executed is illustrated in detail in figure 4.
Figure 4: Fortran code of Runge Kutta for set of first order differential equations.
RESULTANTS and DISCUSSIONS
Comparison between the analytical and the numerical results
Analytical and numerical results that describe solutions with both methods in this analysis are summarized in table 1.
Table 1: Results of the exact and the numerical solution.
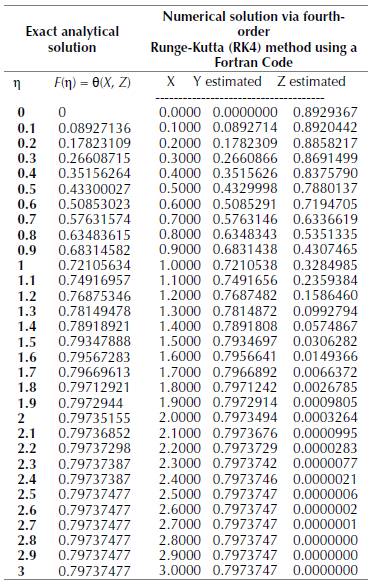
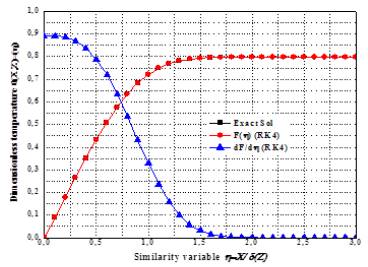
Figure 5 shows a comparison between the resolution results of the equation predicted by the analytical method and the numerical data derived from the Fortran code, the two sets of results of which are plotted in the same figure. On the basis of figure 5, it can be seen that the two curves are fairly identical, while observing that the dimensionless temperature θ gradually and gradually increases to the abscissa Z = 0.7, then loops and arches a little, by varying its path until it reaches the position Z = 1.7 where it stabilizes at a constant value 0.79 along the tube until the outlet of the fluid stream. In the same figure, the derivative function which is physically interpreted as the variation of the thermal transfer coefficient (h) indicated in blue color which is a solution of our system of differential equation by the Runge Kutta method decreases exceptionally as it moves away from the inlet region and then reaches the value zero on the abscissa Z = 1.6 until the exit of the flow. Figure 5 indicates that the present analytical results are in good agreement with the numerical results and theoretical analysis calculated using a fourth order Runge Kutta method. However, with RK04 approach, the method provides an extremely accurate approximation.
Figure 5: Comparison of exact and fourth-order Runge Kutta (RK4) numerical solutions.
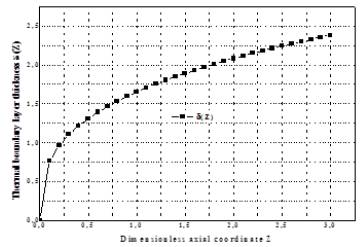
Figure 6 depicts variation of thermal boundary layer thickness with axial position. The thickness of the boundary layer gradually elongates from zero moving in the direction of the flow of the fluid when the fluid enters the tube and eventually leads to the center of the tube and invades the whole of the pipe. The wall shear stress is the highest at the pipe inlet where the thickness of the boundary layer is smallest, and decreases gradually to the fully developed value. Therefore, the pressure drop is higher in the entrance regions of a pipe, and the effect of the entrance region is always to increase the average friction factor for the entire pipe. This increase may be significant for short pipes, but is negligible for long ones. It can be seen that directly at the wall is a thin layer where the velocity is considerably lower than it is at some distance from the wall. The thickness of this layer increases along the tube from front to back. The fluid velocity in a pipe changes from zero at the wall because of the no-slip condition to a maximum at the pipe center.
Figure 6: Thermal boundary layer thickness distribution by analytical method.
The heat transfer coefficient
Depending on the axial position, the heat flux from the wall to the fluid, we can calculate it directly using the following formula:

By usual notation, we define the heat transfer coefficient h (z) as follows:
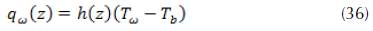
Where is the bulk or cup-mixing average temperature. The mathematical definition of the bulk average temperature is given by the following expression:
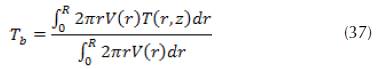
Where 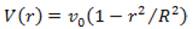 is the velocity field. The heat transfer coefficient is related to the temperature gradient at the tube wall, we can estimate it as follows:
is the velocity field. The heat transfer coefficient is related to the temperature gradient at the tube wall, we can estimate it as follows:

We can define the Nusselt number as a dimensionless heat transfer coefficient.
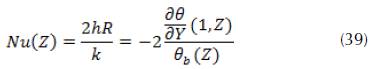
Where  is the dimensionless bulk average temperature
is the dimensionless bulk average temperature
When the thermal boundary layer is thin in the thermal entrance region, the average bulk temperature Tb can be approximated by the temperature of the fluid entering the tube T0.
As a result, the heat transfer coefficient in this input region is defined as:
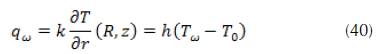
Changing into dimensionless variables and defining a Nusselt number Nu=2hR/k we can write the following:
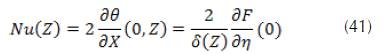
By substituting and , the approximate Nusselt number obtained in the thermal entrance region is given by the following form.
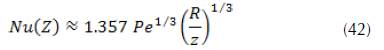
By comparing with the exact solution, we can draw that this result is a good approximation in the range:

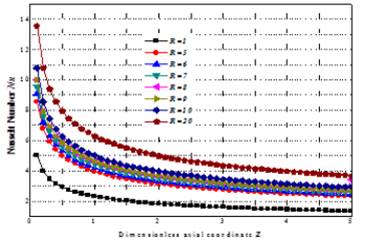
Figure 7 exhibits the Nusselt number versus axial distance, Z obtained in the thermal entrance region, for different Reynolds numbers. As expected, the Nusselt number, Nu(Z), enhances by increasing the tube radius, and that this effect is magnified near the entrance. When Z is greater than a certaine distance all the plots become nearly flat, indicating a thermally fully-developed condition. Indeed, when fluid enters the tube with tube walls at a different temperature from the fluid temperature, thermal boundary layer starts growing. After some distance downstream (thermal entry length) thermallyfully developed condition is eventually reached.
Figure 7: Nusselt number in the thermal entrance region versus axial position for different tube radius.
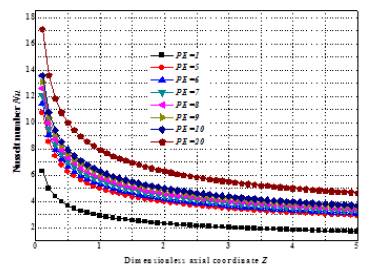
Figure 8 shows the effect of the Péclet number on the Nusselt number at a various axial distance. It’s clearly seen, the Nusselt number increases with the increasing Péclet number. As can be seen, the Péclet number has a much more pronounced effect on the Nusselt values for positions near the tube entrance. However the curve exhibits the same overall behavior-larger Nu at small Z and more or less constant value of large Z. It is evident that the local Nusselt number decreased in the entry region as the thermal boundary layer developed. It reached a constant value independent of heat flux and Reynolds number in the thermally fully developed region. Hence, the heat transfer coefficient (h) is infinite in the beginning (boundary layers just building up), then decays exponentially to a constant value when flow is fully developed (thermally) and thereafter remains constant. The results show that the value of the Nusselt number starts high and decrease rapidly along the length of the tube.
Figure 8: Nusselt number in the thermal entrance region versus axial position with various Peclet numbers
Conclusions
This paper presented an analytical and numerical solution to the Levèque approximation problem in order to predict the temperature field and boundary layer thickness at thermal entrance fully developed region through a circular tube with boundary condition at the axial coordinate origin. The exact solution methodology was based on the similarity variable and the generalized integral transform technique while the numerical approach is based on the fourth-order Runge Kutta technique for a linear system of ordinary two-variable differential equations programmed in Visual Fortran v5.0. The solution method was verified to lead to converging values which are in accordance with physically expected results. After demonstrating the convergence of the solution, the Nusselt number distribution of different Péclet values was analyzed, and the results are also in accordance with expected literature values. As final comments one should mention that the same solution procedure can be used for any dynamically developed velocity profile, as it occurs in many other occasions. Also, the methodology can be easily extended to other configurations such as other channel geometries, different wall heating conditions, and vicious and other flow heating effects.
References
License
Copyright (c) 2017 ali belhocine, Wan Zaidi Wan Omar

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.