Modelado de la sismicidad colombiana como una red compleja espacio-secuencial

Introducción

Buscar patrones en el marco espacial y temporal de los eventos sísmicos ha ayudado en la identificación de los bordes de las placas tectónicas, así como en la caracterización de sus movimientos a través del manto terrestre. Esta información ha permitido la construcción de herramientas para evaluar el riesgo sísmico (Lay & Wallace, 1995). La predicción de la ubicación y el tiempo de origen de un terremoto es una pregunta abierta de investigación, y diferentes trabajos se han enfocado en identificar precursores de eventos de gran magnitud, tales como eventos sísmicos precursores (McGuire et al., 2005), variaciones magnéticas (Doda et al., 2013) o emisiones de gas (Nikolopoulos, 2015), entre otros. Los trabajos relacionados muestran que no hay resultados de pronóstico concluyentes, y se sugiere que la posibilidad de predecir de manera confiable un terremoto se limita a un marco de tiempo de varios años (Donnellan et al., 2015).

Para la búsqueda de patrones temporales en sismología, la aplicación de leyes empíricas, como es el caso de las leyes de Gutenberg-Richter y Omori, han permitido comprender algunas de las complejidades de los fenómenos sismológicos. La ley de Gutenberg-Richter establece que la frecuencia de los terremotos sigue una distribución de ley de potencia con respecto a la energía liberada. Así, para un terremoto de magnitud M se espera que ocurran cerca de 10 veces más terremotos con una magnitud de M-1 (Gutenberg & Richter, 1944). Por su parte, la ley de Omori establece que la tasa de réplicas después de un terremoto importante disminuye de manera algebraica con respecto al tiempo transcurrido desde la ocurrencia del evento en cuestión (Utsu et al., 1995).

El trabajo de Abe y Suzuki (2003) muestra que la sismicidad se puede representar como una intrincada red espacial de eventos. Esto, para el caso del sur de California. Los autores afirman que la sismicidad sigue una geometría fractal comúnmente observada en los sistemas complejos que se encuentran en estado de desequilibrio. Por otra parte, se ha observado que la distribución de los tiempos entre terremotos sigue una distribución de ley de potencia, lo cual evidencia la naturaleza intrincada de la actividad sísmica (Abe & Suzuki, 2002). León et al. (2018) observaron que la red de eventos sísmicos en Colombia sigue la estructura de red de pequeño mundo. Sin embargo, los resultados reportados son para redes espaciotemporales bidimensionales, en las cuales no se incluyó la profundidad. De igual manera, la información de la red de eventos sísmicos en Colombia ha sido utilizada para construir un sistema que permite la anotación automática de sismos, así como reconocer automáticamente eventos de otras fuentes diferentes a las tectónicas (León et al., 2020).

En este trabajo se construyen redes de sismos en tres dimensiones, considerando la latitud, longitud y profundidad de los eventos, así como su secuencia temporal. Se compara la estructura de las redes aleatorias y las redes de pequeño mundo. Los resultados revelan que las redes son del segundo tipo, independientemente del tamaño de celda o la granularidad utilizada para construirlas. Así, la red de pequeño mundo muestra que el esfuerzo y la energía en la región se liberan de acuerdo con una estructura, lo cual se ve reflejado en la presencia de hubs y en las relaciones que tienen estos con el resto de la red en general. En este sentido, este documento presenta cómo la estructura de redes da información acerca de los mecanismos de liberación de energía y las fuentes que recurrentemente producen eventos sísmicos en Colombia.

Redes complejas y sismicidad en Colombia

Una secuencia de terremotos es una serie de eventos sísmicos que ocurren en el espacio y el tiempo, los cuales pueden ser representados como una red compleja. Según Gao et al. (2016), la literatura reporta diferentes métodos para construir redes complejas a partir de series de tiempo en campos como la dinámica climática, las funciones cerebrales y los sistemas de tráfico, entre otros. El catálogo de eventos sísmicos para una región en un determinado periodo de tiempo sigue una secuencia temporal. Por lo tanto, un catálogo de sismicidad se puede estudiar como una serie de tiempo de eventos y, por tanto, como una red compleja. Algunos trabajos relacionados con el estudio de catálogos de eventos sísmicos como redes complejas son León et al. (2018), Pastén et al. (2018) y Chorozoglou et al. (2017).

Se han desarrollado diferentes formas de construir redes de sismos, i.e., celdas como nodos y eventos como nodos, grafos de visibilidad, entre otros (León et al., 2022). De acuerdo con Abe y Suzuki (2011), las redes de sismos se construyen dividiendo una región en celdas, y se selecciona una celda como nodo cuando ocurre un evento sísmico en ella, los nodos se relacionan entre sí de acuerdo con la secuencia temporal que ocurre entre los eventos. En León et al. (2018) se crearon redes de sismos de este tipo, pero sin tener en cuenta la profundidad, mapeando los eventos sísmicos de la región de Colombia en una cuadrícula 2D. Para generar dicha cuadrícula, se definió el tamaño de la celda, y posteriormente se conectaron las celdas de acuerdo con la secuencia de los eventos sísmicos. De forma similar, se puede incluir la profundidad del evento sísmico y construir una red 3D, generando cubos que tienen en cuenta el lugar del evento sísmico y su profundidad. Así, se define el tamaño del cubo y se relacionan los cubos entre sí de acuerdo con la secuencia de eventos. Este trabajo modela la sismicidad en Colombia de acuerdo con una red 3D.

En este trabajo se adiciona la dimensión de profundidad para obtener una comprensión más detallada del fenómeno de la sismicidad en Colombia. Esta comprensión es crucial para desarrollar modelos que permitan describir de manera precisa la complejidad de la sismicidad en la región. Para estudiar la complejidad y la estructura de las redes complejas, se describen numerosos parámetros y medidas relacionadas. Muchas de las características inherentes a los sistemas complejos se observan en las redes, tales como la auto-similitud, la fractalidad o la escalabilidad (Boccaletti et al., 2006). Por otra parte, existen diferentes tipos de redes complejas, i.e., de pequeño mundo, libres de escala y aleatorias (redes Erdös-Rényi). Las redes aleatorias fueron inicialmente estudiadas por Erdös y Rényi (1960) y pueden ser reproducidas por el modelo que lleva su nombre (Erdös & Rényi, 1959). Así, se pueden describir las redes en las cuales dos nodos se relacionan de acuerdo con una distribución de probabilidad binomial. Esto quiere decir que, en este tipo de redes, la decisión de generar un vínculo entre dos nodos corresponde a lanzar una moneda, y todos los nodos tienen la misma probabilidad de estar conectados.

Las redes de pequeño mundo estudiadas por Watts y Strogatz (2011) tienen una estructura más compleja que una red aleatoria Erdös-Rényi. Por lo general, esta estructura se observa mediante dos métricas del grafo: el coeficiente de agrupamiento global (GCC) y la longitud de camino promedio (APL). Es decir, una red que tiene una estructura de pequeño mundo muestra nodos hub, grupos dentro de la estructura de relaciones y una conectividad alta, entre otras características que no se encuentran en las redes Erdös-Rényi. En este trabajo se estudia experimentalmente si la red de sismicidad en Colombia (incluyendo la profundidad, i.e., 3D) sigue un patrón de red Erdös-Rényi o un patrón de pequeño mundo (small-world).

Este estudio utiliza una métrica para analizar la tipología de la red conocida como small-worldness (S), la cual expresa la no aleatoriedad de una red. Esta métrica indica que el GCC de una red de pequeño mundo es mayor que el de una red aleatoria y que su APL es mayor o igual al de una red aleatoria. Para calcular la small-worldness, es necesario obtener el GCC y APL de una red Erdös-Rényi con características de tamaño y conectividad similares a la red observada. En otras palabras, S se calcula comparando el GCC y APL de la red observada y los de una red aleatoria Erdös-Rényi (Humphries & Gurney, 2008). Por lo tanto, para caracterizar una red como de pequeño mundo, su small-worldness debe ser mayor que 1.

Para analizar la small-worldness de las redes sísmicas, se deben considerar varios factores, incluyendo el tamaño de la red, el número de iteraciones utilizadas en el análisis, el umbral de magnitud aplicado y el tipo de catálogo de terremotos utilizado. Además, considerar eventos profundos puede generar patrones de red distintos, especialmente en regiones con diferencias significativas en la actividad sísmica a diferentes profundidades. Otros trabajos similares a los de Abe y Suzuki (2009, 2012) pueden ayudar a comprender la complejidad del fenómeno sísmico e integrarlo con algoritmos de aprendizaje automático.

Metodología construcción del catálogo de datos

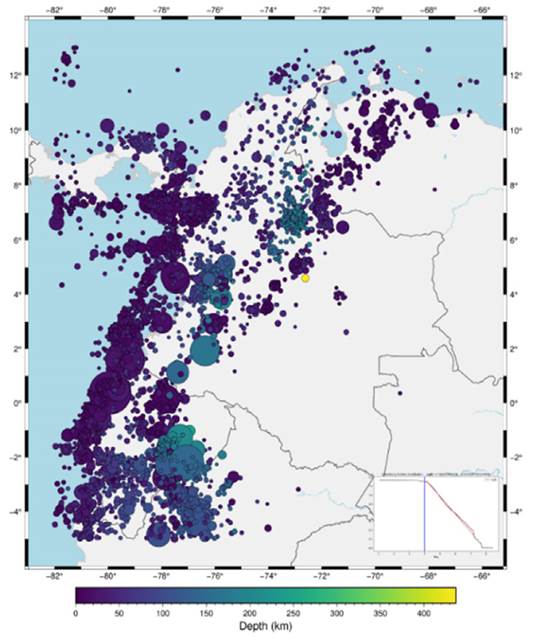
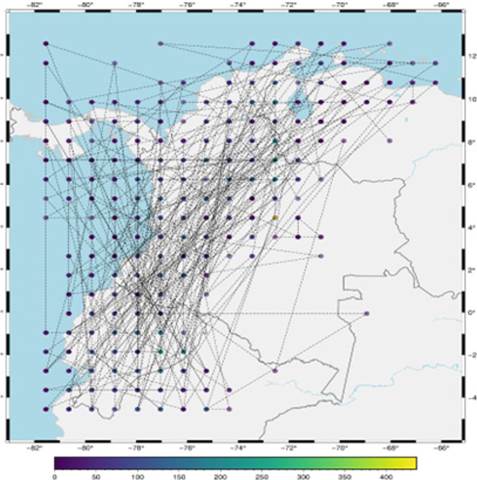
El catálogo de eventos usado para este estudio se descargó del USGS-NEIC (United States Geological Survey - National Earthquake Information Center) para la región cercana a Colombia. Se escogió este catálogo y no el del Servicio Geológico Colombiano porque es más completo para eventos que ocurrieron antes de 1990. Se configuraron latitudes mínimas y máximas de -5 y 13° respectivamente, así como longitudes mínimas y máximas de -82 y -66°. El período escogido para los eventos del catálogo comprende entre el 1 de enero de 1975 y el 18 de enero de 2021, para un total de 6950 eventos. La magnitud mínima para analizar los datos se calculó a partir de la distribución Gutenberg-Richter del catálogo, como se muestra en la Figura 1, donde el eje X es la magnitud y el eje Y es el logaritmo del número de eventos. La línea oscura es entonces el logaritmo del número de eventos con magnitudes mayores o iguales a la magnitud referida en el eje X, y la línea roja es la parte lineal de esta gráfica, tomando solo los datos con magnitudes mayores a la referida por la línea azul, que en este caso es 4.0. La línea se ajusta a una magnitud de hasta 7.5 porque no hay muchos eventos con magnitudes mayores a este valor. Con esta distribución, se puede elegir una magnitud de 4.0 para la completitud del catálogo, es decir, hay confianza de que todos los eventos con magnitudes mayores a 4.0 para el período seleccionado hacen parte del catálogo. Esta magnitud constituye el límite para elegir los eventos con los que se construirán las redes de sismos, lo cual resulta en un catálogo final de 5797 eventos. Asimismo, la Figura 1 muestra los eventos sísmicos y su ubicación en el mapa para las longitudes y latitudes descritas en las líneas anteriores. El tamaño de los eventos se ilustra según su magnitud, y su color corresponde a la profundidad de los eventos.

Figura 1: Distribución Gutenberg-Richter del catálogo estudiado.

Así, la distribución Gutenberg-Richter de todos los eventos en el catálogo de la región, construido a partir del número total de eventos N con magnitud igual o superior a cada valor M en el eje X, muestra un conjunto completo de magnitudes mayores a 4.0. Como se muestra en la Figura 1, a partir del ajuste de N * exp(a - bM), se obtienen los parámetros a = 7.88 y b = -0.99. Así, hay 5797 terremotos con magnitudes mayores a 4.0 entre el 1 de enero de 1975 y el 18 de enero de 2021. Hay otros catálogos de agencias colombianas (Vargas et al., 2018), pero ninguno de ellos se remonta tan atrás en el tiempo como el catálogo del USGS, y, para nuestro análisis, es fundamental contar con el mayor lapso de tiempo posible, en aras de una buena comprensión de la sismicidad de la región.

La ubicación de estos eventos corresponde al límite de cinco placas tectónicas, de acuerdo con Sornette (2003). Esta compleja región de estudio de múltiples placas se ve afectada por la acción combinada de las placas sudamericanas (este), caribeñas (norte), bloques andinos del norte (centro), Cocos (Panamá y Centroamérica) y Nazca (oeste) (Sornette, 2003). La presencia e influencia de todas estas placas indica una zona con una actividad sísmica alta y compleja que vale la pena analizar con técnicas computacionales.

Teniendo en cuenta lo anterior, la separación temporal entre eventos es relativamente pequeña. De los 5797 eventos seleccionados, la mitad ocurrió con una separación temporal de menos de 41 horas entre eventos consecutivos, y el 80 % con una separación temporal de menos de 118 horas (casi cinco días). Por lo tanto, es altamente probable que dos eventos consecutivos con magnitud mayor que 4.0 ocurran con una separación temporal menor de cinco días.

Se utilizó un método similar a la técnica descrita por Abe y Suzuki (2004a) para crear la red. Los eventos sísmicos de la Figura 1 se mapearon en una cuadrícula 3D para que todas las celdas tuvieran el mismo tamaño, y cada celda se identificó como un nodo de la red si reportaba un evento sísmico. Para este trabajo, se asumió una conversión de grados-km de 111 km/grado, por lo que los eventos sísmicos de nuestros conjuntos de datos se mapearon en una cuadrícula de aproximadamente 2000 km de largo y 1900 km de ancho.

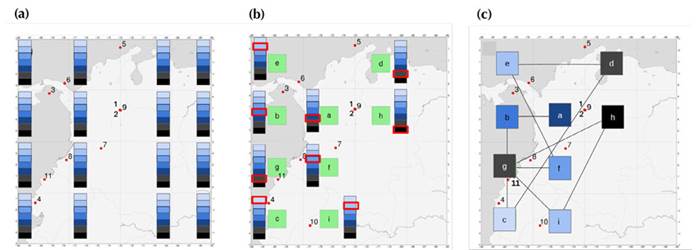
Como se muestra en la Figura 2, una celda se seleccionó como nodo si el epicentro de un evento sísmico estaba dentro de ella. De esta manera, se construyó una celda cúbica con un tamaño dado para alto y largo, y se tuvieron en cuenta las profundidades de los eventos en la celda (Figura 2a). Esta Figura muestra una escala de profundidad de azul claro (baja profundidad) a negro (alta profundidad). En este trabajo se analizaron redes con diferentes tamaños de celda cúbica, i.e., de 10 a 100 km. Se etiquetó cada celda según su longitud, latitud, tamaño y profundidad si en ella ocurrieron eventos sísmicos (Figura 2b). Para cada tamaño de celda, se creó una red (una red para 10 kms, otra para 20kms y así sucesivamente), seleccionando los nodos en los que ocurrieron los eventos y estableciendo enlaces entre nodos siguiendo una secuencia temporal, es decir, enlazando eventos sucesivos (Figura 2c).

Figura 2: Diagrama de la red de sismos generada con base en su secuencia espaciotemporal e incluyendo la profundidad

De esta manera, la red representa una secuencia de eventos, junto con su posición y profundidad. Para analizar dicha red, se ignoraron los bucles (un nodo que se enlaza consigo mismo) y las conexiones múltiples entre cualquier par de nodos.

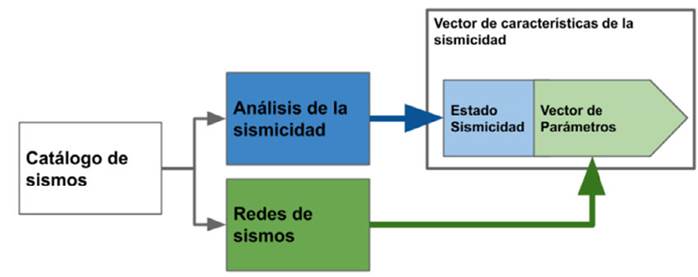
El proceso que sigue el desarrollo del estudio sigue los pasos descritos en el esquema de la Figura 3, los cuales se construyen a partir del catálogo de sismos. Se construyeron las redes de sismos para diferentes tamaños de celdas, así como matrices de adyacencia, que posteriormente serían la entrada del programa de análisis de redes complejas. Estas matrices se analizaron tomando como referencia el estudio de redes complejas y redes de sismicidad en Colombia de León et al. (2018). Las métricas analizadas fueron el número de nodos, el número de enlaces, el grado medio, el APL y el coeficiente de agrupamiento para cada tamaño de celda propuesto. También se obtuvo la representación gráfica de las redes. Los scripts se desarrollaron en Wolfram Mathematica. La Tabla 1 presenta los resultados de cada red para cada tamaño de celda y sus respectivas métricas.

Figura 3: Esquema de construcción de redes de sismicidad.

Tabla 1: Características de las redes estudiadas

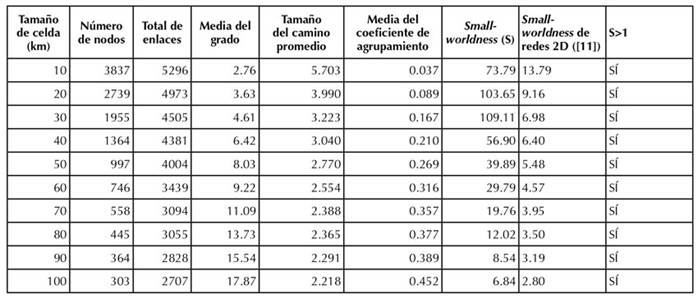
Las herramientas y software utilizados fueron Python ver 3.11 (van Rossum & Python Development Team, 2013) y Wolfram Mathematica v. 13.1 (Wolfram, 2022). Python es un lenguaje de programación ampliamente usado, a través del cual se procesaron los datos del catálogo de eventos sísmicos y se construyeron las matrices de adyacencia para cada uno de los tamaños de celda. Estos archivos fueron importados a Wolfram Mathematica para el análisis de redes complejas. Las funciones utilizadas fueron VertexCount, EdgeCount, DegreeCentrality, BetweennessCentrality, MeanClusteringCoefficient y GraphDistanceMatrix. Adicionalmente, se aplicaron 100 simulaciones para dos tipos de redes aleatorias (modelo Erdös-Rényi) y redes de pequeño mundo (modelo Watts y Strogatz): RandomGraph, WattsStrogatzGraphDistribution y BarabasiAlbertGraphDistribution.

Resultados

Este artículo presenta un análisis de la red de sismicidad en la región de Colombia y Ecuador, la cual utiliza diferentes tamaños de celdas (10 y 100 km). Se observó que las redes obtenidas son de tipo pequeño mundo. La distribución del grado se asemeja a una distribución de Poisson, la cual se utiliza en el análisis de redes de pequeño mundo porque representa una distribución aleatoria de los nodos y conexiones. En una red de pequeño mundo, los nodos se conectan no solo con sus vecinos directos, sino también con otros nodos más lejanos. Sin embargo, las conexiones con nodos lejanos son eventos menos frecuentes. Dos características de las redes pequeño mundo son estudiadas regularmente en la literatura (Watts & Strogatz, 2011): el coeficiente de agrupamiento y la longitud media de los caminos más cortos. En este tipo de redes, hay un alto coeficiente de agrupamiento y una baja longitud media de los caminos más cortos, es decir, la red tiene hubs y grupos, tiene una estructura de centro-periferia y es eficiente, pues se puede alcanzar cualquier nodo en pocos pasos. Los resultados de estás métricas se presentan en la Tabla 1.

De acuerdo con León et al. (2018), la estructura de la red sísmica en la región de Colombia y Ecuador es una red en estado de no equilibrio, donde la información y el estrés pueden propagarse de manera no aleatoria en la red. En este trabajo se confirma que la red no es aleatoria y que las características de la distribución del grado, el coeficiente de agrupamiento y la longitud media de los caminos más cortos lo confirman. En la Tabla se han consignado los resultados del cálculo de la small-worldness para redes de sismos 2D, de manera que se puedan comparar con los resultados obtenidos al considerar la profundidad de los eventos.

En León et al. (2018), las redes se construyen en dos dimensiones y la profundidad no se tiene en cuenta. Un aporte de este trabajo es el desarrollo de las redes incluyendo la profundidad. Esto muestra que no solo las zonas siguen una estructura de red no aleatoria, sino también las profundidades en las que ocurren los eventos sísmicos. Así, esta herramienta permite suponer que la estructura de relaciones que subyace a los eventos sísmicos está continuamente liberando estrés por medio de zonas y profundidades que conforman agrupaciones, lo cual permite liberar energía. De igual forma, dicha energía fluye por esta red hacia la periferia de la red en pocos pasos. Consideramos que esta información podría tener implicaciones prácticas para la gestión del riesgo sísmico en Colombia.

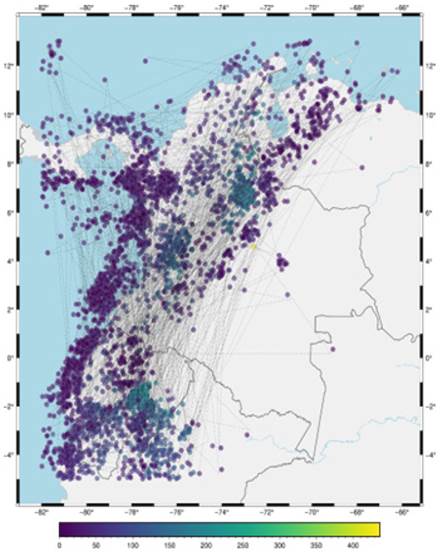
La Figura 4 muestra un análisis de la sismicidad desde la perspectiva de la red, con tamaños de celda de 10 km (Figura 4a) y 100 km (Figura 4b). Las Figuras 4 y (5 muestran estructuras de redes de una complejidad mayor a las redes aleatorias, y se observan agrupaciones de nodos que parecen comunidades de sismos localizadas en zonas como el nido sísmico de Bucaramanga o algunas en Ecuador y cerca del océano Pacífico, así como también algunas a lo largo de la zona de subducción entre la placa de Nazca y la placa Sudamericana (en la costa del Pacífico colombiano) y cerca de Venezuela. El nido sísmico de Bucaramanga ha sido estudiado ampliamente (Schneider et al., 1987; Frohlich et al., 1995) y sigue siendo una región de interés (Poli et al., 2016).

Figura 4: Nodos de sismos.

Figura 5: Celdas de sismos.

Lo mismo aplica para la actividad sísmica a lo largo de la zona de subducción. Por lo tanto, tener diferentes escalas de observación del fenómeno permite detectar regiones que sísmicamente activas a partir de un catálogo dado sin la necesidad de un experto. Este resultado no es necesariamente evidente al observar los datos en un mapa, como se muestra en la Figura 5. En este sentido, la construcción de las redes sísmicas para diferentes tamaños de celdas permite detectar automáticamente regiones con actividad sísmica importante, o eventos específicos en zonas y profundidades que desencadenan otros eventos.

La Figura 6 muestra que, para todas las redes observadas entre 10 y 100 km, los valores de small-worldness son mayores que 1. Se observa que, para las celdas entre 15 y 30 km, hay un pico en el valor de small-worldness. Estos resultados sugieren que las redes observadas se parecen más a una red de pequeño mundo que a una red aleatoria, y permiten representar las secuencias de los eventos sísmicos de esta manera, con una estructura que se aleja del equilibrio.

Figura 6: Small-worldness para cada tamaño de celda.

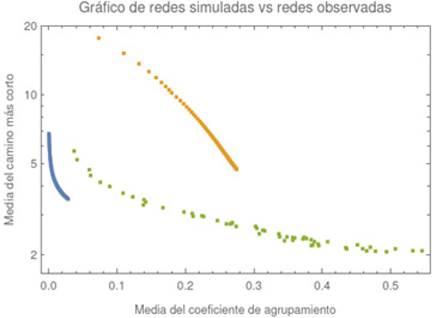
Para evaluar la robustez de las propiedades de la red encontradas para diferentes tamaños de celda, se realizaron comparaciones con 100 simulaciones para dos tipos de redes aleatorias (modelo Erdös-Rényi) y redes de pequeño mundo (modelo Watts y Strogatz). Para ello, se utilizó el número de vértices de las redes observadas y el número de los enlaces obtenidos para cada tamaño de celda (Tabla 1). En cada caso, se simularon redes sísmicas con características similares a las observadas, incluyendo el número de vértices y el grado promedio. Por ejemplo, para redes aleatorias, se mantuvo el mismo tamaño y grado medio, pero, para redes de pequeño mundo, se utilizó el mismo tamaño y una probabilidad de reconexión de 0.25, partiendo de un grafo 2k-regular. Las simulaciones se realizaron utilizando el software Mathematica de Wolfram Research Inc. La Figura 7 muestra una gráfica de APL vs. GCC para las redes sísmicas (verde), las redes aleatorias simuladas aleatorias (azul) y las de pequeño mundo (naranja), indicando la media de la distribución de valores para las 100 simulaciones en cada punto de la curva.

Figura 7: Mapa de pequeño mundo para redes aleatorias, redes observadas y redes de pequeño mundo.

Para los datos que se muestran en la Figura 7, tanto para las redes sísmicas como para las simuladas, el APL disminuye de la misma manera. Para valores bajos de APL, que corresponden a tamaños de celda más grandes (granularidad gruesa en el muestreo para crear la red), el comportamiento de la red sísmica parece ser mejor si se reproduce mediante una estructura de pequeño mundo (naranja). Para demostrar este punto, la Tabla 1 presenta el coeficiente de pequeño mundo, calculado utilizando la Ecuación (1) en la red sísmica. Este resultado muestra que las redes con granularidad fina (tamaños de celda más pequeños, más nodos) tienen un coeficiente de pequeño mundo más alto, lo cual se debe principalmente a un GCC pequeño para las redes aleatorias en comparación con las redes sísmicas. Aunque el parámetro de pequeño mundo es más alto con redes más finas, es importante notar que, para todos los casos, S > 1, lo que significa que, para las redes de celdas cúbicas de diferentes tamaños (10 y 100 km), la red resultante es de pequeño mundo en cada caso.

En cuanto a las técnicas de análisis, se observó que la configuración de los experimentos de simulación con las reglas propuestas genera redes que comparten características con lo observado en la literatura y en los datos de redes 3D aquí presentados. Se observa un comportamiento de pequeño mundo pequeño en el gráfico de APL vs. GCC, y el grado promedio y las medidas de small-worldness también son evidencias de este tipo de red.

Conclusiones

Se encontró que la red de sismos de Colombia, incluyendo la profundidad, puede ser caracterizada como una red de pequeño mundo. Estudios similares en otras regiones del mundo han llegado a una conclusión similar (e.g.,Abe & Suzuki, 2011). Según León et al. (2018), la red de sismos en dos dimensiones también es de este tipo. En este sentido, uno de los aportes de este trabajo es la inclusión de la profundidad de los eventos, lo cual proporciona una imagen más completa del fenómeno sísmico en la región. Nuestros resultados son claves debido a que en la región colombiana existen varias placas tectónicas interactuando entre sí a diferentes profundidades y en diferentes zonas del mapa. Esta complejidad requiere incluir la profundidad como una característica necesaria para comprender el fenómeno de la sismicidad en la zona.

De acuerdo con la Figura 4, el parámetro small-worldness, que mide qué tanto de la red es de pequeño mundo, es mucho mayor en las redes que consideran la profundidad con respecto a los resultados publicados en León et al. (2018) (Tabla 1). En estas redes de sismos hay una distribución similar a la de Poisson, lo que no se pudo observar en las redes de sismos 2D, donde la small-worldness decrece monótonamente al incrementar el tamaño de las celdas. Este comportamiento de la small-worldness es interesante porque sugiere rangos de tamaños de celda que mejoran la detección de hubs o zonas de interés para estudiar el fenómeno de la sismicidad. Valores muy altos de small-worldness indican que, dado el elevado número de nodos, la red mantiene una estructura con las características propias de las redes de pequeño mundo (alto coeficiente de Clustering y longitudes de caminos cortas) en rangos que se alejan de las redes aleatorias tipo Erdös-Rényi. Esto quiere decir que las redes observadas se alejan del equilibrio.

Conocer el tipo particular de red, ya sea aleatoria o de pequeño mundo, es de especial importancia en términos de sus características físicas (o estadísticas), pues podría existir una correlación entre la liberación de estrés en todo el sistema y la estructura de la red sísmica. De esta forma, utilizar el enfoque de redes sísmicas a profundidad en una región donde interactúan varias placas tectónicas puede proporcionar información intrínseca y útil que de otra manera estaría oculta, especialmente debido a que la región sísmica de análisis es única y poco estudiada. Por lo tanto, la caracterización de las redes sísmicas podría ayudar a descubrir aspectos relacionados con las características físicas o estadísticas del fenómeno.

Por ejemplo, la red sísmica de Colombia, a diferentes escalas de celda (10 a 100 km), muestra la importancia del ‘nido’ de Bucaramanga en la dinámica de la sismicidad de la región, independientemente del tamaño de celda utilizado para construir las redes. En este sentido, un nido sísmico se caracteriza por tener una alta tasa de actividad que está aislada de la actividad cercana, y el nido de Bucaramanga representa la mayor concentración de sismicidad de profundidad intermedia en el mundo, lo cual demuestra la importancia sismológica de este lugar. El hecho de que la actividad en esta área no genere un impacto mediático significativo se debe principalmente a que los eventos de este nido ocurren a una profundidad media de 160 km, por lo que rara vez se sienten en otras partes de Colombia, incluso en la misma Bucaramanga.

Nuestros resultados resaltan esta región debido al número de eventos que ocurren en ella y sus profundidades. Esto sugiere que este lugar no está exactamente aislado del resto de la actividad en la región, sino que puede tener una influencia importante en la dinámica de los eventos sísmicos. Algo similar sucede con la sismicidad asociada al proceso de subducción en el Pacífico colombiano. La subducción se da cuando una placa tectónica se desliza por debajo de otra, lo cual hace que se generen eventos sísmicos, muchas veces de gran magnitud, a lo largo de toda la superficie de contacto entre las dos placas (Lallemand et al., 2005; Stern, 2002). Esta interacción entre placas, que genera eventos a diferentes profundidades, cobra también importancia y relevancia en estos resultados, ya que muestra que la agrupación de eventos y/o celdas para una región se da también a profundidad.

Los resultados de los estudios realizados por Abe, Pastén y Suzuki (2011) concluyeron que las redes sísmicas en otras regiones son de pequeño mundo o de escala libre, pero su caracterización varía según el tamaño de las celdas. Las réplicas a menudo regresan al lugar del sismo principal, lo que sugiere que estos eventos pueden convertirse en nodos centrales de una red. En este sentido, el trabajo de Abe y Suzuki (2007, 2012) mostró una forma confiable de distinguir entre sismos principales y réplicas. En nuestro caso, las redes sísmicas tienen un comportamiento similar, y se observa claramente que el tamaño de las celdas cambia el grado, el coeficiente de agrupamiento y la distribución de la longitud del camino en la red resultante. Sin embargo, de acuerdo con los valores de small-worldness, cada red fue consistentemente de pequeño mundo. De forma similar a los resultados en León et al. (2018), las redes obtenidas en este trabajo incluyen la profundidad y mantienen el comportamiento observado en trabajos previos.

Al simular redes aleatorias y de mundo pequeño de diferentes tamaños de celda, se evidencia que las conclusiones encontradas por Abe, Pastén y Suzuki (2011) son similares a los valores obtenidos en este trabajo.

El uso de una disposición que optimiza la densidad de los nodos permite resaltar aquellos pertenecientes a zonas de alta sismicidad. Este efecto es particularmente interesante en el caso de un tamaño de celda de 100 km, lo cual sugiere la existencia de varias zonas sísmicas activas significativas. En el otro extremo, en la red sísmica construida con un tamaño de celda de 10 km, vemos un único grupo significativo, pero con el mayor número de eventos. Esta diferencia en ambas redes podría ser relevante para proponer una metodología que permita encontrar la zona con mayor sismicidad utilizando celdas pequeñas, para luego identificar zonas complementarias mediante tamaños de celda más grandes. Este resultado puede ser de interés para la creación de un sistema autónomo que defina etiquetas en los eventos importantes que deban ser estudiados y clasificados más detalladamente en un catálogo. Por lo tanto, la representación de la sismicidad mediante redes podría ayudarnos a entender la forma en que ocurren los eventos. El cambio de estructura de red permite entender la autoorganización del sistema de sismos para liberar estrés eficientemente, llevando la mayor cantidad de energía a los hubs y repartiéndola por la red hacia la periferia. Esta representación permite pensar los eventos sísmicos como precursores de otros y, al incluir la profundidad en el análisis, reconocer cuáles eventos pueden disipar más energía que otros. Así, la profundidad se convierte en un elemento clave para comprender las zonas de mayor actividad e identificar aquellas que activan a otras en eventos posteriores.

La metodología de las redes se utiliza para diferentes tamaños de celda y ventana. Estos parámetros pueden modificar el tipo de red y las características que se observan en tamaños muy pequeños. Así, se pueden obtener redes no conectadas y, en el caso contrario, redes totalmente conectadas. Este estudio muestra que, previo al trabajo con redes de sismos, es necesario estudiar los parámetros para construirlas, pues estos pueden producir diferentes tipologías de red (e.g., redes no conectadas, totalmente conectadas o aleatorias), algunas sin ninguna complejidad. Esta investigación muestra un método para explorar todas las redes obtenidas para distintos tamaños de celda y utilizar la métrica de small-worldness, en aras de identificar las redes que ofrecen mayor información. Como trabajo futuro, se propone explorar medidas de entropía, ganancia de información y divergencias para estudiar las redes y la información que ofrece sobre el fenómeno de la sismicidad.

Como trabajo futuro, se propone integrar estos resultados en un sistema de pronóstico de eventos sísmicos para la zona colombiana. Para generar modelos de predicción, sería necesario seguir el tiempo entre eventos como parte de las reglas entre nodos. De manera similar, estudiar la coocurrencia entre nodos centrales y seguir los nodos más conectados también podría proporcionar información útil para diseñar un modelo de pronóstico a partir de redes de sismos