DOI:
https://doi.org/10.14483/udistrital.jour.reving.2017.1.a04Published:
2017-01-30Issue:
Vol. 22 No. 1 (2017): January - AprilSection:
Industrial EngineeringModelos de Localización para Cadenas Agroalimentarias Perecederas: una Revisión al Estado del Arte
Facility Location Models in Perishable Agri-Food Chains: a Review
Keywords:
Localización de Instalaciones, Cadena de Suministro Agro-Alimentaria, Productos Perecederos (es).Keywords:
Location of facilities, supply chain Agro-Food, perishable products (en).Downloads
References
J. A. Orjuela C, C. A. Castañeda C y M. E. Calderón, «Análisis de la Cadena de Valor en las Estructuras Productivas de Uchuva y Tomate de Árbol en la Provincia de Sumapaz y el Distrito Capital,» Ingeniería, vol. 13, nº 2, pp. 4-12, 2008.
X. Zhao y J. Dou, «A hybrid particle swarm optimization approach for design of agri-food supply chain network,» Proceedings of 2011 IEEE International Conference on Service Operations, Logistics and Informatics, pp. 162-167, 2011.
J. A. Orjuela Castro y I. A. Chavarrio Colmenares , «Caracterización de la Cadena de Abastecimiento de Panela para la Provincia de Bajo Magdalena-Cundinamarca,» Ingeniería, vol. 16, nº 2, pp. 107-124, 2011.
K. Govindan, A. Jafarian, R. Khodaverdi y K. Devika, «Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food,» International Journal of Production Economics, pp. 9-28, 2014.
F. Boudahri, Z. Sari, F. Maliki y M. Bennekrouf, «Design and optimization of the supply chain of agri-foods: Application distribution network of chicken meat,» 2011 International Conference on Communications, Computing and Control Applications, CCCA 2011, 2011.
M. M. Herrera Ramírez y J. A. Orjuela Castro, «Perspectiva de Trazabilidad en la Cadena de Suministros de Frutas: Un Enfoque desde la Dinámica de Sistemas,» Ingeniería, vol. 19, nº 2, 2014.
FAO, «Pérdidas y desperdicio de alimentos en el mundo,» 2011.
M. Zhang y J. Yang, «Optimization modeling and algorithm of facility location problem in perishable commodities emergency system,» Proceedings - Third International Conference on Natural Computation, pp. 246-250, 2007.
O. Ahumada y J. R. Villalobos, «Application of planning models in the agri-food supply chain: A review,» European Journal of Operational Research, p. 5, 2009.
F. A. Pérez Mantilla y F. J. Torres Delgado, «Modelos de inventarios con productos perecederos: revisión de literatura,» Ingeniería, vol. 19, nº 2, 2014.
W. Di, J. Wang, B. Li y M. Wang, «A location-inventory model for perishable agricultural product distribution centers,» 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce, AIMSEC 2011 - Proceedings, pp. 919-922, 2011.
A. F. Ruiz Moreno, A. L. Caicedo Otavo y J. A. Orjuela Castro, «Integración Externa en las Cadenas de Suministro Agroindustriales: Una Revisión al Estado del Arte,» Ingeniería, vol. 20, nº 2, pp. 9-30, 2015.
Z. Firoozi, N. Ismail, S. Ariafar, S. H. Tang, M. K. M. A. Ariffin y A. Memariani, «Effects of Integration on the Cost Reduction in Distribution Network Design for Perishable Products,» Mathematical Problems in Engineering, pp. 1-10, 2014.
D. Tong, F. Ren y J. Mack, «Locating farmers' markets with an incorporation of spatio-temporal variation,» Socio-Economic Planning Sciences, pp. 149-156, 2012.
M. T. Lucas y D. Chhajed, «Applications of location analysis in agriculture: a survey,» Journal of the Operational Research Society, pp. 561-578, 2004.
S. Validi, A. Bhattacharya y P. J. Byrne, «A case analysis of a sustainable food supply chain distribution system-A multi-objective approach,» International Journal of Production Economics, pp. 71-87, 2014.
R. Akkerman, P. Farahani y M. Grunow, «Quality, safety and sustainability in food distribution: a review of quantitative operations management approaches and challenges,» OR Spectrum, pp. 863-904, 2010.
X. Chen y C.-y. Zhong, «An Improved Genetic Algorithm for Location Problem of Logistic Distribution Center for Perishable Products,» International Asia Conference on Industrial Engineering and Management Innovation (IEMI2012) Proceedings, pp. 949-959, 2013.
S. Chopra y P. Meindl, Administración de la Cadena de Suministro, Mexico: PEARSON Prentice Hall, 2008, p. 554.
B. M. Beamon, «Supply chain design and analysis: Models and methods,» International Journal of Production Economics, pp. 281-294, 1998.
Z. Ling y M. Zhang, «Optimization of Supply Chain Design Based on Knowledge Discovery of Distribution Network,» 2009 International Joint Conference on Artificial Intelligence, pp. 769-772, 2009.
S. Yu, «Supply Chain Distribution Network - Optimized Design Model and Its Solution Based on Time Constraints,» 2012 Second International Conference on Intelligent System Design and Engineering Application, pp. 941-945, 2012.
I. J. Moreno Castañeda, J. L. Roa Canal y J. A. Orjuela Castro, «Caracterización De La Logística De La Cadena De Abastecimiento Agroindustrial Frutícola En Colombia,» Bogotá, 2012.
MinSalud; FAO, «Perfil Nacional De Consumo De Frutas Y Verduras,» 2013.
CORPOICA, «Escenario Actual De CTI En El Sector Hortofrutícola : Análisis Y Retos Futuros.,» 2013.
H.-S. Hwang, «A food distribution model for famine relief,» Computers & Industrial Engineering, pp. 335-338, 1999.
R. Carro Paz y D. Goncález Gómez, «Localización de instalaciones,» Buenos Aires, 2012.
Ş. Erengüç, N. Simpson y A. J. Vakharia, «Integrated production/distribution planning in supply chains: An invited review,» European Journal of Operational Research, pp. 219-236, 1999.
C. E. H. ReVelle, «Location analysis: A synthesis and survey,» European Journal of Operational Research, pp. 1-19, 2005.
A. Weber, «Uber den Standort der Industrien. 1. Teil: Reine Theorie des Standortes, Tu¨bingen, Germany, Translated as On the Location of Industries,» p. 153, 1909.
H. Hotelling, «Stability in competition,» The Economic Journal, pp. 41-57, 1929.
W. Christaller, Central Places in Southern Germany, Prentic-Hall, 1933.
A. Losch, The Economics of Location, New Haven: Yale University Press, 1954.
C. ReVelle, H. Eiselt y M. Daskin, «A bibliography for some fundamental problem categories in discrete location science,» European Journal of Operational Research, pp. 817-848, 2008.
Q. Meng, Y. Huang y R. L. Cheu, «Competitive facility location on decentralized supply chains,» European Journal of Operational Research, pp. 487-499, 2009.
M. Melo, S. Nickel y F. Saldanha-da-Gama, «Facility location and supply chain management – A review,» European Journal of Operational Research, pp. 401-412, 2009.
M. Melo, S. Nickel y F. Saldanha da Gama, «Dynamic multi-commodity capacitated facility location: a mathematical modeling framework for strategic supply chain planning,» Computers & Operations Research, pp. 181-208, 2006.
A. Klose y A. Drexl, «Facility location models for distribution system design,» European Journal of Operational Research, pp. 4-29, 2005.
R. Sridharan, «The capacitated plant location problem,» European Journal of Operational Research, pp. 203-213, 1995.
S. H. Owen y M. S. Daskin, «Strategic facility location: A review,» European Journal of Operational Research, pp. 423-447, 1998.
S. Z.-l. S. Zhi-lin y W. D. W. Dong, «Location Model of Agricultural Product Distribution Center,» 2007 International Conference on Management Science and Engineering, pp. 117-120, 2007.
Q. Xiaohui y Y. Wen, «Studies on spatio-temporal collaboration model for location analysis of vegetable & fruit logistics,» 6th International Conference on Fuzzy Systems and Knowledge Discovery, FSKD 2009, pp. 619-626, 2009.
M. V. Marulanda, G. I. Leguizamón y K. Y. Niño Mora, «Solución al problema de localización (cflp) a través de búsqueda tabú y relajación lagrangeana, caso de estudio: industria de productos alimentarios,» Purntr, 2010.
K. Yang, Y. Liu y G. Yang, «An improved hybrid particle swarm optimization algorithm for fuzzy p-hub center problem,» Computers & Industrial Engineering, pp. 133-142, 2012.
E. Morganti y J. Gonzalez-Feliu, «City logistics for perishable products. The case of the Parma's Food Hub,» Case Studies on Transport Policy, 2014.
H. Etemadnia, S. J. Goetz, P. Canning y M. S. Tavallali, «Optimal wholesale facilities location within the fruit and vegetables supply chain with bimodal transportation options: An LP-MIP heuristic approach,» European Journal of Operational Research, pp. 648-661, 2015.
J. Jouzdani, S. J. Sadjadi y M. Fathian, «Dynamic dairy facility location and supply chain planning under traffic congestion and demand uncertainty: A case study of Tehran,» Applied Mathematical Modelling, pp. 8467-8483, 2013.
W. Neungmatcha, K. Sethanan, M. Gen y S. Theerakulpisut, «Adaptive genetic algorithm for solving sugarcane loading stations with multi-facility services problem,» Computers and Electronics in Agriculture, pp. 85-99, 2013.
A. H. Hiassat y A. Diabat, «A Location Inventory Routing Problem with Perishable Products,» Proceedings of the 41st International Conference on Computers & Industrial Engineering, pp. 386-391, 2010.
X. Zhao y Q. Lv, «Optimal Design of Agri-Food Chain Network: An Improved Particle Swarm Optimization Approach,» 2011 International Conference on Management and Service Science, pp. 1-5, 2011.
K. Khalili-Damghani, A.-R. Abtahi y A. Ghasemi, «A New Bi-objective Location-routing Problem for Distribution of Perishable Products: Evolutionary Computation Approach,» Journal of Mathematical Modelling and Algorithms in Operations Research, 2015.
A. Federgruen, G. Prastacos y P. H. Zipkin, «An Allocation and Distribution Model for Perishable Products,» Operations Research, pp. 75-82, 1986.
X. R. Huang y R. H. Xie, «A model on location decision for distribution centers of emergency food logistics,» 2009 2nd International Conference on Information and Computing Science, ICIC 2009, pp. 232-235, 2009.
K. Diatha, R. Karumanchi y S. Garg, «Mobile Enabled Operations Management Using Multi-Objective Based Logistics Planning For Perishable Products,» Computers and Industrial Engineering 42, pp. 16-18, 2012.
Z. Drezner y C. H. Scott, «Location of a distribution center for a perishable product,» Mathematical Methods of Operations Research, pp. 301-314, 2013.
W. Gong, D. Li, X. Liu, J. Yue y Z. Fu, «Improved two‐grade delayed particle swarm optimisation (TGDPSO) for inventory facility location for perishable food distribution centres in Beijing,» New Zealand Journal of Agricultural Research, pp. 771-779, 2007.
J. Orjuela, I. Castañeda, J. Canal y J. Rivera, «La logística en la cadena de frutas,» Frutas y Hortalizas, nº 39, pp. 10 - 15, 2015.
J. A. Orjuela Castro, L. E. Vidal Morales , A. A. Masmela Cortes y J. Rivera Velasco, «Logística Logística en la Cadena Hortícola (Olerícola),» Revista Frutas & Hortalizas, vol. 41, nº 1, Mayo-Junio 2015.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2017.1.a04
Modelos de Localización para Cadenas Agroalimentarias Perecederas: una Revisión al Estado del Arte
Facility Location Models in Perishable Agri-Food Chains: a Review
Lizeth Andrea Sanabria Coronado
Universidad Distrital Francisco José de Caldas- Facultad de Ingeniería-Bogotá, Colombia. lizeth asanabria@hotmail.com
Andres Mauricio Peralta Lozano
Universidad Distrital Francisco José de Caldas- Facultad de Ingeniería-Bogotá, Colombia. amperaltal@hotmail.com
Javier Arturo Orjuela Castro
Universidad Distrital Francisco José de Caldas- Facultad de Ingeniería-Bogotá, Colombia. jorjuela@udistrital.edu.co
Recibido: 03-05-2016. Modificado: 17-08-2016. Aceptado: 10-10-2016.
Resumen
Contexto:El problema de la localización de instalaciones en cadenas de suministros de productos agrícolas perecederos no ha sido suficientemente estudiado, sin embargo, el tema en los últimos años ha tomado interés debido a la preocupación por el consumo de alimentos frescos y saludables, aspecto relevante en países con potencial productor en alimentos hortofrutícolas.
Método: Se realizó una revisión sistemática del estado del arte del problema de localización de instalaciones para alimentos agrícolas con énfasis en perecederos; se consultaron las bases de datos: Science Direct, IEEE Xplore, SpringerLink, JSTOR, Scopus y Google Scholar, de 135 artículos de localización en alimentos, finalmente se seleccionaron 31 donde contemplan los modelos de localización en cadenas de suministro de alimentos, con énfasis en perecederos, basados en el criterio de la última déCada 2004-2015.
Resultados:
En la revisión se propone una tipología para la clasificación de variables contempladas en los modelos, se establecieron las variables no contempladas en los modelos, pertinentes para países con las características de Colombia. Se identificaron las funciones objetivo, comúnmente usadas, así como las restricciones específicas para las Cadena de Suministro Alimentaria (CSA) y los drivers logísticos más utilizados en estos modelos. Se identifican líneas de futuras investigación, respecto a variables a incluir en modelos de localización para CSA de perecederos (CSAP) en contexto de países montañosos.Conclusiones: Decisiones estratégicas relevantes como la localización de instalaciones son de importancia durante el diseño de la CSA y de su red de distribución, dado el carácter perecedero de los alimentos frescos. Sin embargo, el tema ha sido poco tratado debido especialmente a la dificultad para el modelamiento y al número de variables a considerar en las CSAP. Se requieren modelos que contemplen la perecibilidad, las pérdidas y el comportamiento estocástico de algunas variables. Países montañosos como Colombia abren puertas a investigaciones que modelen el cambio en los climas, pisos térmicos, condiciones de viaje y su incidencia en la perecibilidad de los alimentos.
Palabras clave: Cadena de suministro agro-alimentaria, localización de instalaciones, productos perecederos.
Idioma: Español
Abstract
Context:The problem of locating facilities in supply chains of perishable agricultural products has not been widely addressed, however, this issue in recent years has taken great interest because of concerns about the consumption of fresh and healthy food, important aspect in countries with fruits food producer potential.
Method: A systematic review of the state of the art on facility location problems for perishable agricultural products was conducted. The following databases were searched: Science Direct, IEEE Xplore, SpringerLink, JSTOR, Scopus and Google Scholar. From an initial collection of 135 papers obtained with a generic search query for food location, 31 were finally selected for review focusing on food supply chain location model, within a publication date ranging from 2004 to 2015.
Results: Based on the review, a typology of variables considered and not considered in models pertinent to conditions relevant to countries such as Colombia, is proposed. Objective functions commonly used, specific restrictions for Food Supply Chain (FSC) and logistical drivers most commonly considered in these models were also identified. Future research, regarding variables to be included in FSC models location for perishables in context of mountainous countries were identified.
Conclusions: Strategic decisions such as the location of facilities are of great importance for the design of the fresh food supply chain and its network, given the perishability. However, the issue has been poorly evaluated especially due to the difficulty of modeling and the large number of variables to consider in this type of chain. Models that include the perishability, losses and stochastic behavior of some variables are required. Colombia can benefit from more research in location models of perishable food, particularly the impact on perishability due to its particular conditions of great variety of climates, mountainous landscapes along with a limited transport and road infrastructure.
Keywords: Location of facilities, supply chain Agro-Food, perishable products.
1. Introducción
La cadena de suministro agroalimentaria (CSA) es una red de organizaciones que trabajan juntas, en diferentes procesos y actividades, con el fin de llevar los productos agrícolas de la granja a la mesa y satisfacer las demandas de los consumidores [1], [2], está conformada por productores, mayoristas, distribuidores, corredores, empresas de servicios, empresas al por menor y los consumidores [3], [4]. Se diferencia de otras CS por la importancia que desempeñan factores como la calidad y la seguridad alimentaria [5], [6]; según la FAO (FAO, 2011) más del 50% de las frutas producidas en América Latina se pierden o se desperdician antes de llegar a su destino final.
Un proceso complicado en la CSA es la distribución de alimentos perecederos con calidad [4]. Un producto se dice que es perecedero si alguna de sus características presenta deterioro con respecto a los requisitos de los productores o del cliente [7], [8]. Los productos perecederos comienzan a deteriorarse desde el momento en que se producen, parte de su pérdida se debe al paso del tiempo [9], a los cambios frecuentes de temperatura y al inadecuado mantenimiento de la calidad a lo largo de la cadena [4], [9].
Las CSA de frescos y perecederos se caracterizan por una vida corta de los alimentos, el transporte rápido [4], vida útil limitada, variabilidad en la demanda y precios; esto hace las cadenas más complejas y difíciles de manejar [2], ya que solamente pueden ser trasladados en la CSA durante un lapso de tiempo máximo, luego de ser cosechados [11]. En este tipo de productos una correcta gestión logística permite una reducción de los costos logísticos y ofrecer mejores alimentos a los consumidores, con precios más bajos [10] [7].
La preocupación por la calidad de los alimentos, la salud y el medio ambiente por parte de los consumidores se ha incrementado, para ello se busca que el tiempo de permanencia y envió entre las instalaciones sea el menor posible, por lo tanto, la localización de las instalaciones en la CSA contribuye con este propósito al mantener el alimento fresco [11]. El problema de localización de instalaciones (PLI) agrícolas tiene relevancia en los países en desarrollo, donde la producción agrícola no se encuentra concentrada y el tamaño medio de las explotaciones es pequeño comparado con el número de agricultores, el PLI en la agricultura es de un tamaño considerable magnitud, consideran la ubicación de múltiples instalaciones, heterogeneidad y limitaciones de capacidad [12], en los últimos años se ha incluido el medio ambiente y la competitividad de la CS al problema [13], [14].
En los problemas de localización los centros de distribución son nodos importantes de los sistemas logísticos, [15], [16] su ubicación determina las restricciones de las redes y afecta directamente la eficiencia y la eficacia de la operación misma [17], [18], [19]. A diferencia de un producto industrial, el producto agrícola perecedero tiene un menor valor, mayor nivel de consumo, un proceso de distribución más complejo, una vida útil corta y es más difícil de gestionar en el almacén. Estos factores se ven reflejados en mayores costos logísticos que derivan en un aumento en el precio de venta [9], estos elementos derivan en la necesidad de establecer variables y parámetros específicos para el PLI en CSA de perecederos.
Con base en lo anterior este artículo se centra en la revisión de la literatura de los trabajos relacionados con la localización de instalaciones específicamente en las CSA perecederas, con el objetivo de identificar la forma como se ha abordado en el PLI el carácter perecedero de los alimentos frescos e identificar las formas de solución y posibles aplicaciones en mercados emergentes. La motivación del mismo se centra en el contexto colombiano, donde existen diversas problemáticas en la distribución logística para este tipo de cadenas, relacionadas con la gestión del proceso, el ruteo y la localización de los nodos o instalaciones dentro de la red [20].
Respecto a los nodos de transferencia, existen dos dificultades, la primera atañe a la ubicación de los centros de acopio donde ingresa los alimentos frescos que provienen de los municipios, se alista y acondiciona para ser enviada a mayoristas, minoristas y plantas procesadoras [21]. La segunda dificultad está relacionada con los puertos, debido a su ubicación en la Costa Caribe y Pacifica, los trayectos de envió terrestres son extensos, lo cual genera daños en el producto.
A pesar que en el país se han invertido recursos en la construcción de centros de acopio a nivel municipal y departamental, los resultados no han sido los esperados, dado que los únicos centros de acopio que funcionan de manera aceptable son los que constituyen las grandes Centrales de Abastos de las principales ciudades del país [22]. En ese sentido la localización de instalaciones jugaría un papel fundamental en el mejoramiento del desempeño logístico de la CSA de perecederos, ya que el diseño de la red de distribución es una decisión crítica en la gestión de operaciones por los costos, tiempo y calidad de alimento [23].
A partir de la revisión de la literatura, el artículo busca responder a las preguntas: ¿por qué es importante la ubicación de instalaciones en países con alto potencial en CSA de perecederos como Colombia?, ¿cuáles tipos de modelos han sido aplicados para la ubicación de instalaciones en las CSA de perecederos?,¿ Cual formulación de modelos se utilizan con mayor frecuencia en CSA de perecederos?,¿cuáles son los métodos de solución aplicados al PLI de CSA de perecederos?, ¿serán aplicables estos modelos y métodos a las características de la CSA de Colombia?
El presente artículo se desarrolla de la siguiente manera: en la Sección 2 se presenta la metodologí del levantamiento, selección y clasificación de la información. En la Sección 3, la definición y clasificación de la localización de instalaciones en CSA y en la Sección 4 la discusión y conclusiones.
Metodología
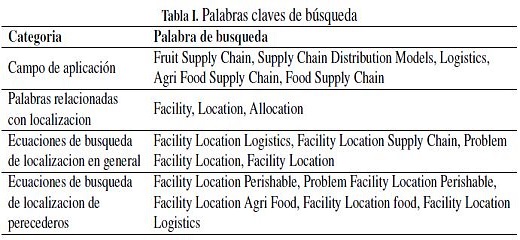
Para el desarrollo del artículo se consultaron las siguientes bases de datos: Science Direct, IEEE Xplore, Springer Link, JSTOR, Scopus y Google Scholar. Las palabras clave de búsqueda se presentan en la Tabla I. Las búsquedas se realizaron en Title, Abstract y Keywords en cada una de las bases de datos.
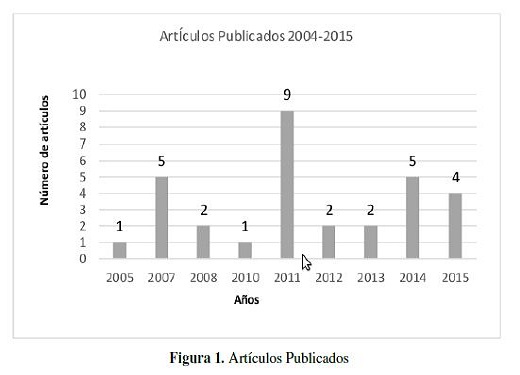
La Figura 1 presenta el consolidado de las bases de datos Scopus, IEEE Xplore, SpringerLink y JSTOR, de la cantidad de artículos publicados utilizando las ecuaciones de búsqueda: Facility Location Agri-Food y Facility Location Perishable, en el entorno de ingenierías, localización, logística y cadenas de suministro. Se observa que el número de publicaciones en productos perecedero han sido pocas a través de los años.
Luego de realizar una revisión exhaustiva de la literatura se identificaron los tipos de PLI usados con mayor frecuencia en la CSA, se construyó una visión general y se completó con la búsqueda de problemas aplicados específicamente a productos perecederos, también se identificaron los tipos de formulación empleados y los métodos de solución aplicados.
3. Localización de instalaciones en cadenas agroalimentarias
La localización de instalaciones es: “el proceso de elegir un lugar geográfico entre varios para realizar las operaciones de determinado actor” [24], se relaciona con los centros de distribución (CD), fábricas y centros de acopio (CA), entre otros, que deben ser seleccionados y asignados para ser atendidos en la cadena, por los diferentes actores [25]. Los problemas de localización se refieren al modelado, formulación y solución para la ubicación de instalaciones [26]. El campo de la teoría de la localización y el modelado tiene sus raíces en la primera mitad del siglo 20 con los trabajos desarrollados por Weber [27], Hotelling [28], Christaller [29] y Losch [30]. En la actualidad sigue siendo un campo activo [31].
Las decisiones de localización son un aspecto crítico para garantizar que una CS sea eficiente, debido a que una mala ubicación dará lugar a un exceso de costos reflejados durante la vida útil de las instalaciones [32]. El establecimiento de nuevas instalaciones, la ampliación, reducción y reubicación de instalaciones hacen parte del nivel estratégico de decisión en la CS, suelen ser proyectos a largo plazo e implican actividades que consumen tiempo y capital [33], [34].
La capacidad, el nivel de comercialización y la calidad de los productos dependen en parte de la ubicación de las instalaciones y la relación existente con los demás agentes en la red logística [35]. La ubicación de instalaciones se combina frecuentemente con decisiones de inventario y producción [33]. Este tipo de decisiones tienen en cuenta los costos, rentabilidad, tiempos de respuesta, cercanía a determinados lugares de acuerdo a las características del sector o cadena evaluados [24].
Los modelos de ubicación y asignación comprenden formulaciones que varían en complejidad desde un modelo lineal simple hasta modelos probabilísticos no lineales, cambian ampliamente en cuanto a los supuestos fundamentales, complejidad matemática y rendimiento computacional. Los algoritmos de soluci]ón incluyen, entre otros, la búsqueda local y enfoques basados en programación matemática [35].
3.1. Tipos de problemas de localización
En esta sección se presenta una revisión al estado del arte de los tipos de problemas de localizión enfocado en productos perecederos, la notación utilizada se presenta en Anexo I, la cual se basa en ReVelle et al. [31]. El primer problema de ubicación de instalaciones se plantea por el matemático Torricelli, es aplicado a tres clientes y una instalación, con el objetivo de minimizar la suma de las distancias euclidianas entre ellos. Los modelos de ubicación y asignación comprenden formulaciones que varían en complejidad desde un modelo lineal simple hasta los modelos probabilísticos no lineales, cambian ampliamente en cuanto a los supuestos fundamentales, complejidad matemática y rendimiento computacional. Los modelos simples intentan localizar una sola instalación y los complejos podrían localizar “p” instalaciones. Los problemas pueden ser capacitados o no capacitados. Las limitaciones de capacidad permiten que la demanda de un cliente se pueda satisfacer por varias instalaciones, lo que deriva en un problema mas complejo [26].
En los modelos capacitados existe un conjunto de ubicaciones potenciales para las plantas, que suministrarán a un grupo de clientes de bienes, el problema busca encontrar el subconjunto de instalaciones o plantas que minimice los costos totales fijos y de transporte, de tal manera que la demanda de todos los clientes pueda ser satisfecha sin violar las restricciones de capacidad, cada planta tiene una capacidad potencial o un nivel máximo de servicio [36].
Según Owen [37] los modelos de localización se pueden dividir en estocásticos, determinísticos, dinámicos y continuos. A continuación serán descritos los tipos de problemas de localización utilizados para la CSA con énfasis en perecederos, se presenta la formulación clásica de cada tipo y se especifica cuales son las variables y restricciones que se han incluido para este tipo de cadenas . Son presentados los problemas P-Mediana, P-Centro, P-Cobertura, Hubs, Multi-producto, Servicios Múltiples y capacitados.
A continuación se presenta el modelo general de los problemas P-Mediana [31]:
FO
Restricciones:
En la función objetivo (1) se minimiza la distancia media ponderada de la demanda. La restricción (2) asegura que se asigne a cada nodo de demanda una instalación candidata, mientras que la (3) controla que solo se asigne aquellas instalaciones localizadas. Por su parte la restricción ( 4) controla que se abra el número de instalaciones requeridas y las restricciones ( 5) y (6) definen las variables de decisión como binarias.
En la CSA los problemas P-Mediana se utilizan para la ubicación de un solo tipo de instalación principalmente centros de distribución [38], [39], [7], dado el tipo de alimento que se comercializa en estas cadenas es importante la localización de plazas y mercados para los agricultores [11]. Al igual que en los modelos P-Mediana generales, los modelos aplicados a productos agrícolas tienen como objetivo principal la minimización del costo total, que incluye entre otros los costos logísticos, de transporte, de construcción y de operación en cada una de las instalaciones. Los pocos trabajos que incluyen el caracter perecedero lo hacen a través de costos de penalización, costos de perdida y costo de desperdicio, estos modelos añaden la temporalidad y el espacio debido al caracter perecedero de los productos agrícolas, la perdida de producto y tasas de descomposición [7], [38], [39], [11].Para su aplicación en alimentos perecederos, los autores Xiaohui [39] y Zhang [2] tuvieron en cuenta el carácter perecedero como una restricción adicional dentro del modelo. La logística de frutas y verduras es diferente a la de otro tipo de productos, debido a la facilidad que tienen para perder sus propiedades, genera un alto nivel de desperdicio y un mayor costo logístico [39]. En ese sentido Zhang [7] desarrolla una función de perdida penalizada con un costo, la cual esta relacionada con la velocidad y la distancia entre la instalación y el punto de demanda.
La ecuación (7) calcula la cantidad de producto perdido en la trasferencia desde el punto i hasta el punto j y las ecuaciones (8) y (9) obtienen el valor de la perdida total en el sistema evaluado. Por su parte Xiaohui [39] realiza un análisis similar al de Zhang con respecto al cálculo del costo de perecibilidad, pero combina variables espacio y tiempo con el fin de eliminar la discrepancia existente entre la ubicación del consumidor y el productor. El autor presenta la ecuación (10 para calcular el costo del carácter perecedero.
Tong [11] quien tambien trabajo el problema P-Mediana en productos perecederos, solamente considero el crecimiento poblacional como criterio para la localización de las instalaciones, sin incluir la perecibilidad de los productos.
3.1.2. Problemas de cobertura
En este tipo de modelos se busca suplir la demanda de diferentes nodos, con una distancia o tiempo máximo aceptable, es decir un plazo determinado. Reduciendo el costo total de la ubicación de instalaciones y maximizando el nivel de servicio hacia cualquiera de los clientes en el problema. La demanda de un nodo o cliente se dice que esta cubierta, si la distancia o el tiempo entre este y su instalación más cercana no es mayor a un valor especificado previamente [26]. La función objetivo y la primera restricción de los problemas P-Cobertura difieren del modelo P- Mediana [31]:
FO
Restricciones:
La función objetivo (11) maximiza el número de demandas cubiertas, la restricción (12) garantiza que se ubiquen suficientes instalaciones para cubrir la demanda, también contiene las tres restricciones (4),(5),(6) del modelo P-Mediana.
Se ha encontrado un estudio que aplica el problema de cobertura en la agroindustria, Marulanda et al. [40] buscan la ubicación de plantas de producción, su objetivo es la cobertura de una mayor demanda al menor costo, determinan el número necesario de plantas, con el fin de soportar la toma de decisiones para la expansión de una empresa. En las formulaciones no se ha tenido en cuenta la vida útil, los desperdicios, o el carácter perecedero de los productos agrícolas, el enfoque de las funciones ha sido la reducción de costos teniendo en cuenta la demanda, apertura y cierre de nuevas instalaciones. Sin embargo, el modelo propuesto por Marulanda [40] presenta un enfoque interesante teniendo en cuenta la capacidad limitada de las instalaciones a ubicar en la CS, generando una mayor aproximación al estado real de la misma, para lo cual agrega la ecuación (13).
3.1.3. Problemas P-Centro
El problema P-Centro es también conocido como MinMax, busca reducir al mínimo las distancias máximas entre cualquier demanda y su centro de distribución más cercano Este tipo de modelos son utilizados para determinar la ubicación de una instalación sobre cualquier lugar de una red establecida, a los cuales se les denomina, problemas de centro absoluto [37]. Las soluciones al problema P-Centro se dividen típicamente en dos. La primera denominada centros de nodo en la que las instalaciones elegibles estan restringidas a los vértices de la red y la segunda, centros absolutos en los que la instalacion podría estar en cualquier lugar dentro de la red [26]. A los elementos que diferencia el modelo de los anteriores [31]:
F.O:
Restricciones:
La función objetivo junto a la restricción (14) mínimiza la distancia máxima entre cliente y la instalación. Además de las restricciones (2), (3), (4), (5), (6), aparece la restricción (15) la cual limita el número de instalaciones a una cantidad preestablecida.
Los problemas P-Centro han sido trabajados tanto para productos agrícolas perecederos, para la ubicacion de CD [41], como para la agroindustria en la localizacion de plantas de procesamiento encontrando el centro de gravedad del conjunto de clientes [5]. En las funciones objetivo del problema, en alimentos perecederos, se encuentran el minimizar los costos de ubicación y transporte [5] y la minimización del tiempo máximo del recorrido entre instalaciones [41]. Yang et al. [41] considera el carácter perecedero de los productos como una restricción adicional con tiempos de entrega. La duración de una entrega es importante para alimentos porque influyen en su calidad y la satisfacción del cliente, por lo tanto, los tiempos de viaje son considerados en el modelo como un factor de competencia. Para ello propone las siguientes ecuaciones en su modelo matemático, la (16) hace referencia a la función objetivo en donde se busca reducir el tiempo de transporte a lo largo de las rutas de la red y la (17) garantiza que el camino o ruta seleccionada es valida siempre y cuando exista asignación de nodos.
Tanto Yang [41] como Boudahri [5] agregan al modelo decisiones de transporte con miras al mejoramiento del desempeño de la CS, adicionalmente Boudahri [5] incluye decisiones de asignación.
3.1.4. Problemas de localizacion Hub
Los problemas de localización Hub surgen en contextos en los que los clientes requieren el transporte entre un gran número de pares origen-destino, en las redes Hub se requiere que los clientes viajen desde su origen a un eje central y de allí se dirijan ya sea a su destino o a otro Hub y así sucesivamente hasta su destino final [26]. Las redes Hub consideran grafos no dirigidos y la existencia de flujo entre cada par de nodos. El número de Hubs puede ser fijo o variables. Si el conjunto de los centros se conoce, el problema tiene como solución la ruta más corta, de lo contrario el problema es NP-complejo [35]. Klose [35] propone el modelo general. La función objetivo (18) minimiza los costos fijo y variables del envío y ubicación de las instalaciones.
La ecuación ( 19) asegura que la suma de las porciones de demanda no sea mayor al 100 %, la ecuación (20) controlan el número de instalaciones a ubicar.
F.O:
Restricciones:
Para la logística de los productos perecederos es importante una buena ubicación de las instalaciones en centros de distribución urbana eficaces y viables [42]. Los problemas de localización tipo Hub en alimentos agrícolas perecederos buscan el diseño de una red de distribución al por mayor con conexiones eficientes. Se han trabajado diferentes tipos de objetivos como la minimización de los costos totales de la red incluyendo costos de transporte y localización, la minimización del tiempo máximo del recorrido entre instalaciones [43].
Para productos perecederos se han tenido en cuenta los tiempos y la distancia de envío, la satisfacción de la demanda total [43] y la duración en las entregas como factor de competencia al relacionarlo con la calidad y satisfacción del cliente, la distancia máxima de entrega, capacidad limitada de los Hub, consolidación del flujo que se envía y escenarios difusos en los tiempos de viaje. [41] . Etemadnia et al. [43] en su modelo considera la cantidad de producción y demanda (21) (22), y la capacidad de las instalaciones tanto con límite superior como inferior (23-24).
3.1.5. Problema multi-producto
En aquellos casos donde no sea posible agregar la demanda, la producción, la manipulación y los costos de distribución, será necesario acudir a un modelo multi-producto donde, por ejemplo, la capacidad de los nodos, la demanda y los flujos estan separados con respecto a grupos de productos homogéneos [35]. Klose [35] presenta el siguiente modelo general de este tipo de problemas:
La función objetivo (25) minimiza los costos fijos y variables de proveer los productos, incluye la ecuación (19) presentada anteriormente, la (26) y (27) prohíbe asignar productos a los depositos cerrados y que se entregue cuando no esta disponible en el almacén. Mientras la restricción (28) controla que sea asignada por lo menos alguna porcion de demanda a cada instalación.
En los problemas multi-producto en perecederos la función objetivo común es la minimización de los costos totales que incluyen los costos de ubicación, producción, transporte, los costos de implementación [2] y costos de inversión [44], se han contemplado modo de transporte, inventario, capacidad de las instalaciones [44], tipo de alimento a producir en cada planta y cantidad a enviar entre las instalaciones [2], algunos modelos incluso abarcan la planificación completa de la CS, considerando la incertidumbre de la demanda [44]. Se han enfocado en la reducción de distancias y costos, e incluso se ha incluido la congestion vehicular y los diversos de actores de una misma cadena. No se han encontrado investigaciones que tengan en cuenta el carácter perecedero de los productos, ni el estado de los mismos durante el movimiento en cadena.
Zhao [2] propone un modelo matemático en el que tiene en cuenta productos frescos, semi- procesados y procesados. Para cada uno de ellos construye una serie de restricción que calculan la cantidad de productos disponibles para suplir la demanda de los eslabones que intervienen. Dadas las características de este trabajo se expone a continuación el conjunto de restricciones que presentan mayor perecibilidad.
3.1.6. Problemas de servicios múltiples
En este tipo de problemas se distingue entre los modelos de elección del cliente y los modelos de asignación. Los de elección del cliente deciden la instalación donde ir, es un sistema apropiado para el sector minorista, en especial cuando el planificador de instalaciones tambien se encarga de decidir que instalación suministra a un cliente determinado [26].
Neungmatcha et al. [45] proponen un modelo para la industria azucarera y la ubicación de estaciones teniendo en cuenta la planeación del transporte y distribución, el objetivo es la minimización de los costos de transporte y de operación, busca el número de instalaciones a abrir y relaciona a los cultivadores con las estaciones que cada uno de estos debera suplir. En servicios múltiples los trabajos en CSA no se ha tenido en cuenta el factor perecedero a lo largo del viaje del producto. El modelo se presenta a continuación:
Este modelo se desarrolló con el objetivo de minimizar el costo total en cualquier período en un ano agrícola (32), incluye el costo de transporte de un campo a una estación de carga y desde la estación de carga de un ingenio azucarero. La restricción (33) asegura que la capacidad de servicio de cada estación no deberá exceder su capacidad y utiliza la ecuación la (2) que asegura que todos los campos se asignaran a una sola estación, la (34) restringe el número total de estaciones abiertas, para que no exceda el número total de estaciones candidatas, la (35) asegura que la cantidad total de la caña de azúcar se puedan atender por las estaciones.
3.2. Tipos de modelado y métodos de solución
Una vez identificados los problemas de localización aplicados a alimentos se procedió a revisar los diferentes tipos de modelado matemático y los métodos de solución utilizados con énfasis en perecederos. Los algoritmos de solución incluyen, entre otros, la búsqueda local y enfoques basados en programación matemática. [35]. En la revisión literaria se identificaron que los autores han utilizado para el problema de alimentos agrícolas perecederos modelos de programación lineral, programación entera mixta (lineal y no lineal) y programación entera binaria y, los métodos utilizados para la solución algoritmos genéticos, heurísticas y meta-heurísticas.
3.2.1. Programación lineal
Boudahri et al. [:5] presentan un modelo de programación lineal que busca encontrar el centro de gravedad de los grupos de clientes, ubicar y asignar los mataderos en la cadena de distribución de carne de pollo, tiene en cuenta la capacidad de las instalaciones y de los vehículos. El objetivo es minimizar los costos de ubicación y de transporte. El modelo es capacitado y contempla las coordenadas geográficas de cada uno de los puntos posibles en seleccionar y asignar, la distancia entre nodos y el transporte.
Tong et al. [11] proponen un modelo de localización que tiene como objetivo seleccionar los lugares y los horarios de servicios de mercados de agricultores realizados directamente al cliente final de la CS. El modelo propuesto tiene en cuenta la variabilidad de la demanda a lo largo del tiempo, la distancia y el número de viajes de los clientes hacia dichos lugares de venta. El problema es no capacitado y trata aspectos como la red de distribución, la distancia entre nodos y el crecimiento poblacional.
3.2.2. Programación entera mixta
Hiassat y Diabat [46] plantean un modelo para la ubicación de las instalaciones que afectan a la empresa durante períodos de tiempo significativamente mas largos que otros. Determinan cuantos almacenes hay que abrir, donde localizarlos y que clientes asignar a los mismos. Existe un solo proveedor que distribuye a múltiples minoristas con demanda determinística a traves de un conjunto de centros de distribución, de un producto perecedero con cierta vida útil. El modelo incluye la localización, los inventarios y el costo de ruteo. El objetivo es reducir el costo. Zhao y Lv [47] diseñan un modelo para la ubicación de instalaciones, en donde se selecciona la capacidad de producción y el modo de transporte para el diseño de la CSA de manzanas. El objetivo es reducir los costos de producción y transporte. La solución se realiza a través de enjambre de partículas. Zhao y Dou [2] proponen un modelo para optimizar la CSA agrícolas con el objetivo de reducir los costos de producción y transporte de la cadena. Con el modelo buscan ubicar las instalaciones de manera óptima y con ello determinar la capacidad máxima de producción, el tipo de alimento a producir en cada planta, la selección de la cantidad a trasportar y el modo de transporte utilizado en la distribución. Para la solución del problema se utiliza enjambre de partículas. Yang et al. [41] presentan un modelo de programación entera mixta p-hub en entornos difusos (suponen elementos difusos en el tiempo de viaje y entre los nodos de origen-destino). El objetivo es minimizar el tiempo de recorrido máximo entre cada instalación. Se resuelve a través de enjambre de partículas.
Neungmatcha et al. [45] presentan un modelo solucionado a través de un algoritmo genético adaptativo, en el cual tienen como principal objetivo hallar la ubicación óptima para la instalación de las estaciones en una CS de la caña de azúcar, intentando maximizar el uso de la capacidad total. El modelo es tratado como un problema multi-servicio donde se tiene en cuenta el tipo y número de estos, y se espera minimizar el costo total. El modelo considera la capacidad de las instalaciones y la asignación de los clientes.
Govindan et al. [4] proponen un modelo de optimización multi-objetivo en una CSA de perecederos, el cual integra la sostenibilidad, el cálculo del número y ubicación de las instalaciones, optimiza la cantidad de los productos entregados y las rutas a traves de las cuales se realiza la distribución. Los autores proponen un modelo capacitado de doble eslabón con ventanas de tiempo, buscando reducir las emisiones de gases de efecto invernadero, utiliza para la solución un hibrido de dos algoritmos (Multi objective particle swarm optimization - Multi objective variable neighborhood search).
Etemadnia et al. [43] examinan la ubicación de instalaciones en una CSA perecederos para facilitar la transferencia entre los lugares de producción y consumo. Para ello proponen un modelo de programaci& entera mixta donde el objetivo es la minimización del costo total de la red, incluyendo los gastos de transporte y el costo de localizar cada una de las instalaciones. Adicional a esto los autores realizan un estudio por escenarios variando parámetros tales como, las distancias de viaje y la capacidad de cada instalación. La solución del problema se hace a través de una heurística.
3.2.3. Programación entera mixta no lineal
Zhi-lin y Dong [38] desarrollan un modelo de optimización para la ubicación de instalaciones. Se centran en el problema de seleccionar la mejor ubicación para el centro de distribución de alimentos agrícolas en China, que represente el menor costo posible, otorgando un análisis económico en cuanto a la construcción y operación de dicho centro. A diferencia de otros los trabajos en programación lineal, los autores tienen en cuenta una tasa de descomposició constante, sin embargo, no relaciona un costo de perdida. Inicialmente se conocen los puntos de ubicación y no tiene en cuenta la capacidad de las instalaciones.
Jouzdani et al. [44] proponen un modelo para la ubicación de instalaciones y la planificación de la CS de leche. El objetivo del modelo es la ubicación óptima de instalaciones y determinan los volúmenes de producción con bajos costos de transporte, consideran el tráfico de las vías y la incertidumbre de la demanda. Tienen en cuenta los posibles cambios en el sistema de transporte y producción, la cantidad de alimento a procesar y el inventario a mantener. Los puntos de ubicación se establecen en una red conocida.
Firoozi et al. [10] trabajan un problema de integración entre el control de inventarios y la ubicación de instalaciones. Los autores consideran de importancia aspectos de manera simultánea en la toma de decisiones, consideran en el costo de transporte y reabastecimiento, afectando de esta manera la política óptima de inventario. Para la solución del problema se hace uso de un algoritmo memético. Se considera que las demandas en los centros de distribución son estocásticas, se manejan puntos potenciales de ubicación conocidos y costos de transporte.
Damghani
3.2.4. Programación entera binaria
Weimin et al. [9] consideran un problema de diseño de red de distribución donde se busca decidir los sitios en los cuales deben estar ubicados los centros de distribución de productos agrícolas perecederos. Con la premisa de que cada centro tiene la capacidad suficiente para servir a su zona de consumo, además de que cada zona acepta productos de solo un centro de distribución. El objetivo es minimizar el costo total, el cual incluye los costos de ubicación, los costos de inventario, los costos de transporte y los costos de pérdida por deterioro. Para la solució del problema utilizan un algoritmo genéico.
Como se observa algunos de los trabajos reseñados no solamente describen con claridad el tipo de modelado matemático utilizado, también mencionan y representan la forma y métodos utilizados en la solución y optimización de los problemas. Se identificó que, para la solución de los problemas de localización de instalaciones en la cadena agrícola de perecederos, se utilizan en general: algoritmos genéticos, heurísticas y meta-heurísticas.
A continuación se realiza una clasificación con aquellos trabajos en los cuales no se presenta con claridad el tipo de modelado matemático, pero si la forma de solución.
3.2.5. Heurísticas y meta-heurísticas
Federgruen et al. [49] presentan un modelo de asignación de productos perecederos, distribuido desde un centro regional para un conjunto dado de ubicaciones con demanda aleatoria. Consideran un problema combinado de asignación de inventario disponible en dicho centro y la forma como se van a realizar las entregas. Se utiliza un algoritmo para la solución y se busca la reducción del costo en cuanto a distribución y transporte.
Zhang y Yang [7] plantean un modelo de optimización para la ubicación de instalaciones en el sistema de emergencia de productos perecederos básicos. Dicho modelo tiene como objetivo la minimización de los costos logísticos bajo limitaciones de tiempo, consideran los costos de transporte y aquellos que representan la pérdida de producto a lo largo de la red de distribución. Los autores establecen un centro de servicio en un área determinada con el fin de asegurar que se abastece la demanda, es decir un punto de demanda es atendido por una instalación, las instalaciones se pueden ubicar tanto en los bordes de la red, como en los vertices, con el fin de lograr la eficiencia de toda la red. Se plantea una heurística para la solución del problema.
Xiaohui y Wen [39] propusieron un modelo para la selección del lugar más adecuado para ubicar los centros de distribución tanto para frutas y verduras en Beijing. El modelo considera la relación espacio-tiempo, con el objetivo de eliminar la discrepancia en el tiempo y lugar entre el productor y el consumidor final del alimento, reducen los costos logísticos y los desperdicios, ofreciendo de manera conveniente y eficiente las frutas a los diversos mercados. En este trabajo se utilizó una heurística con el propósito de reducir la complejidad del problema.
Huang y Xie [50] proponen un modelo de solución al problema de ubicación de centros de distribución en la logística alimentaria de emergencia. En la decisión de localización se tomó en cuenta la eficiencia, la seguridad, la fiabilidad y la incertidumbre en los eventos de emergencia. Desarrollan el modelo bajo la premisa de que la correcta ubicación de los centros de distribución es importante para asegurar que el sistema tenga alta eficiencia, lo que significa una respuesta más rápida, menor tiempo de entrega y costo de operación más bajo cuando ocurren eventos de emergencia. Para la solución del problema se combinan redes neuronales con un algoritmo de colonia de hormigas, dentro de una red de posibles nodos a seleccionar.
Marulanda et al. [40] trabajan el problema de localización de plantas de producción con restricción de capacidad, lo aplican a una empresa que produce y comercializa productos de panadería y repostería en diversas regiones de Colombia. Buscan cubrir la mayor demanda posible con la instalación de una o más plantas de producción al menor costo. El problema es solucionado a través de Relajación Lagrangeana y Búsqueda Tabú.
Diatha et al. [51] proponen un modelo de formulación matemática multi-objetivo de ruteo y localización para en el mercado de hongos, lo solucionan con una heurística. Se conocen los posibles lugares donde se ubicaran los centros de distribución y se asigna un canal de distribución. Se busca minimizar los gastos, las distancias y los tiempos de respuesta, teniendo en cuenta ventanas tiempo.
Drezner y Scott [52] plantean un modelo que combina decisiones de inventario y localización de instalaciones para productos perecederos. Consideran la ubicación de un único centro de distribución que sirve un número finito de puntos de venta. El objetivo del modelo es reducir al mínimo el costo total, compuesto por los costos de inventario y los costos de transporte desde el centro de distribución hasta los puntos de venta. Se conocen los puntos potenciales para la ubicación de las instalaciones, la demanda se modela con una función de densidad y se utilizan las Heurística GWA (Algoritmo Weiszfeld Generalizado) y BTST (triángulo grande, triángulo pequeño), para la solución.
3.2.6. Algoritmos genéticos
Gong et al. [53] analizan de manera conjunta el problema de inventarios e instalación de ubicaciones para productos perecederos agrícolas en China. A través de un algoritmo, buscan reducir al mínimo el costo total de transporte, el nivel de inventarios y la cantidad de desperdicios a lo largo de la CS, encuentran la mejor distribución de los productos.
Chen y Zhong [15] describen un algoritmo genético mejorado para la solución de problemas de ubicación de centros de distribución de productos perecederos, consideran áreas restrictivas, tales como lagos y zonas administrativas. Los autores incluyen el impacto que tiene el carácter perecedero de los productos sobre el costo de distribución global. En el modelo se buscan establecer las zonas de distribución y sus respectivas rutas de manera factible.
4. Discusión
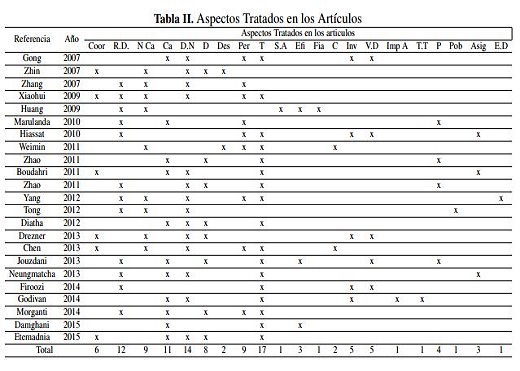
A lo largo de la revisión se ha destacado que los productos agrícolas tienen un alto nivel de consumo, un proceso de distribución complejo, un precio bajo, una vida útil corta y difícil gestión de almacén, lo cual según [9] se ve reflejado en mayores costos logísticos. Sin embargo, la cantidad de publicaciones que se encuentran sobre el tema es escasa, comparada con la literatura referente a cadenas no agrícolas. Esto podría deberse a la complejidad que representa el modelado en este tipo de cadenas dado el número de eslabones y actores que participan, así como las variables especificas a tener en cuenta. Como se evidencia a lo largo del art´iculo de revision aspectos como la seguridad alimentaria, impacto ambiental y el factor perecedero de los productos no se ha tratado ampliamente, a pesar de que tal como lo plantea [32] en los problemas de localización son aspectos críticos para garantizar que una CSA tenga altas medidas de desempeño. En la Tabla II, en la cual se presentan los principales aspectos tenidos en cuenta por cada uno de los autores en los artículos de productos perecederos consultados.
Coor: Coordenadas; R.D: Red de Distribución; NCa: No capacitado; Ca: Capacitado; D.N: Distancia nodos; D: Distribución; Des: Descomposición; Per: Perecedero; T: Transporte; S.A: Seguridad Alimentaria; Efi: Eficiencia; Fia: Fiabilidad; C: Calidad; Inv: Inventario; V.D: Variabilidad Demanda; ImpA: Impacto Ambiental; T.T: Tiempo de trabajo; P: Producción; Pob: Población; Asig: Asignación; E.D: Entornos Difusos.
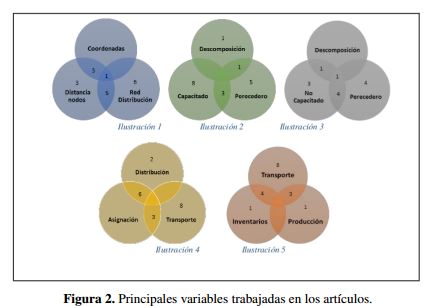
A partir de la revisión de la literatura se propone una tipología mediante de las variables tratadas en los artículos segun tipos y cantidad empleada las cuales son presentadas en la figura 2. En la Ilustración 1, se muestra la forma en que los autores conciben la relación de distancia entre nodos candidatos e instalaciones, las variables utilizadas en este tipo son coordenadas, distancia entre nodos y red de distribución. En la Ilustración 2 se encuentran las variables específicas de los productos perecederos, mostrando el número de artículos que han tenido en cuenta el carácter de perecibilidad, la descomposición del producto y la capacidad de las instalaciones.
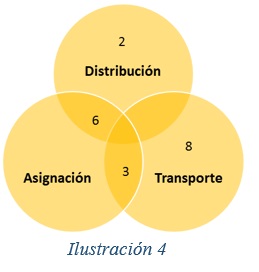
Por otra parte, la Ilustración 3 clasifican en modelos no capacitados, se observa que existe un mayor número de artículos que tienen en cuenta la capacidad de las instalaciones, pero en pocas ocasiones se considera la perecibilidad y la descomposición. Las Ilustraciones 4 y 5 clasifican el problema de localización según los “drivers” logísticos, si se han tratado de manera individual o como diadas, la Ilustración 4 contempla las decisiones de distribución, asignación, mientras la 5 las referidas a transporte o ruteo, produccion e inventarios, siendo transporte el de mayor frecuencia.
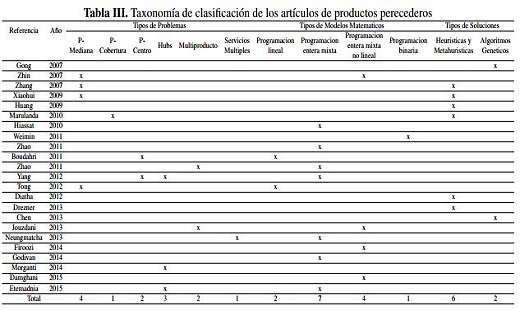
Finalizada la definición de la tipología según las variables que se utilizan con mayor frecuencia en la literatura científica de los problemas de localización de productos perecederos, se realiza una clasificación de los artículos de acuerdo al tipo de problema, modelo matemático y tipo solución que se han utilizado Tabla III.
Se identifica que el tipo de modelo matemático más utilizado es la programación entera mixta, esto se debe a un número grande de variables, parámetros y sub índices que los modelos generalmente incluyen, al contemplar características propias de las CS de productos agrícolas de perecederos. De igual manera se encuentra que dado la complejidad de los modelos, NP-Hard, se hace necesario la utilización de heurísticas y Meta-heurísticas que aproximen una solución al óptimo de cada modelo planteado.
En lo que respecta a las funciones objetivos, los modelos utilizan principalmente la minimización del costo total, incluyen costos de transporte, inventario y de producción. No es común la inclusió , en la formulación matemática, del carácter perecedero de los alimentos, en algunos casos se representa dicha característica como un costo, un tiempo máximo de transporte ligado a la vida útil o como una función de deterioro del mismo.
5. Conclusiones
El interés en las cadenas agroalimentarias se ha incrementado principalmente por la importancia que ha adquirido el consumo de productos frescos alrededor del mundo. Decisiones estratégicas relevantes como la localización de instalaciones son de importancia durante el diseño de la CS y de su red de distribución dado el carácter perecedero de los productos frescos. Sin embargo, el tema ha sido poco tratado debido especialmente a la dificultad para el modelado, así como el tipo y cantidad de variables a considerar en este tipo de CS.
Todo esto conlleva que a pesar de que en los últimos años ha ido en aumento el número de investigaciones y trabajos sobre las cadenas agroalimentarias a lo largo del mundo, principalmente en países desarrollados que buscan fortalecerse especialmente en frutas y verduras, aún existe espacio para investigaciones y propuestas en donde se incluyan en un solo modelo variables como capacidad, tipo de instalación, perecibilidad de los alimentos, perdidas y comportamiento estocástico de la demanda, con el fin de buscar modelos que permitan la toma de decisiones para mejorar el desempeño de las cadenas.
En estos países es necesaria la correcta ubicación de los centros de acopio, centrales mayoristas , empresas procesadoras, las plataformas logísticas y los puertos, así como la ubicación de los consumidores, en los modelos deben contemplarse su funcionalidad, evolución de capacidad y un adecuado diseño de modelos de gestión, contemplando las costumbres comerciales y sus implicaciones en los flujos, tales como la infraestructura y características de la flota. Existen alimentos perecederos como las frutas, en los cuales no se ha tenido en cuenta aspectos como los cambios de temperatura, humedad relativa y pisos térmicos, esenciales para garantizar la vida útil de la fruta y su calidad, que en países con cordilleras como Colombia se hace fundamental. Esto abren puertas a futuras investigaciones que modelen el carácter perecedero de las frutas teniendo en cuenta cambios climáticos, factores internos y externos, no solo al penalizarlo como un costo adicional sino que realmente represente los estados y las condiciones en su viaje a través de los diferentes eslabones de la CSA.
Es importante que en los modelos futuros se contemple tipos de transporte que permitan conservar durante el mayor tiempo posible las características organolépticas de los alimentos, tales como atmósferas modificadas y controladas, actualmente se limitan a identificar el tiempo en el cual la fruta pierde su calidad. Analizando la relación costo-beneficio al reducir las pérdidas de producto por descomposición y aumentando la calidad del producto. La mayor parte de la pérdida después de la cosecha ocurre en los procesos de almacenamiento, empaquetamiento y distribución por debilidades en la provisión y coordinación del servicio logístico.
En este estudio se logró identificar los principales modelos, tipologías de modelado y métodos de solución enfocados a las cadenas agrícolas de productos perecederos, exponiendo oportunidades de mejora y brechas en el conocimiento en la investigación científica de este tipo de problemas, con la intención de que puedan ser tratados en proyectos futuros principalmente en países montañosos como Colombia [55], [56] que permitan responder a la demanda de productos frescos conservando la calidad de estos. Asimismo, se identifica que los modelos dinámicos no son empleados para decisiones sobre localización de instalaciones en las CSA de perecederos, no obstante las especificidades de las mismas a través del tiempo. Por lo tanto, este es otro campo abierto para los investigadores.
Referencias
[1] J. A. Orjuela C, C. A. Castañeda C y M. E. Calderón, “Análisis de la Cadena de valor en las estructuras productivas de uchuva y tomate de arbol en la provincia de Sumapaz y el Distrito Capital”. Ingeniería, vol. 13, no 2, pp. 4-12,2008.
[2] X. Zhao y J. Dou, “A Hybrid Particle Swarm Optimization Approach for Design of Agri-Food Supply Chain Network”. Proceedings of 2011 IEEE International Conference on Service Operations, Logistics and Informatics, pp. 162-167, 2011
[3] J. A. Orjuela Castro y I. A. Chavarrio Colmenares , “Caracterización de la cadena de abastecimiento de panela para la provincia de Bajo Magdalena-Cundinamarca”. Ingeniería, vol. 16, no 2, pp. 107-124, 2011.
[4] K. Govindan, A. Jafarian, R. Khodaverdi y K. Devika, “Two-Echelon Multiple-Vehicle Location-Routing Problem with Time Windows for Optimization of Sustainable Supply Chain Network of Perishable Food”. International Journal of Production Economics, pp. 9-28, 2014.
[5] F. Boudahri, Z. Sari, F. Maliki y M. Bennekrouf, “Design and Optimization of the Supply Chain of Agri-Foods: Application Distribution Network of Chicken Meat”. 2011 International Conference on Communications, Computing and Control Applications, CCCA 2011, 2011.
[6] M. M. Herrera Ramírez y J. A. Orjuela Castro, “Perspectiva de Trazabilidad en la cadena de suministros de frutas: un enfoque desde la dinamica de sistemas”. Ingeniería, vol. 19, no 2, 2014.
[7] M. Zhang y J. Yang, “Optimization Modeling and Algorithm of Facility Location Problem in Perishable Commodities Emergency System”. Proceedings - Third International Conference on Natural Computation, pp. 246-250, 2007.
[8] O. Ahumada y J. R. Villalobos, “Application of Planning Models in the Agri-Food Supply Chain: a Review”. European Journal of Operational Research, p. 5, 2009.
[9] F. A. Pérez Mantilla y F. J. Torres Delgado, “Modelos de inventarios con productos perecederos: revisión de literatura”. Ingeniería, vol. 19, no 2, 2014.
[10] W. Di, J. Wang, B. Li y M. Wang, “A Location-Inventory Model for Perishable Agricultural Product Distribution Centers”. 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce, AIMSEC 2011 - Proceedings, pp. 919-922, 2011.
[11] A. F. Ruiz Moreno, A. L. Caicedo Otavo y J. A. Orjuela Castro, “Integración externa en las cadenas de suministro agroindustriales: una revision al estado del arte”. Ingeniería, vol. 20, no 2, pp. 9-30, 2015.
[12] Z. Firoozi, N. Ismail, S. Ariafar, S. H. Tang, M. K. M. A. Ariffin y A. Memariani, “Effects of Integration on the Cost Reduction in Distribution Network Design for Perishable Products”. Mathematical Problems in Engineering, pp. 1- 10, 2014.
[13] D. Tong, F. Ren y J. Mack, “'Locating Farmers' Markets with an Incorporation of Spatio-Temporal Variation”. Socio-Economic Planning Sciences, pp. 149-156, 2012.
[14] M. T. Lucas y D. Chhajed, “Applications of Location Analysis in Agriculture: a Survey”. Journal of the Operational Research Society, pp. 561-578, 2004.
[15] S. Validi, A. Bhattacharya y P. J. Byrne, “A Case Analysis of a Sustainable Food Supply Chain Distribution System-a Multi-Objective Approach”. International Journal of Production Economics, pp. 71-87, 2014.
[16] R. Akkerman, P. Farahani y M. Grunow, “Quality, Safety and Sustainability in Food Distribution: a Review of Quantitative Operations Management Approaches and Challenges”. OR Spectrum, pp. 863-904, 2010.
[17] X. Chen y C.-y. Zhong, “An Improved Genetic Algorithm for Location Problem of Logistic Distribution Center for Perishable Products”. International Asia Conference on Industrial Engineering and Management Innovation (IEMI2012) Proceedings, pp. 949-959, 2013
[18] S. Chopra y P. Meindl, Administración de la cadena de suministro , Mexico, PEARSON Prentice Hall, 2008, p. 554.
[19] B. M. Beamon, “Supply Chain Design and Analysis: Models and Methods”. International Journal of Production Economics, pp. 281-294, 1998.
[20] Z. Ling y M. Zhang, “Optimization of Supply Chain Design Based on Knowledge Discovery of Distribution Network”. 2009 International Joint Conference on Artificial Intelligence, pp. 769-772, 2009.
[21] S. Yu, “Supply Chain Distribution Network - Optimized Design Model and Its Solution Based on Time Constraints”. 2012 Second International Conference on Intelligent System Design and Engineering Application, pp. 941-945, 2012.
[22] I. J. Moreno Castañeda, J. L. Roa Canal y J. A. Orjuela Castro, “Caracterización de la logística de la cadena de abastecimiento agroindustrial frutícola en Colombia”. Bogotá, D. C., 2012.
[23] MinSalud; FAO, Perfil nacional de consumo de frutas y verduras. Autor, 2013.
[24] CORPOICA, Escenario actual de CTI en el sector hortofrutícola : analisis y retos futuros. Autor, 2013.
[25] H.-S. Hwang, “A Food Distribution Model for Famine Relief”. Computers & Industrial Engineering, pp. 335-338, 1999.
[26] R. Carro Paz y D. González Gómez, Localizacion de instalaciones. Buenos Aires, 2012.
[27] S. Erenguc¸, N. Simpson y A. J. Vakharia, “Integrated Production/Distribution Planning in Supply Chains: an Invited Review”. European Journal of Operational Research, pp. 219-236, 1999.
[28] C. E. H. ReVelle, “Location Analysis: a Synthesis and Survey”. European Journal of Operational Research, pp. 1-19, 2005
[29] A. Weber, “Uber den Standort der Industrien. 1. Teil: Reine Theorie des Standortes, Tu bingen, Germany, Translated as On the Location of Industries”. p. 153, 1909.
[30] H. Hotelling, “Stability in Competition”. The Economic Journal, pp. 41-57, 1929.
[31] W. Christaller, Central Places in Southern Germany. Prentic-Hall, 1933.
[32] A. Losch, The Economics of Location. New Haven, Yale University Press, 1954.
[33] C. ReVelle, H. Eiselt y M. Daskin, “A Bibliography For Some Fundamental Problem Categories In Discrete Location Science”. European Journal of Operational Research, pp. 817-848, 2008.
[34] Q. Meng, Y. Huang y R. L. Cheu, “Competitive Facility Location on Decentralized Supply Chains”. European Journal of Operational Research, pp. 487-499, 2009.
[35] M. Melo, S. Nickel y F. Saldanha-da-Gama, “Facility Location And Supply Chain Management–A Review”. European Journal of Operational Research, pp. 401-412, 2009.
[36] M. Melo, S. Nickel y F. Saldanha da Gama, “Dynamic Multi-Commodity Capacitated Facility Location: a Mathematical Modeling Framework for Strategic Supply Chain Planning”. Computers & Operations Research, pp. 181-208, 2006.
[37] A. Klose y A. Drexl, “Facility Location Models for Distribution System Design”. European Journal of Operational Research, pp. 4-29, 2005.
[38] R. Sridharan, “The Capacitated Plant Location Problem”. European Journal of Operational Research, pp. 203- 213, 1995.
[39] S. H. Owen y M. S. Daskin, “Strategic Facility Location: a Review”. European Journal of Operational Research, pp. 423-447, 1998.
[40] S. Z.-l. S. Zhi-lin y W. D. W. Dong, “Location Model of Agricultural Product Distribution Center”. 2007 International Conference on Management Science and Engineering, pp. 117-120, 2007.
[41] ] Q. Xiaohui y Y. Wen, “Studies on Spatio-Temporal Collaboration Model for Location Analysis of Vegetable & Fruit Logistics”. 6th International Conference on Fuzzy Systems and Knowledge Discovery, FSKD 2009, pp. 619-626, 2009.
[42] M. V. Marulanda, G. I. Leguizamon y K. Y. Niño Mora, “Solución al problema de localización (cflp) a través de busqueda tabú y relajación lagrangeana, caso de estudio: industria de productos alimentarios”. Purntr, 2010.
[43] K. Yang, Y. Liu y G. Yang, “An Improved Hybrid Particle Swarm Optimization Algorithm for Fuzzy P-Hub Center Problem”. Computers & Industrial Engineering, pp. 133-142, 2012.
[44] E. Morganti y J. González-Feliu, “City Logistics For Perishable Products. The Case of the Parma's Food Hub”. Case Studies on Transport Policy, 2014.
[45] H. Etemadnia, S. J. Goetz, P. Canning y M. S. Tavallali, “Optimal Wholesale Facilities Location within the Fruit and Vegetables Supply Chain With Bimodal Transportation Options: an LP-MIP Heuristic Approach”. European Journal of Operational Research, pp. 648-661, 2015.
[46] J. Jouzdani, S. J. Sadjadi y M. Fathian, “Dynamic Dairy Facility Location and Supply Chain Planning Under Traffic Congestion and Demand Uncertainty: a Case Study of Tehran”. Applied Mathematical Modelling, pp. 8467- 8483, 2013.
[47] W. Neungmatcha, K. Sethanan, M. Gen y S. Theerakulpisut, “Adaptive Genetic Algorithm for Solving Sugarcane Loading Stations with Multi-Facility Services Problem”. Computers and Electronics in Agriculture, pp. 85-99, 2013.
[48] A. H. Hiassat y A. Diabat, “A Location Inventory Routing Problem with Perishable Products”. Proceedings of the 41st International Conference on Computers & Industrial Engineering, pp. 386-391, 2010.
[49] X. Zhao y Q. Lv, “Optimal Design of Agri-Food Chain Network: An Improved Particle Swarm Optimization Approach”. 2011 International Conference on Management and Service Science, pp. 1-5, 2011.
[50] K. Khalili-Damghani, A.-R. Abtahi y A. Ghasemi, “A New Bi-objective Location-routing Problem for Distribution of Perishable Products: Evolutionary Computation Approach”. Journal of Mathematical Modelling and Algorithms in Operations Research, 2015..
[51] A. Federgruen, G. Prastacos y P. H. Zipkin, “An Allocation and Distribution Model for Perishable Products”. Operations Research, pp. 75-82, 1986.
[52] X. R. Huang y R. H. Xie, “A Model on Location Decision for Distribution Centers of Emergency Food Logistics”. 2009 2nd International Conference on Information and Computing Science, ICIC 2009, pp. 232-235, 2009.
[53] K. Diatha, R. Karumanchi y S. Garg, “Mobile Enabled Operations Management Using Multi-Objective Based Logistics Planning For Perishable Products”. Computers and Industrial Engineering 42, pp. 16-18, 2012
[54] Z. Drezner y C. H. Scott, “Location of a distribution center for a perishable product”. Mathematical Methods of Operations Research, pp. 301-314, 2013.
[55] W. Gong, D. Li, X. Liu, J. Yue y Z. Fu, “Improved Two-Grade Delayed Particle Swarm Optimisation (TGDPSO) for Inventory Facility Location for Perishable Food Distribution Centres in Beijing”. New Zealand Journal of Agricultural Research, pp. 771-779, 2007.
[56] FAO, “Pérdidas y desperdicio de alimentos en el mundo”. Autor, 2011.
[57] J. Orjuela, I. Castañeda, J. Canal y J. Rivera, “La logística en la cadena de frutas”. Frutas y Hortalizas, no 39, pp. 10 -15, 2015.
[58] J. A. Orjuela Castro, L. E. Vidal Morales , A. A. Masmela Cortes y J. Rivera Velasco, “Logística en la cadena hortícola (Olerícola)”. Revista Frutas & Hortalizas, vol. 41, no 1, Mayo-Junio 2015.
Anexo I:Notación utilizada en el artículo
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

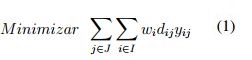
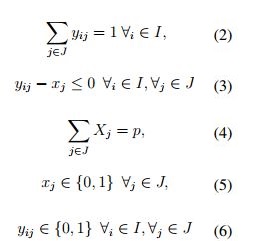
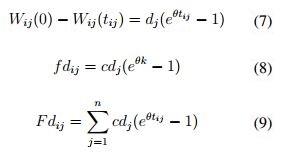
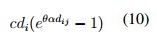
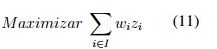
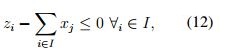
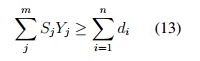
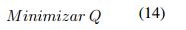
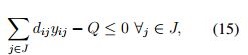
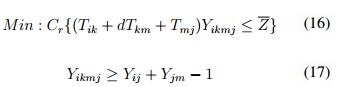
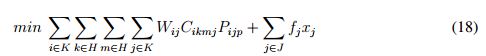
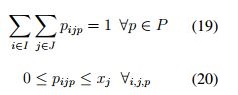
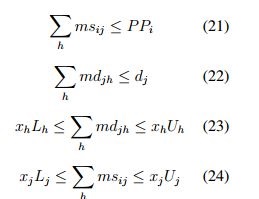
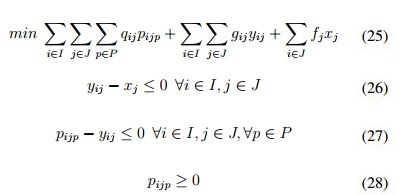
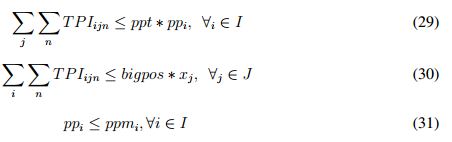
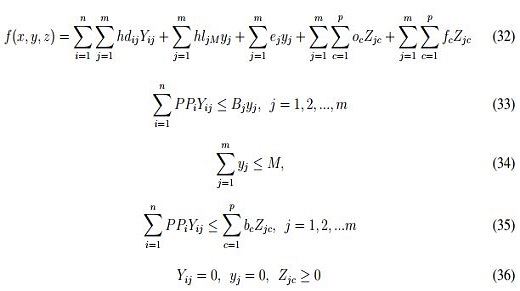




2.jpg)










