DOI:
https://doi.org/10.14483/23448393.16921Published:
2020-10-02Issue:
Vol. 25 No. 3 (2020): September - DecemberSection:
Special Section: Best Extended Articles - WEA 2015Mathematical Model for Centralized Supply Chains with Decisions Involving Shared Resources
Modelo matemático para cadenas logísticas centralizadas con decisiones de recursos compartidos
Keywords:
Cadenas de suministro centralizadas, optimización bajo incertidumbre, recursos compartidos (es).Keywords:
Centralized supply chains, optimization under uncertainty, sharing resources (en).Downloads
References
D. P. Van Donk and T. Van Der Vaart, “A case of shared resources,uncertainty and supply chain integration in the process industry”, International Journal of Production Economics, vol. 96, no. 1, pp. 97–108, 2005. https://doi.org/10.1016/j.ijpe.2004.03.002
A. Mateen and A. K. Chatterjee, “Vendor managed inventory for single-vendor multi-retailer supply chains”, Decision Support Systems, vol. 70, pp. 31–41, 2015. https://doi.org/10.1016/j.dss.2014.12.002
A. M. Attiaa, A. M. Ghaithanb and S. O. Duffuaa, “A multi-objective optimization model for tactical planning of upstream oil and gas supply chains”, Computers and Chemical Engineering, vol. 128, pp. 216–227, 2019. https://doi.org/10.1016/j.compchemeng.2019.06.016
E. Huanga et al., “Multi-objective optimization for sustainable renewable jet fuel production: A case study of corn stover based supply chain system in Midwestern U.S.”, Renewable and Sustainable Energy Reviews, vol. 115, 2019. https://doi.org/10.1016/j.rser.2019.109403
J. Zarei and M. Amin-Naseri, “An integrated optimization model for natural gas supply chain”, Energy, vol. 185, pp. 1114–1130, 2019. https://doi.org/10.1016/j.energy.2019.07.117
C. Cheng, P. Yang, Q. Mingyao and L. Rousseau, “Modeling a green inventory routing problem with a heterogeneous fleet”, Transportation Research Part E: Logistics and Transportation Review, vol. 97, pp. 97–112, 2017. https://doi.org/10.1016/j.tre.2016.11.001
S. H. Chung and C. Kwon, “Integrated supply chain management for perishable products: Dynamics and oligopolistic competition perspectives with application to pharmaceuticals”, International Journal of Production Economics, vol. 179, pp. 117–129, 2016. https://doi.org/10.1016/j.ijpe.2016.05.021
M. Gebicki, E. Mooney, S. J. Chen and L. M. Mazur, “Evaluation of hospital medication inventory policies”, Health Care Management Science, vol. 17, no. 3, pp. 215–229, 2014. http://doi.org/10.1007/s10729-013-9251-1
L. C. Coelho, J.-F. Cordeau and G. Laporte, “Consistency in multi-vehicle inventory-routing”, Transportation Research Part C: Emerging Technologies, vol. 24, pp. 270–287, 2012. https://doi.org/10.1016/j.trc.2012.03.007
F. Morales, C. Franco and G. Mendez-Giraldo, “Dynamic inventory routing problem: Policies considering network disruptions”, International Journal of Industrial Engineering Computations, vol. 9, no. 4, 2018. http://doi.org/10.5267/j.ijiec.2017.11.001
A. Baboli, J. Fondrevelle, R. Tavakkoli-Moghaddam and A. Mehrabi, “A replenishment policy based on joint optimization in a downstream pharmaceutical supply chain: centralized vs. decentralized replenishment”, International Journal of Advanced Manufacturing Technology, vol. 57, pp. 367–378, 2011. https://doi.org/10.1007/s00170-011-3290-x
F. Rayat, M. Musavi and A. Bozorgi-Amiri, “Bi-objective reliable location-inventory-routing problem with partial backordering under disruption risks: A modified AMOSA approach”, Applied Soft Computing, vol. 59, pp. 622–643, 2017. https://doi.org/10.1016/j.asoc.2017.06.036
C. Franco, E. R. López-Santana and J. C. Figueroa-García, “Solving the interval green inventory routing problem using optimization and genetic algorithms”, in Communications in Computer and Information Science, vol. 742, pp. 556–564, 2017. https://doi.org/10.1007/978-3-319-66963-2_49
F. Morales, C. Franco and G. A. Mendez-Giraldo, “Success probability applied to inventory routing problem with time windows”, in Communications in Computer and Information Science, vol. 742, pp. 522–531, 2017. https://doi.org/10.1007/978-3-319-66963-2_49
A. C. Amaroa and A. P. Barbosa-Povoa, “Planning and scheduling of industrial supply chains with reverse flows: A real pharmaceutical case study”, Computers and Chemical Engineering, vol. 32, pp. 2606–2625, 2008. https://doi.org/10.1016/j.compchemeng.2008.03.006
E. López, G. A. Méndez and C. Franco, “Diseño de cadenas de distribución con demanda bajo incertidumbre: una aproximación de programación lineal difusa”, Revista Ingeniería, vol. 18, pp. 68–84, 2013. https://doi.org/10.14483/udistrital.jour.reving.2013.2.a05
J. Kim, B. D. Chung, Y. Kang and B. Jeong, “Robust optimization model for closed-loop supply chain planning under reverse logistics flow and demand uncertainty”, Journal of Cleaner Production, vol. 196, pp. 1314–1328, 2018. https://doi.org/10.1016/j.jclepro.2018.06.157
C. L. Quintero-Araujo, A. Gruler, J. Ángel and J. Faulin, “Using horizontal cooperation concepts in integrated routing and facility‐location decisions”, International Transactions in Operational Research, vol. 26, no. 2, pp. 551-576, 2017. https://doi.org/10.1111/itor.12479
J. Ángel, J. Faulin, E. Perez-Bernabeu and N. Josewoiez, “Horizontal Cooperation in Vehicle Routing Problems with Backhauling and Environmental Criteria”, Procedia. Social and Behavioral Sciences, vol. 111, pp. 1133–1141, 2014. https://doi.org/10.1016/j.sbspro.2014.01.148
C. Caballini, S. Sacone and M. Saeednia, “Cooperation among truck carriers in seaport containerized transportation”, Transportation Research Part E: Logistics and Transportation Review, vol. 93, pp. 38–56, 2016. https://doi.org/10.1016/j.tre.2016.05.007
R. Uthayakumar and S. Priyan, “Pharmaceutical supply chain and inventory management strategies: Optimization for a pharmaceutical company and a hospital”, Operations Research for Health Care, vol. 2, no. 3, pp. 52–64, 2013. https://doi.org/10.1016/j.orhc.2013.08.001
W. Wakeland, S. Cholette and K. Venkat, “Food transportation issues and reducing carbon footprint,” in Green Technologies in Food Production and Processing. Boston: Springer, 2012.
A. Cozzolino, S. Rossi and A. Conforti, “Agile and lean principles in the humanitarian supply chain: The case of the United Nations World Food Programme”, Journal of Humanitarian Logistics and Supply Chain Management, vol. 2, no. 1, pp. 16–33, 2012. http://doi.org/10.1108/20426741211225984
C. Franco, E. R. López-Santana and J. C. Figueroa-García, “A Mathematical Model Under Uncertainty for Optimizing Medicine Logistics in Hospitals”, in Applied Computer Sciences in Engineering. WEA 2018. Communications in Computer and Information Science, vol. 916. Cham: Springer, 2018. https://doi.org/10.1007/978-3-030-00353-1_5
C. Franco, V. Augusto, T. Garaix, E. Alfonso-Lizarazo, M. Bourdelin and H. Bontemps, “Strategic territorial deployment of hospital pharmacy robots using a stochastic p-robust optimization approach”, in 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE), Munich 2018, pp. 390–395.
C. Franco and J. C. Figueroa-García, “A column generation-based algorithm for solving combined inventory and routing problems,” Ingeniare. Revista chilena de ingeniería, vol. 24, no. 2, pp. 305–313, 2016. http://dx.doi.org/10.4067/S0718-33052016000200012
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 1 de junio de 2020; Revisión recibida: 31 de agosto de 2020; Aceptado: 15 de septiembre de 2020
Abstract
Context:
Cooperation in supply chain management is an important issue considering the global performance of the different echelons of a specific supply chain. In this sense, applying logistic strategies such as VMI (Vendor Managed Inventory) allows a system to manage distribution processes from a central point or depot. Additionally, the components of the chain work more closely with it, which allows increasing global performance, instead of individually developing each sector.
Method:
A stochastic mathematical model is proposed which considers a network of customers, where products are delivered from a central depot. These customers can share part of their product with the central depot for redistribution, aiming to minimize shortage for other customers. A mathematical model is proposed which includes the elements involved in distribution processes. It is then reformulated to consider shortage and the linearization of some of its elements.
Results:
Results show that implementing or adapting logistic strategies, such as managing from a central point and sharing resources along the supply chain, allows companies to reduce the complexity of some decisions and improve performance.
Conclusions:
Implementing logistic strategies such as centralized management and sharing resources along a supply network allows companies to reduce the complexity of some decisions and, in turn, improve their performance.
Keywords:
Centralized supply chains, optimization under uncertainty, sharing resources..Resumen
Contexto:
La cooperación en la administración de las cadenas de suministro es un factor importante si se tiene en cuenta el desempeño global de los diferentes sectores de una cadena específica. En este sentido, aplicar estrategias logísticas como el VMI (Vendor Managed Inventory) permite a un sistema administrar los procesos de distribución desde un punto o depósito central. Asimismo, los componentes de la cadena trabajan más de cerca con la misma, lo cual permite incrementar el desempeño global, en vez de desarrollar cada sector individualmente.
Método:
Se propone un modelo estocástico que considera una red de clientes, donde el envío de productos se realiza desde un depósito central. Los clientes de esta red pueden compartir parte de su producto con el depósito central para redistribución, en aras de minimizar los faltantes de otros clientes. Se propone un modelo matemático que incluye los elementos involucrados en los procesos de distribución, que después se reformula para considerar el faltante y la linearización del algunos de sus elementos.
Resultados:
Los resultados muestran que implementar o adaptar estrategias logísticas, tales como la administración desde un punto central y compartir los recursos a través de la cadena de suministro, permite a las compañías reducir la complejidad de algunas decisiones y mejorar su desempeño.
Conclusiones:
La implementación de estrategias logísticas tales como la administración centralizada y el uso de recursos compartidos a través de una red de suministro permite a las compañías reducir la complejidad de algunas decisiones y, a su vez, mejorar el desempeño global.
Palabras clave:
Cadenas de suministro centralizadas, optimización bajo incertidumbre, recursos compartidos..Introduction
Information systems have had a fast development in last decades, so their integration into supply systems became a key task to implement different strategies, with the purpose of obtaining better overall results. For companies that mainly use roads to distribute products, appropriate management of goods and availability have become an important factor to satisfy customer requirements or demands.
Thus, companies should perfom two tasks factors within the distribution process: (i) satisfying customer requirements and (ii) managing inventory levels. It is desirable to have a balance among inventory levels, costs, service levels, and speed of response, since lower inventory levels could mean lower inventory costs, but also shortages and/or lower service levels.
Correct coordination between different echelons of a supply chain can ensure an improvement in its global performance, and there is evidence of how linking internal processes or decisions to suppliers and customers lead to improvements due to integration and cooperation [1]. Thus, that which leads to distribute goods through a central depot or agency also leads to the implementation of vendor-managed inventory strategies [2]. This kind of logistic systems also shares resources with different echelons of the supply chain, which allows improving its overall performance. These resources can be used by a central depot to be delivered to other echelons with higher shortage risk or to reduce service levels.
This paper is then focused in a supply chain model with a central depot that shares resources with different echelons through coordinated decisions. The paper is organized as follows: section 2 consists of a literature review; in section 3, the proposed mathematical model is presented; section 4 comprises the analysis and results; and finally, conclusions are explained in detail.
Literature review
Several approaches have addressed the problem of distributing goods to a set of customers. For instance, Attiaa, Ghaithanb, and Duffuaa [3] develop a model for an oil and gas supply chain. They proposed a mathematical model that considers different echelons of the oil and gas supply chain from the production fields to final demand terminals using two objective functions: i) minimization of total costs and ii) maximization of revenue. It also solved a three-period example with a sensitivity analysis to finally determine the final price of the oil distributed through the network. A similar study was done by Huanga et al. [4], where jet fuel distribution in accordance with production decisions was modeled using a multi-objective four-stage supply chain optimization model which considers total production costs and green emissions (a gas supply chain problem was also solved by Zarei and Amin-Naseri [5]).
Other studies aim to optimize distribution processes without considering special conditions such as the specific type of goods/products (those general problems can be solved using classic inventory routing problem models and their extensions). The problem addressed here consists to make distribution decisions over a planning horizon, a set of customers, vehicle capacity constraints, and customer inventory capacities. Furthermore, customers have their own demand that changes over time, as well as varying inventory capabilities. This problem has been previously studied in the literature with different extensions and variations. Some authors have developed some exact methods for analyzing different sizes of network instances in a deterministic environment [6] -[9]. Other authors consider uncertainty mostly over the demand and travel times [10] -[12] and other extensions [7], [13] -[15]. Fuzzy uncertainty was considered by López, Méndez, and Franco [16] for a design/distribution problem over supply chain networks with fuzzy demands (represented as fuzzy numbers) as an uncertainty source whose solution was provided as a three-stage linear optimization model.
Reverse logistic supply chain problems involving recycling products under uncertainty were solved by Kim, Chung, Kang, and Jeong, who proposed [17] the use of robust representation of uncertainty in two stages: i) a deterministic model and ii) adaptation of robust constraints. Some simulation-aided experiments were performed to emulate uncertain conditions and determine how robust variables work.
Nowadays, the global economy and highly competitive markets force companies to develop innovative strategies to achieve a high level of services to customers, so cooperation and collaboration between different echelons becomes an important strategy to improve performance at different levels of the supply chain. For example, the work by Quintero-Araujo, Gruler, Ángel, and Faulin [18] is based on the concept of vertical/horizontal cooperation, where metaheuristics were used for analyzing collaboration strategies in a distribution network with shared resources for three different scenarios: i) non-cooperative, ii) semi-cooperative, and iii) fully cooperative. In their study, iii) showed lower costs as a result of less depots being opened and reduced routing costs.
A backhaul-based horizontal cooperation analyzing the effects of the cooperation and the environmental impact of road transportation was developed by Ángel, Faulin, Perez-Bernabeu, and Josewoiez [19]. Additionally, Caballini, Sacone, and Saeednia [20] used cooperation for drayage operations, where time windows, trip deadliness, and fleet size were considered over several experiments focused to analyze the number of trips, carrier profit, and others over an Italian real dataset.
This paper proposes a cooperation-inclusion model, where goods are delivered from a depot to a set of customers who can share them with the depot in order to satisfy requirements coming from customers in the network. Some healthcare, food, and humanitarian operations problems use a similar approach [21] -[25].
Proposed mathematical model
Demands are one of the main uncertainty sources in time horizon planning-based supply chains, so, in this paper, we considered them as stochastic variables. In this model, central depot determines replenishment/sharing decisions (similar to those strategies considered in VMI models [26]. In this sense, the main idea of the model is to determine when the product on inventory of a customer can be shared with the central depot for redistribution, aiming to minimize the stock outs of the network. The proposed mathematical model works with a planning horizon T, where a set of customers N or distribution points that belong to the network and the node n = 0 correspond to the central depot. All customers have their own initial inventory levels II n , and the central depot has its own, represented by II 0 . For each time period, there is an amount of product Q t available at the central depot that can be distributed along the network. Also, each node of the network must guarantee a minimum percentage of safety stock R sn given stochastic demands d nt . Key notations, set definitions, parameters and decision variables are defined as follows:
Sets:
T = Set of planning horizon
N = Set of customers
Parameters:
II n = Initial inventory levels at customer n ∈ N
II 0 = Initial inventory levels at customer at central depot
Q t = Amount of product available that can be used by the central depot at period t ∈ T
Rs n = Risk index of safety stock of customer n ∈ N
d nt = Stochastic demand at customer n ∈ N at time period t ∈ T
r n = Risk aversion of customer n ∈ N of delivering product to the central depot
Decision variables:
x nt = Amount of product delivered by the central depot to customer n ∈ N at period t ∈ T
y nt = Amount of product shared by customer to the central depot n ∈ N at period t ∈ T
z nt = Amount of product available that can be used to satisfy the demand by customer n ∈ N at period t ∈ T
I nt = Final inventory levels of customer n ∈ N at period t ∈ T
SS n = Safety stock of customer n ∈ N
The mathematical model proposed is as follows:
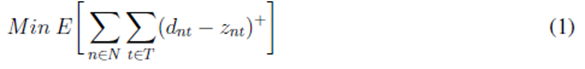
Subject to:
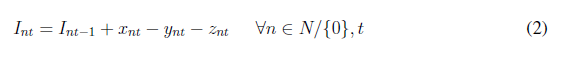
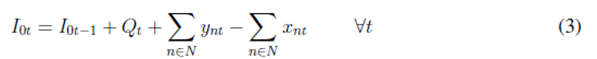
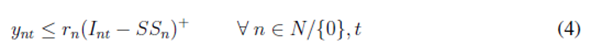

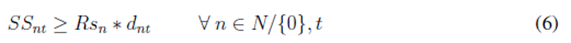

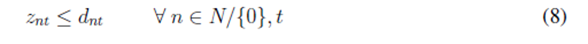

The objective function (1) aims to minimize expected shortages over the network for all periods of time. Constraint (2) represents customer inventory levels represented by the amount of product that comes from the central depot and the amount of product shared with the central depot in order to support other distribution points. The same idea goes to (3), where inventory levels are modeled for the central depot considering the amount of available product, the distributed product, and returns coming from other nodes of the network. Constraint (4) ensures the central depot to receive the amount of delivered product only if safety stocks are greater than inventory levels.
Constraint (5) sets the minimum inventory levels for each customer, given predefined safety stock levels. Those safety stocks are determined by Eq. (6) as the amount of product that customers are unable to share with the central depot due to uncertain demands. Constraint (7) ensures that the amount of product delivered from the central depot cannot exceed its availability. Eq. (8) guarantees that the amount of product sent to satisfy demands cannot exceed the customer demands. Finally, Eq. (9) defines the codomain of all decision variables.
Note that both the objective function (1) and constraint (4) are nonlinear. To linearize the objective function, we have added the new variable ω nt and the following constraint:
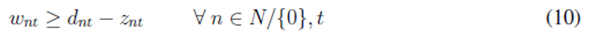
Eq. (4) is also modified by adding a new binary variable g nt as follows:
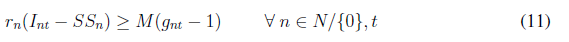
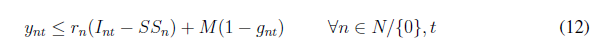

As the demand is assumed to be stochastic, uncertain demands are modeled by using possible scenarios. Therefore, we added a set of S scenarios indexed by the superscript ω. Finally, the complete mathematical model is as follows:

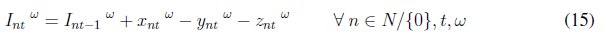
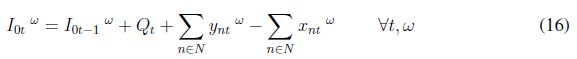
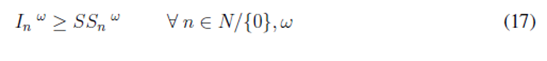

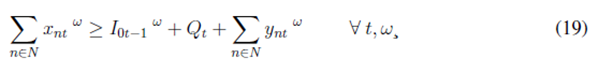
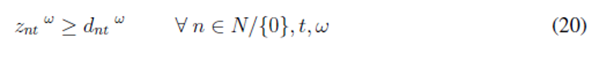
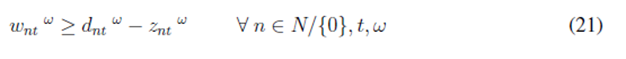
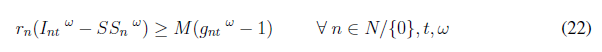
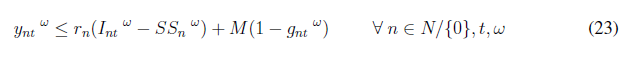
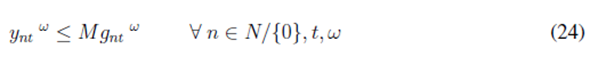
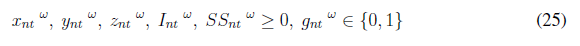
Experimentation
To test the proposed model, we used the instances presented by Coelho, Cordeau, and G. Laporte [9]. Three sets of probabilities were used to define and analyze scenarios:
-
Average: scenarios with the same probability of occurrence
-
Extreme values with lower probability: scenarios with probabilities higher than 0,25
-
Extreme values with higher probability: scenarios with probabilities higher than 0,75
Then, for each customer, different demand values were generated using different scenarios over different periods of time. In this sense, we generated the random variable
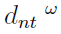 using the instances proposed by Coelho, Cordeau, and G. Laporte [9] and the demand values to generate the different scenarios as previously shown with the aforementioned probabilities. Three performance measures were implemented to analyze the obtained results:
using the instances proposed by Coelho, Cordeau, and G. Laporte [9] and the demand values to generate the different scenarios as previously shown with the aforementioned probabilities. Three performance measures were implemented to analyze the obtained results:
-
Shortage: it is the shortage amount per customer, measured as the maximum and expected values of shortage.
-
Product share: it is the amount of product shared to the central depot. Maximum values for the planning horizon and expected values are presented.
-
Product delivered to the customers: it is defined as the expected value delivered to each customer per period.
An instance composed by 5 customers, 3 time periods, and a safety stock risk index and risk aversion of 0,2 per customer was implemented. Results are shown in Table I. To solve the proposed model, we used the Xpress-MP optimization software.
Table I: Results of the first configuration.
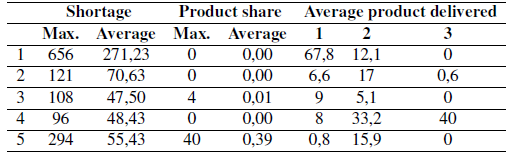
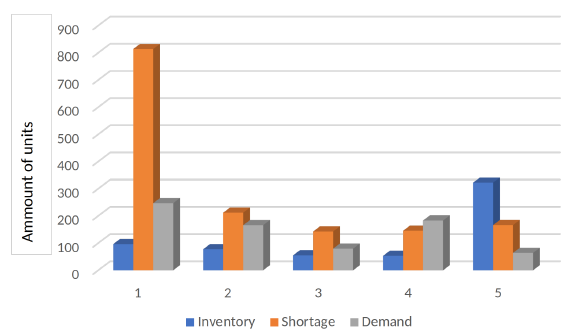
Table I shows that, given the risk aversion and safety stock levels, the amount of shared product to the central depot is low with higher shortage levels. Fig. 1 shows the average amount of shortage inventory and demands of all customers.
Figure 1: Comparison of behavior among customers.
It is clear that customers do not share product to the central depot when they have short demands, which implies higher shortage levels. Only customer 5 reports inventory levels greater than shortage/ demand levels.
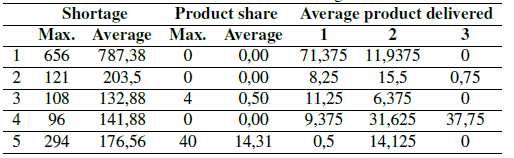
The second probability scenario is presented in Table II. When comparing this scenario to Table I, lower demand levels are more probable, as well as, consequently, higher shortage average evels, whose maximum values remain the same regardless of average levels, so the amount of delivered product to customers from the central depot increases.
Table II: Results of the second configuration.
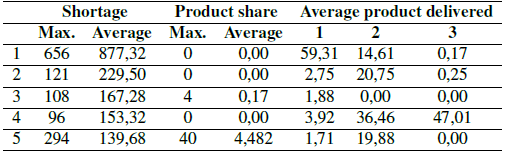
Finally, Table III shows the probability scenario. Again, both shortage levels for most customers and the amount of product delivered from the central depot increase.
Table III: Results of the third configuration.
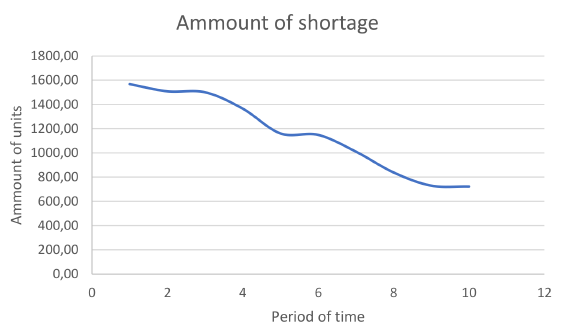
One of the main goals of this model is to evaluate the impact of sharing risks (or the desire of sharing products coming from custromers’ own depots) with the central depot. To analyze the impact of this risk, an additional experiment was performed, whose results show that, given some demand levels, sharing risks decrease total system shortage (see Fig. 2). This leads us to think that integration is key in improving system performance.
Figure 2: Variation of shortage versus the desire of sharing products to the central depot.
Conclusions
In this paper, we presented a mathematical model for a supply network composed of a central depot and a set of customers with stochastic demands. The idea of collaboration among supply chain echelons consists of sharing resources to a central depot, which are then redistributed to other customers with stockout or demand peaks. This sharing strategy was implemented as a parameter of the model.
Experiments showed that, if the customers’ resource sharing willingness desire increased (understood as customer risk), the total system shortage could be reduced, which implies collaboration among all supply chain echelons. The proposed model can be used as a tool for planning resources in a distribution network with high demand variability so their resources can be managed by a central depot.
Future work could include multi-product management problems and larger supply chain networks. This model does not require the implementation of different algorithms to solve large scale instances.
References
License
Copyright (c) 2020 Carlos Franco, Juan Carlos Figueroa García, Diana Guzmán Cortés

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










