DOI:
https://doi.org/10.14483/23448393.16357Published:
2022-01-04Issue:
Vol. 26 No. 3 (2021): September - DecemberSection:
Industrial EngineeringModelos logísticos estocásticos aplicados a la cadena de suministro: una revisión de la literatura
Stochastic Logistic Models Applied to the Supply Chain: A Literature Review
Keywords:
modelos estocásticos, logística, cadena de suministro, IRP, LRP, LIP, LIRP (es).Keywords:
Stochastic Models, Logistics, Supply Chain, IRP, LRP, LIP, LIRP (en).Downloads
References
J. A. Orjuela, “Incidencia del diseño de la cadena de suministro alimentaria en el equilibrio de flujos logísticos” (Trabajo de grado - Doctorado), Universidad Nacional de Colombia Sede Bogotá, 2018.
D. L. Rincón, J. E. Fonseca y J. A. Orjuela-Castro, “Hacia un marco conceptual común sobre trazabilidad en la cadena de suministro de alimentos”, Ingeniería, vol. 22, no. 2, pp. 161-189, 2017. http://dx.doi.org/10.14483/udistrital.jour.reving.2017.2.a01 DOI: https://doi.org/10.14483/udistrital.jour.reving.2017.2.a01
M. Koot, M. Mes, and M. E. Iacob, “A systematic literature review of supply chain decision making supported by the Internet of Things and Big Data Analytics”, Comput. Ind. Eng., vol. 154, 2021, 2021. https://doi.org/10.1016/j.cie.2020.107076 DOI: https://doi.org/10.1016/j.cie.2020.107076
M. E. Palmer-Gato, M. Cardós, E. Babiloni y E. Guijarro, “Revisión de modelos de gestión de inventarios para repuestos reparables”, 4th International Conference on Industrial Engineering and Industrial Management XIV Congreso de Ingeniería de Organización, 2010, pp. 1329-1335.
L. A. Sanabria, A. M. Peralta y J. A. Orjuela, “Modelos de localización para cadenas agroalimentarias perecederas: una revisión al estado del arte”, Ingeniería, vol. 22, no. 1, pp. 65-82, 2017. https://doi.org/10.14483/udistrital.jour.reving.2017.1.a04 DOI: https://doi.org/10.14483/udistrital.jour.reving.2017.1.a04
T. Ahmadi, H. Karimi, H. Davoudpour, and S. A. Hosseinijou, “A robust decision-making approach for p-hub median location problems based on two-stage stochastic programming and mean-variance theory: A real case study”, Int. J. Adv. Manuf. Technol., vol. 77, pp. 1943-1953, 2015. https://doi.org/10.1007/s00170-014-6569-x DOI: https://doi.org/10.1007/s00170-014-6569-x
J. A. Orjuela-Castro, J. P. Orejuela-Cabrera, and W. Adarme-Jaimes, “Last mile logistics in mega-cities for perishable fruits”, J. Ind. Eng. Manag., vol. 12, no. 2, pp. 318-327, 2019. https://doi.org/10.3926/jiem.2770 DOI: https://doi.org/10.3926/jiem.2770
F. You, and I. E. Grossmann, “Mixed-integer nonlinear programming models and algorithms for large-scale supply chain design with stochastic inventory management”, Ind. Eng. Chem. Res., vol. 47, no. 20, pp. 7802-7817, 2008. https://doi.org/10.1021/ie800257x DOI: https://doi.org/10.1021/ie800257x
P. A. Miranda, and R. A. Garrido, “A simultaneous inventory control and facility location model with stochastic capacity constraints”, Netw. Spat. Econ., vol. 6, pp. 39-53, 2006. https://doi.org/10.1007/s11067-006-7684-5 DOI: https://doi.org/10.1007/s11067-006-7684-5
C. Das, “Supply and redistribution rules for two-location inventory systems: One-period analysis”, Manage. Sci., vol. 21, no. 7, pp. 765-776, 1975. https://doi.org/10.1287/mnsc.21.7.765 DOI: https://doi.org/10.1287/mnsc.21.7.765
U. S. Karmarkar, “Convex/Stochastic Programming and Multilocation Inventory Problems.”, Nav. Res. Logist. Q., vol. 26, no. 1, pp. 1-19, 1979, doi: https://doi.org/10.1002/nav.3800260102 DOI: https://doi.org/10.1002/nav.3800260102
H. Qu, L. Wang, and R. Liu, “A contrastive study of the stochastic location-inventory problem with joint replenishment and independent replenishment”, Expert Syst. Appl., vol. 42, no. 4, pp. 2061-2072, 2015. https://doi.org/10.1016/j.eswa.2014.10.017 DOI: https://doi.org/10.1016/j.eswa.2014.10.017
S. J. Sadjadi, A. Makui, E. Dehghani, and M. Pourmohammad, “Applying queuing approach for a stochastic location-inventory problem with two different mean inventory considerations”, Appl. Math. Model., vol. 40, no. 1, pp. 578-596, 2016. https://doi.org/10.1016/j.apm.2015.06.010 DOI: https://doi.org/10.1016/j.apm.2015.06.010
A. Diabat, E. Dehghani, and A. Jabbarzadeh, “Incorporating location and inventory decisions into a supply chain design problem with uncertain demands and lead times”, J. Manuf. Syst., vol. 43, pp. 139-149, 2017. https://doi.org/10.1016/j.jmsy.2017.02.010 DOI: https://doi.org/10.1016/j.jmsy.2017.02.010
M. Amiri-Aref, W. Klibi, and M. Z. Babai, “The multi-sourcing location inventory problem with stochastic demand”, Eur. J. Oper. Res., vol. 266, no. 1, pp. 72-87, 2018. https://doi.org/10.1016/j.ejor.2017.09.003 DOI: https://doi.org/10.1016/j.ejor.2017.09.003
Y. Li, H. Guo, and Y. Zhang, “An integrated location-inventory problem in a closed-loop supply chain with third-party logistics”, Int. J. Prod. Res., vol. 56, no. 10, pp. 3462-3481, 2018. https://doi.org/10.1080/00207543.2017.1338781 DOI: https://doi.org/10.1080/00207543.2017.1338781
A. Kuhnle, and G. Lanza, “Investigation of closed-loop supply chains with product refurbishment as integrated location-inventory problem”, Prod. Eng., vol. 13, pp. 293-303, 2019. https://doi.org/10.1007/s11740-019-00885-4 DOI: https://doi.org/10.1007/s11740-019-00885-4
M. M. Fazel-Zarandi, O. Berman, and J. C. Beck, “Solving a stochastic facility location/fleet management problem with logic-based Benders’ decomposition”, IIE Trans., vol. 45, no. 8, pp. 896-911, 2013. https://doi.org/10.1080/0740817X.2012.705452 DOI: https://doi.org/10.1080/0740817X.2012.705452
A. M. Caunhye, Y. Zhang, M. Li, and X. Nie, “A location-routing model for prepositioning and distributing emergency supplies”, Transp. Res. Part E Logist. Transp. Rev., vol. 90, pp. 161-176, 2016. https://doi.org/10.1016/j.tre.2015.10.011 DOI: https://doi.org/10.1016/j.tre.2015.10.011
N. Ghaffari-Nasab, S. G. Ahari, and M. Ghazanfari, “A hybrid simulated annealing based heuristic for solving the location-routing problem with fuzzy demands”, Sci. Iran., vol. 20, no. 3, pp. 919-930, 2013. https://doi.org/10.1016/j.scient.2013.02.006
G. Laporte, F. Louveaux, and H. Mercure, “Models and exact solutions for a class of stochastic location-routing problems”, Eur. J. Oper. Res., vol. 39, no. 1, pp. 71-78, 1989. https://doi.org/10.1016/0377-2217(89)90354-8 DOI: https://doi.org/10.1016/0377-2217(89)90354-8
R. Borges, C. Ferreira, B. Sousa, and S. Barreto, “A taxonomical analysis, current methods and objectives on location-routing problems”, Int. Trans. Oper. Res., vol. 20, no. 6, pp. 795-822, 2013. https://doi.org/10.1111/itor.12032 DOI: https://doi.org/10.1111/itor.12032
W. Xie, Y. Ouyang, and S. C. Wong, “Reliable location-routing design under probabilistic facility disruptions”, Transp. Sci., vol. 50, no. 3, pp. 1128-1138, 2016. https://doi.org/10.1287/trsc.2015.0630 DOI: https://doi.org/10.1287/trsc.2015.0630
S. Gao, Y. Wang, J. Cheng, Y. Inazumi, and Z. Tang, “Ant colony optimization with clustering for solving the dynamic location routing problem”, Appl. Math. Comput., vol. 285, pp. 149-173, 2016. https://doi.org/10.1016/j.amc.2016.03.035 DOI: https://doi.org/10.1016/j.amc.2016.03.035
A. Nadizadeh, H. Hosseini, A. Sadeghieh, and M. B. Fakhrzad, “A location-routing problem model with multiple periods and fuzzy demands”, Data Envel. Anal. Decis. Sci., vol. 2014, pp. 1-24, 2014. DOI: https://doi.org/10.5899/2014/dea-00063
M. Wei, L. Yu, and X. Li, “Credibilistic location-routing model for hazardous materials transportation”, Int. J. Intell. Syst., vol. 30, no. 1, pp. 23-39, 2015. https://doi.org/10.1002/int.21679 DOI: https://doi.org/10.1002/int.21679
S.-H. Huang, “Solving the multi-compartment capacitated location routing problem with pickup-delivery routes and stochastic demands”, Comput. Ind. Eng., vol. 87, pp. 104-113, 2015. https://doi.org/10.1016/j.cie.2015.05.008 DOI: https://doi.org/10.1016/j.cie.2015.05.008
N. Herazo-Padilla, J. R. Montoya-Torres, S. Nieto Isaza, and J. Alvarado-Valencia, “Simulation-optimization approach for the stochastic location-routing problem”, J. Simul., vol. 9, no. 4, pp. 296-311, 2015. https://doi.org/10.1057/jos.2015.15 DOI: https://doi.org/10.1057/jos.2015.15
E. Pekel, and S. Soner Kara, “Solving fuzzy capacitated location routing problem using hybrid variable neighborhood search and evolutionary local search”, Appl. Soft Comput., vol. 83, 2019. https://doi.org/10.1016/j.asoc.2019.105665 DOI: https://doi.org/10.1016/j.asoc.2019.105665
S. Zhang, M. Chen, and W. Zhang, “A novel location-routing problem in electric vehicle transportation with stochastic demands”, J. Clean. Prod., vol. 221, pp. 567-581, 2019. https://doi.org/10.1016/j.jclepro.2019.02.167 DOI: https://doi.org/10.1016/j.jclepro.2019.02.167
J. A. Orjuela-Castro, D. Batero-Manso, and J. P. Orejuela-Cabrera, “Logistics IRP model for the supply chain of perishable food”, Work. Eng. Appl., pp. 40-52, 2018. https://doi.org/10.1007/978-3-030-00353-1_4 DOI: https://doi.org/10.1007/978-3-030-00353-1_4
L. C. Coelho, J.-F. Cordeau, and G. Laporte, “Thirty years of inventory routing”, Transp. Sci., vol. 48, no. 1, pp. 1-19, 2014. https://doi.org/10.1287/trsc.2013.0472 DOI: https://doi.org/10.1287/trsc.2013.0472
A. Federgruen, and P. Zipkin, “A combined vehicle routing and inventory allocation problem”, Oper. Res., vol. 32, no. 5, pp. 1019-1037, 1984. https://doi.org/10.1287/opre.32.5.1019 DOI: https://doi.org/10.1287/opre.32.5.1019
D. F. Batero-Manso, and J. A. Orjuela-Castro, “El problema de ruteo e inventarios en cadenas de suministro de perecederos: revisión de literatura”, Ingeniería, vol. 23, no. 2, pp. 117-143, 2018. https://doi.org/10.14483/23448393.12691 DOI: https://doi.org/10.14483/23448393.12691
A. Gruler, J. Panadero, J. de Armas, J. A. Moreno, and A. A. Juan, “Combining variable neighborhood search with simulation for the inventory routing problem with stochastic demands and stock-outs”, Comput. Ind. Eng., vol. 123, pp. 278-288, 2018. https://doi.org/10.1016/j.cie.2018.06.036 DOI: https://doi.org/10.1016/j.cie.2018.06.036
R. F. Roldán, R. Basagoiti, and L. C. Coelho, “A survey on the inventory-routing problem with stochastic lead times and demands”, J. Appl. Log., vol. 24, pp. 15-24, 2017. https://doi.org/10.1016/j.jal.2016.11.010 DOI: https://doi.org/10.1016/j.jal.2016.11.010
M. K. Rahim, Y. Zhong, E.-H. Aghezzaf, and T. Aouam, “Modelling and solving the multiperiod inventory-routing problem with stochastic stationary demand rates”, Int. J. Prod. Res., vol. 52, no. 14, pp. 4351-4363, 2014. https://doi.org/10.1080/00207543.2014.883470 DOI: https://doi.org/10.1080/00207543.2014.883470
A. A. Juan, S. E. Grasman, J. Caceres-Cruz, and T. Bektaş, “A simheuristic algorithm for the single-period stochastic inventory-routing problem with stock-outs”, Simul. Model. Pract. Theory, vol. 46, pp. 40-52, 2014. https://doi.org/10.1016/j.simpat.2013.11.008 DOI: https://doi.org/10.1016/j.simpat.2013.11.008
J. Brinkmann, M. W. Ulmer, and D. C. Mattfeld, “Short-term strategies for stochastic inventory routing in bike sharing systems”, Transp. Res. Procedia, vol. 10, pp. 364-373, 2015. https://doi.org/10.1016/j.trpro.2015.09.086 DOI: https://doi.org/10.1016/j.trpro.2015.09.086
Y. Adulyasak, J. F. Cordeau, and R. Jans, “Benders decomposition for production routing under demand uncertainty”, Oper. Res., vol. 63, no. 4, pp. 851-867, 2015. https://doi.org/10.1287/opre.2015.1401 DOI: https://doi.org/10.1287/opre.2015.1401
F. Niakan, and M. Rahimi, “A multi-objective healthcare inventory routing problem; a fuzzy possibilistic approach”, Transp. Res. Part E Logist. Transp. Rev., vol. 80, pp. 74-94, 2015. https://doi.org/10.1016/j.tre.2015.04.010 DOI: https://doi.org/10.1016/j.tre.2015.04.010
L. Bertazzi, A. Bosco, and D. Laganà, “Managing stochastic demand in an Inventory Routing Problem with transportation procurement”, Omega, vol. 56, pp. 112-121, 2015. https://doi.org/10.1016/j.omega.2014.09.010 DOI: https://doi.org/10.1016/j.omega.2014.09.010
D. Bertsimas, S. Gupta, and J. Tay, “Scalable robust and adaptive inventory routing”, Optim. Online, pp. 1-29, 2016.
H. W. Bouma, and R. H. Teunter, “The routed inventory pooling problem with multiple lateral transshipments”, Int. J. Prod. Res., vol. 54, no. 12, pp. 3523-3533, 2015. https://doi.org/10.1080/00207543.2015.1082668 DOI: https://doi.org/10.1080/00207543.2015.1082668
Y. Crama, M. Rezaei, M. Savelsbergh, and T. Van Wolensel, “Stochastic inventory routing for perishable products”, Transp. Sci., vol. 52, no. 3, pp. 526-546, 2018. https://doi.org/10.1287/trsc.2017.0799 DOI: https://doi.org/10.1287/trsc.2017.0799
S. Mirzapour Al-e-hashem, Y. Rekik, and E. M. Hoseinhajlou, “A hybrid L-shaped method to solve a bi-objective stochastic transshipment-enabled inventory routing problem”, Int. J. Prod. Econ., vol. 209, pp. 381-398, 2019. https://doi.org/10.1016/j.ijpe.2017.06.020 DOI: https://doi.org/10.1016/j.ijpe.2017.06.020
E. Yadollahi, E.-H. Aghezzaf, and B. Raa, “Managing inventory and service levels in a safety stock-based inventory routing system with stochastic retailer demands”, Appl. Stoch. Model. Bus. Ind., vol. 33, no. 4, pp. 369-381, 2017. https://doi.org/10.1002/asmb.2241 DOI: https://doi.org/10.1002/asmb.2241
E. Yadollahi, E. H. Aghezzaf, J. Walraevens, and B. Raa, “Considering the difference of pre-set service level and actual service level in a safety-stock based SPIRP”, Procedia Manuf., vol. 11, pp. 1933-1939, 2017. https://doi.org/10.1016/j.promfg.2017.07.337 DOI: https://doi.org/10.1016/j.promfg.2017.07.337
A. Rahbari, M. M. Nasiri, and E. Ghorbani, “An inventory routing problem for perishable products with demand and transportation time uncertainty: A robust optimization approach”, The 10th International Conference of Iranian Operations Research Society, 2017 [Online]. Available: https://www.researchgate.net/profile/Mohammad_Mahdi_Nasiri/publication/319644889_An_inventory_routing_problem_for_perishable_products_with_demand_and_transportation_time_uncertainty_A_robust_optimization_approach/links/59b7b2eaa6fdcc7415bfb0fd/An-inventor
P. Y. Alves, A. da Silva, V. Freire, and K. Valdivia, “Sistema para resolver o problema de roteamento e inventário com demanda estocástica e janelas de tempo”, Anais do XIV Simpósio Brasileiro de Sistemas de Informação, 2018, pp. 223-230. DOI: https://doi.org/10.5753/sbsi.2017.6087
B. S. Onggo, J. Panadero, C. G. Corlu, and A. A. Juan, “Agri-food supply chains with stochastic demands: A multi-period inventory routing problem with perishable products”, Simul. Model. Pract. Theory, vol. 97, 2019. https://doi.org/10.1016/j.simpat.2019.101970 DOI: https://doi.org/10.1016/j.simpat.2019.101970
R. Rossi, M. Tomasella, B. Martin-Barragan, T. Embley, C. Walsh, and M. Langston, “The Dynamic bowser routing problem”, Eur. J. Oper. Res., vol. 275, no. 1, pp. 108-126, 2019. https://doi.org/10.1016/j.ejor.2018.11.026 DOI: https://doi.org/10.1016/j.ejor.2018.11.026
E. Yadollahi, E.-H. Aghezzaf, J. Walraevens, B. Raa, and D. Claeys, “Evaluating approximate solution models for the stochastic periodic inventory routing problem”, J. Manuf. Syst., vol. 50, pp. 25-35, 2019. https://doi.org/10.1016/j.jmsy.2018.11.001 DOI: https://doi.org/10.1016/j.jmsy.2018.11.001
E. Nikzad, M. Bashiri, and F. Oliveira, “Two-stage stochastic programming approach for the medical drug inventory routing problem under uncertainty”, Comput. Ind. Eng., vol. 128, pp. 358-370, 2019. https://doi.org/10.1016/j.cie.2018.12.055 DOI: https://doi.org/10.1016/j.cie.2018.12.055
A. Mosca, N. Vidyarthi, and A. Satir, “Integrated transportation - inventory models: A review”, Oper. Res. Perspect., vol. 6, 2019. https://doi.org/10.1016/j.orp.2019.100101 DOI: https://doi.org/10.1016/j.orp.2019.100101
X. Zheng, M. Yin, and Y. Zhang, “Integrated optimization of location, inventory and routing in supply chain network design”, Transp. Res. Part B Methodol., vol. 121, pp. 1-20, 2019. https://doi.org/10.1016/j.trb.2019.01.003 DOI: https://doi.org/10.1016/j.trb.2019.01.003
V. Gaur, and M. L. Fisher, “A periodic inventory routing problem at a supermarket chain”, Oper. Res., vol. 52, no. 6, pp. 813-822, 2004. https://doi.org/10.1287/opre.1040.0150 DOI: https://doi.org/10.1287/opre.1040.0150
A. Ahmadi Javid, and N. Azad, “Incorporating location, routing and inventory decisions in supply chain network design”, Transp. Res. Part E Logist. Transp. Rev., vol. 46, no. 5, pp. 582-597, 2010. https://doi.org/10.1016/j.tre.2009.06.005 DOI: https://doi.org/10.1016/j.tre.2009.06.005
F. Forouzanfar, and R. Tavakkoli-moghaddam, “Using a genetic algorithm to optimize the total cost for a location-routing-inventory problem in a supply chain with risk pooling”, J. Appl. Oper. Res., vol. 4, no. 1, pp. 2-13, 2012.
N. Nekooghadirli, R. Tavakkoli-Moghaddam, and V. R. Ghezavati, “Efficiency of a multi-objective imperialist competitive algorithm: A bi-objective location-routing-inventory problem with probabilistic routes”, J. AI Data Min., vol. 2, no. 2, pp. 105-112, 2014.
R. Tavakkoli-Moghaddam, F. Forouzanfar, and S. Ebrahimnejad, “Incorporating location, routing, and inventory decisions in a bi-objective supply chain design problem with risk-pooling”, J. Ind. Eng. Int., vol. 9, 2013. https://doi.org/10.1186/2251-712X-9-19 DOI: https://doi.org/10.1186/2251-712X-9-19
N. Nekooghadirli, R. Tavakkoli-Moghaddam, V. R. Ghezavati, and S. Javanmard, “Solving a new bi-objective location-routing-inventory problem in a distribution network by meta-heuristics”, Comput. Ind. Eng., vol. 76, pp. 204-221, 2014. https://doi.org/10.1016/j.cie.2014.08.004 DOI: https://doi.org/10.1016/j.cie.2014.08.004
D. Chen, D. Chen, G. Sun, and G. Liu, “Combined location routing and inventory problem of e-commerce distribution system with fuzzy random demand”, Int. J. Hybrid Inf. Technol., vol. 7, no. 5, pp. 429-442, 2014. DOI: https://doi.org/10.14257/ijhit.2014.7.5.39
S. M. Seyedhosseini, A. Bozorgi-Amiri, and S. Daraei, “An integrated location-routing-inventory problem by considering supply disruption”, iBusiness, vol. 6, no. 2, pp. 29-37, 2014. http://dx.doi.org/10.4236/ib.2014.62004 DOI: https://doi.org/10.4236/ib.2014.62004
B. Liu, H. Chen, Y. Li, and X. Liu, “A pseudo-parallel genetic algorithm integrating simulated annealing for stochastic location-inventory-routing problem with consideration of returns in e-commerce”, Discret. Dyn. Nat. Soc., vol. 2015, 2015. https://doi.org/10.1155/2015/586581 DOI: https://doi.org/10.1155/2015/586581
M. Zhalechian, R. Tavakkoli-Moghaddam, B. Zahiri, and M. Mohammadi, “Sustainable design of a closed-loop location-routing-inventory supply chain network under mixed uncertainty”, Transp. Res. Part E Logist. Transp. Rev., vol. 89, pp. 182-214, 2016. https://doi.org/10.1016/j.tre.2016.02.011 DOI: https://doi.org/10.1016/j.tre.2016.02.011
Z. Rafie-Majd, S. H. Pasandideh, and B. Naderi, “Modelling and solving the integrated inventory-location-routing problem in a multi-period and multi-perishable product supply chain with uncertainty: Lagrangian relaxation algorithm”, Comput. Chem. Eng., vol. 109, pp. 9-22, 2018. https://doi.org/10.1016/j.compchemeng.2017.10.013 DOI: https://doi.org/10.1016/j.compchemeng.2017.10.013
F. Rayat, M. M. Musavi, and A. Bozorgi-Amiri, “Bi-objective reliable location-inventory-routing problem with partial backordering under disruption risks: A modified AMOSA approach”, Appl. Soft Comput. J., vol. 59, pp. 622-643, 2017. https://doi.org/10.1016/j.asoc.2017.06.036 DOI: https://doi.org/10.1016/j.asoc.2017.06.036
M. R. Gholamian, and M. Heydari, “An inventory model with METRIC approach in location-routing-inventory problem”, Adv. Prod. Eng. Manag., vol. 12, no. 2, pp. 115-126, 2017. https://doi.org/10.14743/apem2017.2.244 DOI: https://doi.org/10.14743/apem2017.2.244
S. Nakhjirkan, and F. Mokhatab Rafiei, “An integrated multi-echelon supply chain network design considering stochastic demand: A genetic algorithm based solution”, Promet - Traffic & Transportation, vol. 29, no. 4, pp. 391-400, 2017. https://doi.org/10.7307/ptt.v29i4.2193 DOI: https://doi.org/10.7307/ptt.v29i4.2193
E. Dehghani, N. Behfar, and M. S. Jabalameli, “Optimizing location, routing and inventory decisions in an integrated supply chain network under uncertainty”, J. Ind. Syst. Eng., vol. 9, no. 4, pp. 93-111, 2016.
E. Asadi, F. Habibi, S. Nickel, and H. Sahebi, “A bi-objective stochastic location-inventory-routing model for microalgae-based biofuel supply chain”, Appl. Energy, vol. 228, pp. 2235-2261, 2018. https://doi.org/10.1016/j.apenergy.2018.07.067 DOI: https://doi.org/10.1016/j.apenergy.2018.07.067
M. Eskandari-Khanghahi, R. Tavakkoli-Moghaddam, A. A. Taleizadeh, and S. H. Amin, “Designing and optimizing a sustainable supply chain network for a blood platelet bank under uncertainty”, Eng. Appl. Artif. Intell., vol. 71, pp. 236-250, 2018. https://doi.org/10.1016/j.engappai.2018.03.004 DOI: https://doi.org/10.1016/j.engappai.2018.03.004
Q. Yuchi, N. Wang, Z. He, and H. Chen, “Hybrid heuristic for the location-inventory-routing problem in closed-loop supply chain”, Int. Trans. Oper. Res., vol. 28, no. 3, pp. 1265-1295, 2018. https://doi.org/10.1111/itor.12621 DOI: https://doi.org/10.1111/itor.12621
S. Nakhjirkan, F. M. Rafiei, and A. H. Kashan, “Developing an integrated decision making model in supply chain under demand uncertainty using genetic algorithm and network data envelopment analysis”, Int. J. Math. Oper. Res., vol. 14, no. 1, pp. 53-81, 2019. DOI: https://doi.org/10.1504/IJMOR.2019.096979
N. I. Saragih, S. N. Bahagia, Suprayogi, and I. Syabri, “A heuristic method for location-inventory-routing problem in a three-echelon supply chain system”, Comput. Ind. Eng., vol. 127, pp. 875-886, 2019. https://doi.org/10.1016/j.cie.2018.11.026 DOI: https://doi.org/10.1016/j.cie.2018.11.026
U. S. Rao, “Properties of the periodic review (R,T) inventory control policy for stationary, stochastic demand”, Manuf. Serv. Oper. Manag., vol. 5, no. 1, pp. 37-53, 2003. https://doi.org/10.1287/msom.5.1.37.12761 DOI: https://doi.org/10.1287/msom.5.1.37.12761
C. R. González y J. S. Nieves, “Solución del problema de optimizacion de inventario de dos escalones con demanda estocastica para una red de distribucion de un solo producto” (Trabajo de grado), Universidad Industrial de Santander, 2018.
E. C. González, O. González y M. Becerra, “Estado del arte del problema de ruteo de vehículos con componentes estocásticos”, Inventum, vol. 13, no. 24, pp. 2-13, 2018. https://doi.org/10.26620/uniminuto.inventum.13.24.2018.2-14 DOI: https://doi.org/10.26620/uniminuto.inventum.13.24.2018.2-14
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 20 de mayo de 2020; Revisión recibida: 2 de junio de 2021; Aceptado: 8 de junio de 2021
Resumen
Contexto:
El análisis de la complejidad de los sistemas conlleva la evolución de los modelos de representación de la realidad, la logística ha avanzado de un contexto empresarial a la cadena de suministro, los modelos básicos de logística con parámetros determinísticos requieren representar el comportamiento real estocástico. En este sentido, aparecen la combinación de los modelos de inventario, la localización y el ruteo con enfoque estocástico aplicados a cadenas de suministro.
Método:
Se desarrolló una revisión sistemática de la literatura en las bases de datos bibliográficas ScienceDirect, ScholarGoogle, SpringerLink, Scopus, SemanticScholar y Scielo, así como en ResearchGate. De los 79 artículos referenciados, el 65 % comprenden entre el 2015 y 2019.
Resultados:
Se identifican y describen los modelos, a partir de lo cual se propone una taxonomía en cuatro combinaciones, tres de modelos diádicos: LIP, IRP, LRP y un modelo tríadico: LIRP. Se identifican los parámetros estocásticos utilizados en los modelos, los tipos de modelos, los métodos de solución, las funciones objetivo contempladas y el número de eslabones de la cadena contemplados, a partir de los cuales se proponen taxonomías de los diferentes tipos de modelos. Por último, se presentan líneas de trabajo para futuras investigaciones.
Conclusiones:
La evolución de modelos determinísticos a estocásticos representa un incremento en la complejidad, lo que obliga a desarrollar nuevos métodos de solución con capacidad de encontrar soluciones factibles. Ha sido de reciente interés el desarrollo de modelos y problemas con medidas de desempeño ambiental, social y riesgo humanitario, en el último periodo toman relevancia modelos tríadicos multiproducto y multiperiodo.
Palabras clave:
modelos estocásticos, logística, cadena de suministro, IRP, LRP, LIP, LIRP..Abstract
Context:
The analysis of the complexity of the systems involves the evolution of the models that representation of reality, logistics has advanced from a business context to the supply chain, basic models of logistics with deterministic parameters must go represent real behavior, stochastic. In this context, the combination of inventory, location and routing models with a stochastic approach applied to supply chains appears.
Method:
A systematic review of the literature was developed in the bibliographic databases, ScienceDirect, ScholarGoogle, SpringerLink, Scopus, SemanticScholar, ResearchGate and Scielo, of the 72 referenced articles, 65 % between 2015 and 2019.
Results:
From the models identified and described, a taxonomy of the models is proposed and classified into 4 kinds, three dyadic models Location Inventory Problem (LIP), Inventory Routing Problem (IRP), Location Routing problem (LRP) and a triadic model Location Inventory Routing Problem (LIRP). The stochastic parameters used in the models, the types of models, the solution methods, the contemplated objective functions, and the number of echelons in the supply chain are established, from which taxonomies of the different types of models are proposed. Lines of work for future research is presented.
Conclusions:
The evolution from deterministic to stochastic models represents an increase in complexity which forces the development of new solution methods with ability to find feasible solutions. The development of models with news measurements of performance as environmental, social and humanitarian have been of recent interest. In the last period, triadic multi-product and multi-period models take on relevance.
Keywords:
Stochastic Models, Logistics, Supply Chain, IRP, LRP, LIP, LIRP..Introducción
La integración de los agentes en la economía global ha incrementado la implementación de prácticas logísticas que mejoren el desempeño de varios actores de la cadena de suministro (CS) [1]. En este sentido, las decisiones logísticas estratégicas, tácticas y operativas son de localización, inventario y ruteo respectivamente, para lo cual los tomadores de decisiones se apoyan en modelos matemáticos y de simulación. Cuando el modelo matemático se acerca al contexto de la vida real aparece la variabilidad, los parámetros determinísticos se hacen variables estocásticas. No obstante, la complejidad del modelado, y en especial de los métodos de solución con variables estocásticas, se convierte en una barrera para su uso. En un entorno de las CS que incluye varios eslabones, se complejiza más el problema, así mismo cuando se evalúan simultáneamente varias decisiones logísticas.
En la incursión a esta temática, los investigadores requieren tener un panorama global y específico de los diferentes modelos que integran la localización, el inventario y el ruteo en la toma de decisiones conjuntas, por lo cual se hace necesario establecer cómo ha evolucionado su modelado matemático, los retos y las tendencias.
La revisión de literatura permite identificar investigaciones relativas al modelado estocástico aplicado en logística de las CS y propender por una taxonomía, y que se observen nuevos estudios que proporcionan una mejor aproximación entre el modelo con lo real en temáticas de investigación en el contexto estocástico. La combinación de dos o tres drivers logísticos (localización, inventario o ruteo) dan origen a modelos diádicos y tríadicos, respectivamente, la revisión incluye aquellos de los que al menos uno de sus parámetros es estocástico y contemplen dos o más eslabones de la CS. No se evidenciaron revisiones de la literatura que contemplaran el modelado tríadico estocástico, tampoco ningún trabajo que revisara estos modelos diádicos bajo un mismo enfoque de investigaciones de operaciones.
Inicialmente se presenta la metodología. Luego se presentan los modelos, que se han dividido en cinco apartes, en el primero se presentan los modelos diádicos y en segundo se presentan los modelos tríadicos, para los dos casos se presenta la taxonomía y características. En los modelos diádicos se presenta el problema de localización-inventario, el problema de localización-ruteo y el problema de inventario-ruteo. En el tercer aparte se presentan los parámetros estocásticos, en el cuarto la función objetivo y en el quinto los métodos de solución, contemplados en todos los modelos diádicos y tríadicos. Finalmente se presentan las conclusiones y trabajos futuros.
Metodología
El presente artículo es resultado de una revisión sistemática de la literatura [2] [3] a través de la búsqueda, la recolección y la síntesis de información, tomada de artículos publicados en revistas científicas, mediante la consulta en ScienceDirect, ScholarGoogle, SpringerLink, Scopus, SemanticScholar y Scielo, así como en ResearchGate, adicionalmente se revisaron tesis de maestría y doctorado. En la revisión se definió la estrategia de búsqueda y los criterios de selección, análisis y síntesis. Para la búsqueda de los modelos estocásticos diádicos y tríadicos, se plantearon cuatro conjuntos de palabras clave, uno por cada tipo de modelo (ver Tabla 1).
*Acrónimos por sus siglas en inglés: Location (L), Inventory (I), Routing (R), Problem (P)
Tabla I: Palabras clave usadas en la revisión

Las palabras clave de cada modelo se combinan mediante operadores booleanos para formar cuatro ecuaciones de búsqueda que se presentan en la Tabla 2, cada ecuación es usada en las bases de datos para título y resumen de los artículos.
Tabla II: Ecuaciones de búsqueda

Con el fin de establecer la evolución del modelado matemático integrando localización, inventarios y ruteo en las CS, así como sus retos y tendencias, se formularon como preguntas orientadoras de la búsqueda: ¿qué es un modelo estocástico en logística de las cadenas de suministro?, ¿dónde se presenta la estocasticidad en cada modelo diádico y tríadico ?, ¿cómo han evolucionado los modelos integrados de logística en las CS a través de los años?
Al aplicar la estrategia de búsqueda, se encuentran artículos que pueden ser útiles o no y documentos duplicados, por lo cual se establecen los siguientes criterios de selección:
-
Identificar documentos duplicados con ayuda de Mendeley
-
El texto debe estar disponible en su totalidad
-
Descartar todos los documentos sobre metodologías de análisis o medición del desempeño de la CS
-
Descartar los documentos con modelos causales o de dinámica de sistemas
-
Identificar los artículos seminales
-
Dar prioridad a los artículos con menos de 5 años
-
El artículo debe contener un modelo de optimización con variables de decisión y parámetros plenamente definidos
-
Al menos uno de sus parámetros debe ser de naturaleza incierta
De los artículos consultados, el 45 % corresponde a ScienceDirect y a ScholarGoogle el 43 %, a SemanticScholar, ResearchGate y Springerlink con 5 %, 4 % y 3 % respectivamente (ver Figura 1). En la selección se tuvo en cuenta la literatura reciente que aborda modelos estocásticos en la CS de los últimos 5 años, así como los artículos considerados seminales, con el fin de determinar tendencias y vacíos del conocimiento, en la Figura 1 se ve un incremento de las publicaciones en los últimos años, con el desarrollo de estos modelos. Para extraer la información de los documentos seleccionados, previamente se crearon cinco categorías para cada tipo de modelo. Estas son: tipo de modelo, características, estocasticidad de los parámetros, funciones objetivo y métodos de solución. Para la tabla, en las columnas se ubican las categorías y en las filas los artículos de cada uno de los modelos en orden cronológico, se marca una x en caso de que el modelo presentado en dicho artículo posea el aspecto nombrado en la columna. Las tablas de taxonomía resultante se muestran para cada modelo en la siguiente sección.
Figura 1: Distribución de los artículos según las bases de datos consultadas y año de publicación
Modelos
Antes de abordar los modelos combinados, diádicos y tríadicos, es importante brindar un contexto sobre los modelos individuales. Un problema de localización abarca una decisión estratégica, la cual consiste en ubicar una instalación entre un conjunto de posibles ubicaciones, cada instalación potencial cuenta con su respectivo conjunto de clientes con demanda por satisfacer. En la CS la ubicación de una instalación busca la mejor relación cobertura/costo [5]. Existen básicamente tres tipos: una sola planta, P-Mediana para ubicar un número N de instalaciones y P-Hub, los cuales se configuran como nodos conectados por arcos, en los que aparecen dos tipos de instalación: nodos Hub que funcionan como receptores y transmisores, y nodos No-Hub que se configuran como nodos receptores o transmisores, es decir origen o destino final de la CS [6]. El problema de localización, al ser un modelo general de la CS, tiene una relación directa con los modelos de inventario y ruteo, donde los costos de los mismos dependen en gran medida de la ubicación de la instalación.
Los modelos de inventario buscan determinar la gestión de los pedidos en términos de cantidad y tiempo con el fin de satisfacer las necesidades del cliente al menor costo posible [4], en este modelo se tienen en cuenta las variables de la cantidad de pedido (Q), el tiempo T que indica cada cuanto pedir y un punto de reorden R, el cual es el nivel de stock indicador para realizar una nueva orden. Los modelos de inventario influyen en las decisiones que toman las organizaciones para asegurar el flujo oportuno de los productos a través de la CS.
El problema de ruteo VRP (por su sigla en inglés, Vehicle Roting Problem) consiste en asignar una flota N de vehículos a un número M de clientes que se encuentran ubicados en diversos puntos geográficos, con el fin de que cada demanda sea atendida incurriendo en el menor costo de transporte. Generalmente, los modelos VRP pueden considerar una flota de uno o múltiples vehículos que pueden compartir la misma capacidad o diferentes. Esto bajo la premisa de que en una ruta se debe cumplir la restricción de que un vehículo inicia y finaliza su recorrido en un centro de distribución y la demanda a satisfacer es menor o igual a la capacidad de la flota asignada a dicha ruta [7].
Históricamente, los problemas de gestión de inventarios, ubicación de instalaciones y ruteo eran considerados por separado en la literatura. No obstante, con la evolución de la investigación en el campo, los tres drivers logísticos en la gestión de la cadena de suministro (GCS) están relacionados. En el presente se realiza la taxonomía y descripción de los modelos diádicos: Location Inventory Problem (LIP), Inventory Routing Problem (IRP) y Location Routing Problem (LRP) y posteriormente los modelos tríadicos Location Inventory Routing Problem (LIRP). Para cada grupo de modelos se realiza una breve introducción y descripción al modelo, su clasificación y taxonomía, resaltando los componentes relevantes en escenarios estocásticos. Dado que los trabajos presentan características similares en la función objetivo y métodos de solución, se destina un aparte para estos dos ítems.
Modelos combinados: diádicos
En este aparte se presentan los modelos diádicos de localización-inventario (LIP), inventario-ruteo (IRP) y localización-ruteo (LRP).
Modelos LIP
En los modelos Location Inventory Problem (LIP) se consideran decisiones estratégicas y tácticas, estos buscan determinar la ubicación para instalar uno o más centros de distribución y luego la asignación de cada minorista a un centro de distribución (CD), también se determina con qué frecuencia ordenar en cada CD, se establecen los niveles de inventario a un mínimo costo total de localización e inventario, y se asegura un nivel específico de servicio [8]. Miranda y Garrido [9] plantean un modelo LIP en un entorno en el que los clientes, cada uno con una demanda estocástica, son asignados a CD, si se asigna un cliente a un CD la instalación puede satisfacer una proporción de la demanda del cliente. La demanda que no satisface el CD asignado puede ser asumida por otra instalación, por lo que, dependiendo de la capacidad y su estado, se decide qué demanda cubre.
Taxonomía LIP
La Tabla 3 muestra 10 artículos de modelos estocásticos de localización-inventario, se presenta el tipo de modelo, las características y variables estocásticas. Para los modelos LIP se encontró que los problemas de asignación P-Mediana con política de inventario Q,R son los más empleados en la literatura, se evidencia que la adición de la variante P-Hub incrementa la complejidad del modelo mayor a modelos P-Mediana [8]. La demanda es la variable estocástica más trabajada en los modelos, en la práctica la demanda es variable en el tiempo.
Notación: PMED: P-Mediana; PHUB: P-Hub; ASG: Asignación; MINS: Múltiples instalaciones; MPD:Múltiples periodos; Q,R: Revisión continua; R,T: Revisión periódica; CA: Capacitado; NOCA: No capacitado; CLSC: Circuito cerrado; DEM: Demanda; T: Tiempo; CA: Capacidad.
Tabla III: Taxonomía LIP, tipo de modelo, características y estocasticidad

En la Figura 2 se observa la taxonomía de los modelos LIP con base en sus características. Los modelos se clasificaron, de una parte, en aquellos con demanda estocástica (SD), configuración Closed-Loop (CL) y política de revisión periódica (R), este modelo será llamado SDCLR, un problema LIP que considera las características anteriormente mencionadas y el SDCLRC, al considerar además la capacidad (C), en el modelo. El segundo tipo es el SDPMR, que considera un problema de P-Mediana con SD y política R para un solo periodo, como derivado de este está el SDPMRMP para múltiples periodos. El tercer tipo son los problemas SDMIQ, que consideran una política de revisión continua (Q), la ubicación de múltiples instalaciones (MI). El SDCPMQ, a diferencia de los demás modelos, considera la demanda y las restricciones de capacidad inciertas (SDCa). La última clasificación propuesta es de los modelos SDTMIQ, con demanda y tiempo estocástico (SDT), con MI y una política Q, al considerar la capacidad en el problema serían SDTMIQC. Cada artículo se incluye en la categoría correspondiente, según sus características presentadas.
Figura 2: Taxonomía para el LIP estocástico
Tipos de modelo - política Q,R y R,T
Respecto a los modelos de revisión periódica R,T y continua Q,R, You y Grossmann [8] y [9] adoptan la política Q,R y asumen que las instalaciones no tienen restricciones de capacidad, puesto que podría sesgar el problema al momento de establecer el valor de [8] establecen que todos los clientes son similares y la demanda está determinada por una distribución normal, por lo que comparten la misma media y varianza, mientras que Hui Qu et al. [12] establecen que cada cliente es independiente, proponen un modelo para un conjunto de clientes distribuidos aleatoriamente, los cuales deben ser agrupados en subconjuntos para ubicar un CD para un subconjunto, con la limitante de que un CD no puede servir a clientes de otros subconjuntos. Por su parte, Das [10] desarrolla un modelo de ubicación de dos instalaciones que tienen un sistema de inventario que revisa periódicamente R,T con fines de reposición y redistribución de existencias, el stock puede transferirse de una ubicación a otra solo una vez en cada periodo.
Tipos de modelo - múltiples periodos
Amiri et al. [15] trabajan el problema de localización con múltiples periodos, teniendo en cuenta que las decisiones de ubicación, apertura y cierre de instalaciones van de la mano con una planificación de escenarios e integra la necesidad de establecer los periodos, en los que se hace necesaria la instalación, además planifican el inventario con políticas de orden de pedido, con el fin de enfrentar la incertidumbre de las demandas que fluctúan en múltiples periodos. La Figura 3 muestra la frecuencia de uso de los modelos de LIP, los modelos utilizados para inventario, compuestos por cuatro subconjuntos y los modelos de localización con cuatro subconjuntos. En inventarios, el 55,5 % de los autores trabaja con modelos Q,R, mientras que el 44,5 % los desarrolla con modelos de revisión periódica (R,T); a su vez, el 63 % de los mismos abarca modelos de localización P-Mediana, de los cuales el 54,4 % trata de asignar los clientes a las respectivas instalaciones.
Figura 3: Frecuencia de uso de tipos de modelo de localización-inventario
Características - tipo de planta
Los modelos múltiples son clasificados en P-Hub o P-Mediana. [10] plantea un modelo P-Mediana en el cual se requiere ubicar dos plantas con demanda aleatoria, para mayor cobertura de clientes posibles con modelo de ubicación de múltiples plantas, en la que se realiza una asignación de conjunto de clientes están los modelos de [9] [12] [10], Karmarkar [11]. Otros autores plantean modelos P-Hub divididos en dos etapas, la asignación de los CD a los proveedores, y de los proveedores a los minoristas, en este modelo los CD serían los nodos Hub, los cuales deben tener en consideración la política de inventario, ya que debe conectar la demanda de los clientes minoristas con la oferta del proveedor [8].
Características - capacitados o no
Miranda y Garrido [9] desarrollaron un modelo de localización e inventario en el que la capacidad de los CD y la demanda de los clientes son estocásticas, busca una solución factible que logre un nivel de servicio determinado al menor costo. Mientras, [12] resuelven un problema con instalaciones sin limitaciones de capacidad ni envío, por lo que el costo no es relevante con respecto a la cantidad de transporte, la reposición es permanente y articulada, cada cliente es asignado a un único centro de distribución. La Figura 4 muestra las publicaciones que consideran las características de los modelos LIP y su frecuencia de uso, el 42,8 % de los modelos tiene capacidad limitada en sus instalaciones, el 57,1 % se enfoca en modelos no capacitados y el 28,6 % desarrolla sus modelos sobre circuitos cerrados.
Figura 4: Frecuencia de uso de características de modelos LIP
En la Tabla 4 se presenta la clasificación de los modelos de LIP según función objetivo y métodos de solución, se nota que todos los modelos se centran en minimizar el costo en el que el 20 % de ellos trabaja funciones multiobjetivo en las que se tiene en cuenta aumentar el nivel de servicio, el cual es impactado por demandas insatisfechas.
Notación: MIN CS: Minimizar costo; N SERV: Nivel de servicio; PE2N: Programación estocástica de dos niveles; PM; Programación matemática; LGRN: LaGrange; AG: Algoritmo genético; RS: Recosido simulado; AED: Algoritmo autoadaptativo basado en evolución diferencial; ME: Métodos exactos; ADA: Algoritmo desarrollado por el autor
Tabla IV: Taxonomía LIP, función objetivo y métodos de solución

Actualmente los modelos de LIP buscan aplicarse a CS multieslabón de bucle cerrado, con una planta híbrida de producción, posibles candidatos a CD y recolectores basados en un modelo de subcontratación con un operador logístico (3PL) [16]. En cuanto a la aplicabilidad del modelo en la CS se aborda el proceso de logística inversa en el cual los CD tienen la capacidad de recolectar productos no conformes. Cuando un modelo implica una CS de bucle cerrado, hace referencia a que la CS es bidireccional, en una dirección se distribuyen los bienes hacia el cliente, en la otra, el cliente envía al centro de manufactura, a través de los CD, productos no conformes o remanentes para ser reprocesados [17]. A nivel de la CS, estos modelos permiten avanzar en el desarrollo de una economía circular, al incentivar el consumo responsable y permitir que el cliente pueda disminuir su huella de carbono y cooperar con la fábrica para recolectar insumos para ser reprocesados. Estos modelos no solo ofrecen una alternativa más limpia, también que un cliente no conforme pueda hacer una devolución y reposición de manera rápida y eficiente.
Modelos LRP
Cuando se abordan los problemas de localización-ruteo se hace referencia a la toma de decisiones estratégicas y operativas, la combinación de los dos modelos puede converger a un menor costo [18], [19], [20]. Laporte et al. [21] plantean que en el modelo LRP surgen dos niveles de decisión, primero ubicar las instalaciones cuya cobertura y distancia hacia los clientes sean las mejores, luego se procede a plantear el ruteo de los vehículos, a menor distancia entre el CD y los clientes, los costos de ruteo serán más bajos y el nivel de servicio aumentará. Generalmente los modelos restringen la posibilidad de libre ubicación de las instalaciones, acotándolas a un conjunto de ubicaciones candidatas con el fin de adaptarlo a una situación real [22], [23]. Naturalmente el LRP pertenece a los problemas NP-Hard, dado que el espacio de soluciones aumenta exponencialmente con la expansión del problema [24].
Taxonomía LRP
En la Tabla 5 se muestran 12 artículos dedicados al estudio de modelos estocásticos de localización-ruteo, se resalta el tipo de modelo, las características y variables estocásticas. En la tabla se encuentran como mayor porcentaje de participación los modelos de múltiples instalaciones, ya que agregan al problema de Location-Routing un número de posibles rutas desde los diferentes centros de distribución. Los modelos de un solo tipo de vehículo se pueden considerar obsoletos para la representación de un sistema actual; sin embargo, son pocos los que trabajan con flotas heterogéneas.
Notación: 1P: Una planta; AS: Asignación; MI: Múltiples instalaciones; MP: Múltiples periodos; CA:Capacitado; PDNS: Penalización por demanda no satisfecha; 1V: Un vehículo; MVHOM: Flota homogénea; MVHET: Flota heterogénea; DEM: Demanda; T: Tiempo; DIST: Distancia; CS: Costo.
Tabla V: Taxonomía LRP, tipo de problema, características y estocasticidad

En la Figura 5 se presenta la clasificación para los modelos LRP, la gráfica cuenta con tres niveles. El primer nivel hace referencia al tipo de flota considerada: un solo vehículo (1V), flota heterogénea (HE) y flota homogénea (HO). En el segundo nivel se encuentran las características de localización como una planta (1P) y múltiples instalaciones (MI). En el tercer nivel se encuentra la estocasticidad que presenta el modelo, si es en demanda (SD), tiempo (ST), distancia (SDI), tiempo y costo (STC), demanda y costo (SDC). Por último, en el modelo SDMIHO hay un trabajo que considera múltiples periodos y otro que incluye estocasticidad en los costos. Cada trabajo de LRP fue clasificado según sus características. Se ve que en la literatura revisada no hay trabajos de flota heterogénea que consideren otros parámetros estocásticos además de la demanda.
Figura 5: Taxonomía para el LRP estocástico
Tipos de modelo
Borges et al. [22] plantean una taxonomía respecto a los modelos LRP con incertidumbre; la tipología para LRP que se propone es una combinación de los modelos de localización y ruteo, se basa en el número de instalaciones y en parámetros estocásticos. De la bibliografía existente entre 2013 y 2019, se pueden plantear tres grupos de modelos. VRPSDC - 1 planta: describe una familia de problemas de ubicación y enrutamiento estocástico que ubican simultáneamente un depósito entre un conjunto de sitios potenciales, la demanda o los clientes pueden tener comportamientos aleatorios, con el objetivo de que la instalación proporcione cobertura a la mayoría de clientes y las distancias sean mínimas [21], [19]. VRPSD - múltiples instalaciones: aborda simultáneamente dos problemas, la ubicación de las instalaciones y el diseño de las rutas de viaje para vehículos entre las instalaciones establecidas y los puntos de demanda existentes, contempla la demanda aleatoria por lo que la ubicación de las instalaciones debe cumplir las restricciones de cobertura y capacidad al igual que la flota de vehículos [23], [27], [20]. VRPSTT - múltiples instalaciones: es un modelo para un entorno dinámico, se consideran factores de tráfico aleatorios y cíclicos, con el objetivo de determinar la solución óptima a través del tiempo, Gao et al. [24] proponen un modelo de localización-asignación con múltiples plantas capacitadas, una flota de vehículos con capacidad homogénea y un factor de congestión vehicular alto, medio o bajo; lo que se traduce en tiempos de viaje inciertos entre las ubicaciones de los clientes. Otro tipo de modelos son los difusos, obtienen mejores resultados cuando los estocásticos no funcionan al ser desconocida o parcialmente conocida la distribución de probabilidad de los parámetros, lo que implica la inclusión de expertos. Wei et al. [26] proponen un modelo de programación con restricciones de oportunidad credibilista (CCP) con el objetivo de encontrar el mejor equilibrio entre el riesgo y el costo de transporte de materiales peligrosos bajo los supuestos de que el costo de transporte y el número de personas son variables difusas.
La Figura 6 muestra la frecuencia de uso de los modelos de LRP, al lado izquierdo los modelos utilizados para localización, compuesto de cuatro subconjuntos y al lado derecho los modelos de ruteo con tres subconjuntos.
Figura 6: Frecuencia de uso de tipo de modelos LRP
En localización, el 69,2 % de los autores trabaja con modelos de múltiples plantas, mientras que el 23 % los desarrolla con modelos de una sola planta; a su vez, el 83 % de los mismos abarca modelos de ruteo con demanda estocástica, mientras uno contempla que la aparición de clientes también presente aleatoriedad.
Características - vehículos y capacidad
Respecto a la característica de vehículos se plantean tres grupos: aquellos que cuentan con un solo vehículo [19], los que tienen una cantidad M de vehículos que pueden ser homogéneos [21], [23], [27] y los de flota heterogénea [29]. El modelo LRP puede contemplar dos restricciones de capacidad: en la planta y en el vehículo [22], algunos autores, para reducir la complejidad del problema, solo asignan capacidad a uno de los dos, ya sea a los vehículos o a la planta. En [21] [19] y [20] plantean modelos con una flota de vehículos idénticos de un proveedor externo que envían los productos, hay un máximo M vehículos disponibles, cada vehículo es responsable de un solo viaje de entrega y la capacidad de cada vehículo está determinada. Por su parte, Nadizadeth et al. [25] presentan un modelo con capacidad limitada de vehículos e instalaciones, y demandas difusas para asignación adecuada de rutas y depósitos. Borges et al. [22] postulan un modelo con un conjunto de instalaciones potenciales capacitadas, en el cual se asignan dos conjuntos de rutas independientes para entrega y recogida.
La Figura 7 muestra la cantidad de publicaciones que consideran las características de los modelos de LRP. Se evidencia que el 83,3 % de los modelos cuenta con una flota de múltiples vehículos similares, el 25 % agrega costos de penalización por demanda insatisfecha y uno de los autores desarrolla un modelo LRP con un solo vehículo. En la Tabla 6 se presenta la clasificación de los modelos de LRP según función objetivo y métodos de solución.
Figura 7: Frecuencia de uso de características de modelos LRP
Notación: MIN CS: Minimizar costo; MIN D: Minimizar distancia; RS: Riesgo; SC: Social; AMB:Ambiental; PM: Programación matemática; PL: Programación lineal; LGR: LaGrange; ABAG: Algoritmo basado en algoritmos genéticos; ABDE: Algoritmo basado en optimización por enjambre de partículas; RS: Recosido simulado; TB: Búsqueda tabú; SIM: Simulación; A GEN; Algoritmo genético; DBEN:Descomposición de Benders; ACH: Algoritmo de colonia de hormigas; ABU: Algoritmo de búsqueda local iterativa; ABEV: Algoritmo de búsqueda de entorno; HAB: Heurística basada en algoritmo de búsqueda;AP: Algoritmo desarrollado por el autor.
Tabla VI: Taxonomía LRP, función objetivo y métodos de solución

El avance de los modelos de Location-Routing facilita a las organizaciones el desarrollo de CS sostenibles, permitiendo aplicar tecnologías más limpias. En [30] desarrollaron un modelo de LRP con demanda estocástica en el cual la flota de vehículos es eléctrica, el problema se centra en suplir la demanda de los clientes y ubicar las estaciones de cambio de batería, dado que los vehículos cuentan con una capacidad limitada de mercancía y de batería, lo cual limita la distancia que pueden recorrer entre los nodos, ya sean clientes o estaciones de carga. En términos de la evolución de los modelos logísticos, se encuentra el interés futuro de trabajar en sostenibilidad y objetivos ambientales de problemas aplicables a CS, en los cuales el objetivo trasciende a desarrollar métodos de entrega que disminuyan la emisión de CO2.
Modelos IRP
Los modelos Inventory Routing Problem datan de hace 30 años, inicialmente se plantearon modelos de VRP añadiendo consideraciones de costos de inventario a los costos de transporte [31], [32], [33]. La metodología de los modelos IRP se basa en la toma de tres decisiones específicas: cuándo atender a los clientes, bajo qué rutas se distribuirán los vehículos, y cuánto se debe enviar a cada uno y almacenar en los depósitos [32], [34], [35]. Los métodos de optimización para IRP estocásticos requieren información acerca de los niveles de inventario actuales e históricos, el comportamiento de la demanda, la ubicación de los nodos, los costos de transporte, así como la capacidad y disponibilidad de vehículos y conductores. La elección de la política de inventario influye de forma significativa en el costo del proceso de optimización [36].
Taxonomía IRP
En la Tabla 7 se muestran 20 artículos dedicados al estudio de modelos estocásticos de IRP en los que se presenta la taxonomía, resaltando el tipo de modelo, las características y variables estocásticas. Se encuentra que la mayoría de trabajos aplicados a Inventory-Routing se enfoca en modelos de ruteo con demanda estocástica y una política de inventario R,T; frente a los modelos estudiados anteriormente, los IRP contienen mayor número de trabajos con flota de vehículos heterogénea. La demanda sigue siendo la variable estocástica predominante.
Parámetros VRPSD: Demanda estocástica; VRPSC: Clientes estocásticos; VRPSDC: Demandas y clientes estocásticos; VRPSTT: Ventanas de tiempo estocásticas; DIN: Dinámico; CA: Capacitado; TR: Trasbordo; PDNS: Penalización demanda no satisfecha; TTR: Tercerización de transporte; 1v: 1 vehículo; MVHO: múltiples vehículos flota homogénea; MVHet: múltiples vehículos flota heterogénea; RyE: Recogida y entrega; EP: Entregas parciales; DE: Demanda; T: Tiempo.
Tabla VII: Taxonomía IRP, tipo de modelo, características y estocasticidad

En la Figura 8 se muestra la clasificación resultante para los modelos IRP. Al igual que con la gráfica del modelo anterior, posee tres niveles. En el primero se encuentra el tipo de flota: 1V, heterogénea (HE) y homogénea (HO). En el segundo nivel se encuentra el tipo de política de inventario, si es de revisión continua (Q) o si es revisión periódica (R). En el tercer nivel se encuentran los parámetros estocásticos nombrados como SD para demanda y SDT para demanda y tiempo. Por último, se encuentran modelos que consideran políticas de ruteo tales como trasbordos (TR), tercerización de la flota (TE) y entregas parciales (EP). En la literatura revisada no se encuentran modelos que consideran política Q y tengan políticas de ruteo, también hay ausencia de modelos con política Q considerando el tiempo estocástico.
Figura 8: Taxonomía para el IRP estocástico
Tipos de modelo
Autores como Roldán et al. [36] y Mosca et al. [55] señalan que en los trabajos IRP estocásticos se distinguen dos grupos, el primero añade limitaciones de inventario para el problema del transporte, mientras el otro considera el vehículo como el “productor” del inventario. Los modelos IRP se pueden clasificar con base en la toma de decisiones según: VRPSD - Q,R: plantea la generación de rutas de uno o varios depósitos para satisfacer la demanda del cliente, considerando una política de reorden continua. De otra parte, los modelos de colas y procesos markovianos se han utilizado ampliamente para representar sistemas de inventarios, en especial cuando se considera un único proveedor, con frecuencia se utiliza el sistema M/M/1, en el que las demandas llegan con una distribución Poisson y los tiempos de servicio son representados por una distribución de probabilidad exponencial [36]. VRPSD R,T: este tipo de modelado es el más común, ampliamente usado en CS alimentarias, el ritmo de reorden hace que sea fácil tomar decisiones operativas [56] y [57]. Onggo et al. [51] y Crama et al. [45] plantean el problema multiperiodo con productos perecederos en donde se implementa una política de reabastecimiento (R,T) y de distribución con toma de decisión centralizada (VMI), incluyen la distribución de la demanda y la relación de equilibrio entre el costo de enrutamiento, y el costo del desperdicio. La Figura 9 muestra el uso de los modelos IRP. El 82,3 % de los autores establece una política de inventario de revisión continua, el 17,7 % restante los desarrolla con modelos Q,R, todos los autores trabajan con demanda estocástica, de ellos el 70 % lo desarrolla con flota de vehículos múltiples homogéneos, mientras el 25 % cuenta con flota múltiple heterogénea, el 5 % restante trabaja en modelos con un solo vehículo.
Figura 9: Frecuencia de uso de tipo de modelo IRP
Características - capacidad y flota
En su mayoría los modelos IRP son capacitados, los modelos de inventario tienen un nivel máximo de almacenamiento y contemplan dos tipos de capacidad: en almacén con nivel máximo de inventario y la flota con o sin restricciones de capacidad [35]. Brinkmann et al. [39] plantean un modelo de distribución de bicicletas con un nivel máximo de inventario (portabicicletas) y con M vehículos, se debe garantizar un número de portabicicletas vacío para que puedan ser parqueadas. Yadollahi et al. [53] plantean métodos de solución para modelos estocásticos con flota de capacidad limitada e inventario máximo, y Rossi et al. [52] un modelo capacitado para centros de combustible y vehículos para ruteo. Coelho et al. [32] describen un modelo con un número M de vehículos homogéneos que realizan una ruta por periodo de tiempo. Por su parte Nikzad et al. [54] y Niakan y Rahimi [41] plantean modelos con vehículos heterogéneos, capacidades y costos diferentes, para agregar complejidad en la asignación de vehículos a las rutas. Mientras Yadollahi et al. [47] y Rahbari et al. [49] trabajan con una flota homogénea que sale del mismo depósito hacia un conjunto N de clientes minoristas. Se evidencia gran interés por desarrollar mejores métodos de solución, Crama et al. [45] plantean una política de ordenamiento sencilla con buen desempeño, mejoras estadísticas y económicas significativas, que se logran cuando se utilizan métodos de solución más avanzados. Solo un trabajo tenía restricción de ventanas de tiempo, aunque deterministas [50]. En la Tabla 8 se presenta la clasificación de los modelos de IRP según función objetivo y métodos de solución.
Notación: MIN CS: Minimización de costo; MIN T: Minimización de tiempos; MIN D: Minimización de distancia; N Ser: Nivel de servicio; AMB: Nivel ambiental; P E 2 N: Programación estocástica de dos niveles; OP R: Optimización robusta; DLGR: Descomposición de LaGrange; R SIM: Recocido simulado; D B: Descomposición de Benders; H AD: Algoritmo de despliegue; SIM: Simulación, AEBD: Algoritmo evolutivo basado en descomposición, HDFBD: Heurística de dos fases basada en descomposición, A BLI:Algoritmo búsqueda local interactiva; ME: Métodos exactos; HAB: Heurística basada en algoritmos de búsqueda.
Tabla VIII: Taxonomía IRP, función objetivo y métodos de solución.

El enfoque de programación estocástica de dos etapas para problemas Inventory-Routing generalmente incluye las variables de decisión de inventarios en la segunda etapa, lo cual aumenta el número de restricciones con parámetros inciertos y el número de variables específicas; en su lugar, considerar las desviaciones en las restricciones como variables de segunda etapa genera robustez al modelo y se disminuye el tiempo de cálculo (54). Además, al comparar el modelo propuesto con dos modelos clásicos, uno sin restricciones y otro con restricciones probabilísticas, se demuestra que en condiciones de interrupción de la CS, el modelo propuesto es más sólido. Los enfoques de solución deterministas son eficientes en tiempo, aunque poseen mala calidad en el resultado, pero con una parametrización adecuada es posible mejorar la calidad de estas soluciones, [53] proponen un mecanismo de asignación de stock de seguridad que comparado con el método de solución de aproximación promedio de muestra (SAA) resulta en menor tiempo y costo computacional, en términos de la CS para instancias de gran escala, se obtiene un resultado apropiado en un tiempo razonable.
Modelos triádicos: LIRP
Correspondiente a la combinación del inventario, localización y ruteo (LIRP, por su sigla en inglés Location-Inventory-Routing Problem), dada su complejidad en cuanto a la temporalidad en el modelado y su naturaleza NP-Hard, los artículos son escasos; a la luz de esta revisión se propone una primera clasificación de estos modelos.
Taxonomía LIRP
La Tabla 9 presenta 20 artículos de modelos estocásticos de localización-inventario-ruteo con la taxonomía, resaltando el tipo de modelo, las características y variables estocásticas. En la literatura revisada se encuentra que la mayoría de trabajos se realiza con modelos de múltiples instalaciones, con el objeto de ser aplicables a gran escala en la representación de la CS, los modelos requieren ser capacitados para que las políticas de inventario que se definan se ajusten al tamaño del almacén y a la capacidad de la flota, la decisión de asignación de múltiples instalaciones responde al trabajo de modelos de inventario multieslabón. Igual que los modelos diádicos, la demanda sigue siendo la variable estocástica predominante en los modelos.
Tabla IX: Taxonomía LIRP, tipo de modelo, características y estocasticidad

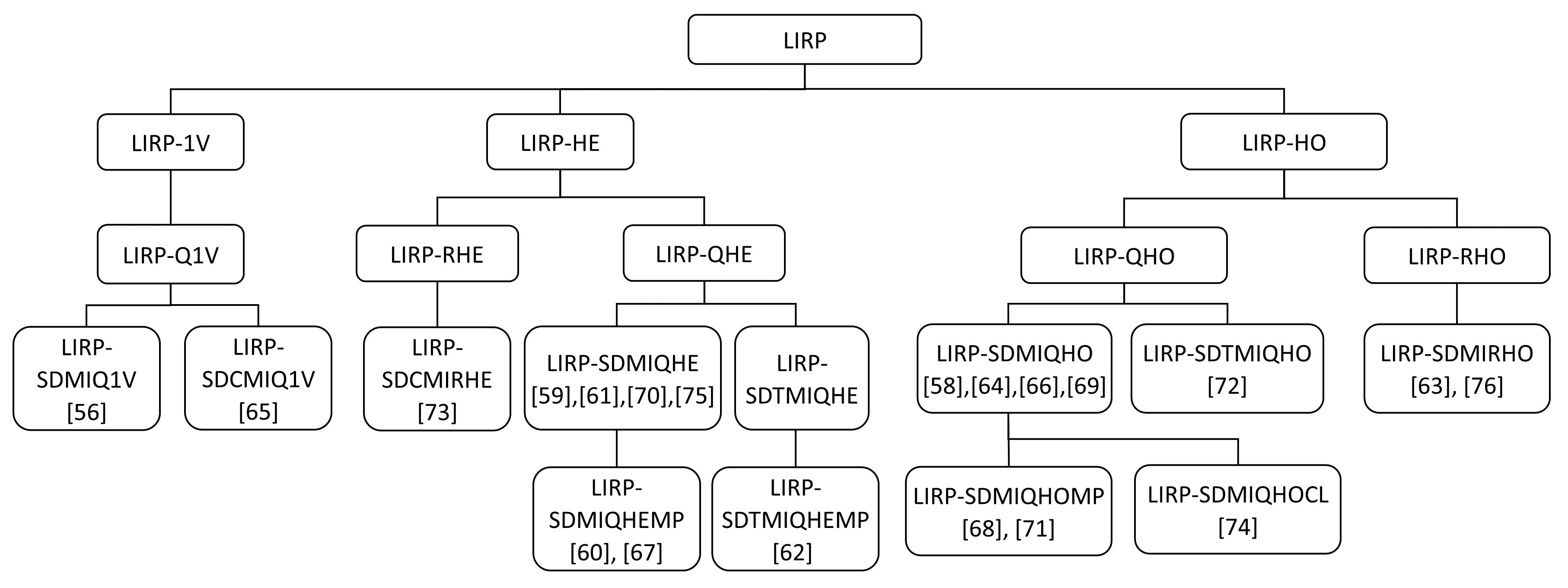
En la Figura 10 se muestra la clasificación para los modelos LIRP estocásticos. La gráfica cuenta con cuatro niveles. En el primer nivel se encuentra el tipo de flota: 1V, heterogéneas (HE) y homogéneas (HO). En el segundo nivel esta la política de inventario Q,R. Para el tercer nivel se encuentra que todos los modelos contemplan múltiples instalaciones (MI) y los parámetros estocásticos SD, SDT y SDC. El último nivel incluye características tales como múltiples periodos (MP) y Closed-Loop (CL). Se evidencia que en la literatura consultada no hay trabajos que consideren políticas de ruteo, en este caso no se combina el uso de las políticas R con tiempos inciertos.
Figura 10: Taxonomía para el LIRP estocástico
Clasificación
La mayoría de los artículos son de un solo producto y un periodo de planeación, con horizonte de planeación finito o infinito, no consideran parámetros dinámicos. La Figura 11 muestra los artículos LIRP según el tipo de modelo que presentan en los tres problemas individuales:
Figura 11: Frecuencia de uso de tipo de modelo LIRP
El 82,3 % de los autores establece una política de inventario de revisión continua para los modelos IRP, el 17,7 % restante los desarrolla con modelos R,T; teniendo en cuenta el modelo de ruteo, todos los autores trabajan sobre problemas con demanda estocástica, de los cuales el 70 % lo desarrolla con flota múltiple de vehículos homogéneos, mientras el 25 % cuenta con flota múltiple de heterogéneos, el 5 % restante trabaja en modelos con un solo vehículo, un trabajo IRP considera una restricción de ventana de tiempo determinística.
LIRP según política de inventario
Los modelos LIRP por definición abordan la CS; sin embargo, la política de inventario puede ser tomada para uno o varios eslabones. De los artículos consultados, el 52 % aplica una política de revisión continua y el 12 % una política R,T, que es aplicada frecuentemente en un solo eslabón, Rao [77], referenciado en [78], ha demostrado que la política Q,R domina a la R,T por su desempeño de los costos generados a largo plazo.
Política R,Q en un único eslabón y varios eslabones
Rayat et al. [68] modelan un LIRP estocástico que considera el riesgo de ruptura en el flujo de la CS, representado mediante una probabilidad, con una política de revisión continua para un solo eslabón, múltiples periodos y multiproducto, en donde el reabastecimiento considera un backordering parcial, es decir que parte de las ventas pendientes se pierde y la otra parte se queda como pedido pendiente. Con una estrategia de centralización del inventario y el riesgo, se pueden reducir los efectos negativos de la variabilidad de la demanda de los clientes y alcanzar niveles adecuados de servicio a los clientes, bajo esta premisa Forouzanfar y Tavakkoli [59], Tavakkoli et al. [61] modelan un problema LIRP con inventario de revisión continua para un CD. En el mismo sentido, Nakhjirkan y Mokhatab [70] modelan un LIRP para cuatro eslabones, con inventario en el CD. Asadi et al. [72] proponen un diseño para la CS con una política s-1,S para el reabastecimiento en dos de los tres eslabones considerados. Se modela como una cadena de Markov con la demanda Poisson y tiempos de entrega desde el proveedor con una distribución exponencial. Con la misma política s-1,S, Dehghani et al. [71] plantean un sistema de colas para el inventario, cuyas decisiones son determinar el nivel de inventario y el stock de seguridad para los CD y los minoristas.
Política R,T en un eslabón
Eskandari et al. [73] desarrollan un modelo de optimización para una CS sostenible multiobjetivo de sangre, multiproducto perecedero, consideran datos inciertos en un desastre natural. Aplican una política de inventario periódico para un eslabón con demanda difusa, demuestran que un incremento en el costo de mantenimiento no tiene un impacto significativo en la función objetivo para este tipo de problema. Saragih et al. [76] proponen un modelo, aplicable a problemas de gran escala, con política de inventario ordenar-hasta, en tres eslabones involucrados y demanda con distribución normal, a fin de reducir los costos de escasez y determinar el inventario de seguridad apropiado.
Características - modelos capacitados
Los modelos pueden tener restricciones de capacidad en la flota o en los almacenes. Un problema con flota capacitada restringe la cantidad de productos que pueden ser enviados por las diferentes rutas, se debe decidir qué cantidad o número de clientes satisfacer [65]. Rafie et al. [67] establecen un modelo cuya flota tiene capacidad limitada para CD qué usan vehículos con horario. Ahmadi y Azad [58] proponen un modelo en el que se conocen todos los niveles de capacidad posibles para el conjunto de CD. Por su parte Seyedhosseini et al. [64] desarrollan un modelo en el cual se presentan disrupciones aleatoriamente, lo cual puede representar una pérdida de capacidad de la instalación o la indisponibilidad. En la Figura 12 se observa la distribución de los artículos consultados para LIRP teniendo en cuenta el tamaño de la flota.
Figura 12: Frecuencia de uso de características de modelo LIRP
La mitad de autores trabaja sobre modelos cuya flota de vehículos es mayor a uno y con características similares (50 %), seguido de modelos con múltiples vehículos y de características diferentes (40 %), solo el 10 % trabaja con problemas de un solo vehículo. En la Tabla 10 se presenta la clasificación de los modelos de LIRP según función objetivo y métodos de solución.
Notación: MINCS: Minimizar costo; MIN T: Tiempo; RS: Riesgo; SC: Social; N SER: Nivel de servicio; AMB: Ambiental; PM: Programación matemática; LGRN: LaGrange; AG: Algoritmo genético; ADEP: Algoritmo de optimización por enjambre; AIC: Algoritmo imperialista competitivo; RS: Recosido simulado; TB: Búsqueda tabú; EEP: Estrategia de evolución de Pareto; SIM: Simulación; AEBD: Algoritmo evolutivo basado endescomposición; ME: Métodos exactos; HAB: Heurística basada en algoritmos de búsqueda; ABA: Algoritmo de búsqueda de la armonía; ADA: Algoritmo desarrollado por el autor.
Tabla X: Taxonomía LIRP, función objetivo y métodos de solución

Las principales limitantes para modelos tríadicos de gran escala son la falta de linealidad y el cálculo respecto al enrutamiento de vehículos, por ello, en [56] se implementa un método para reducir la dimensión del problema y un método de solución basado en la descomposición de Benders, lo que resulta computacionalmente mejor que utilizar optimizadores o el algoritmo de aproximación externa (OA). Esto se realiza considerando un solo producto y un solo proveedor; sin embargo, al considerar múltiples productos y proveedores la complejidad aumenta, tanto así que el método de solución propuesto no es eficiente; por tanto, esta propuesta va enfocada a cadenas como autos, redes de comunicación y redes de transporte de agua urbana. [76] también consideran un único producto y único proveedor, además de una flota homogénea; la contribución radica en que las decisiones de inventario se realizan en los tres eslabones considerados. Para resolver dicho problema emplean una heurística de dos fases, fase 1: solución inicial y fase 2: mejora de la solución inicial mediante recocido simulado. Estos casos de estudio son modelos difícilmente generalizables; considerar múltiples productos, múltiples proveedores y ventanas de tiempo incrementan considerablemente la complejidad, implicando un reto a investigaciones futuras y hacia los métodos de solución.
Parámetros Estocásticos
En el siguiente aparte se presenta la distribución de los parámetros estocásticos en los modelos diádicos y tríadicos, la demanda, el tiempo, el costo y la capacidad son algunos de los parámetros más abordados en los modelos logísticos, la Figura 13 muestra la frecuencia de los parámetros estocásticos en cada modelo.
Figura 13: Frecuencia de uso de los parámetros estocásticos en los modelos diádicos y tríadicos
A nivel general, la demanda es el parámetro estocástico más común en los modelos diádicos, pues en el 85 % de los artículos revisados esta es la variable principal, seguida del tiempo cuya representación es del 15 % en los trabajos; la razón por la cual la demanda es la variable estocástica con mayor frecuencia en la distribución corresponde a que, en representación de una organización, este es uno de los parámetros con mayor variación en el tiempo, que generalmente se representan con una distribución de probabilidad. En los modelos tríadicos la demanda estocástica es tenida en cuenta en el 75 % de los trabajos consultados y el tiempo en un 15 %.
Función objetivo
En este aparte se presenta la distribución de la función objetivo de los modelos logísticos, donde encontramos que la mayoría concentra sus medidas de desempeño en factores como minimización de costo, tiempo, distancia, impacto ambiental, mejorando el nivel de servicio y beneficio social. La Figura 14 muestra la frecuencia de la función objetivo en cada problema.
Figura 14: Frecuencia de uso de la función objetivo en los modelos diádicos y tríadicos
En los modelos diádicos el costo es el objetivo más utilizado con un 86 %, dado que las empresas buscan obtener mayor utilidad con la minimización. En los artículos de inventarios, el nivel de existencias es calculado como objetivo en el 68,2 %, la distancia también es representativa en los modelos de localización (25 %) y ruteo (52,4 %).
Dado que el total de los artículos de LIRP tiene en cuenta la minimización del costo en la función objetivo, no se muestra en la Figura 14. La mitad de los modelos tiene función multiobjetivo (50 %), en la cual el 15 % se basa en la minimización del tiempo, el 5 % en maximizar el nivel de servicio y el 5 % en disminución del riesgo. En los modelos tríadicos se destaca que algunos autores (25 %) tienen en cuenta el criterio ambiental, al ser un problema abordado desde el 2010. Se evidencia que es un enfoque relevante en los últimos años, siendo la disminución de las emisiones de dióxido de carbono la más frecuente, como en [72], [73], [75]. El 10 % contempla el beneficio social entre los objetivos, Zhalechian et al. [66] contemplan la afectación al ambiente de los procesos y el factor de beneficio social en la creación de nuevos empleos, Eskandari et al. [73] plantean un modelo basado en la CS de plaquetas y sangre, para maximizar los efectos sociales y reducir el impacto ambiental. En la literatura se evidencia un reciente interés por atender otros objetivos diferentes al costo, pues en la evolución de las organizaciones aumenta el interés por desarrollar modelos sostenibles, que mitiguen los impactos negativos a nivel social y ambiental.
Métodos de solución
Los métodos de solución se pueden clasificar en cuatro categorías para los modelos NP-Hard: métodos exactos, heurísticas, metaheurísticas y simulación. En la Figura 15 se presenta la clasificación de los trabajos revisados que emplearon métodos exactos o simulación para encontrar la solución del problema. La investigación en el campo de los modelos logísticos con componentes estocásticos es relevante en el mundo académico, una razón es la complejidad en la búsqueda de los métodos de solución; este tipo de problemas difícilmente son optimizables, y el objetivo se direcciona a buscar soluciones factibles y aproximadas a un valor óptimo [79]. Cabe recalcar que los métodos de optimización exacta son utilizados como base para validar el modelo en instancias pequeñas y comparar el desempeño y la calidad de solución de los algoritmos empleados por los autores.
Figura 15: Taxonomía para los métodos de solución de los modelos diádicos y tríadicos
En la Figura 16 se encuentra una clasificación más detallada de los métodos de solución metaheurística que fueron utilizados para solucionar los modelos. Las metaheurísticas están inspiradas en comportamientos naturales, tales como la evolución, la física o la biología. Los trabajos clasificados en algoritmos genéticos y el recocido simulado son los más utilizados para resolver modelos diádicos y tríadicos; mientras los algoritmos de búsqueda de armonía y el basado en evolución diferencial son menos utilizados.
Figura 16: Taxonomía para las metaheurísticas empleadas en los modelos diádicos y tríadicos
En la Figura 17 se muestra el porcentaje en el uso de métodos de solución para cada conjunto de modelos. Para modelos IRP se observa que los métodos exactos son bastante utilizados para la validación y comparación en el desempeño (36 %), mientras las metaheurísticas presentan un 28 % y la simulación un 23 %. Los modelos LRP, a diferencia del resto de modelos, presentan una fuerte inclinación hacia la consideración de parámetros difusos mediante programación difusa [20] [26] [29] [25]. Para la solución de estos modelos se usan con mayor frecuencia métodos heurísticos, seguidamente metaheurísticas (31 %), métodos exactos (21 %) y simulación (14 %). Por su parte, el LIP es el modelo con menor atención por parte de los investigadores, los métodos exactos representan el 60 %, las metaheurísticas el 30 % y las heurísticas el 10 %; en la revisión no se encontró la simulación como método.
Figura 17: Porcentaje de uso de los métodos de solución en los modelos diádicos
El método de solución más utilizado para la resolución de los modelos LIRP son las metaheurísticas, le siguen los métodos exactos, las heurísticas y la simulación. El LIRP, dada su naturaleza NP-Hard y su mayor complejidad, requiere métodos de solución más sofisticados; aunque en instancias pequeñas, los métodos exactos resuelven el problema en un tiempo razonable para el tomador de decisiones.
En la Figura 17 se muestran los métodos de solución empleados en el modelo LIRP estocástico. Los métodos de solución aplicados mediante algoritmos para estos modelos, se caracterizan por tener una estructura jerárquica que resuelve en tres etapas, la primera etapa da solución estrictamente al problema de localización, la segunda y la tercera dan solución al problema de inventario o ruteo, el orden depende del autor (76).
Conclusiones y trabajos futuros
En un marco histórico la revisión de la literatura muestra cómo la complejidad aumenta exponencialmente cuando sus componentes son tratados con variables aleatorias, por lo que los métodos matemáticos y las técnicas de optimización tradicionales demandan tiempo y recursos computacionales en exceso, generando soluciones ineficientes. Por lo tanto, los autores buscan métodos de solución acordes con esta complejidad, las heurísticas y metaheurísticas que resuelven problemas con amplias cantidades de variables y restricciones logran una rápida convergencia en soluciones factibles y en algunos casos soluciones óptimas.
En el campo investigativo ha sido de interés el desarrollo de modelos multiobjetivo, en los que se supera el objetivo de rentabilidad empresarial, aparecen otros objetivos tales como la maximización del beneficio social, el factor social, la generación de nuevos empleos, la cobertura de servicios de salud, y la reducción del impacto ambiental, de los tiempos de atención a una emergencia o un desastre natural en que se vean implicadas vidas humanas.
Los trabajos futuros en LIP deben considerar que en la práctica las CS cuentan con más de un CD, si bien en temas de localización pueden ubicarse o dar apertura a varios de estos, al momento de realizar la asignación cada minorista es atendido por un solo CD; para estudios futuros, se sugiere trabajar el supuesto de que un minorista puede ser atendido por varios de los CD que se abrieron, es un tema que requiere ser más tratado [13]. Futuras líneas de investigación pueden ser la integración de políticas de inventario bajo el contexto de demandas no estacionarias [15], la incorporación del riesgo de ruptura de la CS [14] y los métodos de validación de los resultados obtenidos en las investigaciones [17].
La mayoría de los modelos LRP encuentran limitaciones en ventanas de tiempo, se encuentran pocos modelos con esta característica, por lo que algunos autores establecen que los tiempos de recorrido y la carga de combustible son constantes, es decir independientes de la carga que transportan los automotores, es necesario añadir estas características para una aproximación del modelo a la realidad [19], [29], [30].
Las líneas futuras de investigación en IRP requieren el planteamiento de problemas con estaciones de carga, mantenimiento y operación, capacidades de carga, velocidad y tiempo para lograr mejor empalme del modelo con situaciones cotidianas que logren aportar mayores beneficios a empresas logísticas (PL). [54], [50]. Respecto al LIRP, dado la juventud de estos modelos, se identifica una fuente importante de trabajo investigativo, donde se destaca la necesidad de estudiar modelos LIRP multiproducto y multiperiodo [64], modelos de tres niveles (proveedor, CD, cliente) con políticas de ruteo mixtas, en las que un vehículo pueda ir desde el proveedor al cliente, back order y entregas parciales.
Referencias
License
Copyright (c) 2022 Ricardo Andrés Cuervo Cruz, Javier Martínez Bernal, Javier Arturo Orjuela-Castro

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.












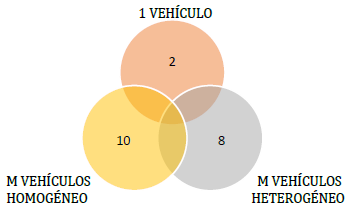



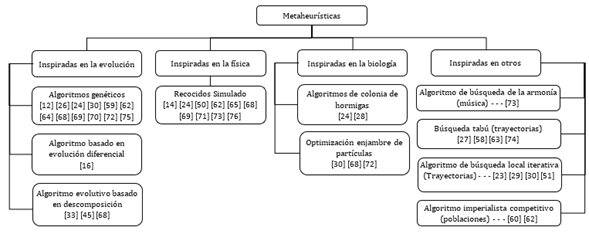
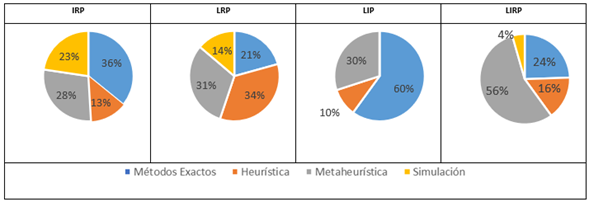



2.jpg)










