DOI:
https://doi.org/10.14483/23448393.13248Publicado:
2018-05-31Número:
Vol. 23 Núm. 2 (2018): Mayo - AgostoSección:
Inteligencia ComputacionalNew Algorithms for δγ-Order Preserving Matching
Nuevos Algoritmos para Búsqueda de Orden δγ
Palabras clave:
String searching, experimental algorithm analysis, strings similarity metric. (en).Descargas
Referencias
MIDI Association. Midi official webpage. [Online]. Available https://www.midi.org/".
Peter Brass. Advanced Data Structures. Cambridge University Press, 2008".
https://doi.org/10.1017/CBO9780511800191
Emilios Cambouropoulos, Maxime Crochemore, Costas Iliopoulos, Laurent Mouchard, and Yoan Pinzon. Algorithms for computing approximate repetitions in musical sequences. International Journal of Computer Mathematics, 79(11):1135–1148, 2002".
https://doi.org/10.1080/00207160213939
Tamanna Chhabra, M. Oguzhan Kulekci, and Jorma Tarhio. Alternative algorithms for order-preserving matching. In Jan Holub and Jan Zdárek, editors, Proceedings of the Prague Stringology Conference 2015, pages 36–46, Czech Technical University in Prague, Czech Republic, 2015".
Tamanna Chhabra and Jorma Tarhio. Order-preserving matching with filtration. In Proceedings of the 13th International Symposium on Experimental Algorithms - Volume 8504, pages 307–314, New York, NY, USA, 2014. Springer-Verlag New York, Inc.".
https://doi.org/10.1007/978-3-319-07959-2_26
Tim Crawford, Costas S. Iliopoulos, and Rajeev Raman. String-Matching Techniques for Musical Similarity and Melodic Recognition. Computing in Musicology, 11:71–100, 1998".
Maxime Crochemore, Costas S. Iliopoulos, Tomasz Kociumaka, Marcin Kubica, Alessio Langiu, Solon P. Pissis, Jakub Radoszewski, Wojciech Rytter, and Tomasz Wale´n. Order-Preserving Incomplete Suffix Trees and Order- Preserving Indexes, pages 84–95. Springer International Publishing, Cham, 2013".
https://doi.org/10.1007/978-3-319-02432-5_13
Maxime Crochemore, Costas S. Iliopoulos, Tomasz Kociumaka, Marcin Kubica, Alessio Langiu, Solon P. Pissis, Jakub Radoszewski, Wojciech Rytter, and Tomasz Walen. Order-preserving suffix trees and their algorithmic applications. CoRR, abs/1303.6872, 2013".
Maxime Crochemore, Costas S. Iliopoulos, Tomasz Kociumaka, Marcin Kubica, Alessio Langiu, Solon P. Pissis, Jakub Radoszewski, Wojciech Rytter, and Tomasz Wale’n. Order-preserving indexing. Theor. Comput. Sci., 638(C):122–135, July 2016".
https://doi.org/10.1016/j.tcs.2015.06.050
Mark de Berg, Otfried Cheong, Marc van Kreveld, and Mark Overmars. More geometric data structures: Windowing. Computational Geometry: Algorithms and Applications, pages 219–241, 2008".
Simone Faro and M. Oguzhan Kulekci. Efficient algorithms for the order preserving pattern matching problem. CoRR, abs/1501.04001, 2015".
Peter M Fenwick. A new data structure for cumulative frequency tables. Software: Practice and Experience, 24:327–336, 1994".
https://doi.org/10.1002/spe.4380240306
Paweł Gawrychowski and Przemysław Uznanski. Order-preserving pattern matching with k mismatches. Theoretical Computer Science, 638:136 – 144, 2016". Pattern Matching, Text Data Structures and Compression Issue in honor of the 60th birthday of Amihood Amir".
Md Mahbubul Hasan, ASM Shohidull Islam, Mohammad Saifur Rahman, and M Sohel Rahman. Order preserving pattern matching revisited. Pattern Recognition Letters, 55:15–21, 2015".
https://doi.org/10.1016/j.patrec.2014.11.013
Md Mahbubul Hasan, ASM Sohidull Islam, Mohammad Saifur Rahman, andMSohel Rahman. Order preserving prefix tables. In International Symposium on String Processing and Information Retrieval, pages 111–116. Springer, 2014".
Inc IMDb. John Williams imdb profile. [Online]. Available http://www.imdb.com/name/
Inc IMDb. Star Wars: Episode V - The Empire Strikes Back (original title) imdb page. [Online]. Available http://www.imdb.com/title/tt0080684/".
Jinil Kim, Peter Eades, Rudolf Fleischer, Seok-Hee Hong, Costas S. Iliopoulos, Kunsoo Park, Simon J. Puglisi, and Takeshi Tokuyama. Order-preserving matching. Theoretical Computer Science, 525:68 – 79, 2014. Advances in Stringology".
https://doi.org/10.1016/j.tcs.2013.10.006
Marcin Kubica, Tomasz Kulczynski, Jakub Radoszewski, Wojciech Rytter, and Tomasz Walén. A linear time algorithm for consecutive permutation pattern matching. Information Processing Letters, 113(12):430–433, 2013".
https://doi.org/10.1016/j.ipl.2013.03.015
Inbok Lee, Juan Mendivelso, and Yoan J. Pinzón. γδ– Parameterized Matching, pages 236-248. Springer Berlin Heidelberg, Berlin, Heidelberg, 2009".
Juan Mendivelso. Definition and solution of a new string searching variant termed γδ -parameterized matching. Master's thesis, National University of Colombia, Bogota, Colombia, 2010".
Juan Mendivelso, Inbok Lee, and Yoan J. Pinzón. Approximate Function Matching under δ- and γ- Distances, pages 348–359. Springer Berlin Heidelberg, Berlin, Heidelberg, 2012".
Juan Mendivelso, Camilo Pino, Luis F. Ni-o, and Yoan Pinzón. Approximate Abelian Periods to Find Motifs in Biological Sequences, pages 121–130. Springer International Publishing, Cham, 2015".
https://doi.org/10.1007/978-3-319-24462-4_11
Juan Mendivelso and Yoan Pinzón. A novel approach to approximate parikh matching for comparing composition in biological sequences. In Proceedings of the 6th International Conference on Bioinformatics and Computational Biology (BICoB 2014), 2014".
Rafael Niquefa. Definition and solution of a new approximate variant of the order preserving matching problem. Master's thesis, Universidad Nacional de Colombia, 2017".
Rafael Niquefa, Juan Mendivelso, Germán Hernández, and Yoan Pinzón. Order Preserving Matching under δγ-approximation. In Congreso Internacional de Ciencias Básicas e Ingeniería, 2017".
Rafael Niquefa, Juan Mendivelso, Germán Hernández, and Yoan Pinzón. Segment and fenwick trees for approximate order preserving matching. In Workshop on Engineering Applications, pages 131–143. Springer, 2017".
https://doi.org/10.1007/978-3-319-66963-2_13
Thomas Scarff. MIDI note numbers. [Online]. Available http://www.electronics.dit.ie/staff/
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 14 de abril de 2018; Revisión recibida: 14 de mayo de 2018; Aceptado: 28 de mayo de 2018
Resumen
Contexto:
El emparejamiento de cadenas según el orden compara la estructura de las cadenas de texto. Sin embargo, sus áreas de aplicación requieren mayor flexibilidad en el criterio de comparación. Este artículo avanza en esta dirección al extender [ 27].
Método:
Se define la búsqueda de orden-δϒ como una variante aproximada del problema de emparejamiento de cadenas según orden. Se proponen dos soluciones basadas en árboles de segmentos y árboles Fenwick: segtree BA and bitBA.
Resultados:
La eficiencia de los algoritmos propuestos se muestra experimentalmente comparándolos con los algoritmos presentados en [26 ] (naiveA y updateBA). Además, se presentan aplicaciones.
Conclusiones:
A pesar de que la complejidad en tiempo de peor-caso de los algoritmos propuestos (a decir, O(nm log m)) es mayor que la complejidad de update BA (Θ(nm)), su cota baja Ω(n log n) los hace más eficientes en práctica. También se muestran aplicaciones del enfoque propuesto en recuperación de música y análisis del mercado de acciones con ejemplos reales.
Palabras clave:
Análisis experimental de algoritmos, búsqueda de texto, métrica de similitud..Abstract
Context:
Order-preserving matching regards comparing the relative order of symbols within different strings. However, its application areas require more flexibility in the matching paradigm. We advance in this direction in this paper that extends our previous work [27].
Method:
We define δϒ-order preserving matching as an approximate variant of order-preserving matching. We devise two solutions for it based on segment and Fenwick trees: segtreeBA and bitBA.
Results:
We experimentally show the efficiency of our algorithms compared to the ones presented in [26] (naiveA and updateBA). Also, we present applications of our approach in music retrieval and stock market analysis.
Conclusions:
Even though the worst-case time complexity of the proposed algorithms (namely, O(nm log m)) is higher than the Θ(nm)-time complexity of updateBA, their Ω(n log n) lower bound makes them more efficient in practice. On the other hand, we show that our approach is useful to identify similarity in music melodies and stock price trends through real application examples.
Keywords:
String searching, experimental algorithm analysis, strings similarity metric, Language: English.1. Introduction
Stringology is the branch of computer science that is dedicated to the study of problems in which sequences are involved. One of the main problems of interest in stringology is string matching, which consists of finding the occurrences of a pattern P within a text T both defined over a given alphabet Σ. Let T0...n−1 represent a length-n string defined over Σ. The symbol at the position i of a string T is denoted as Ti . Also, Ti...j represents the substring of the text T from the position i to the position j, i.e. Ti...j = Ti Ti+1 · · · Tj , where it is assumed that 0 ≤ i ≤ j < n. In particular, we are interested in each length-m substring that starts at position i of the text, i.e. Ti...i+m−1 , 0 ≤ i ≤ n − m, which we call text window and denote as T i in the rest of the paper. Then, the output of the exact string matching problem should list all the positions i, 0 ≤ i ≤ n − m, such that Pj = Ti+j for all 0 ≤ j ≤ m − 1.
In this paper, two variants of the problem of exact search of patterns are combined: the δϒ- matching problem and the order preserving matching problem. Both of them consider integer alphabets. The δϒ-matching problem consists of finding all the text windows in T for which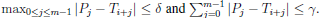 ≤ γ. This is denoted as
≤ γ. This is denoted as 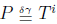 . We can seethat δ limits the individual error of each position while γ limits the total error. Then, δϒ-matching has applications in bioinformatics, computer vision and music information retrieval, to name some. Cambouropoulos et al. [3] was perhaps the first to mention this problem motivated by Crawford’s work et al. [6]. Recently, it has been used to make flexible other string matching paradigms such as parameterized matching [20], [21], function matching [22] and jumbled matching [23], [24 ].
. We can seethat δ limits the individual error of each position while γ limits the total error. Then, δϒ-matching has applications in bioinformatics, computer vision and music information retrieval, to name some. Cambouropoulos et al. [3] was perhaps the first to mention this problem motivated by Crawford’s work et al. [6]. Recently, it has been used to make flexible other string matching paradigms such as parameterized matching [20], [21], function matching [22] and jumbled matching [23], [24 ].
On the other hand, order-preserving matching considers the order relations within the numeric strings rather than the approximation of their values. Specifically, the output of this problem is the set of text windows whose natural representation match the natural representation of the pattern. The natural representation of a string is a string composed by the rankings of each symbol in such string. In particular, the ranking of symbol Ti of string T0...n−1 is:
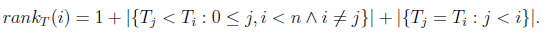
Then, the natural representation of T is nr(T) = rankT (0)rankT (1) · · · rankT (n−1). Therefore, order preserving matching consists of finding all the text windows T i such that nr(P) = nr(Ti ). Note that this problem is interested in matching the internal structure of the strings rather than their values. Then, it has important applications in music information retrieval and stock market analysis. Specifically, in music information retrieval, one may be interested in finding matches between relative pitches; similarly, in stock market analysis the variation pattern of the share prices may be more interesting than the actual values of the prices [18]. Since Kim et al. [18] and Kubica et al. [19] defined the problem, it has gained great attention from several other researchers [4[, [5 ], [7 ]- ]9 ], [11], ]14], [14 ], ]15 ].
Despite the extensive work on order-preserving matching, the only approximate variant in previous literature, to the best of our knowledge, was recently proposed by Uznan´ ski and Gawrychowski [13 . In particular, they allow k mismatches between the pattern and each text window. Then, they regard the number of mismatches but not their magnitude. In this paper, we propose a different approach to approximate order-preserving matching that bounds the magnitude of the mismatchethrough the δϒ distance. Specifically, δ is a bound between the ranking of each character in the pattern and its corresponding character in the text window; likewise, ϒ is a bound on the sum of all such differences in ranking. Thus, δ and ϒ respectively restrict the magnitude of the error individually and globally across the strings. We define δϒ-order-preserving matching as the problem of finding all the text windows in T that match the pattern P under this new paradigm. This paper is an extended version of the work [27] presented in the Workshop on Engineering Applications 2017. Furthermore, some of its contents were developed in the Master’s Thesis [25].
We first defined the notion of δγ-order preserving matching in ]26]. Now, in this paper, we provide a more formal definition and two new algorithms for this problem in Section 2. Then, we present some experimental results of the proposed algorithms and discuss some applicacions in Section 3. Finally, the concluding remarks are presented in Section 4.
2. Methods
In Section 2.1 we formally define δϒ-order preserving matching while we present its solutions in Section 2.2.
2.1. Definition of δϒ -order preserving matching problem (δϒ -OPMP)
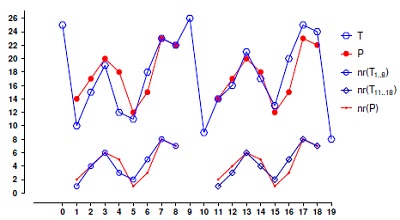
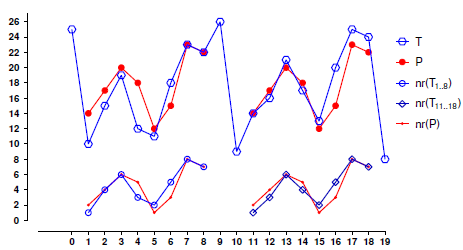
The motivation to define δϒ -order-preserving matching stems from the observation that the application areas of order-preserving matching, mainly stock market analysis and music information retrieval, require to search for occurrences of the pattern that may not be exact but rather have slight modifications in the magnitude of the rankings. For example, let us assume that the text T presented in Figure 1 is a sequence of stock prices and that we want to determine whether it contains similar occurrences of the pattern P (also shown in this figure). Under the exact order-preserving matching paradigm, there are no matches, but there are similar occurrences at positions and 1 and 11. In particular, T1...8 and T11...18 are similar, regarding order structure, to the pattern. This similarity can be seen even more clearly if we consider natural representations of these strings (also shown in Figure 1). Next we formally define these notions
Figure 1: Order preserving matching under _ approximation example.
Definition 1 (δϒ -order-preserving match )
Let X = X0...m−1 and Y = Y0...m−1 be two equallength strings defined over Σσ . Also, let δ, γ be two given numbers (δ, γ ∈
N). Strings X and Yare said to δγ-order-preserving match, denoted as 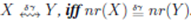 .
.
Given δ = 2, γ = 6, X = (10, 15, 19, 12, 11, 18, 23, 22) and Y = (14, 17, 20, 18, 12, 15, 23, 22i 22) 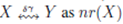 = (1, 4, 6, 3, 2, 5, 8, 7i, nr(Y ) = (2, 4, 6, 5, 1, 3, 8, 7i and nr(X )
= (1, 4, 6, 3, 2, 5, 8, 7i, nr(Y ) = (2, 4, 6, 5, 1, 3, 8, 7i and nr(X )  γ nr(Y ).
γ nr(Y ).
Problem 1 (δγ-order-preserving matching)
Let P = P0...m−1 be a pattern string and T = T0...n−1 be a text string, both defined over Σσ . Also, let δ, γ be two given numbers (δ, γ ∈
N). The δγ-order-preserving matching problem is to calculate the set of all indices i, 0 ≤ i ≤ n − m,satisfying the condition P satisfying the condition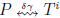 . From now on δγ-OPMP.
. From now on δγ-OPMP.
2.2.Algorithms for the δϒ -OPM
In this section, we present two algorithms that solve the δϒ -OPMP: one that uses segment trees (Section 2.2.1) and the other utilizes Fenwick trees (Section 2.2.2).
2.2.1. Segment tree based algorithm (segtree BA)2 10
[ ] [ ] RMQ RMQ i i minI ndex, [i, i + m - 1 m oldV alue changedI ndex
-
buildSegTree( T , 0, n − 1 ): Builds a segment tree with T0 , T1 , . . . , Tn−1 and returns the root node. The complexity is O(n) .
-
updateSegTree(minIndex, i, x): Sets Ti to x. The complexity is O(lg n).
-
querySegTree(minI ndex, i, j): Returns the index of the minimum value among Ti , Ti+1, . . . , Tj . If there are several minimum values, the leftmost (smallest index) is chosen. The complexity is O(lg n)
Figure 2: Segment tree based algorithm: segtreeBA. The totalcomplexityof the algorithm is then O(nm lg n) with a lower bound of Ω(n lg n).
2.2.2.Fenwick tree based algorithm ( bitBA )
The Binary Indexed Tree (BIT ) or Fenwick tree, is a data structure that can be used to maintain and query cumulative frequencies [12]. In particular, it is mainly used to efficiently calculate prefix sums in an array of numbers. Based on this data structure, we propose the algorithm called bitBA (see Figure 3). The BIT data structure could be considered then as an abstraction of an integer array of size n indexed from 1, i.e., a bit encapsulate A = A1 A2 · · · An . The version we are going to use has two operations:
-
sumUpT o(tree, i): Returns A1 + A2 + . . . + Ai . The complexity is O(lg n).
-
addAt(tree, i, x): Sums x to Ai . The complexity is O(lg n)
The algorithm has a preprocessing phase in which the data structures needed to solve the δϒ - OPMP are created. This is done with a complexity of Θ(n + n lg n + m lg m). The term n is due to the creation of the BIT. The term n lg n is due to the creation of
Tnr
and the term m lg m is due to the creation of
Pnr
. In the searching phase, it iterates over all possible positions in the text T to find the existing matches. For each position i to be considered, the algorithm uses the BIT to get the rank of every symbol in the searching window
Ti...i+m−1
, and then each rank in the window is compared with each rank in
Pnr
to check if
Ti
is a δϒ -order preserving match. This operation is evaluated using the function isAMatch(
P,Ti,δ,ϒ
); in particular, this function returns true
iff
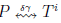 I and this takes O(m lg m + m). Each rank calculation using the BIT costs O(lg n). Then the total complexity of the algorithm is O(nm lg n), but with a lower bound of Ω(nlg n).
I and this takes O(m lg m + m). Each rank calculation using the BIT costs O(lg n). Then the total complexity of the algorithm is O(nm lg n), but with a lower bound of Ω(nlg n).
In the preprocessing phase, the algorithm first creates the natural representations of the pattern P and the text T (
Pnr and Tnr
, respectively). Then, it creates a BIT which is an encapsulation of an array with n positions numbered from 1 to n. Then assigns 1 the positions 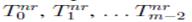
(Lines 1 to 5 in Figure 3). In the searching phase, for each candidate position i, the algorithm computes the rank of each symbol Ti+j , 0 ≤ j ≤ m − 1 using sumUpT o(i + j). After checking if there is a match at position i, the BIT must be updated in each iteration to consider symbol Ti+m (line 7 in Figure 3). And the BIT must be updated so it does not consider the position i in the next search window (line 9 in Figure 3).
Figure 3: BIT based algorithm: bitBA.
3. Results
In Section 3.1 we present experimental results on the proposed algorithms while we present applications for δϒ -order preserving matching in Section 3.2.
3.1.Experiments on Artificial Data
In this section, we describe the experimental setup we designed to evaluate the performance of the proposed algorithms. We compare our algorithms with two baseline algorithms: The naive algorithm, which we call naiveA, and updateBA, presented in [26]. The former, whose time complexity is Θ(nm lg m), considers all possible positions in the text and, for each one of them, verifies if there is a match in Θ(m lg m + m) time. The latter algorithm, whose time complexity is Θ(nm), is based on linear update and verification.
We present the experimental framework (Section 3.1.1) and describe the data generation (Section 3.1.2). Then, we discuss the results obtained (Section 3.1.3). Finally we show the results of the experiments intended to study how the algorithms segtreeBA and bitBA behave in the worstcase scenario for all experiment instances (Section 3.1.4).
3.1.1. Experimental setup
Hardware and software: All the algorithms were implemented using C++. The computer used for the experiments was a Lenovo ThinkPad with a processor Intel(R) Core(TM) i7 4600u CPU @ 2.10GHz 2.69 GHz and installed RAM memory of 8GB. The computer was running 64-bit Linux Ubuntu 14.04.5 LTS. The C++ compiler version was g++ (Ubuntu 4.8.4-2ubuntu1 14.04.3) 4.8.4.
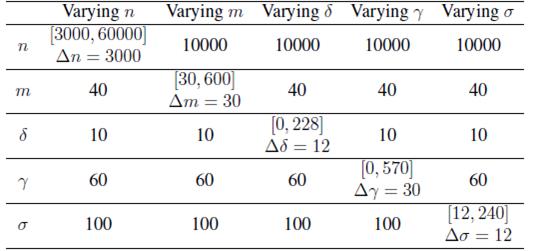
Parameters: To show how our solution behaves with different configuration of the different parameters, we perform five types of experiments. In each experiment, we vary one of the given parameters n, m, δ, ϒ and σ, and let the other four parameters fixed at a given value. We chose the fixed values after several attempts via try and error to find values that produced results varying from no matches to matches near the value of n. For each experiment type, we performed five different experiments and took the median as the value to plot, making the median of five experiments the representative value for a experiment configuration of values n m, δ,ϒ and σ. The variation of the parameter values for each experiment type is presented in Table I.
Table I: Experimental values of n m, δ,γ and σ
3.1.2. Random data generation
An experiment consists of two stages. The first stage is the pseudo-random generation of a text T of length n and the pattern P of length m. The second stage is the execution of the algorithms on the generated strings P and T . The random generation of each character of both the pattern P and the text T is done by calling a function that pseudo-randomly and selects a number between 1 and σ with an uniform probability distribution, i.e., all symbols have the same probability to appear in a position and for that reason, on average, every symbol in the alphabet will appear with the same frequency on an arbitrary generated string.
3.1.3. Experimental results and analysis
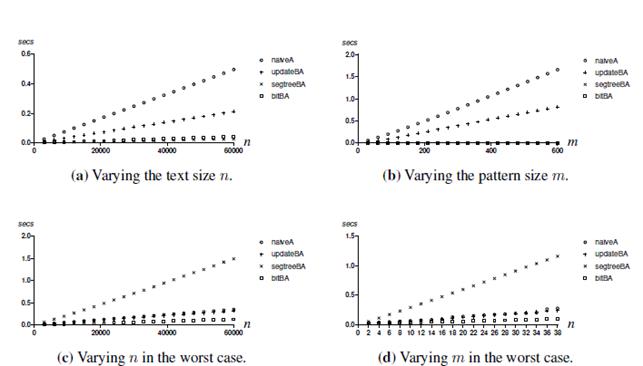
The first result to highlight is the fact that, in every experiment, the naive algorithm always has the worst performance, as expected. We found that the size of the alphabet and the parameters δ and ϒ have practically no impact on the execution time of any of the algorithms, they all show nearly constant time behavior. Figures 4a and 4b verify the theoretical complexity analysis that states that n and m are the parameters that really determine the growth in the execution time of all the algorithms. In Figure 4a, m is a constant and n is a variable while in Figure 4b, n is a constant and m is a variable. It is important to notice that, under these conditions, the graphs are expected to be linear and the experiments verify that.
Figure 4: Experimental results of comparing the four algorithms by varying different parameters
In the figures where we show the result of varying the parameter n and the parameter m, (Figures 4a-4b), we can see that the best two algorithms are the based on data structures (segtreBA and bitBA). This despite the fact that these two algorithms have a higher upper bound on their complexities in relation with the first two algorithms (naive A and updateBA). This result can be explained by the fact that the lower bound on the data structure based algorithms is considerably lower in comparison with the other two. The lower bound of the data structures based algorithms is Ω(n lg n) and the lower bound of the naiveA and update BA is the same as their upper bound meaning they are Θ(nm lg m) and Θ(nm) respectively. This can be understood by taking into account that the first two algorithms check for a match after a natural representation of every window is completely obtained; on the contrary, data structure based algorithms break the calculation of a given natural representation of a window if at some point the δ or ϒ restriction do not hold.
Given the result of the experiments, it is safe to say that the algorithms based on data structures are faster in most cases, especially if they are going to be used in applications where very few matches are expected to appear. This is due to their lower bound of complexity. We test two different implementations of the segment tree data structure: one based on classes and pointers, and the other based on an array. Ultimately, we recommend to chose the array based as representative for the segment tree based solution and the experiments plots show their results. The array-based segment tree is almost twice time faster than the classes-based implementation.
3.1.4.Worst case experiments on segtreeBA and bitBA
Taking into account that the first two algorithms, naiveA and updateBA both have complexities in Big Theta notation, i.e. their worst case is the same as their best case, the experiments described so far are enough for their experimental analysis. For the data structures based algorithms a more particular kind of experiment is needed, i.e. the worst case experimental analysis. For this algorithms the worst case is when there is a match in every candidate position. An easy way to generate data for the worst case is when all the symbols in both the pattern P and the text T are the same. Other way to generate worst cases scenarios for this two algorithms is when either both P and T are strictly increasing or both are strictly decreasing. Results from this experiments show a fast degradation in experimental performance of the segtreeBA algorithm, but a very slow degradation of the bitBA algorithm. Results of this last experiments are shown in Figures 4c and 4d.
3.2. Applications
In this section we show a couple of applications of the defined problem, in music and finance.
3.2.1.Application in music
For the music application example, we choose the main theme from The Imperial March, soundtrack of the film series Star Wars [17] composed by John Williams [16] also known as the Darth Vader’s theme because it represents him. This melody sounds every time this villain has a significant scene. Here we use an integer alphabet abstraction of a music piece, where each note of the melody is an integer. This abstraction of music takes into account only the pitch leaving out other aspects as silences, note duration, harmony, or instrumentation, but it gives a very good idea of the possible applications in music retrieval. The alphabet for music applications could be for example the given by the MIDI (Musical Instrument Digital Interface) technical standard [1], [28]. In the MIDI standard, the first note, 0 is a C note of the octave 0 (the lowest octave), note 1 is a C # of the same octave and so on. There could be up to note 127 which will be a G in the 10th octave.
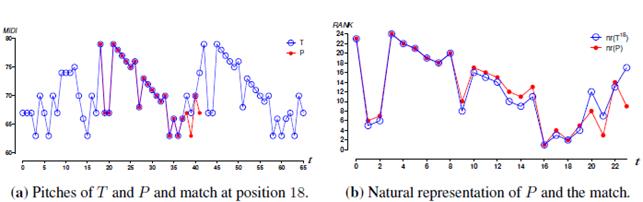
We draw an example of δϒ -OPM with the same musical piece. We consider a 66-pitch excerpt of the main melody as the text T = T 0...65 , and from the same except we extract T42...65 as the pattern P (see Figure 5a). For δ = 8 and ϒ = 32, we found a match in position 18 which for professional musicians, and even non professional musicians, sounds very similar to the pattern. Namely,Gabriela Rojas, a professional musician from the National University of Colombia Conservatory found the match similar to the pattern. The parameters δ and γ were chosen by attempting different values of both starting from 0 and increasing them until more matches were found. Furthermore, we can see in Figure 5a how similar the pitches of the pattern and the match are. In Figure 5b we show the similarity of their natural representation . This gives us an idea of possible applications in musical retrieval of approximate string matching. This can be useful for the advanced music students in order to help them with the theoretical analysis of the scores so they can look for melodic similarities or differences either in the same piece or comparing different pieces.
Figure 5: Darth Vader’s theme from Star Wars by John Williams (Excerpt).
3.2.2. Application in finance
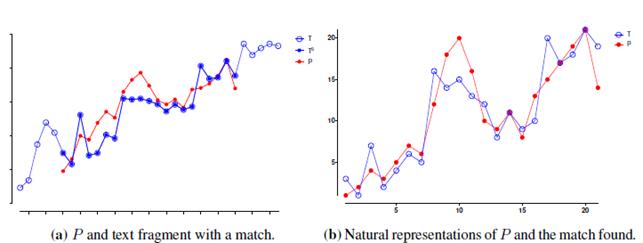
For the finance application we choose to analyse the stock price of the Facebook company. We take the history of the stock price of Facebook from May 18 2012 to March 31 2017 as the text T (the size of this text is 1225). As the pattern, we take the 21-day period starting in February 28 2017 up to March 28 2017. Take into account that not all days the stock actions change, for that reason we choose 21 days which is approximately the amount of days the stock actions change in a month. In Figure 6a we show the pattern and the portion of the text that we found to be the most similar to the pattern. In this figure we omit the y and x axes labels because we want to show the similarity in shape of the pattern and the search window, not the similarity in absolute values which indeed is quite different. In fact the values in the pattern to search are values lower than 34 and the text window found has values greater than 100. Finally, in Figure 6b we show the natural representation (or ranks) of both the pattern P and the match found. We can see that they have a similar structure. We selected the pattern randomly and then attempted to find its matches with different values for δ and ϒ. Given that a 21 day period is not a short period, it was expected that we just found one match in the given text window.
Figure 6: Stock price of the Facebook company from May 18 2012 to March 31 2017.
4. Conclusions and Discussion
We define a new variant of the string matching problem, the δϒ -order preserving matching problem (δϒ -OPMP). This new variant provides the possibility of searching a pattern according to the relative order of the symbols as the order preserving matching problem. But it also gives more flexibility to the search by allowing error in the individual ranking comparisons through the parameter δ. And also, the proposed problem gives a bound for the global error in the comparison of a pattern against a text window through ϒ. This new variant has at least the same applications as the order preserving matching problem.
Our experimental results on randomly generated data show that in most cases, given the uniformly data generation, the proposed algorithms work faster than the naive solution and updateBA. One question that remains open is if an algorithm with better worst case time complexity than O(nm) can be designed; other question that also remains open is that if an algorithm with better lower bound than Ω(n lg n) can be obtained. We show experimental results on the worst cases of the bitBA and segtree BA. We conclude that the degradation in performance in the segtreeBA algorithm is much more notorious than the degradation of bitBA. It still remains open to prove empirically that we can device an experimental setup where the best worst-case algorithm, updateBA experimentally beats the other three algorithms. Given the theory behind the big O notation, we can say that such experimental setup exist.
We show two applications with real data in music and finance. In music we use our findings to search for a portion of a melody in the melody itself. Those two portions of the melody are also very similar according to professional musicians consulted. For the financial application, we show how similar the changes in stock prices are despite the difference in their absolutes values. An aspect left to explore related to the applications is to establish whether, in the finance application, the tools presented here can be useful to device or complement algorithms/techniques to make predictive analysis of stock price changes. In music, our contributions can be useful to design tools for advanced music students in order to help them with the theoretical analysis of the scores so they can look for melodic similarities or differences either in the same piece or comparing different pieces. Also composers could see the δγ-OPMP, as a tool to check the perception they have about the similarity of musical ideas developed in different ways in one or several pieces of their own. For the musicologist this could be a way to track the development of one composer’s musical ideas throughout their life and to analyze the way the composer evolves.
References
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.






2.jpg)