DOI:
https://doi.org/10.14483/udistrital.jour.reving.2013.2.a06Published:
2013-11-06Issue:
Vol. 18 No. 2 (2013): July - DecemberSection:
Special Section: Best Papers "VI Symposium on Optimization".Towards Solving Matrix Games with Interval Type-2 Fuzzy Uncertainty through Linear Optimization
Hacia la solución de juegos matriciales con incertidumbre difusa Tipo-2 a través de optimización lineal
Keywords:
Fuzzy linear programming, Type-2 fuzzy sets, Games theory (en).Keywords:
programación Lineal Difusa, Conjuntos difusos Tipo-2, Teoría de juegos (es).Downloads
References
C. R. Bector and Suresh Chandra. Fuzzy Mathematical Programming and Fuzzy Matrix Games. Springer-Verlag, 2005.
R. E. Bellman and Lofti A. Zadeh. Decision-making in a fuzzy environment. Management Science, 17(1):141–164, 1970.
D. Butnariu. Fuzzy games a description of the concept. Fuzzy Sets and Systems, 1:181–192, 1978.
D. Butnariu. Advances in Fuzzy Set Theory and Application, volume 1, chapter Solution concept for n-Person games. North-Holland Publishing, 1979.
L. Campos. Fuzzy linear programming models to solve fuzzy matrix games. Fuzzy Sets and Systems, 326(1):275–289, 1989.
Carlos Celemin and Miguel Melgarejo. A proposal to speed up the computation of the centroid of an interval Type-2 fuzzy set. Advances in Fuzzy Systems, 2013:17, 1993.
Li Cunlin and Zhang Qiang. Nash equilibrium strategy for fuzzy non-cooperative games. Fuzzy Sets and Systems, 176(1):46–55, 2011.
George Dantzig. Linear Programming and Extensions. Princeton University Press, 1963.
Juan Carlos Figueroa. An iterative procedure for fuzzy linear programming problems. In 2011 Annual Meeting of the North American Fuzzy InformationProcessing Society (NAFIPS), pages 1–6. IEEE, 2011.
Juan Carlos Figueroa. A general model for linear programming with interval type-2 fuzzy
technological coeffi cients. In 2012 Annual Meeting of the North American Fuzzy Information
Processing Society (NAFIPS), pages 1–6. IEEE, 2012.
Juan Carlos Figueroa and Germa´n Herna´ndez. Computing optimal solutions of a linear programming problem with interval type-2 fuzzy constraints. Lecture Notes in Computer Science, 7208:567–576, 2012.
Juan Carlos Figueroa-Garc´ıa. An approximation method for type reduction of an interval Type2 fuzzy set based on -cuts. In Proceedings of FEDCSIS 2012, 1-6. IEEE, 2012.
Juan Carlos Figueroa-Garc´ıa and German Herna´ndez. A transportation model with interval type-2 fuzzy demands and supplies. Lecture Notes in Computer Science, 7389(1):610–617,2012.
George J. Klir and Tina A. Folger. Fuzzy Sets, Uncertainty and Information. Prentice Hall, 1992.
George J. Klir and Bo Yuan. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, 1995.
Moussa Larbani. Non cooperative fuzzy games in normal form: A survey. Fuzzy Sets and Systems, 160:3184–3210, 2009.
Miguel Melgarejo. Implementing Interval Type-2 Fuzzy processors. IEEE Computational Intelligence Magazine, 2(1):63–71, 2007.
Miguel Alberto Melgarejo. A Fast Recursive Method to compute the Generalized Centroid of
an Interval Type-2 Fuzzy Set. In Annual Meeting of the North American Fuzzy Information
Processing Society (NAFIPS), pages 190–194. IEEE, 2007.
Jerry Mendel. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice Hall, 1994.
Jerry M. Mendel and Feilong Liu. Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set. IEEE Transactions on Fuzzy Systems, 15(2):309–320, 2007.
L. Monroy, M.A. Hinojosa, A.M. Mrmol, and F.R. Fernandez. Set-valued cooperative games
with fuzzy payoffs. the fuzzy assignment game. European Journal of Operational Research,
(1):85–90, 2013.
J.F. Nash. Non cooperative games. Annals of Mathematics, 54:286–295, 1951.
John Von Neumann and Oskar Morgenstern. Theory of Games and Economic Behavior. Princeton University Press, 1944.
V. Vijay, S. Chandra, and C.R. Bector. Bimatrix games with fuzzy payoffs and fuzzy goals.
Fuzzy Optimization and Decision Making, 3:327–344, 2004.
L.A. Zadeh. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets and Systems, 1:3–28, 1978.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
TOWARDS SOLVING MATRIX GAMES WITH INTERVAL TYPE-2 FUZZY UNCERTAINTY THROUGH LINEAR OPTIMIZATION
HACIA LA SOLUCIÓN DE JUEGOS MATRICIALES CON INCERTIDUMBRE DIFUSA TIPO-2 A TRAVÉS DE OPTIMIZACIÓN LINEAL
Juan Carlos Figueroa García, Universidad Nacional de Colombia-Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. jcfigueroag@udistrital.edu.co
Germán Hernández, Universidad Nacional de Colombia. Bogotá, Colombia. gjhernandezp@gmail.com
Carlos Franco, Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. kafraud@hotmail.com
Recibido: 25/09/2013 - Aceptado: 10/12/2013
ABSTRACT
This paper presents some theoretical and computing considerations about how to deal with fuzzy uncertainty in the parameters of the classical games model. Indeed, when multiple experts are involved in a game situation, then their opinions lead to have uncertainty since most of the times they are not agree to each others. This kind of uncertainty can be modeled using Type-2 fuzzy sets, which implies a specialized methods and sub-models.
Some considerations about the use of Type-2 fuzzy sets and what does this imply when computing solutions, are presented. A general model which includes this kind of uncertainty is defined on the base of the extension principle and α-cuts representation theorem. A possible way for solving this model is glimpsed and put down for discussion and implementation.
Key words: Fuzzy linear programming, Type-2 fuzzy sets, Games theory.
RESUMEN
Este artículo presenta algunas consideraciones computacionales y teóricas acerca de cómo incluír incertidumbre difusa en los parámetros de un problema clásico de juegos. De hecho, cuando varios expertos están involucrados en un problema de juegos, todas sus opiniones llevan a pensar en una fuente incertidumbre, ya quemuchas veces esos expertos no están de acuerdo entre sí. Ese tipo de incertidumbre puede modelarse mediante conjuntos difusos Tipo-2, lo que implica usar modelos y métodos especiales para llegar a una respuesta adecuada.
Se presentan algunos aspectos importantes acerca del cálculo de soluciones en presencia de este tipo de incertidumbre. Un modelo general que incluye incertidumbre difusa Tipo-2 es presentado, el cual se basa en el principio de extensión y el teorema de representación de α-cortes. Un posible método de solución es puesto a consideraci ón para discusión e implementación.
Palabras clave: Programación Lineal Difusa, Conjuntos difusos Tipo-2, Teoría de juegos.
1. INTRODUCTION AND MOTIVATION
Recently, analysis of both incomplete and uncertainty-based information have lead to develop appropriate method for solving more complex problems. One of the most developed tools are fuzzy sets, which are based on the idea of projecting a variable x ∈ X to the domain [0, 1] using a linguistic label (word) A that represents a concept itself. Thus, the perception of an expert about X is represented through a membership function, μA(x).
Classical zero-sum games do not include uncertainty in their payments matrix (even when decisions are uncertain in practice). This payment matrix represents the value of the retribution and/or losses that each player has in regards to the other, where that payments matrix was initially defined in a deterministic way.
Now, when linguistic uncertainty about the perception of multiple experts about a game situation, then some interesting questions around the use of Type-2 fuzzy sets for involving uncertainty begin to appear, so this paper is focused on providing a theoretical basis for designing specialized models and methods to solve this kind of problems. A good introduction about classical fuzzy sets methods, and fuzzy linear programming models applied to matrix games is provided by Bector and Chandra [1]. In general, the proposals of Cunlin and Qiang [7], Vijay, Chandra and Bector [24], Butnariu [3], and Campos [5], which are based on linear programming methods to find a crisp solution of a fuzzy game, could be extended to a Type-2 fuzzy environment.
This paper is divided into five principal sections. In Section 1 the Introduction and Motivation is presented. In Section 2, the classical two-players game is described, and its LP formulation presented. In Section 3, some basics on Type-2 fuzzy sets are introduced. In Section 4, a Type-2 fuzzy games model is presented. Section 5 presents a proposal for solving this kind of problems under uncertainty, and finally in Section 6 some concluding remarks are suggested.
1.1 A discussion
When a problem is deterministic, a large variety of methods can be used to solve it, at least conceptually, regardless of their complexity. Uncertainty clouds the definition of optimality and makes the decision process that much more difficult due to our inability to predict outcomes with certainty.
Games decision problems often involve another individual who may be an antagonistic opponent. We must make decisions knowing that the result will be governed in part by the actions of a competitor. In this way, a deterministic point of view would not be an appropriate approach, since the payments of the game sometimes are defined by experts who express such opinions using words instead of crisp numbers.
Now, when multiple experts are asked for defining a payment matrix in a game situation, then multiple perceptions are involved. This leads us to think in how to deal with those opinions, using well known methods for finding a solution of the game, such as linear programming, fuzzy sets, and fuzzy equations.
However, the use of the judgement of multiple experts implies the development of special measures and methods. One of the most useful tools is, in this case, the theory of Type-2 fuzzy sets, may help us to deal with the perception of multiple people thinking about a concept (e.g. a word) regarding to a variable, or a payoff in our case.
There are some special models to address matrix games when fuzzy uncertainty is involved, mostly focused on obtaining a crisp solution of the game using linear programming models, and some additional suppositions. Campos [5] proposes to solve the game using a full satisfaction degree of all fuzzy sets by maximizing chance constrained models, possibilistic models, and triangular fuzzy sets. Bector and Chandra [1] extended some of the results of Campos to games involving both fuzzy payoffs and fuzzy goals. Until the current date, there is no any report on specialized literature (recognized journals and books) referring to the use of Type-2 fuzzy linguistic uncertainty, which is common in practical applications involving experts.
2. THE CLASSICAL TWO-PLAYERS GAME
A two-players game is a situation where two actors are trying to make a move to earn the best possible benefits, given the possible moves of the other player. This implies that each player has to know how much does a move is paying or charging to its budget, so a move gives gains to a player while its opponent losses.
In this problem, all payments can be represented by using a payment matrix namely A, where each element aij represents the payoff of the player 1, where a negative value means that player 1 has to pay aij to 2. The set Nm is the set of possible moves of Player 1, and the set Nn is the set of possible moves of Player 2. Note that i ∈ Nm , and j ∈ Nn . A generic example of A is shown next.
where aij ∈ R, i ∈ Nm and j ∈ Nn.
This matrix A is commonly defined using crisp payoffs, so there is only one strategy which maximizes the decision making process. this decision making process is based on a max - min principle. This principle seeks to get the maximum incomes selected from the worse possible movings made by the opponent, so the decision is to do a move i which has the maximum of the minimum payoffs given all the possible moves j of the opponent.
2.1 Mathematical formulation
Basically, the mathematical formulation of a two-players game is intended to find the optimal frequency of moves which maximizes the the value of the game. To do so, a player has to do the move (Ai), x*i times to obtain the best expected payoff (aij). The mathematical programming formulation for the Player I is as follows:
where x ∈ Rm, aij ∈ Rnxm. xi is the probability that each decision has to be taken.
The first LP model for games was provided by Dantzig [8] based on the seminal works of Neumann and Morgenstern [23], and Nash [22]. His proposal is based on defining an auxiliary variable v, equivalent to the min operator. The solution is then provided by the simplex method since it is a full LP problem, so it has been widely applied in many practical situations. The LP formulation of the above model (Player I) is shown next.
where x ∈ Rm, aij ∈ Rnxm. xi is the probability that each decision has to be taken. v is an auxiliary variable which operates as 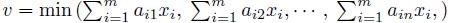
A Type-2 fuzzy set is an ordered pair 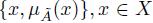 , where A is its linguistic label and à represents uncertainty around the word A. Their mathematical definitions are taken from Mendel [19] and Klir and Yuan [14]:
, where A is its linguistic label and à represents uncertainty around the word A. Their mathematical definitions are taken from Mendel [19] and Klir and Yuan [14]:
where fx(u)/u is the secondary membership function of à over x ∈ X, and u is its domain of uncertainty. A special kind of Type-2 fuzzy sets are called Interval Type-2 fuzzy sets (IT2FS) in which fx(u) is defined as 1. Hence, an Interval Type-2 fuzzy set 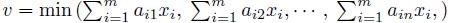 is composed by an infinite amount of Type-1 fuzzy sets in two ways: primary fuzzy sets Jx weighted by secondary fuzzy sets fx(u) = 1. In other words
is composed by an infinite amount of Type-1 fuzzy sets in two ways: primary fuzzy sets Jx weighted by secondary fuzzy sets fx(u) = 1. In other words
and its extended representation is:
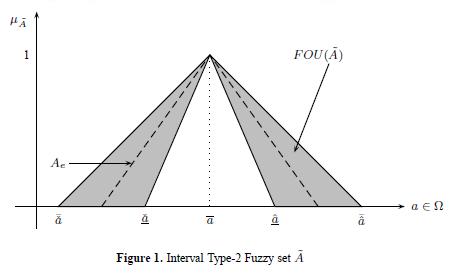
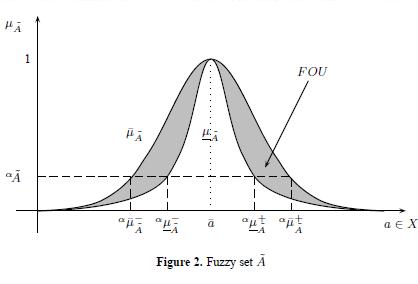
A graphical example of the IT2FS set à is shown in Figure 1.
Here, 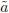 is an Interval Type-2 fuzzy set defined over an universe of discourse
is an Interval Type-2 fuzzy set defined over an universe of discourse 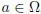 , its support supp(
, its support supp(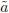 ) is enclosed into the interval
) is enclosed into the interval 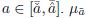 is a linear Type-2 fuzzy set with parameters
is a linear Type-2 fuzzy set with parameters 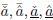 and
and 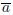 . FOU is the Footprint of Uncertainty of the Type-2 fuzzy set and Ae is a Type-1 fuzzy set embedded in the FOU.
. FOU is the Footprint of Uncertainty of the Type-2 fuzzy set and Ae is a Type-1 fuzzy set embedded in the FOU.
Uncertainty about A is conveyed by the union of all primary memberships into the FOU of Ã, (FOU(Ã)), i.e.
Therefore, the FOU involves all the embedded Jx characterized by the secondary membership function fx(u)/u, in this case 1/u. An FOU is bounded by two membership functions: an Upper membership function (UMF)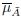 and a Lower membership function (LMF)
and a Lower membership function (LMF) 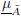 having e embedded sets (Ae).
having e embedded sets (Ae).
Some proposals based on the use of classical fuzzy sets (a.k.a Type-1 fuzzy sets) were proposed by Butnariu [3], [4], Vijay et al [24], Monroy et al [21], and Cunlin and Qiang [7]. A good survey about the topic has been provided by Larbani [16]. All those contributions were based on the idea of having imprecision handled through Type-1 fuzzy sets, so our proposal is based on the idea of having linguistic uncertainty handled through Type-2 fuzzy sets.
Indeed, Type-1 fuzzy games handle imprecision around the payoffs A using a linguistic label provided by a single expert through its perception about A. Type-2 fuzzy sets involve uncertainty provided by multiple experts about the payoffs using the same linguistic label. This way, the proposed approach attempts to handle group matrix games (seen as multiple experts) instead of single players, which is commonly presented in economics, industry, negotiation problems, etc.
Now, our proposal for involving Type-2 fuzzy uncertainty in the payoffs matrix of a games problem, is presented next (for Player I):
where x ∈ Rm, 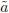 ij ∈ Rnxm. xi is defined as a Type-2 fuzzy set.
ij ∈ Rnxm. xi is defined as a Type-2 fuzzy set.
In this proposal, the payoffs matrix has been defined by multiple experts, each one having a different perception about each payoff. This leads us to think that a new framework for solving this kind of problems, is needed. To do so, three key aspects has to be analyzed before designing a method for solving this problem. The three key aspects are the following:
- An optimization principle.
-
A decomposition method for each
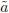 ij.
ij.
- A Type reduction strategy.
4.1 The fuzzy decision making principle
A first approach to find an appropriate way for modeling this problem is given by the Zadeh’s Extension principle (see Zadeh [2], [25], and Klir [14]), which is presented as follows
This theorem is useful to project any function (z = f (x1, x2, ... , xn), in this case) into a fuzzy set using the membership functions A1(x1), A2 (x2), ... , An(xn) of Xi. In practice, there is an important problem when applying this theorem: it leads to NP-hard implementations since we need to compute all the possible combinations of Xi, so as Xi is continuous, then we have to compute an infinite amount of z and afterwards μz.
But not all is lost, there is a way to compute the set μz using a mapping of Ai(xi) instead of Xi. This is by using α-cuts and the Representation Theorem of a fuzzy set (See Klir and Yuan [15]), which is presented in next subsection.
4.2 The extended representation theorem
This theorem simplifies the computation of any f(x) in presence of fuzzy sets (see Klir and Yuan [14]). In our case z = f(x*) leads to f(Ai)(z). The α-cut of a Type-1 fuzzy set A is:
This theorem allows to represent any fuzzy set through α-cuts instead of mapping X. This way, we can map μA(x) to compute a function of the values of f -1(μA) → x, and finally compute functions of fuzzy sets. Now, it is possible to extend the α-cut of A to the α-cut of Ã(See Figueroa [12]), which results in the following:
A graphical representation of αà is provided in Figure 2.
Thus, we can use (15) and Definition 4.1 to compose z as required by (12) to be solved by using (2), (3) and (4), so we can extend these results to a Type-2 fuzzy environment, as follows:
Note that as α-cuts are computed, we need to solve 4 times an LP model. This leads to have multiple optimal solutions inregards to α, so we need to compute a crisp measure of the behavior of f(xi)(z) to become our results operational. The most common way to defuzzify this kind of problems is by using a Type-reduction strategy. In next section, we present the most popular Type-reduction algorithm for computing the centroid (expected value) of a Type-2 fuzzy set.
4.3 Centroid of a Type-2 fuzzy set
The idea of computing the centroid of any convex measure is to obtain a measure of its expected value. In this way, IT2FSs lead to have interval-valued centroids, which means that there is an infinite amount of possible centroids embedded into the FOU of Ã. Those centroids are bounded by two boundaries yl and yu, y ∈ [yl , yu ].
Wu and Mendel in [20] and [9] defined the Enhanced Karnik-Mendel algorithms for Type-reduction (centroid) of an IT2FS. The EKM algorithm for computing yl is as follows1
- Sort xi (i = 1, 2, ...,N) in increasing order, and call the sorted xi by the same name, but now, x1 ≤ x2 ≤ ... ≤ xN. Match the weights wi with their respective xi and renumber them so that their index corresponds to the renumbered xi.
- Set k = [N/2.4] (the nearest integer to N/2.4), and compute
- Find switch point k’ (1 ≤ k ≤ N - 1) such that
- Check if k’ = k. If yes, stop, set yl = y, and call k as L. ’
- Compute s = sign(k’ - k), and
- Set y = y’, a = a’, b = b’, and k = k’. Go to step 3).
Note that this algorithm is based on a map of x, and we have obtained a map of α. To do so, we encourage the reader to use the results of Figueroa [12] and Melgarejo [6], [17], [18] to get appropriate results.
5. TOWARDS COMPUTING A SOLUTION
As the problem of computing Type-2 fuzzy LPs is very recent (See Figueroa [10]-[13]), the optimization process of a Type-2 fuzzy game becomes an interesting problem. We point out that this is not a problem of applying any other Type-1 fuzzy model using the UMF and LMF of the FOU of Ã, since it makes no sense. This is a problem of having infinite Type-1 fuzzy sets into the FOU of Ã, so the idea is to deal with its FOU instead to solve an infinite amount of fuzzy LPs.
Although we do not present an example, we present the following methodology for computing a solution of an LP fuzzy game model when having a Type-2 fuzzy payoff matrix:
- Select one of the following options:
- Optimize using the fuzzy decision making principle, if so
- Select k ∈ N α-cuts
- Compute all the α-cuts of à using Definition 4.1
- Solve the 4k LP related problems (See Figure 2) using (2), (3) and (4)
- Compose f(xi)(z) using step (iii) and equation (18)
-
Compose a new set
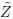 using (15)
using (15)
- Compute yl and yu using [12]
- Return [yl, yu] as the interval of expected values of the game
- Optimize using interval optimization, if so
- Compute yl and yu of à using [17], [18], and [6]
- Solve the 2 LP related problems using yl and yu in (2), (3) and (4)
- Compose zl as the optimal solution of the LP coming from yl
- Compose zu as the optimal solution of the LP coming from yu
- Return [zl, zu] as the interval of optimal solutions of the game
As we can see, the computation of optimal solutions in LP problems leads to compute multiple LP problems, and therefore compute a set of possible choices that the analyst can use, given a particular perception about the payoffs matrix.
This is especially useful when having linguistic uncertainty and/or ambiguity around aij, since the game can start change using different values of aij, at different uncertainty degrees. Note that both methods can lead to different results, so the decision about which one of the two proposed ways should be selected will affects the final results.
Remark 5.1
Note that z is a function of ãij, which are perceptions about the payoffs of the game. This way, f(xi)(z) is a function of the perceptions as well, so what a fuzzy optimal solution means is an optimal decision made over a particular perception of the experts of the system. To resume, the sense of optimality is intimately related to what the experts perceives about ãij, not a single solution of the problem.
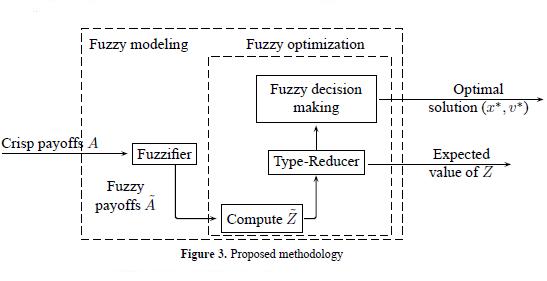
This way, our proposal can be displayed as follows
Figure 3 shows a proposal for handling Type-2 fuzzy games, where the idea is that the analyst fuzzyfies their perception of the experts by defining Ã, then compute 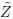 which needs to be defuzzified into two steps: Type-reduction and fuzzy decision making. Finally, the analyst can use one of the two proposed ways to find a solution of the game (centroid or interval optimization), or even other fuzzy decision making methods.
which needs to be defuzzified into two steps: Type-reduction and fuzzy decision making. Finally, the analyst can use one of the two proposed ways to find a solution of the game (centroid or interval optimization), or even other fuzzy decision making methods.
The games decision making problem increases its complexity when including linguistic uncertainty around the concept of payoffs, using words and fuzzy sets for words. The presented paper presents a methodology to solve games in these conditions.
The presented methodology (see Figure 3) is based on well-known results which needs to be experimented in simulated and/or real scenarios. The reader should notice that what we propose is based on intensive computing of multiple LPs, since the proposal is not based on reducing computations but finding a solution.
There is a need for using natural language in optimization problems, for which our proposal has been designed. Although the use concepts and perceptions could lead to ambiguous theoretical issues, the use of Type-2 fuzzy sets has opened the door to handle uncertainty around words and concepts.
Finally, experimentation and exemplification of the presented results are the next step in fuzzy modeling. The extension of our proposal to General Type-2 fuzzy sets is also a future step of our results. However, computing complexity and computing costs still are to date, a problem for extensive exemplification.
REFERENCES
- C. R. Bector and Suresh Chandra. Fuzzy Mathematical Programming and Fuzzy Matrix Games. Springer-Verlag, 2005.
- R. E. Bellman and Lofti A. Zadeh. Decision-making in a fuzzy environment. Management Science, 17(1):141-164, 1970.
- D. Butnariu. Fuzzy games a description of the concept. Fuzzy Sets and Systems, 1:181-192, 1978.
- D. Butnariu. Advances in Fuzzy Set Theory and Application, volume 1, chapter Solution concept for n-Person games. North-Holland Publishing, 1979.
- L. Campos. Fuzzy linear programming models to solve fuzzy matrix games. Fuzzy Sets and Systems, 326(1):275-289, 1989.
- Carlos Celemin and Miguel Melgarejo. A proposal to speed up the computation of the centroid of an interval Type-2 fuzzy set. Advances in Fuzzy Systems, 2013:17, 1993.
- Li Cunlin and Zhang Qiang. Nash equilibrium strategy for fuzzy non-cooperative games. Fuzzy Sets and Systems, 176(1):46-55, 2011.
- George Dantzig. Linear Programming and Extensions. Princeton University Press, 1963.
- Juan Carlos Figueroa. An iterative procedure for fuzzy linear programming problems. In 2011 AnnualMeeting of the North American Fuzzy Information Processing Society (NAFIPS), pages 1-6. IEEE, 2011.
- Juan Carlos Figueroa. A general model for linear programming with interval type-2 fuzzy technological coefficients. In 2012 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), pages 1-6. IEEE, 2012.
- Juan Carlos Figueroa and Germán Hernández. Computing optimal solutions of a linear programming problem with interval type-2 fuzzy constraints. Lecture Notes in Computer Science, 7208:567-576, 2012.
- Juan Carlos Figueroa-García. An approximation method for type reduction of an interval Type-2 fuzzy set based on α-cuts. In Proceedings of FEDCSIS 2012, 1-6. IEEE, 2012.
- Juan Carlos Figueroa-García and German Hernández. A transportation model with interval type-2 fuzzy demands and supplies. Lecture Notes in Computer Science, 7389(1):610-617, 2012.
- George J. Klir and Tina A. Folger. Fuzzy Sets, Uncertainty and Information. Prentice Hall, 1992.
- George J. Klir and Bo Yuan. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, 1995.
- Moussa Larbani. Non cooperative fuzzy games in normal form: A survey. Fuzzy Sets and Systems, 160:3184-3210, 2009.
- Miguel Melgarejo. Implementing Interval Type-2 Fuzzy processors. IEEE Computational Intelligence Magazine, 2(1):63-71, 2007.
- Miguel Alberto Melgarejo. A Fast Recursive Method to compute the Generalized Centroid of an Interval Type-2 Fuzzy Set. In Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), pages 190-194. IEEE, 2007.
- Jerry Mendel. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Prentice Hall, 1994.
- Jerry M. Mendel and Feilong Liu. Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set. IEEE Transactions on Fuzzy Systems, 15(2):309-320, 2007.
- L.Monroy, M.A. Hinojosa, A.M.Mrmol, and F.R. Fernandez. Set-valued cooperative games with fuzzy payoffs. the fuzzy assignment game. European Journal of Operational Research, 225(1):85-90, 2013.
- J.F. Nash. Non cooperative games. Annals of Mathematics, 54:286-295, 1951.
- John Von Neumann and Oskar Morgenstern. Theory of Games and Economic Behavior. Princeton University Press, 1944.
- V. Vijay, S. Chandra, and C.R. Bector. Bimatrix games with fuzzy payoffs and fuzzy goals. Fuzzy Optimization and Decision Making, 3:327-344, 2004.
- L.A. Zadeh. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets and Systems, 1:3-28, 1978.
1To save space, we only show the computation of yl. Further details can be found in [20] and [10].
Este trabajo está autorizado por una Licencia Attribution-NonCommercial-NoDerivs CC BY-NC-ND.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.



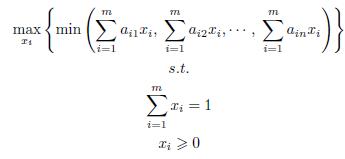
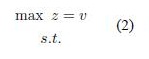
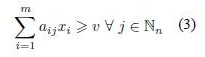
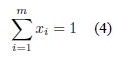
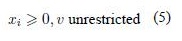
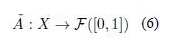
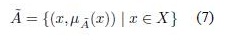
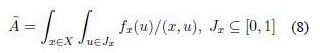
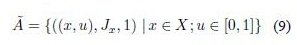
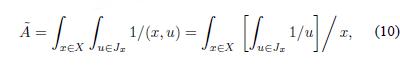
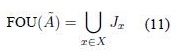
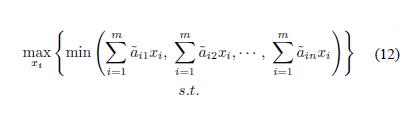
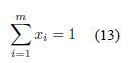
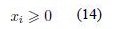
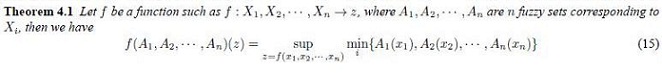
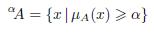
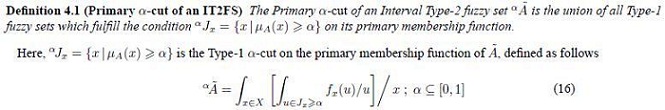
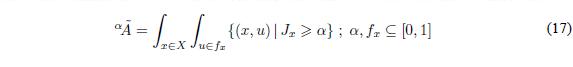
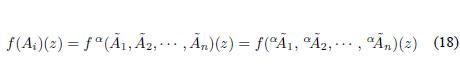
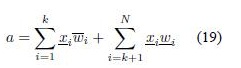
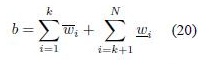
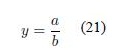
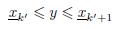
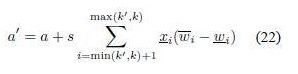
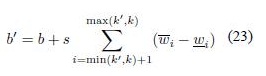
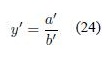




2.jpg)










