Ciencia, Investigación, Academia y Desarrollo

Ingeniería, 2006-00-00 vol:11 nro:1 pág:62-67

Cascadas conservadoras aplicadas a la predicción de tráfico multifractal

Conservative Cascades for Multifractal Traffic Prediction

Lidia Soraya Contreras Ávila

Miembro Grupo de Investigación Telecomunicaciones, GITUD, Universidad Distrital.

Gabriel Armando Ospina García

Miembro Grupo de Investigación Telecomunicaciones, GITUD, Universidad Distrital.

Marco Aurelio Alzate Monroy

Miembro Grupo de Investigación Telecomunicaciones, GITUD, Universidad Distrital.

Resumen

En este artículo proponemos un novedoso método de predicción de tráfico que se basa en el análisis estadístico de los coeficientes de un modelo wavelet multifractal del tráfico obser vado. La evaluación del predictor es computacionalmente eficiente, pues se reduce a una ecuación muy sencilla sobre los coeficientes de la transformada wavelet. Simultáneamente, como se está considerando una gran cantidad de características estadísticas de orden superior en un amplio rango de escalas de tiempo, el método logra una alta exactitud. En el artículo verificamos estas características del predictor aplicándolo sobre distintas trazas reales de tráfico.

Palabras clave: predicción de tráfico, tráfico multifractal, cascadas multiplicativas.

Abstract

In this paper we propose a novel traffic prediction method, based on the statistical analysis of the coefficients of a multifractal wavelet model. The predictor is computationally efficient because it is based on a simple equation on the coefficients of the wavelet transform. It is also highly accurate because it takes into account several higher order statistics over a wide range of time scales. We verify these characteristics using the predictor over several real traffic traces.

Keywords: traffic prediction, multifractal traffic, multiplicative cascades.

1. INTRODUCCIÓN

El tráfico en redes modernas de comunicaciones se distingue por la presencia de ráfagas, las cuales tienen un significativo impacto en el desempeño de dichas redes [1]. Esta presencia de ráfagas se puede originar de dos maneras diferentes. Por un lado, si {X(t), t≥ 0} es el número de bytes por segundo que está llegando a un enlace en el instante t, la presencia de ráfagas puede obedecer a las dependencias que haya en el proceso sobre largos períodos de tiempo. Así pues, si {X(t), t≥0} es un proceso estacionario de segundo orden, su función de autocorrelación puede ser no sumable (dependencia de rango largo, LRD), lo cual se ha explicado mediante la distribución de cola pesada de los archivos que se comparten en las redes modernas o de los tiempos de conexión de las sesiones que se establecen sobre las mismas. Por otro lado, la presencia de ráfagas también puede explicarse mediante la acción de protocolos de control de red sobre los flujos de datos, que generan dependencias a menores escalas de tiempo [2].

La primera fuente de presencia de ráfagas temporales genera fenómenos de escala sobre un amplio rango de escalas grandes de tiempo (segundos o más), y obedecen a la superposición de un gran número de procesos on/off, por lo que los modelos fractales (especialmente gaussianos, como el ruido gaussiano fraccional) son de gran aplicabilidad. La segunda fuente de presencia de ráfagas de amplitud genera fenómenos de escala sobre una amplio rango de escalas pequeñas de tiempo (milisegundos o menos) y es altamente no gaussiana, pues el alto índice de dispersión implicaría un gran número de muestras negativas en la tasa instantánea de llegadas de cualquier proceso gaussiano [3]. Así pues, se necesita un nuevo modelo para este tipo de fenómenos de escala y, en ese sentido, las cascadas conservadoras son un prometedor concepto para representar el tráfico moderno a pequeñas escalas de tiempo [4].

Con el fin de implementar mejoras en la administración de redes de comunicaciones, es importante conocer aquello que va a ocurrir en el próximo instante de tiempo, y esto es posible aplicando un algoritmo de predicción a los datos históricos de la señal. Conociendo esta información futura, pueden llevarse a cabo procedimientos más elaborados, tales como medición de recursos disponibles, estimación de tráfico cruzado, técnicas de control de acceso, de control de congestión, etc.

El Modelo Wavelet Multifractal [3] es un importante modelo de tráfico ya que captura las principales características estadísticas del tráfico en redes de comunicaciones, con gran eficiencia computacional. Sin embargo, y a pesar que desde 1996 se ha propuesto explotar la predecibilidad del tráfico [5], son pocos los algoritmos desarrollados para predecir muestras futuras de trazas tráfico reales, pues casi siempre se buscan sólo aproximaciones en baja frecuencia (promedios en largas ventanas de tiempo para reducir la variabilidad) [6][7]. Nosotros consideramos la traza observada del tráfico como una serie de tiempo y explotamos su multifractalidad para predecir muestras futuras de la serie en múltiples escalas de tiempo, con lo que capturamos la alta variabilidad que tiene un gran impacto en el desempeño de la red [2].

En la siguiente sección se establece un marco de referencia en el que se definen las cascadas multiplicativas y los procesos multifractales, y se muestra el análisis de una traza real de tráfico. En la sección 3 se describe el algoritmo de predicción propuesto. La sección 4 muestra resultados numéricos que permiten observar las bondades del predictor. Finalmente se proponen algunas conclusiones acerca de la utilidad del método de predicción.

2. ASPECTOS TEÓRICOS

Una cascada es un proceso que divide un conjunto dado en subconjuntos cada vez más y más pequeños de acuerdo con alguna regla geométrica, preservando alguna característica de la medida del conjunto inicial. Considérese, por ejemplo, el número de bytes que llegan a un nodo de conmutación durante un intervalo I de una hora, µ(I)=N₀. Supongamos que durante la primera media hora, I(0), llegan µ(I(0))=p.N₀ bytes y durante la segunda media hora, I(1), llegaron µ(I(1))= (1-p).N₀ bytes, donde p∈(0,1), de manera que se conserva el número original de bytes en el intervalo original de una hora, I. Ahora dividamos cada subintervalo de media hora, I(0) e I(1), en dos subintervalos de un cuarto de hora cada uno, [I(0,0), I(0,1)] y [I(1,0), I(1,1)], y asignemos la misma fracción de bytes a cada subintervalo: µ(I(0,0)) = p².N₀, µ(I(0,1)) = (1-p).N₀, µ(I(1,0)) = p.(1-p).N₀, µ(I(1,1))=(1-p)².N₀. Iterando este proceso, en la etapa l encontraremos que el número de bytes que llegaron en el intervalo I(j₁,j₂,...,j_l) es µ(j₁,j₂,...,j_l)=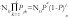

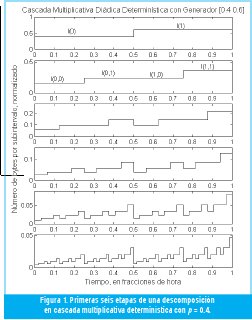
donde j_k∈{0,1}, p₀=p, p₁=(1-p), n es el número de ceros que hay en la secuencia (j₁, j₂, ..., j_l), y la longitud del intervalo es 2^-l horas. Así hemos construido una cascada determinística que preserva el número total de bytes que llegan durante la hora observada, repartiéndolos en subintervalos diádicos. La figura 1 muestra el proceso para p=2/5, normalizando las medidas con respecto a N₀. Cada barra representa el número (normalizado) de bytes que llegaron en el intervalo correspondiente (dos intervalos de media hora en la gráfica superior hasta 64 intervalos de 56.25 segundos en la gráfica inferior). Es evidente la autosemejanza estricta del objeto generado, pues cada mitad de cada figura es una copia exacta de la figura anterior, rescalizada en tiempo (por 1/2) y en amplitud (por p ó 1-p, dependiendo si es la mitad derecha o la mitad izquierda). Si en cada etapa l la medida del intervalo de una hora es µ_l(I), en el límite del proceso se obtiene la medida binomial µ∞(I), la cual es una medida de probabilidad singular y multifractal para cualquier p≠1/2 [8].

Por supuesto, la anterior descomposición forma una cascada determinística y, como tal, no resulta de interés para modelar el tráfico de una red. En la l-ésima etapa de una cascada aleatoria, una fracción W(j₁,j₂,...,j_l-1,0) de la medida del intervalo I(j₁,...,j_l-1) se le asigna a la primera mitad de dicho intervalo, I(j₁,...,j_l-1,0), y otra fracción W(j₁,j₂,...,j_l-1,1) se asigna a la segunda mitad, I(j₁,...,j_l-1,1), donde las W(.) son variables aleatorias no negativas, independientes e idénticamente distribuidas, con valor medio 0.5. Nótese que, en este caso, la cascada sólo conserva el valor promedio de la medida original, N₀. Para modelamiento de tráfico en redes, es necesario que la cascada preserve la medida original, como lo hace la cascada determinística, pero que ofrezca flexibilidad para ajustar las estadísticas de la cascada a las estadísticas observadas en trazas reales, como lo hace la cascada aleatoria. Con ese propósito se define la cascada conservadora, que preserva la medida y ofrece una alta flexibilidad estadística, haciendo W(j₁, j₂,...,j_l-1,1)= 1 - W(j₁, j₂,...,j_l-1,0), como en el cómputo de una medida binomial [9].

Al tratar de representar funciones temporales con características complejas (como la medida de una cascada conservadora) mediante una expansión en series de potencias, estas presentan potencias no enteras para una o varias diferencias de tiempo, es decir:

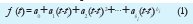
A estas potencias no enteras se les llama singularidades h_i de la función y se presentan para tiempos t_i particulares o instantes de singularidad.

Si en la función se presenta un valor único de singularidad hi=H para todos los puntos singulares t_i, éste representa el grado de irregularidad en todas las escalas de tiempo, y es llamado Parámetro de Hurst. A este tipo de procesos se les conoce como monofractales [10].

Los modelos que han surgido para la caracterización de tráfico de redes basados en movimiento browniano fraccional (fBm) y ruido gaussiano fraccional (fGn) son procesos monofractales.

En los procesos multifractales las irregularidades locales cambian de una escala a otra, de manera que hi varía con el tiempo ti siguiendo relaciones no lineales. Los instantes de singularidad ti de una traza particular se pueden encontrar fácilmente explotando las propiedades multiescala de la transformada wavelet, si utilizamos bases con un número adecuado de momentos desvanecientes [11]. Si, para cada posible valor de la singularidad hi calculamos la dimensión fractal de su soporte,

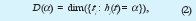
obtenemos el espectro de singularidad [8][9][10], el cual cuantifica la falta de linealidad de la traza de una manera muy compacta. Mientras en una cascada aditiva (como fbm) el espectro de singularidad corresponde al punto (H,1), donde H es el parámetro de Hurst, en una cascada multiplicativa (como la medida binomial de una cascada conservadora) el espectro de singularidad toma la forma de una función convexa [10].

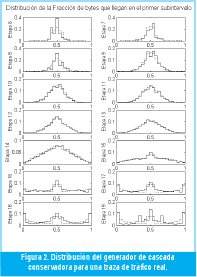
Consideremos, por ejemplo, la representación como cascada conservadora de la famosa traza BC_pAug89 [12], a la cual llegaron un millón de paquetes en un período de 3142.8 segundos. Este período de tiempo será nuestro intervalo unitario I = [0,1), compuesto aproximadamente de 2²⁰ subintervalos de 3 ms cada uno. La medida total del intervalo es µ(I) = 434 292 031 bytes, de los cuales llegaron 225 561 469 bytes en la primera mitad del intervalo, I(0) = [0, 1/2), y 208 730 562 en la segunda mitad, I(1) = [1/2, 1), de manera que en la primera etapa el generador W(0) toma el valor 0.51938, aproximadamente, y W(1)=1-W(0) = 0.48062. De la misma manera calculamos los correspondientes valores del generador durante 20 etapas de descomposición en cascada multiplicativa. La figura 2 muestra la distribución muestral de la fracción de bytes que van al primer subintervalo en cada etapa de descomposición.

3. PREDICCIÓN BASADA EN EL MODELO DE CASCADAS CONSERVADORAS

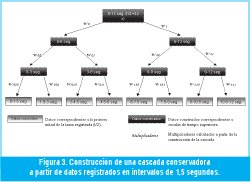
El procedimiento implementado, permite predecir el siguiente número de paquetes, con solo estimar el multiplicador W(j₁,j₂,...,j_l-1,1) correspondiente a un nivel anterior deseado. El hecho de que se lleve a cabo solo una predicción por muestra, reduce significativamente el error que se comete en el procedimiento total. Para ilustrar el procedimiento, obsérvese la figura 3; la cantidad de paquetes que llegarán entre los segundos 10.5 y 12 se puede predecir con solo estimar el multiplicador W(1,1,1), sin importar que no se conozcan W(1,1) o W(1).

Mediante la figura 4, se explicará de forma detallada el algoritmo de predicción. Con líneas continuas se muestra la cascada conservadora del instante de tiempo actual; con líneas punteadas se ilustra la que corresponde a un instante de tiempo futuro.

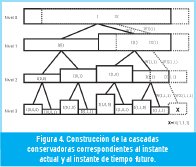
La terminología de la figura 4 se utilizará para calcular el número de paquetes que llegarán en el siguiente período del nivel 3 (X)

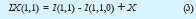
Donde

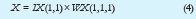
de manera que

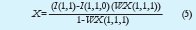
De esta forma se puede deducir el número de paquetes X, con solo calcular el multiplicador WX(1,1,1).

De forma similar, se pueden deducir expresiones en las que se presenta X en términos de multiplicadores de niveles superiores en la cascada. A continuación se muestra la expresión para hallar X a partir de WX(1,1).

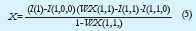
Realizando el mismo procedimiento se puede generalizar una expresión para hallar X a partir de cualquier multiplicador W de la cascada, así:

donde A es el número del nivel de la cascada en que se realizará la predicción, B es el numero del nivel al que corresponde el multiplicador que se estimará, U es la cantidad de unos (separados por comas) y C es la cantidad de ceros dentro del paréntesis (separados por comas).

Así pues, usando la taza de tráfico medida, se construye la cascada conservadora, comenzando desde el nivel a predecir (mínima escala de tiempo) y yendo hacia escalas superiores en la cascada. Este proceso se itera para obtener los multiplicadores y los valores del tráfico en el rango de escalas de interés. Posteriormente, se selecciona él último nivel de multiplicadores, que son los pertenecientes a la escala de tiempo de la predicción, y con ellos se implementa un algoritmo de predicción lineal. Este predictor lineal proporciona el valor del siguiente multiplicador (WX) de este nivel, donde WX Î (0, 1). Con este valor se resuelve la ecuación 5, para calcular el número de paquetes que llegarán en el siguiente instante de tiempo.

Obsérvese que, aunque una propiedad deseable de la transformada wavelet de un proceso multifractal es la independencia de los multiplicadores a una misma escala, existe una correlación remanente que es la que nosotros explotamos mediante el predictor lineal [13]. En efecto, la propiedad blanqueadora de la transformada wavelet depende del número de momentos desvanecientes de la wavelet madre [11] y nosotros usamos la wavelet de Haar, que tiene sólo un primer momento desvaneciente.

4. RESULTADOS NUMÉRICOS

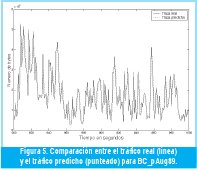
Usando el anterior procedimiento, predijimos la segunda mitad de las trazas BC_pAug89, BC_pOct89[12] y algunas películas populares en formato MPEG-4[16], todas en la escala de un segundo, con las que obtuvimos relaciones señal a ruido (SNR) entre 8 y 22 dB. La figura 5 se refiere a la primera traza, con la que obtuvimos una relación señal a ruido de 9.6 dB. Los resultados con otras trazas no se muestran por falta de espacio.

Las medidas de desempeño obtenidas con el predictor multifractal se comparan muy favorablemente con las reportadas anteriormente mediante predicción lineal usada directamente sobre la traza de tráfico [15] y mediante un estimador basado en la esperanza condicional [16].

5. CONCLUSIONES

Propusimos un método novedoso para predecir el tráfico futuro, con base en el análisis estadístico de los coeficientes de un modelo wavelet multifractal del tráfico observado. A manera de conclusiones, mencionamos algunas de las bondades del predictor propuesto:

• A través del algoritmo implementado se logró conseguir una estimación de tráfico futuro que se ajusta con alta precisión a la señal real, de acuerdo con las mediciones de relación señal a ruido.


• Una predicción capaz de seguir la traza de tráfico con sus complejas características de variabilidad representa un avance importante con respecto a aquellos predictores que usan la media muestral en el pasado reciente como predicción del tráfico futuro, pues la variabilidad tiene efectos dramáticos en el desempeño de la red [2].


• Es importante destacar que el algoritmo impone una muy reducida carga computacional, lo cual sugiere su uso en aplicaciones de tiempo real. Dada la naturaleza multiescala del predictor, estas aplicaciones pueden ir desde el ajuste de tasas de transmisión en las fuentes, hasta la admisión de flujos en los puntos de acceso, pasando por la administración de recursos en los nodos.

6. REFERENCIAS BIBLIOGRÁFICAS

[1] M. ALZATE. Introducción al Tráfico Autosimilar en redes de comunicaciones. Revista Ingeniería, Universidad Distrital, Vol. 6, N. 2, 2001.

[2] M. ALZATE. Modelos de Tráfico en Análisis y Control de Redes de Comunicaciones. Revista INGENIERIA, Universidad Distrital, Vol. 9, No. 1, 2004

[3] R. RIEDI, M.CROUSE, V.RIBEIRO and R. BARNIUK. A Multifractal Wavelet Model with Application to Network Traffic. Transactions on Information Theory, Vol. 45, No. 3, April 1999.

[4] V.RIBEIRO, R.RIEDI, R.BARANIUK. Wavelets And Multifractals For Network Traffic Modeling And Inference. Department of Electrical and Computer Engineering, Rice University, 2001

[5] G. GRIPENBERG and I. NORROS, On the prediction of fractional Brownian motion. Journal of Applied Probability, vol. 33, pp. 400-410, 1996.

[6] T. TUAN and K. PARK. Congestion control for self-similar network traffic. In «Self-similar network traffic and performance evaluation», edited by K. Park and W. Willinger, John-Wiley and sons, 2000.

[7] G. HE, Y. GAO J. HOU and K. PARK. A case for exploiting self-similarity of Internet traffic in TCP Congestion Control. Technical report, Department of Electrical Engineering, The Ohio State University, 2002

[8] R.RIEDI. Multifractal processes. Journal on Stochastic Processes and Applications, preprint, 1999.

[9] P. CHAINAIS, R RIEDI, and P.ABRY. On non-scale-invariant infinitely divisible cascades. IEEE Transactions on Information Theory, Vol. 51, No. 3, pp. 1063-1083, 2005.

[10] L. AMARAL. A Brief Overview of Multifractal Time Series. PhysioNet Research, http://www.physionet.org/tutorials/ multifractal

[11] M. ALZATE. Uso de la Transformada Wavelet en el Estudio de Tráfico Fractal. Revista Ingeniería, Universidad Distrital, Vol. 7, N. 1, 2002

[12] Lawrence Berkley National Laboratory, The Internet Traffic Archive, http:// ita.ee.lbl.gov/html/contrib/BC.html, April 29, 2000.

[13] TEWFIK and M. KIM. Correlation structure of the discrete wavelet coefficients of fractional brownian motion. IEEE Trans. Info. Theory, 38:904-909, 1992.

[14] J. VEGA. Aplicación del efecto de memoria a largo plazo en control de congestión en redes modernas de comunicaciones. Universidad Distrital, Tesis de Maestría en Teleinformática, 2003.

[15] M. ALZATE y J. VEGA. Predecibilidad del Tráfico en Redes Modernas de Comunicaciones. Revista Ingeniería, Universidad Distrital, Vol. 7, No. 2, 2002.

[16] Video Traces Research Group, Arizona State University, http:/ /trace.eas.asu.edu/ TRACE/ pics/FrameTrace/mp4/

Lidia Soraya Contreras Ávila
Es Ingeniera Electrónica de la Universidad Distrital (2005). Desarrolló su trabajo de grado en análisis, síntesis y predicción de tráfico fractal y multifractal, participando en el Grupo de Investigación en Telecomunicaciones, GITUD.

Gabriel Armando Ospina García
Obtuvo el título de Ingeniero Electrónico de la Universidad Distrital en 2005, donde desarrolló su trabajo de grado dentro del Grupo de Investigación en Telecomunicaciones, GITUD.

Marco Aurelio Alzate Monroy
Es ingeniero electrónico de la Universidad Distrital (1989) y Máster en Ingeniería Eléctrica de la Universidad de los Andes (1991). Actualmente adelanta su doctorado en la Universidad de los Andes en colaboración con la Universidad del Sur de la Florida y la Universidad de Maryland. Es profesor de la Facultad de Ingeniería de la Universidad Distrital, donde participa en el grupo de investigación en telecomunicaciones, malzate@gemail.com / malzate@udistrital.edu.co