DOI:
https://doi.org/10.14483/23448393.12726Published:
2018-05-31Issue:
Vol. 23 No. 2 (2018): May - AugustSection:
Computational IntelligencePronóstico de Divisas Latinoamericanas con Modelos de Volatilidad Estática y Estocástica
Forecasting Latin-American Currency Exchange using Models with Static and Stochastic Volatility
Keywords:
Paridades, Divisas, pronóstico, Heston, Black-Scholes, Diebold-Mariano. (es).Keywords:
Parities, Forex, forecast, Heston, Black-Scholes, Diebold-Mariano. (en).Downloads
References
Zhi-Min Ling, Thao Vo, Siu-May Ho, Ying Shiau, Yeng-Kaung Peng, Yung-Tao Lin,"Real-time in-line defect disposition and yield forecasting system"US 5598341 A 28 de enero 1997."
J.J. Echavarría, D. M. Vásquez y M. Villamizar, "Impacto de las intervenciones cambiarias sobre el nivel y la volatilidad de la tasa de cambio en Colombia" Revista Borradores de Economía, vol. 561, no. 1, 2009, pp. 12-69."
J. A. Avellaneda, C. M. Ochoa y J. C. Figueroa, "Comparación entre un sistema neuro difuso auto organizado y un modelo arimax en la predicción de series económicas volátiles" Revista Universidad Distrital, vol. 17, no. 2, 2012."
G. Rodríguez, "Modeling Latin-American stock markets volatility: Varying probabilities and mean reversion in a random level shift model." Magazine Review of Development Finance, vol. 6, no. 1, 2016, pp. 26-45."
https://doi.org/10.1016/j.rdf.2015.11.002
C. I. Pati-o y J. C. Alonso, "Evaluación de pronósticos para la tasa de cambio en Colombia" Revista Universidad Icesi Colombia, Vol. 96, No. 1, 2005, pp. 13-29."
E. F. Firacative, "Aplicación del modelo CAPM para la valoración de acciones en el mercado integrado latinoamericano MIL." Tesis Maestría, Universidad Nacional, Bogotá, 2015."
E. Cartagena, "METODOLOGÍA PARA LA ESTIMACIÓN DEL DRIFT DE LA TASA DE CAMBIO (USD/COP) A TRAVÉS DE MODELOS BAYESIANOS." Revista en contexto, vol. 1, no. 7, 2017, pp. 36-45."
F. Villada, W. Mu-oz y M. Henao, "Pronóstico de las tasas de cambio. una aplicación al yen japonés mediante redes neuronales artificiales" La Revista Scientia et Technica, vol. 1, no. 30, 2006, pp. 233-238."
G. Benavides y C. Capistran, "Pronóstico de la Volatilidad del Tipo de Cambio: el Desempe-o Superior de Combinaciones Condicionales de Pronósticos de Series de Tiempo y Pronósticos Implícitos en Opciones" Revista Banco de México, vol. 1, no. 1, 2009, pp. 9-28."
A. Ortiz, F. Venegas y M. D. Bustamante, "Valuación de opciones europeas sobre amx-l, walmex-v y gmexico-b" Revista El Trimestre Económico, vol. 4, no. 324, 2014, pp. 943-988."
https://doi.org/10.20430/ete.v81i324.135
F. C. Klebaner, Introduction to Stochastic Calculus with Applications, Singapore: Imperial College Press, 2012."
S. Shreve, Stochastic Calculus for Finance II: Continuous-Time Models, New York: Springer-Verlag, 2004."
https://doi.org/10.1007/978-1-4757-4296-1
R. G. Brown, Smoothing, Forecasting and Prediction of Discrete Time Series (Dover Phoenix Editions).Dover Publications, 2004."
R. C. Merton, "Theory of Rational Option Pricing The Bell Journal of Economics and Management Science" La Revista RAND Corporation, Vol. 4, no. 1, 1973, pp. 141-183."
F. Black y M. Scholes, "The Pricing of Options and Corporate Liabilities" The Journal of Political Economy, vol. 81, No. 3, 1973, pp. 637-654."
https://doi.org/10.1086/260062
A. C. Harvey and N.G. Shephard, "Estimation and Testing of Stochastic Variance Models" Revista Suntory and Toyota International Centres for Economics and Related Disciplines, vol. 4, no. 268, 1993, pp. 232-345."
J. C. Cox, J. E. Ingersoll and S. A. Ross, "A Theory of the Term Structure of Interest Rates" Revista Econometric Society, vol. 53, no. 2, 1985, pp. 385-407."
https://doi.org/10.2307/1911242
D. Heath, R. Jarrow y A. Morton, "Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claims Valuation" Revista Econometric Society, vol. 60, no. 1, 1992, pp. 77-105."
https://doi.org/10.2307/2951677
L. Bergomi, Stochastic Volatility Modeling,New York: Chapman and Hall/CRC,2015."
S. L. Heston, "A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options" Revista The Review of Financial Studies, vol. 6, no. 2, 1993, pp. 327-343."
https://doi.org/10.1093/rfs/6.2.327
F. X. Diebold y R. S. Mariano, "Comparing Predictive Accuracy" Revista Journal of Business and Economic Statistics, vol. 13, no. 2, 1993, pp. 253-265."
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 20 de diciembre de 2017; Revisión recibida: 2 de mayo de 2018; Aceptado: 24 de mayo de 2018
Resumen
Contexto:
El mercado de divisas es conocido como el mercado más liquido en el sistema financiero. Su fuerte. Repercusión en la economía se encuentra atada a la capitalización y el impulso que este mercado proporciona a través del aumento de las inversiones y por ende de efectos macroeconómicos que se encuentra implícitos en el desarrollo de la economía, Por esta razón, es relevante estudiar modelos de predicción del comportamiento de las principales divisas latinas.
Método:
Se plantean dos modelos para el pronóstico y la identificación de factores implícitos en los comportamientos de estas monedas. El primer modelo planteado corresponde al de Black-Scholes, el cual permite obtener el precio futuro de la divisa basándose en procesos de precio integrando, un proceso Wiener y se reconoce una volatilidad estática. El segundo modelo es Heston, el cual describe la evolución de la volatilidad de un activo subyacente y asume una volatilidad estocástica. En la presente investigación.
Resultados:
Luego de la aplicación de las dos metodologías que se propusieron se evalúa la eficiencia de los dos modelos por medio del Test de Diebold-Mariano, con el fin de identificar el modelo de pronóstico que mejor se adapta al comportamiento real de las paridades.
Conclusiones:
En resultado de la investigación se identifica que modelo de Heston brinda un mejor ajuste al pronóstico, asumiendo volatilidad aleatoria en el corto plazo para cada una de las divisas, mientras que al largo plazo presenta mayor ajuste el modelo Black-Scholes, se evidencia que cuanto mayor sea el tiempo de pronóstico, mayor incertidumbre se presentara y mayor error de pronóstico.
Palabras clave:
Black-Scholes, Diebold-Mariano, divisas, Heston, paridades, pronóstico, Idioma: Español.Abstract
Context:
The currency market is known as the most liquid market in the financial system. Its strong repercussion in the economy is tied to the capitalization and the impulse that this market offers through the increase of investments and therefore of macroeconomic effects that is found in the development of the economy, For these reasons, it is relevant to study models that predict the behavior of the main Latin currencies.
Method:
Two models are proposed for the prognosis and the identification of factors implicit in the behavior of these currencies. The first proposed model corresponds to the Black-Scholes, which allows obtaining the future price of the currency based on integrating price processes, a Wiener process and a static volatility is recognized. The second model is Heston, which describes the evolution of the volatility of an underlying asset and assumes a stochastic volatility.
Results:
After the application of the proposed mmodels, their efficiency are evaluated by means of the Diebold- Mariano Test, in order to identify the forecast model that best adapts models, their efficiency areto the real behavior of the parities.
Conclusions:
It is identified that the Heston model offers a better fit to the forecast, assuming random volatility in the short term for each of the currencies, while the long term presents the largest adjustment of the Black
& Scholes model, It is evident that the longer the forecast time, the greater the uncertainty and the greater the prediction error.
Keywords:
Black-Scholes, Diebold-Mariano, currencies, Heston, Parities, forecast, Language: Spanish.1. Introducción
La predicción de entornos dinámicos ha tomado relevancia a través de los años y con la aleatoriedad de sistemas cambiarios relativamente flexibles [1], los cuales han incrementado el inclinado interés en la predicción de estos entornos. Un ejemplo claro de esto, es el mercado de divisas, el cual es uno de los activos financieros más transados y volátiles a nivel mundial. Las divisas corresponden a un mercado de tipo flotación libre, es decir, responde a estímulos como: flujos de capital, importaciones y exportaciones, inflación, entre otros. Concerniente a esto, los bancos centrales se convierten en uno de los agentes del mercado financiero interesados en predecir futuras fluctuaciones, importantes para la toma de decisiones en políticas macroeconómicas.
En correspondencia a lo anterior, América Latina constituye una de las zonas con mayor volatilidad e impacto en sus tasas de cambio, por concernir a una economía emergente y por sus fuertes lazos de comercio internacional con países desarrollados especialmente con Estados Unidos, es por ello, que la presente investigación se centra en desarrollo el pronóstico de divisas latinoamericanas, frente al dólar, de los países de Colombia, México, Brasil, Argentina, Perú y Chile, en el periodo de 2014-2017 con un horizonte de tiempo de uno y veintiún días.
La investigación sobre pronóstico en estas divisas, se desarrollan mediante procesos de difusión del modelo Black-Scholes, que asume volatilidad constante y el modelo de Heston, que asume volatilidad estocástica estos modelos permiten explicar el pronóstico de las divisas, teniendo en cuenta el factor de la volatilidad, finalmente, estos son evaluados por medio de criterios de selección de indicadores estadísticos como el RSME, Promedio de Errores al Cuadrado, y el test de Diebold-Mariano, teniendo en cuenta criterios de predicción de modelos lineales aplicados generalmente en las predicciones desarrolladas por bancas centrales
2. Antecedentes
Derivado de la alta volatilidad que presenta el mercado de divisas y la necesidad de explicar su comportamiento, se han realizado diferentes investigaciones, en el contexto latinoamericano, que permiten evidenciar la importancia y del estudio y evaluación de estos activos financieros, por lo que se convierten en el punto de partida para el desarrollo de la presente investigación.
En el contexto colombiano, [2] presenta la evaluación del impacto de las intervenciones cambiarias sobre el nivel y la volatilidad de la tasa de cambio en Colombia sobre las compras de divisas durante el período 20002008. En este lapso de tiempo, se compran US 18.000 millones con cambios significativos de intensidad en ciertos años que devaluó la tasa de cambio y redujo su volatilidad. Este trabajo utiliza metodologías que permiten evaluar la estabilidad de los parámetros de la ecuación de media y de volatilidad para el modelo E-GARCH en forma simultánea.
Es importante tener en cuenta que la aplicación de metodologías que permitan la caracterización de la variabilidad en los rendimientos de los mercados bursátiles son características importantes para representar el comportamiento financiero, por lo que el presente estudio [3] aplica como método que permite asignar el modelo que mejor se ajusta a la predicción de la serie, por medio de la aplicación de un modelo ARIMAX y un modelo SONFS para la serie colombiana Pacific Rubiales en una prueba de aleatoriedad, homoscedasticidad y ausencia de correlación. Esta investigación permite evidenciar la importancia que tiene la inclusión de nuevas variables que permitan la reducción desde un punto de vista más aproximado, teniendo en cuenta patrones de variabilidad dentro de la acción de Pacific Rubiales, pruebas que permitan ver las bondades de la aplicación no solo de procesos autor regresivos, sino de modelos computacionales que faciliten la sincronización de nuevas técnicas.
De otro modo, se encuentran otro tipo de aplicaciones en este caso el de un modelo RLS (Regersion lineal simple) [4], donde se identifico la volatilidad de los retornos diarios para Argentina, Brasil, Chile, México y Perú. La volatilidad en estos mercados latino es evidente, por lo cual se reemplazan los modelos de probabilidad constante por un modelo que permita registrar los cambios de probabilidad en donde se registren perdidas en sus retornos. Teniendo en cuenta la magnitud y dirección de estas variaciones que derivan el cambio en los niveles habituales de los retornos y por ende de los precios desviando la velocidad de reversión a su media. Por lo anterior, este estudio aplica bajo la perspectiva del modelo básico de RLS una variables sobre la combinación de probabilidades variable y un RLS que tuvo en cuenta la reversión a su media, permitiendo así tener en cuenta que los parámetros son variables altamente significativas que tienen especial importancia bajo la metodología de la reversión a la media como factor principal. El muestreo aleatorio se encuentra implícito en la estimación de factores temporales, es por ello que este estudio aplica no solo la variabilidad de la metodología RLS, sino, además de ello, la inclusión de modelos donde la presencia del cambio de nivel cobra vital importancia, modelos ARFIMA y GARCH en donde los efectos son de memoria larga y considera la predicción de la historia, a diferencia de los modelos RLS donde todas sus variables inciden que es mejor pronosticar en un conjunto de variabilidades.
En cuanto a la evaluación de pronóstico, [5] hacen una evaluación para la tasa de cambio en Colombia y se analiza la capacidad de predicción dentro de la muestra de cuatro modelos de tasa de cambio nominal durante el período 1984 - 2004. A través de los años, Colombia ha cambiado sus modelos económicos conocidos, pero recientemente los movimientos de la tasa de cambio no pueden ser explicados por los modelos convencionales; sin embargo, se evalúan modelos de la década de 1990 que pueden explicar los movimientos de la tasa de cambio actual para lo cual se usa el error medio al cuadrado y el coeficiente de desigualdad de Thell, estos se comparan con un camino aleatorio y la condición de paridad del poder adquisitivo, lo que arrojó como resultado en el documento que ningún modelo logra superar al camino aleatorio.
Teniendo en cuenta la afinidad y la vinculación ente las finanzas y la valoración de estas en relación con los riesgos asociados, es importante tener en cuenta [6] la repercusión económica con la que cuenta en el sector financiero y la aplicación de otras que permitan la aproximación a la valoración de los mercados, este estudio permite la asociación del mercado MILA (Mercado Integrado Latinoamericano) por medio del CAMP, teniendo en cuenta la rentabilidad que se espera del mismo y la aproximación teórica con el entorno.
El mercado financiero colombiano se ha visto afectado a través del año por la volatilidad presente en el tipo de cambio USD/COP [7], partiendo de esto, se propone una nueva metodología de pronostico planteada por la cual consiste en mejorar la predicción de la TRM por medio de la aplicación de los modelos bayesianos, la cual tiene como factor principal la información histórica presente en el comportamiento de la TRM en el mercado.
Otro estudio relacionado al pronóstico de divisas, lo realiza [8] sobre las tasas de cambio del yen japonés mediante redes neuronales artificiales, donde muestra la aplicabilidad de las redes neuronales artificiales al mercado de divisas mediante el estudio de la tasa de cambio del yen japonés con respecto al dólar americano. Según estudios, las predicciones otorgadas por un modelo estocástico lineal no son tan precisas como las que entregan las no lineales, debido al comportamiento no lineal de las tasas de cambio esto lleva a necesitar nuevos métodos de estudio basados en redes neuronales, ya que estas permiten establecer relaciones lineales y no lineales; para ello, se le da a la red neuronal dos tipo de datos, un histórico de serie de datos y los seis indicadores económicos que más afectan el comportamiento del dólar americano.
Por su parte, [9] realiza la investigación sobre el pronóstico de la volatilidad del tipo de cambio, donde hace una comparación entre combinaciones de pronósticos de volatilidad en opciones y series de tiempo comparado con series individuales y pronósticos híbridos, dando a conocer una superioridad de las combinaciones de pronósticos de la volatilidad. La aplicación es para pronósticos de volatilidad del tipo de cambio peso mexicano frente a dólar estadounidense, los resultado muestran que la combinación del pronóstico GARCH y lo pronósticos de IV del tipo de cambio son superiores, afirmando que las combinaciones de modelos son mejores que las series individuales.
Referente a la investigación que plantea [10] sobre la valuación de opciones europeas con el modelo de volatilidad de Heston, se desarrolla uno de los principales productos negociados en las bolsas de derivados en México haciendo una comparación entre la fórmula de Black-Scholes para la evaluación de opciones, teniendo en cuenta que uno de los supuestos argumentados por esta metodología no es acorde con la evolución del mercado, por ello, se genera un discrepancia entre la valoración de este en comparación con el modelo de Heston de volatilidad estocástica, donde se quiere verificar empíricamente, el parámetro de correlación controla el sesgo de la función de la densidad de Heston.
Dichas investigaciones, se convierten en insumos básicos para el desarrollo de la presente investigación referente al pronóstico de divisas latinoamericanas y permiten validar la importancia de investigar estos temas de gran impacto en el mercado financiero y real.
3. Marco teórico
Se asume que los rendimientos de las divisas manifiestan un comportamiento de distribución normal, por lo tanto, aplicándolo a la teoría de movimientos brownianos y a los procesos de difusión, se identifican que se pueden modelar los mismos asumiendo µ = 0 y σ = √(t ), puesto que se encuentran en un espacio muestra w. Por lo anterior, se evalúa el comportamiento de las divisas latinoamericanas mediante estos procesos de difusión que buscan la manera de medir los rendimientos de futuros a partir de información histórica o aportadas por las [F ],quienes proporcionan la información de los modelos, por lo que se adaptan estos procesos.
3.1. Teoría de probabilidad
En el ámbito financiero muy poco se conoce sobre las áreas de conexión que permiten entender el contexto matemático que integra las finanzas tal y cómo se conocen, en este contexto, la matemática brinda un factor fundamental integrado especialmente por la teoría de la probabilidad y de todos los procesos estocásticos, que desde el punto de vista matemático-financiero ha permitido concebir de manera más consistente lo que en la última década se ha conocido en las finanzas como su componente matemático. Teniendo en cuenta lo anterior, todos los procesos matemáticos que sobrevienen en el ámbito financiero ocurren dentro del espacio de probabilidad comprendido por eventos aleatorios, aquellos que no se pueden predecir dentro de los números reales; por lo tanto, todo aquello que ocurre en un ámbito financiero es conocido como una probabilidad ( Ω, F, P ), donde cada una de estas partes conforma el cálculo de probabilidades dentro de un posible evento aleatorio X en un valor real a partir de una función f (x) definida en Ω con un espacio de probabilidad en un intervalo [0,1]. En términos financieros la probabilidad se define como [11] “El valor fijo limite hacia el que tiende a aproximarse la frecuencia de aparición de un resultado cuando crece el número de observaciones que se realizan en situaciones similares”, lo que quiere decir que la probabilidad de los eventos financieros se encuentra directamente asociada con la recurrencia de los sucesos, permitiendo de esta forma predecir en cierta manera qué acontecimiento puede o no ocurrir dentro del rango de probabilidad definido [0,1], teniendo en cuenta la esperanza del suceso o evento E(X). De lo anterior se difiere que: teniendo un conjuntoΩ y F un s-algebra de subconjuntos de W, Donde se define una filtración [Ft ](t ≥ 0) como una familia de subconjuntos σ-algebra F [11]. En un proceso estocástico se genera una filtración dada por

Cabe destacar que un proceso estocástico X es adaptado a una filtración Ft para cada t ≥ 0, Xt , donde es una variable aleatoria Ft medible.
3.2. Modelos de proceso de difusión
Es una variable aleatoria xt, la cual no se discierne, se comporta a futuro, se conoce que cuenta con dos parámetros µ y σ , de lo cual se infiere que cada uno de estos parámetros tiene validez dentro de los procesos de difusión propuestos y generar de esta manera posibles comportamientos en un horizonte de tiempo futuro.
Movimiento browniano
La observación de un movimiento aleatorio de una partícula suspendida en un fluido produjo quizá el modelo matemático más importante en la predicción de variables aleatorias, mejor definido como el movimiento browniano. En 1826 Robert Brown observo en las partículas de polen sumergidas en un fluido (líquido o gas) un movimiento aleatorio producido por los choques contra moléculas de dicho fluido; desde entonces cautivó la atención de sin fin de científicos hasta que, posteriormente, Bachelier (en 1900) introduce el movimiento browniano (MB) para modelar las fluctuaciones de la bolsa parisina. El MB o proceso de Wiener en (Ω, F, P) es un proceso aleatorio, definido [14]:

Donde se infiere que:
-
Sus trayectorias son continuas, sus incrementos son independientes. Si 0 ≤ t1 ≤ .... ≤ tn entonces [12]
-
Son variables independientes.
-
Wt = 0 , Wt −Ws representan una variables gaussiana con media cero y varianza t − s, es decir [12]
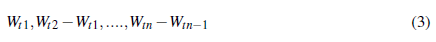

Donde se debe tener en cuenta que X se comporta de manera normal cuando: (X ∼ N(µ , σ 2)), hay una distribución de probabilidad comprendida por [12]

Para tener en cuenta:
Movimiento browniano, proceso de trayectoria continua que se encuentra definido por (Ω, F, P), Donde:
-
B 0 = 0.
-
Bt − Bs independiente a Fs y distribuido normalmente [0,1]
El movimiento browniano es un proceso gaussiano, ya que cuenta con σ 2 = 1, se dice que (Wt ) es un MB estándar; sin embargo, si lo anterior no se cumple se puede realizar un cambio de variable 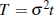 o al considerar un nuevo espacio que se encuentra definido por
o al considerar un nuevo espacio que se encuentra definido por 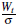 .
.
De lo anterior se define que Wt ∼ N(0, t ). Donde se asegura que los movimientos dados por los incrementos en el precio son estacionarios.
El MB, teniendo en cuenta las trayectorias continuas, quiere decir, que siempre existe una versión continua que defina MB (Wt ), lo que quiere decir que la normalidad, los incrementos dados en los precios son continuos.
Un movimiento browniano (Wt ) cumple :
-
Covarianza γ (t , s) = cov(Wt ,Ws) = mint , s.
-
Variación cuadrática en las trayectorias sobre [0, T ] es t P − c.s.
-
Variación en las trayectorias sobre [0, T ] es t P − c.s.
Movimiento Geométrico Browniano
Un movimiento browniano Wt definido por [12]:

Donde se deduce que el proceso definido por Yt es un movimiento geométrico browniano, el cual es obtenido a partir de una transformación exponencial del movimiento browniano con derivada, el cual se encuentra definido como [12]

Donde se parte para determinar un t fijo, la va Yt tienen una distribución log-normal con [12]
-
Media µt.
-
varianza σ 2t .
-
es decir: In (Yt ) ∼ N(µt , σ 2t ).
El movimiento geométrico browniano (Yt ) se define [12]:

-
Donde Y0 puede tomar valores de cualquier variable aleatoria
Este movimiento representa la tendencia y la variabilidad de los precios de los instrumentos de forma exponencial, su aplicación a través del promedio de los rendimientos y la forma en la que se implementa el proceso de difusión, permiten obtener buenos resultados de forma sencilla.
Black-Scholes
Uno de los principales modelos que tiene su mayor utilidad para simular y modelar el comportamiento de activos financieros es el modelo de Black-Scholes, ya que este incluye lµ , σ dentro de sus parámetros y, además de ello, utiliza el método de difusión del movimiento browniano, de esta manera, a través de (6), se genera el modelo de Black-Scholes.
Basado en el movimiento geométrico browniano, [15] implementaron uno de los primeros modelos para explicar los cambios en los rendimientos de los instrumentos financieros, este modelo consta de una ecuación que permite determinar el precio de uno o más activos financieros.
El modelo tiene un continuo de ciclos comprendidos en t∈ [0, T ] y consta de dos activos [15].
-
B = (Bt )t ε [0,T ] que evolución determinítica según:
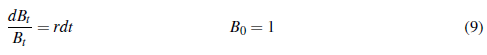
Donde r es la tasa de interés presente en cada magnitud de tiempo. B representara´ el bono final.
Dado los anteriores conceptos que permiten definir y conceptualizar todos los acontecimientos aleatorios que suceden dentro del campo probabilístico y financiero, se presenta el modelo Heston, el cual obtiene las características de las probabilidades neutrales al riesgo, a partir de las cuales se obtiene la formula Black-Scholes (1972) para evaluar opciones o bajo metodologías de pronóstico.
Fisher Black y Myron Scholes proponen un modelo de valoración de opciones que permite, a través de una ecuación diferencial estocástica, calcular el precio de un activo. Uno de sus parámetros a tener en cuenta es la volatilidad del precio de un activo y su tasa libre de riesgo, la volatilidad en este modelo es considerada constante, por lo tanto, al hacerla variable podía extender de manera natural a un modelo más complejo. El modelo de Heston describe el cambio en el precio de un activo, asumiendo que la volatilidad es variable y estocástica.
En el modelo de Black-Scholes asume una variación en el precio de un activo (St) en un periodo de tiempo (dt) que será igual al precio en un instante de tiempo (t) por su tasa de crecimiento/decrecimiento (r), más el cambio generado por la volatilidad, el cual se modela por medio de una constante 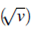 multiplicado por el crecimiento de un movimiento geométrico browniano (W1) evidenciado en la ecuación (10) que se puede encontrar en [16].
multiplicado por el crecimiento de un movimiento geométrico browniano (W1) evidenciado en la ecuación (10) que se puede encontrar en [16].

Teniendo en cuenta un modelo de volatilidad estocástica en donde se agrega una ecuación extra a la actual para evidenciar la correlación existente entre dos movimientos brownianos que posee un sistema en concreto, el modelo de Heston se representa de la siguiente manera:


Donde:
-
Para una tasa de cambio (St ), la cual representa el precio de una divisa en términos de otra.
-
W1 y W2 son movimientos brownianos con correlación,, de lo cual se entiende que cuando uno de los procesos manifiesta un incremento el otro lo hará de la misma forma o, por el contrario, si uno se manifiesta decreciente el otro lo tendrá
El modelo de Black-Scholes cuenta con ciertos supuestos: (a) el activo constituye una acción que no genera dividendos. (b) el precio del activo es dirigido por un movimiento geométrico browniano, es decir, el precio tiene un comportamiento log-normal y los rendimientos del mismo son de comportamiento común; (c) u principal supuesto se define en que la volatilidad del precio del activo se mantiene constante a través del tiempo, es decir, que es constante; (d) el mercado es líquido y divisible; es decir, podemos vender o comprar el activo en cualquier fracción de unidad.
Como se evidencio´ anteriormente, para obtener el proceso de Black-Scholes se considera un movimiento browniano (Wt )t ε [0,t ] definido sobre un espacio fijo muestra (Ω, F, FtW ℙ). Donde el cambio del precio del activo St al tiempo t , es determinado por el movimiento browniano [12].

Donde
-
µ ∈ ℝ: rendimiento medio esperado
-
σ > 0 : volatilidad instantánea por cada unidad de tiempo.
-
dWt: modela las fluctuaciones propias del mercado del subyacente y del MB
Por último, cabe destacar que el modelo de Black-Scholes asume dentro de su implementación una volatilidad constante, es decir, que para este modelo la volatilidad es estacionaria, por lo cual es importante la aplicación de un método que implemente una volatilidad estocástica en el tiempo.
Modelo de equilibrio general de CIR
Dado que se presume que el comportamiento de las divisas latinoamericanas tienen una alta volatilidad, se hace necesaria la implementación de un modelo más robusto que describa el comportamiento de los rendimientos en el futuro; por lo cual, al asumir que una divisa tiene una volatilidad alta se define que habría que modelarla, y dentro de los procesos de difusión el modelo de Heston permite asumir una volatilidad cambiante utilizando como herramienta un modelo de media de reversión que no permite tasas negativas, también conocido como el modelo de equilibrio de CIR (Cox, Ingresoll, Ross).
El modelo de CIR [17] puede definirse como un proceso finito de números que integra procesos de aleatoriedad constantes a escala, por lo que un solo activo puede asignarse a un número finito de agentes con preferencias idénticas y que logarítmicamente se puedan seleccionar como agentes potenciales de inversión [17], por lo que el mercado tiene definición desde el momento descrito donde se invierten los recursos, el consumo tiene un nivel de solvencia por lo cual los individuos descritos invierten en activos, y el resto de su riqueza la prestan o se endeudan en un mercado ha contado con un tipo de interés de equilibrio.
Los activos siguen un comportamiento de difusión multivariante, el cual está definido por un proceso markoviano representado en un conjunto de valores de cada una las variables, las cuales determinan la situación de la economía en el momento. Cabe resaltar que en una situación de equilibrio, todo capital que se invierte en los procesos físicos con aleatoriedad y se determina el tipo de interés con discriminación hacia el riesgo se define mediante la metodología del modelo CIR, el cual obtiene un proceso de difusión para el tipo de interés en función [18]:
Donde Wt es un proceso de Wiener (modela el factor de riesgo de mercado al azar) y κ , rt y σ son los parámetros. El parámetro κ corresponde a la velocidad de ajuste, θ para la media y σ la volatilidad. La tendencia del modelo descrita por, k(θ − rt ) es exactamente la misma que se encuentra en el modelo de Vasicek. Donde se asegura la reversión a la medida de la tasa de interés hacia el valor a largo plazo θ , donde σ mide la variación de la tasa de interés alrededor de la media.
La desviación estándar del factor, / evita la posibilidad de tasas de interés negativas para todos los valores positivos de k un y µ . Una tasa de interés de cero también esta´ impedido si la condición dada 2ab≥σ 2.
En general, cuando la tasa (
rt
) es cercana a cero la desviación estándar 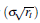 también se vuelve muy pequen˜ a, que amortigua el efecto de choque al azar del mercado. En consecuencia, cuando la tasa se acerca a cero, su evolución se encuentra en el factor de derivación que impulsa la tasa hacia el alza (hacia el equilibrio); este proceso se encuentra definido dentro de la suma de cuadrados aplicado en el proceso de Ornstein-Uhlenbeck. El modelo CIR representa un proceso ergódico, y posee una distribución estacionaria, el mismo que se ve aplicado dentro del modelo de Heston para modelar la Volatilidad estocástica [19].
también se vuelve muy pequen˜ a, que amortigua el efecto de choque al azar del mercado. En consecuencia, cuando la tasa se acerca a cero, su evolución se encuentra en el factor de derivación que impulsa la tasa hacia el alza (hacia el equilibrio); este proceso se encuentra definido dentro de la suma de cuadrados aplicado en el proceso de Ornstein-Uhlenbeck. El modelo CIR representa un proceso ergódico, y posee una distribución estacionaria, el mismo que se ve aplicado dentro del modelo de Heston para modelar la Volatilidad estocástica [19].
-
Teniendo en cuenta los anteriores conceptos propuestos para la construcción del modelo de heston
Modelo de Volatilidad Estocástica - Heston
Modelos ARCH-GARCH
Teniendo en cuenta que el comportamiento de las series temporales en las finanzas contiene características inherentes a su naturaleza, la volatilidad representa una de las más importantes de ellas, y como consecuencia, el continuo interés por tratar de predecirla. En 1982 Engle introduce la primera aproximación a los modelos autor regresivos condicionales heterosedasticos ARCH, el cual define los procesos estocásticos como una sucesión ordenada de variables cuya distribución se encuentra definida invariantes antes calores dispersos. En general la este modelo se encuentra atado a que el supuesto más importante se encuentre dado por considerar que la información pasada de una variable observada y su volatilidad.
Se describe como:

Donde este a su vez representa un proceso de ruido banco, el cual se encuentra conformado por variables estacionarias no correlacionadas con características muéstrales como media cero y varianza marginal constante. Un proceso estacionario que sigue un proceso ARCH garantiza que la varianza es positiva y que para que dicho proceso sea estacionario, es decir, que sea independiente a su historia, se debe representar como σ(t )2 Los modelos ARCH consiguen describir el comportamiento de la varianza condicionada y por ende describen los procesos de volatilidad presente en el comportamiento de las series temporales.
En 1986 Bollerslev desarrolló una ampliación de los modelos ARCH, esta adaptación consiste en introducir retrasos r de la varianza condicionada a la cual hacen referencia este tipo de modelos, se entiende entonces que los modelos GARCH actúan bajo el supuesto de normalidad con media 0 y varianza 1. Este modelo permite garantizar que la varianza sea positiva y, además de ello, que esta se encuentre condicionada al tiempo garantizando momentos de orden superior. En la aplicación del modelo de volatilidad estocástica Heston en esta investigación se aplicó el modelo ARCH-GARCH para la modelación y obtención de la volatilidad presente en las series temporales de las divisas latinoamericanas a estudiar.
Modelo Heston
Propuesto por Steven Heston [20], este modelo describe la evolución de la volatilidad de un activo subyacente donde se asume una volatilidad estocástica, es decir que la variación del activo no es persistente ni determinıstica, pues representa un proceso netamente aleatorio. La importancia de este modelo se sitúa en que es uno de los modelos más robustos en el ´ámbito financiero, ya que integra procesos de precios y un proceso para la inclusión de la volatilidad, bajo el supuesto de que su comportamiento no tiene tendencia negativa y presenta reversión a la media.
El modelo de Heston fue uno de los primeros en introducir al mercado la explicación del fenómeno de la curva sonrisa, tomado como característica principal en el modelo es la presentación de una fórmula cerrada para el precio con el supuesto de correlación entre el precio del activo la volatilidad presente, a continuación, se evidencia la dinámica estocástica que conduce a la volatilidad en el modelo.
-
La dinámica estocástica que conduce a la volatilidad en el modelo de Heston supone una acción St , sigue un proceso estocástico de la forma [20] :

-
µ ∈ R: representa el retorno esperado del precio del activo subyacente.
-
( Wt )t >0: movimiento browniano sobre un espacio muestral con filtración aumentada (Ωw, F w,
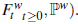
-
σt: volatilidad instantánea de la presión del activo que sigue un proceso Ornstein-Uhlenbeck, por lo cual tiene un varianza Vt sigue un proceso de tipo CIR.
-
Inclusión del proceso de cir, la varianza instantánea:
-
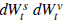 son procesos de Wiener ( paseos aleatorios) con ρ de correlación , o equivalente con dt covarianza p
son procesos de Wiener ( paseos aleatorios) con ρ de correlación , o equivalente con dt covarianza p
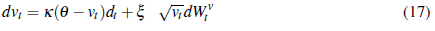
Los parámetros en cada una de las ecuaciones anteriormente representadas
-
µ es la tasa de rendimiento del activo.
-
θ es el tiempo de varianza o varianza media de los precios a largo plazo, como t tiende a infinito el valor esperado de vt tiende a θ.
-
κ es la velocidad a la que las variaciones vuelven a θ.
-
ε es la volatilidad de la volatilidad, es decir vol. de vol. y determina la varianza de vt .
3.3. Pronóstico y evaluación
Metodología Rolling
Optimizar los modelos de pronostico cobra vital importancia desde la perspectiva de la dinámica presente en los mercados financieros y en particular en el de divisas, ya que teniendo en cuenta los enfoques de la economía global, este cobra vital importancia a la hora de hablar de expansión y crecimiento económico-financiero para los países, lo que vitaliza el supuesto volatilidad contante y estocástica y, en particular, el objetivo de optimizar los modelos que permita un mayor grado de acercamiento a la realidad que viven los mercados financieros hoy por hoy. En lineamiento con ello se aplica la metodología de Rolling Forecast, el cual es un pronosticó dinámico del comportamiento de las variables, se aplica para series periódicas donde las previsiones recogen las últimas tendencias del mercado, por lo que a medida que va incrementando la serie de datos lo últimos aportados por la misma son los que generan la tendencia y demás características presentes en las series temporales, al usar una metodología Rolling para las predicciones de divisas se puede lograr un mejor desempeño de las metodologías y, por ende, un mejor pronosticó de las variables a intervalos de tiempo futuro.
Estadístico de error
Bajo criterios estadísticos, los errores de la estimación surgen en la estimación de calores a interés y se encuentran sujetas a la diferencia presente entre una muestra y otra. En relación con ello, los estadísticos de error pueden ser expresados como términos de valoración que permitan dar una conclusión acerca de si el error muestra es deseado y controlado. En este orden de ideas, se tiene en cuenta el error cuadrático medio como factor de evolución entre las dos metodologías de pronosticó propuestas, en la cual se mide el promedio de errores al cuadrado estimados bajo cada uno de los modelos. El RMSE es una función de riesgo, la cual permite calcular cuál es la máxima pérdida cuadrática producida por la aleatoriedad. Este estimador permite tener en encuentra la varianza de la estimación y el sesgo recogido en esta valoración, es por ello que se toma como una medida de selección entre modelos que puedan pronosticar mejor, desde la perspectiva de insesgamiento y de mínimo error.
Test Diebold-Mariano:
El test de Diebold y Mariano [ 21] es un test predictivo que intenta determinar de manera comparativa cual de los dos modelos de pronósticos planteados genera mejores resultados poblacionalmente. Esta comparación se hace bajo los errores de los modelos como se expuso anteriormente. Fue propuesto en 1995 para las aplicaciones empíricas, donde se pronostican una o más series de tiempo de las variables de interés; a partir de lo anterior, se formula la pregunta ¿cuál de los modelos pronostica mejor?”, de ahí el desarrollo de esta prueba que brinda una solución a este interrogante. En conclusión dependiendo del grado de correlación serial entre los errores de pronostico y el tamaño de la muestra T se seleccionara´ el mejor pronostico de adaptación. Para la obtención de este (Diebold y Mariano, 1995):


Para saber si un modelo es mejor que otro se realiza la siguiente hipo´ tesis nula en donde se sugiere que los dos modelos propuestos tienen igual alcance de predicción
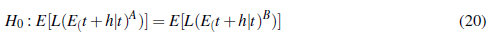
Y, por ´último, se propone la hipótesis alterna, algún modelo es mejor que el otro en alcance de predicción.
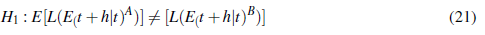
4. Metodología
Existen muchos elementos que se pueden abordar y desarrollar en la investigación sobre temas relacionados con el pronóstico de activos financieros. Esta investigación se inicia con la recolección de suficiente información de cada una de las cotizaciones de las paridades de estudio, realiza la evaluación de volatilidad variable y aplica los modelos de Black-Scholes y Heston; finalmente, los resultados también son evaluados, todo esto con el fin de generar un mejor pronosticó, muy próximo a la realidad. A continuación se presenta de manera general, la metodología realizada en esta investigación.
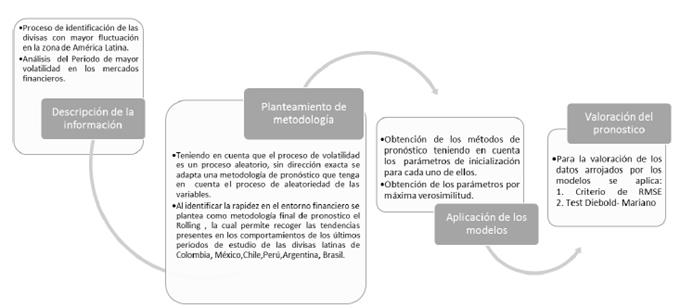
Se aplica la metodología de Black-Scholes y la metodología de Heston a uno y a veintiún días, teniendo en cuenta periodos de predicción a un corto y mediano-largo plazo, la estimación de parámetros se realiza a partir del histórico para el modelo de Black-Scholes, por su parte para el modelo de Heston se estima la volatilidad bajo la aplicación de modelos ARCH-GARCH y para la correlación se utiliza la estadística de descomposición propuesta por Cholesky; es importante tener en cuenta que la estimación de parámetros para cada uno de los modelos es de manera independiente. El pronosticó se realizó mediante la aplicación de la Simulación de Montecarlo bajo el pronosticó dinámico, también llamado Rolling, con horizontes de tiempo a uno y a veintiún días. Por ´ultimo la evaluación se realiza mediante análisis graficó, estadística de error y la aplicación del test de Diebold y Mariano, que permite comparar las dos metodologías a corto y a mediano plazo lo anterior permite evaluar si los supuestos clásicos que frecuentemente analizan para modelar estas variables se cumplen empíricamente en función de la precisión de los pronósticos Figura 1).
Figura 1.: Etapas Metodológicas
4.1. Descripción de la información
En la selección de las divisas aplicables para esta investigación, se tuvieron en cuenta las que representan mayor importancia en el entorno latinoamericano y, además de ello en las que se generan mayores fluctuaciones en sus cotizaciones del mercado de divisas, estas son el insumo para la obtención de los pronósticos comporta mentales en un horizonte de tiempo a uno y veintiún días .Teniendo en cuenta el insesgamiento presente en la obtención de dichos pronósticos, toma mayor relevancia la selección del método que mejor se adecué a los factores poblacionales incidentes sobre cada activo, para posteriormente evaluar las características de los pronósticos y la obtención del mejor para cada paridad.
Para la selección de la información en primera instancia se realizó un análisis del comportamiento de las variables, incluyendo todas las divisas presentes en el mercado latino. En relación con ese análisis se seleccionaron las que presentaban mayor fluctuación frente al dólar, por lo que su pronóstico es más difícil de realizar.
De lo anterior que la metodología de esta investigación tiene como punto de partida la obtención de la cotización en un periodo comprendido 19-03-2014/20-03-2017 datos diarios , de cada una de las diferentes paridades como la colombiana, mexicana, brasilera, argentina, peruana y chilena todas atadas al dólar estadounidense de las cuales se obtuvieron los rendimientos diarios de cada activo, los cuales proporcionan el insumo principal para de desarrollo de los modelos de Black-Scholes y Heston. Fuente de información Bloomberg.
4.2. Propuesta metodológica
La optimización los modelos de pronosticó tiene vital importancia desde la perspectiva de la dinámica presente en los mercados financieros y, en particular, en el de divisas, ya que teniendo en cuenta los enfoques de la economía global este tiene total validez a la hora de hablar de expansión y crecimiento económico-financiero para los países lo que vitaliza el supuesto volatilidad contante y estocástica y en particular el objetivo de optimizar los modelos que permita un mayor grado de acercamiento a la realidad que viven los mercados financieros hoy por hoy. En lineamiento con ello se aplica a la metodología de Rolling Forecast el cual es un pronóstico dinámico del comportamiento de las variables, el cual se aplica para series periódicas donde las previsiones recogen las últimas tendencias del mercado, por lo que a medida que va incrementando la serie de datos lo últimos aportados por la misma, son los que generan la tendencia y demás características presentes en las series temporales, al usar una metodología Rolling para las predicciones de divisas se puede lograr un mejor desempeño de las metodologías y, por ende, un mejor pronóstico de las variables a intervalos de tiempo futuro.
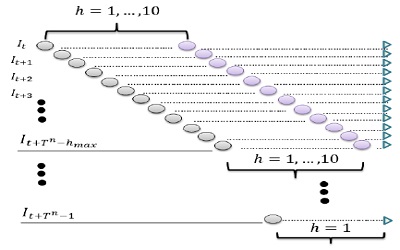
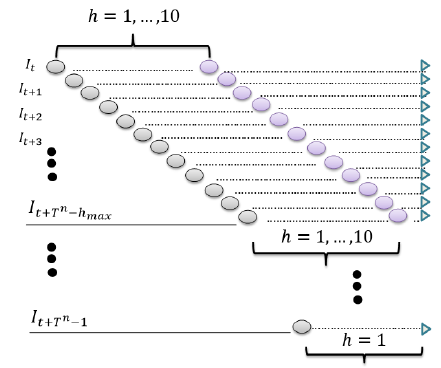
Para la aplicación y obtención de los pronósticos para cada uno de los modelos se procedió aplicar una metodología Rolling, la cual consiste en ir ingresando un dato adicional a la serie e ir pronosticando; de esta manera, de los nuevos datos ingresados a la serie tienen mayor importancia, pues tienen en cuenta la tendencia del mercado y por ende se tiene la facilidad de responder más rápidamente a los choques inherentes frente al mismo. En este caso diez pronósticos futuros por cada observación añadida a la muestra. Es decir que para estos modelos genera un pronosticó máximo de (hmax = 21), teniendo en cuenta los parámetros de estimación para la muestra anteriormente definidos. El proceso se repite con los parámetros reestimados utilizando como conjunto de información (I(t+1)), en donde la muestra inicial (It) de estimación y se adiciona la siguiente observación como se evidencia en la Figura 2. A posteriori se procede a hacer la evaluación del pronosticó.
Figura 2: Metodología para pronostico
4.2.1. Obtención de los métodos
Teniendo en cuenta la constante aplicación de los principales agentes interesados en pronosticar el comportamiento futuro de las divisas y, para este caso, las divisas latinoamericanas, se plantean las variables de entrada del modelo clásico aportado por Black-Scholes anteriormente expuesto y en relación con ello se aplica el modelo de Heston debilitando el principal supuesto de volatilidad constante que aportan los modelos clásicos lineales, esto con el fin de determinar si a través del tiempo se cumplen supuestos de adaptación de la serie teniendo en cuenta un contexto netamente determinıstico. Por lo anterior, que se tengan en cuenta los siguientes parámetros de entrada desarrollados para cada uno de los modelos dentro del lenguaje de programación aportado por el software Matlab.
-
Modelo Black-Scholes: como se identificó en la presentación del marco teórico para la obtención de este modelo se tiene en cuenta los parámetros: µ , σ , dWt
-
En otras palabras se calcula la media de los retornos, y la variación de los mismos, posteriormente se asigna a cada parámetro que compone el modelo de BS (número de simulaciones, horizonte de tiempo, media de la varianza los retornos, varianza de los retornos y precio inicial) para la aplicación de n iteraciones con pronóstico a uno y veintiún días. Luego de obtener el modelo BS se calcula su RMSE para uno de los horizontes de pronósticos que se aplicaron en el modelo.
-
Modelo Heston: para la aplicación de este modelo se tienen en cuenta los parámetros1: µ, θ , κ y ε , como se describió anteriormente.
Como se puede identificar en los parámetro que componen el modelo de Heston, aunque ninguno es igual a los expuestos en el modelo de Black-Sholes-Merton, su identificación y afinación al diferir de un solo parámetro en donde se contradice el primer supuesto del modelo de BSM de que el comportamiento de la volatilidad es estable , pues para este modelo e corresponde a la variable presente en los precios que es la volatilidad de la volatilidad, y se asume como principal supuesta que hay una volatilidad explicita en el comportamiento de los precios; por lo anterior, el proceso de obtención de los parámetros para este modelo difiera en la primera parte , pues primero se debe hacer la obtención de la medida de volatilidad en el comportamiento de las series temporales para luego aplicar e identificar los siguientes parámetros como se detalla a continuación:
-
En primera instancia teniendo en cuenta la serie de los retornos y se procede a la obtención de la serie de la volatilidad de los mismo aplicando la metodología una metodología ARCH (Tabla I)
Tabla I: Obtención volatilidad
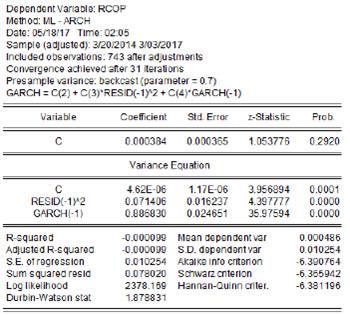
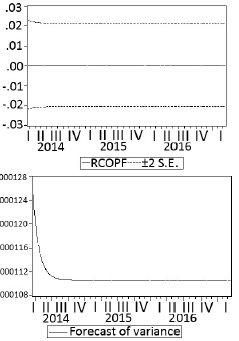
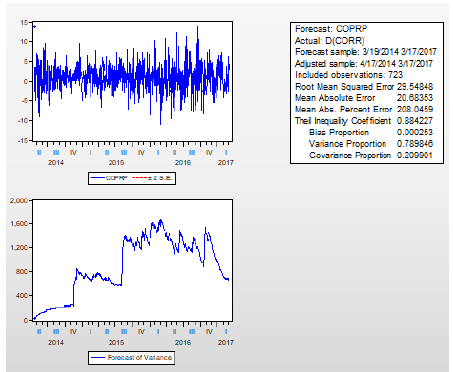
Con respecto a la Figura 3, donde se aplica el proceso ML-ARCH para la variable COP, se evidencia que el correlograma asociado a los residuos y los errores al cuadrado no representan significancia, por lo que los residuos siguen un comportamiento de normalidad y homocedasticidad, por lo cual el comportamiento de las variables no guarda correlación estadística con su historia, es decir, la variable siempre tomara´ un valor distinto sin afectar su varianza.
Figura 3.: Comportamiento volatilidad
Con el modelo anteriormente propuesto, y teniendo en cuenta las variables expuestas, se define que es viable realizar la predicción teniendo en cuenta lo intervalos de confianza en los que estarán oscilando los valores de predicción, aplicando de manera precisa la varianza de error que se ha aplicado en manera de estimación. El anterior proceso fue aplicado para las seis divisas tenidas en cuenta en esta investigación metodológica.
-
Aplicación del modelo inmerso en el modelo de Heston (equilibrio de CIR) en donde partir de la serie de la volatilidad de los retornos se estiman sus tres parámetros alpha (media de reversión), nu (media q), sigma (volatilidad de la volatilidad) y rho (correlación varianza rendimiento).
-
Por último, se aplica en totalidad el modelo de Heston teniendo los parámetros anteriormente obtenidos y asumiendo una volatilidad estocástica para cada una de las variables (media de la varianza de los retornos, numero de simulaciones, horizonte de tiempo, volatilidad estocástica, precio inicial, correlación varianza, rendimiento, media de reversión, media q, volatilidad de la volatilidad). Teniendo en cuenta que para la aplicación de este se tiene el mismo horizonte de tiempo en el pronóstico de sus iteraciones y por ultimo calcula RMSE.
A continuación se hace la aplicación de pruebas de normalidad e independencia dentro de cada una de las series para las divisas de los países de Colombia, Brasil, Chile, México, Perú y Argentina. Teniendo en cuenta supuestos de Heterosedasticidad en las series, invertibilidad y pruebas de bondad.
A continuación se hace la aplicación de pruebas de normalidad e independencia dentro de cada una de las series para las divisas de los países de Colombia, Brasil, Chile, México, Perú y Argentina. Teniendo en cuenta supuestos de Heterosedasticidad en las series, invertibilidad y pruebas de bondad.
Análisis gráfico, de la serie corta con frecuencia hacia su media y variabilidad persisten tente, lo cual indica que la serie puede ser aleatoria, por lo cual tiene sentido tener en cuenta una volatilidad aleatoria y el planteamiento de modelos que modelen la volatilidad de manera aleatoria (Figura 4).
Figura 4: Verificación de supuestos
El aspecto de la FAC y FACP corresponde a las pruebas para garantizar que la serie sea o no una seria estacionaria. En este caso se observa el decaimiento no truncado en algunas partes de cada correlograma, por lo que se puede ver una fase de identificación de perdida para proponer el modelo autor regresivo y, posteriormente, aplicar el modelo a la estimación y comprobación de volatilidad de las series (Tabla II).
Tabla II: Verificación de supuestos
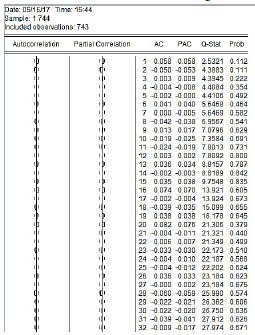
Validación de los modelos de estimación que describen el comportamiento de la serie donde se evidencia el análisis de residuos, coeficientes y la bondad de ajuste presente en las series temporales; de esta manera, se comprueba que los residuos de los modelos de estimación tienen comportamientos de compatibilidad con ruido blanco, por lo cual tiene total validez el pronóstico de las series teniendo en cuenta independencia en las mismas (Tabla III).
Tabla III: Verificación de supuestos
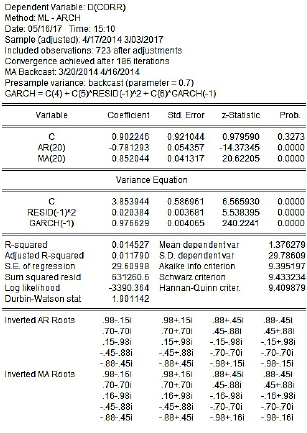
Teniendo en cuenta cada una de las series, se aplica el test de heterosedasticidad para confirmar que las perturbaciones presentes en las series temporales no sean constantes a lo largo del tiempo, como se evidencia en la Tabla IV. En este caso se confirma el supuesto y eso permute considerar como un modelo de predicción heterosedástico de varianza del error condicional de las variables explicativas variable a lo largo del tiempo.
Tabla IV: Verificación de supuestos
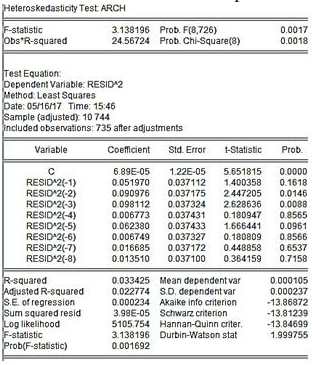
Por lo anterior se puede considerar que las pruebas de inclusión de normalidad de las series temporales se adaptaron de acuerdo con los supuestos de volatilidad aleatoria bajo el supuesto del comportamiento de cada una de las variables de descripción.
5. Resultados empíricos
Los resultado arrojados por los dos modelos de evaluación, se encuentran incluidos en el intervalo de comprendido del 19-03-2014/ 21-03 2017 para el pronosticó individual y del 19-03-2014/18-04-2017 para los dos métodos en combinación al pronosticó de veintiún días. En ambos casos, se utilizaron los datos en la misma periodicidad y se realiza la estimación de las paridades y los periodos adicionales para la divisa colombiana. Los resultados finales de los métodos de predicción son representados en las tablas según espacio de tiempo y se muestran los diferentes estadísticos de RMSE para la evaluación de los pronósticos en los dos horizontes considerados para las paridades de cada país, por último se evaluaron las dos medidas de las muestras por medio de los siguientes criterios.
Eficiencia del modelo propuesto frente a modelos clásicos de un solo factor ( Black-Scholes), a través del test de Diebold-Mariano
-
RMSE: el error cuadrático medido anteriormente y obtenido en cada uno de los modelo y en cada uno de las iteraciones evaluadas, constituye un estimado para el desempeño de los modelos.
-
Test Diebold-Mariano: se evalúan los errores a un día, determinando la diferencia del valor pronosticado con el modelo (BS-Heston) y el precio de cierre real, se tuvo en cuenta el error que da como resultado en el paso anterior se eleva al cuadrado. Por último la aplicación para el test a veintiún días varía en que se toma la serie de datos obtenida por los dos modelos (BS-Heston), la serie inicial de los precios de cierre. El error que da como resultado en el paso anterior se eleva al cuadrado
5.1. Análisis de resultados
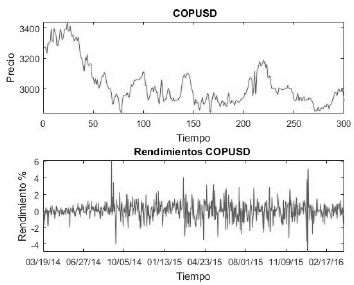
En la Figura 5, se observa el comportamiento en el periodo de tiempo de estudio de la divisa colombiana atendiendo las inconsistencias de los mercados y, además de ello, al porcentaje de retorno asociado a la paridad USD-COP.
Figura 5: Precio-Rentabilidad
Aplicando la metodología expuesta en esta investigación a un horizonte de tiempo de un día se evidencia que:
-
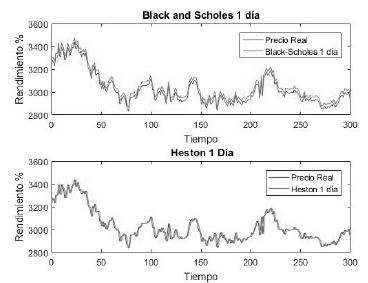
El modelo de Black-Scholes-Merton a un día se demuestra en la primera parte de la Figura 6, por lo cual se identifica el desfase entre el comportamiento del precio real y la metodología aplicada para el pronosticó, lo que quiere decir que, aunque la brecha entre este modelo y la realidad es pequeña, demuestra que existen diferencias con respecto al comportamiento en el mercado real, a diferencia de la segunda parte de la Figura 6, donde el comportamiento del precio real, en contraste con la metodología del modelo de Heston donde a simple vista no se logra identificar brecha alguna, lo que nos da una perspectiva de que el modelo que mejor se adapta a los parámetros iniciales requeridos por el activo es el modelo de Heston, se asume una volatilidad estocástica.
Figura 6: Modelos COP h=1
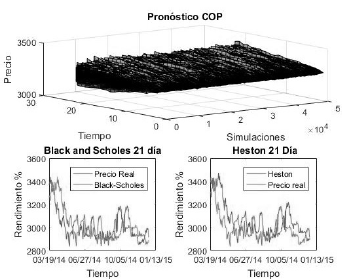
Figura 7: Precio-rentabilidad
-
Considerando el comportamiento del mercado financiero asociado se identifica en la primera parte los posibles escenarios en que puede converger el precio de la divisa colombiana durante un periodo n de tiempo bajo una metodología estocástica. Por último, se puede identificar que para la aplicación bajo una ventana de tiempo de mediano plazo (h=21) se identifica que analizar el comportamiento de las variables es mucho más complejo pues, la brecha entre el precio en que oscila la variable en su realidad con el de las dos metodologías propuestas solo se puede identificar mediante la aplicación de estadísticos de error que permitan la distinción y la valoración del mejor método, ya que a simple vista se podrá deducir que es indiferente cuál de las dos metodologías se aplique para el pronosticó a h=21 días.
-
Para las cinco variables de divisas restantes (Brasil, Chile, Argentina, México y Perú) se hizo el mismo proceso de análisis anteriormente evidenciado
5.2. Evaluación de pronóstico
Analizando el pronosticó con horizonte de tiempo a un día, se identifica que el alcance del modelo de Heston que tiene mejor predicción a un día de manera ascendente son: Perú, México, Argentina, Chile, Brasil y Colombia. Analizando el pronosticó con horizonte de tiempo a veintiún días, y teniendo en cuenta los choques inherentes que se presentan en la naturaleza de los mercados en una ventana de tiempo más amplia, el alcance de los modelos es más variable de esta forma se identifica que:
-
Para el modelo de Black-Scholes-Merton, el asumir una volatilidad constante a una condición de tiempo más amplia genera un mejor pronosticó para las divisas de México, Argentina y Colombia.
-
Para el modelo de Heston se concluye que para una ventana de tiempo de mediano plazo y teniendo en cuenta los choques de las economías expuestas es mejor asumir una volatilidad estocástica para los países de Perú´, Chile y Brasil.
Evaluación a un día con RMSE
En las previsiones a un día se aplican los modelos BS y Heston, donde el estimador mide el promedio de los errores al cuadrado, es decir, la diferencia entre el estimador y lo que se estima. De lo cual en esta primera parte se puede evidenciar el RMSE de los modelos para cada una de las divisas como se muestra en la Tabla V
-
Cabe anotar que el RMSE también es un factor de evaluación de efectividad de los modelos de predicción a un día para este caso
-
De donde para la previsión a un día se encuentra la Tabla V, donde se considera la muestra completa final del mejor modelo para un horizonte de 1. Teniendo en cuenta el RMSE se entiende además como una función de riesgo, correspondiente a la estimación del valor esperado de la pérdida del error al cuadrado o pérdida cuadrática. Por lo anterior, se quiere que el RMSE sea lo más pequeño posible. De lo anterior se concluye que: para cada uno de los modelos individuales (por paridad de divisa) el mejor modelo de estimación a corto plazo es Heston, Argentina: Heston, Perú: Heston, Chile: Heston. Por lo cual se puede evidenciar que para la evaluación de modelos de pronosticó a un día con RMSE el modelo que brinda mejor resultado teniendo en cuenta sus errores es el modelo de Heston
Tabla V: RMSE
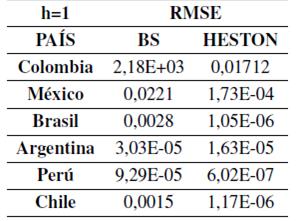
Por otro lado encontramos la evaluación del pronosticó a través test Diebold y Mariano Se basa en los errores de cada uno de los modelos teniendo en cuenta que el modelo de Heston incluye la estimación de la volatilidad por medio de un ARCH.
-
Teniendo en cuenta la información aportada en la Tabla VI, se evidencia que el P-valué para esta prueba es cero, por lo cual lo cual indica que Heston fue muy superior en términos de predicción diaria para todas las paridades de divisas frente al comportamiento predictivo que tuvo Black-Scholes por lo cual rechazó H0 y el mejor modelo de pronosticó es el aportado por Heston
Tabla VI: Test-DM
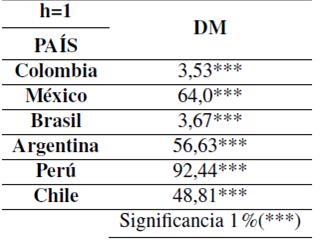
Evaluación a un día con RMSE veintiún días
En efecto el RMSE para este horizonte de tiempo tiene la misma interpretación en función de riesgo y, además, en valor esperado para los dos modelos, por lo cual para una previsión a veintiún días y teniendo en cuenta la aplicación de la volatilidad empírica del modelo de Heston se puede evidenciar en la Tabla VII se tiene que:
-
El modelo de Black-Scholes demuestra menores errores en su predicción y una función de riesgo menos alta para las divisas de Colombia y Brasil, por lo que este brinda un mejor cálculo en su predicción en un horizonte de tiempo a veintiún días.
Para el modelo de Heston se identifica que los RMSE más pequeños obtenidos por el modelo en comparación con BS y por tanto con los que obtiene un nivel de riesgo menor y una estimación más precisas se aplica en un horizonte de veintiún días para México, Argentina, Perú y Chile véase (Tabla VII).
Tabla VII.: RMSE
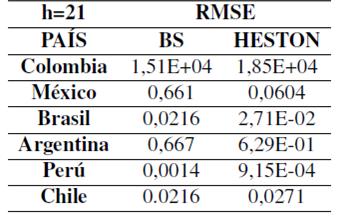
Ahora bien, teniendo en cuenta la información consignada en la Tabla VIII donde se tiene en cuenta el valor del test y con respecto a este se estima e valor del P-valué se evidencia que a partir de los estimados se entiende que:
-
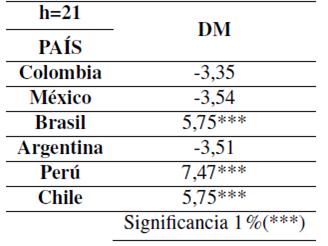
A pesar de los errores del RMSE para la divisa colombiana, mexicana, argentina se evidencia que es indiferente el pronosticar con un modelo de Black-Scholes o Heston según el P-valué arrojado por el valor del test de diferenciación, se acepta H0 para las divisas anteriormente mencionadas. De igual forma, teniendo en cuenta el valor del test, se demuestra que además de las diferencias de RMSE el modelo de Heston proporciona una mayor precisión al mediano plazo con respecto a modelo de Black-Scholes para las paridades de Brasil, Perú y Chile, teniendo en cuenta que la hipótesis nula se define bajo la perspectiva de igualdad de predicción para los dos modelos y en ese orden de ideas se rechaza la hipótesis nula y el mejor modelo de pronosticó sigue siendo el aportado por Heston, para los otros casos el mejor es el de BS.
Tabla VIII: Test-DM
6. Conclusiones
La presente investigación se ha enfocado al análisis de los patrones temporales intrínsecos asociado con sus procesos estocásticos generadores de volatilidad presentes en los mercados de divisas asociados a América Latina para seis países específicos, mediante la aplicación de metodologías que validen supuestos de volatilidad constante en estos mercados.
En la evaluación de pronósticos en Rolling para los modelos de Black-Scholes y Heston demuestra que a corto plazo el método que mejor se adapta a las estimaciones de las variables es modelo de Heston, ya que se incluye la volatilidad aleatoria y esta recoge todos los efectos presentes en el corto plazo. En el mediano plazo el modelo más preciso varía, ya que no está afectando en gran medida la volatilidad que mide las variaciones presentes en el mismo periodo de tiempo.
Por lo cual se debe tener en cuenta que para un mediano-largo plazo tiene más sentido manejar una volatilidad no condicional sino constante, para algunos países, es decir, una volatilidad incondicional, pero en el corto hay que reconocer las variaciones condicionales al tiempo.
Al modelar la volatilidad condicionada de los rendimientos de las divisas latinoamericanas, se identifica un mejor ajuste en el modelo del pronosticó de Heston para el corto plazo, por lo que se podría inferir que este modelo tiene relevancia en las decisiones de corto plazo para la totalidad de las divisas a las cuales se aplicó, de lo anterior que a un mediano plazo su efectividad no se aplique en igual proporción a todas las divisas. Al verifica con la pruebas de ARCH LM se verifico que existía dentro de los datos una estructura de auto correlación en la volatilidad, lo cual permitió reconocer que la varianza se encuentra condicionada y la volatilidad no es contante, por lo que la alternativa de Heston cobra vida dentro de la estimación a futuro de las divisas latinoamericanas.
Acknowledgements
7. Agradecimientos
En memoria del ser que toco mi vida y mi alma, Aura María Hernández quien me enseño el valor de la vida y la responsabilidad que viene inmersa en ella. A mis directores de tesis, Miller Ariza, Andrés Martínez y Gloria Bohórquez, quienes fueron orientación teórica- Práctica en el desarrollo de esta investigación.
Referencias
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










