DOI:
https://doi.org/10.14483/23448393.2696Published:
2000-11-30Issue:
Vol. 6 No. 2 (2001): July - DecemberSection:
Science, research, academia and developmentIntroducción al tráfico autosimilar en redes de comunicaciones
Keywords:
Modelos de tráfico, autosimilitud, dependencia de rango largo, distribución de cola pesada, movimiento browniano fraccional (es).Downloads
References
P. Abry and D. Veitch. Wavelet Analysis of Long-Range-Dependent Traffic. IEEE Trans. Information Theory, 44(1):2-15, 1998.
A. Adas and A. Mukherjee. On resource management and QoS guarantees for long-range dependent traffic. GIT-CC-94/60 1994.
M. Alzate. Análisis de la Eficiencia en el Uso de la Capacidad Asignada a Conversaciones Telefónicas. Revista INGENIERIA, Universidad Distrital, 1993
M. Alzate. Estimación del Tono de Señales de Voz Mediante la Transformada Wavelet. III Simposio de Procesamiento de Señales, Universidad de los Andes, 1994
M. Alzate. Obtención de Bases Wavelets Ortonormales Mediante el Diseño de Bancos de Filtros de Reconstrucción Perfecta. IV Simposio de Procesamiento de Señales, Universidad de los Andes, 1995.
M. Alzate. Conmutación de Paquetes de Voz. X Congreso Nacional y I Andino de Telecomunicaciones, 1995.
M. Alzate. Modelos de Tráfico en Redes de Comunicaciones. Reporte de Investigación de la Maestría en Teleinformática de la Universidad Distrital, marzo de 1995.
M. Alzate. Tráfico de Voz en ATM Sometido a Control de Admisión por Leaky Bucket. Revista INGENIERIA, enero-marzo, 1996.
M. Alzate. Generation of Simulated Fractal and Multifractal Traffic. IX Congreso Nacional de Estudiantes de Ingeniería de Sistemas, Bogotá, 2000.
M. Alzate. Active Networking and Congestion Control under SelfSimilar Traffic. Institute for System Research, Technical Report, to appear in 2002.
M. Arlitt and C. Williamson. Web Server Workload Characterization: The search for Invariants. IEEE/ACM Trans. Networking, 5(5):631-645, 1997.
J. Beran. Statistics for Long Memory Processes. Chapman and Hall, New York, 1994.
J. Beran, R. Sherman, M. Taqqu and W. Willinger. Long-Range Dependence in VBR video traffic. IEEE. Trans. Commun. 43:1566-1579, 1995.
O. Boxma and J. Cohen. The M/G/1 Queue with Heavy-tailed Service Time Distribution. IEEE J. Selected Areas in Commun. 16:749-763, 1998.
M. Crovella, M. Taqqu and A. Betsavros. Heavy-Tailed Probability Distributions in the WWW, In "A practical guide to Heavy Tails", Adler, Feldman and Taqqu, editors. Birkhauser, 1998.
M. Crovella and A. Bestavros. Self-similarity in WWW traffic. IEEE/ACM Trans. Networking, 5:835-846, 1997.
A. Erramili, O. Narayan and W. Willinger. Experimental queueing analysis with LRD packet traffic. IEEE/ACM Trans. Networking, 4:209-223, 1996.
A. Feldman, A. Gilbert, P. Huang and W. Willinger. Dynamics of IP Traffic: A Study of the Role of Variability and the Impact of Control. Proc. ACM SIGCOM'99, 1999.
P. Flandrin. Wavelet Analysis and Synthesis of Fractional Brownian Motion. IEEE Trans. Inf. Theory, 38:910-917, 1992.
V. Frost and B. Melamed. Traffic Modeling for Telecommunications Networks. IEEE Commun. Mag. 32(3):7081, 1994.
A. Gilbert, W. Willinger and A. Feldman. Scaling analysis of conservative cascades with application to network traffic. IEEE Trans. Information Theory, 45(3):971-991, 1999.
T. Gyires. Using Active Networking for Congestion Control in High-Speed Networks with Self-Similar Traffic. 0-7803-6583-6 © 2000 IEEE.
T. Hagiwara, H. Doi, H. Tode and H. Ikeda. High-Speed Calculation Method of the Hurst Parameter Based on Real Data. LCN 2000.
D. Heyman and T. Lakshman. What are the Implications of LRD for VBR Traffic Engineering? IEEE/ACM Trans. Networking, 4(3):301, 1996.
Internet Traffic Archive. BC_pAug89, http://www.acm.org/ sigcomm/ITA/index.html.
W. Leland, M. Taqqu, W. Willinger and D. Wilson. On the selfsimilar nature of Ethernet Traffic. IEEE/ACM Trans. Networking, 2:1-15, 1994.
S. Ma and C. Ji. Modeling Heterogeneous Network Traffic in Wavelet Domain. IEEE/ACM Trans. Networking, 9(5):634-649, 2001.
B. Mandelbrot and J. VanNess. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev., 10:422-437, 1968.
I. Norros. On the Use of Fractional Brownian Motion in the Theory of Connectionless Networks. IEEE J. Selected Areas in Commun. 13(6):953-962, 1995.
K. Park and W. Willinger. Self-Similar Network Traffic and Performance Evaluation. John Wiley and Sons, New York, 2000.
M. Parulekar and A. Makowski. M/G/ Input Processes. Proc. IEEE Infocom'97, 1997.
V. Paxson and S. Floyd. Wide-Area Traffic: The Failure of Poisson Modeling. IEEE/ACM Trans. Networking, 3:226-244, 1995.
R. Riedi, et. al. A Multifractal Wavelet Model with Application to Network Traffic. IEEE Trans. Inf. Theory, 45(3):992-1018, 1999.
M. Schwartz. Telecommunication Networks: Protocols, Modeling and Analysis. Prentice Hall, N.Y. 1989.
M. Taqqu, W. Willinger and V. Teverovsky. Estimators for Long-Range Dependence: An Empirical Study. Fractals 3(4):785-798, 1995.
A. Tewfik and M. Kim. Correlation structure of the discrete wavelet coefficients of fractional brownian motion. IEEE Trans. Info. Theory, 38:904-909, 1992.
B. Tsybakov and N. Georganas. Self-Similar Processes in Communications Networks. IEEE Trans. Inf. Theory, 44(5):17131725, 1998.
D. Veitch and P. Abry. A Wavelet-Based Joint Estimator of the Parameters of LRD. IEEE Trans. Inf. Theory, 45(3):878-897, 1999.
W. Willinger, M. Taqqu, R. Sherman and D. Wilson. Self-Similarity Through High Variability: Statistical Analysis of Ethernet LAN Traffic at the Source Level. IEEE/ACM Trans. Networking, 5(1):71-86, 1997.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2001-00-00 vol:6 nro:2 pág:6-1
Introducción al tráfico autosimilar en redes de comunicaciones
Marco Aurelio Alzate Monroy
Resumen
El tráfico se modela mediante un proceso estocástico que representa la demanda que los usuarios de una red de comunicaciones imponen sobre los recursos de la red. Originalmente se consideró que los tiempos entre llegadas de las demandas de los usuarios eran independientes entre sí, así como la cantidad misma de la demanda (tiempos entre llamadas y duración de las llamadas, tiempos entre llegada de paquetes y longitud de los paquetes, tiempos entre solicitud de conexiones y duración de las sesiones, etc.). Posteriormente se vio la necesidad de incluir el efecto de la correlación existente entre estas variables, para lo cual se desarrollaron modelos más elaborados en los que la correlación decaía exponencialmente con el tiempo. Sin embargo, recientemente se ha evidenciado que, en las redes modernas de comunicaciones, la correlación entre estas variables no decae tan rápidamente y puede persistir a través de muchas escalas de tiempo. Este fenómeno, que afecta significativamente el desempeño de las redes de comunicaciones, se puede representar adecuadamente mediante modelos de tráfico fractal o autosimilar. En este artículo se presentan los conceptos más básicos involucrados en el estudio de estos modelos, con el fin de facilitar al lector su introducción a la literatura especializada sobre el tema.
Palabras clave: Modelos de tráfico, autosimilitud, dependencia de rango largo, distribución de cola pesada, movimiento browniano fraccional.
Abstract
Traffic is modeled as an stochastic process representing the demand that users impose on the resources of a communication network. Originally, both the demand interarrival times and the demand amounts were considered as sequences of independent variables (call durations, packet lengths, file sizes, etc.). Later on, it became apparent that the correlation among these variables were so important that new models with exponentially decaying correlations were developed. However, recent evidence has shown that the correlation among these variables can decay much slower and persists through several time scales. This phenomenon, that impacts the network performance significatively, can be represented via fractal or self-similar models. In this paper we present the most basic concepts involved in the study of these models, hoping to help the reader to be better prepared for reading the especialized literature on the subject.
Key words: Traffic modeling, self-similarity, longrange dependence, heavy-tailed distributions, fractional brownian motion.
I. INTRODUCCIÓN
Aunque los fenómenos de autosimilitud en el tráfico de las actuales redes de comunicaciones se descubrió hace ya casi una década[26], en nuestro medio no se ha querido abordar el tema formalmente pues todavía se le considera como un aspecto "muy avanzado" de la teleinformática. Sin embargo, los efectos que este fenómeno produce en el desempeño de las redes exigen que iniciemos inmediatamente el estudio del tema. En efecto, los modelos tradicionales de tráfico permiten fácilmente controlar la variabilidad de la demanda y, por consiguiente, con ellos resulta relativamente fácil ejercer control de tráfico de manera que se puedan garantizar algunos niveles mínimos de calidad de servicio. Desafortunadamente, el fenómeno de la autosimilitud puede conducir a estructuras complejas de correlación en las que la variabilidad se extiende a muchas escalas de tiempo, invalidando las técnicas de control diseñadas para dichos modelos tradicionales de tráfico[30]. Así pues, estamos obligados a revisar todos nuestros esquemas de asignación de recursos, control de congestión y dimensionamiento de redes a la luz de este fenómeno observado en el tráfico de las redes de comunicaciones.
Puesto que la principal dificultad para empezar a abordar estos temas es el tratamiento matemático que se le da en la literatura especializada, se ha querido presentar en este artículo la definición de los principales conceptos involucrados en el tema general del tráfico autosimilar en redes de comunicaciones de una manera relativamente sencilla, con la esperanza de ofrecer al lector mejores herramientas para abordar el tema del tráfico autosimilar en la literatura especializada y, porqué no, para conducir su propia investigación al respecto. Por supuesto, si queremos hacer un estudio serio del tema debemos ubicarnos al nivel de abstracción matemática que se necesita y por eso la presentación de los conceptos no puede dejar de ser formal. En consecuencia, aquí se supone de parte del lector un conocimiento general de la teoría de probabilidades con algunos fundamentos básicos de procesos estocásticos, tal como el conocimiento que se imparte en un curso típico de pregrado en un programa de ingeniería electrónica o de sistemas.
En el artículo se presentan brevemente las principales técnicas de modelamiento de tráfico, haciendo especial énfasis en cómo la autocorrelación de los modelos tradicionales decae exponencialmente con el tiempo, en abierta contradicción con las medidas observadas recientemente. Luego se discute la necesidad de un nuevo modelo que capture las estructuras complejas de correlación observadas en tráfico real y se muestra cómo los modelos autosimilares satisfacen esta necesidad. Posteriormente se definen los conceptos fundamentales involucrados en el modelamiento autosimilar del tráfico, tales como autosimilitud determinística, autosimilitud estocástica exacta, autosimilitud de segundo orden, autosimilitud asintótica de segundo orden, dependencia de rango largo, distribución de cola pesada, movimiento browniano fraccional y ruido gaussiano fraccional. Finalmente se mencionan algunas técnicas de síntesis de movimiento browniano fraccional así como mecanismos para estimación de parámetros a partir de trazas muestrales.
Este es el primero de una serie de cuatro artículos sobre el tema. En el segundo artículo se mencionará como la transformada wavelet se convierte en una herramienta ideal para detección, estimación y síntesis de tráfico autosimilar. En el tercer artículo se describirá el efecto del tráfico autosimilar sobre el comportamiento dinámico de las colas en elementos de red tales como enrutadores y multiplexores. En el cuarto y último artículo se describirán aspectos adicionales como control de congestión, ingeniería de tráfico y dimensionamiento de redes considerando la autosimilitud en el tráfico.
II. MODELAMIENTO DE TRÁFICO
Para estudiar el tráfico, esto es, la medida de la demanda que los usuarios de una red de comunicaciones imponen sobre los recursos de la red, se utilizan modelos matemáticos del comportamiento de los usuarios. En particular, se representan los patrones de llegada de las demandas que los usuarios producen, donde estas demandas se pueden medir en términos de paquetes, celdas, llamadas, flujos, conexiones, bits, o cualquier otra unidad de información adecuada. Estos patrones de llegada se representan mediante alguna secuencia de tiempo que los identifique, tal como los instantes de llegada, {Tn, nÎZ}, o el número de llegadas hasta el instante t, {N(t), tÎR}, o la secuencia de tiempos entre llegadas, {An, nÎZ}, etc. Por supuesto, como estas secuencias son representaciones del mismo fenómeno, se encuentran íntimamente relacionadas entre sí[7]:

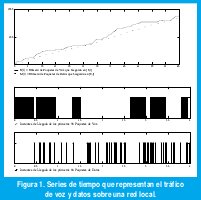
La Figura 1(a) muestra un minuto de dos secuencias del tipo {N(t), tÎR}, mientras que las Figuras 1(b) y 1(c) muestran los primeros cuatro segundos de las correspondientes secuencias del tipo {Tn, nÎZ}. Se trata de la llegada de paquetes de voz y datos en una red local con servicios integrados de voz y datos[6].
Lo primero que se puede obser var es la impredecibilidad de las secuencias, lo que obliga a modelar las series de tiempo {Tn, nÎZ}, {N(t), t ÎR} o {An, nÎZ}, como realizaciones de procesos estocásticos. Los correspondientes modelos estocásticos deben capturar las principales características estadísticas del tráfico en cuanto a su impacto en el desempeño de las redes. Por ejemplo, mientras las llegadas de paquetes de datos de la Figura 1(c) pueden modelarse como un simple proceso de Poisson con una intensidad adecuada, las llegadas de paquetes de voz de la Figura 1(b) deberán modelarse mediante un proceso que tenga en cuenta la correlación entre las llegadas impuesta por los intervalos de actividad e inactividad del usuario. Este simple ejemplo ilustra, pues, la necesidad de desarrollar distintos modelos de tráfico para diferentes tipos de servicio.
En efecto, a medida que avanza el desarrollo de las telecomunicaciones, se han propuesto distintos modelos de tráfico que han resultado muy exitosos (hasta ahora) para el análisis de desempeño de las redes de comunicaciones y, por consiguiente, para el diseño de mecanismos de control que permitan asegurar una determinada calidad de servicio a los usuarios. Por ejemplo, desde los comienzos mismos de la telefonía hasta comienzo de los años 80 se consideró que la llegada de llamadas a una central telefónica obedecía a un proceso de Poisson y que la duración de las llamadas estaba exponencialmente distribuida, con total independencia entre llamadas[34]. Estas suposiciones resultaron ampliamente validadas por las mediciones reales de tráfico y permitieron desarrollar métodos de diseño para asegurar una calidad de servicio dada (que en este caso era un único parámetro para todos los usuarios: Probabilidad de bloqueo). Recordemos que en un proceso de Poisson las llegadas se producen a intervalos exponencialmente ditribuidos con total independencia entre ellos, esto es,
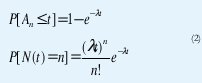
Esta total independencia hace que la aplicación de este modelo resulte muy fácil en análisis de desempeño y diseño de redes de comunicaciones. De hecho, el éxito de este modelo en las redes telefónicas motivó su aplicación al tráfico de datos durante los 70's, con igual éxito a pesar de que las predicciones del modelo no resultaban tan exactas. En este caso, la medida de la calidad de servicio también era una sola para todos los usuarios (retardo promedio) y así resultaba fácil desarrollar métodos de diseño para asegurar una calidad de servicio dada [34].
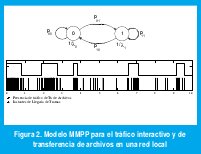
Sin embargo, con la digitalización total de las redes y el aumento abrumador de las capacidades de transmision en los enlaces, además de la voz y los datos surgieron nuevos tipos de servicio como imágenes y video, los cuales se empezaron a integrar en una misma red de comunicaciones. Por supuesto, el modelo de Poisson para estos nuevos tipos de tráfico resulta inválido, pues no puede esperarse independencia entre los tiempos entre llegadas. Así pues, a partir de los años 80's se han venido desarrollando nuevos modelos de tráfico que tienen en cuenta esta correlación entre tiempos de llegada. El proceso de llegada de paquetes de voz de la figura 1(b), por ejemplo, podría modelarse mediante un proceso determinístico Markovianamente modulado (MMDP): El abonado transita de activo a inactivo de acuerdo con una cadena de Markov de dos estados, en el estado activo genera paquetes a una tasa constante y en el estado inactivo no genera paquetes[6]. Otro ejemplo es el de la figura 2, en el que se muestra el tráfico sobre una red LAN con datos interactivos permanentes y sesiones esporádicas de transferencia de archivos. Este tráfico compuesto se podría modelar mediante una cadena de Markov de dos estados. En cada estado, la llegada forma un proceso de Poisson con distinta intensidad, por lo que se trata de un Proceso de Poisson Markovianamente modulado (MMPP)[7]. Estos tipos de modelos capturan mucha de la correlación entre llegadas que impacta el desempeño de la red y cuyo efecto no se observa con el modelo de Poisson. Los modelos MMPP han sido especialmente útiles en el modelamiento de tráfico de video con tasa variable de bits, como MPEG2, en las que la transición entre tipos de tramas I, P y B constituye una cadena de Markov, cada una con su respectiva tasa promedio de llegadas tipo Poisson [7].
Otros modelos recientes incluyen modelos de flujo continuo, útiles en aquellos casos en los que cada unidad de información (celda, paquete, bit, etc.) representa una carga infinitesimal para la capacidad de los medios de transmisión. Igualmente se han empleado modelos autoregresivos en los que el número de paquetes que llegan en un intervalo de tiempo dado se puede predecir a partir de una combinación lineal del número de llegadas en los anteriores k intervalos, siendo el error de predicción una secuencia de variables aleatorias independientes e idénticamente distribuidas[7].
Todos estos modelos recientes permiten capturar la correlación existente entre llegadas de paquetes a corto plazo. Esto es, al calcular la autocovarianza de los procesos estocásticos correspondientes se encuentra que la velocidad a la que esta decae en el tiempo es exponencial, como en (3).
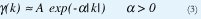
Sin embargo, mediciones y estudios recientes han demostrado que la autocorrelación en muchísimas trazas de tráfico reales decae de una manera hiperbólica con el tiempo [ver (4)], de manera que que el número de llegadas por segundo en un instante no sólo depende de lo que pasó hace unas milésimas de segundo sino también de lo que pasó hace unos segundos e, inclusive, hace algunos miles de segundos[30].
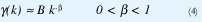
Los modelos de tráfico autosimilar se han desarrollado precisamente para poder capturar los efectos de este fenómeno, que se reportó por primera vez en 1994 con el famoso trabajo de Leland, Taqqu, Willinger y Wilson [26]. Este trabajo sentó las bases para el inmenso caudal de resultados de investigación que muestran la autosimilitud como una característica ubicua cuando se observa empíricamente el tráfico en redes modernas. Desde entonces se han reportado evidencias de autosimilitud en casi todos los aspectos de las redes modernas de comunicaciones tanto LAN como WAN, bajo IP y bajo ATM, con enlaces de cobre, de fibra óptica o inalámbricos, en la navegación por la web o en la transferencia de archivos, etc.[30]
Hoy en día la autosimilitud se considera un concepto fundamental para comprender la naturaleza dinámica del tráfico, el desempeño de las redes y los procedimientos de control de tráfico que buscan proporcionar una calidad de servicio dada. En efecto, el descubrimiento de que el tráfico puede ser fundamentalmente diferente a como hasta ahora se ha venido considerando exige reexaminar el panorama de las redes de comunicaciones y reconsiderar muchas de sus premisas básicas[32].
¿Porqué tantos modelos distintos y la necesidad de adicionar un modelo más, el del tráfico autosimilar? Un modelo de tráfico sólo puede considerarse correcto si las técnicas de inferencia estadística utilizadas sobre trazas de tráfico real permiten concluir que estas muestras de tráfico son consistentes con el modelo. Claramente, el hecho de que estadísticamente se pueda encontrar consistencia entre un modelo y una traza muestral no significa que no hayan otros modelos que se ajusten igualmente bien (o mejor). En este sentido, los modelos de tráfico autosimilar han demostrado una gran consistencia con las medidas observadas, las cuales evidencian fenómenos de escala en las redes modernas de comunicaciones.
Es de anotar que, por ejemplo, los modelos MMPP y autosimilares han demostrado ser igualmente válidos para representar el tráfico de una fuente de video MPEG2[13], incluyendo las principales medidas de desempeño de un conmutador que acepta este tipo de tráfico[24]. Por supuesto, dado que el modelo MMPP sólo considera la autocorrelación entre intervalos de tiempo muy próximos entre sí, las técnicas de análisis de desempeño y de diseño de métodos de control de tráfico resultan mucho más fáciles que con el modelo autosimilar, por lo que el modelo MMPP es el preferido entre estas dos alternativas igualmente válidas[24]. Sin embargo, el inmenso volumen de diversas medidas de tráfico de altísima calidad empiezan a develar inconsistencias entre los modelos tradicionales y las medidas observadas, especialmente en lo referente a estructuras de correlación que se expanden a lo largo de diferentes escalas en el tiempo. Estos fenómenos, en cambio, son inmediatamente capturados por los modelos de tráfico autosimilar, los cuales se vuelven cada vez más importantes en la medida en que el desarrollo de las redes de telecomunicaciones revelan el impacto de estos fenómenos de escala en el desempeño de las redes[32].
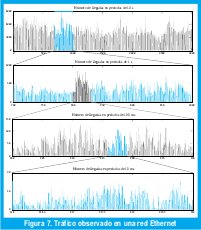
También es de anotar que para análisis y control de desempeño en redes de comunicaciones es importante tener en cuenta cómo se comportan los procesos de tráfico ante la re-escalización (la observación de los fenómenos de tráfico a diferentes escalas de tiempo), ya que el almacenamiento de paquetes en buffers y la asignación de ancho de banda a flujos de paquetes se pueden considerar como operaciones sobre el proceso re-escalizado. Específicamente, si un proceso markoviano se re-escaliza adecuadamente en el tiempo, el proceso que resulta pierde rápidamente la dependencia y se comporta como una secuencia de variables aleatorias independientes e idénticamente distribuidas. Una de las características más deseadas de este tipo de procesos, de acuerdo con la teoría de las grandes desviaciones, es que los "eventos raros" (como la ocurrencia prolongada de un exceso de llegadas) tiene una probabilidad exponencialmente pequeña. Este comportamiento se explica por la poca correlación entre eventos que se suceden relativamente separados en el tiempo[30]. En cambio, si un proceso autosimilar se re-escaliza en el tiempo, los fenómenos de variabilidad persistirán de una escala de tiempo a otra (invarianza a la escala), como se puede apreciar más adelante en las figuras 7 y 8[26]. Enseguida se definen más técnicamente todas estas ideas.
III. CONCEPTOS FUNDAMENTALES SOBRE TRÁFICO AUTOSIMILA
La autosimilitud y la fractalidad describen el fenómeno en el que cierta propiedad de un objeto se preserva con respecto a la escalización en el tiempo o en el espacio. Este fenómeno sucede en imágenes naturales, en el subdominio de convergencia de ciertos sistemas dinámicos y en muchas series de tiempo (como los procesos de tráfico que nos interesan). En un objeto autosimilar o fractal, sus partes magnificadas se asemejan a la forma del objeto completo, donde la semejanza se mide en algún sentido adecuado.
3.1 Autosimilitud determinística
Mediante la iteración de cierto procedimiento se puede obtener, por simple construcción, la forma más sencilla de autosimilitud. Un buen ejemplo es el copo de nieve de Von Koch (Figura 3), que se construye dividiendo cada línea en tres segmentos iguales y remplazando el segmento de la mitad por dos segmentos iguales, como en un triángulo equilátero. Si el procedimiento se repite para cada nuevo segmento indefinidamente, cualquier pequeña porción de la curva de Von Koch puede magnificarse para reproducir, exactamente, una porción mayor. Esta propiedad se conoce como "Autosimilitud exacta".

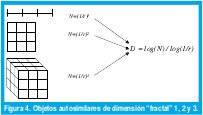
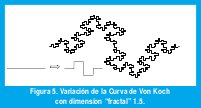
Obsérvese que un segmento de línea es un objeto unidimensional autosimilar pues puede dividirse en N segmentos idénticos, cada uno de ellos escalizado por el factor r=N-1. Igualmente, un cuadrado es un objeto bidimensional autosimilar pues puede dividirse en N cuadrados idénticos, donde el lado de cada uno de ellos se ha escalizado por un factor r=N-1/2. Finalmente, un cubo es un objeto tridimensional autosimilar que puede dividirse en N cubos idénticos, donde el lado de cada uno de ellos se ha escalizado por un factor r=N-1/3 (Figura 4). Generalizando, un objeto D-dimensional autosimilar puede dividirse en N copias más pequeñas de si mismo donde el lado de cada copia se ha escalizado por un factor r=N-1/D. Así pues, la dimensión de un objeto autosimilar compuesto por N partes idénticas en las que cada lado ha sido escalizado por un factor r es D=log(N) / log(1/r). En el caso de la curva de Von Koch, cada segmento de línea se convierte en N=4 subsegmentos, cada uno de los cuales se escaliza por un factor r=1/3, de manera que su dimensión es D=log(4)/log(3)=1.26. Como ésta es una dimensión fraccional, a estos objetos autosimilares se les llama también fractales (FRACTional DimensionAL). La figura 5 muestra una variación del copo de nieve de Von Koch de dimensión fractal 1.5.
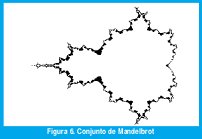
Otros objetos fractales pueden surgir de los subdominios de convergencia de ciertos sistemas dinámicos. Por ejemplo, el famoso conjunto de Mandelbrot está formado por los puntos c que no escapan a infinito bajo la iteración c=c+c2, como muestra la figura 6.
3.2 Autosimilitud estocástica
La autosimilitud estocástica, como la determinística, se puede ilustrar visualmente. En la figura 7(a) observamos el número de paquetes que transitan por un segmento de una red Ethernet[25], en períodos de 10 s, esto es, la barra que aparece en el instante t de la gráfica corresponde al número de paquetes que pasaron por ese segmento de la red en el intervalo (t, t+10). En la figura 7(b) magnificamos por un factor 10 una porción de la figura 7(a), de manera que reducimos la granularidad a 1 s. Este proceso lo repetimos en las figuras 7(c) y 7(d), que tienen granularidades de 0.1 y 0.01 segundos respectivamente, esto es, la barra que aparece en el instante t de la figura 7(d) corresponde al número de paquetes que pasaron por ese mismo segmento de la red en el intervalo [t, t+0.01).
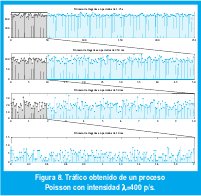
Debemos admitir que las cuatro gráficas de la figura 7 se parecen mucho entre si. Sin embargo, a diferencia de los objetos fractales determinísticos, cada gráfica no es una reproducción exacta de la gráfica anterior. Por supuesto, sería mucho pedir si esperásemos dicha fractalidad en un proceso tan aleatorio como la llegada de paquetes a una red Ethernet. Pero si consideramos que el tráfico observado es una traza muestral de un proceso estocástico y restringimos la similitud a ciertas estadísticas de las series de tiempo reescalizadas, descubriremos fácilmente autosimilitud exacta en los objetos matemáticos abstractos y autosimilitud aproximada en las realizaciones específicas, como la de la figura 7. De hecho, basta comparar las gráficas de la figura 7 con las de la figura 8, que muestran las llegadas de acuerdo con un proceso de Poisson, con magnificaciones por un factor 5. En éste último, a medida que consideramos intervalos de tiempo mayores, las llegadas en cada intervalo varían menos, tanto que a intervalos Δt de más de cuatro segundos se obtiene un número prácticamente constante de llegadas igual a 400×Δt. En cambio, la variabilidad en el proceso de tráfico de la red Ethernet parece ser invariante a la escala.
Para medir la autosimilitud estocástica se pueden utilizar las estadísticas de segundo orden que capturan la variabilidad de los procesos. De hecho, la invarianza a la escala se puede definir en términos de la función de autocorrelación, pues el decrecimiento polinómico (en vez de exponencial) de esta función es la manifestación de la dependencia de largo rango que, en una importante clase de procesos, es equivalente a la autosimilitud.
3.2.1 Autosimilitud, Autosimilitud de Segundo Orden, Autosimilitud Asintótica de Segundo Orden y Dependencia de Rango Largo
Consideremos un proceso estocástico de tiempo discreto {X(t), tÎZ}, donde X(t) es el número de paquetes que llegan en el intervalo (t-1,t]. El proceso acumulativo lo llamaremos {Y(t), tÎZ}, donde Y(t) es el número total de paquetes que han llegado hasta el instante t, de manera que X(t)=Y(t)-Y(t-1). Para utilizar X(t) como un modelo de tráfico, querríamos que este proceso fuera "estacionario", esto es, que su comportamiento no cambie con desplazamientos en el tiempo. De otra manera X(t) perdería su atractivo como una descripción compacta de un fenómeno supuestamente manejable. Decimos que el proceso estocástico {X(t), tÎZ} es estrictamente estacionario si la distribución conjunta de las variables aleatorias (X(t1), X(t2),..., X(tn)) es la misma distribución conjunta de las variables (X(t1+k), X(t2+k),..., X(tn+k)), para todo nÎN, t1,t2,...,tn, kÎZ. Esta estacionariedad estricta es demasiado restrictiva, pues nosotros vamos a trabajar, principalmente, con estadísticas hasta de segundo orden. Por eso preferimos una forma más débil de estacionariedad, la estacionariedad de segundo orden (o estacionariedad en el sentido amplio), según la cual las estadísticas de primer y segundo orden como el valor esperado, µ (t)=E[X(t)], y la función de autocovarianza, y (t,s)= E[(X(t)-µ (t)) (X(s)-µ (s))], son invariantes a desplazamientos en el tiempo. Esto es,
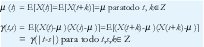
En adelante vamos a suponer que µ y σ2=y(0) existen y son finitos. Más aún, por simplicidad vamos a suponer que µ=0.
Consideremos el proceso agregado con nivel de agregación m, X<m>, obtenido del proceso original X mediante la siguiente suma normalizada:
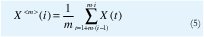
Esto es, hacemos una partición de {X(t), t∈Z} en bloques no sobrelapados de tamaño m, y promediamos los valores de cada bloque. El promedio del i-ésimo bloque es el valor de la i-ésima variable aleatoria del proceso agregado {X<m>(i), i∈Z}. Denotemos la autocovarianza de X<m>(i) mediante y<m>(k). Bajo la suposición de estacionariedad de segundo orden, podemos hacer las siguientes definiciones:
X(t) es exactamente auto-similar de segundo orden con parámetro de Hurst H∈(1/2, 1) si
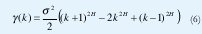
para todo k>0.
X(t) es asintóticamente auto-similar de segundo orden con parámetro de Hurst H∈(1/2, 1) si
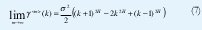
para todo k>0.
Nótese la importancia de que el parámetro de Hurst se encuentre en el intervalo abierto (½,1): Si H=1/2, las correlaciones (6) y (7) se hacen cero y obtenemos nuevamente la independencia que queremos evitar. Si H=1 tenemos que y(k) es constante para todo k, esto es, la función de autocorrelación es siempre 1 y la aleatoriedad desaparece. La condición H<1/2 es artificiosamente irreal y con H>1 se pierde la estacionariedad de X(t). Por eso cuando se habla de autosimilitud como en (6) ó (7), siempre se considera el rango de H entre ½ y 1.
Si X(t) es exactamente autosimilar de segundo orden, y(k) = y<m>(k) para todo m>0. De esta manera, la autosimilitud de segundo orden implica que la estructura de correlación se preserva bajo la agregación en tiempo (en forma exacta o asintótica según se satisfaga (6) ó solamente (7)).
La forma de las funciones de autocorrelación de las ecuaciones (6) y (7) no es arbitraria. En efecto, consideremos un proceso estocástico en tiempo continuo, {Y(t),≥ t0}. De acuerdo con las definiciones deter ministicas de autosimilitud, la versión estocástica más natural sería la invarianza de la distribución a la escala, esto es, Y(t) es exactamente autosimilar con parámetro de Hurst H si

Pero este proceso no podría ser estacionario puesto que si la media µ y la varianza σ2 fueran independientes del tiempo, necesitaríamos µ=a-Hµ y s2=a-2Hσ2, lo cual requiere µ=σ2=0. Esto es, Y(t) sólo puede ser estacionario si fuera degenerado, Y(t)0 ∀t. De hecho, con un poco de manipulación matemática, podemos encontrar que la autocovarianza de Y(t) es
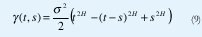
Como una simple verificación, nótese que y(t,t)= σ2 t2H. En efecto, usando t=1 en (8) y renombrando a como t, obtenemos Y(t)=d tHY(1). Elevando al cuadrado y tomando el valor esperado a cada lado obtenemos el mismo resultado, donde σ2=E[Y(1)2].
Consideremos ahora el respectivo proceso de incrementos X(t)=Y(t)-Y(t-1). Expandiendo X(t)X(s) en términos de Y, tomando el valor esperado y utilizando (9), encontramos que la autocovarianza de X no depende de los valores absolutos de t y s sino sólo del valor relativo k=(t-s), exactamente como en (6). Por esa razón es que se define una forma de autosimilitud menos restrictiva que (8), que es la autosimilitud de segundo orden (exacta o asintótica) definida anteriormente mediante (6) y (7).
Por supuesto, el proceso agregado X<m> tampoco es arbitrario. En efecto, nótese que
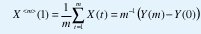
de manera que, de (8),
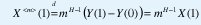
Esto es, las distribuciones de X y X<m> también están relacionadas por una simple relación de escala que involucra el parámetro de Hurst H:

Por eso las definiciones de autosimilitud de segundo orden (exacta y asintótica) exigen que X y m1-HX <m> tengan la misma estructura de autocorrelación (para todo m ó para m grande).
Respecto al parámetro H, de (10), Var(X<m>) =m2H-2 Var(X). Viendo X<m> como una media muestral de tamaño muestral m, si las muestras fuesen independientes sabemos que la varianza de X<m> sería Var(X<m>)=m-1Var(X), que es el caso con H=½. Para ½<H<1, la relación es
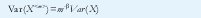
con 0<β<1 y H=1-β/2.Esta relación indica una estructura de dependencia muy particular entre las muestras X(t), la cual hace que la convergencia de Var(X<m>) hacia cero, a medida que crece el tamaño muestral m, sea más lenta que m-1.
Más aún, considerando la función de autocorrelación r(k)=y(k)/Var(X), una aproximación asintóticamente exacta es
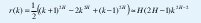
y, para ½<H<1, el comportamiento asintótico de r(k) es r(k)=ck-β, con 0<β<1. Esto es, la función de autocorrelación decae muy lentamente (hiperbólicamente), lo que conduce a la propiedad de que la función de autocorrelación es no sumable:

Cuando r(k) decae hiperbólicamente de manera tal que la condición (11) se cumple, decimos que el proceso estacionario X(t) tiene una dependencia de rango largo. Una definición esencialmente equivalente se puede dar en el dominio de la frecuencia, diciendo que la densidad espectral Γ(v) debe satisfacer la relación
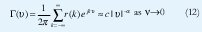
para algún c>0 y 0 < a=2H-1 < 1. Esta divergencia de la densidad espectral cerca al origen indica una importante contribución de los componentes de baja frecuencia.
Nótese la diferencia conceptual entre autosimilitud y dependencia de rango largo. Hay procesos autosimilares que no poseen dependencia de rango largo y viceversa. Sin embargo, bajo la restricción ½<H<1, existe una doble implicación entre autosimilitud y dependencia de rango largo y por eso muchas veces se usan como conceptos idénticos.
3.2.2 Movimiento Browniano Fraccional y Ruido Gaussiano Fraccional
El ejemplo más importante para procesos (exactamente) autosimilares corresponde al movimiento browniano fraccional y al ruido gaussiano fraccional[28]. Y(t), t∈R, es un movimiento browniano fraccional con parámetro 0<H< 1 si Y(t) es gaussiano, exactamente autosimilar y tiene incrementos independientes. Al proceso de incrementos X(t)=Y(t+1)-Y(t) se le conoce como ruido gaussiano fraccional.
Para introducir estos procesos, podemos empezar por recordar el movimiento browniano,
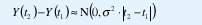
Suponiendo que Y(0)=0, obtenemos Y(t)~N(0,σ2|t|), de manera que Y(at)~a1/2N(0, σ2 |t|). De acuerdo con (8), el movimiento browniano es exactamente autosimilar con parámetro H=1/2. Su proceso de incrementos X(t)=Y(t+1)-Y(t)~N(0, σ2) es ruido blanco gaussiano. Este es un ejemplo perfecto de un proceso autosimilar que no sólo no tiene dependencia de rango largo sino que es completamente nocorrelacionado (¡de hecho, los incrementos del movimiento browniano son independientes!). Con ½ <H<1, el movimiento browniano fraccional obedece a
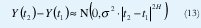
de manera que se trata de un proceso no estacionario con función de autorregulación
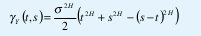
como en (9). Su proceso de incrementos X(t)= Y(t+1)-Y(t) sigue siendo ~ N(0,σ2), pero ahora con función de autocorrelación
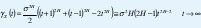
que se reduce a γX(t)=0 si H=1/2.
Es fácil utilizar la estructura de correlación de un movimiento browniano fraccional para generar trazas muestrales. Por ejemplo, en 1920 Wiener desarrolló un algoritmo que es una extensión natural de la construcción de VonKoch: el desplazamiento aleatorio del punto medio[9]. Si YH(t) es un movimiento browniano fraccional con E[(YH(t+1)-YH(t))2= σ2, de acuerdo con (13) y suponiendo por simplicidad que YH(0)=0, obtenemos E[YH(t)2] = σ2|t|2H. Así pues, si escogemos YH(0)=0 y YH(1) como una muestra de una variable aleatoria normal con media cero y varianza σ2, podemos generar una muestra del punto medio así: YH(1/2) = 0.5[YH(1) + YH(0)] + Δ1, donde Δ1 es una variable aleatoria normal con media cero y varianza σ22-2H[1-22H-2], de manera que se satisfaga (13) para t2=1/2 y t1=0 así como para t2=1 y t1=1/2. Similarmente, YH(1/4) = 0.5[YH(1/2) + YH(0)] + Δ2, donde Δ2 es una variable aleatoria normal con media cero y varianza σ24-2H[1-22H-2]. En general, YH(1/2n) = 0.5[YH(1/2n-1)+YH(0)]+ Δn, donde Δn es una variable aleatoria normal con media cero y varianza σ22-2nH[1-22H-2]. (Nótese que ésta es sólo una aproximación porque, aunque Var[YH(1/2n)-YH(0)]= Var[YH(1/2n-1)-YH(1/2n)]=...= Var[YH(1)-YH((2n-1)/ 2n)]= σ22-2nH, no es cierto que Var[YH(a+1/2n) YH(a)]= σ22-2nH para todo a). La figura 9 muestra un programa en Matlab para generar trazas de movimiento browniano fraccional mediante desplazamiento del punto medio y una salida típica.
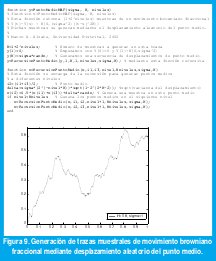
Por supuesto, existen muchas técnicas adicionales. Por ejemplo, haciendo uso de (12), podemos usar síntesis espectral de movimiento browniano fraccional. En efecto, sabemos que al filtrar ruido blanco con un filtro lineal con respuesta en frecuencia H(f), el espectro de potencia a la salida es proporcional a |H(f)|2. Correspondientemente, si expresamos la señal X(t) como
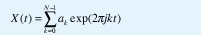
es suficiente con escoger los ak aleatoriamente de manera que E(|ak|2) sea proporcional a k -β para obtener S(f) proporcional a f-β , donde β=2H+1. Nótese que, aunque en (12) usamos a=2H-1 para el proceso de incrementos (ruido browniano fraccional), aquí usamos β=2H+1 para el proceso agregado (movimiento browniano fraccional). Este concepto puede extenderse fácilmente a multiples dimensiones, como se muestra en la figura 10 [9].
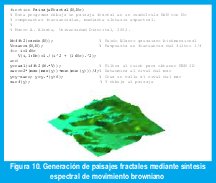
Muchas técnicas semejantes a estas pueden utilizarse para generar trazas muestrales de tráfico fractal modelado como movimiento browniano fraccional. Una de ellas es de especial interés para nosotros pues surge de una posible explicación del fenómeno de la autosimilitud en redes de comunicaciones a partir de las distribuciones de probabilidad de variables tales como el tamaño de los archivos de las páginas web, los tiempos de conexión de muchas sesiones y/o conexiones, etc. Se trata del multiplexaje de cierta clase de procesos on/off, como se explica en la siguiente sección.
3.2.3 Distribuciones con Colas Pesadas: ¿Porqué la Fractalidad?
Una variable aleatoria Z tiene una distribución de cola pesada si
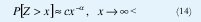
donde c es una constante positiva y 0<a<2 es el parámetro de forma o índice de la cola de la distribución. Aunque existen definiciones técnicamente más sutiles que involucran funciones de variación lenta, los conceptos principales se pueden extraer de esta definición ligeramente más restrictiva pero mucho más práctica.
Obsérvese de (14) que la cola de la distribución decae hiperbólicamente en contraste con las distribuciones de cola liviana, como las distribuciones exponencial o gaussiana, cuyas colas decrecen exponencialmente. Igualmente, la varianza de Z es infinita (si 0<a<2) e incluso el valor medio puede ser infinito si 0<a≤1. La propiedad (14) se cumple para todo x en el caso de la distribución de Pareto,
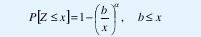
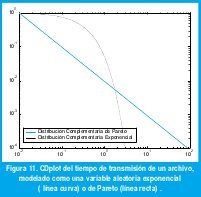
donde 0<a<2 es el parámetro de forma y b>0 es el parámetro de localización. La varianza de una variable aleatoria con distribución de Pareto es infinita. El valor medio es ab/(a-1) si a>1, o infinito si a≤1. La figura 11 compara la función de distribución complementaria en escala log-log (CDplot) para una distribución exponencial y una distribución de Pareto que representan el tiempo de transmisión de un archivo. Aunque ambas distribuciones tienen el mismo valor medio, sólo uno de cada 10000 archivos tarda más de 3 segundos en el caso exponencial, mientras que 3 de cada mil lo hacen en el caso de Pareto.
La principal característica de una variable aleatoria con distribución de cola pesada es su variabilidad extrema, esto es, puede tomar valores extremadamente grandes con una probabilidad no despreciable. Al tomar muestras de dicha variable, la gran mayoría de valores serán pequeños pero algunos valores serán muy grandes, de manera que la convergencia de la media muestral es lenta, especialmente si a se aproxima a 1. Otra característica importante de estas variables aleatorias es la predecibilidad. Supongamos que la duración de una conexión a una red es una variable aleatoria con cola pesada y queremos averiguar cuál es la probabilidad de que la conexión persista en el futuro, dado que ha estado activa por t segundos. Con distribuciones de cola liviana (asintóticamente exponencial), la predicción es independiente de t, de manera que nuestra incertidumbre no disminuye al condicionar en mayores períodos de actividad. Pero con distribuciones de cola pesada, entre mayor sea el período de actividad observado, mayor es la certeza de que la conexión persista en el futuro.
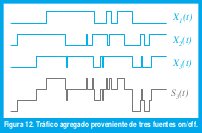
Debido a dicha predicibilidad, las variables aleatorias con distribución de cola pesada conducen a procesos estocásticos con dependendencia de rango largo. En efecto, considérese un modelo de N fuentes independientes de tráfico, Xi(t), i∈[1,N] donde cada fuente es un proceso de renovación on/off y en los que tanto los períodos de actividad como los de inactividad son independientes e idénticamente distribuidos. Sea SN(t) = ∑i =1..N Xi(t) el tráfico agregado en el instante t, como se representa en la figura 12. El proceso acumulativo YN(at) se define como ∫0at SN(τ)d τ, donde a>0 es un factor de escala. Si Xi(t) mide el número de paquetes por segundo que genera la fuente i en el instante t, YN(at) mide el número total de paquetes generados hasta el instante at.
Si la duración de los períodos de actividad, τON, es una variable aleatoria con distribución de cola pesada y parámetro de forma 1<a<2, se puede demostrar [39] que el proceso acumulativo YN(at) se comporta como un movimiento browniano fraccional en el sentido de que, para N y a grandes,
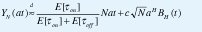
donde BH (t) es un movimiento browniano fraccional con varianza 1 y parámetro H=(3-a)/2, mientras c es una constante positiva que sólo depende de las distribuciones de τON y τOFF.
3.2.4 Estimación del parámetro H
Al modelar tráfico como movimiento browniano fraccional, debemos ajustar el valor medio, la varianza y el parámetro H para que correspondan con los respectivos estimados estadísticos tomados de mediciones de tráfico real. Más allá de la lenta convergencia de los estimadores tradicionales para la media y la varianza, no existe mayor dificultad en obtener valores adecuados para estos dos parámetros (claro, si la ergodicidad es una suposición válida). Sin embargo, la estimación del parámetro H es mucho más difícil. Una de las técnicas más utilizadas es el diagrama varianza-tiempo, basado en (10). En efecto, tomando las varianzas a ambos lados de (10) obtenemos Var[X<m>] = m-βVar[X], con β =2(1-H). Tomando el logaritmo a cada lado de la ecuación anterior obtenemos
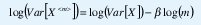
de manera que al graficar log(Var[x<m>]) contra log(m) obtendremos una curva cuya pendiente es 2(H-1).
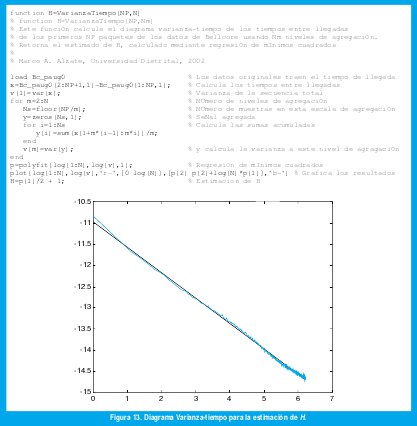
Cuando se tiene una serie de tiempo suficientemente larga como para estimar con suficiente precisión la varianza de las series agregadas (5) para un amplio rango de valores de m, podemos construir la gráfica anterior usando dichas estimaciones. Si detectamos algún tipo de alineación con una pendiente entre -1 y 0, podemos interpretarla como un fenómeno de dependencia de largo rango y la pendiente (obtenida mediante regresión lineal) resulta un estimador de 2(H-1). La figura 13 muestra un ejemplo obtenido de los 100000 primeros paquetes de [25]. La curva verde es el diagrama varianza-tiempo y la curva negra es el ajuste de mínimos cuadrados, que produce una pendiente de 0.6, para una estimación de H igual a 0.7. (Nótese que esta técnica de estimación no es solo valida para movimiento browniano fraccional sino para todo proceso con dependencia de largo rango, para lo cual toca encontrar un m0 mínimo a partir del cual se detecte alineación antes de efectuar la regresión).
3.2.5 Otros Métodos y Otros Modelos
Existen muchos otros métodos para estimación de parámetros de procesos autosimilares, tales como el análisis R/S, el periodograma o el estimador de Whittle [35,23]. Todos ellos han demostrado ser útiles en diferentes situaciones, a pesar de ciertas dificultades inherentes a cada uno de ellos. Sin embargo, una técnica de estimación de parámetros de procesos autosimilares que está ganando cada vez más popularidad es la de la transformada wavelet [4].
Efectivamente, como la autosimilitud se refiere a la invarianza en la escala de diferentes estadísticas de los procesos de tráfico y la transformada wavelet se diseñó para estudiar señales en el dominio de la escala[5], existe una afinidad natural entre los fenónemos autosimilares y la transformada wavelet. Más aún, los coeficientes wavelets de procesos autosimilares reproducen la autosimilitud entre escalas (la distribución de los coeficientes a la escala j es idéntica a la distribución de los coeficientes a la escala 0 previamente escalizados por 2j(H+1/2)) y son estacionarios dentro de cada escala; más aún, si la wavelet madre tiene un número suficiente de momentos desvanecientes, la correlación entre los coeficientes es prácticamente cero[1]. Así pues, basta con graficar el logaritmo de la energía de la traza muestral de tráfico versus la escala para detectar autosimilitud (mediante alineaciones) y estimar el parámetro Hurst (mediante regresión lineal). Más aún, como la generación de los procesos estocásticos correspondientes a los coeficientes wavelets es estadísticamente eficiente, la transformada wavelet también se constrituye en una excelente técnica de síntesis de procesos fractales[19].
Igualmente existen otros modelos diferentes al movimiento browniano fraccional tales como los procesos FARIMA(p,d,q) [2] o los procesos M/G/∞ [31]. Sin embargo, aquí también han habido desarrollos mucho más recientes en los que el tráfico de red se modela directamente en el dominio de la escala mediante wavelets [27]. Más aún, existe una clase de procesos de escala generalizados cuyo comportamiento no se puede describir mediante un único exponente de escala (movimiento browniano multifraccional, procesos multifractales, cascadas multiplicativas, etc.). Estos modelos permiten unas estructuras de escala mucho más ricas y, en ese sentido, han demostrado ser muy útiles en el modelamiento de tráfico. De hecho, la multifractalidad se ha evidenciado en trazas muestrales de tráfico debido al efecto de cascada multiplicativa que producen los protocolos de la red[33]. Para todos estos fenómenos, los modelos wavelet multifractales (MWM) han demostrado ser de gran utilidad[33].
IV. CONCLUSIONES
Los modelos tradicionales de tráfico son insuficientes para explicar muchas de las características observadas en el tráfico de las redes modernas de comunicaciones, especialmente en cuanto a las estructuras complejas de correlación que se extienden a muchas escalas. Los modelos de tráfico autosimilar capturan los efectos de estas estructuras de correlación. En este artículo se presentaron definiciones sencillas de conceptos importantes en el modelamiento de tráfico mediante procesos autosimilares. En particular, se definió la autosimilitud determinística y las diferentes formas de autosimilitud estadística (exacta, de segundo orden, asintótica de segundo orden), la dependencia de largo rango, la distribución de cola pesada, el movimiento browniano fraccional y el diagrama varianza-tiempo. Finalmente se mencionó muy brevemente cómo la transformada wavelet se convierte en una herramienta muy útil no sólo para detección, estimación y síntesis sino para modelamiento mismo de tráfico.
REFERENCIAS BIBLIOGRÁFICAS
[1] P. Abry and D. Veitch. Wavelet Analysis of Long-Range-Dependent Traffic. IEEE Trans. Information Theory, 44(1):2-15, 1998.
[2] A. Adas and A. Mukherjee. On resource management and QoS guarantees for long-range dependent traffic. GIT-CC-94/60 1994.
[3] M. Alzate. Análisis de la Eficiencia en el Uso de la Capacidad Asignada a Conversaciones Telefónicas. Revista INGENIERIA, Universidad Distrital, 1993
[4] M. Alzate. Estimación del Tono de Señales de Voz Mediante la Transformada Wavelet. III Simposio de Procesamiento de Señales, Universidad de los Andes, 1994
[5] M. Alzate. Obtención de Bases Wavelets Ortonormales Mediante el Diseño de Bancos de Filtros de Reconstrucción Perfecta. IV Simposio de Procesamiento de Señales, Universidad de los Andes, 1995.
[6] M. Alzate. Conmutación de Paquetes de Voz. X Congreso Nacional y I Andino de Telecomunicaciones, 1995.
[7] M. Alzate. Modelos de Tráfico en Redes de Comunicaciones. Reporte de Investigación de la Maestría en Teleinformática de la Universidad Distrital, marzo de 1995.
[8] M. Alzate. Tráfico de Voz en ATM Sometido a Control de Admisión por Leaky Bucket. Revista INGENIERIA, enero-marzo, 1996.
[9] M. Alzate. Generation of Simulated Fractal and Multifractal Traffic. IX Congreso Nacional de Estudiantes de Ingeniería de Sistemas, Bogotá, 2000.
[10] M. Alzate. Active Networking and Congestion Control under SelfSimilar Traffic. Institute for System Research, Technical Report, to appear in 2002.
[11] M. Arlitt and C. Williamson. Web Server Workload Characterization: The search for Invariants. IEEE/ACM Trans. Networking, 5(5):631-645, 1997.
[12] J. Beran. Statistics for Long Memory Processes. Chapman and Hall, New York, 1994.
[13] J. Beran, R. Sherman, M. Taqqu and W. Willinger. Long-Range Dependence in VBR video traffic. IEEE. Trans. Commun. 43:1566-1579, 1995.
[14] O. Boxma and J. Cohen. The M/G/1 Queue with Heavy-tailed Service Time Distribution. IEEE J. Selected Areas in Commun. 16:749-763, 1998.
[15] M. Crovella, M. Taqqu and A. Betsavros. Heavy-Tailed Probability Distributions in the WWW, In "A practical guide to Heavy Tails", Adler, Feldman and Taqqu, editors. Birkhauser, 1998.
[16] M. Crovella and A. Bestavros. Self-similarity in WWW traffic. IEEE/ACM Trans. Networking, 5:835-846, 1997.
[17] A. Erramili, O. Narayan and W. Willinger. Experimental queueing analysis with LRD packet traffic. IEEE/ACM Trans. Networking, 4:209-223, 1996.
[18] A. Feldman, A. Gilbert, P. Huang and W. Willinger. Dynamics of IP Traffic: A Study of the Role of Variability and the Impact of Control. Proc. ACM SIGCOM'99, 1999.
[19] P. Flandrin. Wavelet Analysis and Synthesis of Fractional Brownian Motion. IEEE Trans. Inf. Theory, 38:910-917, 1992.
[20] V. Frost and B. Melamed. Traffic Modeling for Telecommunications Networks. IEEE Commun. Mag. 32(3):7081, 1994.
[21] A. Gilbert, W. Willinger and A. Feldman. Scaling analysis of conservative cascades with application to network traffic. IEEE Trans. Information Theory, 45(3):971-991, 1999.
[22] T. Gyires. Using Active Networking for Congestion Control in High-Speed Networks with Self-Similar Traffic. 0-7803-6583-6 © 2000 IEEE.
[23] T. Hagiwara, H. Doi, H. Tode and H. Ikeda. High-Speed Calculation Method of the Hurst Parameter Based on Real Data. LCN 2000.
[24] D. Heyman and T. Lakshman. What are the Implications of LRD for VBR Traffic Engineering? IEEE/ACM Trans. Networking, 4(3):301, 1996.
[25] Internet Traffic Archive. BC_pAug89, http://www.acm.org/ sigcomm/ITA/index.html.
[26] W. Leland, M. Taqqu, W. Willinger and D. Wilson. On the selfsimilar nature of Ethernet Traffic. IEEE/ACM Trans. Networking, 2:1-15, 1994.
[27] S. Ma and C. Ji. Modeling Heterogeneous Network Traffic in Wavelet Domain. IEEE/ACM Trans. Networking, 9(5):634-649, 2001.
[28] B. Mandelbrot and J. VanNess. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev., 10:422-437, 1968.
[29] I. Norros. On the Use of Fractional Brownian Motion in the Theory of Connectionless Networks. IEEE J. Selected Areas in Commun. 13(6):953-962, 1995.
[30] K. Park and W. Willinger. Self-Similar Network Traffic and Performance Evaluation. John Wiley and Sons, New York, 2000.
[31] M. Parulekar and A. Makowski. M/G/ Input Processes. Proc. IEEE Infocom'97, 1997.
[32] V. Paxson and S. Floyd. Wide-Area Traffic: The Failure of Poisson Modeling. IEEE/ACM Trans. Networking, 3:226-244, 1995.
[33] R. Riedi, et. al. A Multifractal Wavelet Model with Application to Network Traffic. IEEE Trans. Inf. Theory, 45(3):992-1018, 1999.
[34] M. Schwartz. Telecommunication Networks: Protocols, Modeling and Analysis. Prentice Hall, N.Y. 1989.
[35] M. Taqqu, W. Willinger and V. Teverovsky. Estimators for Long-Range Dependence: An Empirical Study. Fractals 3(4):785-798, 1995.
[36] A. Tewfik and M. Kim. Correlation structure of the discrete wavelet coefficients of fractional brownian motion. IEEE Trans. Info. Theory, 38:904-909, 1992.
[37] B. Tsybakov and N. Georganas. Self-Similar Processes in Communications Networks. IEEE Trans. Inf. Theory, 44(5):17131725, 1998.
[38] D. Veitch and P. Abry. A Wavelet-Based Joint Estimator of the Parameters of LRD. IEEE Trans. Inf. Theory, 45(3):878-897, 1999.
[39] W. Willinger, M. Taqqu, R. Sherman and D. Wilson. Self-Similarity Through High Variability: Statistical Analysis of Ethernet LAN Traffic at the Source Level. IEEE/ACM Trans. Networking, 5(1):71-86, 1997.
Marco Aurelio Alzate Monroy
Ingeniero Electrónico de la U. Distrital, Máster en Ingeniería Eléctrica de la Universidad de los Andes. Se desempeñó como docenteinvestigador en la División de Investigación del ITEC, Telecom, y luego se vinculó a la Facultad de Ingeniería Electrónica de la Universidad Distrital, donde actualmente se desempeña como profesor asociado. En este momento adelanta su disertación doctoral en Ingeniería Eléctrica en la Universidad de Maryland.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










