DOI:
https://doi.org/10.14483/23448393.2853Publicado:
2008-11-30Número:
Vol. 8 Núm. 1 (2003): Enero - JunioSección:
Ciencia, investigación, academia y desarrolloAproximación a un modelo de despacho óptimo de flujo de agua en una red de acueducto
Palabras clave:
Despacho óptimo, modelo dinámico de planeación de producción, flujo en redes, flujo de costo mínimo, optimización lineal. (es).Descargas
Referencias
SHU, Yang, YUNG-Hsin Sun, Optimization of Regional Water Distributions System With Blending Requirements. Journal Of Water Resourses Planning and Managment. Vol 126, Nro4. July August 2000
AHUJA, Ravindra K; MAGNANTI, Thomas y ORLIN, James B. Network Flows. New Yersey, 1993
AHUJA, Ravindra K; MAGNANTI, Thomas y ORLIN, James B. Network Flows. New Yersey, 1993
HIDROSAN LTDA Ingenieros Consultores. Estudio y Actualización de las Estaciones de Bombeo. EAAB-ESP
TEA LTDA CONSULTORIAS, Actualización de la Proyección de la Demanda de Agua. Informe Ejecutivo. EAAB-ESP, 1999
INGETEC S.A. INGESTUDIOS. Modelo de evaluación financiera Concesión Planta Tibitoc. EAAB-ESP. 1996
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2003-00-00 vol:8 nro:1 pág:58-63
Aproximación a un modelo de despacho óptimo de flujo de agua en una red de acueducto
Rafael Guillermo García Cáceres
Miembro y Director del Grupo de Investigación Logísticos Pontificia Universidad Javeriana.
Mónica López Castro
Funcionario de la Empresa de Acueducto de de Bogotá.
José Fidel Torres Delgado
Profesor asociado, Universidad de los Andes.
Resumen
Este artículo presenta una nueva formulación de optimización de modelos dinámicos de despacho óptimo. Se tomó como caso específico de estudio la Empresa de Acueducto y Alcantarillado de BogotáESP. El modelo contempla en el análisis del sistema, el suministro de agua desde embalses hasta zonas de servicio; el modelo permite tomar decisiones respecto a volúmenes óptimos de agua por periodo de tiempo de tratamiento en las plantas y tiempos óptimos de bombeo de tal manera que se minimicen los costos de operación del sistema. Dentro de la formulación propuesta se incluyen elementos como: flujos bidireccionales, comportamiento de tanques de almacenamiento, consumos de agua de los embalses, estructura de costos lineal a tramos, demandas de agua de sectores hidráulicos, cotas de flujo en las tuberías que conforma la red matriz de acueducto y capacidades de los embalses, plantas, tanques y estaciones de bombeo.
Palabras clave: Despacho óptimo, modelo dinámico de planeación de producción, flujo en redes, flujo de costo mínimo, optimización lineal.
Abstract
This article presents a new formulation based in the better use of dynamic models in optimum planning and shipping. The specific case is the study of the water and sewerage system of Bogotá. This model includes the analysis of the system; the act of supplying water from ponds to zones of service, allows taking decisions referent to eminently good volumes of water for periods of time in plants of treatment and better pumping time. In this order, the model helps to minimize the operation costs in the system. This formulation manage elements like: two-directional flows, the behavior of store deposits, the consumption of water in ponds, the piece-linear structure of costs, demands of water from hydraulic sectors, lower and upper levels of flow in the pipe line that conforms the water matrix network, and the capacity of plants of treatment, ponds, tanks and pumping stations.
Key words: optimum planning and shipping dynamic models, network flows, minimum cost flow, linear optimization.
I. ANTECEDENTES
El problema de despacho óptimo de agua en una red de acueducto no ha sido tratado en la bibliografía; sin embargo se destaca un trabajo de distribución de agua en distritos[1] en donde se incluye una restricción de calidad de agua de tipo no lineal, además de las restricciones típicas del modelo de redes de flujo de costo mínimo.
II. INTRODUCCIÓN
Las empresas encargadas de la comercialización de agua potable, se enfrentan a la búsqueda de soluciones locales sin tomar en cuenta que sus decisiones aisladas afectan el comportamiento de los otros subsistemas. Conscientes de ésta necesidad, se efectúo este trabajo, con el objetivo de encontrar un modelo matemático que determine la cantidad óptima a ser despachada en cada planta a una zona de servicio específica, bajo las restricciones del sistema, con el menor costo posible y bajo un horizonte de planeación predefinido.
Las restricciones que contempla el modelo son: oferta de agua de los embalses abastecedores, capacidad máxima de tratamiento en las plantas, flujo máximo en la red, tiempo máximo de bombeo, dinámica oferta-demanda de los tanques de control-compensación, conservación de masa, manejo de arcos bidireccionales y de costos lineales a tramos y demanda en los sectores hidráulicos.
Los costos variables involucrados corresponden a: Tratamiento del agua cruda, bombeo en la red, costo por compra de agua bajo una estructura de costos lineal a tramos y uso del recurso hídrico.
III. DESARROLLO NOTACIÓN
Se presentan la simbología utilizada
1. Conjuntos y subconjuntos relacionados con la formulación del modelo
- N representa el conjunto de nodos de la red
- A representa el conjunto de arcos de la red
- K representa los periodos del horizonte de planeación.
- B representa el conjunto de los nodos plantas de tratamiento pertenecientes a la empresa de acueducto y es un subconjunto de N.
- C representa el conjunto de arcos que contienen estaciones de bombeo y es un subconjunto de A.
- D representa el conjunto de nodos de las fuentes de abastecimiento de agua cruda y es un subconjunto de N.
- G representa el conjunto de plantas con comportamiento de costos lineal a tramos, y es un subconjunto de A.
- E representa el conjunto de nodos que contienen a los arcos bidireccionales, y es un subconjunto de N.
- F representa el conjunto de arcos bidireccionales y es un subconjunto de A.
- L representa el número de tramos de escala de tarifas, del conjunto de plantas de tratamiento que se administran mediante costos lineales a tramos.
2. Parámetros
- bik representa la demanda u oferta del nodo i, en el periodo k.
- Qij representa el caudal proporcionado por el sistema de bombeo i j.
- Ui1 representa el volumen inicial ocupado por el fluido en el tanque i.
- CTi representa la capacidad máxima de volumen del tanque i.
- Si,j representa la Capacidad máxima del arco (i,j).
- Pi representa la capacidad máxima de la planta i
- fk representa la proporción de cambio en la demanda promedio (dp) para el periodo k de planeación.; de tal manera que para el caso de los nodos demanda bik = dp * fk
- αl representa la cota l-ésima de volumen superior asociada al mismo rango de consumo, fijado por la negociación entre las plantas que utilizan costeo lineal a tramos y la empresa de acueducto.
3. Costos
a. Costo de Tratamiento
- Cada planta de tratamiento determina la calidad del agua tratada; a través de recetas de producción que dependen de las físico químicas y bacteriológicas del agua cruda. El modelo tendrá en cuenta el costo de tratamiento por m3 de la planta i, representado por CTi, j, para todos los nodos i que pertenezcan al conjunto de plantas (B). Este debe calcularse tomando en cuenta el consumo de cada una de las sustancias químicas utilizadas, Cloro, sulfato de aluminio líquido, sulfato de aluminio granulado, polímero, cal hidratada, cal viva y pre-cal, por m3 de agua cruda tratada.
b. Costo de Bombeo
- Una estación de bombeo es una estructura que contiene un conjunto de bombas hidráulicas alimentadas por energía eléctrica; cuyo objetivo fundamental es la elevación de la cabeza de agua. La energía consumida depende de la potencia de las bombas y de la cantidad de tiempo de bombeo. Sus especificaciones técnicas le aseguran un caudal constante del fluido bombeado.
CBi, j representa el costo de energía asociado a todos los arcos (i , j) que pertenezcan al conjunto de bombas (C). Este se toma de la tarifa de energía correspondiente.
El caudal debe ser estimado mediante un software de simulación como Watercad. Haciendo las conversiones necesarias se halla la expresión de la energía consumida en términos del caudal. Esta es mostrada a continuación:
Energía = Potencia × Tiempo
Donde
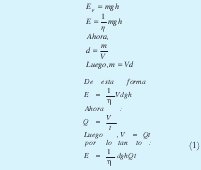
Reduciendo esta constante a
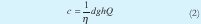
Se tiene la ecuación:
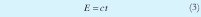
Donde:
Ep = Energía potencial
c= constante asociada a la estación de bombeo, dada en watios
m = masa
V; = volumen
d = densidad
h = eficiencia
t = tiempo
g = gravedad
Q = caudal
h = altura
E = energía consumida
La energía está en función del tiempo de tal manera que definimos éste como una variable de decisión para cada estación de bombeo Tki,j en segundos. Como la constante c, está en vatios, y la tarifa se cobra en $/Kwh, entonces se realiza la siguiente conversión:
Donde ci,j, es igual a la constante c perteneciente a la estación (i,j).
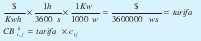
c. Costo de Uso del Recurso Hídrico
El costo de uso del recurso hídrico esta asociado a la tarifa que cobran, las entidades reguladoras a la empresa de acueducto, por tomar el agua en los embalses, tratarla, suministrarla y posteriormente devolverla como agua residual. Este costo cambia de acuerdo con el embalse.
El modelo tendrá en cuenta el costo de uso del recurso hídrico del embalse i, representado por: CUi, j, como el costo por metro cúbico de agua cruda suministrada desde el embalse i, para todos los i que pertenezcan al conjunto de embalses D
d. Costos Lineal a Tramos
En el caso del acueducto de Bogotá existen concesiones entre el estado y administradores privados del recurso hídrico. Dentro del contrato establecido por la empresa de acueducto y dichos administradores privados se estableció una escala de tarifas lineal a tramos asociado a rangos de volumen suministrado.
Cklij representa el costo de tratamiento de la planta i en el l-ésimo intervalo lineal a tramos correspondiente al intervalo de volumen αl-1 a al en el periodo k., para todas las plantas de tratamiento del conjunto G.
Estos costos se establecen como porcentajes de la tarifa plena, correspondiente al rango inferior de volumen de consumo mínimo establecido.
e. Función Objetivo
La ecuación de costo estaría dada por:
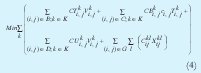
4. Variables de Decisión.
Las variables determinadas para el sistema objeto de estudio son:
- Vki,j Número de metros cúbicos de agua suministrada por la planta i al sector hidráulico j en el periodo de tiempo k:
- Tki,j Tiempo de bombeo de la estación i en el periodo k:
- Xkli,j Número de metros cúbicos de agua consumida en el l-ésimo intervalo de volumen αl-1 a αl; suministrada por la planta i, al sector j en el periodo k,
- Dki Gradiente del volumen del tanque i en el periodo k, esta variable es no restringida.
5. Restricciones
a. Costos Lineal a Tramos
Las ecuaciones que modelan la escala de costos lineales a tramos se muestran a continuación:
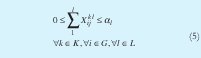
b. Balance de Masa [2]
Esta ecuación de nodos se muestra a continuación:
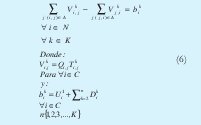
c. Capacidad en los tanques de compensación y control
El modelo debe contemplar restricciones de capacidad en tanques de control y compensación de la red matriz de distribución. El sistema en buena parte es regulado por los tanques que tienen una función tanto de oferta como de demanda, de tal manera que cuando la demanda de agua varía, el tanque debe ser ajustado a un nivel tal que permita satisfacer la demanda en forma continua.
El efecto de los gradientes de volumen de agua en los tanques es muy importante, debido a que ellos modelan la inercia del proceso; permitiendo que el modelo capture la dinámica del sistema.
Para asegurar que los cambios no excedan la capacidad máxima y mínima (0), de los tanques, se restringe a esta condición el volumen acumulado histórico; como se muestra a continuación:
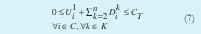
d. Capacidad de las plantas
Las plantas tienen una cota máxima de capacidad de tratamiento, y una mínima determinada en cero.
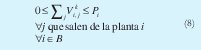
e. Capacidad en los Arcos
El rango de volumen que puede pasar por un arco en un período de tiempo se encuentra entre cero y un límite superior; este depende del caudal del agua que lo recorre y el periodo de planeación (H en unidades de tiempo). El caudal debe ser calculado mediante simulación, escogiéndose la estimación máxima alcanzada en un número estadísticamente significativo de ejecuciones. El volumen es estimado de la siguiente manera.
f. Restricciones de no negatividad
Con la excepción de los gradientes que son variables no restringidas, todas las variables del sistema son variables no negativas.
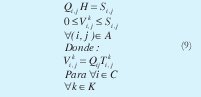
g. Transformaciones en la Red
El abastecimiento de la red en algunos puntos de demanda se hace desde diferentes fuentes, lo que implica que pueda existir en diferentes periodos de tiempo flujo en doble sentido. Esto también ocurre en algunos segmentos de red próximos a los tanques de abastecimiento.
Para asegurar que la red sea dirigida y cumpla con los supuestos del modelo de flujo de costo mínimo en redes, se utilizo la siguiente transformación:[3]
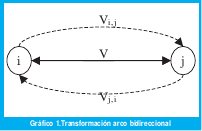
En el gráfico 1 cada arco bidireccional se convierte en dos arcos dirigidos; se puede demostrar que las dos nuevas variables no pueden ser básicas simultáneamente. Las ecuaciones que surgen con la transformación son:
Ecuación de balance de masa:
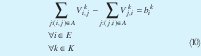
La ecuación de capacidad en los arcos, se transforma como sigue:
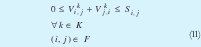
IV. RESULTADOS
A manera de validación se probó el modelo en un sector de la red de acueducto de Bogotá; este segmento corresponde a la red alta Vitelma que por su complejidad fue seleccionada. Esta red esta compuesta por dos plantas de tratamiento (Vitelma y La Laguna), cuatro fuentes de abastecimiento (embalses los Tunjos, Chizacá y La Regadera y el río San Cristóbal), catorce tanques y ocho estaciones de bombeo. Los parámetros fueron suministrados por la EAAB-ESP a partir de estudios previos, sobre eficiencias en las estaciones de bombeo[4] , calculo de proyecciones de demanda[5] y costeo de la concesion Tibitoc[6].
Se dejó el parámetro Ui1 como variable. Los resultados del flujo óptimo en los arcos procedentes del conjunto de nodos que pertenecen a las plantas de tratamiento se muestran en la siguiente tabla Los resultados no mostrados corresponden a variables que toman el valor cero.
El horizonte de planeación en este caso corresponde a un día dividió en 5 periodos de tres horas cada uno y por lo tanto H = 14400 segundos.
Los resultados correspondientes al conjunto que incluyen las plantas de tratamiento se muestran en la siguiente tabla I:

Los resultados del flujo óptimo en los arcos procedentes del conjunto de nodos que pertenecen a los embalses suministradores de Agua cruda se muestran en la tabla II:

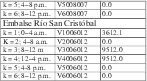
Los resultados de los tiempos de bombeo en algunos de los arcos procedentes del conjunto de nodos que contienen las estaciones de bombeo se muestran en la tabla III:
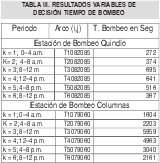
Se observa una gran dinámica en el flujo en los arcos de tal manera que los tanques mantienen unos niveles óptimos que minimizan los costos del agua. En la tabla IV, se presentan los resultados variables de decisión asociadas.
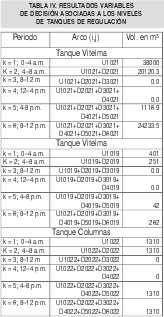
Esta salida incluye unas condiciones iniciales que son escogidas por el modelo (estas normalmente son fijadas), haciendo que el costo total del periodo diario sea el mínimo posible, debido a que algunos tanques tienen la suficiente capacidad para surtir inicialmente al sistema sin ningún costo, como resultado de la no contabilización del valor del agua en sus depósitos. El problema no pierde generalidad al ser este un estado transitorio de partida y simplemente pueden ser registrado al sumar su costo a la solución, identificando únicamente el lugar de procedencia del agua de los tanques.
Las variables Ui1 tomaron el valor máximo posible y que corresponde a la capacidad máxima de la planta, como era de esperarse, haciendo que no se utilizaran varias de las estaciones de bombeo.
El modelo seleccionó los embalses con costo mínimo apara abastecer las plantas de tratamiento.
El modelo utilizó ambas plantas: La Laguna que tiene un costo menor y Vitelma que tiene mayor capacidad de tratamiento.
Los tiempos de utilización de las estaciones de bombeo fueron consistentes con sus eficiencias asociadas, de tal manera que fueron mayores a menor eficiencia.
Finalmente, se observa gran dinámica de bombeo por periodo, producto de la topología particular de la red, que se apoya fuertemente del efecto regulador de los tanques. El tiempo de bombeo en algunas estaciones es considerable en algunos periodos.
V. CONCLUSIONES
Este trabajo presenta un nuevo modelo de optimización para el despacho óptimo de agua en una red de distribución. Aspectos claves son el modelaje del bombeo en la red, el modelaje lineal a tramos de la estructura de costos de una planta de tratamiento, el modelaje dinámico de los tanques y su efecto regulador en la red, el cálculo del costo de la energía a partir de ecuaciones físicas, el modelaje de la calidad del agua a partir de recetas de producción y el cálculo de los límites superiores utilizando la estimación del caudal del flujo y ecuaciones físicas.
El modelo permite la toma de decisiones a partir de la determinación de la participación de cada planta en la satisfacción de la demanda en los sectores hidráulicos y la determinación de los tiempos de bombeo en cada estación. Otra característica importante del modelo es su linealidad y su rápida convergencia en programas de optimización como LINDO o CPLEX.
VI. REFERENCIAS BIBLIOGRÁFICAS
[1] SHU, Yang, YUNG-Hsin Sun, Optimization of Regional Water Distributions System With Blending Requirements. Journal Of Water Resourses Planning and Managment. Vol 126, Nro4. July-August 2000
[2] AHUJA, Ravindra K; MAGNANTI, Thomas y ORLIN, James B. Network Flows. New Yersey, 1993
[3] AHUJA, Ravindra K; MAGNANTI, Thomas y ORLIN, James B. Network Flows. New Yersey, 1993
[4] HIDROSAN LTDA Ingenieros Consultores. Estudio y Actualización de las Estaciones de Bombeo. EAAB-ESP
[5] TEA LTDA CONSULTORIAS, Actualización de la Proyección de la Demanda de Agua. Informe Ejecutivo. EAAB-ESP, 1999
[6] INGETEC S.A. - INGESTUDIOS. Modelo de evaluación financiera Concesión Planta Tibitoc. EAAB-ESP. 1996
Rafael Guillermo García Cáceres
Profesor Asistente Pontificia Universidad Javeriana, Director del Grupo de Investigación Logísticos.
Mónica López Castro
Funcionaria de la Empresa de Acueducto y Alcantarillado de Bogotá.
José Fidel Torres Delgado
Profesor Asociado Universidad de los Andes
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)