DOI:
https://doi.org/10.14483/23448393.19091Published:
2022-11-20Issue:
Vol. 28 No. 1 (2023): January-AprilSection:
Biomedical EngineeringUna Revisión de los sistemas de control aplicados a los simuladores de rodilla
A Review on Control Systems Applied to Knee Simulators
Keywords:
knee simulator, control strategies, biomedical control, dynamic systems (en).Keywords:
simulador de rodilla, estrategias de control, control biomédico, sistemas dinámicos (es).Downloads
References
A. Zavatsky, “A kinematic-freedom analysis of a flexed-knee-stance testing rig,” J. Biomech., vol. 30, no. 3, pp. 277–280, mar 1997. [Online]. Available: https://doi.org/10.1016/S0021-9290(96)00142-X
K. M. Varadarajan, R. E. Harry, T. Johnson, and G. Li, “Can in vitro systems capture the characteristic differences between the flexion–extension kinematics of the healthy and TKA knee,” Med. Eng. Phys., vol. 31, no. 8, pp. 899–906, oct 2009. [Online]. Available: https://doi.org/10.1016/j.medengphy.2009.06.005 DOI: https://doi.org/10.1016/j.medengphy.2009.06.005
O. Szklar, “Development of an unconstrained two-force dynamic simulator for the human knee joint,” M.S. thesis, Dep. Mech. Eng., McGill Univ., Montreal, Canada, 1985. [Online]. Available: https://escholarship.mcgill.ca/concern/theses/p5547s51j
T. M. Guess and L. P. Maletsky, “Computational Modeling of a Dynamic Knee Simulator for Reproduction of Knee Loading,” J. Biomech. Eng., vol. 127, no. 7, pp. 1216–1221, dec 2005. [Online]. Available: https://doi.org/10.1115/1.2073676 DOI: https://doi.org/10.1115/1.2073676
L. P. Maletsky and B. M. Hillberry, “Simulating Dynamic Activities Using a Five-Axis Knee Simulator,” J. Biomech. Eng., vol. 127, no. 1, pp. 123–133, feb 2005. [Online]. Available: https://doi.org/10.1115/1.1846070 DOI: https://doi.org/10.1115/1.1846070
J. Victor, L. Labey, P. Wong, B. Innocenti, and J. Bellemans, “The influence of muscle load on tibiofemoral knee kinematics,” J. Orthop. Res., vol. 28, no. 4, pp. 419–428, 2009. [Online]. Available: https://doi.org/10.1002/jor.21019 DOI: https://doi.org/10.1002/jor.21019
D. De Jongh, W. Wargnye, and R. De Keyser, “Control of knee flexion in a knee simulator,” M.S. thesis, Fac. Eng. Archit., Ghent Univ., Ghent, Belgium, 2014. [Online]. Available: https://lib.ugent.be/catalog/rug01:002153765
A. Steinbruck, C. Schroder, M. Woiczinski, A. Fottner, P. E. Muller, and V. Jansson, “The effect of trochlea tilting on patellofemoral contact patterns after total knee arthroplasty: an in vitro study,” Arch. Orthop. Trauma Surg., vol. 134, no. 6, pp. 867–872, jun 2014. [Online]. Available: https://doi.org/10.1007/s00402-014-1956-1 DOI: https://doi.org/10.1007/s00402-014-1956-1
A. Chevalier, C. M. Ionescu, and R. De Keyser, “Analysis of robustness to gain variation in a fractional-order PI controller for knee joint motion,” in ICFDA’14 Int. Conf. Fract. Differ. Its Appl. 2014. IEEE, jun 2014, pp. 1–6. [Online]. Available: https://doi.org/10.1109/ICFDA.2014.6967359 DOI: https://doi.org/10.1109/ICFDA.2014.6967359
J. R. Fuller and E. Ness, Instrumentación quirúrgica: teoría, técnicas y procedimientos. Panamericana, 2007.[Online]. Available: https://books.google.com.mx/books?id=yBwepEJsqZQC
P. S. Walker, G. W. Blunn, D. R. Broome, J. Perry, A. Watkins, S. Sathasivam, M. E. Dewar, and J. P. Paul, “A knee simulating machine for performance evaluation of total knee replacements,” J. Biomech., vol. 30, no. 1, pp. 83–89, jan 1997. [Online]. Available: https://doi.org/10.1016/S0021-9290(96)00118-2
R. Bourne, J. Goodfellow, and J. O’Connor, “A functional analysis of various knee arthroplasties,” Trans. 24th Annu. Orthop. Res. Soc., pp. 21–23, 1978.
N. Arnout, L. Vanlommel, J. Vanlommel, J. P. Luyckx, L. Labey, B. Innocenti, J. Victor, and J. Bellemans, “Post-cam mechanics and tibiofemoral kinematics: a dynamic in vitro analysis of eight posterior-stabilized total knee designs,” Knee Surg. Sports Traumatol. Arthrosc., vol. 23, no. 11, pp. 3343–3353, nov 2015. [Online]. Available: https://doi.org/10.1007/s00167-014-3167-2 DOI: https://doi.org/10.1007/s00167-014-3167-2
A. B. Zavatsky, “A kinematic-freedom analysis of a flexed-knee-stance testing rig,” J. Biomech., vol. 30, no. 3, p. 278, 1997. DOI: https://doi.org/10.1016/S0021-9290(96)00142-X
C. K. Fitzpatrick, M. a. Baldwin, C. W. Clary, L. P. Maletsky, and P. J. Rullkoetter, “Evaluating knee replacement mechanics during ADL with PID-controlled dynamic finite element analysis,” in Orthop. Res. Soc. 2012 Annu. Meet., vol. 37, 2012, Poster. [Online]. Available: https://www.ors.org/abstract-search/
C. W. Clary, C. K. Fitzpatrick, L. P. Maletsky, and P. J. Rullkoetter, “The influence of total knee arthroplasty geometry on mid-flexion stability: An experimental and finite element study,” J. Biomech., vol. 46, no. 7, pp. 1351–1357, apr 2013. [Online]. Available: https://doi.org/10.1016/j.jbiomech.2013.01.025 DOI: https://doi.org/10.1016/j.jbiomech.2013.01.025
F. Fitzwater, A. Lenz, and L. Maletsky, “Modeling of a Dynamic Knee Simulator With Advanced PID Controller to Evaluate Joint Loading Conditions,” in Vol. 4A Dyn. Vib. Control. American Society of Mechanical Engineers, nov 2014, pp. 1–2. [Online]. Available: https://doi.org/10.1115/IMECE2014-38932 DOI: https://doi.org/10.1115/IMECE2014-38932
C. K. Fitzpatrick, M. A. Baldwin, C. W. Clary, L. P. Maletsky, and P. J. Rullkoetter, “Evaluating knee replacement mechanics during ADL with PID-controlled dynamic finite element analysis,” Comput. Methods Biomech. Biomed. Engin., vol. 17, no. 4, pp. 360–369, mar 2014. [Online]. Available: https://doi.org/10.1080/10255842.2012.684242 DOI: https://doi.org/10.1080/10255842.2012.684242
C. A. McLean and A. M. Ahmed, “Design and Development of an Unconstrained Dynamic Knee Simulator,” J. Biomech. Eng., vol. 115, no. 2, pp. 144–148, may 1993. [Online]. Available: https://doi.org/10.1115/1.2894114 DOI: https://doi.org/10.1115/1.2894114
A. Steinbr¨uck, C. Schr¨oder, M. Woiczinski, A. Fottner, P. E. M¨uller, and V. Jansson, “Patellofemoral contact patterns before and after total knee arthroplasty: an in vitro measurement,” Biomed. Eng. Online, vol. 12, no. 1, p. 58, 2013. [Online]. Available: https://doi.org/10.1186/1475-925X-12-58 DOI: https://doi.org/10.1186/1475-925X-12-58
A. Chevalier, A. Hernandez, C. M. Ionescu, M. Verstraete, and R. De Keyser, “Closed-loop Identiffication of a Multivariable Dynamic Knee Rig,” IFAC-PapersOnLine, vol. 48, no. 28, pp. 116–121, 2015. [Online]. Available: https://doi.org/10.1016/j.ifacol.2015.12.110 DOI: https://doi.org/10.1016/j.ifacol.2015.12.110
S. De Coninck, J. Smis, J. Victor, P. De Baets, and M. Verstraete, “Computational modeling of a dynamic knee simulator,” Int. J. Sustain. Constr. Des., vol. 6, no. 2, p. 8, jul 2015. [Online]. Available: https://doi.org/10.21825/scad.v6i2.1124 DOI: https://doi.org/10.21825/scad.v6i2.1124
A. Chevalier, C.-M. Ionescu, and R. De Keyser, “Control of knee joint motion in a dynamic knee rig,” in 34th Benlux Meet. Syst. Control, 2015, p. 23. [Online]. Available: https://lib.ugent.be/catalog/pug01:5944203
L. Chen, K. Gordon, and M. Hurtig, “Design and validation of a cadaveric knee joint loading device compatible with magnetic resonance imaging and computed tomography,” Med. Eng. Phys., vol. 36, no. 10, pp. 1346–1351, oct 2014. [Online]. Available: https://doi.org/10.1016/j.medengphy.2014.06.017 DOI: https://doi.org/10.1016/j.medengphy.2014.06.017
M. A. Verstraete and J. Victor, “Possibilities and limitations of novel in-vitro knee simulator,” J. Biomech., vol. 48, no. 12, pp. 3377–3382, sep 2015. [Online]. Available: http://doi.org/10.1016/j.jbiomech.2015.06.007 DOI: https://doi.org/10.1016/j.jbiomech.2015.06.007
Q. Nollet and C. Ionescu, “Control of the ground reaction force in a dynamic knee rig,” M.S. thesis, Fac. Eng. Archit., Ghent Univ., Ghent, Belgium, 2017. [Online]. Available: https://lib.ugent.be/catalog/rug01:002367297
A. Chevalier, M. Verstraete, C. Ionescu, and R. De Keyser, “Decoupled Control for the Bicycling UGent Knee Rig: Design, Implementation, and Validation,” IEEE/ASME Trans. Mechatronics, vol. 22, no. 4, pp. 1685–1694, aug 2017. [Online]. Available: https://doi.org/10.1109/TMECH.2017.2696708 DOI: https://doi.org/10.1109/TMECH.2017.2696708
R. J. Reynolds, P. S. Walker, and J. Buza, “Mechanisms of anterior-posterior stability of the knee joint under load-bearing,” J. Biomech., vol. 57, pp. 39–45, may 2017. [Online]. Available: https://doi.org/10.1016/j.jbiomech.2017.03.016 DOI: https://doi.org/10.1016/j.jbiomech.2017.03.016
A. Chevalier, B. De Vlieger, M. Verstraete, C. M. Ionescu, and R. De Keyser, “Decoupled PID control with gain adaptation for a cycling dynamic knee rig,” in 2016 IEEE Int. Conf. Syst. Man, Cybern. IEEE, oct 2016, pp. 002 779–002 784. [Online]. Available: https://doi.org/10.1109/SMC.2016.7844660 DOI: https://doi.org/10.1109/SMC.2016.7844660
A. Chevalier, B. De Vlieger, M. Verstraete, C. Ionescu, and R. De Keyser, “A Data-driven Gain Adaptation Mechanism for Flexible Usability in the UGent Knee Rig,” IFAC-PapersOnLine, vol. 50, no. 1, pp. 12 210–12 215, jul 2017. [Online]. Available: https://doi.org/10.1016/j.ifacol.2017.08.2339 DOI: https://doi.org/10.1016/j.ifacol.2017.08.2339
A. Chevalier, M. Verstraete, R. De Keyser, and M. Loccufier, “Specimen-specific control in the UGent Knee Rig using gain adaptation,” Control Eng. Pract., vol. 76, no. 76, pp. 104–111, jul 2018. [Online]. Available: https://doi.org/10.1016/j.conengprac.2018.04.012 DOI: https://doi.org/10.1016/j.conengprac.2018.04.012
T. R. Abo-Alhol, C. K. Fitzpatrick, C. W. Clary, A. J. Cyr, L. P. Maletsky, P. J. Laz, and P. J. Rullkoetter, “Patellar mechanics during simulated kneeling in the natural and implanted knee,” J. Biomech., vol. 47, no. 5, pp. 1045–1051, mar 2014. [Online]. Available: https://doi.org/10.1016/j.jbiomech.2013.12.040 DOI: https://doi.org/10.1016/j.jbiomech.2013.12.040
R. B. Durairaj, J. Shanker, P. Vinoth Kumar, and M. Sivasankar, “A Study on Development of Knee Simulator for Testing Artificial Knee Prosthesis,” in Lect. Notes Mech. Eng., 2012, pp. 351–360. [Online]. Available: https://doi.org/10.1007/978-81-322-1007-8 DOI: https://doi.org/10.1007/978-81-322-1007-8_32
A. Tecame, M. Ferrari, B. Violante, G. Calafiore, R. Papalia, and P. Adravanti, “Are contemporary femoral components sizing and design likely to affect functional results in TKA? A mathematical model of an implanted knee to predict knee forces,” Musculoskelet. Surg., vol. 102, no. 3, pp. 289–297, dec 2018. [Online]. Available: https://doi.org/10.1007/s12306- DOI: https://doi.org/10.1007/s12306-018-0533-0
-0533-0
K. A. Weimer, T. M. Guess, K. A. Dodd, and L. P. Maletksy, “Development and Validation of a Subject-Specific Computational Human Knee Model in a Dynamic Knee Simulator,” in ASME 2007 Summer Bioeng. Conf. American Society of Mechanical Engineers, jun 2007, pp. 407–408. [Online]. Available: https://doi.org/10.1115/SBC2007-176613 DOI: https://doi.org/10.1115/SBC2007-176613
A. Chevalier, “The knee joint motion in a force and position controlled knee rig: modeling, implementation and validation,” Ph.D. Dissertation, Fac. Eng. Archit., Ghent Univ., Ghent, Belgium, 2019. [Online]. Available: http://hdl.handle.net/1854/LU-8630995
A. Chevalier, J. Victor, S. Herregodts, and M. Loccufier, “Descending Staircase in the UGent Knee Rig: a Feasibility Study,” IFAC-PapersOnLine, vol. 54, no. 15, pp. 430–435, 2021. [Online]. Available: https://doi.org/10.1016/j.ifacol.2021.10.294 DOI: https://doi.org/10.1016/j.ifacol.2021.10.294
N. Arnout, J. Victor, A. Chevalier, J. Bellemans, and M. A. Verstraete, “Muscle loaded stability reflects ligament-based stability in TKA: a cadaveric study,” Knee Surg. Sports Traumatol. Arthrosc., vol. 30, no. 2, pp. 612–620, feb 2022. [Online]. Available: https://doi.org/10.1007/s00167-020-06329-2 DOI: https://doi.org/10.1007/s00167-020-06329-2
C. McLean, “Design, development and performance evaluation of a dynamic knee simulator,” M.S. thesis, Dep. Mech. Eng., McGill Univ., Montreal, Canada, 1990. [Online]. Available: https://escholarship.mcgill.ca/concern/theses/gt54kp343
A. Sauer, C. Thorwaechter, I. Dupraz, A. Maas, A. Steinbrueck, T. M. Grupp, and M. Woiczinski, “Isolated effects of patellar resurfacing in total knee arthroplasty and their relation to native patellar geometry,” Sci. Rep., vol. 12, no. 1, p. 12979, dec 2022. [Online]. Available: https://doi.org/10.1038/s41598-022-16810-2 DOI: https://doi.org/10.1038/s41598-022-16810-2
J. A. Shaw and D. G. Murray, “Knee Joint Simulator,” Clin. Orthop. Relat. Res., no. 94, pp. 15–23, jul 1973.[Online]. Available: https://doi.org/10.1097/00003086-197307000-00004 DOI: https://doi.org/10.1097/00003086-197307000-00004
C. Maag, A. Metcalfe, I. Cracaoanu, C. Wise, and D. D. Auger, “The development of simulator testing for total knee replacements,” Biosurface and Biotribology, vol. 7, no. 2, pp. 70–82, jun 2021. [Online]. Available: https://doi.org/10.1049/bsb2.12001 DOI: https://doi.org/10.1049/bsb2.12001
F. W. Werner, L. G. Sutton, T. Hamblin, and J. Clabeaux, “Development of a Deep Knee Bend Knee Simulator,” J. Biomech., vol. 40, no. July, p. S97, jan 2007. [Online]. Available: https://doi.org/10.1016/S0021-9290(07)70094-5 DOI: https://doi.org/10.1016/S0021-9290(07)70094-5
P. Rullkoetter, S. McGuan, and L. Maletsky, “Development and verification of a virtual knee simulator for TKR evaluation,” in 45th Annu. Meet. Orthop. Res. Soc., California, 1999, p. 973.
F. Schall, A. M. Seitz, S. Hacker, S. van Drongelen, S. I. Wolf, A. Ignatius, and L. Dürselen, “German Society of Biomechanics (DGfB) Young Investigator Award 2019: Proof-of-Concept of a Novel Knee Joint Simulator Allowing Rapid Motions at Physiological Muscle and Ground Reaction Forces,” Front. Bioeng. Biotechnol., vol. 7, no. SEP, pp. 1–10, sep 2019. [Online]. Available: https://doi.org/10.3389/fbioe.2019.00244 DOI: https://doi.org/10.3389/fbioe.2019.00244
P. S. Walker, G. W. Blunn, D. R. Broome, J. Perry, A. Watkins, S. Sathasivam, M. E. Dewart, and J. P. Paul, “A knee simulating machine for performance evaluation of total knee replacements,” J. Biomech., vol. 30, no. 1, p. 84, 1997. 9 DOI: https://doi.org/10.1016/S0021-9290(96)00118-2
J. D. DesJardins, P. S. Walker, H. Haider, and J. Perry, “The use of a force-controlled dynamic knee simulator to quantify the mechanical performance of total knee replacement designs during functional activity,” J. Biomech., vol. 33, no. 10, pp. 1231–1242, oct 2000. [Online]. Available: https://doi.org/10.1016/S0021-9290(00)00094-4 DOI: https://doi.org/10.1016/S0021-9290(00)00094-4
B. White, D. D’Lima, A. Drueding, J. Cox, F. Carignan, and S. Dean, “A Simulator Study of TKR Kinematics Using Modeled Soft-Tissue Constraint: Virtual Soft-Tissue Control for Knee Simulation,” J. ASTM Int., vol. 3, no. 8, p. 100251, 2006. [Online]. Available: https://doi.org/10.1520/JAI100251 DOI: https://doi.org/10.1520/JAI100251
B. F. White, “Prosthetic Simulator With Soft Tissue Modeling,” US patent 7 823 460 B2, Nov. 2, 2010. 10, 11
——, “System and method for joint motion simulation,” CA patent 2 779 013 A1, May 12, 2011. 10, 11
C. K. Fitzpatrick, C. Maag, C. W. Clary, A. Metcalfe, J. Langhorn, and P. J. Rullkoetter, “Validation of a new computational 6-DOF knee simulator during dynamic activities,” J. Biomech., vol. 49, no. 14, pp. 3177–3184, oct 2016. [Online]. Available: https://doi.org/10.1016/j.jbiomech.2016.07.040 DOI: https://doi.org/10.1016/j.jbiomech.2016.07.040
F. J. Carignan and B. F. White, “Method And Apparatus For Joint Motion Simulation,” US patent 9 351 857B, may, 2016.
AMTI Force and Motion, “ADL Knee Simulator Description and Specifications,” 2020, [Online]. Available: www.schmidtbiomedical.com/images/AMTIADLKNEEbrochure.pdf (accessed Aug. 01, 2022).
——, “ADL Knee Simulator Specifications,” 2020, [Online]. Available: http://www.amti.biz/AMTI-Knee-Simulator.pdf (accessed Jan. 03, 2022). 10, 11
J. D. DesJardins, S. A. Banks, L. C. Benson, T. Pace, and M. LaBerge, “A direct comparison of patient and force-controlled simulator total knee replacement kinematics,” J. Biomech., vol. 40, no. 15, pp. 3458–3466, jan 2007. [Online]. Available: https://doi.org/10.1016/j.jbiomech.2007.05.022 DOI: https://doi.org/10.1016/j.jbiomech.2007.05.022
A. Abdelgaied, J. Fisher, and L. M. Jennings, “A comparison between electromechanical and pneumatic-controlled knee simulators for the investigation of wear of total knee replacements,” Proc. Inst. Mech. Eng. Part H J. Eng. Med., vol. 231, no. 7, pp. 643–651, jul 2017. [Online]. Available: https://doi.org/10.1177/0954411917696519 DOI: https://doi.org/10.1177/0954411917696519
ProSim, “Knee Wear Simulator (Independent Stations) Overview,” 2017, [Online]. Available: http://www. prosim.co.uk/pdf/uk/KneeWear ENG.pdf (accessed Aug. 01, 2022)
X.-H. Wang, X. Dong, B.-Z. Zhu, L. Jiang, Z.-M. Jin, T. Suguro, and C.-K. Cheng, “A preclinical method for evaluating the kinematics of knee prostheses,” Med. Eng. Phys., vol. 66, pp. 84–90, apr 2019. [Online]. Available: https://doi.org/10.1016/j.medengphy.2019.03.003 DOI: https://doi.org/10.1016/j.medengphy.2019.03.003
EndoLab Mechanical Engineering GmbH, “The EndoLab® Knee Simulator,” 2022, [Online]. Available: https://www.endolab.org/simulator-knee-implants.asp (accessed Aug. 01, 2022)
A. J. Clark and D. N. Maue, “Load dynamics compensation circuit for servohydraulic control systems,” US patent WO 85/03 573, Aug. 15, 1985.
MTS Systems Corporation, “Bionix ® Knee Wear Simulator,” 2010, [Online]. Available: https://www.mts.com/media/biomedical/pdfs/brochures/100-201-737aBionixKneeWear.pdf?as=1 (accessed Jan. 03, 2022).
B. D. Schulz, S. Paul J. Leska, D. J. Willis, and H. F. Fahrendorff, “Orthopedic simulator with a multi-axis slide table assembly,” US patent 7 913 573 B2, Mar. 29, 2011.
MTS Systems Corporation, “MultiPurpose TestWare,” 2014, [Online]. Available: https://www.mts.com/cs/groups/public/documents/library/dev 002042.pdf (accessed Feb. 10, 2022).
Shore Western, “Shore Western Control System,” 2019, [Online]. Available: http://www.shorewestern.com/controls.php (accessed Dec. 03, 2019).
——, “Shore Western Control System SWCS,” Monrovia, 2019, [Online]. Available: http://www.hydratec.co. uk/downloads/SC6000.pdf (accessed Dec. 03, 2019).
——, “Knee Wear Simulator,” 2017, [Online]. Available: http://www.shorewestern.com/Documents/PDFs/Knee.pdf (accessed Aug. 01, 2022).
E. Bahc¸e and E. Emir, “Investigation of wear of ultra high molecular weight polyethylene in a soft tissue behaviour knee joint prosthesis wear test simulator,” J. Mater. Res. Technol., vol. 8, no. 5, pp. 4642–4650, sep 2019. [Online]. Available: https://doi.org/10.1016/j.jmrt.2019.08.008 DOI: https://doi.org/10.1016/j.jmrt.2019.08.008
——, “Wear and validation of posterior stabilized knee prosthesis with the knee simulator,” Mater. Technol., vol. 36, no. 6, pp. 356–363, may 2021. [Online]. Available: https://doi.org/10.1080/10667857.2020.1759934 DOI: https://doi.org/10.1080/10667857.2020.1759934
N. Campbell, “Design of a Knee Simulator for the Testing of Total Knee Prostheses,” M.S. thesis, Dep. Biomed. Eng., Univ. Cape Town, Rondebosch, South Africa, 2008. [Online]. Available: http://hdl.handle.net/11427/3228
I. C. Burgess, M. Kolar, J. L. Cunningham, and A. Unsworth, “Development of a six station knee wear simulator and preliminary wear results,” Proc. Inst. Mech. Eng. Part H J. Eng. Med., vol. 211, no. 1, pp. 37–47, jan 1997. [Online]. Available: https://doi.org/10.1243/0954411971534665 DOI: https://doi.org/10.1243/0954411971534665
ISO 14243-1, “Implants for surgery - Wear of total knee-joint prostheses - Part 1: Loading and displacement parameters for wear-testing machines with load control and corresponding environmental conditions for test,” 2002. [Online]. Available: https://www.iso.org/standard/23256.html
ISO 14243-3, “Implants for surgery - Wear of total knee-joint prostheses - Part 3: Loading and displacement parameters for wear-testing machines with displacement control and corresponding environmental conditions for test,” 2014. [Online]. Available: https://www.iso.org/standard/56649.html
ASTM, “ASTM F3141, Standard Guide for Total Knee Replacement Loading Profiles,” 2017. [Online]. Available: https://doi.org/10.1520/F3141-17A DOI: https://doi.org/10.1520/F3141-17A
Lucideon, “Wear Testing - Load-Control vs. Displacement-Control,” Webinar Recording, 2020, [Online]. Available: https://www.lucideon.com/healthcare/insight-hub/lucideon-webinars/load-control-vs-displacement-control-webinar-recording (accessed Aug. 01, 2022).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 15 de febrero de 2021; Revisión recibida: 25 de julio de 2022; Aceptado: 29 de agosto de 2022
Resumen
Contexto:
Los mecanismos de simulación y/o desgaste de articulaciones han sido estudiados y aplicados en sistemas biomecánicos de rodilla por más de 30 años. Sin embargo, estos no han sido ampliamente reportados en cuanto a sus estrategias de control y/o automatización. El objetivo de este trabajo es presentar los avances del desarrollo tecnológico de las diferentes plataformas y modelos de simuladores de rodilla, con base principalmente en las plataformas de Oxford y Stanmore.
Método:
Se realizó una revisión exhaustiva de las patentes de equipos comerciales y artículos científicos.El enfoque utilizado consideró la cinemática y dinámica de las plataformas y los modelos de control, los actuadores, la interfaz y el método de sintonización empleados, así como las pruebas desarrolladas y el error del sistema.
Resultados:
No se han reportado sistemas biomecánicos de rodilla de manera generalizada en lo que a sus estrategias de control y/o automatización se refiere, debido a que muchos de ellos son comerciales y patentados. Existen plataformas que están certificadas bajo ciertos estándares, pero solo dependen de la variable controlada. Adicionalmente, se presenta una comparación detallada de los distintos tipos de plataformas existentes, en la cual destacan los modelos hidráulicos con controladores PID.
Conclusiones:
Existe un área de oportunidad para proponer nuevas alternativas de diseños y/o estrategias de control para simuladores de rodillas Esto, a su vez, abre la posibilidad de proponer nuevos diseños de alguna otra articulación, así como mejoras a los modelos existentes.
Palabras clave:
simulador de rodilla, estrategias de control, control biomédico, sistemas dinámico..Abstract
Context:
Simulation and wear joint mechanisms have been studied and applied in knee biomechanical systems for more than 30 years. However, these have not been widely reported with regard to their control and/or automation strategies. This work aims to present the advances made in the technological development of the different platforms and models of knee simulators, based mainly on the Oxford and Stanmore platforms.
Method:
An exhaustive review of commercial equipment patents and scientific papers was conducted. The approach considered the kinematics and dynamics of the platforms and the control models actuators, interface, and tuning method used, as well as the tests conducted and the system error.
Results:
Biomechanical knee systems have not been widely reported, as far as their control and/or automation strategies are concerned, because many of them are commercial and patented. Some platforms are certified under certain standards but depend only on the controlled variable. In addition, a detailed comparison of the different types of existing platforms is presented, highlighting the hydraulic models with PID controllers.
Conclusions:
There is an area of opportunity to propose new design alternatives and/or control strategies for knee simulators. This, in turn, opens the possibility of developing new designs for other joints, as well as improved models of existing ones.
Keywords:
knee simulator, control strategies, biomedical control, dynamic systems..Introducción
Los sistemas tecnológicos modernos utilizados en la ingeniería biomecánica han tenido gran aplicación durante los últimos años. Estas tecnologías abarcan mecanismos para estudios in vitro de prótesis utilizadas en diferentes tipos de artroplastia, pruebas de ortesis, exoesqueletos e incluso asistentes de rehabilitación. Todos, con el fin de devolver la motilidad y función normal a una articulación del cuerpo humano.
Durante las últimas tres décadas, desde el diseño de la plataforma de rodilla Oxford para pruebas biomecánicas de la rodilla 1, esta articulación ha sido extensamente estudiada en diversas áreas, principalmente en la artroplastia de rodilla. La ventaja de estos sistemas es que se pueden establecer diferentes condiciones de prueba y evaluarlas en el mismo espécimen, i.e., en condiciones bien controladas que no se pueden simular en sujetos vivos. Esto incluye evaluar la cinemática de la rodilla bajo condiciones de carga específicas 2 o millones de ciclos repetitivos 2 de alguna actividad de la rodilla, como lo es el ciclo de marcha. Este tipo de pruebas han sido operadas bajo controladores PID o alguna de sus variantes en desplazamiento y fuerza en trabajos como 3)-(8 por mencionar algunos ejemplos.
En este artículo se presenta un resumen de los principales tipos de controladores utilizados en sistemas biomecánicos de rodilla. El objetivo principal es determinar las características del tipo de variable controlado, el tipo de actuador, la técnica de control utilizada y el tipo de sistema. Aunque existen numerosos estudios y diferentes tipos de sistemas como las órtesis, este trabajo se centra en las plataformas dinámicas de rodilla, ya que existe mención de que algunos controladores tienen aplicación para los sistemas de órtesis y de simulación de rodilla 9.
Como objeto de interés se busca recabar información sobre controladores aplicados a sistemas biomecánicos complejos, donde el estudio de la cinemática y dinámica es de gran importancia, haciendo énfasis en que los controladores convencionales pueden no presentar un buen rendimiento en sistemas potencialmente no lineales o inestables.
Ergo, existe la limitante de que no se puede hacer un estudio comparativo de cuál controlador es el más adecuado para los sistemas biomecánicos de rodilla. Esto, debido a que no hay suficientes estudios documentados de diferentes controladores que hayan sio probados en un mismo dispositivo.
Materiales y métodos
En este estudio se desarrolló una revisión exhaustiva de la literatura a través de bases bibliográficas como IEEE Xplore, ScienceDirect, SpringerLink, SchoolarGoogle y Scopus; de bases de patentes como Google Patents, WIPO y FPO; y de repositorios de tesis de posgrado de diferentes instituciones y catálogos, hojas de especificaciones y patentes de fabricantes de simuladores de rodilla.
En la revisión se definieron parámetros como la estrategia de control, la variable controlada, el tipo y la cantidad de los actuadores y el desempeño ante el seguimiento de trayectorias. Por último, se clasificaron los principales tipos de sistemas encontrados, identificando las características principales de cada tipo.
Sistemas de pruebas de remplazo total de rodilla
En un remplazo total de rodilla (TKR, Total Knee Replacement) o artroplastia total de rodilla (TKA, Total Knee Arthroplasty), las superficies desgastadas de la articulación son reemplazadas total o parcialmente por un implante de rodilla 10). Estos implantes han sido probados y evaluados en plataformas como la de Oxford 1 o la de Stanmore 11. El primer tipo involucra un ensamble del tobillo y la cadera, que permite el movimiento de los seis grados de libertad de la rodilla 1, con la desventaja de que puede presentar fallos en pruebas a largo plazo 11. El segundo tipo asume que los componentes femoral y tibial se mantienen fijos y restringidos, considerando que la flexión-extensión simule cualquier actividad requerida. Además, se anticipa que cada prueba pueda ser realizada hasta por 30 millones de ciclos 11.
Modelos basados en la configuración Oxford
La plataforma original de rodilla de Oxford (OKR, Oxford Knee Rig) fue desarrollada en 1978 por 12 y usada para el estudio de varias artroplastias de rodilla. Esta consiste en un ensamble de “cadera” y “tobillo”, los cuales se combinan para permitir los seis grados de libertad de movimiento de la rodilla.
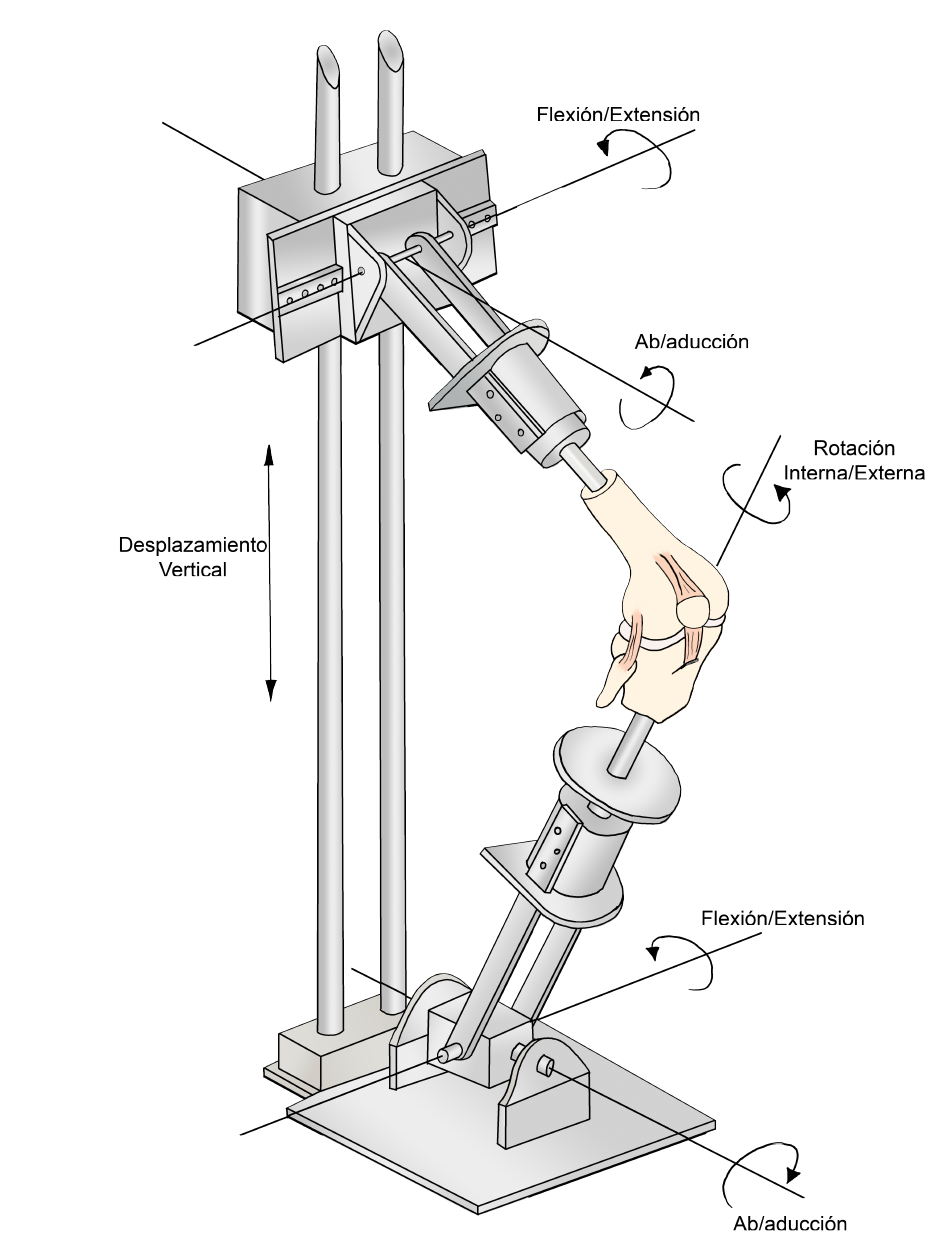
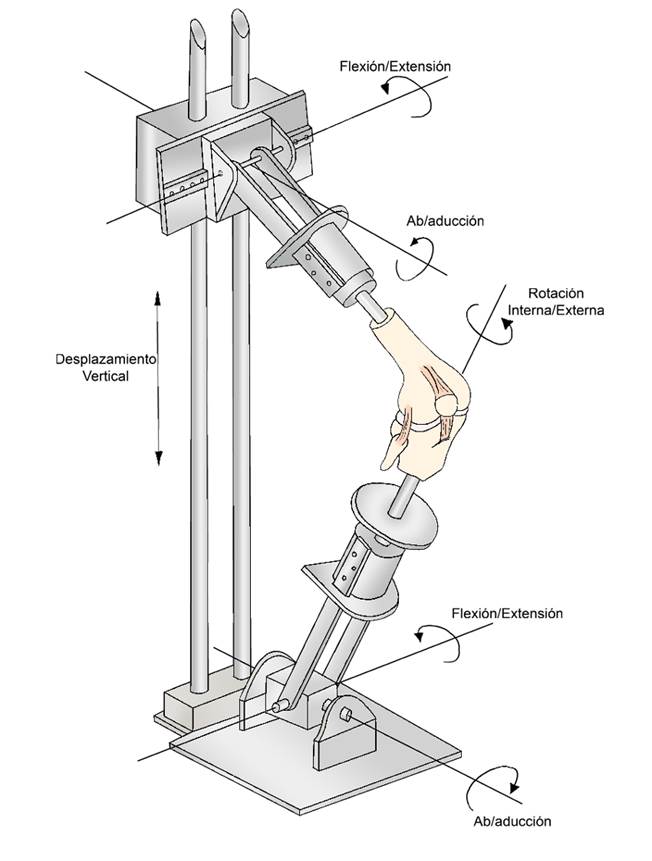
Este sistema incluye tres rotaciones: flexión-extensión, interna-externa y abducción-aducción; y tres traslaciones: anterior-posterior, medial-lateral y proximal-distal. Solo el ángulo de flexión es controlado directamente; todas las demás rotaciones y traslaciones son gobernadas por una fuerza de tensión que debe ser aplicada simulando el cuádriceps 1, 13. El esquema de este sistema se puede apreciar en la Fig. 1.
Figura 1: Esquema del simulador de rodilla OKR). Adaptado de 14.
Dependiendo de la investigación realizada, algunos modelos como el de Kansas utilizan actuadores servo-hidráulicos 4), (15)-(18 debido a los rápidos movimientos y elevadas cargas requeridas para simular las actividades de la rodilla. En otros casos se utilizan motores a pasos para controlar las cargas de la articulación y generar el ángulo de flexión deseado, e.g., el de McGill University 19 o en el simulador diseñado por McMaster University 5. También se emplean ampliamente los servomotores en actuadores lineales, ya sea para el desplazamiento vertical o para el control de la fuerza del cuádriceps 7),(8),(20)-(23. En los modelos basados en la plataforma de Oxford ha sido utilizado LabVIEW para programar el código del controlador y la interfaz de usuario 5)-(8), (20), (22), (24)-(28. En (3)-8),(15),(17),(18),(20)-(23),(25)-(31 se han implementado controladores Proporcional-Integral-Derivativos (PID) o alguna de sus variantes, (P, PI o PD). De todos los simuladores existentes en la literatura, los más reportados son los de la Universidad de Kansas y la Universidad de Gante.
Simulador de la Universidad de Kansas y Purdue
El dispositivo de Kansas 4, basado en el modelo de Purdue, permite simular las actividades de la rodilla en tiempo real mediante actuadores servo-hidráulicos. Para evaluar los movimientos de la rodilla, existen cinco ejes de control que consisten en tres cargas (traslaciones) y dos torques (rotaciones) 4),(5. Cada eje de control tiene un sensor de posición y fuerza que mide la retroalimentación y opera en cualquier modo, de control o carga. Se utilizó un controlador digital (Instron 8580, Canton, MA) para operar el simulador de rodilla, en el cual se pueden definir perfiles de posición o carga en los cinco ejes de manera simultánea 4), (5), (15), (17), (18.
El sistema utiliza un lazo de control PID 4), (5), (15), (17), (18, donde se muestrea la retroalimentación del lazo de control a 5 KHz. Los comandos y datos entre el controlador y el operador son transferidos a una computadora utilizando el bus de comunicación IEEE 488.2 mediante una interfaz de usuario creada en LabVIEW (5).
En 5, durante las simulaciones, cuando eran operados los actuadores de manera independiente, estos presentaban un excelente seguimiento de sus perfiles correspondientes. Sin embargo, durante las simulaciones dinámicas, existían interacciones entre los actuadores, por lo que se emplearon un acoplamiento cruzado entre la carga vertical y el momento de flexión del tobillo para mejorar la respuesta. Para la sintonización del controlador, se menciona que los valores de las ganancias fueron ajustados individualmente, sin describir el método utilizado. Posteriormente se hicieron pequeños ajustes con base a la retroalimentación durante la simulación de actividades con todos los ejes. Estos ajustes de ganancias fueron determinados de manera experimental durante simulaciones de flexión profunda de la rodilla 5.
En otros trabajos se aplicaron métodos de sintonización mediante algoritmos de programación para obtener los parámetros del controlador 18. Para probar el sistema, se utilizaron una trayectoria senoidal para la flexión y la carga vertical a una frecuencia de 0,3 Hz, incrementada dos y tres veces, para examinar la respuesta bajo diferentes condiciones. También se realizaron pruebas con un perfil del ciclo de marcha a 1 Hz. Mientras que el seguimiento de los perfiles era bueno para actividades relativamente simples y lentas, las simulaciones más complicadas como el ciclo de marcha mostraron un decremento en la precisión de los lazos de control, donde la mayoría de la validación de los perfiles mostraba una tendencia al error del 6% 5. Aunque los componentes del simulador fueron diseñados para soportar el ciclo de marcha a velocidades de hasta 2 Hz y una fuerza de 2400 N, los errores bajo estas condiciones son inaceptables, por lo que se sugiere mejorar el acoplamiento cruzado e incluir la fricción en el modelo.
En otras pruebas se realizaron ángulos de flexión profunda de hasta 120º, encontrando diferencias de 0,5º, 65N, 1,6 %, 0,8 Nm y 17 N para el ángulo de flexión, la carga articular, la carga medial-lateral, el torque interno-externo y la fuerza anteroposterior respectivamente 15), (18.
Simulador de la Universidad de Gante
Este simulador está basado en el modelo Oxford y ha sido modificado varias veces. En su propuesta inicial, se trabajó con el control de la flexión de la rodilla, utilizando un actuador lineal 7. En su siguiente versión, se describieron tres actuadores lineales: uno que simula los cuádriceps y dos que simulan la articulación del tobillo 21)-(23), (25. Chevalier et al. mencionan que controlar las fuerzas y movimientos aplicados en el simulador no es una tarea fácil, por lo cual proponen un control PD aplicado a cada motor para un sistema que se contempla como inestable y multivariable 21), (23.
Chevalier et al. utilizan LabVIEW como interfaz para programar un controlador PID 7), (22), (25)-(27). Aunque no se describe la estrategia de sintonización, las variables controladas son el ángulo del fémur y la fuerza aplicada a los cuádriceps. Para ambos casos se aplicó un perfil sinusoidal, donde el error en el movimiento angular representó menos del 1,5% y los resultados en cuanto a fuerza fueron menores al 3,6% 22.
Arnout et al. utilizan el simulador de Gante actuado por medio de dos motores 13: uno para mover la cadera verticalmente, mientras que el segundo aplica carga a una correa, la cual simula el tendón del cuádriceps y dos fuerzas constantes de 50 N cada una. Mediante resortes, el estudio simula la carga de los isquiotibiales medial y lateral 13. Se menciona que el primer motor genera una flexión controlada entre 30 y 130º en 10 s, mientras que el segundo motor tira el tendón del cuádriceps de tal manera que mantiene una fuerza vertical de 150 N en el tobillo 13.
Usando LabVIEW en el mismo simulador fue desarrollado y probado otro control, subdividido en tres lazos de control independientes, con su respectivo lazo de retroalimentación 25. Los primeros dos lazos controlan la posición horizontal y vertical del tobillo mediante un lazo de control PID. El tercer lazo de control es dedicado a la fuerza del cuádriceps, que depende de la fuerza vertical del tobillo. El algoritmo empleado utiliza un control PID para hacer coincidir la fuerza actual del cuádriceps con su valor objetivo, basándose en la señal de retroalimentación de la fuerza vertical del tobillo. Para evaluar la precisión del lazo de control del tobillo, se utilizó una señal seno y coseno como referencia para los ejes horizontal y vertical respectivamente, donde se obtuvo un error del 0,1% para el movimiento horizontal y 0,2% para el vertical, ambos con un retardo de fase del 0,68 %. Para el caso del control de la fuerza vertical en el tobillo, se puso como objetivo una fuerza constante de 100 N, donde el error permanecía por debajo de los 3,6 N 25.
Como se mencionó anteriormente, el modelo Oxford no fue pensado para movimientos cíclicos, por lo que la universidad de Gante desarrolló nuevas configuraciones para ampliar su funcionabilidad, cambiando el número de actuadores y permitiendo así el estudio de actividades más complejas como el movimiento de bicicleta, utilizado en terapias de rehabilitación 29; y bajar escaleras 25. Chevalier et al. modificaron su simulador hasta utilizar cinco actuadores 26), (27), (29)-(31: un actuador para el cuádriceps, dos actuadores para los isquiotibiales (medial y lateral) y dos para el posicionamiento horizontal y vertical del tobillo 29. A partir de estas configuraciones, el simulador fue considerado como un sistema de múltiples entradas y múltiples salidas (MIMO, Multiple Input, Multiple Output), el cual puede tener fuertes interacciones entre las variables. Si estas últimas no se conocen, el sistema puede ser tratado como múltiples sistemas de una entrada una salida (SISO, Single Input, Single Output) 21.
En la configuración de cinco actuadores se identificaron las interacciones que existen entre las entradas y salidas 29, por lo que se eligió utilizar una estrategia de control desacoplado para contrarrestar esta interacción cruzada e incrementar el desempeño del controlador. Para obtener un desempeño adecuado, las ganancias del controlador PID fueron sintonizadas utilizando la herramienta Frequency Response toolbox (FRtool) de Matlab. Además, en el diseño de los controladores se usaron las siguientes especificaciones: tiempo de asentamiento <0,5 s, porcentaje de sobre impulso de <30% y robustez >0,55. Con estas especificaciones se obtuvieron las ganancias adecuadas para cada controlador, con intervalos de error de ±5% para el posicionamiento horizontal y vertical del tobillo y de la fuerza del cuádriceps, y un error dentro del ±10% para los isquiotibiales medial y lateral 29.
Chevalier et al. probaron una estrategia que incluye control desacoplado con control prealimentado (feedforward control) 31, esta vez con una descripción más detallada entre las interacciones cruzadas entre las variables manipuladas y controladas, comparando el control desacoplado y el no desacoplado y obteniendo un mejor desempeño cuando se usa el primero, que compensa dichas interacciones cruzadas. Los autores también mencionan que, con cada espécimen probado en su simulador, se requieren ganancias específicas, mientras que las estrategias de diseño probadas utilizan parámetros de sintonización que no cambian (31. Para solucionar este problema de ganancias, se propone un mecanismo de “adaptación” en el que se determinan las ganancias en un corto pre-experimento donde el tobillo sigue cierta trayectoria 30.
Conforme han avanzado los estudios en la implementación de controladores, desde un PID a un control desacoplado con feedforward, se ha ido mejorando el desempeño, probando controladores que indican una mejor respuesta ante las problemáticas que se presentan.
Resumen de las principales características de control de simuladores basados en el modelo Oxford
Al ser los simuladores de Gante y Kansas los más reportados en la literatura, la Tabla I resume las características más importantes de estos y otros simuladores. En estos modelos se pueden distinguir varias características comunes: dependiendo de la complejidad de los movimientos, se utilizan de tres a cinco actuadores servo-hidráulicos en los que se controla posición o fuerza, y se utiliza LabVIEW para el desarrollo de la interfaz. En estos simuladores se utilizó principalmente un algoritmo de control PID, al cual se le aplicó una señal de prueba sinusoidal, simulando una flexión completa o una sentadilla, obteniendo errores dentro de un rango del ±10% para las pruebas y resultados reportados.
Tabla I: Resumen de las características de los controladores aplicados en simuladores tipo Oxford

Algo que cabe destacar de estos simuladores y el controlador es que las trayectorias y señales de prueba utilizadas no representan, en su mayoría, un movimiento cotidiano de la rodilla como lo es el ciclo de marcha, sino que se realizan flexiones, principalmente con movimientos sinusoidales a velocidades de ciclo lentas menores a 1 Hz, sometidas a fuerzas constantes, esto debido quizás a la naturaleza de las pruebas biomecánicas para las que fueron hechos los simuladores, donde comúnmente utilizan especímenes de rodilla de cadáveres humanos. Estos, al ser diferentes unos de otros, requieren ganancias específicas en sus controladores o la necesidad de aplicar controladores con mecanismos de adaptación o más avanzados como el feedforward con control desacoplado.
En la siguiente sección se presenta un modelo utilizado para pruebas de prótesis, así como las diferentes características desde su construcción hasta la forma en que se realizan las pruebas biomecánicas.
Simuladores basados en el modelo Stanmore
Este modelo fue diseñado en 1996, en aras de que se pudieran reproducir hasta 30 millones de ciclos en cada prueba, por lo que el simulador debía ser lo suficientemente adaptable para aplicar diferentes condiciones de prueba y su operación debía estar basada en el control de análisis de datos derivados del ciclo de marcha 11. Este dispositivo controla cuatro de los seis grados de libertad de la rodilla mediante actuadores hidráulicos, donde la máquina es capaz de controlar la rotación de la flexión-extensión en el fémur, la fuerza axial en el fémur que produce un desplazamiento axial sin restricciones en su mecanismo, la fuerza anterior-posterior en la tibia que produce un desplazamiento restringido por tejidos blandos, y el momento de la rotación interna-externa de la tibia 11.
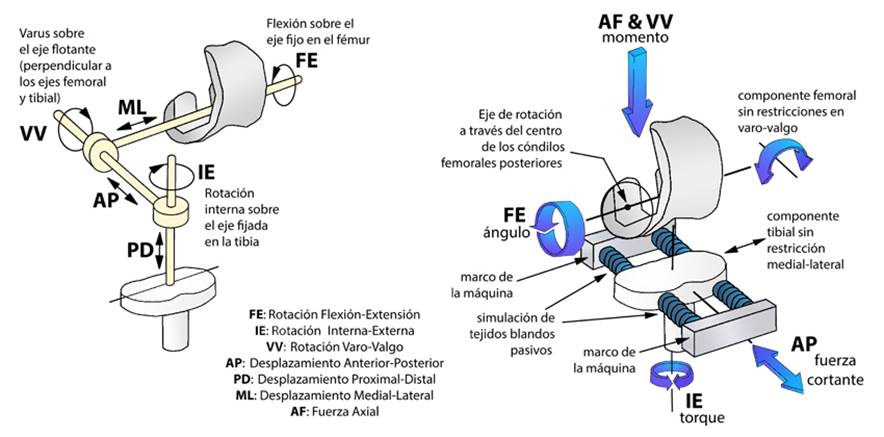
La Fig. 2 muestra la disposición mecánica del simulador de rodilla que sigue el sistema de coordenadas establecido por Grood y Suntay 16 para el modo de desplazamientos y rotaciones y el modo de fuerzas y momentos. Este modelo permite una configuración basada en momentos y fuerzas así como una configuración basada en desplazamientos lineales y angulares.
Figura 2: Esquema del simulador de rodilla Stanmore. Adaptado de 46.
El simulador de Stanmore requiereque el sistema de control sea adaptable a una amplia gama de características de entrada y que posea la capacidad de desarrollar las fuerzas y desplazamientos necesarios para ser aplicados a la rodilla 11.
Adicionalmente se menciona que la elección de actuadores hidráulicos es preferible para la reproducción de trayectorias del ciclo de marcha con altas tasas de cambio. No obstante, si el sistema requiere frecuencias menores a 2 Hz y baja precisión, un sistema neumático podría ser más viable y menos costoso 11.
Aunque en este tipo de simuladores se reportan parámetros de interés específico para el diseño de controladores, se presentan porcentajes de error en cuanto al desempeño del seguimiento de las trayectorias (traking performance) del ciclo de marcha. Existen estudios donde el simulador muestra una buena respuesta ante el seguimiento de los perfiles de fuerza y desplazamiento del ciclo de marcha, con un error promedio RMS de 1,01% para el ángulo de flexión, 2,84% para la fuerza axial, 6,41% para la fuerza anterior-posterior y 3,86% para el torque axial 47.
Otro modelo que trata sobre estudios de control es el AMTI ADL Knee Simulator 48)-(54. En 48), (50), (51 se utiliza un algoritmo de control de aprendizaje iterativo (ILC), reduciendo el tiempo de ajuste del simulador, donde los datos de previas iteraciones son almacenados en la memoria de la computadora y se calcula una nueva señal de control al completar cada ciclo. Este algoritmo reporta errores promedio RMS de 0,5% para la fuerza axial, 0,7% para la flexión, 2,0% para el desplazamiento anteroposterior y 1,7% para el desplazamiento anterior-posterior 48.
Este tipo de mecanismo se ha convertido en uno de los más usados para pruebas de prótesis, por lo que los modelos existentes han sido comercializados y no hay información científica detallada de los mismos. Se pueden encontrar trabajos de los modelos existentes más utilizados, donde se resumen las principales características de rango de carga y desplazamiento, así como de las condiciones de prueba en cuanto a velocidad, temperatura y lubricación 42. En otros casos, las fuentes de información principales son las patentes, páginas de internet y hojas de especificaciones de los fabricantes.
La Tabla II describe los principales modelos y algunas de sus características útiles para el desarrollo e implementación de controladores. En este caso no se muestra la señal de prueba, ya que todos los simuladores de este tipo han sido probados con las trayectorias del ciclo de marcha.
Tabla II: Características de simuladores tipo Stanmore
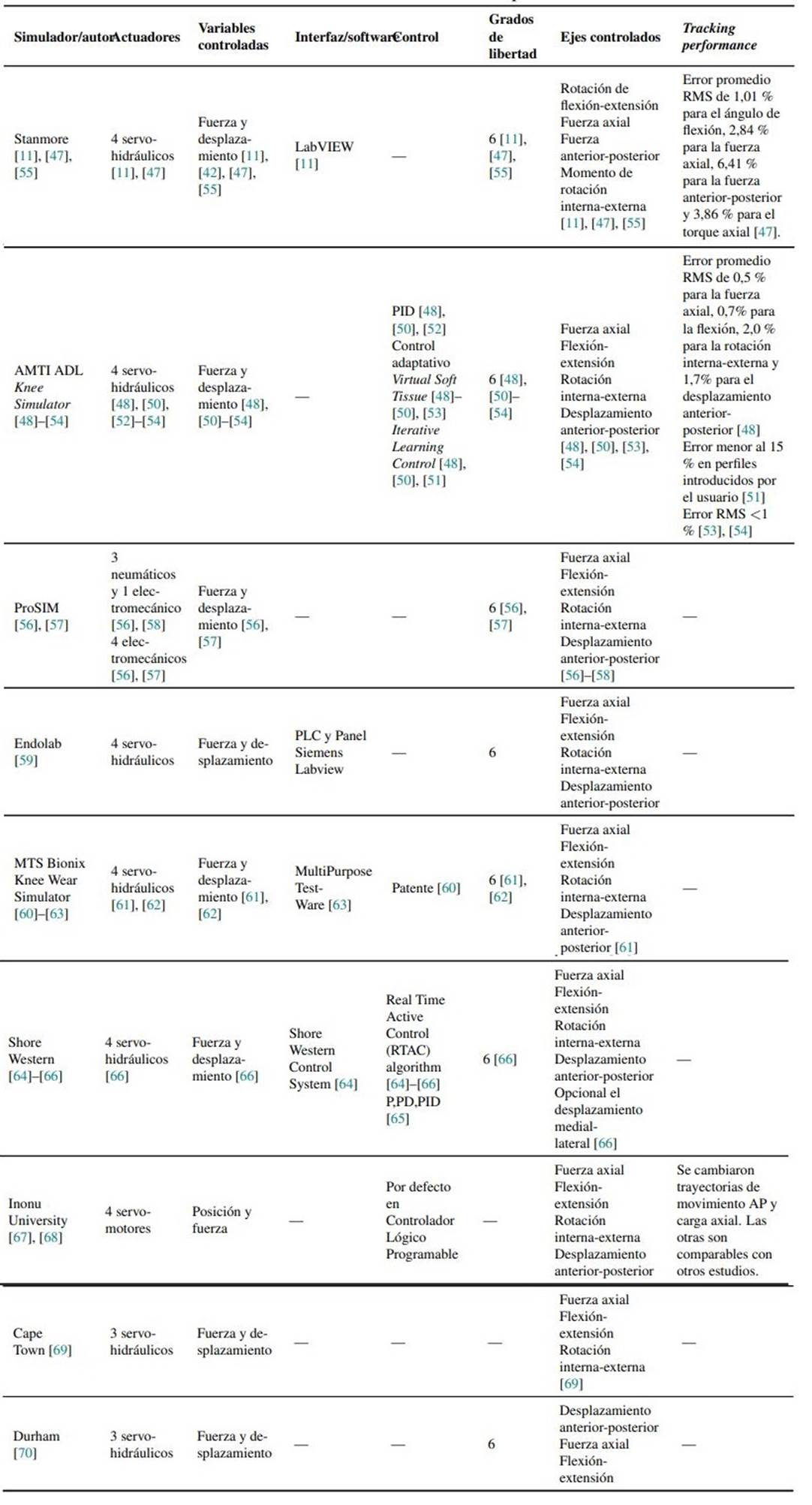
Todos los modelos de la Tabla II han sido comercializados y trabajan bajo estándares o normas como la ISO 14243. La mayoría de los fabricantes no indican los algoritmos de control utilizados para reproducir los movimientos de la rodilla durante el ciclo de marcha. La información de interés que proporcionan es: los tipos de actuadores utilizados, las variables controladas y el error obtenido en la reproducción de los movimientos. Considerando que estos simuladores trabajan bajo una norma, y que esta depende de la variable controlada, se han estudiado las ventajas y desventajas del uso de la norma ISO 14243 para el control de fuerza 71 y el control de desplazamiento 72. Se recomienda utilizar el modo de control de fuerza para los diseños altamente congruentes, constreñidos y con pivote medial, mientras que el modo de control del desplazamiento podría utilizarse para los diseños poco congruentes, poco constreñidos interna o externamente y placas tibiales planas 42. La Tabla III presenta una comparación de la norma ISO 14243-1 para el control de fuerza y la ISO 14243-3 para el control de desplazamiento, donde se observa que la elección de la norma adecuada para el simulador puede ser determinante en el tipo de prótesis diseñada y las pruebas deseadas. En caso de requerir simular movimientos de actividades cotidianas como subir y bajar escaleras, sentarse/pararse y hacer sentadillas, entre otras, es necesario recurrir a normas como la ASTM F3141-17a 73, que muestra diferentes perfiles de carga para pruebas de TKR.
Tabla III: Ventajas y desventajas del control de fuerza y desplazamiento para pruebas de implantes de rodilla 74

Discusión
El objetivo general del presente trabajo fue estudiar las diferentes plataformas y modelos de simuladores, enfocándose principalmente en la recopilación de información de controladores aplicados en sistemas biomecánicos de rodilla. La literatura muestra que los simuladores de rodilla son ampliamente utilizados y desarrollados para investigaciones de interés. El principal problema radica en que estos desarrollos quedan como reproducciones basadas en modelos existentes, a los que se les realizan mejoras o adaptaciones necesarias para los estudios requeridos. Tal fue el caso en las variantes del simulador de Oxford.
Las variantes del modelo Oxford se han limitado a la aplicación de controladores tipo PID. La literatura plantea que esto se debe a que los fabricantes de actuadores proporcionan un controlador con tal característica para el control de desplazamiento y/o fuerza mediante algoritmos PID, el cual es suficiente para la reproducción de trayectorias sinusoidales o formas de onda regulares. Sin embargo, cuando se requiere la reproducción de movimientos más complejos como el ciclo de marcha, se ha visto la necesidad de probar técnicas de control avanzadas para la reproducción de dichos movimientos.
El modelo Stanmore y sus variaciones son más utilizados para investigaciones en áreas ortopédicas y tribológicas, entre otras, pues pueden reproducir movimientos más complejos y con mayor precisión que el modelo anterior. Además, estos pueden ser utilizados para pruebas que involucran millones de ciclos, considerando que estos modelos cuentan con condiciones estandarizadas en pruebas de control de fuerza y desplazamiento (ISO 14243-1/3) 71, 72. Dicho modelo tiene la desventaja de que no hay estudios documentados de las estrategias de control utilizadas en estos dispositivos. No obstante, se puede encontrar, en hojas de especificaciones y patentes, una breve descripción de la manera de controlar sus actuadores, con esquemas de control y descripción de algoritmos o algunos de sus parámetros de desempeño, lo cual sugiere similitudes en el tipo de actuadores utilizados, las variables controladas y el error obtenido en la reproducción de movimientos.
Conclusiones
Después de realizar una investigación detallada de la documentación existente, se ha identificado que, aun después de más de treinta años de estudio y aplicación, los sistemas biomecánicos de rodilla no han sido ampliamente reportados en cuanto a sus estrategias de control y/o automatización. Las similitudes y diferencias entre las plataformas revisadas, como las de Oxford y Stanmore, así como los tipos de actuadores involucrados en la reproducción de movimientos en el sistema mecánico, muestran la existencia de un área de oportunidad para proponer nuevas alternativas de diseño y/o estrategias de control para simuladores de rodilla.
En los modelos derivados de Oxford ha sido suficiente aplicar controladores basados en un PID para el tipo de pruebas realizadas, donde los movimientos son simples perfiles sinusoidales o valores constantes. Esto sugiere la posibilidad de estudiar y aplicar métodos de control avanzado para la reproducción de movimientos más complejos de manera cíclica y acelerada, no solo en el modelo Oxford, sino en nuevos desarrollos basados en el modelo Stanmore. Aunque el modelo Stanmore puede reproducir movimientos de actividades cotidianas con controladores avanzados, las estrategias de control que mencionan algunos fabricantes no están reportadas en la literatura. La ausencia de este tipo de información permite vislumbrar un área de estudio enfocada a la aplicación de controladores a sistemas biomecánicos complejos de este tipo, sobre todo considerando el uso de actuadores no hidráulicos.
La necesidad de usar este tipo de simuladores en diferentes tipos de pruebas relacionadas con la articulación de rodilla -o incluso otro tipo de articulaciones- abre un nuevo campo de investigación en el área de control, automatización y mecánica para el desarrollo de nuevas plataformas que cumplan con los intereses de estudio de investigaciones relacionadas con la biomecánica de la rodilla u otras articulaciones.
Acknowledgements
Agradecimientos
Al CONACyT, por el financiamiento del proyecto No. 2250-6 del FOINS
Referencias
License
Copyright (c) 2022 José Armando Olvera Balderas, Julio César Sosa-Savedra, Rubén Ortega González, José Dolores Oscar Barceinas Sánchez

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










