DOI:
https://doi.org/10.14483/23448393.2312Published:
2005-11-30Issue:
Vol. 11 No. 1 (2006): January - JuneSection:
Science, research, academia and developmentSintonización de ecualizadores difusos basada en técnicas de agrupamiento y mapas autoorganizados
Tuning based on clustering and selforganizing maps for fuzzy equalization
Keywords:
ecualizadores difusos, extracción de datos, mapas autoorganizados, agrupamiento (es).Downloads
References
F. Albu, A. Mateescu, J.C.M Mota, B. Dorizzi. Adaptive Channel Equalization Using Neural Network, ITS '98 Proceedings, vol. 2, pp 438-441. 1998.
Q. Liang, J. M. Mendel «Equalization of Nonlinear Time-Varying Channels Using Type-2 Fuzzy Adaptive Filters», IEEE Transaction on Fuzzy Systems, vol. 8, No 5, pp 551-563. October 2000.
S. K. Patra, B. Mulgrew, «Efficient Architecture for Bayesian Equalization Using Fuzzy Filters», IEEE Transactions on Circuits and Systems, vol. 45, No. 7, pp 812-820. July 1998.
G.D. Forney Jr. Maximum-Likelihood sequence estimation of digital sequences in the presence of inter-symbol interference. IEEE Transactions on Information Theory, vol. IT-18, pp 363378. May. 1972.
F. Olarte, P. Ladino, M. Melgarejo, «Hardware realization of fuzzy adaptative filters for non linear channel equalization», proceedings of the XV International Symposium on Circuits and Systems, Kobe, Japan, May 2005.
A.K. Jain, M.N Murty y P.J. Flynn. Data Clustering: A review. ACM Computer Surveys, vol 31, N° 3 , pp. 264-323. 1999.
B. Martin del Brio y A. Sanz. Redes Neuronales y Sistemas Difusos. Editorial Alfa Omega, México.2002.
J. Vesanto, E. Alhoniemi. Clustering of the Self-Organizing Map, IEEE Transactions On Neural Networks, Vol. 11, No. 3, pp 586-600. May 2000.
Batchelor, Bruce G.: Pattern Recognition: Ideas in Practice. New York: Plenum Press,pp. 71-72. 1978.
J.J. Blake , L.P. Maguire, «The implementation of fuzzy systems, neural networks and fuzzy neural networks using FPGAs», Information Sciences 112 ,pp 151-168. 1998.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación, Academia y Desarrollo
Ingeniería, 2006-00-00 vol:11 nro:1 pág:68-74
Sintonización de ecualizadores difusos basada en técnicas de agrupamiento y mapas autoorganizados
Tuning based on clustering and self-organizing maps for fuzzy equalization
John Figueroa
Ingeniero Electrónico de la Universidad Distrital Francisco José de Caldas. Miembro del Laboratorio de Automática, Microelectrónica e inteligencia Computacional (LAMIC).
Diego Corrales
Ingeniero Electrónico de la Universidad Distrital Francisco José de Caldas.
Resumen
Este artículo presenta dos algoritmos de sintonización de ecualizadores difusos para canales de comunicación de orden dos, basados en técnicas de agrupamiento y mapas autoorganizados. También se presenta los resultados de pruebas experimentales realizadas a cada uno de los algoritmos con el fin de caracterizar su comportamiento ante variaciones de los parámetros del canal.
Palabras clave: ecualizadores difusos, extracción de datos, mapas autoorganizados, agrupamiento.
Abstract
This paper present two novel algorithms for tuning second order fuzzy equalizers. The algorithms are based on data clustering and selforganizing maps techniques. In addition, this paper presents some experimental results concerning the behavior of both algorithms when the parameters of the channel vary.
Key words: data mining, fuzzy equalization, tuning.
1. INTRODUCCIÓN
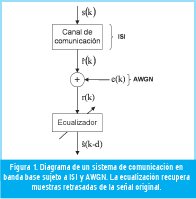
La ecualización de canales es una herramienta utilizada para remover los efectos de distorsión que un canal de comunicaciones introduce en los datos que se transmiten. Dos de los efectos determinantes en la distorsión de la información, y que afectan principalmente la tasa máxima de transmisión, son el ISI (Interferencia Inter.-Símbolos) y el AWGN (Additive White Gaussian Noise) [1] [3]. La función del ecualizador de canal es reconstruir los símbolos transmitidos desde la fuente mediante la observación de la señal que recibe con ruido e interferencia [3]. En la Figura 1 se muestra el diagrama de un sistema de comunicación ecualizado.
Se han propuesto varias técnicas para ecualización de canal basadas en redes neuronales, filtros inversos, teoría de probabilidades y otras [1]-[4]. Cada método tiene parámetros variables que modifican el ecualizador y permiten adaptarlo a una condición dada. El proceso de adaptación del ecualizador al canal se conoce como sintonización del ecualizador. En esta etapa se introducen cadenas de bits de prueba para determinar los parámetros del canal y calibrar el ecualizador. De esta forma el ecualizador se ajusta a las condiciones del canal, y trabaja correctamente mientras dichas condiciones se conserven.
Cuando el comportamiento del canal no es constante durante un intervalo de trabajo del ecualizador, se dice que el canal es variante en el tiempo, y la ecualización puede no ser válida en algún momento. Para este caso el sistema de sintonía debe realizar entrenamientos continuos y modificar los parámetros del ecualizador para que trabaje correctamente [1] [2] [5]. Si dichos parámetros se modifican adecuadamente y con rapidez suficiente, se podrá garantizar una actualización permanente del ecualizador que mejore el rendimiento del canal.
En este trabajo se exploran dos metodologías con las que se puede construir un sintonizador: agrupamiento y mapas auto-organizados. Estos dos métodos buscan extraer la información de centro y desviación estándar para cada grupo den-tro de una denominada constelación de estados, que caracteriza al canal. Los datos obtenidos permiten actualizar los parámetros del ecualizador difuso de acuerdo con las variaciones del canal.
Este artículo se organiza de la siguiente manera: en la sección 2 se hace una pequeña introducción a la ecualización de canales de comunicación, los ecualizadores difusos y de dónde surge la necesidad de la sintonización. Después, en la sección 3, se mencionan algunas generalidades sobre agrupamiento y mapas autoorganizados. La sección 4 describe cada uno de los algoritmos basados en las técnicas estudiadas en la sección 3. En la sección 5 se explicarán algunas pruebas de rendimiento y sus resultados. Para finalizar, en la sección 6 se comentarán las conclusiones de la investigación.
2. ECUALIZACIÓN DE CANAL Y SINTONÍA DEL ECUALIZADOR
En canales de comunicación lineales de orden dos, la interferencia entre símbolos provoca que la muestra presente, a la salida del canal, dependa de la muestra presente original y de su muestra anterior [1] [3]. De forma análoga, para evaluar la información a la salida del canal se toma una muestra presente y una anterior, que se grafican sobre el plano real. Este plano es llamado constelación de estados [2] [5] y mediante su análisis se puede determinar el símbolo original transmitido.
En la constelación se forman grupos de datos cercanos. La forma y tamaño de estos grupos depende de las características del ISI y del nivel de ruido. Cada grupo de datos hace referencia a un mismo símbolo transmitido desde la fuente, haciendo que la ecualización tenga lugar infiriendo el valor del símbolo correspondiente para cada par de muestras provenientes del canal [2] [5].
En la Figura 2 se muestra la constelación de estados para un canal de orden dos, del cual se conoce sus coeficientes y además se ha extraído parámetros característicos de cada grupo. Estos parámetros son la media y la desviación del grupo de datos, que son utilizados por el ecualizador difuso para generar las funciones de pertenencia.
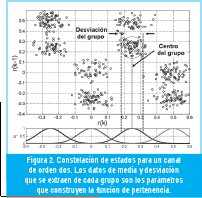
En la ecualización, las funciones de pertenencia evalúan cada punto que ingresa a la constelación y obtienen un factor de distancia con respecto a los centros ajustados por el sintonizador. Este factor de distancia determina la participación de los estados de canal asociados a cada centro. Luego tiene lugar un bloque de inferencias que combina los estados de canal con los valores de salida de la función de pertenencia. Finalmente, se realiza la defusificación mediante la sumatoria de todas las combinaciones y su paso a través de una función signo para obtener los estados de canal ecualizados. Esta metodología de ecualización se describe detalladamente en Olarte [5]
3. TÉCNICAS DE EXTRACCIÓN DE PARÁMETROS
A continuación se revisan dos técnicas de extracción de datos que pueden ser empleadas en la extracción de los parámetros del canal para la sintonización del ecualizador: agrupamiento y mapas autoorganizados.
3.1. Agrupamiento
Los algoritmos de agrupamiento extraen valores representativos de las muestras de entrada. Estos valores se usan para reunir las muestras en una serie de grupos o clusters que se conoce habitualmente como diccionario.
Las funciones de densidad de probabilidad suelen tener una moda o un máximo en una región. Es decir, las observaciones tienden a agruparse en torno a una región del espacio de patrones cercana a la moda. Las técnicas de agrupamiento analizan el conjunto de observaciones disponibles para determinar la tendencia de los patrones a agruparse. Estas técnicas permiten realizar una clasificación asignando cada observación a un grupo, de forma que cada grupo sea más o menos homogéneo y diferenciable de los demás [6].
Los métodos de agrupamiento asocian un patrón a un grupo siguiendo algún criterio de disimilitud. Algunas medidas de disimilitud habituales son la distancia euclidiana, la distancia euclidiana nor malizada, la distancia euclidiana ponderada, la distancia de Mahalanobis y la distancia City Block [6]. Las medidas de disimilitud deben ser aplicables entre pares de patrones, entre un patrón y un grupo y finalmente, entre pares de grupos.
Hay dos tipos de algoritmos de agrupamiento: los que van creando grupos de pequeño tamaño, incluso inicialmente con un solo componente, y los que van fusionando hasta obtener clusters de tamaño superior. Diferentes versiones de algoritmos se diferencian por las reglas que usan para unir grupos o separarlos. El resultado final es un árbol de grupos denominado dendrograma, que muestra como los grupos se relacionan unos con otros.
3.2. Mapas autoorganizados
Los SOM (por sus siglas en ingles SelfOrganizing Maps) o mapas autoorganizados, pueden ser utilizados como algoritmo de agrupamiento de datos a partir de procesos de entrenamiento [7] [8]. Este agrupamiento hace que la proyección de los datos sobre el mapa distribuya sus características de forma gradual.
Los SOM son algoritmos no-supervisados [7], eso quiere decir, que no usan la etiqueta de los datos para el entrenamiento. Sin embargo, en la mayor parte de los casos se usa algún tipo de etiqueta para visualizar los datos correctamente. Se denominan también algoritmos competitivos porque en el entrenamiento se modifica una sola neurona a la vez, lo cual significa que la representación de cada zona del espacio de entrada está concentrada por neuronas, no distribuida.
El número de unidades que forman la red así como su topología, distribución de las neuronas y forma de la red, se determinan antes de empezar el proceso de entrenamiento. Durante el proceso de aprendizaje el SOM se comporta como una red elástica, deformándose para adaptarse a la estructura de los datos que se le presentan. De esta manera la red aproxima la función de densidad de probabilidad de los datos iniciales, situando un mayor número de nodos donde el espacio de entrada es más denso y menos nodos donde los datos están más dispersos.
4. ALGORITMOS PROPUESTOS
Hay que tener en cuenta que el algoritmo de sintonía que se use con un ecualizador debe cumplir dos características importantes: el margen de error en la estimación de los parámetros y el tiempo de procesamiento deben ser mínimos, para poder ser usado en un sistema de tiempo real asociado a una aplicación hardware. Teniendo en cuenta esto, se proponen dos algoritmos: uno que usa técnicas de agrupamiento y otro que usa una variación de un mapa autoorganizado. A continuación se describe cada uno.
4.1. Algoritmo basado en agrupamiento
El sintonizador propuesto en esta parte se basa en una estrategia de agrupamiento mixta, que toma elementos de técnicas típicas como k-medias e ISODATA [6]. El algoritmo se caracteriza por usar operaciones típicas como suma, resta, multiplicación y división, que implican una baja complejidad computacional. La forma como opera el algoritmo es la siguiente.
El algoritmo hace uso de una trama de entrada de n elementos. Esta se segmenta en tres partes que se usan en las distintas etapas del algoritmo. En la primera etapa se halla el máximo y el mínimo de los datos del primer segmento de la trama original, para hallar los centros de los clusters semilla. El espacio bidimensional se divide en 16 grupos de igual tamaño, distribuidos como una matriz de cuatro por cuatro.
Con los datos del segundo segmento de trama se hallan los grupos que corresponden a estados de canal. Cada dato es asociado a un grupo. La pertenencia a un grupo se determina calculando la distancia del dato a cada uno de los centros de los grupos. La menor distancia indica a que grupo pertenece el dato. Cada grupo esta representado por un registro de acumulación, en el cual se van sumando los datos que corresponden a ese grupo. Adicionalmente hay un registro de conteo, por cada grupo, que se incrementa en uno cada vez que un dato es sumado.
Al procesar todos los datos de este segmento se determinan los grupos que más veces fueron activados. El umbral de selección se determina asumiendo una distribución uniforme de los datos en todos los grupos. Debido a la forma en que se distribuyen los datos en la constelación de un canal de orden dos, son ocho los grupos representativos de estados de canal. Para cada uno se calcula el centro real (media) haciendo una división entre el registro de acumulación y el registro de conteo.Con los datos restantes se obtienen las desviaciones para cada grupo. El procedimiento es similar al que se realiza para obtener la media, la diferencia radica en que en lugar de acumular el dato, se almacena en un registro la mayor distancia que se obtiene para cada grupo. Esto se realiza mediante una comparación: si la distancia calculada para ese dato y su respectivo grupo es mayor que la que hay en el registro, pasa ser la nueva desviación, si no, se deja el dato que se tenía acumulado. Al final cada registro va a tener la mayor distancia que se presentó entre el centro del grupo y los datos. Por la simetría y la dispersión de los grupos que se forman en la constelación de estados, esta distancia se puede asumir como la desviación estándar.
Hay que tener en cuenta que el algoritmo entrega los parámetros sólo al terminar de procesar toda la trama inicial
4.2. Algoritmo basado en Mapas Autoorganizados
El algoritmo de búsqueda de centros y desviaciones mediante SOM consta de tres fases.
La primera fase es la generación de una grilla inicial de neuronas, para lo que se utiliza una trama corta que define las fronteras de la constelación. Dentro de estas fronteras se crea una matriz de 16 neuronas equiespaciadas, valor que duplica los posibles estados para un canal de segundo orden.
En la segunda fase se entrenan las neuronas iniciales con una trama de mayor longitud. Las neuronas representan los centros de los grupos, y cada una de ellas se desplaza cierta proporción de distancia cuando una muestra entrante cae en sus proximidades. Para calcular la proximidad de una muestra a cada neurona se utiliza una medición de distancia del tipo City Block, luego del cálculo se busca la menor distancia y se hace desplazar la neurona en dirección a la muestra entrante. El valor de distancia que recorrerá la neurona diminuye linealmente y de forma radial alejándose de la neurona, es decir que entre más alejada esté la muestra entrante, menor será la distancia que se desplace el centro.
Luego de la segunda fase se realiza una reducción de neuronas donde se determinan las ocho que mejor representan la constelación. Esta reducción se basa en el número de veces que cada una fue movida por una muestra.
La tercera fase consiste en la extracción de los parámetros del canal. Mediante un proceso de entrenamiento similar al de la segunda fase se ajustan finamente las ocho neuronas y con ellas se extraen los centros definitivos.
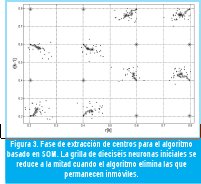
Para la extracción de las desviaciones se utiliza otro mapa autoorganizado que se monta sobre el primero una vez se ha logrado la reducción de centros (fin de la segunda fase). Esta red, al igual que su predecesora, se actualiza con cada muestra que ingresa a la constelación y crea una neurona por cada centro. Esta neurona se actualiza de forma proporcional a su distancia desde la muestra actual hasta el centro del grupo activado. En la figura 3 se muestra la aplicación del algoritmo sobre una constelación de doscientas muestras.
5. PRUEBAS Y RESULTADOS
Para determinar el desempeño de cada algoritmo en la extracción de los parámetros del canal, se propone una serie de pruebas para ser implementadas en software. En estas pruebas se utiliza el modelo de ecualizador difuso propuesto por Patra y Mulgrew [3]. La función que realiza la ecualización requiere la trama de datos y los parámetros que caracterizan las funciones de pertenencia, luego de procesarlas entrega la trama de datos recuperada.
Para generar las tramas de datos de prueba se usa un modelo de canal de segundo orden, no lineal, reportado típicamente en la literatura [2]:
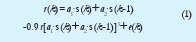
Los coeficientes a1 y a2 determinan la varianza en el tiempo de la función y la posición de los clúster en la constelación de estados. Las muestras de entrada s(k) y s(k-1) son, respectivamente, la muestra presente y la muestra anterior. Que aparezcan estas dos muestras define el orden del canal. La componente e(k) representa el AWGN.
Se proponen dos pruebas de desempeño para los algoritmos. En la primera se varían las condiciones de ruido en el canal y el número de muestras suministradas para realizar la ecualización. En la segunda se evalúa la complejidad computacional asociada a cada algoritmo partiendo de las operaciones que se realizan. A continuación se comentan en detalle las pruebas y los resultados obtenidos para cada algoritmo.
5.1. Pruebas de rendimiento para diferentes condiciones de canal
En esta prueba el ecualizador se sintoniza con los parámetros extraídos con cada algoritmo y se calcula el BER (Bit Error Rate) para una trama de entrenamiento. El nivel de BER se utiliza como parámetro de evaluación de la prueba.
La longitud de la trama de entrenamiento se varía desde 100 muestras hasta 350 muestras. La relación señal a ruido se varía desde 12dB hasta 22dB. Cada entrenamiento se repite 100 veces para calcular un valor de BER medio que asegure la confiabilidad de los resultados.
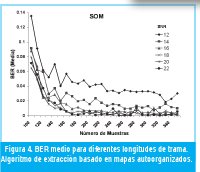
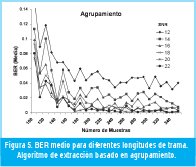
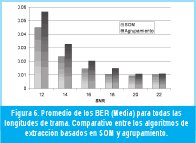
En las Figuras 4 y 5 se puede observar que el BER medio para longitudes de trama superiores a 180 muestras se mantiene por debajo de 0.06, tanto para el algoritmo basado en agrupamiento como para el algoritmo basado en SOM. También se observa que en el algoritmo basado en SOM los valores de BER medio para todas las relaciones SNR son, en promedio, menores que para el algoritmo de agrupamiento. En la Figura 6 se muestran los valores de BER (Media) promedio para todas las longitudes de trama de prueba. Igualmente se observa que el algoritmo basado en SOM tiene los menores valores de BER. También se observa que la diferencia en el desempeño entre los dos algoritmos disminuye a medida que la relación señal a ruido aumenta.
5.2. Evaluación de la complejidad computacional de los algoritmos propuestos
La complejidad computación de los algoritmos de extracción propuestos es función del número de operaciones necesarias para lograr un resultado. Para la evaluación de los algoritmos se considera la ecuación que establece la complejidad de un algoritmo en términos del número de operaciones y un factor de ponderación asociado a cada una:
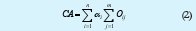
donde:
n= Número de operaciones diferentes.
m= Número de operaciones del mismo tipo.
O= Operación.
α= Factor de ponderación de complejidad o coeficiente de penalización.
El factor de ponderación está relacionado con el costo computacional de las operaciones. Para efectos prácticos, el algoritmo que obtenga el menor resultado se considera como el algoritmo computacionalmente menos complejo.
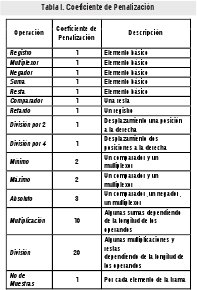
En la Tabla I se presentan las operaciones y los coeficientes de penalización asociados a cada una de ellas. El valor de cada coeficiente se calcula teniendo en cuenta el número de operaciones básicas que se usan para construir determinada función [10]. Una operación básica tiene un punto de penalización.
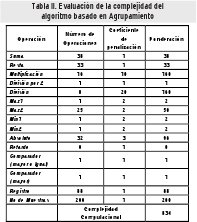
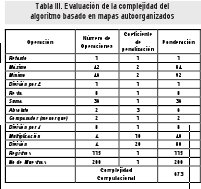
En la Tabla II y la Tabla III se muestra el cálculo de la complejidad computacional para cada uno de los algoritmos. Observando cada una de las fases de operación se determina el tipo y el número de operaciones que se usan. Estos resultados son ponderados con los coeficientes de la Tabla I y totalizados para determinar el valor de complejidad. Al comparar la información que suministran las tablas, se determina que el algoritmo basado en mapas autoorganizados ofrece una menor complejidad computacional.
6. CONCLUSIONES
Se han presentado dos métodos de sintonía para ecualizadores difusos, basados en técnicas de agrupamiento y mapas Autoorganizados. Mediante la observación de los datos de un canal, que esta afectado por ISI y por AWGN, los algoritmos de sintonía son capaces de extraer las medias y las desviaciones que el ecualizador emplea para calibrar sus funciones de pertenencia y recuperar adecuadamente los datos originales.
Las pruebas de rendimiento muestran que el algoritmo basado en mapas autoorganizados ofrece niveles de BER menores que el algoritmo basado en agrupamiento, probado para diferentes longitudes de trama y diferentes niveles de ruido. Adicionalmente, el cálculo de la complejidad computacional para cada algoritmo, que parte de la revisión del número de operaciones empleadas y de la complejidad de cada una, también arroja resultados favorables para el algoritmo basado en mapas autoorganizados por una reducción en la complejidad computacional de cerca del 20%, comparado con el algoritmo basado en técnicas de agrupamiento.
El siguiente paso en esta investigación es la reevaluación y adecuación del algoritmo basado en mapas autoorganizados para su implementación en una plataforma hardware y posterior acoplamiento al ecualizado difuso descrito en Olarte [5].
7. AGRADECIMIENTOS
Agradecemos al Laboratorio de Automática, Microelectrónica en Inteligencia Computacional, LAMIC, el permitir desarrollar con ellos este trabajo y brindar el apoyo necesario en las consultas y resultados de investigación anteriores. También agradecemos al Ingeniero Miguel Melgarejo MSc. por su permanente asesoría en nuestra labor investigativa y la revisión y aportes a este artículo.
8. REFERENCIAS BIBLIOGRÁFICAS
[1] F. Albu, A. Mateescu, J.C.M Mota, B. Dorizzi. Adaptive Channel Equalization Using Neural Network, ITS '98 Proceedings, vol. 2, pp 438-441. 1998.
[2] Q. Liang, J. M. Mendel «Equalization of Nonlinear Time-Varying Channels Using Type-2 Fuzzy Adaptive Filters», IEEE Transaction on Fuzzy Systems, vol. 8, No 5, pp 551-563. October 2000.
[3] S. K. Patra, B. Mulgrew, «Efficient Architecture for Bayesian Equalization Using Fuzzy Filters», IEEE Transactions on Circuits and Systems, vol. 45, No. 7, pp 812-820. July 1998.
[4] G.D. Forney Jr. Maximum-Likelihood sequence estimation of digital sequences in the presence of inter-symbol interference. IEEE Transactions on Information Theory, vol. IT-18, pp 363378. May. 1972.
[5] F. Olarte, P. Ladino, M. Melgarejo, «Hardware realization of fuzzy adaptative filters for non linear channel equalization», proceedings of the XV International Symposium on Circuits and Systems, Kobe, Japan, May 2005.
[6] A.K. Jain, M.N Murty y P.J. Flynn. Data Clustering: A review. ACM Computer Surveys, vol 31, N° 3 , pp. 264-323. 1999.
[7] B. Martin del Brio y A. Sanz. Redes Neuronales y Sistemas Difusos. Editorial Alfa Omega, México.2002.
[8] J. Vesanto, E. Alhoniemi. Clustering of the Self-Organizing Map, IEEE Transactions On Neural Networks, Vol. 11, No. 3, pp 586-600. May 2000.
[9] Batchelor, Bruce G.: Pattern Recognition: Ideas in Practice. New York: Plenum Press,pp. 71-72. 1978.
[10] J.J. Blake , L.P. Maguire, «The implementation of fuzzy systems, neural networks and fuzzy neural networks using FPGAs», Information Sciences 112 ,pp 151-168. 1998.
John A. Figueroa R.
Ingeniero electrónico de la Universidad Distrital Francisco José de Caldas, Bogotá. Proyecto de grado meritorio por la Realización Hardware de un Algoritmo de Sintonía Automática para Ecualizadores Difusos de Canales de Comunicación No Lineales de Orden Dos. Actualmente trabaja en el diseño de un sistema de trazabilidad para el Sistema de Abastecimiento Alimentario de Bogotá (SAAB). e-mail: jafigueroar@udistrital.edu.co
Diego A. Corrales C.
Ingeniero electrónico de la Universidad Distrital Francisco José de Caldas, Bogotá. Proyecto de grado meritorio por la Realización Hardware de un Algoritmo de Sintonía Automática para Ecualizadores Difusos de Canales de Comunicación No Lineales de Orden Dos. Actualmente trabaja en el centro interactivo Maloka como investigador en el área de Educación en Tecnología. e-mail: dacorralesc@yahoo.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)