DOI:
https://doi.org/10.14483/23448393.3495Published:
1999-11-30Issue:
Vol. 5 No. 1 (2000): January - JuneSection:
Science, research and developmentDiseño de un algoritmo genético para un sistema logístico de distribución
Keywords:
Logística empresarial, logística de distribución, algoritmos genéticos, secuenciación de vehículos. (es).Downloads
References
Montaña, Yara. (1998). Logística, cómo responder a las necesidades y exigencias crecientes del cliente. Revista Clase Empresarial. N°65 (noviembre). Santafé de Bogotá, D.C., Colombia.
Fea, Ugo. (1995). Hacia un Nuevo Concepto de Empresa. Editorial Alfaomega Marcombo. Barcelona, España.
Bonson, Enrique. (1999). Tecnologías Inteligentes para la Gestión Empresarial. Ed. Alfaomega -- Rama. Barcelona, España.
Braidot, Nestor. (1992). Marketing total. Ed. Macchi. Buenos Aires, Argentina.
Martinich, Joseph. (1997). Production and Operations Management. John Wiley and Sons. Missouri, USA.
Arbones, Eduardo. (1989). Logística Empresarial. Ed. Marcombo. Barcelona, España.
Badiru, Adedeji. (1992). Expert Systems Applications in Engineering and Manufacturing. Ed. Prentice Hall. New Jersey, USA.
Hicks, Donald. (1999). The State of supply Chain Strategy. Revista Solutions N°8 Vol 31. (august). Atlanta, USA.
Spalding, Jan. (1998). Transportation Industry Takes the Ri ght-of-Way in the Supply Chain. Revista Solutions N°7 Vol 30. (July). Atlanta, USA.
Savoie, Brian. (1998). The Last Word on Supply Chain Improvement. Revista Solutions N°10 Vol 30. (October). Atlanta, USA.
Gen, M y Cheng, R. (1997). Geneti c Algorithms and EngineeringDesign. Ed. Wiley. USA.
Larrañaga, L. ¡Error! Marcador no definido.. Departamento de ciencias de la computación e Inteli gencia Artificial Universidad del País Vasco.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencia, Investigación y Desarrollo
Ingeniería, 2000-00-00 vol:5 nro:1 pág:20-27
Diseño de un algoritmo genético para un sistema logístico de distribución
Germán Méndez Giraldo
Doctor en Ciencias Técnicas Universidad Central de las Villas "Marta Abreu". Magister en Ingeniería Industrial Universidad de los Andes, Especialista en Informática Industrial Universidad Distrital, Profesor de la Facultad de Ingeniería Universidad Distrital. Consultor empresarial.
Resumen
Para las organizaciones productivas es importante mejorar la función de servicio al cliente, entendiendo a ésta como una función que depende de muchas variables entre las que priman la calidad del producto o del servicio, el precio y el tiempo de entrega. Para mejorar la función de servicio al cliente se ha incorporado a la gestión de las actividades del negocio la Logística Empresarial que se compone de la logística de suministros, la de manufactura y la de productos; ésta última encargada de llevar el bien a manos del cliente.
La Logística se basa en juicios de la experiencia, modelos matemáticos y otras técnicas clásicas, sin embargo, por las condiciones reales del sistema, éstas, quedan cortas brindando soluciones parciales e incompletas, por tal razón hoy en día, se buscan otras herramientas novedosas como algoritmos genéticos que mejoran sustancialmente esta situación. El presente artículo muestra el diseño de un algoritmo genético para resolver el problema de distribución convencional y que consisten en determinar las rutas y los medios de transporte para suplir distintas demandas en puntos remotos. Además se contrasta con la técnica convencional más utilizada para este propósito, demostrando la reducción en un 30% del costo generado.
Palabras Claves: Logística empresarial, logística de distribución, algoritmos genéticos, secuenciación de vehículos.
Abstract
For manufacturing business is interesting to improve the customer's service function, this is a function that depends on many variables which the more important are: quality, price and lead time. For this reason in the manufacturing organizations are incorporated the Business Logistic that composed for supply, manufacturing and distribution logistic, the last is occupied of merchandise transshipment to customer and clients.
The Logistic is based on experience, mathematical models and other classic techniques, but for the real manufacturing systems, these tools are inadequate and give poor solutions, for that, today analysts offer novelty applications such as Genetic Algorithms. In this article is presented a design of Genetic Algorithm to solve the distribution problem that consist on finding the paths and vehicles to transshipment the products to remotes points. In addition, it is compared with the most conventional tool used for this propone, and demonstrated the cost reduce in a 30%.
Key words: Enterprise logistic, distribution logistic, genetic algorithm, vehicles sequences.
O. INTRODUCCIÓN
Las organizaciones productivas basan sus estrategias competitivas en la logística empresarial que no es más que todo el conjunto de actividades que permiten una vinculación de todos los actores de un sistema de producción: Proveedor - Transformador - Consumidor [1].
Esta cadena logística, para su conveniente gestión, ha sido dividida en tres grandes áreas claramente definidas: logística de suministro, donde lo importante es el flujo de materiales desde el proveedor hasta el transformador; logística de manufactura, que involucra toda la gestión de los bienes en el proceso productivo y la logística de distribución cuyo objetivo consiste en colocar el bien en manos del cliente [2].
Para la empresa productora y en general cualquier organización empresarial su comportamiento se liga a la función de servicio que brinde, dicha función aumenta conforme a los niveles de calidad real y percibida aumenten (supermodularidad), asimismo aumenta cuando los precios y tiempos de entrega disminuyen (submodularidad). Cualquier esfuerzo encaminado a la reducción de costos y por ende de los precios de venta, disminuir los defectos e inconformidades del bien frente a sus especificaciones y por acortar los plazos de entrega, son bienvenidos y están en el orden del día de la logística empresarial [3].
Y aunque no exista un punto que pueda considerarse más importante que otro dentro de la cadena logística, si es bien conocido que al final de dicha cadena esta función de servicio se vuelve más crítica, ya que por un lado, se tiene un mayor contacto con el cliente que es el eje de trabajo logístico y por otro, en esta etapa de distribución se trabaja con un producto terminado cuyo valor agregado es más alto y costoso para la organización [4]. Es por ello que se aborda la problemática de distribución física de los bienes/servicios a través de técnicas no convencionales, ya que las convencionales no ofrecen soluciones adecuadas al caso de colocación de las mercancías en manos del cliente, las principales técnicas consisten en modelos convencionales de transporte cuya solución cae en el campo de la programación lineal y la programación entera [5], sin embargo, desconocen los efectos no convexos de los costos causados por el uso de recursos.
Otras técnicas como la teoría de grafos abordan y resuelven los problemas de distribución, algoritmos como el de Etiquetas o el de Dikjstra resuelven efectivamente problemas de rutas mínimas, flujos máximos o costos mínimos, sin embargo caen en problemas propios de su ejecutoria algorítmica elevando su tiempo de ejecución al contemplar costos no lineales.
Esto ha desencadenado el uso de modelos heurísticos que se basan en el buen juicio y la experiencia, de los cuales se descata el Método del Ahorro que permite realizar las secuencias del despacho de vehículos y que en últimas determina medios de transporte asignados a rutas de distribución. Sin embargo sólo contempla restricciones de un solo tipo y su extensión a varias características limitantes implica una modificación a su algoritmo. Como si fuera poco se consume más esfuerzo y tiempo en determinar una "buena solución" [6].
Algunos enfoques modernos que se pueden utilizar y entre los que vale la pena mencionar son los sistemas expertos, las redes neuronales, la lógica difusa y los algoritmos genéticos entre otros [7], pero que han sido menos tratados y menos aún implementados.
I. PROBLEMA DE SECUENCIAS DE VEHÍCULOS
Este tipo de problema concierne a un conjunto de clientes, todos con dirección y demanda de servicio de un solo producto aunque en extensiones se puede abordar un conjunto o portafolio de productos. A todos estos clientes se les suministra desde un solo punto, de donde se despachan una serie de vehículos [8].
El problema consiste en diseñar a costo mínimo, rutas de estos vehículos basadas en las siguientes restricciones:
- Se debe satisfacer la demanda de servicio por unidad de tiempo de cada cliente.
- El tiempo total de servicio o bien la distancia total de recorrido no debe exceder una cantidad prefijada. Esto suele suceder cuando se tienen restricciones de tipo legal o sindical.
- Existe un intervalo de tiempo en el cual el cliente debe ser atendido. [9], [10].
Surge entonces la necesidad de desarrollar un procedimiento matemático que resuelva el problema de establecer la red de distribución más adecuada desde el punto de vista de costos y tiempos de entrega, para tal efecto se construye el algoritmo genético como alternativa de solución.
II. ALGORITMOS GENÉTICOS
1. Definición
Es un modelo matemático con origen en la biología, que toma una población de soluciones y aplica sobre ella una prueba de aptitud que juzga su desempeño y es perturbada por medio de operadores genéticos, es un proceso evolutivo, para generar una nueva población, proceso que se repite hasta obtener una generación muy cercana al óptimo.
2. Aplicaciones
Una de las áreas en que los algoritmos genéticos se desempeñan bastante bien es en la optimización. Un Algoritmo Genético (A.G.) es muy robusto, esto significa que trabaja con una amplia gama de problemas. Al comparar los algoritmos de optimización más tradicionales, las mayores diferencias son:
- Los algoritmos genéticos trabajan con una versión codificada de los parámetros;
- Ellos no buscan desde un punto único, pero sí desde una población de puntos;
- Ellos usan información de resultados en vez de derivados u otro conocimiento auxiliares;
- Ellos usan reproducción estocástica en vez de reglas determinísticas.
Muchos problemas pueden verse como problemas de optimización.
Los problemas de optimización son modelos formulados matemáticamente con muchos parámetros independientes que resultan en una función llamada de aptitud. Esta función de aptitud describe la calidad del modelo (o individuo) para el conjunto de parámetros. En la función de aptitud se puede modelar toda clase de demandas conflictivas [11]. En general se define una función como:
f (x1, x2,x3,...,xn)
Donde x1, x2,x3,...,xn son los parámetros independientes que necesitan ser determinados. Si se quiere usar un algoritmo genético se necesita asegurarse que esta función sea siempre mayor que cero. Los campos de aplicación usuales son: Diseño asistido por computador (CAD), pronósticos financieros, programas de producción, exploración petrolera, control de robots, en combinaciones con redes neuronales y por supuesto en el campo de la logística.
3. Elementos
Basados en la selección natural, se considera lo siguiente:
- El algoritmo opera sobre una población de individuos.
- Cada individuo es una solución potencial alproblema determinado.
- Después de una población inicial generada aleatoriamente, el algoritmo evoluciona mediante tres operadores:
- La selección que es igual a la supervivencia de la estrategia elite. La clave es la preferencia de los mejores individuos (estrategia elite), permitiendo pasar sus genes a la próxima generación. El desempeño de cada individuo depende de su aptitud que puede ser determinada por una función objetivo o por un juicio subjetivo.
- El crossover que representa la mezcla entre individuos. De dos individuos elegidos de la población elite, en un ligar elegido aleatoriamente dentro de sus cadenas de bits se efectúa un corte, los valores de las dos cadenas se intercambian hasta este punto, por ejemplo: S 1= 000000 y S2 = 111111 y el punto de crossover es 2, entonces: S1'=110000 yS2'. 001111.
Los dos nuevos hijos creados de este mezcla se ubican en la próxima generación de la población, por la recombinación de partes de los mejores individuos, el proceso crea mejores individuos [12]. - La mutación que introduce modificaciones aleatorias. Con una baja probabilidad, un grupo de los nuevos individuos tendrán algunos de sus bits alterados, su propósito radica en mantener la diversidad dentro de la población e inhibir la convergencia prematura.
Los tres aspectos más importantes al usar algoritmos genéticos son:
- Definición de la función objetivo.
- Definición e implementación de la representación genética.
- Definición e implementación de los operadores genéticos.
Una vez definidos los anteriores aspectos, se presenta el algoritmo genético para el caso de secuencias de vehículos.
III. METODOLOGÍA
1. Definición del Caso
Como se ha mencionado, el problema consiste en determinar la secuencia de vehículos más apropiada a un problema específico, en este trabajo se presenta el caso de una red de distribución que consta de una Fábrica y 20 centros de distribución o depósitos; cada uno posee un valor dij que representa la distancia entre un punto i y el punto j. Se dispone de varios medios de trabajo (k), y cada uno de ellos posee una capacidad Qk de transportar carga, adicionalmente se ha colocado un límite máximo en kilómetros a recorrer por día y su correspondiente valor que se compone de un valor fijo y otro variable, restricciones de cumplimiento de las necesidades de cada almacén, cumplir con la jornada laboral de los conductores y que los vehículos retornen a la fábrica al final de su ruta.
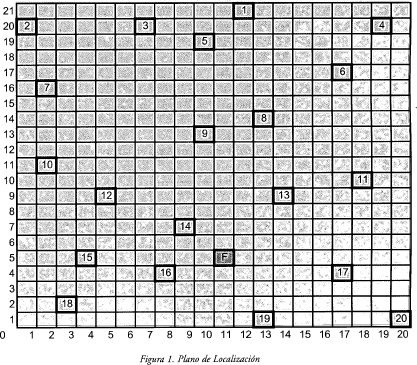
Las distancias se calcularon mediante un mapa de localización (figura 1) y aplicando la ecuación de distancia euclideana: dij= [(xj-xi)2 + (yj-yi)2]12 .
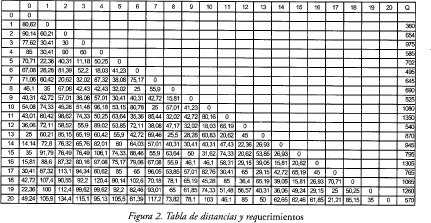
En la figura 2, se 13 resenta la tabla de distancias entre nodos y los requerimientos de los depósitos, se dispone de 4 medios de 2 toneladas y 4 medios 3 toneladas, sin embargo estos recursos son excesivos como se demuestra más adelante.
2. Generación del Algoritmo Genético
En la construcción del algoritmo genético se siguieron los pasos descritos en los procesos de las figuras 3 y 4.
DIAGRAMA DE BLOQUES ALGORITMO GENETICO
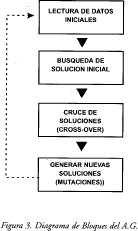
DIAGRAMA DEL PROGRAMA
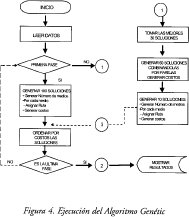
En la figura 3 se muestra globalmente las etapas para generar el A.G. como se enuncio anteriormente, en la figura 4 se muestran los pasos seguidos de manera global en la ejecución del desarrollo del algoritmo. A continuación se presenta en más detalle la construcción del algoritmo genético para resolver el problema de la secuencia de vehículos.
2.1 Elementos constitutivos del Algoritmo Genético
Especie o Individuo: La solución al problema de secuencias se da por un vector compuesto de parámetros o segmentos, en este caso la especie no será de naturaleza binaria sino de tipo flotante y los segmentos a trabajar son 2: El primero que representa los tipo de vehículo a utilizar, el segundo, que muestra el orden de visita a los diferentes depósitos o destinos.
- Población: Atendiendo a los teóricos ya mencionados, sobre la conveniencia de poblaciones relativamente grandes [12], se trabaja con una población de 100 individuos.
- La función de aptitud: Es una función de costo de transporte que involucra componentes dados por el costo de activar los vehículos, el costo proveniente de la carga a transportar por distancia recorrida y un costo de penalización cuando se violan las restricciones.
- Restricciones: Cada vehículo tiene una capacidad en volumen y en peso, la cual no puede ser excedida, adicionalmente, a cada depósito debe llegar la cantidad exacta de sus demandas o requerimientos; finalmente, los vehículos por disposiciones laborales, no pueden exceder una cantidad máxima de kilómetros a recorrer.
- Función de Penalización: Cada vez que se viole una o varias de las restricciones por parte de las especies, el valor de la función de aptitud toma un valor correspondiente a K*10 d. Donde K es el valor de la suma de activar todos los vehículos, mas el valor de recorrer todas las distancias multiplicado por la suma de las cargas a transportar, d es una constante de ampliación y que se recomienda que sea el valor del número de dígitos significativos de la cantidad más grande.
- La Selección o Supervivencia de la Elite, se garantiza mediante la generación de una función de costo, la cual se ordena en forma ascendente. Esta especie se conforma de dos vectores de punto flotante, el primero determina el nodo visitado y el segundo el medio de transporte utilizado. En caso de no ser una especie factible, se penaliza con un valor como el ya descrito. Para seleccionar las especies a cruzar, se trabaja con la elite, es decir las 30 mejores soluciones que en la fase siguiente se cruzan para generar otras 60 soluciones.
- El crossover que representa la mezcla entre individuos se realiza ligando los dos segmentos constitutivos de las especies, es decir, los tipos de vehículos a utilizar en su orden y los depósitos a visitar en un orden específico. Se conjuga entonces, un segmento de depósitos a visitar de la primera especie con un segmento de vehículos a utilizar de la segunda especie; se genera su costo como en el punto anterior. Los dos nuevos hijos creados de este mezcla se ubican en la próxima generación de la población. - La mutación o modificación aleatoria se genera como en la primera solución, es decir, mediante la generación de variables aleatorias y que se expone más adelante.
- El Criterio de detención permite determinar la convergencia de la solución, pero debe cuidar que esta solución (óptimo local) no se encuentre en un valor alejado del óptimo global, para ello se debe perturbar al sistema de tal suerte que se cumpla con lo anterior, esto se puede hacer cambiando la estructura de la elite y del crossover.
2.2. Detalle del Algoritmo Genético
- Paso Inicial: Leer los datos básicos de demanda de los distintos depósitos. Así mismo leer los medios disponibles de transporte con sus respectivos atributos de peso, volumen, leer las restricciones impuestas al sistema y los parámetros constitutivos de la función de aptitud. Hacer Fase igual a uno, Hacer Función de Aptitud anterior igual a K. Paso Uno: Si es una Fase distinta a la uno el número de especies a generar es 10 de lo contrario el número de especies a generar es 100.
- Paso Dos: Para el número de generaciones a realizar se debe calcular un conjunto de 8 números aleatorios que determinen el tipo de vehículo a utilizar, mediante una probabilidad de ocurrencia que se recalcula cada vez con los vehículos disponibles, esto produce un segmento de la especie que es el orden en que se van a utilizar los vehículos. Luego se genera otro conjunto de números aleatorios (distintos) igual a 20, para determinar la secuencia de ciudades a visitar y que también se recalcula basado en las probabilidades de las ciudades que todavía no se han marcado como visitadas.
- Paso Tres: Para cada especie se determina su factibilidad, es decir, en el orden en que se generaron los vehículos se asigna la carga según el mínimo valor de la capacidad del medio (dada por volumen y/o peso) o de la carga remanente a transportar. Luego se procede a despachar según el orden de los depósitos a visitar, para ello se controla que la demanda del depósito no este satisfecha y que no exceda el número máximo de kilómetros a recorrer. Si sobran vehículos por que no hay carga remanente a transportar no se activan para no generar costos. Finalmente, de todo este proceso, se calcula el valor de la función de aptitud, en caso de haberse violado una o más restricciones se penaliza la función.
- Paso Cuatro: Si es la Fase uno ir al Paso Cinco, si no, seleccionar las primeras 30 especies y de la Fase anterior y conformar grupo Elite, generar número aleatorios según probabilidad de ocurrencia del grupo elite remanente y por parejas combinar las especies según lo mencionado en el crossover, obteniendo dos nuevos individuos. Luego generar el valor de la función de aptitud tal y como se explico en el Paso Tres.
- Paso Cinco: Generar una población de 100 individuos obtenida de los Pasos Dos y Cuatro. Ordenar esta población de manera ascendente según la función de aptitud calculada anteriormente.
- Paso Seis: Comparar valor de la función de aptitud actual con función de aptitud anterior, si son iguales se incrementa etiqueta de repetición en uno. De lo contrario se actualiza valor de función de aptitud, el valor de la etiqueta de repetición vuelve a cero, se incrementa la Fase y se va al Paso Uno. Si la etiqueta de repetición es mayor o igual a 5 y menor o igual a 10, se cambia el proceso de crossover, esto se hace en el Paso Siete. Si la etiqueta de repetición es mayor a 10 el proceso de búsqueda termina y se acepta como la mejor solución el valor de la especie ubicada en el primer puesto de la Fase actual.
- Paso Siete: Se modifica el crossover como se mencionó alterando el proceso de búsqueda y aceptando la técnica de Simulated Annealing [11], [12], a partir de especies de baja evolución. Esto quiere decir que de las 100 especies de la población se toman las 20 mejores y las 20 peores y se cruzan como en el paso 4 obteniendo 80 especies, las 20 restantes se toman del proceso de mutación. En este paso también se procede a evaluar la factibilidad de la solución mediante el cálculo de la función de aptitud. Este proceso continua en Cinco pero las soluciones ahora serán dadas por este paso.
Vale la pena destacar que las valoraciones se hacen sólo con "especies buenas" o factibles, de esta forma se logra generar rápidamente un conjunto relativamente bueno de soluciones y que potencialmente se aproximan al óptimo. Como la evaluación sería muy difícil de realizar manualmente para evaluar la conveniencia de la técnica se desarrolló un programa en Visual Basic, para ejemplificar se muestra una pantalla de resultados en la figura 5.
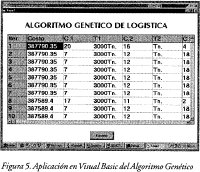
3. Resultados
Para analizar las bondades de utilizar esta herramienta, se compara frente a una de las técnicas más utilizadas para la secuenciación de vehículos, es decir la que utiliza el método de ahorro. Esta técnica consiste en escoger el máximo ahorro en desplazamientos partiendo del concepto expuesto a continuación.
Si hay dos nodos destino: A y B, que deben ser surtidos de un nodo fuente F, se supone que la distancia de F a A es DFA, que es igual a la distancia de A a F DAF y la distancia de F a B es DFB, igual a la distancia DBF ahora se supone una distancia de A a B como DAB, que es igual a la distancia de B a A por simetría. Si se visita los dos nodos destino a partir del nodo fuente, se obtiene una distancia total dada por DT= DFA + DAF + DFB + DBF, pero si se visita primero un nodo y luego a partir de este se visita el otro, se tiene una distancia equivalente dada por DT1 = DFA + DAB + DBF, el ahorro consiste en restar DT - DT1. Ahorro = DFA + DFB - DAB .
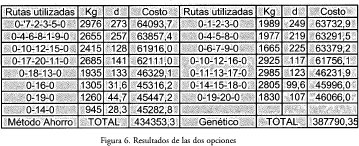
Se visitan los nodos de acuerdo al ahorro de manera descendente, cuidando de respetar las restricciones impuestas al sistema, como la capacidad del sistema y la distancia recorrida. A partir de este procedimiento se obtienen los resultados que se muestran en la figura 6.
En general se obtiene una diferencia a favor del 12% y la utilización de sólo 7 de los 8 medios de transporte disponibles, con lo que obtiene un 18 % adicional. Además se mejora la utilización de los recursos por cuanto en promedio hay un mayor desplazamiento de estos.
IV. CONCLUSIONES RECOMENDACIONES
En el mundo de los negocios donde se busca incansablemente elevar los niveles de productividad (eficiencia y eficacia simultáneas), la logística entendida como la rama del conocimiento dedicada a la gestión de la cadena cliente-proveedor, ha demostrado su bondad para mejorar los niveles de servicio al cliente basados en el aumento de la calidad, la disminución de costos y reducción de los plazos de entrega, principalmente. Aunque la logística comprende muchos tópicos, en la actualidad resulta de interés resolver el problema de despacho de bienes a los clientes, para ello se han utilizado técnicas basadas en las heurísticas conocidas como los algoritmos de ruteo, sin embargo este tipo de solución aunque sea simple suele ser impracticable cuando la magnitud de los nodos (puntos de destino) es grande.
Los algoritmos genéticos permite dar respuesta a uno de los inconvenientes más complicados presentados en la Investigación de Operaciones, resolver los problemas de solución combinatoria. Estas búsquedas se basan en la teoría de supervivencia y mejoramiento de las especies, donde estas son ubicadas en los vectores solución.
Para atender adecuadamente a los algoritmos genéticos se recomienda que los datos de entrada sean adecuados, esto es que las distancias sean reales, las capacidades de los medios y los demás atributos como volumen, peso y costo. Posteriormente, se debe considerar un número de especies a generar y que en cualquier caso no deben ser inferiores a 50, así como rutinas de crossover y de mutación consistentes con el tipo de problema a resolver.
REFERENCIAS
[1] Montaña, Yara. (1998). Logística, cómo responder a las necesidades y exigencias crecientes del cliente. Revista Clase Empresarial. N°65 (noviembre). Santafé de Bogotá, D.C., Colombia.
[2] Fea, Ugo. (1995). Hacia un Nuevo Concepto de Empresa. Editorial Alfaomega Marcombo. Barcelona, España.
[3] Bonson, Enrique. (1999). Tecnologías Inteligentes para la Gestión Empresarial. Ed. Alfaomega - Rama. Barcelona, España.
[4] Braidot, Nestor. (1992). Marketing total. Ed. Macchi. Buenos Aires, Argentina.
[5] Martinich, Joseph. (1997). Production and Operations Management. John Wiley and Sons. Missouri, USA.
[6] Arbones, Eduardo. (1989). Logística Empresarial. Ed. Marcombo. Barcelona, España.
[7] Badiru, Adedeji. (1992). Expert Systems Applications in Engineering and Manufacturing. Ed. Prentice Hall. New Jersey, USA.
[8] Hicks, Donald. (1999). The State of supply Chain Strategy. Revista Solutions N°8 Vol 31. (august). Atlanta, USA.
[9] Spalding, Jan. (1998). Transportation Industry Takes the Ri ght-of-Way in the Supply Chain. Revista Solutions N°7 Vol 30. (July). Atlanta, USA.
[1O] Savoie, Brian. (1998). The Last Word on Supply Chain Improvement. Revista Solutions N°10 Vol 30. (October). Atlanta, USA.
[11]Gen, M y Cheng, R. (1997). Geneti c Algorithms and EngineeringDesign. Ed. Wiley. USA.
[12] Larrañaga, L. ¡Error! Marcador no definido. Departamento de ciencias de la computación e Inteli gencia Artificial Universidad del País Vasco.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)