Ciencia, Investigación, Academia y Desarrollo

Ingeniería, 2006-00-00 vol:11 nro:2 pág:80-87

Identificación y programación de asignaturas a ofrecer en un programa de especialización

Identification and schedule of courses that should be offer by a specialization program

Germán A. Méndez Giraldo

Investigador del Grupo Simulación y Sistemas Expertos.

Juan Pablo Caballero Villalobos

Investigador del Grupo Zentech.

Lindsay Álvarez Pomar

Directora del Grupo de Investigación Simulación y Sistemas Expertos.

Resumen

El presente artículo ilustra una propuesta alterna de solución para el problema de selección y programación de asignaturas que se origina en los programas de especialización al inicio de cada periodo académico. El resultado que se espera es una programación de las asignaturas que mayor satisfacción proporcione tanto a los estudiantes como a la dirección del programa. Como primera alternativa de solución al problema, se empleó la optimización matemática mediante un modelo de programación mixta para decidir qué cursos ofrecer, pero este enfoque no resultó exitoso desde el punto de vista práctico.

Ante las dificultades prácticas encontradas, se propone el uso combinado de dos técnicas metaheurísticas de amplio reconocimiento en la literatura por sus capacidades para abordar problemas de alta complejidad: algoritmos genéticos y búsqueda tabú. El primero de ellos se utiliza para realizar el proceso de selección de las asignaturas a ofrecer durante el periodo. La segunda técnica se empleó para realizar la programación de las asignaturas seleccionadas. El diseño de las metaheurísticas es innovador y se encontraron resultados en un tiempo relativamente corto teniendo en cuenta la magnitud del problema.

Palabras clave: Programación lineal entera, Metaheurísticas, Algoritmos genéticos, Búsqueda tabú, Secuenciación con tiempo.

Abstract

This paper presents an alternative proposal for a solution of an existing problem for specialization programs. At the beginning of each academic period, academic programs have to select and schedule diverse courses. The expected result is a timetable that offers the greatest satisfaction to students and the direction of the program. As a first approach to solve the problem, a mathematical optimization was utilized through a mixed programming model in order to decide which courses to offer. However, this approach was not successful from a practical point of view.

Due to the difficulties encountered from the practical point of view, a combined use of two meta heuristics techniques was proposed. These techniques have been widely recognized by the literature because of its capacities of facing high complexity problems: genetic algorithms and tabu search. The Genetic Algorithms were used to perform the selection process of the courses to be offered during the academic period, while Tabu search was used to define the scheduling of the selected courses. The design of the met heuristics is innovative and the results were presented in a relatively short period of time for the magnitude of the problem.

Key words: Linear and Integer programming, Metaheuristics, Genetic Algoritms, Tabu Search, Timetabling problems.

1. INTRODUCCIÓN

Las universidades deben decidir sobre cuáles y qué número de cursos deben ofrecer semestralmente en los diferentes programas que ofrecen, con el fin de satisfacer restricciones tanto de la universidad como de los estudiantes.

Se debe ofrecer cursos de manera que se garantice usos racionales de los recursos con que cuenta, es decir, la universidad intentará minimizar el uso de los recursos, sin dejar de lado la calidad de los mismos, que no será objeto del presente estudio; los recursos a tener en cuenta serán cuantificables, teniendo en cuenta que en algunos casos las universidades formulan políticas con el fin de regular este uso, como por ejemplo la exigencia de un número mínimo de estudiantes inscritos para que pueda ser ofrecido un curso y un número máximo por curso.

Problemas de este tipo se han trabajado en la literatura bajo la denominación "timetabling problems", sin embargo, el problema tratado en este artículo, presenta unas restricciones específicas que hacen que la búsqueda de soluciones deba abordarse con un enfoque diferente a los encontrados en la literatura consultada.

2. DESCRIPCIÓN DEL PROBLEMA

Con el fin de analizar un tipo especial de problema que se presenta en las especializaciones y que no ha sido analizado antes bajo este enfoque, y con el ánimo de exponer las ventajas de la metodología propuesta, se tomó como caso específico de análisis el de una Universidad de Bogotá, Colombia, que solicitó no ser citada con nombre propio en el presente artículo.

El problema que se tomó como ejemplo, se enmarca en un programa de postgrado que está diseñado para tener una duración de tres semestres; para obtener el título los estudiantes deben cursar dieciséis materias obligatorias y dos electivas.

En lo posible, la especialización programa una sola clase de cada asignatura a la semana y no necesariamente los cursos inician en la misma fecha, pero sí son ofrecidos todos a la misma hora; sin embargo la universidad intenta programarlos de lunes a jueves, para dejar el viernes como un día para cubrir clases que eventualmente no hayan podido ser dictadas. La programación de las materias que se ofrecen cada semestre se hace en el periodo académico de dieciocho semanas.

Por otro lado, los estudiantes desean terminar sus estudios en el menor tiempo posible, de manera que semestralmente deberían inscribir el número máximo de materias posibles para lograr este fin, que es igualmente benéfico para la universidad y que se constituye en un factor muy importante para el enfoque del problema.

Otro tipo de relaciones restrictivas afecta el problema, como son los cruces de los horarios, las materias obligatorias y electivas y el número máximo de materias que debido al tiempo, puede ofrecer la universidad. Sin embargo, ninguna asignatura tiene prerrequisitos y cada una tiene una intensidad horaria distinta. Adicionalmente, la especialización debe garantizar a sus estudiantes que puedan terminar su especialización en tres semestres, o que si pierden materias, puedan tomar las materias en el menor tiempo posible.

Se pretende entonces determinar la programación de materias que debe ofrecer un programa de especialización, haciendo uso mínimo de los recursos de la universidad y garantizando que los estudiantes nivelados puedan ver todas las materias posibles. De la misma manera, se pretende tener en cuenta todas las restricciones y los datos reales que son propios de la instancia específica, con el fin de hacer una validación real de la metodología propuesta.

3. ESTADO DEL ARTE

En la consulta bibliográfica realizada, no se ha encontrado solución a este tipo específico de problema, sin embargo, puede enmarcarse dentro de los problemas tipo "cronograma" (timetabling).

El problema de asignación de cursos ha sido abordado desde diversos perspectivas como los mencionados en el trabajo de revisión del estado del arte presentado por Schaerf [2]; adicionalmente algunas variaciones interesantes de este tipo de problema y sus enfoques para solucionarlos emplean diferentes técnicas meta heurísticas como Tabu Search[1], en su trabajo Schaerf asigna profesores a los cursos que se pueden ofrecer; tiene en cuenta restricciones típicas de estos sistemas como no asignar más de un curso al mismo profesor en el mismo tiempo, que junto con otras restricciones se convierte en un problema de tipo NP completo[1].

Abramson[3] abordó el problema de timetabling para asignar estudiantes, profesores, salones y horarios, teniendo en cuenta las restricciones propias de este tipo de sistemas, obteniendo también resultados satisfactorios.

Hinkin y Thompons[4] identifican este problema como el más importante de Administración Hotelera de la Universidad de Cornell. Crearon un programa que realiza la asignación de salones teniendo en cuenta los prerrequisitos de las materias y los deseos de los estudiantes de ver determinadas electivas que responden a las necesidades del mercado y que cambian constantemente. Otros autores como Goltz, Küchler y Matzke[5] han realizado sus propias aplicaciones y han hecho unión de técnicas para resolverlo.

Capara, Fischetti y Toth [6] solucionaron el problema de timetabling para trenes, teniendo en cuenta la capacidad de cada uno y el conjunto de estaciones en las que deben detenerse. Utilizaron programación entera y relajación lagrangiana, obteniendo resultados que han sido implementados en varias ferrovías.

Los artículos encontrados trabajan problemas que, aunque enmarcados dentro del tipo timetabling problems, no solucionan exactamente el mismo problema desde diferentes ópticas, sino que trabajan con restricciones distintas, como sucede con el problema que se trata en el presente estudio.

4. PROPUESTA INICIAL DE SOLUCIÓN

Se propuso como primera aproximación, abordar el problema en dos fases (ver figura 1): la primera fase utiliza un modelo de programación entera, mediante el cual se identificaría el conjunto de materias que se abrirían en el periodo académico. Las materias seleccionadas en esta primera fase se deben programar en el semestre mediante una meta-heurística buscando garantizar que todos los estudiantes puedan cursar el número de materias establecido por semestre o el número de materias que le hace falta para cumplir con los requisitos de grado.

Inicialmente se planteó el siguiente modelo de programación entera para la primera fase propuesta:

Conjuntos:

m = materias {1,2, .. ,M}
a = alumnos {1,2, .. ,A}
Sa = materias a cursar en el siguiente semestre, en las que está interesado el alumno
e = conjunto de electivas

Parámetros:

Sm: número de sesiones en un semestre para materia m
Pa: Peso asignado a cada alumno (5 nivelado, 1 ha perdido materias)
T: Semanas disponibles en el semestre
Km: costo por abrir materia m
D: número de días a la semana en las que se dictará clase
MIN: Número mínimo de estudiantes para abrir cualquier materia
MAX: Número máximo de estudiantes para abrir cualquier materia
Ea : Número máximo de electivas que puede cursar el alumno a

Variables:
X_a,m: variable binaria que toma el valor de cero si el estudiante no toma la materia m y uno si el estudiante toma la materia m
Y_m: variable binaria que toma el valor de cero si no se abre la materia m y uno si se abre la materia m

Función Objetivo:

Consiste en minimizar el costo de ofrecer cada una de las asignaturas que indica la variable Ym y maximizar los pesos (prioridades) asignados a los estudiantes.

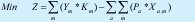
Restricciones:

Restricción que garantiza que el número de estudiantes inscritos en cada materia cumpla el requisito de estudiantes mínimos que se exigen por políticas de la especialización.

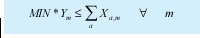
Restricción que garantiza que el número de estudiantes inscritos en cada materia cumpla el requisito de estudiantes máximos por asignatura que se exigen por políticas de la especialización y por capacidad de los salones.

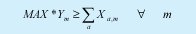
El número de sesiones correspondiente a las materias que pueda inscribir un estudiante, debe ser a lo sumo el máximo de disponibilidad de tiempo en el semestre.

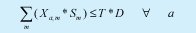
El número de asignaturas electivas que toma cada estudiante, debe ser a lo sumo el número máximo permitido por la especialización en cada semestre.

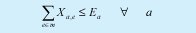
El conjunto de materias que cada estudiante puede ver se determina al eliminar las materias ya cursadas de las materias que debe cursar en la especialización para obtener su grado, esta información configura una matriz binaria de la siguiente forma:

La formulación propuesta presenta el inconveniente de no poder resolverse óptimamente mediante programas comerciales en tiempos razonables[3] debido al número de variables binarias que contempla, lo que lo hace impráctico optar éste enfoque. Para un conjunto de datos de prueba con cincuenta alumnos, diez y ocho materias, el modelo contempla novecientas dieciocho variables binarias.

Sin embargo, y conociendo las limitaciones anteriormente mencionadas, se intentó solucionar una primera instancia del problema con diez estudiantes y cinco materias mediante el software GAMS, sin que al cabo de tres horas de procesamiento hubiera arrojado una solución óptima. Por este motivo se hizo necesario explorar otros enfoques para el problema tratado.

5. PROPUESTA FINAL DE SOLUCIÓN

Se propone la utilización de algoritmos genéticos para la determinación de las materias que se abrirían en el semestre y búsqueda tabú para la programación de las asignaturas elegidas.

5.1. Cromosoma Algoritmo Genético

El cromosoma que usará el algoritmo genético para determinar el conjunto de materias a abrir es un vector binario de m números, donde un 1 en la i-ésima posición del vector indica que la materia i se abrirá para el próximo semestre y un cero en esta misma posición indica que no se abrirá (figura 2).

La evaluación de la conveniencia de abrir este conjunto de materias se establecerá utilizando búsqueda tabú para determinar aproximadamente la mejor programación de éstas en el semestre.

5.2. Cromosoma Búsqueda Tabú

El cromosoma utilizado por la búsqueda tabú está dado por el conjunto de materias que se abrirán según el cromosoma del genético (Figura 3).

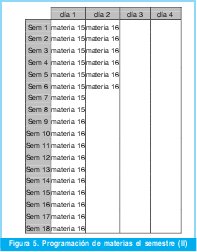
Tal como se mencionó, las materias deben programarse en el periodo académico de diez y ocho semanas y es altamente deseable que las sesiones de cada materia se programen el mismo día de la semana. Adicionalmente, se debe tener en cuenta que en el semestre se cuenta con la posibilidad de dictar un máximo de 72 sesiones sin que se presente ningún cruce (18 semanas * 4 días a la semana).

El cromosoma de búsqueda tabú representa una programación de las materias especificadas por el cromosoma del algoritmo genético. La programación total del semestre se obtiene al asignar todas las sesiones de cada materia consecutivamente en los espacios posibles y según el orden de aparición de las materias en el cromosoma (Figura 4 y 5).

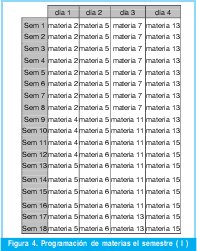
En la figura 4 y 5 se muestra la programación de las materias para el cromosoma ilustrado en la Figura 3.

Inicialmente se pensó que esta programación permite obtener una matriz de cruce de materias (MCM) que tiene una conformación binaria, donde cero significa que las materias no se cruzan y uno, que se cruzan (Figura 6).

Esta matriz compendia la relación entre cada par de materias abiertas según la programación hecha y permitiría ver si dos materias podían verse simultáneamente sin que se presentaran cruces.

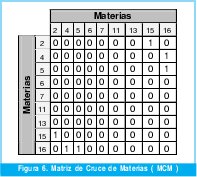
Sin embargo, en la implementación no fue utilizada la MCM debido a que la bondad de la secuencia de cada conjunto de materias está dado por la permisión en la inscripción del número máximo de materias a cada estudiante; lo que significa que cada vez que un estudiante "inscribe" una materia, esta puede tener cruce con otra, así, cada vez que se realiza esta operación, se restringe el grupo de materias que puede inscribir y el número de instrucciones en la implementación se hacía bastante extenso.

Se pensó también en la utilización de una Matriz de Opciones de los Estudiantes (MOE) conformada por ceros y unos con dimensión número de estudiantes por número de materias, en dónde un cero en la entrada i,j de la matriz significa que el i-ésimo estudiante no puede ver la j-ésima materia (ya la cursó y aprobó), y un uno en esa misma posición significa que sí puede cursarla. Dicha matriz (MOE) se usó como parte de los datos de entrada para el algoritmo genético.

5.3. Evaluación del Cromosoma Genético

El Algoritmo genético identifica un conjunto de materias que se va a abrir; mediante Búsqueda Tabú se halla la secuencia en la que se programará y a través de otra Búsqueda Tabú se halla la secuencia en la cual cada estudiante escogerá el conjunto de materias dada la programación actual, de manera que se maximice el número de materias que se pueden ver (Figura 7).

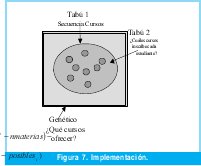
Utilizando la información disponible de las asignaturas que cada estudiante puede cursar (Tabú), el conjunto de cursos que se pueden abrir (Genético) y una programación de los cursos (Tabú), se evalúa la conveniencia de la solución propuesta buscando maximizar la siguiente expresión:

Donde:

i = Conjunto de Estudiantes

Pi = Variable binaria. Donde 1 indica que el estudiante i puede ver el número mínimo de materias, 0 indica que el estudiante i no puede ver el número mínimo de materias con la programación actual.

MINi = Número de materias que debe tomar en el semestre.

posibles_i = Número de materias máximo que puede inscribir el alumno i con la programación actual.

TMAT = Número total de materias que podría abrir la especialización.

nmaterias = Número de materias que se abrirán en el semestre (tamaño del cromosoma de búsqueda tabú).

La relación existente entre Pi , MINi , y posibles i está dada por:

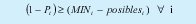
Una solución encontrada es factible si el valor de la función Objetivo es mayor o igual a (Número de estudiantes * 1000), indicando que para todo estudiante se ha garantizado que pueda cursar el número mínimo de materias establecido.

5.4. Cálculo del número máximo de asignaturas que puede inscribir cada estudiante

Mediante Búsqueda Tabú se encuentra una secuencia de los cursos y basado en ella, se inicia entonces un proceso de "inscripción" para cada estudiante, donde se elige una asignatura que es la que empieza a restringir el proceso. Luego se elige una segunda asignatura y así sucesivamente, hasta encontrar una combinación que permita inscribir y cursar el mayor número de materias.

5.5. Operadores genéticos y parámetros de las meta-heurísticas

Los vecinos que explorará la búsqueda tabú para la programación de las materias son las parejas adyacentes en el cromosoma.

Para el algoritmo genético se plantea el uso del operador de recombinación de un punto aleatorio, estrategia de evolución de mejores entre padres e hijos de una generación, torneo como estrategia de selección, mutación implementada como el intercambio aleatorio del valor de un gen (0 a 1, o de 1 a 0).

6. INSTANCIAS DEL PROBLEMA

Se usaron los datos cuando el programa estaba en su segundo semestre y se esperaba el ingreso de veinte nuevos estudiantes para el siguiente semestre, totalizando cerca de 55 estudiantes. El número de estudiantes que se tiene presupuestado una vez se estabilice la especialización es de 70 alumnos repartidos en los tres semestres.

Las materias se relacionan a continuación:

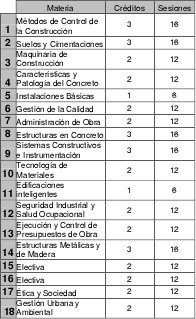
La implementación se realizó en Visual Basic para Excel y se corrió para el problema real actual de la especialización (55 estudiantes y 18 materias) y para problemas aleatorios (60 estudiantes y 18 materias). En las instancias propuestas se encontraron soluciones en un tiempo promedio de 58 minutos con una desviación estándar de 7,3 minutos, satisfaciendo el 83% de los estudiantes en 79% de las veces.

7. CONCLUSIONES

Como conclusión principal se tiene que el problema afrontado tiene una alta complejidad que impide el uso intuitivo de una sola técnica y se hizo necesario mezclarlas para proporcionar una solución al mismo. La unión ha sido interesante desde el punto de vista académico y soluciona un problema real de bastante complejidad.

Es importante notar que el cálculo de la función objetivo para cada cromosoma implica la resolución de dos problemas combinatorios dentro de otro problema combinatorio y aunque se sabe que existe suficiente tiempo para ejecutar el proceso y que éste sólo debe realizarse dos veces por año, el tiempo de corrida es significativo. Sin embargo la implementación genera buenas soluciones al problema, lo que lo hace bastante práctico, porque puede reemplazar el proceso empírico con el que se toman actualmente las decisiones.

El problema estudiado reviste bastante complejidad porque programa las materias para cada estudiante, es decir, realiza la búsqueda de buenas inscripciones para cada uno. De manera que la especialización puede realizar la inscripción de las materias basado en los reportes de la implementación.

Aunque este problema se encuentra encasillado dentro de los "timetabling" por su origen, también podría ser visto como un problema de asignación de estudiantes a cursos. Sin embargo, aunque se clasifica en los problemas de "timetabling", se observa que estos difieren notablemente entre ellos por las características propias de los entornos para los cuales se desarrollan.

Las técnicas de Búsqueda Tabú y Algoritmos Genéticos facilitan las implementaciones de problemas nuevos, debido a que por su estructura, puede ser usado el código de un problema cualquiera para resolver otro, cambiando la función objetivo y "calibrando" los parámetros.

El lenguaje de programación utilizado no es el más apropiado para resolver este problema con el enfoque propuesto, debido a la cantidad de accesos a memoria que debe realizar, así que debería experimentarse implementando la propuesta en un lenguaje de más alto desempeño como C.

REFERENCIAS BIBLIOGRÁFICAS

[1] Schaerf, Andrea. Tabu Search Techniques for Large High-School Timetabling Problems. Proceeding of the 13th National Conference of the American Asociation for artificial Intelligence. 1996

[2] Schaerf, Andrea. A survey of Automated Timetabling. Artificial Intelligence Review. Kluwer Academic Publishers, Netherlands, 1999.

[3] Abramson, D. Constructing School Timetables using Simulated Annealing: Sequential and Parallel Algorithms. Division of information technology departament of communication and electronic engineering Royal Melbourne Institute of Technology. Melbourne. 1991

[4] Hinkin, Timothy, Thompson, Gary. SchedulExpert: Scheduling Courses in the Cornell University School of Hotel Administration. Interfaces. 2002

[5] Goltz, Hans-Joachim, Küchler, Georg and Matzke, Dirk. Constraint-Based Timetabling for Universities. German National Research Center for Information Technology. Berlin

[6] Caprara, Alberto, Fischetti, Matteo and Toth, Paolo. Modeling and Solving the Train Timetabling Problem. Informs. 2002

[7] Andrea Rossi and Gino Dini. Dynamic Scheduling of FMS using a real ­ time genetic algorithm. International Journal of Production Research. 2000. Vol. 38. N.1. 1-20.

[8] Krishnamoorthy C.S. and Rajeev S. Artificial Intelligence and Expert Systems for Engineers. Indian Institute of Technology Madras. CRC. 2000.

[9] Méndez, Germán. Diseño de un Algoritmo Genético para un Sistema Logístico de Distribución. Revista Ingeniería. Vol. 2. Año 2001.

[10] Tadao Murata. Petri Nets: Property, Análisis and Applications. Proceedings of the IEEE. Vol 77. N 4. April 1989.

[11] Pinedo, Michael and Chao, Xiuli. Operations Scheduling with Applications in Manufacturing and Services. Irwin/ McGraw Hill. 1999.

[12] Méndez, Germán. Gerencia de Manufactura-Función de Planeación. U.D.F.J.C. 2003.

[13] Gómez Gómez, A.; Parreño Fernández, J y Fernández Quesada, I. Aplicaciones De Los Algoritmos Genéticos En La Industria. Escuela Técnica Superior De Ingenieros Industriales De Gijón. Universidad De Oviedo.

[14] Prada Romero, Jairo Fernando. Aplicación de un Algoritmo Genético al Problema Job Shop Scheduling. CIFI. Universidad de los Andes. Memo de Investigación No 482. Santafé de Bogotá. Marzo de 1998

[15] Mejía, Gonzalo. Notas de la clase Programación de Producción. Maestría en Ingeniería Industrial. Universidad de los Andes. Semestre I de 2003

Germán Méndez Giraldo, Ph.D.
Nació en Bogotá, Colombia. es Ingeniero Industrial de la Universidad Distrital. Magíster, Universidad de Los Andes. Doctor, Universidad Central de Las Villas, Santa Clara, Cuba. Se ha desempeñado como Jefe de Producción en industrias nacionales y multinacionales. Gerente y Coordinador de proyectos. Consultor y asesor empresarial. Es profesor de tiempo completo de la Facultad de Ingeniería de la Universidad Distrital. Ha desempeñado diversos cargos dentro de la Institución como: coordinador de la Especialización en Ingeniería de Producción, de la Maestría en Ingeniería Industrial, Jefe de la Oficina de Relaciones Interinstitucionales y Rector Encargado.

Actualmente es coordinador de la línea de Investigación en Simulación y Dinámica del Sistema, se desempeña como profesor en el área de Investigación de Operaciones en la Universidad Distrital Francisco y pertenece como investigador al grupo Simulación y Sistemas Expertos, donde realiza estudios sobre Metaheurísticas, Sistemas Expertos y PyME. gmendez@udistrital.edu.co

Juan Pablo Caballero Villalobos, M.Sc.
Nació en Honda, Colombia. Es Ingeniero Industrial de la Pontificia Universidad Javeriana. Magíster en Ingeniería Industrial, Universidad de Los Andes de Bogotá. Ha trabajado en empresas como MABE Colombia S.A., Internet Securities Inc y la Pontificia Universidad Javeriana, en donde actualmente desempeña el cargo de jefe de la sección de producción. Pertenece al grupo de investigación Zentech del departamento de procesos productivos, donde realiza investigación en la aplicación de técnicas metaheurísticas a la resolución de problemas de programación de la producción y problemas combinatorios relacionados. juan.caballero@javeriana.edu.co

Lindsay Alvarez Pomar, M.Sc.
Nació en Florencia, Colombia. Es Ingeniera Industrial de la Universidad Distrital Francisco José de Caldas. Magíster en Ingeniería Industrial en la Universidad de Los Andes. Se desempeña actualmente como Coordinadora del Proyecto Curricular en Ingeniería Industrial de la Universidad Distrital Francisco José de Calda y como profesora asistente en el área de Investigación de Operaciones en la misma universidad. Dirige el grupo de investigación Simulación y Sistemas Expertos donde realiza estudios sobre Metaheurísticas, PyME y Teoría de juegos. lalvarez@udistrital.edu.co