DOI:
https://doi.org/10.14483/23448393.19423Publicado:
2024-01-13Número:
Vol. 29 Núm. 1 (2024): Enero-AbrilSección:
Inteligencia ComputacionalMethodology for Inventory Management in Neighborhood Stores Using Machine Learning and Integer Linear Programming
Metodología para la gestión de inventario en tiendas de barrio utilizando aprendizaje de máquina y programación lineal entera
Palabras clave:
Machine learning, inventory, constrained optimization, demand estimation (en).Palabras clave:
Aprendizaje de máquina, inventario, optimización restringida, estimación de la demanda (es).Descargas
Referencias
F. E. Castro and J. A. Oviedo, "Tiendas de barrio a la vanguardia de la competitividad," in XIX Congreso Internacional AECA, 2017, pp. 72.
E. J. Albarracín and S. C. Erazo, “Influencia de las tecnologías de la información y comunicación en el rendimiento de las micro, pequeñas y medianas empresas Colombianas,” Estudios Gerenciales, vol. 30, no. 133, pp. 355-364, 2014. https://doi.org/10.1016/j.estger.2014.06.006 DOI: https://doi.org/10.1016/j.estger.2014.06.006
J. M. Caicedo and J. M. Quiceno, “Situación actual de la tienda de barrio frente a la aparición de la nuevas superficies ARA y D1 en la ciudad de Manizales,” Undergraduate thesis, Univ. Manizales. Manizales, Caldas, Colombia. [Online]. Available: https://ridum.umanizales.edu.co/xmlui/handle/20.500.12746/2080
Semana, “El fenómeno D1: la revolución de las tiendas de descuento,” 2016. [Online]. Available: https://www.semana.com/edicion-impresa/caratula/articulo/como-funcionan-las-tiendas-d1/218767/
Portafolio, “Los tenderos no conocen a un competidor directo: la cadena D1,” 2016. [Online]. Available: https://www.portafolio.co/negocios/tenderos-conocen-competidor-directo-cadena-d1-495847
J.M. Paúcar, E. Vargas, “Propuesta de mejora de la gestión de inventarios en una empresa del sector retail,” Undergraduate thesis, Univ. Peruana Ciencias Aplicadas, Fac. Ing., Lima, Perú. [Online]. Available: http://hdl.handle.net/10757/623832
M. Ulrich and H. Jahnke, "Classification-based model selection in retail demand forecasting," Int. J. Forecast., vol. 30, no. 1, pp. 209-223, 2022. https://doi.org/10.1016/j.ijforecast.2021.05.010 DOI: https://doi.org/10.1016/j.ijforecast.2021.05.010
M. Doszyń, "Expert systems in intermittent demand forecasting," Procedia Comp. Sci., vol. 192, pp. 3598-3606, 2021. https://doi.org/10.1016/j.procs.2021.09.133 DOI: https://doi.org/10.1016/j.procs.2021.09.133
F. Tao and Q. Qi, "Data-driven smart manufacturing," J. Manuf. Syst., vol. 48, part C, pp. 157-169, 2018. https://doi.org/10.1016/j.jmsy.2018.01.006 DOI: https://doi.org/10.1016/j.jmsy.2018.01.006
J. A. Arango and J. A. Giraldo, “Gestión de compras e inventarios a partir de pronósticos Holt-Winters y diferenciación de nivel de servicio por clasificación ABC,” Scientia et Technica, vol. 18, no. 4, pp. 743-747, Dec. 2013. https://doi.org/10.22517/23447214.7171
J. E. Montemayor, Métodos de pronósticos para negocios, Monterrey, Nuevo León, México: Tecnológico de Monterrey. [Online]. Available: http://hdl.handle.net/11285/621230
T. Tanizaki and T. Hoshino, "Demand forecasting in restaurants using machine learning and statistical análisis," Procedia CIRP, vol. 79, pp. 679-683, 2019. https://doi.org/10.1016/j.procir.2019.02.042 DOI: https://doi.org/10.1016/j.procir.2019.02.042
J. P. Usuga and S. Lamouri, "Trends in machine learning applied to demand & sales forecasting: A review," presented at International Conference on Information Systems, Logistics and Supply Chain, Jul. 2018, Lyon, France. [Online]. Available: https://hal.science/hal-01881362
D. A. Collier and J. R. Evans, Administración de operaciones, Boston, MA, USA: Cengage, 2019.
T. Boone and R. Ganeshan, "Forecasting sales in the supply chain: Consumer analytics in the Big Data era," Int. J. Forecast., vol. 35, no. 1, pp. 170-180, 2019. https://doi.org/10.1016/j.ijforecast.2018.09.003 DOI: https://doi.org/10.1016/j.ijforecast.2018.09.003
A. Kumar and R. Shankar, "A Big Data driven framework for demand-driven forecasting with effects of marketing-mix variables," Ind. Marketing Manag., vol. 90, pp. 493-507, 2020. https://doi.org/10.1016/j.indmarman.2019.05.003 DOI: https://doi.org/10.1016/j.indmarman.2019.05.003
S. Chopra, "The evolution of omni-channel retailing and its impact on supply chains," Transport. Res. Procedia, vol. 30, pp. 4-13, 2018. https://doi.org/10.1016/j.trpro.2018.09.002 DOI: https://doi.org/10.1016/j.trpro.2018.09.002
S. Mou and D.J. Robb, "Retail store operations: Literature review and research directions," European J. Oper. Res., vol. 265, no. 2, pp. 399-422, 2018. https://doi.org/10.1016/j.ejor.2017.07.003 DOI: https://doi.org/10.1016/j.ejor.2017.07.003
E. Casado and M. La Civita, "Estimated time of arrival sensitivity to aircraft intent uncertainty," IFAC-PapersOnLine, vol. 51, no. 9, pp. 162-167, 2018. https://doi.org/10.1016/j.ifacol.2018.07.027 DOI: https://doi.org/10.1016/j.ifacol.2018.07.027
M. A. Sellitto and E. Balugani, "Spare parts replacement policy based on chaotic models", IFAC-PapersOnLine, vol. 51, no. 11, pp. 945-950, 2018. https://doi.org/10.1016/j.ifacol.2018.08.486 DOI: https://doi.org/10.1016/j.ifacol.2018.08.486
F. Hamilton and A. Lloyd, "Hybrid modeling and prediction of dynamical systems", PLoS Comp. Biology, vol. 13, no. 7, pp. 1-20, 2017. https://doi.org/10.1371/journal.pcbi.1005655 DOI: https://doi.org/10.1371/journal.pcbi.1005655
J. C. Sanclemente, “La reputación del tendero de barrio ante su mercado y sus consecuencias,” PhD thesis, Univ. EAFIT, Medellín, Colombia . [Online]. Available:
Servinformación, “Estudio revela que los tenderos barranquilleros madrugan más que los bogotanos”, 2019. [Online]. Available: https://www.colombia.com/actualidad/nacionales/barranquilleros-madrugan-mas-que-los-bogotanos-241787
eSemanal, “Estudio global de la cadena de suministro de retail”, 2020. [Online]. Available: https://esemanal.mx/2020/07/estudio-global-de-la-cadena-de-suministro-de-retail/
El Espectador, “Un estudio comparó las tiendas de barrio de bogotá con las de barranquilla”, 2019. [Online]. Available: https://www.elespectador.com/bogota/un-estudio-comparo-las-tiendas-de-barrio-de-bogota-con-las-de-barranquilla-article-879317/
R. Gaku, "Demand forecasting procedure for short life-cycle products with an actual food processing enterprise," Int. J. Comp. Intel. Syst., vol. 7, no. 2, pp. 85-92, 2014. https://doi.org/10.1080/18756891.2014.947121 DOI: https://doi.org/10.1080/18756891.2014.947121
J. E. Hanke and D. W. Wichern, Pronósticos en los negocios, 9th ed., Mexico DF, Mexico: Pearson Educación, 2010.
P. L. Meyer and C. P. Campos, Probabilidad y aplicaciones estadísticas, Mexico DF, Mexico: Fondo Educativo Interamericano, 1973.
M.T. Farrell, A. Correa, "Gaussian process regression models for predicting stock trends,” Relation, vol. 10, pp. 3414–3423,. https://api.semanticscholar.org/CorpusID:16646484
B. Schölkopfa and A. J. Smola, Learning with kernels: Support vector machines, regularization, optimization, and beyond, Cambridge, MA, USA: MIT press, 2002.
C. M. Bishop, Pattern recognition and machine learning (information science and statistics), 1st ed., New York, NY, USA: Springer, 2006.
K. S. Shanmugan and A. M. Breipohl, Random signals: Detection, estimation and data analysis, Hoboken, NJ, USA: Wiley, 1988.
C. E. Rasmussen, "Gaussian processes in machine learning,” in Advanced Lectures on Machine Learning, O. Bousquet, U. von Luxburg, and G. Rätsch, Eds., Berlin, Heidelberg, Germany: Springer, 2003, pp. 63-71.
C. Krzysztof and C. K. Williams, "Empirical evaluation of Gaussian Process approximation algorithms," Master's thesis, S. Informatics, Univ. Edinburgh, 2011. [Online]. Available: https://homepages.inf.ed.ac.uk/ckiw/postscript/Chalupka2011diss.pdf
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 25 de mayo de 2022; Aceptado: 29 de agosto de 2023
Abstract
Context:
Nowadays, inventory management poses a challenge given the constant demands related to temporality, geographic location, price variability, and budget availability, among others. In neighborhood shops, this process is manually done based on experience (the data generated are ignored), which is sometimes not enough to respond to changes. This shows the need to develop new strategies and tools that use data analysis techniques.
Method:
Our methodology predicts the weekly demand for 14 common products in neighborhood stores, which is later refined based on investment capital. The method is validated using a database built with synthetic information extracted from statistical sampling. For the prediction model, three supervised learning models are used: support vector machines (SVM), AutoRegressive models (Arx), and Gaussian processes (GP). This work proposes a restricted linear model given an inversion and the predicted quantity of products; the aim is to refine the prediction while maximizing the shopkeeper’s profit. Finally, the problem is solved by applying an integer linear programming paradigm.
Results:
Tests regarding the prediction and inventory adjustment stages are conducted, showing that the methodology can predict the temporal dynamics of the data by inferring the statistical moments of the distributions used. It is shown that it is possible to obtain a maximum profit with a lower investment.
Conclusions:
Our method allows predicting and refining inventory management in a neighborhood store model where quantities are managed to maximize the shopkeeper’s profits. This opens the way to explore this approach in a real scenario or to introduce new techniques that can improve its performance.
Keywords:
machine learning, inventory, constrained optimization, demand estimation..Resumen
Contexto:
En la actualidad, la administración del inventario representa un reto dadas las constantes exigencias de temporalidad, ubicación geográfica, variabilidad en los precios, disponibilidad presupuestal, entre otros. En las tiendas de barrio, este proceso se realiza de forma manual y con base en la experiencia (se ignoran los datos generados), lo que en ocasiones no es suficiente para responder a los cambios. Esto muestra la necesidad de desarrollar nuevas estrategias y herramientas que utilicen técnicas de análisis de datos.
Método:
Nuestra metodología predice la demanda semanal para 14 productos comunes en tiendas de barrio, la cual se refina posteriormente en función del capital de inversión para optimizar la ganancia. El método se valida a través de una base de datos construida con información sintética extraída a partir de muestreo estadístico. Para la predicción, se utilizan tres modelos de aprendizaje supervisado: máquinas de soporte vectorial (SVM), modelos AutoRegresivos (ARx) y procesos Gaussianos (GP). Luego, se plantea un modelo lineal restringido dada una inversión y las cantidades pronosticadas; el propósito es refinar la predicción maximizando la ganancia del tendero. Finalmente, el problema se soluciona aplicando un paradigma de programación lineal entera.
Resultados:
Se realizan pruebas para las etapas de predicción y ajustes del inventario, donde se demuestra que la metodología logra predecir la dinámica temporal de los datos infiriendo los momentos estadísticos de las distribuciones utilizadas. Se muestra que es posible obtener una máxima ganancia con un monto menor de inversión.
Conclusiones:
Nuestra metodología que permite predecir y refinar la gestión de inventario en un modelo de tienda de barrio en el que las cantidades se administran para maximizar las ganancias del tendero. Lo anterior abre el camino para explorar este enfoque en un escenario real o introducir nuevas técnicas que puedan mejorar su desempeño.
Palabras clave:
aprendizaje de máquina, inventario, optimización restringida, estimación de la demanda.Introduction
Over the years, the world economy has oriented its markets towards globalized supply and demand. In the case of Colombia, this process started in the 90s with the beginning of the economic opening, when new competitors were allowed to enter the market, many of which were foreign producers. Due to this situation, several economic sectors disappeared, as it was not possible to compete with the wide range of products and prices in offer (1, 2).
In light of the above, a large number of international companies entered the Colombian market, especially in the retail sector, which represents 56 % of retail sales. Within this business paradigm, large sales chains such as Éxito, Carrefour (today Jumbo), Carulla, Olímpica, Super Inter, and Makro stand out. These companies assess the procurement of supplies based on efficiency indicators, aiming to maximize the return on investment. However, there is a second model that concerns the neighborhood convenience stores of the traditional channel. The most noticeable difference between these two models corresponds to administration, which is carried out by the owner or head of the family unit in the second case (1, 2).
Despite stiff competition, neighborhood stores have survived due to their closeness to the final consumer, their trust and empathy with customers, and the payment methods offered (interest-free credit). Neighborhood stores have been hit hard by the advent of large discount store chains, such as ARA, D1, and Justo & Bueno, which aim to get closer to the end customer and compete with low prices (3, 4). Therefore, the traditional channel in Colombia must improve, update, and transform its processes, specifically in making decisions on the projection of supply and demand, as well as in inventory rotation 5.
In general terms, the store administrator manages the investments in the purchase of the products offered according to their expertise and knowledge acquired from the market. It should be stressed that this is a subjective forecasting method based on experience. This strategy generates a high bias in facing the uncertainties presented by changes in the demand for certain items according to the season and the economic variations in prices, state policies, and social events 6.
Likewise, it has been identified that demand forecasting is a common problem in supply chains. Here, the objective is to achieve greater precision and less error. According to 7, given the diversity of demand patterns, it is unlikely that any single demand forecasting model can offer the highest accuracy across all items. On the other hand, managers frequently have more information that should be considered to improve forecast results. For example, they know customer habits and purchase intentions, among others 8. A better forecast should include all this information. However, this requires more advanced methods than those offered by the prediction techniques of machine learning.
Considering the above, artificial intelligence (AI) and machine learning techniques have been proposed in the literature, aiming to reduce bias and provide business units with decision-making tools under a data-based paradigm, largely because AI models allow them to carry out forecasting with regard to the demand for items 9. In the state of the art, two major stages are identified in which these procedures are focused. The first involves collecting and characterizing the data, with the purpose of describing the behavior of the products and its variability over time. In the second stage, different machine learning techniques are used to estimate computational models that can predict and reproduce the dynamics of the data, so that the sales dynamics can be emulated over time for a set of specific items (10-13).
Usually, the forecast of pure units or goods follows a uniform or normal probability distribution 14. More specialized developments introduce planning aspects that drive the supply chain as customer expectations increase, shortening delivery times, and pressure for resource optimization 15. On the other hand, demand forecasting is generally carried out using machine learning techniques. An example of this is the use of neural networks, which emulate the forecast of items through a non-linear function in time. Historical sales data are included in the network design in combination with the effectiveness of advertising, promotions, and marketing events. However, this model is sensitive to the network architecture (i.e., the number of hidden layers and the value of neurons per layer), which affects the generality of the method 16. Other methods also predict demand, such as the Auto Regressive Moving-Average (ARMA), Support Vector Machine (SVM), Multiple Linear Regression (MLR), and Random Forest models, showing competitive results adjusted to reality. Still, this approach predicts the quantities of products required without considering the investment and profit capabilities of the shopkeeper (17, 18). Other works demonstrate the application of chaotic methods, such as (19-21), achieving demand adjustment.
As of today, the sudden changes in the market have generated new paradigms of competition. These circumstances are experienced by emerging businesses such as neighborhood stores 22. Studies such as 23) show that more than 90 % of the data generated by these businesses are not exploited and are not used to make sense of the changing dynamics of the market. There are success stories where machine learning has been used to better predict and manage expenses 23. This optimizes business profits, thus allowing for small businesses’ economic survival. Some sources claim that including these methodologies can add significant value to their demand forecasting processes, while more than half state that they can improve other eight critical supply chain capabilities 24.
The above-mentioned study added that retailers with the technology to predict these changes model contingency plans and options and quickly adapt their supply chain strategy to meet high demand and avoid excess inventory. Those who cannot do it risk falling behind with sales not meeting the goals, in addition to incurring losses through waste 23. This research describes and structures a methodology for forecasting the quantities needed to order certain products in neighborhood stores. The method proposes a linear model to maximize the shopkeeper’s profits based on an available investment value that, combined with a machine learning procedure, allows inferring the amounts to be requested. This method constitutes an alternative detached from the traditional paradigm of neighborhood stores, which is built daily and considers the last order requested, ignoring the behavior in sales and the dynamics of customers 25.
This proposal employs three models for sales forecasting, i.e., the performance of an SVM, a Gaussian process (GP), and an ARx model are examined using synthetic data generated via statistical sampling according to the Probability Distribution Function (PDF) that is accentuated to the sales of the products under analysis. The selection criteria for the PDFs of the products studied are in accordance with 14, which suggests using uniform or Gaussian PDFs for products offered in neighborhood stores. Additionally, the methodology proposes error metrics and statistical analysis to evaluate and validate each of the models selected in this research. The results show that our proposal allows maximizing the shopkeeper’s profits by considering the dynamics in sales and the available investment. The main contributions of this research are the following:
-
A methodology to forecast sales (demand) for a neighborhood store over a specific period which maximizes the shopkeeper’s profits while considering the dynamics of demand and the number of products to invest in.
-
A comparative study that evaluates the performance of forecast models applied to the prediction of demand in neighborhood stores.
-
A validation procedure to measure the performance of each step in the proposed method.
This paper is organized as follows. Section 2 presents the basic nomenclature. Section 3 describes the proposed methodology, as well as the validation procedure, and the results obtained are shown in section 4. In the final section, the concluding remarks of our research are presented.
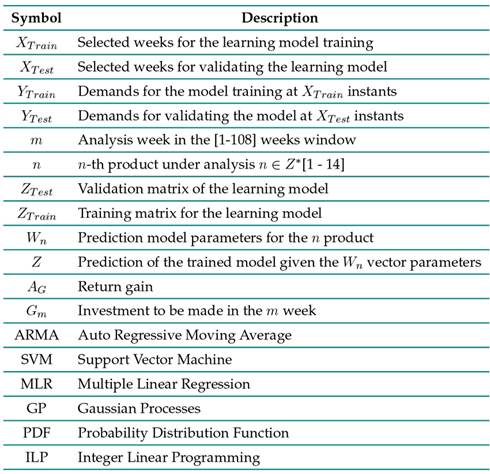
Basic nomenclature
Table I: Paper nomenclature
Methodology
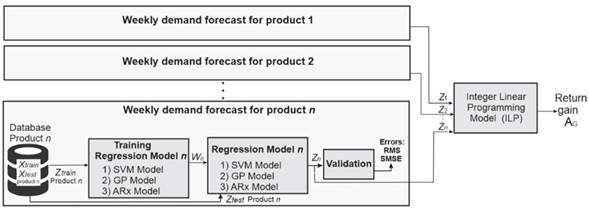
Fig. 1shows the implemented method in a block diagram. In short, it consists of three phases: firstly, a database with information on the demands per week for 14 everyday items offered in neighborhood stores; secondly, a regression model that emulates the prediction Z = {Z 1 Z 2 . . . Z n }, where Z n is the prediction of the n-th product; and, finally, an integer linear programming model that refines the weekly orders to maximize the profit return A G given a weekly investment rate. Traditionally, inventory management models include a systematic methodology to establish inventory control policies for products. This allows determining the security list, the reorder point, or when the order must be placed 26). This research aims to reduce the overall costs by predicting the demand for key products in neighborhood stores. It analyzes projected profits based on the model’s predictions. It must be acknowledged that this study does not encompass all aspects of defining inventory control policies.
Figure 1: Implemented methodology
Database
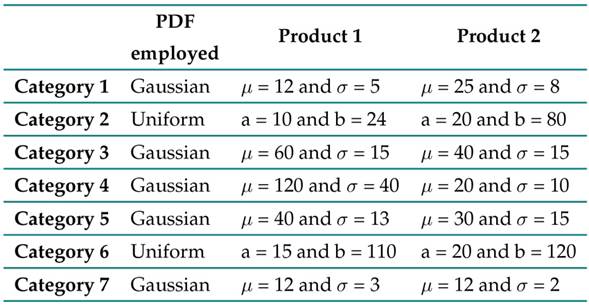
In this study, seven categories that cover 14 product varieties in neighborhood stores were selected, as summarized in Table II. Each product is independent, so all analyses are proposed and done for each one of them.
Table II: Selected categories and products
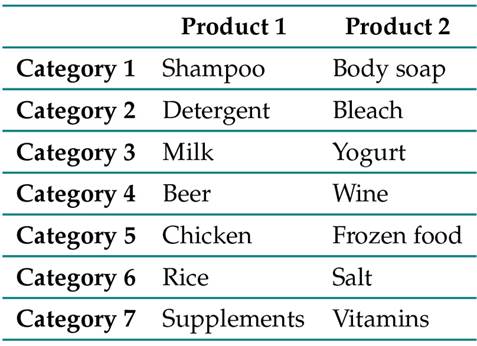
This selection was done by visiting shopkeepers in neighborhoods of Pereira (these items were selected since they were representative of the sales during the analyzed time horizon) and identifying common items such as those shown in Table II. Additionally, the variability in their demand was validated, finding that some exhibit a temporary behavior, as is the case of category 6 (products of great demand on celebration dates, i.e., holidays, commemorative days, among others).
Conversely, other items show a stable behavior over time, as is the case of the products in categories 5 and 7. The literature states that the demand follows a certain PDF, which, in the case of basic products, can be adjusted to a normal or uniform behavior 27. Due to the above, it is possible to generate synthetic data from a statistical sample while assuming a PDF for each category, establishing the distribution parameters for each item ( Table III).
Table III: Definition of the model for data generation
The expected values u
Y
(where Y is the weekly demand) and the standard deviation σ
Y
of the distribution given in Table III, are summarized in Table IV. The first moments for a normal and uniform distribution are u
Y
= µand 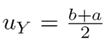 , respectively. Similarly, the variance in the case of a Gaussian and uniform PDF is σ
Y
= σ and
, respectively. Similarly, the variance in the case of a Gaussian and uniform PDF is σ
Y
= σ and
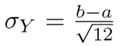 14.
14.
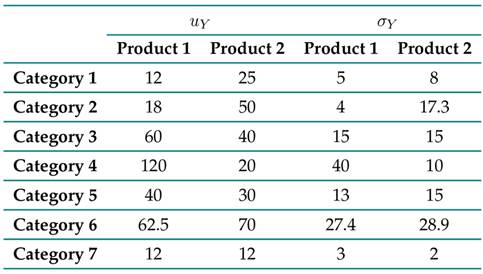
Table IV: Expected values and distributions from Table III
Thus, the demand per week (for each product) was sampled over a time window of 78 weeks, i.e., the data generated emulate the dynamics of the demands per product for this sales interval. Once the database was formed, it was segmented as follows: X = {X T rain , Y T rain , X T est , Y T est }. Then, a characteristic was added to the vectors X T rain and X T est which models the increase or decrease in the number of requested units of a product with respect to the previous week. Eq. (1) shows the transformation for the Y T rain case, following a similar procedure for Y T est .
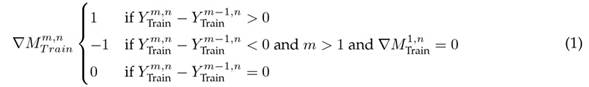
The sub-index m refers to the analyzed week for product n (defined in Table II). Eq. (1) indicates that, if the value of
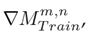 , there was an increase when ordering product n in week m regarding the m − 1 period. On the other hand, a value of
, there was an increase when ordering product n in week m regarding the m − 1 period. On the other hand, a value of
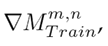 implies a stable behavior in week m regarding the moment m − 1. This descriptor seeks to guide the learning model at the moments when changes occur in the demands of the n products. For more details, the reader should consult (28). With these changes, the terms are defined as follows:
implies a stable behavior in week m regarding the moment m − 1. This descriptor seeks to guide the learning model at the moments when changes occur in the demands of the n products. For more details, the reader should consult (28). With these changes, the terms are defined as follows:
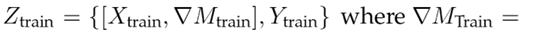
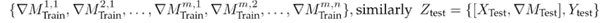
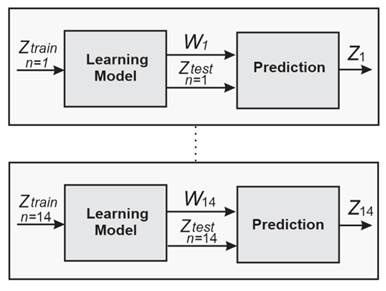
Regression model
This phase is divided into two processes: model training and simulation. The first process consists of computing the set of parameters W n given the demands per week for an item n of a specific category. On the other hand, the simulation process consists of predicting the behavior regarding the future demands of product n once the parameters W n
Model training
Fig. 2 shows each of the stages that make up the training phase. In short, it consists of a database that integrates synthetic data of demands per week for a family of products, as well as a supervised learning model to emulate the dynamics of weekly demands. The purpose is to transfer the data content to the model through a learning rule that allows finding the set of parameters W n .
Figure 2: Prediction model diagram
Supervised learning model
In this paper, three supervised options for state-of-the-art training are examined. Each of these is described below.
SVM
The use of an SVM as a prediction model is mainly due to its robustness against data with noise. It is a widely studied method, and it is easy to implement. This method is characterized by being a linear model in the W n parameters, which are tuned by minimizing a regularized error function subject to a set of linear constraints.
Generally, the problem is usually transformed into an equivalent dual one by applying the KKT (Karush-Kuhn-Tucker) conditions, obtaining a quadratic representation that allows the value W n to be inferred when it is solved. Once the parameter values W n are known, the model is trained. However, the equivalent objective function will depend on some variables assumed to be known, such as the Z T rain data set, as well as the Kernel structure (covariance function) (29, 30).
ARx Model
The acronym ARx refers to an autoregressive model of exogenous terms. It involves an input signal in its structure. Eq. 2 shows this model. The meaning of each term is shown in Table V.
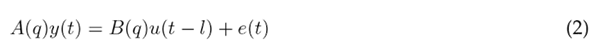
Table V: Nomenclature associated with the ARx model

The set of parameters to infer W n corresponds to the set of values of the coefficients a n a and b n b . These are tuned via least squares through the Z T rain dataset. Then, once the values of W n are known, the model is determined for any value of t, assuming that W n is known. For more details, the reader can refer to 31.
Gaussian process (GP)
Contrary to previous methods, the GP introduces a probabilistic non-linear prediction function, preventing a fixed structure in the model. From its base, the model assumes that the nature of the data follows a Gaussian distribution function established by a mean function m(x) and a covariance cov(x, x). In the literature, cov(x, x) is also known as Kernel, so the model training consists of tuning the parameters of m(x) and cov(x, x) (i.e., W n ) given the input X T rain and output Y T rain (Z T rain ) dataset. The prediction process (once the model has been trained) is performed from the mean predictive function, as shown in Eq. (3).
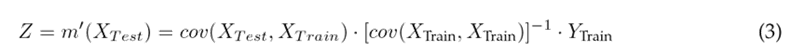
where m ′ (x 1) is the prediction in space x 1 given the input x and the corresponding output y. An interesting feature of the GP allows computing the evolution of uncertainty (Eq. (4)) in the prediction using the predictive standard value (Eq. (3)), where σ(m ′ (x 1)) evaluates the uncertainty (variance) of m ′ (x 1). The GP implicitly assumes that the function m ′ 1(x 1) obeys - as does m(x) − a Gaussian behavior 32.

Validation
In this process, the performance of the trained models is evaluated through the dataset (X T est , ∇M T est ) and the corresponding prediction Z (Fig. 2). In the first place, the effective error is used as a performance metric (Eq. (5)) where E is the RMS error between the synthetic data validation vector and the prediction of the model 30. Here, N refers to the size of the vector Y T est .

This metric allows evaluating the fidelity of the trained model to emulate the prediction process of product demands. However, the Y
T est
and Y
T rain
data must be normalized to avoid bias regarding strong changes. In this work, they are normalized with respect to the mean value of the data as follows:
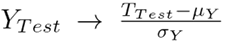 A similar transformation applies to YT rain. Thus, Eq. (5) is transformed into the following expression:
A similar transformation applies to YT rain. Thus, Eq. (5) is transformed into the following expression:

On the other hand, Eq. (7) defines the form of the standardized mean squared error (SMSE) (33):
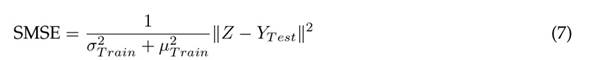
where
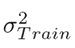 and µ
T rain
are the variance and arithmetic mean of the Y
T est
data. The metric given in Eq. (6) has the purpose of evaluating the stability of the prediction model Z when considering changes in the training data Z
T rain
.
and µ
T rain
are the variance and arithmetic mean of the Y
T est
data. The metric given in Eq. (6) has the purpose of evaluating the stability of the prediction model Z when considering changes in the training data Z
T rain
.
Integer linear programming model (ILP)
Z is an expected value of the demand. However, the shopkeeper will not always have sufficient resources to meet the quota established by the prediction model, which is why a strategy that refines the suggested Z values through a linear optimization model is adopted. The objective function to be minimized is presented in Eq. (8).
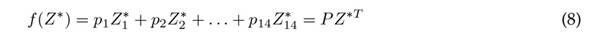
where Z ∗ = (Z1∗, Z2∗, . . . , Z1∗4) are the quantities demanded weekly to be refined for each of the items defined in Table II, and P = (p 1 , p 2 , p 3 , p 14) denotes the corresponding percentages of profit from the sale of each product. The restrictions associated with the maximum number of items allowed are as follows:
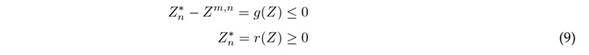
where Z m,n refers to the predictions of item n(n : 1 : 14) for week m. Therefore, Eq. (9) yields 28 linear constraints given a value of m. Finally, the equality associated with the investment in week m is
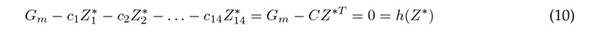
where C = (c 1 , c 2 , c 3 . . . , c 14) are the purchase costs per item. Now, the refined quantities Z ∗ are found by solving the following ILP problem (Eq. (11)) for an investment G associated with week m.
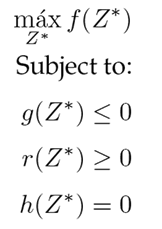
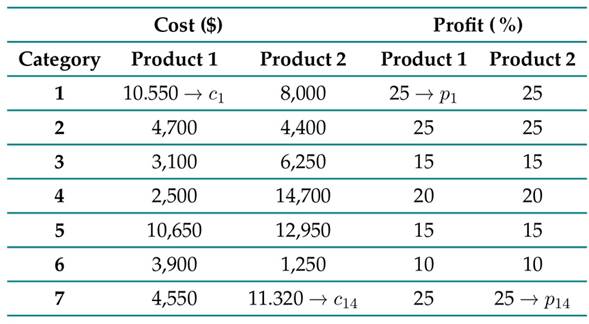
Note that the presumption of solving the problem stated in Eq. (11) is due to the fact that the quantities to be refined have a discrete characteristic. The values of P and C have been extracted from the portal www.megatiendas.co, and they are condensed in Table VI.
Table VI: Definition of the values for the percentage gain vector P and the cost per product C
Experiments
The test procedures evaluated the performance of the learning rules and the ILP. For the first case, the performance of the three strategies was evaluated by computing the values of E and SMSE (Eqs. (6) and (7)) for the prediction Z produced by the model and the test dataset Y T est . Out of the 78 weeks, the first 55 were selected with their corresponding demands to build the vectors X T rain , Y T rain , and ∇M T rain . Then, with the other weeks (56 to 78), the validation array X T est , Y T est , and ∇M T est was made. The test in Algorithm 1 shows the process that summarizes the above.
For the case of GP and SVM, a radial basis covariance function (RBF) with scale factor ρ 2 was assumed (32). This parameter was tuned given the Z T rain dataset. The GPML (34) toolbox was used to train (find W n ) and validate the GP (the value of ρ 2 was also tuned with this toolbox). For the SVM, MATLAB’s regression toolbox in MATLAB was employed. In this case, a value of τ 2 = 0, 001 (length scale) was set for the tests. The results are presented by means of tables and figures depicting the behavior of each model. In the case of the GP, the results are based on Eqs. (3) and (4). Finally, based on the results, the best prediction model was selected in order to evaluate the performance of the ILP.
The experiments carried out in the ILP consist of validating the problem stated in (11). For this purpose, weekly test investments G m , are defined. Thus, the refined quantities Z ∗ are calculated given the weekly investment G m and Z m,n . Finally, the expected return earning rate A G is calculated according to the suggested amount Z ∗ by the model in week m (Eq. (11)). Algorithm 2 shows a summary of the refinement process of the quantities Z and the profits for each of the weeks m under analysis.

Results
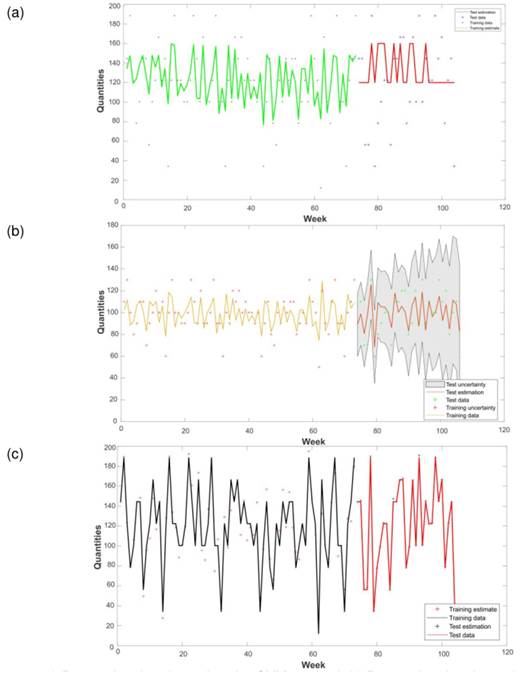
This section presents the analysis and discussion of the results obtained by implementing the methodology and performing the validation tests proposed in the methodology section. Fig. 3 shows the demand estimation made via the proposed prediction methods for product 14. In 3c, it can be seen that the ARx is the predictor that manages to capture the trend of the data and the demand variability for the item in the time window.
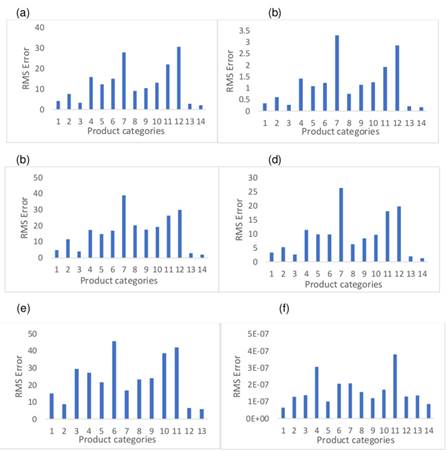
Fig. 3b shows GP’s low performance, as it fails to predict the variability of the demands when estimating an average value. Although the SVM manages to improve the prediction concerning the GP, this variation is not enough to emulate the dynamics of the weekly demands of the products (Fig. 3a). The quantitative results are shown in Fig. 3b. The results regarding the effective errors are condensed (Eq. (5)) once the Monte Carlo experiment has been simulated (Algorithm 1). As per Fig. 4b, the ARX shows a lower error when compared to the SVM (Fig. 4d) and the GP (Fig. 4f), which corroborates the results shown in Fig. 3. It is noteworthy that the minimum error for the training demands is reached by GP (Fig. 4e). This suggests that the model is overtrained, which explains the result in Fig. 3b. On the other hand, Fig. 4d shows that the SVM responds adequately to products with low variability, as is the case of the items in categories 1 and 7 (Table II).
Figure 3: a) Demand estimation using the SVM method. b) Demand estimation using the GP method. c) Demand estimation using the ARX method
Figure 4: a) Training RMS error for the ARX method. b) Test RMS error for the ARX method. c) Training RMS error for the SVM method. d) Test RMS error for the SVM method. e) Training RMS error for the GP method. f) Test RMS error for the GP method
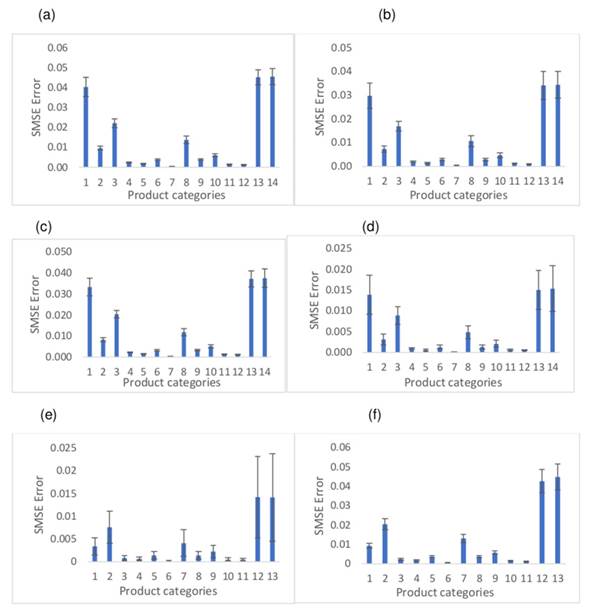
Fig. 5 synthesizes the results for the SMSE metric. The GP fails to stabilize in the training phase regarding the categories {1,2,7, 12, 13}. On the other hand, the SVM and the ARx exhibit a similar qualitative behavior in all the product categories under study, both in the training stage and during the validation. The results suggest that the prediction computed by the three methods evaluated is stable. This corroborates what is evidenced in Figs. 5 and 6, where the change in the datasets Z T rain and Z T est fails to capture the dynamics of the data, nor does it significantly reduce the effective errors, mainly in the case of the SVM and the GP. The above insinuates that they fail to satisfactorily emulate the behavior of the demands. This may be due to the nature of the application, where the analysis time window (104 weeks) is restricted for these models.
Figure 5: a) Training RMS error for the ARX method. b) Test RMS error for the ARX method. c) Training RMS error for the SVM method. d) Test RMS error for the SVM method. e) Training RMS error for the GP method. f) Test RMS error for the GP method
Table VII summarizes the results obtained by calculating the first expected value and the variance of the predictors for each of the studied products’ demands. The ARx manages to approach the theoretical statistics, which is a significant result, suggesting that it manages to capture the variability and the mean value of the distributions associated with each of the demands. However, although the SVM and the GP approach the first theoretical moment of the data, they fail to capture the variability; these predictors have a variance bias in this application.
Table VII: Results regarding the expected value and variance for each of the predictors
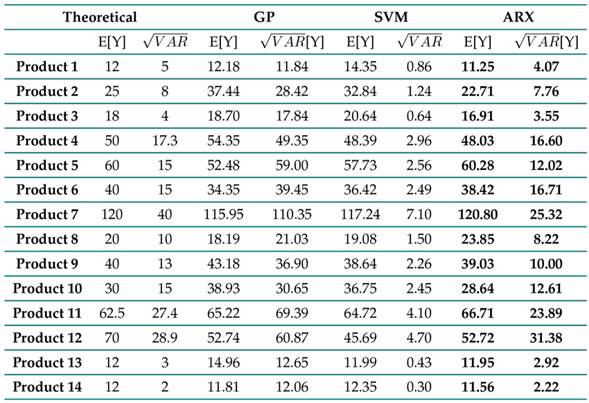
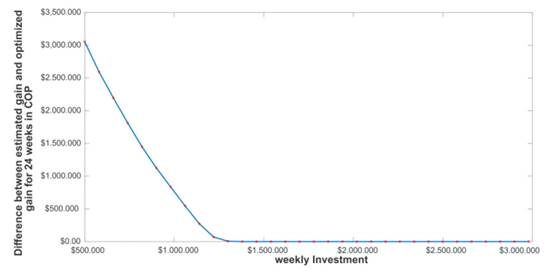
Given that the ARx exhibits a good performance in estimating the demands in each of the categories, and considering that the SVM and GP do not reach competitive performances (Table VII, Figs. 3, 4, 5), the outputs Z inferred by the ARx are selected to build the integer programming model described in Eq. (11) in such a way that it is possible to refine the quantities Z by defining a weekly investment index to determine Z ∗. Fig. 6 shows the difference between the profits when considering a sufficient investment to acquire the amounts Z versus the profits gained when examining a smaller investment to obtain Z ∗ in a cumulative period of 22 weeks. Notice how, in the linear programming method, the profits approach the maximum values as the investment grows. This is an expected result since the formulation aims to provide further weight to the products with the highest profit; the method suggests the amounts that maximize profit to the shopkeeper. It should be noted that, from an investment of 1.200.000 COP, it is possible to obtain the same profit as the one obtained with the Z amounts, i.e., the values suggested by the ARx.
Figure 6: Difference between the profit projected by the estimation of the product and the profit obtained by the integer programming model for 22 weeks of analysis
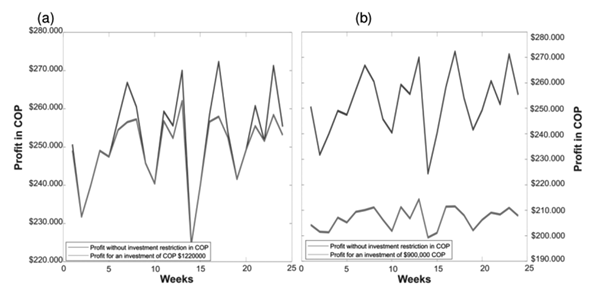
Fig. 7a shows the expected profit for 22 weeks according to the amounts Z.It also shows the profit for the amounts Z ∗ corresponding to an investment of 1.220.000 COP. This shows that the linear programming model does not affect the trend of expected profits. Note that this result is still valid for smaller investments (Fig. 7b), and it is important because the method guarantees proportionality in profits, even if the investment is low.
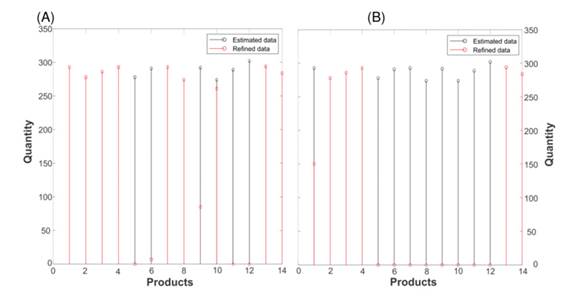
Fig. 8 shows how the solution to the problem given by Eq. (11) refines the number of products and prioritizes those that generate greater profits. For example, in Fig. 8a, the model gives priority to products 1, 2, 3, 4, 13, and 14 when comparing them against the utility portions defined in Table 7. They coincide with the items that report the highest percentage of utility per sale. Similarly, it should be noted (Fig. 8b) that, as the investment value increases, the amounts Z ∗ tend to equal the values of Z, which corrects the results reported in Figs.6 and 7.
Figure 7: a) Expected profit with Z vs. profit obtained with Z
∗ for 22 weeks, corresponding to an investment of 1.220.000 COP. b) Expected profit with Z vs. profit obtained with Z
∗ for 22 weeks given an investment of 920.000 COP
Figure 8: a) Estimated amounts for the 14 products in 22 weeks vs. refined amounts for a weekly investment of 500.000 COP. b) Estimated amounts for the 14 products in 22 weeks vs. refined amounts for a weekly investment of 1.000.000 COP
Conclusions
In this research, a methodology is designed and implemented with the aim of estimating the demand for products sold in neighborhood stores. This is achieved based on the history of the weeks of sales for previous months and weeks. This method estimates demand and suggests which products to buy in order to maximize profit based on an available investment cost. Based on the results, it is observed that the model proposed in Eq. (11) is functional to the extent that the investment available per week is not sufficient to acquire the amounts Z. This is inferred by analyzing that reported in Figs. 8a and 8b, where the behavior of the amounts Z and Z ∗ is described as an investment value. The aforementioned is an expected result because, at a higher level of investment, the amounts Z ∗ are closer to Z. Therefore, it is concluded that the refinement process of the proportions of Z becomes unnecessary at high levels of investment.
On the other hand, the results show that, for this application, the ARx is the model that is closest to the data dynamics (Table VII), managing to reproduce the first moment and the variance of the probability distributions assumed in Table III. This is verified by analyzing the values of the effective errors reported in Fig. 4b, where the ARx proves to be more competitive than the SVM and the GP.
The differences per product regarding the behavior of the effective error for the studied learning models can be explained by analyzing some categories’ variances. For example, from Table IV, items 11 and 12 have a high variability concerning the others, i.e., they exhibit a greater range of fluctuation in demand. Note that, in these particular cases, the effective error is significantly higher when compared to products with low variability, as for those belonging to category 1. The above suggests that the prediction models’ yields are sensitive to solid changes in demand.
As further work, the proposed method must incorporate other relevant variables, allowing for qualitative and/or quantitative variables to be weighted in order to refine the Z quantities. This is essential, given that, in a competitive environment such as the neighborhood grocery store market, the supply of different products should not be strictly conditioned as being a problem of maximizing the shopkeeper’s profits according to the items that yield the highest profit. However, on the contrary, it should consider the client’s needs, so that these are incorporated into the strategy for calculating Z ∗. On the other hand, it is also important to validate this methodology with different neighborhood stores, as well as to measure the possible impact of the methodology, for it is imperative to build software that allows the shopkeeper to manage it with ease. This information can be valuable to grow the model and thus correlate other variables currently unknown to the method
Acknowledgements
Acknowledgements
The authors would like to thank Universidad Tecnológica de Pereira and Universidad de Valle for their support during this project.
References
Licencia
Derechos de autor 2023 Carlos Alberto Henao-Baena, Bibiana Zuluaga-Zuluaga, Julian Galeano-Castro, Edward Jhohan Marín-García, Andrés Felipe Calvo-Salcedo

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.






2.jpg)