DOI:
https://doi.org/10.14483/23448393.2744Publicado:
2003-11-30Número:
Vol. 9 Núm. 1 (2004): Enero - JunioSección:
Ciencia, investigación, academia y desarrolloModelos de Tráfico en análisis y control de Redes de Comunicaciones
Descargas
Referencias
N. Abramson "Multiple Access Communications: Foundations for Emerging Technologies", IEEE Press, 1994
P. Abry and D. Veitch. "Wavelet Analysis of Long-Range-Dependent Traffic". IEEE Trans. Information Theory, 44(1):2-15, 1998.
P. Abry, P. Flandrin, M. Taqqu and D. Veitch. "Wavelets for the Analysis and Synthesis of Scaling Data", In "Self-Similar Network Traffic and Performance Evaluation", K. Park and W. Willinger, editors. John Wiley and Sons, New York, 2000.
P. Abry, D. Veitch and P. Flandrin "Long-Range Dependence: Revisiting Aggregation with Wavelets". Blackwell publishers ltd. 1999
A. Adas and A. Mukherjee. "On resource management and QoS guarantees for long-range dependent traffic". GIT-CC-94/60 1994.
R. Albert and L. Barabasi. "Statistical mechanics of complex networks". Reviews of Modern Physics, Volume 74, January 2002.
M. Alzate, "Multiplexaje de voz y datos", Universidad de los Andes, Tesis de Maestria MIE-90-II-1, Departamento de Ingeniería Eléctrica, 1990.
M. Alzate y F. Vega. "Predecibilidad del tráfico en redes modernas de telecomunicaciones". Revista Ingeniería, Universidad Distrital FJC, 2003.
M. Alzate. "Conmutación de Paquetes de Voz". X Congreso Nacional y I Andino de Telecomunicaciones, 1995.
M. Alzate. "Framing ATM Cells for Satellite Onboard Switching". Revista INGENIERIA, Universidad Distrital, 2000.
M. Alzate. "Generation of Simulated Fractal and Multifractal Traffic". IX Congreso Nacional de Estudiantes de Ingeniería de Sistemas, Bogotá, 2000.
M. Alzate. "Introducción al Tráfico Autosemejante en Redes de Comunicaciones". Revista INGENIERIA, Universidad Distrital, 2001.
M. Alzate. "Uso de la Transformada Wavelet para el Estudio de Tráfico Fractal en Redes de Comunicaciones". Revista INGENIERIA, Universidad Distrital, 2002.
M. Alzate. "Probability of Imminent Failure as a Routing Metric in a High-Mobility Wireless Ad Hoc Network". 8th International Conference on Cellular and Intelligent Communications, Seoul, Korea, 2003.
M. Alzate. "Análisis de la Eficiencia en el Uso de la Capacidad Asignada a Conversaciones Telefónicas". Revista INGENIERIA, Universidad Distrital, 1993
M. Alzate. "Tráfico de Voz en ATM Sometido a Control de Admisión por Leaky Bucket". Revista INGENIERIA, enero-marzo, 1996.
M. Alzate. "Procesamiento Digital de Señales en el Modelamiento y Análisis de Redes de Comunicaciones", Documento interno de los grupos de investigación en DSP y Telecomunicaciones la Universidad Distrital (GI-DSP-UD y GITUD), Octubre 2003.
M. Alzate. "Simulation model for MPEG-II Video Traffic", ENEE 608 class project final report, University of Maryland, spring 1998.
M. Alzate and S. Suárez "Ant Routing of fractal traffic", IEEE ANDESCON 2004.
S. Appleby and S. Steward. "Mobile software agents for control in telecommunications networks". BT Technology Journal, vol. 12, No. 2, april 1994.
M. Arlitt and C. Williamson. "Web Server Workload Characterization: The search for Invariants". IEEE/ACM Trans. Networking, 5(5):631-645, 1997.
ATM Forum "Traffic Management Specification" af-tm0056.000, April 1996
P. Bak. "How Nature works: the science of self organized criticality". Copernicus, NY, 1996.
A-L. Barabasi and E. Bonabeau. "Scale-free networks". Scientific American, may 2003.
J. Baras. "Control Problems in Modern Communication Networks". ENEE769 syllabus, University of Maryland, Spring 2001.
J. Baras, A. Ephremides, R. La and S. Ulukus "Vertical Protocol Integration in Wireles Adhoc Networks", A proposal to the NSF, 2002.
J. Beran, R. Sherman, M. Taqqu and W. Willinger. "LongRange Dependence in VBR video traffic". IEEE. Trans. Commun. 43:1566-1579, 1995.
J. Beran. "Statistics for Long Memory Processes". Chapman and Hall, New York, 1994.
S. Blake et.al. "An architecture for differentiated services" IETF RFC 2475, December 1998.
E.Bonabeau, M.Dorigo and G.Theraulaz. "Swarm Intelligence: From Natural to Artificial Systems", Oxford University Press, 1999.
O. Boxma and J. Cohen. "The M/G/1 Queue with Heavy-tailed Service Time Distribution". IEEE J. Selected Areas in Commun. 16:749-763, 1998.
D. Bertsekas and R. Gallager. "Data Networks", 2nd edition, Prentice-Hall, NJ, 1992.
J. Burns, T. Ott, J. Kock and A. Krzesinski "Path Selection and Bandwidth Allocation in MPLS networks: a non-linear programming approach", ITCOM'01, SPIE, 2001
J. Carlson and J. Doyle. "Highly Optimized Tolerance: Robustness and design in complex systems". http:// www.physics.ucsb.edu/~complex/pubs/hot2.ps
M. Coates, R. Castro and R. Nowak. "Maximum Likelihood network topology identification from edge-based unicast measurements". Rice University ECE department, Technical report TREE-0107, August 2002.
M. Coates, A. Hero, R. Nowak and B. Yu. "Internet Tomography", IEEE Signal Processing Magazine, may 2002.
M. Crovella and A. Bestavros. "Self-similarity in WWW traffic". IEEE/ACM Trans. Networking, 5:835-846, 1997.
M. Crovella, M. Taqqu and A. Betsavros. "Heavy-Tailed Probability Distributions in the WWW", In "A practical guide to Heavy Tails", Adler, Feldman and Taqqu, editors. Birkhauser, 1998.
C. Chang. "Performance Guarantees in Communication Networks", Springer, 2000
R. Cruz. "A Calculus for Network Delay. Part I: Elements in Isolation", IEEE Trans. On Information Theory, Volume 37, Number 1, January 1991.
R. Cruz. "A Calculus for Network Delay. Part II: Network Analysis", IEEE Trans. On Information Theory, Volume 37, Number 1, January 1991.
I. Daubechies. "Ten Lectures on Wavelets". SIAM'92. Philadelphia, 1992.
E.Dinan, D. Awduche and B. Jabbari "Optimal Traffic Partitioning in MPLS Networks", in "Networking 2000", Edited by G. Pujolle, Springer-Verlag, 2000
A. Erramili, O. Narayan and W. Willinger. "Experimental queueing analysis with LRD packet traffic". IEEE/ACM Trans. Networking, 4:209-223, 1996.
A. Erramilli and R. Singh. "An application of deterministic chaotic maps to model packet traffic". Queueing Systems, vol. 20, 1996. Pp. 171-206.
A. Feldman, A. Gilbert, P. Huang and W. Willinger. "Dynamics of IP Traffic: A Study of the Role of Variability and the Impact of Control". Proc. ACM SIGCOM'99, 1999.
P. Fieguth and A. Willisky. "Fractal estimation using models on multiscale trees". IEEE Trans. Signal Proc. 44:1297-1300, 1996.
P. Flandrin. "Wavelet Analysis and Synthesis of Fractional Brownian Motion". IEEE Trans. Inf. Theory, 38:910-917, 1992.
S. Floyd and V. Paxson. "Dificulties in Simulating the Internet", IEEE/ACM Trans. On Networking, Vol. 9, N. 4, August 2001.
V. Frost and B. Melamed. "Traffic Modeling for Telecommunications Networks". IEEE Commun. Mag. 32(3):70-81, 1994.
Y. Gao, G. He and J. Hou. "On Exploiting Traffic Predictability in Active Queue Management", IEEE Infocom 2002, New York, June 2002
Y. Gao, G. He and J. C. Hou. "On Leveraging Traffic Predictability in Active Queue Management", Technical report, Department of Electrical Engineering, The Ohio State University, 2002
A. Gilbert, W. Willinger and A. Feldman. "Scaling analysis of conservative cascades with application to network traffic". IEEE Trans. Information Theory, 45(3):971-991, 1999.
F.W.Glover and M.Laguna. "Tabu Search" Kluwer Academic, 1998.
G. Grimmet and D. Stirzaker. "Probability and Random Processes", second edition, Oxford Science Publications, NY, 1995.
G. Gripenberg and I. Norros, "On the prediction of fractional Brownian motion," Journal of Applied Probability, vol. 33, pp. 400-410, 1996.
T. Gyires, "Using Active Networks for Congestion Control in High-Speed Networks with Self-Similar Traffic", IEEE Intl. Conf. On Systems, Man, and Cybernetics, 2000, Vol. 1.
O. Haggstrom "Finite Markov Chains and Algorithmic Applications", Cambridge University Press, 2002.
T. Hagiwara, H. Doi, H. Tode and H. Ikeda. "High-Speed Calculation Method of the Hurst Parameter Based on Real Data". LCN 2000.
G. He, Y. Gao J. Hou and K. Park. "A case for exploiting selfsimilarity of Internet traffic in TCP Congestion Control", Technical report, Department of Electrical Engineering, The Ohio State University, 2002
D. Heyman and T. Lakshman. "What are the Implications of LRD for VBR Video Traffic Engineering?" IEEE/ACM Trans. On Networking, Vol. 4, N. 3, June 1996.
D. Heyman and D. Lucantoni. "Modeling multiple IP traffic streams with rate limits". In Proceedings of the 17th International Teletraffic Congress, Brazil, December 2001.
P. Huang, A. Feldmann and W. Willinger. "A Non-intrusive, Wavelet-based Approach To Diagnosing Network Performance Problems". Proceeding of ACM SIGCOMM Internet Measurement Workshop 2001, San Francisco, November 2001
J. Hui. "Resource Allocation for Broadband Networks", IEEE Journal on Selected Areas in Communications, Vol. 6, Number 12, December 1988.
IEEE Journal on Selected Areas in Communications, Special issue on Telecommunication Network Design and Planning, Volume 7, Number 8, 1989.
Internet Traffic Archive. BC_pAug89, http://www.acm.org/ sigcomm/ITA/index.html.
S. Kauffman. "The origins of order: self organization and selection in evolution". Oxford University Press, NY, 1993.
L. Kleinrock. "Queueing Systems. Vol. I: Theory. Vol.II: Computer Applications", John Wiley and Sons, NY, 1976.
A. Kulkarni and S. Bush. "Network management and Kolmogorov complexity". IEEE Openarch, 2001
R. La and V. Anantharam. "Optimal Routing Control: gametheoretic approach". 1998 CDC Conference, 1998.
W. Leland, M. Taqqu, W. Willinger and D. Wilson. "On the self-similar nature of Ethernet Traffic". IEEE/ACM Trans. Networking, 2:1-15, 1994.
R. Lewin. "Complexity: life at the edge of chaos". McMillan, NY, 1992.
S. Ma and C. Ji. "Modeling Heterogeneous Network Traffic in Wavelet Domain". IEEE/ACM Trans. Networking, 9(5):634-649, 2001.
B. Mandelbrot and J. VanNess. "Fractional Brownian Motions, Fractional Noises and Applications". SIAM Rev., 10:422-437, 1968.
D. Manolakis, V. Ingle and S. Kogon "Statistical Signal Processing", McGraw-Hill, 2000.
I. Marshall and C. Roadknight. "Adaptive management of an Active Service Network". BT Technol J Vol 18 No 4, pp.78-84, October 2000.
G. McLachlan and T. Krishnan "The EM algorithm and estensions", John Wiley, 1997.
B. Melamed, "An Overview of the TES Process and Modeling Methodology", Performance Evaluation of Computer and Communication Systems, Lecture Notes in Computer Science, Springer-Verlag, 1999
J. Mendes and S. Dorogovtsev. Evolution of networks: From biological nets to the Internet and WWW. Oxford University Press, NY, 2003.
M.Michelle "An introduction to genetic algorithms" MIT Press, Cambridge, MA, 1998
M. Neuts "Matrix-Geometric Solutions in Stochastic Models", Dover Publications, NY, 1994.
I. Norros. "On the Use of Fractional Brownian Motion in the Theory of Connectionless Networks". IEEE J. Selected Areas in Commun. 13(6):953-962, 1995.
T. Ohira and R. Sawatari. "Phase transition in computer network traffic model". Physical review, vol. 58, pp. 193-195, 1998.
K. Park and W. Willinger. "Self-Similar Network Traffic and Performance Evaluation". John Wiley and Sons, New York, 2000.
K. Park and W. Willinger "Self-Similar Network Traffic: An Overview". In "Self-Similar Network Traffic and Performance Evaluation", K. Park and W. Willinger, editors. John Wiley and Sons, New York, 2000.
M. Parulekar and A. Makowski. "M/G/¥ Input Processes". Proc. IEEE Infocom'97, 1997.
V. Paxson and S. Floyd. "Wide-Area Traffic: The Failure of Poisson Modeling". IEEE/ACM Trans. Networking, 3:226-244, 1995.
Petropulu, A. and Nowak, R. "Signal Processing for Networking". IEEE Signal Processing Magazine, May 2002
M. de Prycker "Asynchronous transfer mode solution for BISDN" Ellis Norwood, 1991.
P. Ranjan, E. Abed and R. La. "Nonlinear Instabilities in TCPRED". IEEE Infocom'2002.
E. Rathgeb. "Modeling and Performance Comparison of Policing Mechanisms for Broadband Networks", IEEE Journal on Selected Areas in Communications, Vol. 9, Number 4, April 1991.
V. Ribeiro, R. Riedi, et al. "Multiscale Queuing Analysis of Long-Range-Dependent Network Traffic", Submitted to IEEE Transaction on Networking, 2002.
R. Riedi, et. al. "A Multifractal Wavelet Model with Application to Network Traffic". IEEE Trans. Inf. Theory, 45(3):992-1018, 1999.
R.Riedi, "Multifractal processes," Stochastic Processes and Applications, preprint, 1999.
A. Riska "Aggregate matrix-analytic techniques and their applications", Computer Science PhD dissertation Research, College of Virginia, 2002.
J.Roberts "Traffic Theory and the Internet", IEEE Communications Magazine, January 2001.
J. Roberts "Insensitivity in IP Networks Performance", IPAM Workshop, 2002
M. Schwartz. "Telecommunication Networks: Protocols, Modeling and Analysis". Prentice Hall, N.Y. 1989.
M. Schwartz. "Broadband Integrated Networks", Prentice Hall, NJ, 1996.
S. Shenker and J. Wroclawski "General characterization parameters for integrated service network elements", RFC 2215, IETF, September 1997.
Y. Shu, Z. Jin, L. Zhang, L. Wang and O. W. W. Yang, "Traffic prediction using FARIMA models", ICC'99, vol. 2, pp. 891-895, 1999.
R.V.Sole and S. Valverde. "Information transfer and phase transition in a model of internet traffic". Physica A, vol. 289, pp. 595-605, 2001
R.Srikant. "Control of Communication Networks". In "Perspectives in Control Engineering", T. Samad, Editor. IEEE Press, Piscataway, NJ, 2000.
R. Syski "Introduction to congestion theory in telephone systems", Oliver and Boyd, Edinburgh, 1960
Y. Takahashi, et.al. "ARIMA Model's Superiority over f-ARIMA Model", ICCT2000.
A. Tannenbaum "Computer Networks", 4th edition, Prentice Hall, 2002
M. Taqqu, W. Willinger and V. Teverovsky. "Estimators for Long-Range Dependence: An Empirical Study". Fractals 3(4):785-798, 1995.
D. Tennenhouse et.al. "A survey of ActiveNetwork research". IEEE communications Magazine, vol. 35, No. 1, January 1997.
A. Tewfik and M. Kim. "Correlation structure of the discrete wavelet coefficients of fractional brownian motion". IEEE Trans. Info. Theory, 38:904-909, 1992.
J.F.Traub and A.G.Werschulz. "Complexity and Information", Cambridge University Pres, Cambridge, UK, 1999.
Y. Tsang, M. Coates and R.Nowak. "Nonparametric Internet tomography". IEEE International Conference on Signal Processing, Vol. 3, 2002, pp. 2045-2048.
B. Tsybakov and N. Georganas. "Self-Similar Processes in Communications Networks". IEEE Trans. Inf. Theory, 44(5):1713-1725, 1998.
T. Tuan and K. Park. "Congestion control for self-similar network traffic". In "Self-similar network traffic and performance evaluation", edited by K. Park and W. Willinger, John-Wiley and sons, 2000.
UCB/LBNL/VINT "Network Simulator ns-2", http://www.isi.edu/ nsnam/ns
Y. Vardi "Network Tomography: Estimating Source-Destination Traffic Intensities from Link Data", Journal of the American Statistical Association, vol. 91, No. 433, 1996.
F.Vega. "Aplicación del efecto de memoria a largo plazo en el control de congestión en redes de conmutación de paquetes". Tesis de Maestría, Universidad Distrital, 2003.
F. Vega y M. Alzate. "Determinacion de la Predecibilidad de Trazas de Tráfico Mediante Analisis de Recurrencia". Revista INGENIERIA, Universidad Distrital, 2003
D. Veitch and P. Abry. "A Wavelet-Based Joint Estimator of the Parameters of LRD". IEEE Trans. Inf. Theory, 45(3):878897, 1999.
A.Veres and M.Boda. "The Chaotic nature of TCP congestion control". IEEE Infocom'2000.
J. Walrand "An Introduction to Queueing Networks", PrenticeHall, NJ, 1988.
W. Willinger, and V. Paxson, "Where Mathematics meets the Internet," Notices of the American Mathematical Society, vol. 45, no. 8, Aug. 1998, pp. 961-970.
C. Weinstein. "Fractional Speech Loss and Talker Activity Model for TASI and for Packet-Switched Speech", IEEE Trans. On Comm. Volume 27, Number 11, november 1979.
W. Willinger, M. Taqqu, R. Sherman and D. Wilson. "SelfSimilarity Through High Variability: Statistical Analysis of Ethernet LAN Traffic at the Source Level". IEEE/ACM Trans. Networking, 5(1):71-86, 1997.
W. Willinger and J. Doyle. "Robustness and the Internet: Design and Evolution". Caltech, Pasadena, 2002.
I. Wokoma, L. Sacks and I. Marshall. "Biologically Inspired Models for Sensor Network Design". LCS 119, Springer Verlag, 2002
F.Xue, "Modeling Analysis and Performance Evaluation for self-similar traffic." Ph.D. Dissertation, Tianjin University, June 1998.
J. Yang and I. Lambadaris, "Effective Bandwidths for TES Processes", ITC 2001, Salvador de Bahia, Brazil.
O. Yu and S. Khanvilkar "Dynamic adaptive QoS provisioning over GPRS wireless mobile links", ICC 2002
J. Widmer, R. Denda and M. Mauve, "A Survey of TCP-Friendly Congestion Control", IEEE Network Magazine, june 2001
T.Karagiannis, M.Molle, M.Faloutsos and A.Broido, "A Nonstationary Poisson View of Internet Traffic", IEEE Infocom 2004, Hong Kong, 2004.
Ashwin Sridharan, Roch Guerin and Christophe Diot "Achieving Near-Optimal Traffic Engineering Solutions for Current OSPF/ IS-IS Networks", IEEE Infocom 2003, San Francisco, CA, 2003.
Eric J. Anderson and Thomas E. Anderson "On the Stability of Adaptive Routing in the Presence of Congestion Control", IEEE Infocom 2003, San Francisco, CA, 2003.
M. Alzate and J. Baras "Dynamic Routing in Mobile Wireless Ad Hoc Networks using Link Life Estimates", 38th Conference on Información Sciences and Systems, CISS'04, Princeton University, Princeton, NJ, March 2004, pp. 363-367.
C. Perkins (editor). Ad Hoc Networking. Addison Wesley, 2001
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ingeniería, 2004-00-00 vol:9 nro:1 pág:63-87
Modelos de Tráfico en Análisis y Control de Redes de Comunicaciones
Marco Aurelio Alzate
Miembro de los grupos de GITUD y GIDSP UD. Este trabajo se realizó bajó la supervisión del profesor Néstor M. Peña en el programa doctoral en ingeniería de la Universidad de los Ándes.
Resumen
Este es un artículo tutorial y de revisión en el que se describen los principales modelos de tráfico que se usan actualmente para representar la aleatoriedad en las demandas de los usuarios de redes modernas de comunicaciones, así como la utilización de dichos modelos en el análisis de desempeño de la red y, consecuentemente, en el control de la misma. También se menciona cómo el comportamiento fractal del tráfico moderno conduce al estudio de las redes desde el punto de vista de sistemas complejos. Como conclusión, se sugiere un área de investigación en el tema general de Modelamiento de Tráfico y Control de Redes de Comunicaciones, como es el uso de la predecibilidad del tráfico con dependencia de rango largo, para hacer control más oportuno y eficiente en forma integrada a diferentes niveles de la jerarquía funcional de la red.
I. INTRODUCCIÓN
La teoría de tráfico consiste en la aplicación de modelos matemáticos para explicar la relación que existe entre la capacidad de una red de comunicaciones, la demanda de servicio que los usuarios le imponen y el nivel de desempeño que la red puede alcanzar. Como dicha demanda es de naturaleza estadística, se suele representar mediante algún proceso estocástico adecuado, con lo que se constituyen diferentes Modelos de Tráfico. Así pues, dado un modelo de tráfico particular, el desempeño de la red se podría predecir, en principio, aplicando herramientas adecuadas proporcionadas principalmente por la Teoría de Procesos Estocásticos y otros recursos matemáticos. Los resultados de dicho análisis de desempeño son los puntos de partida para el diseño de mecanismos de control de la red en aspectos tan variados como el control de admisión, el control de flujo, el control de congestión, el control de la memoria en las colas, la asignación de recursos (especialmente la administración dinámica del ancho de banda en los enlaces y de la memoria en los buffers de transmisión), el caché dinámico, el enrutamiento dinámico adaptable, etc.
Un ejemplo tradicional y supremamente exitoso es el de las redes telefónicas, en las que la relación tráfico-desempeño se describe mediante una expresión cerrada y compacta, la fórmula B de Erlang, con la que se calcula la probabilidad de que una llamada sea rechazada, ρB, cuando hay N circuitos sobre los que los usuarios imponen una intensidad de tráfico ρ, definida como el producto de la tasa de llegada de llamadas por la duración promedio de cada llamada:
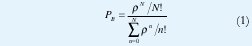
En esta fórmula sólo se supone que las llamadas telefónicas llegan según un proceso estacionario de Poisson, así que la probabilidad de bloqueo no se ve afectada por otras características del tráfico como la distribución de los tiempos de duración de las llamadas.
En redes modernas de comunicaciones, es importante poder encontrar relaciones entre el tráfico y el desempeño, semejantes a la ecuación (1), con las cuales se pueda determinar qué tipos de garantías de servicio pueden ofrecerse. Por supuesto, no podemos esperar que dichas relaciones se puedan expresar de una manera tan compacta como la fórmula de Erlang, pero sí debemos ser capaces de encontrar procedimientos de diseño de redes y de administración de los recursos de la red en los que se tengan en cuenta las características esenciales del tráfico que afectan significativamente las medidas de desempeño y en los que se ignoren las características irrelevantes. Con este propósito, resulta de fundamental importancia desarrollar modelos de tráfico que capturen dichas características.
A lo largo del desarrollo de las redes de comunicaciones en los últimos cien años, se han propuesto diferentes modelos de tráfico, cada uno de los cuales ha resultado útil dentro del contexto particular para el que se propuso. Esto es, al utilizar estos modelos en el estudio de desempeño de redes (mediante análisis o simulación), se obtienen resultados estadísticamente significativos. Este aspecto es importante pues un modelo puede ser tan bueno como otro si ambos satisfacen pruebas de hipótesis adecuadas (en especial, los criterios de ajuste del modelo no sólo deben incluir distribuciones marginales y estructuras de autocorrelación sino que, en últimas, deben predecir con suficiente exactitud las medidas de desempeño de interés). Curiosamente, hasta hace dos décadas, fue muy poco el desarrollo que se hizo en el campo del modelamiento de tráfico propiamente dicho, pues la ingeniería de tráfico se dedicaba al análisis de desempeño de los componentes de la red bajo tráfico Poisson. Sólo recientemente, a partir de la necesidad de prestar servicios integrados con una única estructura de red, el modelamiento de tráfico se ha convertido en una extensa área de investigación en la que el objetivo es desarrollar modelos que predigan el impacto de la carga impuesta por las diferentes aplicaciones sobre los recursos de la red, de manera que se pueda evaluar la calidad de servicio (QoS) ofrecida.
En este artículo se hace un breve resumen de los principales modelos de tráfico que se han propuesto hasta el día de hoy y cómo se pueden deducir a partir de ellos los niveles de desempeño de la red para diseñar procedimientos de control adecuados. Como se hace especial énfasis en ofrecer las definiciones más relevantes, el artículo toma un formato tutorial.
En el siguiente numeral se mencionan los modelos no correlacionados, los cuales se extienden en el numeral tres a procesos con dependencia de rango corto. El numeral 4 se refiere a modelos de tráfico fractal, donde se discute brevemente su predecibilidad. La sección 5 menciona el modelo más usado actualmente en redes IP y ATM, donde se deja de lado la descripción estadística detallada para usar sólo algunos descriptores básicos. El numeral 6 indica cómo la dependencia de rango largo es sólo una manifestación de la complejidad de las redes modernas de comunicaciones, pues también existen otros fenómenos emergentes que sugieren un cambio de paradigma en el diseño, análisis y administración de redes. La sección 7 se refiere a evidencias recientes de comportamiento tipo Poisson en el tráfico agregado sobre enlaces troncales de gran capacidad sujetos a baja utilización. Por último, en la sección 8, se propone un área de investigación relacionada con el modelamiento de tráfico para análisis y control de redes. El artículo termina con unas breves conclusiones en la sección 9.
II. MODELOS DE TRÁFICO NO CORRELACIONADOS
Cuando se agrega el tráfico proveniente de una gran cantidad de usuarios independientes entre ellos, es de esperar que los tiempos entre llegadas de demandas (paquetes, llamadas, flujos, conexiones, ...) a los nodos de ingreso a la red sean no correlacionados, a menos que la magnitud de las demandas (longitud de los paquetes, duración de las llamadas,...) tengan algún tipo de dependencia de rango largo. Esta suposición de independencia respecto al tráfico que ingresa a la red permitió el desarrollo de casi toda la Teoría de Colas, la cual constituye la más exitosa herramienta matemática hasta ahora usada en el análisis y control de redes de comunicaciones. En esta segunda parte del artículo describimos algunos de los modelos de tráfico propuestos bajo dicha suposición.
2.1 Modelos de Tráfico sin Memoria
Un proceso estocástico {A(t), t≥0} que toma valores enteros no negativos es un proceso de Poisson con tasa λ si: (a) A(t) es un proceso de conteo que representa el número total de llegadas que han ocurrido desde el instante 0 hasta el instante t, de manera que A(0)=0 y A(t)- A(s) es el número de llegadas en el intervalo (s, t]. (b) El número de llegadas que ocurren en intervalos de tiempo no sobrelapados son independientes. (c) El número de llegadas en cualquier intervalo de longitud T es una variable aleatoria con distribución de Poisson y parámetro λT [32],
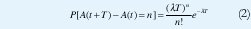
Generalmente, el proceso de Poisson se considera adecuado para modelar el tráfico agregado de un gran número de usuarios similares e independientes, tal como ocurre con las conversaciones telefónicas o el tráfico interactivo de datos (Figura 1(b)). Los tiempos entre llegadas, T, son independientes y exponencialmente distribuidos con promedio 1/&lambda, de manera que el tiempo que toca esperar hasta ver la próxima llegada es independiente del instante en que se empiece a observar, lo cual se conoce como la "falta de memoria" de la distribución exponencial:
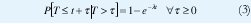
Esta propiedad también aparece en modelos de tiempo discreto en los que, en cada ranura de tiempo, la llegada de un paquete se da con probabilidad p, independientemente de otras ranuras. El número de llegadas en intervalos de n ranuras es una variable binomial (n, p), mientras que el número de ranuras N que toca esperar hasta ver la llegada del próximo paquete es una variable geométrica que también carece de memoria:
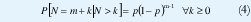
Es esta propiedad de falta de memoria de las distribuciones exponencial y geométrica la que hace posible reducir el cálculo de las principales medidas de desempeño de los elementos de una red de comunicaciones a un simple análisis de una cadena de Markov. Por ejemplo, si los tiempos de servicio en un multiplexor estadístico también son exponenciales, es posible encontrar la distribución estacionaria del número de clientes (paquetes, llamadas, sesiones, etc.) en el multiplexor, N(t), mediante el análisis de un proceso Markoviano de nacimiento y muerte, pues se trataría de una cola M/M, donde la primera Mse refiere a la falta de memoria en el proceso de llegadas y la segunda M se refiere a la falta de memoria en el proceso de servicios [68]. Con dicha distribución es posible encontrar todas las medidas de desempeño de interés tales como retardo promedio, variaciones en el retardo, ocupación de los circuitos y de los buffers de memoria en el multiplexor, probabilidad de rechazo, etc. Bajo otras distribuciones de los tiempos de servicio aún es posible encontrar las principales medidas de desempeño si existe independencia entre los tiempos de servicio (modelos M/GI). En estos casos se puede observar el proceso N(t) en instantes particulares que determinan una cadena de Markov embebida [68] o se pueden analizar los tiempos residuales de servicio [32]. En general, es la falta de memoria del proceso de llegadas la que facilita enormemente el análisis de los elementos de la red, de manera que existen resultados compactos para sistemas con varios servidores, con cupo limitado en las colas, con períodos ociosos en los servidores, con reservas de recursos, con diferentes clases de clientes, con sistemas de acceso múltiple por contención, con sistemas basados en prioridades, etc. Más aún, existen resultados semejantes para redes de colas, basados en el hecho de que la distribución de la ocupación conjunta de las colas se puede expresar mediante el producto de la ocupación marginal de cada una de ellas [120]. Se han desarrollado excelentes técnicas computacionales para la solución de este tipo de redes de colas, tales como soluciones matriciales geométricas [81], técnicas matriciales analíticas [95], o análisis de valor medio [120].
Como todos estos resultados de la teoría de colas condujeron a "fórmulas" que se pueden interpretar como ecuaciones de análisis y diseño de redes de comunicaciones, tal como la fórmula de Erlang (ecuación (1)), no es de sorprender que el modelo de Poisson se haya usado con gran éxito durante cerca de cien años para el análisis y el control de redes telefónicas (POTS) y de redes de datos (p.ej. X.25). En efecto, dada la uniformidad de los servicios y el pequeño rango de capacidades de los medios de transmisión de entonces, las llegadas tanto de conversaciones telefónicas como de paquetes de datos para servicios telemáticos se ajustaban con gran exactitud al modelo de Poisson. En la referencia [65], por ejemplo, se pueden apreciar excelentes ejemplos de cómo este tipo de modelos condujeron a métodos óptimos de diseño topológico de redes de comunicaciones.
Sin embargo, las únicas distribuciones que se caracterizan por su falta de memoria son la exponencial y la geométrica. Si bien esas distribuciones pueden ajustarse con exactitud aceptable al tráfico de las redes modernas de comunicaciones cuando se modela al nivel de flujos de datos, resultan inadecuadas cuando se quiere representar el tráfico a nivel de paquetes de datos, pues los diferentes tipos de flujos generan muy distintos patrones de llegadas de paquetes [96]. Por eso la teoría de colas se ha extendido con modelos de tráfico en los que los tiempos entre llegadas no son necesariamente exponenciales, como se menciona a continuación.
2.2 Modelos de Renovación
Un proceso estocástico {A(t), t≥0} que toma valores enteros no negativos es un proceso de renovación si A(t) = max{n: Tn ≥t}, donde T0=0, Tn=X1+X2+...+Xn, y lo Xi son variables aleatorias no negativas independientes e idénticamente distribuidas [55]. Así pues, los procesos de renovación son una extensión de los modelos de tráfico sin memoria, en los que los intervalos de tiempo entre llegadas de paquetes son independientes e idénticamente distribuidos, aunque no necesariamente exponenciales o geométricos. Evidentemente, el modelo de Poisson es un ejemplo particular de un proceso de renovación. Sin embargo, a diferencia de él, la superposición de procesos de renovación no conduce necesariamente a nuevos procesos de renovación puesto que ahora existe cierta memoria. En efecto, el tiempo que falta esperar hasta ver la llegada del próximo paquete depende de hace cuánto tiempo llegó el último paquete. Aunque esta memoria incrementa la complejidad analítica de los procesos generales de renovación con respecto a los procesos sin memoria, sigue siendo nula la correlación entre los tiempos entre llegadas de paquetes consecutivos, lo cual hace que estos modelos sigan siendo analíticamente tratables para estudiar el desempeño de los elementos de la red. Además tienen la ventaja de permitir escoger una distribución más cercana a la de los tiempos observados entre llegadas. En efecto, muchos de los resultados de los sistemas de colas M/GI/m/q que se mencionaron en procesos sin memoria, se pueden extender a los sistemas GI/ GI/m/q, al menos en forma de aproximaciones de bajo o alto tráfico, o como cotas superiores o inferiores de la medidas de desempeño [68]. Todos estos resultados también se han incorporado a los procedimientos clásicos de análisis y diseño de redes de comunicaciones [32][65].
2.3 Aplicaciones y Deficiencias de los Modelos no Correlacionados
Como ya se ha mencionado, los modelos no correlacionados se han aplicado con enorme éxito en el análisis y control de redes telefónicas y redes teleinformáticas, pues los tráficos de voz y datos interactivos pueden ajustarse con suficiente exactitud a las suposiciones básicas que generan estos modelos. Dada la independencia entre los tiempo de llegada, se ha podido desarrollar toda una completa teoría matemática que modela los efectos de estas demandas sobre recursos limitados de comunicación, como es la Teoría de Colas, ampliamente utilizada en el modelamiento de redes tradicionales de comunicaciones. El principal resultado de este tipo de modelos es la fórmula de Erlang (ecuación (1)), pues con ella se han dimensionado las redes telefónicas durante casi un siglo [104].
Bajo esta misma suposición de independencia se han producido muchos resultados de gran aplicabilidad en cuanto a análisis de mecanismos de acceso a medios de transmisión compartidos [1], análisis de eficiencia de protocolos de retransmisión entre los extremos de una conexión física [98], análisis de retardo de distintas estructuras de conmutación en nodos ATM [89], mecanismos de enrutamiento y balance de carga en redes [33], etc. Inclusive se siguen reportando resultados muy recientes que siguen explotando la versatilidad de este tipo de tráfico.[97][128][43][10]
Sin embargo, las redes modernas de comunicaciones deben ofrecer no sólo servicios de voz y datos sino muchos otros (imágenes, video, audio, texto, control, etc.), cada uno de ellos con muy diferentes criterios de calidad de servicio (QoS) y, en consecuencia, con muy diferentes requerimientos para la red. Esta falta de uniformidad en las demandas y los requerimientos de los usuarios se complementa con una amplio rango de capacidades de transmisión que van desde pocas decenas de kbps hasta varias decenas de Gbps. Esta combinación de nuevas características en las capacidades y en las demandas invalida los resultados tradicionales de la teoría de tráfico que se basaban en modelos no correlacionados, pues el nuevo tráfico sobre las redes es demasiado complejo para ser modelado mediante técnicas desarrolladas para la red telefónica [121][87]. Como consecuencia de la inaplicabilidad de los resultados tradicionales de la Teoría de Colas, actualmente el dimensionamiento de los recursos de red en Internet, por ejemplo, se basa en reglas heurísticas muy sencillas mientras que, en cambio, se dedica un gran esfuerzo al diseño de mecanismos para garantizar niveles mínimos de QoS ante características inciertas del tráfico [29].
III.MODELOS DE TRÁFICO CORRELACIONADO CON DEPENDENCIA DE RANGO CORTO
Con el advenimiento de redes multimedios de banda ancha, en las últimas dos décadas se han tratado de desarrollar nuevas herramientas para modelamiento que tengan en cuenta las características del tráfico real, en especial las correlaciones que existen entre los tiempos entre llegadas, completamente ausentes en los modelos de renovación. Algunos de esos modelos se basan en in- cluir correlaciones que decaen exponencialmente rápido con el tiempo, ya que esos modelos pueden representar con relativa exactitud muchas fuentes reales de tráfico en redes modernas de comunicaciones y todavía permiten cierta tratabilidad matemática. Debido a ese rápido decremento de la correlación, se dice que estos modelos tienen "dependencia de rango corto". A continuación mencionaremos algunos de ellos.
3.1 Tráfico Markovianamente Modulado
Las primeras evidencias de presencia de correlación en el tráfico sobre redes con múltiples servicios se presentaron con la paquetización de la voz, en la que cada fuente transita entre un estado activo (durante el cual genera paquetes a una tasa constante) y un estado inactivo (durante el cual no genera paquetes)[7]. Previamente se utilizaba el esquema TASI -Time Assignment Speech Interpolation- para hacer multiplicación digital de circuitos [122], pero la unidad de tráfico seguía siendo la llamada telefónica. Con voz paquetizada, se puede considerar el paquete como la unidad de tráfico, en cuyo caso existe una correlación no despreciable entre los paquetes en un corto rango de tiempo. Si los períodos de actividad e inactividad se consideran independientes y exponencialmente distribuidos con promedios 1/λ1 y 1/λ2 respectivamente, la actividad de los abonados de voz se puede caracterizar mediante una cadena de Markov de dos estados con tasas de transición λ1 y λ2 entre ellos. Es de notar que, en este caso, la suposición de que los tiempos de duración en cada estado son exponenciales resulta empíricamente válida para los períodos de sonido, pero es muy inexacta para los períodos de silencio [9].
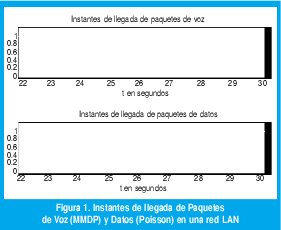
Como una verificación informal de la correlación existente entre los tiempos entre llegadas de paquetes, la figura 1 muestra los instantes de llegada de los paquetes de voz generados por un abonado telefónico y los paquetes de datos generados por 25 terminales interactivas, durante un período de ocho segundos. Mientras el tiempo entre llegadas de paquetes de datos parece independiente de los tiempos entre llegadas anteriores, el tiempo entre llegada de paquetes de voz está altamente correlacionado con los tiempos entre llegadas anteriores debido al proceso de actividad e inactividad.
El anterior modelo de tráfico corresponde a un Proceso Determinístico Markovianamente Modulado (MMDP) mediante una cadena de Markov de 2 estados. Si se multiplexan n abonados telefónicos, el estado de la cadena moduladora de Markov indicaría el número de abonados activos. De esta manera, si durante el estado activo cada abonado genera α paquetes por segundo, en el estado i se estarían generando αi paquetes/segundo.
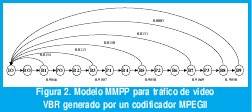
Al modelar otras fuentes de tráfico como video con tasa variable de bits, conviene suponer que la cadena de Markov modula la tasa promedio de un proceso de Poisson, con lo que se generaría un Proceso de Poisson Markovianamente Modulado, MMPP. En [18], por ejemplo, se caracteriza el trafico generado por un codificador MPEG mediante un modelo MMPP en el que la cadena moduladora tiene 15 estados para representar la secuencia de tramas [I,B,P] dentro de un GOP (grupo de imágenes), con excelentes resultados en cuanto a la predicción del desempeño de un sistema de transmisión consistente en un buffer y un enlace. El modelo se representa en la Figura 2.
Existen resultados analíticos que describen el comportamiento de colas de espera sometidas a tráfico MMPP. Por ejemplo, la distribución conjunta del estado de la cadena y la ocupación del buffer se puede representar mediante una cadena multidimensional de Markov, para la cual existen métodos analíticos, como el enfoque geométrico matricial, que permiten calcular la distribución de la ocupación del enlace y, correspondientemente, todas sus medidas de desempeño [81]. Otro método menos exacto pero más fácil de evaluar es el de modelos de flujo continuo en los que se ignoran las unidades individuales de tráfico (mensajes, paquetes, celdas, llamadas o bits) y se modela un fluido continuo caracterizado por una tasa de flujo markovianamente modulada [99]. Esta aproximación es adecuada cuando, dada una escala de tiempo, la cantidad de unidades de tráfico individuales son tantas que el efecto individual de cada unidad es insignificante. Además de la simplicidad conceptual de estos modelos, su evaluación puede ser muy eficiente, pues todo se reduce a un sistema de ecuaciones diferenciales, generalmente lineales y de primer orden [7].
3.2 Otros modelos de tráfico correlacionado basados en Modelos Markovianos
En los procesos tipo fase (PH) los tiempos entre llegadas están dados por los instantes de absorción en una cadena de Markov finita con m estados transientes y un estado absorbente. Modelos anteriores para los tiempos entre llegadas, como la distribución hiperexponencial o la distribución Erlang, son casos particulares de la distribución tipo fase. Existen diferentes técnicas numéricas y analíticas para estudiar el comportamiento de colas tipo PH/PH/S/Q, en los que los tiempos entre llegadas y los tiempos de servicio surgen de procesos tipo fase [81]. Puesto que cualquier distribución se puede aproximar mediante una distribución tipo fase adecuadamente seleccionada, esos resultados pueden ser de gran utilidad para el análisis de casos generalizados de sistemas de colas.
El proceso tipo fase es, en realidad, otro proceso de renovación puesto que después de la absorción, la cadena vuelve a un estado transiente de acuerdo con un vector original de distribución de estados. Por eso se define el Proceso de Llegadas Markovianas (MAP-Markovian Arrival Process) como una generalización de los procesos markovianamente modulados. Este proceso también se asocia con una cadena de Markov finita absorbente pero, en vez de tener un solo vector de probabilidad inicial, se tiene un vector por cada estado transiente de manera que, una vez se ha entrado en el estado absorbente y se ha generado un paquete, el proceso se reinicia con el vector de probabilidad correspondiente al último estado transiente que se visitó. Estos procesos han sido ampliamente estudiados en [81] y sus resultados se han generalizado en [95]. Obsérvese que el proceso de Fase es un MAP en el que la matriz de vectores iniciales tiene todas la filas iguales, mientras que el MMPP es un MAP en el que dicha matriz es diagonal.
El concepto MAP se puede extender al Proceso de MAP por Lotes (BMAP -Batch Markovian Arrival Process-), en el que cada evento MAP genera un lote de llegadas (el tamaño del lote se modela de diferentes maneras). Estos procesos han recibido mucha atención recientemente, pues es posible adecuarlos para modelar las características de correlación observadas en muchos tipos de tráfico sobre Internet [62].
Por último, consideraremos el Proceso Autoregresivo en el que el siguiente tiempo entre llegadas depende explícitamente de los anteriores tiempos entre llegadas, al menos dentro de una ventana de tiempo de longitud determinada [50]. Este modelo es un modelo de Markov de orden superior, lo cual resulta muy apropiado para representar el tráfico proveniente de señales codificadas con tasa variable de bits como en el caso del video comprimido. El proceso autoregresivo más usado corresponde a un modelo lineal de orden p que toma siguiente forma
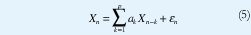
donde Xn es el tiempo entre la llegada del paquete n-1 y el paquete n, los ak son constantes por estimar y las εn son variables aleatorias idénticamente distribuidas, independientes de Xn e independientes entre sí, denominadas "residuos" de la predicción de Xn. A diferencia de los procesos anteriores, este modelo considera explícitamente la autocorrelación del proceso de llegadas, pues los parámetros ak se estiman de acuerdo con las correlaciones muestrales de orden p observadas en las trazas reales de tráfico.
Otro modelo autoregresivo es el modelo TES (Transforma-Expande-Muestrea). Este modelo, que opera con aritmética módulo 1 y no es lineal, consiste en generar probabilidades de llegadas mediante números pseudoaletorios correlacionados e invertir la función de distribución acumulativa de los tiempos entre llegadas [78][127]. Así, con este modelo se pueden ajustar tanto la distribución marginal de los tiempos entre llegadas como la autocorrelación de muestras reales de tráfico.
3.3 Aplicaciones y Deficiencias de los Modelos Correlacionados con Dependencia de Rango Corto
Como se mencionó antes, la Teoría de Colas ha desarrollado importantes resultados bajo estos modelos de tráfico que, cuando se aplican al análisis de desempeño de los nodos de una red de comunicaciones conducen a procedimientos apropiados de asignación de recursos, control de congestión, etc. Por ejemplo, si el tráfico se modela como un proceso de renovación, las probabilidades de pérdidas en el buffer de un multiplexor decaen asintóticamente como K, para grandes valores de K, donde es la utilización del enlace y K es el tamaño del buffer. Con los modelos Markovianamente modulados se puede encontrar un comportamiento diferente que corresponde mucho mejor con la realidad. En efecto, si la transición entre estados toma mucho tiempo (comparada con los tiempos entre llegadas de paquetes consecutivos en cualquiera de esos estados) y el tamaño del buffer es pequeño, la correlación se pierde en la cola pues, para cada estado de la cadena moduladora, el multiplexor alcanza a estabilizarse. Sin embargo, para valores grandes de K, las pérdidas se deben más a ráfagas debidas a la transición hacia estados de alta generación de paquetes. Bajo estas condiciones, el aumento en el tamaño del buffer no mejora significativamente la tasa de pérdidas. Las soluciones exactas mediante el enfoque geométrico matricial predicen con exactitud la primera región, mientras que las soluciones de flujo continuo predicen mejor los resultados bajo aproximación de alto tráfico.
Con este tipo de resultados analíticos se han determinado valores adecuados del número de sesiones que se pueden aceptar de manera que se garantice una calidad de servicio dada, en términos de la características de estos modelos de tráfico en cada sesión (por ejemplo dadas la tasa pico y la tasa promedio de llegadas de cada sesión, cuántas sesiones de cada tipo se pueden aceptar para garantizar una tasa dada de pérdidas, una variación dada en el retardo, etc.). [64] Aunque estos resultados no son tan compactos como la fórmula de Erlang (ecuación (1)) para diseño de redes telefónicas, si proporcionan un marco teórico para hacer una mejor asignación de recursos que las basadas en el ancho de banda promedio (alta utilización pero baja calidad de servicio) o el ancho de banda pico (alta calidad de servicio pero baja utilización de recursos). Más aún, fueron básicamente estos modelos los que condujeron a esquemas de control de congestión basados en moldear el tráfico (traffic shapping), tales como los baldes con fugas (leaky bucket) o los baldes de permisos (token bucket), tan comunes en las modernas redes multiservicios [91].
Todos estos resultados corresponden a un único elemento de la red y no se pueden extender fácilmente al análisis de una red de colas. Cuando el tráfico se modela mediante un proceso de renovación, la independencia permite encontrar el desempeño de la red mediante la combinación apropiada de los desempeños individuales de cada nodo, pues la distribución conjunta de la ocupación de la red es el producto de las distribuciones marginales de los nodos (teorema de Jackson [32]). Con modelos correlacionados no se puede hacer esta simplificación, por lo que los resultados se suelen limitar al cálculo de cotas asintóticas en las medidas de desempeño. En particular, [40][41] propone toda una metodología para cuantificar los efectos de diferentes elementos de la red en cascada, cuando el tráfico en la entrada se regula de manera que el número de llegadas en un intervalo de tiempo de longitud t sea menor o igual α + βt, donde α es la máxima ráfaga que puede llegar en un instante y β es una cota superior para la tasa promedio de llegadas en un intervalo grande de tiempo (leacky bucket, por ejemplo). Esta metodología, denominada "el Cálculo de Cruz", que ha sido ampliamente utilizada en la última década para el dimensionamiento de redes de comunicaciones ATM y TCP/IP, conduce tanto a cotas determinísticas aunque inexactas (se garantiza con total certeza que ningún paquete excede- rá jamás la cota del retardo) como a cotas estocáticas mucho más aproximadas (se garantiza que el 95% de los paquetes, por ejemplo, no excederá la cota) [39]. Estas cotas estocásticas se basan en la teoría de las grandes desviaciones y han conducido al desarrollo de la teoría de "la capacidad efectiva" [39] que, para el caso de fuentes markovianamente moduladas y sus generalizaciones, proporciona herramientas de diseño para dimensionar los recursos de la red de manera que se satisfagan requerimientos de calidad de servicio dados. Una bondad del cálculo de Cruz es que, al modelar el tráfico únicamente mediante las cotas de la máxima ráfaga y de la tasa promedio, se convierte en una metodología adecuada para cualquier modelo de tráfico que permita este tipo de acotamiento, y por tanto no se limita al tráfico con dependencia de rango corto.
Desafortunadamente, mediciones detalladas de tráfico realizadas en la última década revelan una estructura de correlación mucho más rica y compleja en casi todos los tipos de tráfico sobre las modernas redes de comunicaciones, que se extiende a muchas escalas de tiempo, en lo que se conoce como "dependencia de rango largo". Aunque los modelos de tráfico vistos hasta ahora permiten fácilmente controlar la variabilidad de la demanda y, por consiguiente, con ellos resulta relativamente fácil diseñar esquemas de control de tráfico que permitan garantizar niveles mínimos de calidad de servicio, el fenómeno de la dependencia de rango largo hace que la variabilidad se extienda a muchas escalas de tiempo, comprometiendo la validez de las técnicas de control diseñadas para los modelos tradicionales de tráfico[84]. Por esta razón, ha sido necesario desarrollar modelos adicionales de tráfico capaces de representar estas correlaciones [12][112].
IV. MODELOS DE TRÁFICO CORRELACIONADO CON DEPENDENCIA DE RANGO LARGO
Un proceso estocástico {Y(t), t≥0} es un Proceso exactamente autosemejante con parámetro de Hurst H si

esto es, si Y(t) y aHY(at) están idénticamente distribuidas para todo a>0 y t>0 [85]. La autosemejanza se refiere al hecho de que, de acuerdo con la ecuación (6), las características estadísticas del proceso no varían con la escala.
Si Y(t) representa el número de paquetes que han llegado a un enrutador en el intervalo de tiempo [0, t], el correspondiente proceso de incrementos {X(t) = Y(t) - Y(t-1), tZ} representa el número de llegadas en intervalos sucesivos de una unidad de tiempo. Si {X(t), t∈Z} es un proceso estacionario de segundo orden, su función de autocovarianza y(k) satisface la siguiente relación:
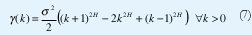
la cual da origen a una definición empíricamente verificable de autosemejanza, como se describe a continuación.
Sea {X(t), t∈Z} un proceso sobre el que se hace una partición en bloques no sobrelapados de tamaño m, y se promedian los valores de cada bloque para obtener el proceso agregado {X<m>(i), t∈Z},
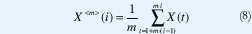
Denotemos la autocovarianza de {X<m>;(i), t∈Z} mediante y<m>(k). Decimos que {X(t), t∈Z} es asintóticamente autosemejante de segundo orden con parámetro de Hurst H si, para todo k>0,
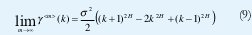
Si {X(t), t∈Z} es asintóticamente autosemejante de segundo orden, su función de autocorrelación, r(k)= (k)/σ2, en el límite, satisface
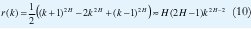
De acuerdo con las ecuaciones (7),(9) y (10),si H=1/2 la autocorrelación se hace cero para todo valor de k, de manera que el proceso de incrementos {X(t), t∈Z} se convierte en un simple proceso de renovación. Si H=1, la autocorrelación se hace uno para todo valor de k, de manera que la aleatoriedad desaparece. Sin embargo, para ½<H<1, de acuerdo con (10), el comportamiento asintótico de r(k) es r(k)= ck-,β con 0<β<1. Esto es, la función de autocorrelación decae muy lentamente (hiperbólicamente), lo que conduce a la propiedad de que la función de autocorrelación es "no sumable":
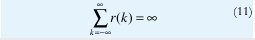
Cuando r(k) decae hiperbólicamente de manera tal que la condición (11) se cumple, decimos que el proceso estacionario {X(t), t∈Z} es un Proceso con Dependencia de Rango Largo (LRD) [85].
La definición de LRD basada en (8) resulta fácilmente verificable mediante mediciones, como muestra la figura 3 [71]. En la primera parte se observa cómo el proceso de agregación según la ecuación (8) mantiene casi inalterable la variabilidad de la tasa promedio de bps,medida en rangos de tiempo que van desde los 10 ms hasta los 10 s, para una traza muestral de tráfico medida en una red LAN [66]. En contraste, al agregar la tasa de llegadas para una traza muestral de tráfico Poisson, la variabilidad es despreciable en rangos superiores a 1 segundo. Mientras en el trafico Poisson cualquier intervalo de 10 s es adecuado para obtener una muy precisa estimación de la tasa promedio de bps que generan los usuarios de la red, en el tráfico real será necesario considerar intervalos mucho mayores.
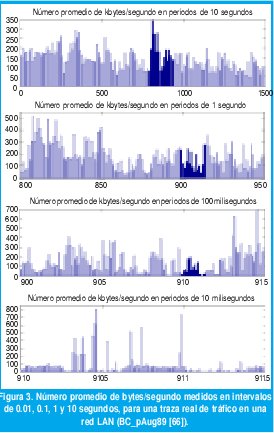
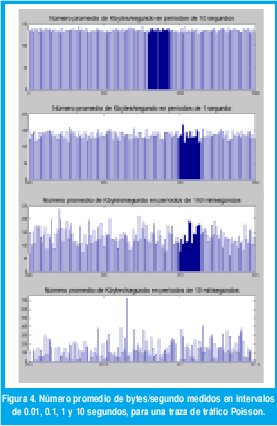
Este fenómeno con trazas reales de tráfico sobre redes Ethernet se reportó por primera vez en 1994, en el famoso trabajo de Leland, Taqqu, Willinger y Wilson [71], el cual sentó las bases para el inmenso caudal de resultados de investigación que muestran la autosemejanza como una característica ubicua cuando se observa empíricamente el tráfico en redes modernas de comunicaciones. Desde entonces se han reportado evidencias de autosemejanza con una ubicuidad abrumadora en casi todos los aspectos de las redes modernas de comunicaciones tanto LAN como WAN, bajo IP y bajo ATM, con enlaces de cobre, de fibra óptica o inalámbricos, en la navegación por la web o en la transferencia de archivos,etc. [21][27][37][38][46][71]. En todos estos casos, es posible ajustar diferentes procesos estocásticos LRD para modelar estas características del tráfico en redes modernas de comunicaciones.
Cabe anotar que, a pesar de las fundamentales diferencias que existen entre autosemejanza exacta, autosemejanza asintótica de segundo orden y dependencia de rango largo, generalmente se usan los términos de Tráfico Autosemejante o Tráfico Fractal para representar a cualquier modelo de tráfico que capture estos fenómenos de invarianza a la escala. En efecto, las trazas dejadas al acumular procesos LRD son curvas fractales en las que la dimensión está directamente relacionada con la pendiente logarítmica de la densidad espectral de potencia. Por esta razón, otro término comúnmente utilizado para procesos LRD es el de Ruido 1/f, refiriéndose al hecho de que una definición esencialmente equivalente de LRD se puede dar en el dominio de la frecuencia, diciendo que la densidad espectral (v) del proceso de incrementos {X(t), t∈Z} debe satisfacer la relación

(donde r() es la función de autocorrelación de X), para algún c>0 y 0<α=2H-1<1.
Por último, debido al comportamiento asintótico de la autocorrelación, r(k) = ckβ- con 0<β <1, de la densidad espectral de potencia,Γ(v)=d|v|-a con 0<α<1, y de la cola de las distribuciones asociadas, P[Z>z]=c zy- con 0<y <2 (ver ecuación (16) más adelante), a los procesos que presentan estos fenómenos de escala se les conoce también como Procesos con Ley de Potencia (power-law).
4.1 Movimiento Browniano Fraccional
{Y(t), t∈R} es un Movimiento Browniano Fraccional (fbm) con parámetro 0<H< 1 si Y(t) es gaussiano, exactamente autosemejante con parámetro H y tiene incrementos estacionarios. Al proceso de incrementos X(t) = Y(t)-Y(t-1) se le conoce como Ruido Gaussiano Fraccional (fgn) [74].
Un caso particular es el movimiento browniano, en el que la varianza entre dos muestras del proceso es proporcional a la distancia entre las dos muestras:
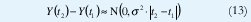
Suponiendo que Y(0)=0, obtenemos Y(t)~N(0,s2|t|), de manera que Y(at)~a-½(0,s2;|t|). De acuerdo con (6), el movimiento browniano es exactamente autosemejante con parámetro H=½ y su proceso de incrementos X(t) = Y(t) - Y(t-1) ~ N(0,s2) es ruido blanco gaussiano. Este es un ejemplo perfecto de un proceso autosemejante cuyos incrementos no sólo no tienen dependencia de rango largo sino que son completamente no-correlacionados (de hecho, los incrementos del movimiento browniano son independientes!). Con ½ <H<1, el movimiento browniano fraccional obedece a
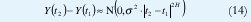
de manera que se trata de un proceso no estacionario con función de autocorrelación
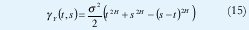
como corresponde a cualquier proceso exactamente autosemejante con incrementos estacionarios. El proceso de incrementos X(t) = Y(t) - Y(t1) sigue siendo ~ N(0,s2), pero su función de autocorrelación no es cero, sino que decae hiperbólicamente con el tiempo según la ecuación (10), de manera que se trata de un proceso LRD.
El movimiento browniano fraccional resulta muy atractivo como modelo de tráfico por dos razones fundamentales. En primer lugar porque, al ser un proceso gaussiano, todavía es posible tratarlo analíticamente. Y en segundo lugar, porque es el proceso que surge de multiplexar un gran número de procesos on/off en los que la distribución de los tiempos de actividad y/o inactividad tiene "cola pesada". Esta razón es de mucho interés puesto que las distribuciones de probabilidad de variables tales como el tamaño de los archivos transferidos mediante FTP, los tiempos de conexión TCP, el tamaño de los objetos multimedios en las páginas Web, la longitud de las escenas en video MPEG, etc., tienen este tipo de distribución (por ejemplo, Pareto o Weibull).
Una variable aleatoria Z tiene una Distribución de Cola Pesada si
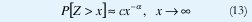
donde c es una constante positiva y 0 <α < 2 es el parámetro de forma o índice de la cola de la distribución (existen definiciones técnicamente más sutiles que involucran funciones de variación lenta, pero los conceptos principales se pueden extraer de esta definición ligeramente más restrictiva pero mucho más práctica).
La principal característica de una variable aleatoria con distribución de cola pesada es su variabilidad extrema, esto es, puede tomar valores extremadamente grandes con una probabilidad no despreciable. Al tomar muestras de dicha variable, la gran mayoría de valores serán pequeños pero algunos pocos valores serán muy grandes y determinarán el comportamiento general de la variable. Por ejemplo, la gran mayoría de archivos en nuestros discos duros son pequeños, pero los pocos archivos grandes que existen son los que ocupan la mayoría del espacio en disco. Otra característica importante de estas variables aleatorias es la predecibilidad. Supongamos que la duración de una conexión a una red es una variable aleatoria con cola pesada y queremos averiguar cuál es la probabilidad de que la conexión persista en el futuro, dado que ha estado activa por t segundos. Con distribuciones de cola liviana (asintóticamente exponencial), la predicción es independiente de t, de manera que nuestra incertidumbre no disminuye al condicionar en mayores períodos de actividad (ecuación (3)). Pero con distribuciones de cola pesada, entre mayor sea el período de actividad observado, mayor es la certeza de que la conexión persista en el futuro.
Debido a dicha predecibilidad, las variables aleatorias con distribución de cola pesada conducen a procesos estocásticos con dependencia de rango largo. En efecto, considérese un modelo de N fuentes independientes de tráfico, Xi(t), i∈[1,N] donde cada fuente es un proceso de renovación on/off en el que tanto los períodos de actividad como los de inactividad son independientes e idénticamente distribuidos. Sea SN(t)=∑i=TNXi(t) el tráfico agregado en el instante t, como se representa en la figura 5. El proceso acumulativo YN(t) se define comof0τ SN(τ)dτ. Si Xi(t) mide el número de paquetes por segundo que genera la fuente i en el instante t, YN(t) mide el número total de paquetes generados hasta el instante t.
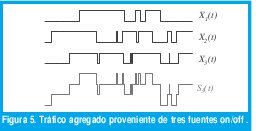
Si la duración de los períodos de actividad, tON, es una variable aleatoria con distribución de cola pesada y parámetro de forma 1<α < 2, se puede demostrar [123] que el proceso acumulativo YN(t) se comporta como un movimiento browniano fraccional en el sentido de que, para N grande,
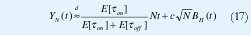
donde BH (t) es un movimiento browniano fraccional con varianza 1 y parámetro H=(3-α)/2, mientras c es una constante positiva que sólo depende de las distribuciones de τON y τOFF.
4.2 Modelos FARIMA
La ecuación (5) mostró la forma de un proceso autoregresivo AR(p), en el cual la traza de tráfico se sintetiza a partir de los residuos de predicción mediante un filtro de sólo polos de orden p, A(z)=1/∑akz-k, con a0=1. Si se añaden q ceros al filtro, se obtiene un proceso autoregresivo (AR(p)) de promedios móviles (MA(q)), o proceso ARMA(p,q), en el que también se incluye una combinación lineal del actual residuo de predicción y los anteriores q-1 residuos mediante un filtro recursivo B(z)/A(z). Si la salida del filtro se integra multiplicando su transformada Z con un integrador (1-z-1)d, d∈N,se obtiene un proceso autoregresivo integrado de promedios móviles (ARIMA(p,d,q)). Un Proceso FARIMA(p,d,q) es un proceso ARIMA(p,d,q) en el que d∈(-0.5, 0.5).
En el caso particular en que d se encuentre en el intervalo abierto (0,1/2), los procesos FARIMA(p,d,q) poseen propiedades LRD. Adicionalmente, y esto es lo más atractivo de los procesos FARIMA, también poseen simultáneamente propiedades SRD (dependencia de rango corto) debido a que se pueden descomponer en dos procesos: uno ARMA(p,q) que se encarga del comportamiento SRD y otro FARIMA(0,d,0) que se encarga del comportamiento LRD. El correspondiente proceso acumulativo es autosemejante con H = d+0.5 [126].
4.3 Modelos M/G/
En un sistema de colas con infinitos servidores en el que las llegadas forman un proceso Poisson y los tiempos de servicio tienen una distribución con cola pesada y parámetro de forma 1<a<2, el proceso {N(t), t≥0}, que representa el número de servidores ocupados en el instante t, es un proceso autosemejante con parámetro de Hurst H=(3-a)/2. Claramente, este modelo es una generalización de la superposición de procesos on/ off y, como tal, tiene mayor versatilidad en cuanto a su capacidad para ajustarse a las características estadísticas observadas en trazas reales de tráfico. De hecho, la relevancia del modelo M/G/∞ para representar el tráfico en redes de comunicaciones surge de diferentes aspectos tales como la asociación con el modelo natural de combinar fuentes on/off, la propiedad deseable de invarianza ante la multiplexación (la superposición de procesos M/G/∞ produce otro proceso M/G/∞), la flexibilidad para capturar las correlaciones positivas en un amplio rango de escalas de tiempo, y su asociación natural con el análisis de la ocupación de los buffers en los nodos de la red. [86].
4.4 Modelos Wavelet Multifractales
El análisis Wavelet es una técnica naturalmente adecuada para el estudio de procesos autosemejantes, puesto que está orientado al estudio multiresolución de señales, el cual permite analizar el comportamiento de la señal a diferentes escalas de tiempo simultáneamente [2][3][4][13]. De hecho, tratándose de procesos fbm, la transformada wavelet (WT) es capaz de transformar un proceso autosemejante con una compleja estructura de correlación en una secuencia de procesos gaussianos, independientes entre sí y no autocorrelacionados (los coeficientes wavelet), pero de manera que la energía de los coeficientes decae hiperbólicamente con la escala de acuerdo con el grado de autosemejanza del proceso original, H [48][109]. Esta decorrelación se acerca al ideal de la transformación KarhunenLoeve (KL), con la ventaja de que, a diferencia de KL, es posible llevar a cabo la WT de una manera muy eficiente mediante las técnicas de procesamiento digital de señales multitasa, y de manera tal que la varianza de los coeficientes wavelet en cada escala conserva la información del grado de autosemejanza del proceso analizado. Por esta razón, la WT se ha convertido en la principal herramienta para detectar, estimar y sintetizar procesos autosemejantes [3][13][118].
Más aún, la WT se ha extendido para generar todo un nuevo modelo de tráfico que no sólo presenta grandes ventajas computacionales sino que captura efectos adicionales observados en trazas de tráfico real, como es la multifractalidad [53].
En un proceso fractal (o "monofractal"), el exponente que gobierna el comportamiento general del sistema es el parámetro de Hurst, H, el cual determina la dependencia de rango largo.
Pero en un conjunto de procesos más generales, ese exponente podría variar con el tiempo como H(t). Para una traza muestral y(t) del proceso {Y(t),t∈R}, los conjuntos E(α)= {t: H(t)=α} descomponen el conjunto de soporte del proceso de acuerdo con sus exponentes H. Para un proceso autosemejante (monofractal), solo existe un exponente H(t)≡H∀t, de manera que E(H) es el conjunto de soporte de Y, y E(a) es vacío para cualquier otro #αH. Muy informalmente, decimos que Y(t) es un Proceso Multifractal si para cada α, E(α) es un conjunto fractal denso en el soporte de {Y(t), t∈R }. La función f: R→R que asigna a cada α el valor de la dimensión fractal de E(a) se denomina "Espectro Multifractal de Y". Para un proceso monofractal, f(α)= 1(α=1) es simplemente el punto (1,1). Si H(t) es continuo y no es constante en ningún intervalo, f(α)=0 ∀a. Pero si el espectro fractal toma una forma no-degenerada, estamosante un proceso multifractal. (para una definición precisa de los procesos multifractales,véase [94]). Es importante distinguir entre un proceso multifractal y un proceso fractal multi-escala, el cual toma distintos valores de H en diferentes rangos de escalas.
El Modelo Wavelet Multifractal (MWM) se refiere a una forma particular de caracterizar y sintetizar procesos multifractales en el dominio de la escala [93], de acuerdo con el concepto de "cascada multiplicativa", como se explica a continuación.
La transformada Wavelet representa una señal unidimensional en términos de versiones desplazadas y dilatadas de una función wavelet,ψ(t), pasabanda y una función de escala, Φ(t), pasabajos. Para algunas funciones wavelet y de escala cuidadosamente seleccionadas, las versiones dilatadas y desplazadas ψjk(t)=2j/2ψ(2jt-k) y Φjk(t)=2j/2(2jt-k) forman una base ortonormal para las funciones de energía finita. La correspondiente expansión en coeficientes wavelet de una "señal" obtenida de una traza muestral de tráfico,
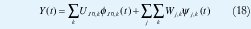
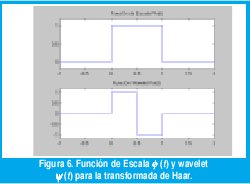
es tal que, para una wavelet y(t) centrada en el instante t=0 y en la frecuencia f=f0, el coeficiente wavelet W/jk da información sobre la amplitud de la señal alrededor del instante 2-jk y la frecuencia 2jk0, mientras que el coeficiente de escala Uj,k da información sobre el promedio local en ese mismo instante, por lo que a j se le llama índice de escala y a k se le llama índice de tiempo. La figura 6 muestra el ejemplo más sencillo de una base wavelet ortonormal conformada por las funciones de escala y wavelet de Haar [93]. Obsérvese que, a una escala j dada, los soportes de fjk(t) y yjk(t) se anidan dentro de los soportes a escalas menos finas, lo cual se constituye en una propiedad fundamental para la definición de los modelos wavelet multifractales.
En efecto, los modelos de tráfico fractal basados en fbm (o fgn) tiene la limitante de que, por ser gaussianas, siempre existirá una probabilidad distinta de cero de generar muestras negativas cuando, por supuesto, el tráfico es inherentemente positivo. Además se ha visto que la distribución del tráfico está llena de picos, a diferencia de la suavidad gaussiana. Más aún, se ha visto que muchas trazas reales de tráfico no sólo exhiben dependencia de rango largo sino que sus correlaciones a corto plazo también poseen comportamientos de escala que no concuerdan completamente con la autosemejanza estricta de estos modelos. Afortunadamente, existe una condición sencilla para garantizar que una señal sintetizada mediante la WT de Haar tenga incrementos no negativos: |Wjk| ≤Ujk para todo j,k. En el MWM esta característica se aprovecha para modelar los coeficientes wavelet mediante Wjk = AjkUjk, donde los multiplicadores A jk son variables aleatorias independientes que toman valores en el intervalo [-1, 1]. De esta manera el MWM es capaz de capturar con gran precisión el espectro de potencia (y, consecuentemente, la dependencia de rango largo) de una traza real de tráfico mediante el ajuste adecuado de las varianzas de los multiplicadores. Simultáneamente, y a diferencia de otros modelos, el MWM también puede reproducir la positividad y las estadísticas de orden superior de trazas reales de tráfico.
La precisión con que se pueden ajustar las estadísticas de tráfico real mediante MWM sugiere que algunos de los mecanismos que moldean el tráfico tienen una estructura inherentemente multiplicativa. Los esquemas aditivos (como la superposición de procesos on/off) reproducen la multiplexación de componentes individuales de tráfico en la red, con gran exactitud para grandes escalas de tiempo. El MWM, en cambio, representa las llegadas como el producto de multiplicadores aleatorios, lo cual se asemeja a la partición y clasificación de tráfico que se hace en las redes modernas de comunicaciones, obteniendo mucho mejores resultados al considerar pequeñas escalas de tiempo.
4.5 Modelos de Mapas Caóticos
La rica estructura de correlación de las trazas medidas de tráfico real sugiere la presencia de un sistema dinámico que las genera. La evidencia de fractalidad indica que dicho sistema sería caótico. Con esta motivación, se ha propuesto la aplicación de mapas caóticos determinísticos de bajo orden para modelar fuentes de tráfico. Por ejemplo, si en la siguiente recurrencia
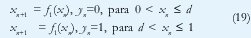
las funciones no-lineales f1(·) y f2(·) satisfacen requerimientos de alta sensibilidad a condiciones iniciales, cada condición inicial definirá una trayectoria en el espacio de fase, de manera análoga a la "realización" de un proceso estocástico. Los paquetes se generarían durante los períodos activos (en los que yn=1). En variaciones del modelo, el sistema podría generar directamente los tiempos entre llegada de paquetes [45] pero, de cualquier manera, el grado de fractalidad del proceso estaría asociado con el exponente de Lyapunov del sistema dinámico.
Esto mapas caóticos no sólo pueden capturar varias de las propiedades fractales observadas en trazas reales [45], sino que pueden sugerir métodos de análisis de desempeño, especialmente en cuanto a características transientes de los sistemas de colas. Por supuesto, aún existen serias dificultades analíticas que deben ser superadas para este tipo de aplicación. Sin embargo, como se verá más adelante en la sección 6, recientemente se han descubierto comportamientos caóticos en los sistemas dinámicos propios de los procesos de control de congestión en redes modernas, con lo que se hace aún más interesante este tipo de modelos.
4.6 Aplicaciones y deficiencias de los modelos correlacionados con dependencia de rango largo
Un modelo de tráfico sólo puede considerarse correcto si las técnicas de inferencia estadística utilizadas sobre trazas de tráfico real permiten concluir que estas muestras de tráfico son consistentes con el modelo. Claramente, el hecho de que estadísticamente se pueda encontrar consistencia entre un modelo y una traza muestral no significa que no hayan otros modelos que se ajusten igualmente bien (o mejor). En este sentido, los modelos de tráfico autosemejante han demostrado una gran consistencia con las medidas observadas.
Es de anotar que, por ejemplo, los modelos MMPP y autosemejantes han demostrado ser igualmente válidos para representar el tráfico de una fuente de video MPEG2[27], incluyendo las principales medidas de desempeño de un conmutador que acepta este tipo de tráfico[61]. Por supuesto, dado que el modelo MMPP sólo considera la autocorrelación entre intervalos de tiempo muy próximos entre sí, las técnicas de análisis de desempeño y de diseño de métodos de control de tráfico resultan mucho más fáciles que con el modelo autosemejante, por lo que el modelo MMPP es el preferido entre estas dos alternativas igualmente válidas[61]. Sin embargo, el inmenso volumen de diversas medidas de tráfico de altísima calidad empiezan a develar inconsistencias entre los modelos tradicionales y las medidas observadas, especialmente en lo referente a estructuras de correlación que se expanden a lo largo de diferentes escalas en el tiempo. Estos fenómenos, en cambio, son inmediatamente capturados por los modelos de tráfico autosemejante, los cuales se vuelven cada vez más importantes en la medida en que el desarrollo de las redes de telecomunicaciones revelan el impacto de estos fenómenos de escala en el desempeño de las redes[87].
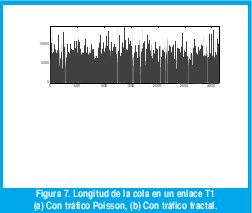
A manera de ejemplo, considérese los dos procesos que se representaron en las figuras 3 y 4. Después de una hora de observación, ambos procesos generaron, en promedio, 1.11 Mbps. De acuerdo con los resultados de las colas con llegadas sin memoria, sería una buena decisión proporcionar un enlace T1 de 1.544 Mbps para transmitir estos flujos de datos entre dos puntos. Sin embargo ocurren resultados sorprendentes al medir la longitud de la cola en función del tiempo. Como muestra la figura 7(a), la longitud de la cola con el tráfico Poisson nunca excede 15 Kbytes, los picos de máxima ocupación sólo duran algunas fracciones de segundo, el retardo promedio de los paquetes, incluyendo la transmisión, es de menos de 8 ms, el retardo máximo sólo llega a 85 ms y no hay congestión en ningún instante. Una situación muy diferente ocurre con el tráfico fractal, como se muestra en la figura 7(b). Necesitaríamos un buffer de 6 Mbytes, 410 veces mayor que el que necesitaríamos con el tráfico de Poisson. Los picos de máxima ocupación duran cientos de segundos, constituyendo largos períodos de fuerte congestión. En promedio, cada paquete tarda 3 s con un retardo máximo de hasta 30 s. Ciertamente, la correlación que exhibe la traza de tráfico LRD durante varias escalas de tiempo resulta desastrosa para el desempeño de la red.
El anterior ejemplo demuestra que es necesario buscar aquellas características del tráfico moderno que resultan relevantes en el análisis de desempeño de las redes de comunicaciones y que, en ese sentido, no se puede ignorar la dependencia de rango largo. Ahora bien, debido a este mismo fenómeno, son pocos los resultados analíticos que se puedan mostrar. Tal vez uno de los más significativos es el de [82], que describe la probabilidad de bloqueo en un sistema con un único servidor cuando la capacidad del buffer es de B paquetes, la utilización es ρ erlangs (tiempo promedio de servicio / tiempo promedio entre llegadas) y el parámetro de Hurst es H. En una forma muy simplificada, esa probabilidad de bloqueo está aproximadamente dada por
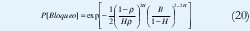
con lo cual se podría dimensionar el buffer para una P[Bloqueo] dada, de la misma manera que la fórmula de Erlang (1) se puede utilizar para redes telefónicas. De hecho, así como la fórmula (1) sólo es válida ante entradas sin memoria, con lo cual se reduce mucho su aplicabilidad actual, la fórmula (20) sólo es válida para entradas fraccionales gaussianas, las cuales son sólo una aproximación al multiplexaje de muchas fuentes on/off independientes.
La gran mayoría de resultados analíticos sobre el desempeño de sistemas de colas se refieren a cotas asintóticas ante aproximaciones de bajo o alto tráfico con modelos específicos de tráfico fractal, casi siempre basados en la teoría de las grandes desviaciones mencionada en el aparte 3.3 [5][31][44][45][126][84] (un excelente resumen de los resultados que hasta el año 2000 se habían obtenido en cuanto al análisis de desempeño con modelos LRD se encuentra en [84]). Entre los resultados más recientes, se destaca el análisis de cola multiescala [92], el cual aprovecha la estructura arborescente de la transformada wavelet del proceso fractal para encontrar la siguiente fórmula para la cola de la distribución de la longitud del buffer, Q:
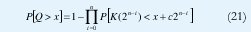
donde K(r) es el número de llegadas en las anteriores r unidades de tiempo, el cual se obtiene directamente de la WT para instantes diádicos r=2m, y c es la capacidad del canal. Esta fórmula se aplica a cualquier proceso de entrada multiescala representado mediante una WT y, en especial, al modelo MWM, en cuyo caso las probabilidades dentro del producto en (21) están dadas por las distribuciones acumulativas de los multiplicadores MWM a cada escala [92]. Este resultado es uno de los primeros en el promisorio campo del análisis de desempeño en el dominio de la escala. De hecho, otros resultados interesantes basados en modelos wavelet son el reportado en [113], en el que se utiliza análisis multiescala para estimar el volumen de tráfico que compite con la fuente de interés a lo largo de la ruta; el reportado en [60], en el que se hace inferencia y detección de aspectos cualitativos del desempeño de la red, el reportado en [73], donde se calcula la probabilidad de bloqueo bajo tráfico fgn generado mediante wavelets, etc. Aunque éstos son apenas incipientes avances dentro de un campo en el que casi todo está por hacerse, muestran las posibilidades de hacer análisis de desempeño en el dominio de la escala.
Si con tráfico SRD (short range dependent) ya existen enormes dificultades analíticas y computacionales para encontrar resultados adecuados en redes de colas, con tráfico LRD aún nos encontramos mucho más atrás, pues inclusive para una sola cola los resultados son sólo aproximados. La gran virtud de estos modelos es que permiten capturar muchas de las características que se han evidenciado cada vez más en el tráfico en redes modernas y, en ese sentido, se hacen más adecuados para estudios de desempeño mediante simulación. Pero aún en estas aplicaciones, los procesos LRD requieren largas simulaciones para llegar a resultados significativos de "estado estable" (como se evidencia al comparar las figuras 3 y 4) [49][107][28][59]. Aunque esta no es una deficiencia fundamental de los modelos sino de los fenómenos que tratan de modelar, no se han desarrollado aún técnicas eficientes para tratar computacionalmente los efectos de las distribuciones de cola pesada. Si bien la síntesis de tráfico fractal puede hacerse eficientemente mediante la transformada wavelet, aún es muy difícil poder determinar condiciones de estabilidad, por ejemplo, o aplicar técnicas clásicas de análisis estadístico cuando las varianzas de los resultados de simulación disminuyen más lentamente que el inverso del número de mediciones.
A pesar de estas dificultades, hoy en día está claro que la autosemejanza es un concepto fundamental para comprender la naturaleza dinámica del tráfico, el desempeño de las redes y los procedimientos de control de tráfico que buscan proporcionar una calidad de servicio dada, tanto que algunos autores opinan que esta autosemejanza exige reexaminar el panorama de las redes de comunicaciones y reconsiderar muchas de sus premisas básicas[87]. Por ejemplo, es importante saber cómo se comportan los procesos de tráfico ante la re-escalización (la observación de los fenómenos de tráfico a diferentes escalas de tiempo), ya que el almacenamiento de paquetes en buffers y la asignación de ancho de banda a flujos de paquetes se pueden considerar como operaciones sobre el proceso re-escalizado. Específicamente, si un proceso markoviano se re-escaliza adecuadamente en el tiempo, el proceso que resulta pierde rápidamente la dependencia y se comporta como una secuencia de variables aleatorias independientes e idénticamente distribuidas. Una de las características más deseadas de este tipo de procesos, de acuerdo con la teoría de las grandes desviaciones, es que los "eventos raros" (como la ocurrencia prolongada de un exceso de llegadas) tiene una probabilidad exponencialmente pequeña. Este comportamiento se explica por la poca correlación entre eventos que se suceden relativamente separados en el tiempo[84]. En cambio, si un proceso autosemejante se re-escaliza en el tiempo, los fenómenos de variabilidad persistirán de una escala de tiempo a otra (invarianza a la escala), como se puede apreciar en las figuras 3 y 4 [71]. En general, deben tenerse en cuenta tanto la dependencia de rango corto como la dependencia de rango largo, pues cada una de ellas genera efectos importantes en el desempeño de las redes [96].
Por otro lado, todavía existe algún debate sobre el verdadero efecto de la dependencia de rango largo sobre los elementos de la red. En efecto, algunos resultados experimentales han demostrado que, con bajos períodos de ocupación, la LRD no afecta la longitud del buffer. Por ejemplo, un modelo de Markov y un modelo autosemejante ajustados a una traza real de video VBR pueden generar las mismas longitudes de cola [61]. O, en algunos contextos particulares, un modelos ARIMA puede resultar superior a un modelo FARIMA [105]. Estos resultados han conducido al procedimiento actual de dimensionamiento de redes según el cual se proporciona una capacidad de transmisión más cercana al pico del tráfico que al promedio y se mantienen reducidas las capacidades de los buffers. Este sobre-dimensionamiento elimina los efectos negativos de la dependencia de rango largo y aún le da algún espacio a la ingeniería de tráfico, pues también se ha demostrado que, cuando se modela al nivel de flujo y no al nivel de paquete, los tiempos entre llegadas y los tiempos de duración de las sesiones son variables aleatorias independientes e, incluso, sin memoria, con lo cual se restablecen las bases del modelamiento markoviano [96]. Aunque estos autores aceptan que las herramientas para modelamiento no pueden ignorar las características del tráfico real y que se necesita desarrollar una nueva teoría de tráfico, también sugieren que las técnicas tradicionales y los resultados clásicos siguen teniendo aplicación y pueden mostrar el impacto de futuras evoluciones alternativas de las redes.
A pesar de la controversia, para todos los autores está claro que la dependencia de rango largo puede tener un efecto significativo en el desempeño de la red y que es necesario ejercer control de las colas en los nodos a nivel de paquete. Ese tipo de controles se suele basar en procesos de realimentación que generan retardos y, por consiguiente, inestabilidad. Afortunadamente, la compleja estructura de correlación del tráfico LRD también ofrece una oportunidad para combatir dicha inestabilidad, y es la posibilidad de predecir el tráfico futuro a diferentes escalas de tiempo.
4.7 Predecibilidad del Tráfico LRD
En casi todos los procesos de control de redes de comunicaciones se puede identificar algún mecanismo de realimentación mediante el cual los componentes de la red responden a la información suministrada tomando alguna acción de control correspondiente. Esta información de realimentación, sin embargo, suele llegar con algún retardo, comprometiendo la oportunidad de la respuesta obtenida. Consideremos, por ejemplo, un mecanismos IADM (Incremento Aditivo, Decremento Multiplicativo) de control de congestión según el cual las fuentes ajustan la tasa de transmisión de acuerdo con la tasa de pérdidas percibida o el retardo experimentado (TCP, por ejemplo). La figura 8 muestra el mecanismo de realimentación correspondiente: Las fuentes distribuyen sus flujos de paquetes en los enlaces de la red mediante la matriz de enrutamiento, con lo cual se determina la cantidad de flujo en cada enlace. De acuerdo con el mecanismos de administración de la cola (FIFO, RED, WFQ, etc.), el uso de cada enlace tendrá un costo en términos de retardo y probabilidad de pérdida. La combinación adecuada de los costos de cada enlace se comunica a las fuentes como un costo total y, de acuerdo con ese costo percibido, las fuentes ajustan la tasa de transmisión incrementándola linealmente si el costo es bajo o decrementándola exponencialmente si el costo es muy alto.
Un paquete emitido en el instante 0 será descartado en un nodo congestionado en un instante posterior t1. Si existen mecanismos ECN (notificación explícita de la congestión), la pérdida podría informársele inmediatamente al transmisor para que disminuya su tasa, en cuyo caso la información llegará ~2t1 segundos después de haber enviado un paquete que, en principio, no debió haber sido enviado. Sin mecanismos ECN, el retardo en la reacción a los fenómenos de congestión es mucho mayor (varios RTTs). Si la fuente hubiera podido predecir que ese paquete iba a ser rechazado, hubiera tomado las acciones de control más oportunamente. Debido a los retardos, los sistemas dinámicos como el de la figura 8 experimentan inestabilidades que afectan muy negativamente la calidad del servicio ofrecido.
Si bien la variabilidad LRD tiene los efectos negativos que hemos visto anteriormente sobre el desempeño de la red, imponiendo serias dificultades a los algoritmos de control de congestión, también es cierto que este tipo de procesos poseen una compleja estructura de correlación que puede ser explotada para "predecir el futuro" [113] y hacer más oportuna la acción de los procesos de control. En diferentes publicaciones se han reportado resultados analíticos de predecibilidad basados en modelos paramétricos fbm y Farima [56][101] o basados simplemente en mediciones sin necesidad de ajustar modelos paramétricos [113][52][117]. Estas propiedades se han utilizado exitosamente en administración activa de colas [51], control de tasa de transmisión en flujos TCP [113], balanceo de carga en redes activas [57], etc.
Como verificación de esta predecibilidad, la figura 9 muestra la probabilidad de que el tráfico en el siguiente segundo caiga en uno de ocho niveles predeterminados dado que el tráfico en el segundo inmediatamente anterior es alto, medio o bajo, de acuerdo con las trazas de tráfico de las figuras 3 y 4. Para el tráfico Poisson, las tres distribuciones son casi idénticas a la distribución incondicional, mientras que para el tráfico Ethernet, la correlación positiva permite predecir con mayor exactitud el nivel de tráfico en el siguiente segundo [8].
Esa predecibilidad se extiende a muchas escalas de tiempo, como se puede observar en la figura 10, donde se grafica la entropía de las distribuciones condicionales ponderadas para cada uno de los ocho niveles en que se dividió la intensidad de tráfico. Claramente, la menor entropía del tráfico Ethernet indica que la incertidumbre en él es menor [8].

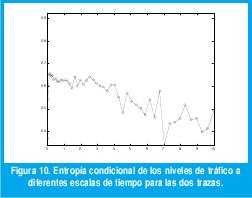
Un aspecto por explotar es la predecibilidad multiescala debida a la fractalidad del tráfico. Esto es, cabe preguntarse si las observaciones hechas a escalas pequeñas (o grandes) de tiempo pueden emplearse para hacer predicción en otras escalas de tiempo. Si así fuera, podríamos explotar el hecho de que es fácil hacer mediciones de tráfico a escalas grandes de tiempo (para control de admisión, por ejemplo) para hacer predicción a escalas menores de tiempo (para control de congestión, por ejemplo). Este es tema de estudio por parte de los autores, quienes ya han obtenido algunos resultados promisorios con la predecibilidad del tráfico [8][116] y con otros fenómenos predecibles en redes de comunicaciones [14].
V. TRÁFICO "ELÁSTICO"
Y TRÁFICO "NO-ELÁSTICO"
La dificultad de definir un proceso estocástico que describa las características estadísticas del tráfico para cada caso particular no puede ser una limitante que restrinja el desarrollo de las redes de comunicaciones. Aunque estos modelos son importantes para estudios de desempeño en actividades de investigación y desarrollo, o para dimensionamiento y administración de redes "offline", en la práctica es aún más importante poder establecer acuerdos de nivel de servicio (SLA) y verificar que esos acuerdos se cumplan tanto por parte de la red como por parte de los usuarios (traffic policing, traffic shaping). Por esa razón, las entidades encargadas de la normalización de procesos en las redes han preferido definir un conjunto de descriptores que se adecúen a cualquier tipo de tráfico y sobre los cuales se puedan establecer dichos acuerdos [22][100]. Estos descriptores corresponden a los modelos de tráfico acotados propios del "cálculo de Cruz", el cual se mencionó antes en la sección 3.3 [40][41]. Estos modelos no tratan de dar una descripción estadística detallada del tráfico sino que se limitan a dar algunas cotas en el número de paquetes que se pueden generar en un intervalo dado de tiempo, con lo cual se pueden determinar cotas para la ocupación de los buffers, para el retardo de los paquetes e, inclusive, para la tasa de pérdidas [39].
El tráfico se puede describir en términos de las características de diferentes objetos tales como paquetes, ráfagas, flujos, sesiones y conexiones, dependiendo de la escala de tiempo de las variaciones estadísticas relevantes. Para los modelos acotados resulta más conveniente caracterizar el tráfico al nivel intermedio de flujos, donde un flujo se define como una sucesión unidireccional de paquetes desde una fuente particular, todos ellos identificados adecuadamente (por ejemplo mediante las mismas direcciones y números de puerto de fuente y de destino). En este contexto, resulta útil distinguir entre flujos elásticos en los que los paquetes corresponden a un documento digital que no necesita transmitirse en tiempo real, y flujos no elásticos en los que los paquetes representan una señal de audio o de video [96]. Las características a nivel de paquete de los flujos elásticos están dadas principalmente por el protocolo de transporte y sus interacciones con la red. De otro lado, los flujos no elásticos tienen característica intrínsecas de tasa de bits (generalmente variable) que se deben preservar aún después de que el flujo atraviese la red. Actualmente, entre el 90 y el 95% de los paquetes en Internet utilizan TCP pues corresponden a la transferencia de diferentes documentos digitales tales como páginas web y archivos de datos. Los algoritmos de control de congestión de TCP hacen que el caudal varíe elásticamente de acuerdo con los cambios aleatorios en las transferencias de documentos. Sin embargo, una pequeña pero creciente proporción del tráfico en Internet corresponde a flujos no elásticos de audio y video que no están sometidos a estos mecanismos de control de congestión [96].
TCP realiza un control en lazo cerrado mediante un algoritmo de incremento aditivo y decremento multiplicativo: La tasa se incrementa linealmente en ausencia de pérdida de paquetes, pero se reduce a la mitad cada vez que ocurre una pérdida. Este comportamiento hace que cada flujo ajuste su tasa promedio de transmisión a un valor que depende de la capacidad y del conjunto de flujos que compiten en cada enlace de la ruta. El ancho de banda disponible se comparte así de una manera más o menos equitativa entre todos los flujos.
El tráfico no elástico está sujeto a un esquema de control de lazo abierto: Se supone que cada flujo que llega tiene ciertas características de tráfico, de manera que la red admite el flujo si se puede mantener la calidad de servicio. Los flujos admitidos son sometidos a control policivo para asegurar que sus características de tráfico se conserven dentro de los valores advertidos.
Para el caso de tráfico elástico, el desempeño está determinado, principalmente, por la manera de compartir el ancho de banda entre los flujos que compiten por él. Un modelo sencillo de procesador compartido indica que el desempeño de caudal promedio es muy poco sensible a las características detalladas del tráfico tales como la distribución del tamaño del flujo [96]. Para el caso de tráfico no elástico, el control en lazo abierto es más simple cuando la red hace multiplexación sin buffers pues, en ese caso, la probabilidad de pérdida de paquetes resulta independiente de cualquier autosemejanza en las variaciones de la tasa de bits de los flujos individuales [96]. Bajo estos modelos, el principal mecanismo para asegurar una alta calidad de servicio es el sobredimensionamiento que, básicamente, significa evitar la sobrecarga asegurando que la capacidad de todos los enlaces sea siempre superior al pico de la demanda.
VI. CAOS Y COMPLEJIDAD EN REDES
Ante las dificultades que presenta el análisis tradicional de la teoría de colas al aplicarse a las redes modernas de comunicaciones, muchos de los problemas técnicos actuales como el control de admisión, el control de flujo, el control de congestión, el control de la memoria en las colas, la asignación de recursos (especialmente la administración dinámica del ancho de banda de los canales y de la memoria en los buffers de transmisión), el caché dinámico, la estimación de las características del canal, la mitigación de la interferencia en enlaces inalámbricos, el incremento de la capacidad mediante técnicas avanzadas de modulación, el enrutamiento dinámico adaptable, la recuperación automática ante fallas, etc., se han reformulado exitosamente en términos de la teoría de control y la optimización [25]. Por ejemplo, el enrutamiento en redes de circuitos virtuales o con conmutación por etiquetas (MPLS) puede formularse como un problema de optimización para el cual, utilizando métodos propios de la teoría de control óptimo, se pueden encontrar soluciones aproximadas que permiten determinar cotas compactas de las medidas de desempeño resultantes [103]. Igualmente, el control de admisión puede reformularse como un problema determinístico de control óptimo sobre un modelo de flujos [103]. Un enfoque novedoso que esta visión del problema de enrutamiento desde la teoría del control y la optimización ha traído, es el de considerar la red como un sistema en el que los usuarios (o los proveedores de servicios) desean seleccionar las rutas para optimizar sus propios objetivos individuales de desempeño. Esto conduce al estudio de sistemas compuestos por usuarios no cooperativos que interactúan para conseguir sus propios objetivos. Un enfoque natural para este tipo de problemas es el de la teoría de juegos y sus diferentes variantes, las cuales se han aplicado exitosamente en la solución de problemas prácticos de enrutamiento [70]. Pero, más interesante aún, este tipo de sistemas se han estudiado en muy diferentes contextos como la mecánica estadística, la biología y la economía, entre otros, donde han conducido a la teoría de sistemas complejos [6][110]. De hecho, al empezar a estudiar los problemas de asignación de recursos y control de congestión en redes IP desde el punto de vista de la teoría de control, se han venido descubriendo comportamientos dinámicos sorprendentes de los protocolos de la red, propios de los sistemas complejos [119].
En particular, considérense las interacciones entre el protocolo de control de congestión en TCP y el algoritmo RED de administración activa de colas, mostradas en la Figura 11. Si el tiempo se discretiza en unidades de RTT (round trip time), en el instante k la fuente TCP genera paquetes a una tasa rk y la cola, que tiene una longitud instantánea qk y una longitud promedio qk__, descarta paquetes con una probabilidad pk. Analizando los detalles de los algoritmos TCP y RED, en [90] llegaron al siguiente modelo ecuaciones de estado para un sistema dinámico no lineal:
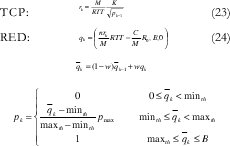
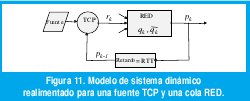
Variando cualquiera de los parámetros del modelo, se descubren diferentes fenómenos de bifurcación que conducen a órbitas periódicas de período arbitrario e, inclusive, al caos [90][119], como muestra la figura 12 para variaciones en w.
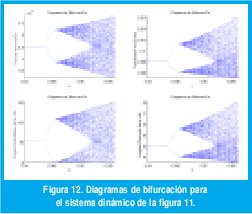
Este descubrimiento tiene muchas implicaciones no sólo en cuanto a la posibilidad de introducir a las redes de comunicaciones la reciente teoría del control del caos, sino como una manera misma de explicar el fenómeno de la fractalidad en los patrones medidos de tráfico. En efecto, se sabe que las trayectorias de sistemas caóticos suelen ser de naturaleza fractal y, de hecho, suelen usarse como generadores de estructuras fractales [45]. Pues bien, el operar "al borde del caos" (EOC -edge of chaos-) es una propiedad de los sistemas complejos de la mecánica estadística que se autoconfiguran para situarse en un estado crítico óptimo (SOC -Self Organized Criticality), y con los cuales podría explicarse la ubicuidad de los fenómenos fractales en la naturaleza [23][67][72]. Varios autores han sugerido esta SOC como una explicación de los comportamientos de escala que han aparecido en las redes de comunicaciones [83][102]. Otros autores sugieren que esta explicación ignora el largo proceso de diseño óptimo que ha habido durante la evolución de las redes de comunicaciones y proponen una asociación entre las modernas redes de comunicaciones y los modelos de complejidad de los sistemas biológicos en los que, mediante evolución, se obtiene robustez contra problemas conocidos o predecibles pero a costa de fragilidad contra otros problemas no predecibles que son cada vez más improbables a medida que la evolución avanza pero, igualmente, pueden ser más catastróficos cuando finalmente se presentan [124]. Estas características de tolerancia altamente optimizada (HOT -Highly Optimized Tolerance-), extensamente compartidas por las redes de comunicaciones, también conducen a fenómenos de fractalidad y comportamientos dinámicos caóticos [34].
Existen otras manifestaciones de complejidad en redes modernas de comunicaciones. Por ejemplo, el concepto de "redes libres de escala" [24] sugiere un comportamiento igualmente fractal en fenómenos tales como la topología de Internet y la estructura de la WorldWideWeb, en los que las conexiones entre nodos siguen una distribución de cola pesada (algunos nodos tienen un inmenso número de conexiones mientras que la mayoría de nodos sólo tienen algunas pocas), lo que suele dar paso a fenómenos autosemejantes. Esta característica de las redes libres de escala las hace robustas contra fallas accidentales pero altamente vulnerables a ataques coordinados (sistemas HOT) [24][79].
Se espera que este nuevo enfoque de las redes de comunicaciones desde la perspectiva del control de sistemas complejos traiga más profundos conocimientos, mayor comprensión y nuevos desarrollos tecnológicos en las redes de comunicaciones actuales y futuras, especialmente en cuanto a la administración misma de las redes [69].
En efecto, el descubrimiento de estos tipos de complejidad en redes de comunicaciones debe conducir a nuevas formas de administración de las mismas. Actualmente, el enfoque de administración se basa en mediciones del "estado" de la red y su almacenamiento en bases de datos distribuidas (la MIB de SNMP, por ejemplo), de manera que los procesos de administración correspondan a máquinas de estado finito aplicadas a modelos de información construidos sobre las MIB [69][106]. Sin embargo, dados todos los fenómenos de escala anteriormente mencionados, no es factible "medir" el estado de la red. De hecho, para simplemente monitorear el desempeño de la red, ya es necesario usar técnicas de inferencia estadística basadas en principios de tomografía [35][111]. Consecuentemente, varios autores han considerado la posibilidad de emplear métodos de los sistemas complejos propios de la biología para el control de redes modernas de comunicación [125]. En efecto, los sistemas biológicos de gran escala han desarrollado, a través de miles de años de evolución, características tales como adaptabilidad a condiciones diversas y dinámicas, alta seguridad y disponibilidad, escalabilidad, autonomía, etc. Todos estas características son deseables en el control de redes de comunicaciones.
Un nuevo paradigma que promete muchas soluciones en este complejo panorama en la administración de redes es el de los agentes de software móviles [20]. Por ejemplo, en redes activas, los usuarios pueden proporcionar a los nodos de conmutación los programas necesarios para los servicios particulares que ellos requieran [108]. Algunos autores proponen utilizar este paradigma para la implementación de técnicas de control genéticas: los nodos (o bacterias) comparten programas componentes de servicio (o genes) mediante paquetes activos (migración plasmídica) para maximizar el número de servicios prestados a los usuarios (alimento digerido), en un esquema de aprendizaje no-supervisado [76][80]. Otro importante ejemplo es el de enrutamiento mediante hormigas, en el que agentes sencillos (hormigas) interactúan mediante estigmergia (comunicación indirecta y asincrónica por depósito de feromonas), de manera tal que generan un sistema complejo auto-organizado (la colonia de hormigas) capaz de resolver complejos problemas de optimización (encontrar la ruta más corta entre el hormiguero y la fuente de comida) [30]. Como todo sistema complejo auto-organizado, los algoritmos de colonia de hormigas crean estructuras espacio-temporales en un medio inicialmente homogéneo, con características de multiestabilidad y presencia de bifurcaciones ante cambios ambientales.
VII. FALTA DE ESTACIONARIEDAD Y LRD
En [130] se reporta un trabajo muy reciente en el que se modela el tráfico sobre canales troncales de Internet a 2.5 Gbps con muy baja utilización. Las trazas observadas a escalas de tiempo de un segundo se ajustan sorprendentemente bien a un modelo no estacionario de Poisson pues, en efecto, se está considerando una altísima agregación de flujos individuales independientes. De hecho, son tantas las fuentes agregadas en tal enlace troncal, que la falta de estacionariedad no pareciera atribuible a variaciones en el número de fuentes activas sino que, según sugieren los autores, dicha falta de estacionariedad se puede deber a la variabilidad de la tasa de llegadas de cada fuente, la cual se transfiere al proceso agregado que, de todas formas, adquiere rápidamente las características de un proceso de Poisson perfecto (muchas fuentes independientes) cuya tasa promedio de llegadas varía con el tiempo.
Lo más interesante es que, a escalas de tiempo superiores, el tráfico troncal muestra dependencia de largo rango, de acuerdo con mediciones empíricas del exponente Hurst, lo cual sugiere una dicotomía en el comportamiento del tráfico altamente agregado, con una delgada frontera entre la falta de estacionariedad de un proceso de Poisson y la dependencia de largo rango de un proceso altamente correlacionado.
Si bien el reporte arriba mencionado abre muchos interrogantes sobre la evolución del tráfico n Internet a medida que crecen sus dimensiones,también refuerza la importancia de considerar el tráfico a diferentes escalas de tiempo para comprender los efectos de su comportamiento a diferentes niveles de la jerarquía funcional, donde cada acción de control sobre la red tiene una "constante de tiempo" determinada. Esto nos motiva aún más a considerar el análisis y el control de las redes de comunicaciones desde la perspectiva del comportamiento multiescala del tráfico sobre las mismas, como se describe a continuación.
VIII. INVESTIGACIÓN SOBRE MODELOS DE TRÁFICO EN ANÁLISIS Y CONTROL DE REDES
El tema general del modelamiento de tráfico y el control de redes modernas de comunicaciones es motivo de una intensa actividad de investigación en el mundo entero, como puede verificarse a partir de la bibliografía propuesta para este artículo. Dentro de las incontables áreas de investigación que se podrían mencionar, los autores de este artículo están interesados en la aplicación de técnicas de procesamiento estadístico de señales en análisis y control de redes de comunicaciones [17][8]. Proponemos verificar la hipótesis de que, explotando las propiedades de dependencia de largo rango del tráfico en redes modernas de comunicaciones, especialmente la predecibilidad, es posible utilizar técnicas de procesamiento estadístico de señales para monitorear y predecir el desempeño de estas redes de manera que se pueda tomar decisiones de control más oportunas y efectivas. En particular, quisiéramos aprovechar las características de correlación del tráfico moderno para predecir la intensidad del tráfico futuro en escalas de tiempo adecuadas a los diferentes procesos de control de una red de comunicaciones, tales como ingeniería de tráfico, ajuste de la tasa de datos en las fuentes, administración activa de colas y planeación general de la red. Si la predicción fuese suficientemente exacta, sería posible tomar acciones integradas de control más oportunas. Más aún, en este sentido se podría explotar la predecibilidad de muchas otras "señales" medidas sobre la red (tasas de pérdidas, retardos, capacidad disponible, movilidad, cambios topológicos, energía almacenada en las baterías de los dispositivos móviles, etc.) para tomar acciones de control en una verdadera integración vertical de protocolos. En [133], por ejemplo, se toman decisiones de enrutamiento de acuerdo con predicciones sobre la duración de los enlaces en redes móviles ad hoc. En este numeral discutimos brevemente dichas posibilidades de investigación.
8.1 Tomografía de Redes
Dada la heterogeneidad y la complejidad de las modernas redes de comunicaciones, cada vez es más difícil realizar tareas como enrutamiento dinámico, verificación de niveles de servicio, detección de problemas de desempeño, etc. En este sentido, una novedosa y promisoria área que apenas está emergiendo es el de la inferencia estadística de las medidas de desempeño de la red a partir de mediciones indirectas, ya sean pasivas o activas (Tomografía de red [36]).
En términos generales, la tomografía de redes consiste en estimar parámetros de desempeño de la red, inferiéndolos a partir de mediciones de tráfico hechas en un subconjunto limitado de los nodos [115]. La aleatoriedad inherente de dichas mediciones exige la adopción de métodos de inferencia estadística, generalmente de naturaleza iterativa debido a la alta dimensionalidad de los problemas. Por ejemplo, si se dispone de la matriz de enrutamiento A= {αij) (donde αij es uno si la iésima ruta utiliza el j-ésimo enlace y cero en otro caso) y se mide el vector de pérdidas y={yi} (donde yi es el logaritmo de la tasa de pérdidas en la iésima ruta), en principio podríamos estimar las tasas de pérdidas en cada enlace,⊕= {⊕j} (donde ⊕j es el logaritmo de la probabilidad de pérdida en el jésimo enlace) mediante la aplicación de algún algoritmo de estimación óptima aplicado sobre el modelo afín y= A⊕+ε, donde ε es un término de ruido correspondiente a las perturbaciones aleatorias de ⊕ y al error en las mediciones y. El mismo modelo se podría aplicar si, por ejemplo, y son las mediciones del retardo entre extremos y se quiere estimar el retardo en cada enlace ⊕, o si y corresponde a mediciones de la intensidad de tráfico en cada enlace y se quiere estimar la intensidad de tráfico entre los extremos de las rutas, ⊕ (en este caso A se debería transponer y el término de error sería cero). Estos problemas tienen soluciones conocidas si el ruido ε es Gaussiano y su matriz de covarianza es independiente de A⊕ (el método recursivo de los mínimos cuadrados [75]). En otros casos se requieren métodos más elaborados como ML-EM (Máxima verosimilitud mediante esperanza-maximización) [77] o MAP-MCMC (máximo-a-posteriori mediante Cadenas de Markov Monte Carlo) [58]. Cuando no se conoce la matriz de enrutamiento A, es necesario estimarla mediante técnicas tomográficas de estimación topológica basadas en medidas entre extremos del grado de correlación que existe entre distintos receptores [35]. En estos casos el modelo a resolver es altamente no-lineal, pues se trata de considerar las medidas y como observaciones ruidosas de los parámetros de desempeño reales,⊕, de acuerdo con una densidad de probabilidad parametrizada por la topología de la red, T. La estimación consiste en encontrar la topología que maximiza la probabilidad de la observación y dado ⊕. Éste es un problema formidable que sólo se puede resolver mediante técnicas aproximadas basadas en reglas heurísticas [36]. Aquí nuevamente, los modelos basados en transformada wavelet son muy promisorios [63][73].
Las observaciones y pueden hacerse mediante mediciones activas, las cuales introducen tráfico de prueba, facilitando así la inferencia del caudal, el retardo, la tasa de pérdidas, la capacidad efectiva, etc., pero incrementando la carga en la red y perturbando su desempeño [36]. Las mediciones pasivas se concentran exclusivamente sobre el tráfico existente en la red, eliminando la interferencia. Sin embargo, dada la dificultad de extraer información útil de estas mediciones, el problema de inferencia se puede volver extremadamente complicado, a menos que se asuman modelos de tráfico muy simplificados [36]. Por esta razón, hasta ahora, tanto la teoría como las aplicaciones de la tomografía de redes se han basado en suposiciones de independencia en el tráfico que, como hemos visto a lo largo de este artículo, son cada vez más irreales. Es la opinión de los autores que, si se usan modelos más realistas que describan el comportamiento estadístico del tráfico sobre la red y se utilizan técnicas de procesamiento estadístico de señales sobre las medidas observadas, no sólo se podrían obtener estimados más exactos de las medidas de desempeño sino que esas medidas así inferidas se podrían utilizar en el control de la red en cuanto a la asignación dinámica y óptima de sus recursos a los flujos que la atraviesan, de una manera integrada entre los niveles de red y de transporte.
8.2 Control de Flujo entre Extremos
Los procedimientos de control de congestión mediante realimentación entre extremos, como en TCP, consisten en que las fuentes de tráfico ajusten su tasa de datos según las medidas de congestión obtenidas de la red. Estas medidas suelen ser indirectas (por ejemplo la ausencia de un reconocimiento, el incremento en el tiempo de ida-y-vuelta, RTT, o la duplicidad de reconocimientos) y llegan a las fuentes después de un retardo significativo, inclusive cuando se usa notificación explicita de la congestión (ECN). Este retardo en el camino de la realimentación hace que las acciones de control no correspondan al estado actual de congestión en la red sino a algún estado previo, lo cual se puede traducir en oscilaciones e inestabilidades que traen efectos desastrosos en la calidad del servicio ofrecido por la red [90]. Muchos esfuerzos de investigación se han concentrado en tratar de mitigar estos efectos negativos del retardo en el lazo de realimentación mediante la estabilización de las colas en los nodos congestionados o próximos a congestionarse. Sin embargo, excepto por un posible procedimiento de ajuste en los nodos de ingreso, no se presta atención a las características estadísticas de cada flujo de tráfico ni del flujo agregado, cuyas variaciones aleatorias generan la necesidad de ajustar continuamente la tasa de datos de las fuentes. Si la información realimentada y/o la decisión tomada por las fuentes obedeciera a un conocimiento más detallado de las variaciones del tráfico, incluyendo sus variaciones futuras en un horizonte de tiempo adecuado, se podrían evitar lo efectos desestabilizadores del retardo de realimentación y se podrían ejercer acciones de control más apropiadas. A manera de ejemplo, en vez de usar algoritmos AIMD -incremento aditivo y decremento multiplicativopara el ajuste de las tasas de transmisión, se podría llegar a un punto de equilibrio estable si los ajustes de optimizan de acuerdo con las características del tráfico agregado.
Es de anotar que este tipo de estudios ya se iniciaron en lo que se refiere a los esquemas de control de flujo en TCP (como se ha descrito en la sección 4.7 de este artículo). Sin embargo, las nuevas tendencias en redes IP incluyen la implementación de servicios con tráfico no-elástico que, como se mencionó en la sección 5, no comparten el ancho de banda disponible de una manera equitativa con los servicios basados en TCP. Por esta razón se han venido proponiendo protocolos "amigables" con TCP para flujos no elásticos que se comporten equitativamente cuando coexisten con flujos alásticos TCP. Un mecanismo basado en ventanas deslizantes, como el de TCP, no es apropiado para este tipo de flujos por la forma de diente de sierra que adopta la tasa instantánea en este tipo de algoritmos. En consecuencia, se procura encontrar mecanismos que adapten la tasa de transmisión al caudal promedio a largo plazo que obtendría un flujo TCP equivalente [129]. En este tipo de esquemas es fundamental contar con un modelo de ancho de banda disponible con el que se pueda predecir el caudal equitativo al cual ajustar la tasa de transmisión. En estas condiciones, un modelo predictivo del tráfico que compite por los recursos de la red podría ser de gran utilidad para estimar dicho promedio a largo plazo, pues permitiría considerar ajustes a mediano plazo que hagan más equitativa la repartición del ancho de banda sin degradar significativamente la calidad del flujo no-elástico.
8.3 Administración Activa de Memoria y Disciplinas de Servicio en las Colas de los Enrutadores
Las disciplinas de servicio determinan el orden en que los paquetes son atendidos y constituyen una manera fundamental de controlar la asignación de recursos en una red de comunicaciones. En general, se trata de formar una cola por cada nivel de prioridad de servicio, de manera que las colas de menor prioridad no se atienden mientras las colas de mayor prioridad no estén desocupadas. Dentro de cada nivel los paquetes se pueden atender en un orden FIFO o se pueden ordenar de acuerdo con etiquetas de QoS. Los flujos pueden corresponder a diferentes niveles de prioridad o se pueden agregar dentro de niveles específicos de prioridad. Sin embargo, la asignación de recursos entre los flujos que pertenecen al mismo nivel de prioridad sigue siendo un problema por resolver. En este sentido, un conocimiento del comportamiento de cada flujo individual sería de gran utilidad.
Por supuesto, la disciplina de servicio no puede resolver por si sola el problema de la administración de recursos dentro de la red porque, a menos que hubiese mucha memoria para absorber las ráfagas de paquetes de manera que se puedan transmistir en posteriores períodos de silencio, la tasa de pérdidas puede ser muy alta durante la presencia de ráfagas, independientemente de la disciplina de servicio. Ni siquiera una capacidad infinita en las colas resolvería el problema pues, aún así, en condiciones de sobrecarga se descartarían todos los paquetes por exceso de retardo. Así pues, se hace necesario desarrollar mecanismos para compartir el espacio en la cola entre aquellos flujos que usen el mismo puerto de salida. Lo ideal sería llevar un registro de los niveles de ocupación de los cupos en la cola por cada flujo, y descartar los paquetes de acuerdo con esos niveles de ocupación. Para diseñar adecuadamente este tipo de gestión de los cupos de la cola sería muy conveniente disponer de un modelo adecuado de la demanda de cupos (y la presencia de ráfagas) en cada flujo individual y en el tráfico agregado.
Es importante notar que el descarte de paquetes es interpretado por TCP (y los algoritmos amigables con TCP) como indicación de congestión, por lo que se convierte en el mecanismo básico de realimentación desde la red hacia los transmisores. El mecanismo clásico en el que los paquetes se descartan si no hay cupos disponibles en la cola (taildrop) informa sobre la congestión cuando ya es muy tarde y genera una sincronización global en la red. Otras posibilidades, como descartar el primero de la cola cuando llega un paquete nuevo a una cola llena, o descartar un paquete escogido aleatoriamente dentro de la cola introducen pequeñas mejoras al hacer que la congestión se notifique más rápidamente al transmisor y que el paquete descartado tenga más probabilidad de pertenecer al flujo que ocupa más recursos. Sin embargo, los tres mecanismos procuran recuperarse de la congestión una vez ésta se presenta en vez de intentar evitarla antes de que se presente. Los enrutadores pueden prevenir la congestión descartando (o marcando) paquetes sleccionados antes de que se agoten los cupos en la cola, en lo que se conoce como Administración Activa de Colas (AQM). El mecanismo más generalmente utilizado es RED (Random Early Detection), en el que los paquetes se descartan aleatoriamente para mantener bajo control la longitud promedio de la cola. Se ha demostrado la dificultad de ajustar los parámetros de RED para mantener un buen desempeño bajo diferentes condiciones de tráfico. Si se dispusiera de un modelo adecuado de las variaciones del tráfico agregado sobre el enrutador, sería posible pensar en un RED que se ajuste a sí mismo en un amplio rango de condiciones de tráfico.
8.4 Ingeniería de Tráfico
La ingeniería de tráfico permite balancear la carga entre los diferentes enlaces de una red, de manera que ninguno de ellos permanezca sobrecargado ni subutilizado. Originalmente, la ingeniería de tráfico se conseguía mediante la manipuación de las métricas de enrutamiento, lo cual sigue siendo una solución válida si se trata de redes muy pequeñas atendiendo muy pocos usuarios. Cuando las redes IP empezaron a crecer, la solución evidente fue utilizar ATM en el centro de la red y colocar los enrutadores IP en la periferia completamente interconectados mediante circuitos virtuales permanentes (PVC). De esta manera, los PVC se pueden configurar independientemente de IP, aunque la ingeniería de tráfico debe llevarse a cabo "fuera de línea" de acuerdo con procesos de optimización globales basados en promedios históricos del tráfico entre los distintos enrutadores. La única posibilidad de permitir algún comportamiento dinámico adaptivo es asignando algunos PVC secundarios para responder a condiciones de falla. Además, este esquema requiere la administración de dos redes diferentes. Por eso la tendencia en redes IP que quieran implementar ingeniería de tráfico es el uso de MPLS, que permite dirigir un flujo de paquetes IP por una ruta determinada, LSP, la cual se puede escoger independientemente de la ruta escogida por el protocolo de enrutamiento (sin embargo, aún existen alternativas adicionales para hacer ingeniería de tráfico sobre OSPF o IS-IS [131]). Más aún, la asignación de un paquete a un LSP dado puede basarse en una gran cantidad de criterios como fuente, destino, aplicación, requerimiento de QoS, etc. Para la aplicación específica de ingeniería de tráfico, MPLS comparte dinámicamente información sobre la topología de la red y el estado de congestión de los enlaces mediante algún algoritmo de señalización adecuado (RSVP o LDP), con lo que se facilita hacer un cálculo "en línea" de las mejores rutas, de acuerdo con la condiciones dinámicas de la red en cada instante.
Estas enormes capacidades de MPLS para hacer una juiciosa implementación de ingeniería de tráfico se ve limitada por la falta de un conocimiento preciso de las caractersticas del tráfico que circula por la red. En efecto, el objetivo de cualquier procedimiento de ingeniería de tráfico es la optimización de algún criterio de desempeño que integre criterios sobre la calidad de servicio vista por los usuarios y eficiencia en el uso de recursos. Debido a la complejidad de los problemas de optimización que se plantean con estos objetivos tan diversos, los modelos estocásticos de partición de tráfico en redes IP basadas en MPLS se suelen restringir a modelos de tráfico tipo Poisson y las decisiones se toman de acuerdo con el estado estimado de la red en cada instante [33][43]. Un conocimiento más detallado de las características del tráfico y de la correspondiente variación dinámica del estado de la red permitiría tomar mejores y más oportunas decisiones de ingeniría de tráfico. Al plantear dichos problemas de optimización para ser resueltos en términos de algoritmos numéricos de optimización típicos, la complejidad puede hacerse excesiva en términos computacionales, por lo que convendría explorar la asignación dinámica de tráfico sobre LSPs preestablecidos mediante técnicas heurísticas, ya sea a través de reglas directas (si se espera que la intensidad de tráfico sobrepase un límite superior thr dentro de los siguientes t segundos, disperse los paquetes sobre un número n( t,thr) de LSPs paralelos [57][116]) o a través de algoritmos bioinspirados de inteligencia computacional (inteligencia de enjambre, algoritmos genéticos, redes neuronales, etc. [17][19]).
8.5 Integración Vertical de Protocolos
Por supuesto, si todos estos esquemas de predicción se utilizan simultáneamente para tomar decisiones de control más adecuadas y oportunas a diferentes niveles de la jerarquía funcional de la red, podrán presentarse una serie de interacciones imprevistas que será necesario estudiar y controlar. De hecho, recientemente se ha verificado que la estabilidad de los algoritmos de enrutamiento adaptivo se puede ver comprometida cuando operan simultáneamente con algoritmos de control de congestión realimentados, debido a la doble realimentación [132]. Este problema sugiere considerar la inferencia y el control predictivo de redes desde el punto de vista de la integración vertical de protocolos. En efecto, se ha propuesto que, en redes de alto desempeño, el enfoque convencional en el que cada nivel se diseña y optimiza independientemente de los demás debe revaluarse para poder explotar las dependencias entre niveles en un esquema de optimización conjunta [26].
IX. DISCUSIÓN Y CONCLUSIONES
Los modelos de tráfico no correlacionados (procesos de renovación, en especial el proceso de Poisson) ofrecen una gran tratabilidad matemática pero no son capaces de capturar muchas de las características más relevantes del tráfico moderno, en particular las asociadas con la autocorrelación observada en el tráfico real. Desde finales de los 80's se han venido proponiendo nuevos modelos basados en procesos estocásticos capaces de capturar los efectos de la correlación a pequeñas escalas de tiempo (MMPP, MMDP, MAP, B-MAP, SMP, AR, TES, etc.) Aunque con estos modelos se reduce la tratabilidad matemática, todavía es posible obtener resultados significativos (analíticos y de simulación) a costos computacionales razonables. Sin embargo la autocorrelación de estos modelos decae exponencialmente rápido con el tiempo, haciéndolos insuficientes para explicar muchas de las características observadas en el tráfico de las redes modernas de comunicaciones, especialmente en cuanto a las estructuras complejas de correlación que se extienden a muchas escalas de tiempo. Los modelos de tráfico autosemejante (fbm, farima, mapas caóticos, M/G/, MWM, etc.) pretenden capturar los efectos de estas estructuras de correlación, en especial el gran impacto que tienen sobre el desempeño de la red. Sin embargo, todavía son muy preliminares los resultados de análisis de desempeño bajo tráfico autosemejante y, más aún, algunos autores creen que ese efecto no es tan relevante cuando se considera el tráfico en unidades de flujos y no en unidades de paquetes.
Debido a estas dificultades en el modelamiento de tráfico (todavía no comprendemos cuáles son las características del tráfico que realmente afectan el desempeño de las redes), los procedimientos actuales de control de redes se basan en modelos de tráfico acotados, los cuales representan las características fundamentales del tráfico en términos de algunos descriptores sencillos tales como la tasa pico y la tasa media. Estos modelos son muy efectivos en cuanto a que conducen a procedimientos de diseño basados en el sobredimensionamiento, con altas tasas de transmisión y poca memoria para los buffers de espera, con los cuales es posible ofrecer garantías de calidad de servicio, aunque a costa de una pobre utilización de los recursos de la red. Sin embargo, para mantener un nivel de calidad de servicio adecuado a medida que la demanda aumenta, las redes modernas de comunicaciones dependen de procedimientos efectivos de control de congestión que permitan usar eficientemente los recursos. La aplicación efectiva de los modelos propuestos de tráfico en un esquema combinado de sobredimensionamiento y administración de ancho de banda es un tema actual de investigación en el que hay mucho por aportar.
La fractalidad del tráfico es apenas una de la manifestaciones de la complejidad de las redes modernas de comunicaciones. En efecto, estas redes están constituidas por una gran cantidad de componentes que interactúan cooperando de alguna manera para dar paso a fenómenos emergentes. Otras manifestaciones de dicha complejidad son la presencia de fenómenos caóticos en su comportamiento dinámico, las leyes de potencia en su crecimiento topológico, la distribución de colas pesadas en los archivos transportados por la red, etc. Este tipo de fenómenos emergentes son cada vez más evidentes en todo tipo de sistemas complejos, los cuales se autoconfiguran para operar en puntos críticos al borde del caos. En el caso de los sistemas biológicos o los sistemas tecnológicos cuidadosamente diseñados, la complejidad se traduce en tolerancia altamente optimizada, esto es, adaptabilidad y robustez a problemas conocidos, pero gran fragilidad ante problemas imprevistos.
Como gran conclusión de todos estos puntos, está claro que nos encontramos en un momento privilegiado del desarrollo de las tecnologías de redes de comunicaciones, en el que contamos con un amplio espacio para hacer aportes importantes mediante actividades de investigación en la frontera del conocimiento. En particular, el artículo termina con la proposición de un área de investigación en la aplicación de técnicas de procesamiento estadístico de señales para monitorear y predecir el desempeño de la red, de manera que se puedan tomar decisiones de control más oportunas y efectivas.
REFERENCIAS BIBLIOGRÁFICAS
[1]N. Abramson "Multiple Access Communications: Foundations for Emerging Technologies", IEEE Press, 1994
[2] P. Abry and D. Veitch. "Wavelet Analysis of Long-Range-Dependent Traffic". IEEE Trans. Information Theory, 44(1):2-15, 1998.
[3] P. Abry, P. Flandrin, M. Taqqu and D. Veitch. "Wavelets for the Analysis and Synthesis of Scaling Data", In "Self-Similar Network Traffic and Performance Evaluation", K. Park and W. Willinger, editors. John Wiley and Sons, New York, 2000.
[4] P. Abry, D. Veitch and P. Flandrin "Long-Range Dependence: Revisiting Aggregation with Wavelets". Blackwell publishers ltd. 1999
[5] A. Adas and A. Mukherjee. "On resource management and QoS guarantees for long-range dependent traffic". GIT-CC-94/60 1994.
[6] R. Albert and L. Barabasi. "Statistical mechanics of complex networks". Reviews of Modern Physics, Volume 74, January 2002.
[7] M. Alzate, "Multiplexaje de voz y datos", Universidad de los Andes, Tesis de Maestria MIE-90-II-1, Departamento de Ingeniería Eléctrica, 1990.
[8] M. Alzate y F. Vega. "Predecibilidad del tráfico en redes modernas de telecomunicaciones". Revista Ingeniería, Universidad Distrital FJC, 2003.
[9] M. Alzate. "Conmutación de Paquetes de Voz". X Congreso Nacional y I Andino de Telecomunicaciones, 1995.
[10] M. Alzate. "Framing ATM Cells for Satellite Onboard Switching". Revista INGENIERIA, Universidad Distrital, 2000.
[11] M. Alzate. "Generation of Simulated Fractal and Multifractal Traffic". IX Congreso Nacional de Estudiantes de Ingeniería de Sistemas, Bogotá, 2000.
[12] M. Alzate. "Introducción al Tráfico Autosemejante en Redes de Comunicaciones". Revista INGENIERIA, Universidad Distrital, 2001.
[13] M. Alzate. "Uso de la Transformada Wavelet para el Estudio de Tráfico Fractal en Redes de Comunicaciones". Revista INGENIERIA, Universidad Distrital, 2002.
[14] M. Alzate. "Probability of Imminent Failure as a Routing Metric in a High-Mobility Wireless Ad Hoc Network". 8th International Conference on Cellular and Intelligent Communications, Seoul, Korea, 2003.
[15] M. Alzate. "Análisis de la Eficiencia en el Uso de la Capacidad Asignada a Conversaciones Telefónicas". Revista INGENIERIA, Universidad Distrital, 1993
[16] M. Alzate. "Tráfico de Voz en ATM Sometido a Control de Admisión por Leaky Bucket". Revista INGENIERIA, enero-marzo, 1996.
[17] M. Alzate. "Procesamiento Digital de Señales en el Modelamiento y Análisis de Redes de Comunicaciones", Documento interno de los grupos de investigación en DSP y Telecomunicaciones la Universidad Distrital (GI-DSP-UD y GITUD), Octubre 2003.
[18] M. Alzate. "Simulation model for MPEG-II Video Traffic", ENEE 608 class project final report, University of Maryland, spring 1998.
[19] M. Alzate and S. Suárez "Ant Routing of fractal traffic", IEEE ANDESCON 2004.
[20] S. Appleby and S. Steward. "Mobile software agents for control in telecommunications networks". BT Technology Journal, vol. 12, No. 2, april 1994.
[21] M. Arlitt and C. Williamson. "Web Server Workload Characterization: The search for Invariants". IEEE/ACM Trans. Networking, 5(5):631-645, 1997.
[22] ATM Forum "Traffic Management Specification" af-tm 0056.000, April 1996
[23] P. Bak. "How Nature works: the science of self organized criticality". Copernicus, NY, 1996.
[24] A-L. Barabasi and E. Bonabeau. "Scale-free networks". Scientific American, may 2003.
[25] J. Baras. "Control Problems in Modern Communication Networks". ENEE769 syllabus, University of Maryland, Spring 2001.
[26] J. Baras, A. Ephremides, R. La and S. Ulukus "Vertical Protocol Integration in Wireles Adhoc Networks", A proposal to the NSF, 2002.
[27] J. Beran, R. Sherman, M. Taqqu and W. Willinger. "LongRange Dependence in VBR video traffic". IEEE. Trans. Commun. 43:1566-1579, 1995.
[28] J. Beran. "Statistics for Long Memory Processes". Chapman and Hall, New York, 1994.
[29] S. Blake et.al. "An architecture for differentiated services" IETF RFC 2475, December 1998.
[30] E.Bonabeau, M.Dorigo and G.Theraulaz. "Swarm Intelligence:From Natural to Artificial Systems", Oxford University Press, 1999.
[31] O. Boxma and J. Cohen. "The M/G/1 Queue with Heavy-tailed Service Time Distribution". IEEE J. Selected Areas in Commun. 16:749-763, 1998.
[32] D. Bertsekas and R. Gallager. "Data Networks", 2nd edition, Prentice-Hall, NJ, 1992.
[33] J. Burns, T. Ott, J. Kock and A. Krzesinski "Path Selection and Bandwidth Allocation in MPLS networks: a non-linear programming approach", ITCOM'01, SPIE, 2001
[34] J. Carlson and J. Doyle. "Highly Optimized Tolerance: Robustness and design in complex systems". http://www.physics.ucsb.edu/~complex/pubs/hot2.ps
[35] M. Coates, R. Castro and R. Nowak. "Maximum Likelihood network topology identification from edge-based unicast measurements". Rice University ECE department, Technical report TREE-0107, August 2002.
[36] M. Coates, A. Hero, R. Nowak and B. Yu. "Internet Tomography", IEEE Signal Processing Magazine, may 2002.
[37] M. Crovella and A. Bestavros. "Self-similarity in WWW traffic".IEEE/ACM Trans. Networking, 5:835-846, 1997.
[38] M. Crovella, M. Taqqu and A. Betsavros. "Heavy-Tailed Probability Distributions in the WWW", In "A practical guide to Heavy Tails", Adler, Feldman and Taqqu, editors. Birkhauser, 1998.
[39] C. Chang. "Performance Guarantees in Communication Networks", Springer, 2000
[40] R. Cruz. "A Calculus for Network Delay. Part I: Elements in Isolation", IEEE Trans. On Information Theory, Volume 37, Number 1, January 1991.
[41] R. Cruz. "A Calculus for Network Delay. Part II: Network Analysis", IEEE Trans. On Information Theory, Volume 37, Number 1, January 1991.
[42] I. Daubechies. "Ten Lectures on Wavelets". SIAM'92. Philadelphia, 1992.
[43] E.Dinan, D. Awduche and B. Jabbari "Optimal Traffic Partitioning in MPLS Networks", in "Networking 2000", Edited by G. Pujolle, Springer-Verlag, 2000
[44] A. Erramili, O. Narayan and W. Willinger. "Experimental queueing analysis with LRD packet traffic". IEEE/ACM Trans. Networking, 4:209-223, 1996.
[45] A. Erramilli and R. Singh. "An application of deterministic chaotic maps to model packet traffic". Queueing Systems, vol. 20, 1996. Pp. 171-206.
[46] A. Feldman, A. Gilbert, P. Huang and W. Willinger. "Dynamics of IP Traffic: A Study of the Role of Variability and the Impact of Control". Proc. ACM SIGCOM'99, 1999.
[47] P. Fieguth and A. Willisky. "Fractal estimation using models on multiscale trees". IEEE Trans. Signal Proc. 44:1297-1300, 1996.
[48] P. Flandrin. "Wavelet Analysis and Synthesis of Fractional Brownian Motion". IEEE Trans. Inf. Theory, 38:910-917, 1992.
[49] S. Floyd and V. Paxson. "Dificulties in Simulating the Internet", IEEE/ACM Trans. On Networking, Vol. 9, N. 4, August 2001.
[50] V. Frost and B. Melamed. "Traffic Modeling for Telecommunications Networks". IEEE Commun. Mag.32(3):70-81, 1994.
[51] Y. Gao, G. He and J. Hou. "On Exploiting Traffic Predictability in Active Queue Management", IEEE Infocom 2002, New York, June 2002
[52] Y. Gao, G. He and J. C. Hou. "On Leveraging Traffic Predictability in Active Queue Management", Technical report,Department of Electrical Engineering, The Ohio State University, 2002
[53] A. Gilbert, W. Willinger and A. Feldman. "Scaling analysis of conservative cascades with application to network traffic". IEEE Trans. Information Theory, 45(3):971-991, 1999.
[54] F.W.Glover and M.Laguna. "Tabu Search" Kluwer Academic, 1998.
[55] G. Grimmet and D. Stirzaker. "Probability and Random Processes",second edition, Oxford Science Publications, NY, 1995.
[56] G. Gripenberg and I. Norros, "On the prediction of fractional Brownian motion," Journal of Applied Probability, vol. 33, pp. 400-410, 1996.
[57] T. Gyires, "Using Active Networks for Congestion Control in High-Speed Networks with Self-Similar Traffic", IEEE Intl. Conf. On Systems, Man, and Cybernetics, 2000, Vol. 1.
[58] O. Haggstrom "Finite Markov Chains and Algorithmic Applications", Cambridge University Press, 2002.
[59] T. Hagiwara, H. Doi, H. Tode and H. Ikeda. "High-Speed Calculation Method of the Hurst Parameter Based on Real Data". LCN 2000.
[60] G. He, Y. Gao J. Hou and K. Park. "A case for exploiting selfsimilarity of Internet traffic in TCP Congestion Control", Technical report, Department of Electrical Engineering, The Ohio State University, 2002
[61] D. Heyman and T. Lakshman. "What are the Implications of LRD for VBR Video Traffic Engineering?" IEEE/ACM Trans. On Networking, Vol. 4, N. 3, June 1996.
[62] D. Heyman and D. Lucantoni. "Modeling multiple IP traffic streams with rate limits". In Proceedings of the 17th International Teletraffic Congress, Brazil, December 2001.
[63] P. Huang, A. Feldmann and W. Willinger. "A Non-intrusive, Wavelet-based Approach To Diagnosing Network Performance Problems". Proceeding of ACM SIGCOMM Internet Measurement Workshop 2001, San Francisco, November 2001
[64] J. Hui. "Resource Allocation for Broadband Networks", IEEE Journal on Selected Areas in Communications, Vol. 6, Number 12, December 1988.
[65] IEEE Journal on Selected Areas in Communications, Special issue on Telecommunication Network Design and Planning, Volume 7, Number 8, 1989.
[66] Internet Traffic Archive. BC_pAug89, http://www.acm.org/sigcomm/ITA/index.html.
[67] S. Kauffman. "The origins of order: self organization and selection in evolution". Oxford University Press, NY, 1993.
[68] L. Kleinrock. "Queueing Systems. Vol. I: Theory. Vol.II:Computer Applications", John Wiley and Sons, NY, 1976.
[69] A. Kulkarni and S. Bush. "Network management and Kolmogorov complexity". IEEE Openarch, 2001
[70] R. La and V. Anantharam. "Optimal Routing Control: gametheoretic approach". 1998 CDC Conference, 1998.
[71] W. Leland, M. Taqqu, W. Willinger and D. Wilson. "On the self-similar nature of Ethernet Traffic". IEEE/ACM Trans. Networking, 2:1-15, 1994.
[72] R. Lewin. "Complexity: life at the edge of chaos". McMillan, NY, 1992.
[73] S. Ma and C. Ji. "Modeling Heterogeneous Network Traffic in Wavelet Domain". IEEE/ACM Trans. Networking, 9(5):634-649, 2001.
[74] B. Mandelbrot and J. VanNess. "Fractional Brownian Motions, Fractional Noises and Applications". SIAM Rev., 10:422-437, 1968.
[75] D. Manolakis, V. Ingle and S. Kogon "Statistical Signal Processing", McGraw-Hill, 2000.
[76] I. Marshall and C. Roadknight. "Adaptive management of an Active Service Network". BT Technol J Vol 18 No 4, pp.78-84, October 2000.
[77] G. McLachlan and T. Krishnan "The EM algorithm and estensions", John Wiley, 1997.
[78] B. Melamed, "An Overview of the TES Process and Modeling Methodology", Performance Evaluation of Computer and Communication Systems, Lecture Notes in Computer Science, Springer-Verlag, 1999
[79] J. Mendes and S. Dorogovtsev. Evolution of networks: From biological nets to the Internet and WWW. Oxford University Press, NY, 2003.
[80] M.Michelle "An introduction to genetic algorithms" MIT Press,Cambridge, MA, 1998
[81] M. Neuts "Matrix-Geometric Solutions in Stochastic Models", Dover Publications, NY, 1994.
[82] I. Norros. "On the Use of Fractional Brownian Motion in the Theory of Connectionless Networks". IEEE J. Selected Areas in Commun. 13(6):953-962, 1995
[83] T. Ohira and R. Sawatari. "Phase transition in computer network traffic model". Physical review, vol. 58, pp. 193-195, 1998.
[84] K. Park and W. Willinger. "Self-Similar Network Traffic and Performance Evaluation". John Wiley and Sons, New York, 2000.
[85] K. Park and W. Willinger "Self-Similar Network Traffic: An Overview". In "Self-Similar Network Traffic and Performance Evaluation", K. Park and W. Willinger, editors. John Wiley and Sons, New York, 2000.
[86] M. Parulekar and A. Makowski. "M/G/¥ Input Processes". Proc. IEEE Infocom'97, 1997.
[87] V. Paxson and S. Floyd. "Wide-Area Traffic: The Failure of Poisson Modeling". IEEE/ACM Trans. Networking, 3:226-244, 1995.
[88] Petropulu, A. and Nowak, R. "Signal Processing for Networking". IEEE Signal Processing Magazine, May 2002
[89] M. de Prycker "Asynchronous transfer mode solution for BISDN" Ellis Norwood, 1991.
[90] P. Ranjan, E. Abed and R. La. "Nonlinear Instabilities in TCP- RED". IEEE Infocom'2002.
[91] E. Rathgeb. "Modeling and Performance Comparison of Policing Mechanisms for Broadband Networks", IEEE Journal on Selected Areas in Communications, Vol. 9, Number 4, April 1991.
[92] V. Ribeiro, R. Riedi, et al. "Multiscale Queuing Analysis of Long-Range-Dependent Network Traffic", Submitted to IEEE Transaction on Networking, 2002.
[93] R. Riedi, et. al. "A Multifractal Wavelet Model with Application to Network Traffic". IEEE Trans. Inf. Theory, 45(3):992-1018, 1999.
[94] R.Riedi, "Multifractal processes," Stochastic Processes and Applications, preprint, 1999.
[95] A. Riska "Aggregate matrix-analytic techniques and their applications", Computer Science PhD dissertation Research, College of Virginia, 2002.
[96] J.Roberts "Traffic Theory and the Internet", IEEE Communications Magazine, January 2001.
[97] J. Roberts "Insensitivity in IP Networks Performance", IPAM Workshop, 2002
[98] M. Schwartz. "Telecommunication Networks: Protocols, Modeling and Analysis". Prentice Hall, N.Y. 1989.
[99] M. Schwartz. "Broadband Integrated Networks", Prentice Hall, NJ, 1996.
[100] S. Shenker and J. Wroclawski "General characterization parameters for integrated service network elements", RFC 2215, IETF, September 1997.
[101] Y. Shu, Z. Jin, L. Zhang, L. Wang and O. W. W. Yang, "Traffic prediction using FARIMA models", ICC'99, vol. 2, pp. 891-895, 1999.
[102] R.V.Sole and S. Valverde. "Information transfer and phase transition in a model of internet traffic". Physica A, vol. 289, pp. 595-605, 2001
[103] R.Srikant. "Control of Communication Networks". In "Perspectives in Control Engineering", T. Samad, Editor. IEEE Press, Piscataway, NJ, 2000.
[104] R. Syski "Introduction to congestion theory in telephone systems", Oliver and Boyd, Edinburgh, 1960
[105] Y. Takahashi, et.al. "ARIMA Model's Superiority over f-ARIMA Model", ICCT2000.
[106] A. Tannenbaum "Computer Networks", 4th edition, Prentice Hall, 2002
[107] M. Taqqu, W. Willinger and V. Teverovsky. "Estimators for Long-Range Dependence: An Empirical Study". Fractals 3(4):785-798, 1995.
[108] D. Tennenhouse et.al. "A survey of ActiveNetwork research". IEEE communications Magazine, vol. 35, No. 1, January 1997.
[109] A. Tewfik and M. Kim. "Correlation structure of the discrete wavelet coefficients of fractional brownian motion". IEEE Trans. Info. Theory, 38:904-909, 1992.
[110] J.F.Traub and A.G.Werschulz. "Complexity and Information", Cambridge University Pres, Cambridge, UK, 1999.
[111] Y. Tsang, M. Coates and R.Nowak. "Nonparametric Internet tomography". IEEE International Conference on Signal Processing, Vol. 3, 2002, pp. 2045-2048.
[112] B. Tsybakov and N. Georganas. "Self-Similar Processes in Communications Networks". IEEE Trans. Inf. Theory, 44(5):1713-1725, 1998.
[113] T. Tuan and K. Park. "Congestion control for self-similar network traffic". In "Self-similar network traffic and performance evaluation", edited by K. Park and W. Willinger, John-Wiley and sons, 2000.
[114] UCB/LBNL/VINT "Network Simulator ns-2", http://www.isi.edu/ nsnam/ns
[115] Y. Vardi "Network Tomography: Estimating Source-Destination Traffic Intensities from Link Data", Journal of the American Statistical Association, vol. 91, No. 433, 1996.
[116] F.Vega. "Aplicación del efecto de memoria a largo plazo en el control de congestión en redes de conmutación de paquetes". Tesis de Maestría, Universidad Distrital, 2003.
[117] F. Vega y M. Alzate. "Determinacion de la Predecibilidad de Trazas de Tráfico Mediante Analisis de Recurrencia". Revista INGENIERIA, Universidad Distrital, 2003
[118] D. Veitch and P. Abry. "A Wavelet-Based Joint Estimator of the Parameters of LRD". IEEE Trans. Inf. Theory, 45(3):878- 897, 1999.
[119] A.Veres and M.Boda. "The Chaotic nature of TCP congestion control". IEEE Infocom'2000.
[120] J. Walrand "An Introduction to Queueing Networks", Prentice- Hall, NJ, 1988.
[121] W. Willinger, and V. Paxson, "Where Mathematics meets the Internet," Notices of the American Mathematical Society, vol. 45, no. 8, Aug. 1998, pp. 961-970.
[122] C. Weinstein. "Fractional Speech Loss and Talker Activity Model for TASI and for Packet-Switched Speech", IEEE Trans. On Comm. Volume 27, Number 11, november 1979.
[123] W. Willinger, M. Taqqu, R. Sherman and D. Wilson. "Self- Similarity Through High Variability: Statistical Analysis of Ethernet LAN Traffic at the Source Level". IEEE/ACM Trans. Networking, 5(1):71-86, 1997.
[124] W. Willinger and J. Doyle. "Robustness and the Internet: Design and Evolution". Caltech, Pasadena, 2002.
[125] I. Wokoma, L. Sacks and I. Marshall. "Biologically Inspired Models for Sensor Network Design". LCS 119, Springer Verlag, 2002
[126] F.Xue, "Modeling Analysis and Performance Evaluation for self-similar traffic." Ph.D. Dissertation, Tianjin University, June 1998.
[127] J. Yang and I. Lambadaris, "Effective Bandwidths for TES Processes", ITC 2001, Salvador de Bahia, Brazil.
[128] O. Yu and S. Khanvilkar "Dynamic adaptive QoS provisioning over GPRS wireless mobile links", ICC 2002
[129] J. Widmer, R. Denda and M. Mauve, "A Survey of TCP-Friendly Congestion Control", IEEE Network Magazine, june 2001
[130] T.Karagiannis, M.Molle, M.Faloutsos and A.Broido, "A Nonstationary Poisson View of Internet Traffic", IEEE Infocom 2004, Hong Kong, 2004.
[131] Ashwin Sridharan, Roch Guerin and Christophe Diot "Achieving Near-Optimal Traffic Engineering Solutions for Current OSPF/ IS-IS Networks", IEEE Infocom 2003, San Francisco, CA, 2003.
[132] Eric J. Anderson and Thomas E. Anderson "On the Stability of Adaptive Routing in the Presence of Congestion Control", IEEE Infocom 2003, San Francisco, CA, 2003.
[133] M. Alzate and J. Baras "Dynamic Routing in Mobile Wireless Ad Hoc Networks using Link Life Estimates", 38th Conference on Información Sciences and Systems, CISS'04, Princeton University, Princeton, NJ, March 2004, pp. 363-367.
[134] C. Perkins (editor). Ad Hoc Networking. Addison Wesley, 2001
Marco Aurelio Alzate Monroy
Ingeniero Electrónico de la Universidad Distrital en 1989 y Master en Ingeniería Electrica en la Universidad de los Andes 1991. Entre 1989 y 1992 fue docente-investigador en la División de Investigación del ITEC Telecom y luego se vinculó a la Facultad de Ingeniería de la Universidad Distrital donde actualmente se desempeña como profesor. En este momento adelanta su disertación doctoral en Ingeniería Electrica y de Computadores en la Universidad de Maryland USA.
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)