Los cinco sólidos geométricos y su expresión simbólica en el arte.

La geometría de la materia y los sólidos regulares: su relación con los procesos artísticos

Sri Aurobindo señala que los cinco sólidos geométricos simbolizan la base de las formas del mundo material, constituido por los cinco estados elementales de la materia que emanan de la energía primordial. Estos están compuestos por el éter, el aire, el fuego, el agua y la tierra, cada uno de los cuales forma “la base de una de las cinco propiedades sutiles de la Energía o Materia: el sonido, el tacto, la forma, el gusto y el olfato, los cuales constituyen el modo en que la mente-sentido percibe los objetos” (Aurobindo, 2011, p. 91). Estos cinco objetos de los sentidos, o cinco modos distintos de tomar consciencia a nivel sensorio del mundo, constituirían los cinco poderes que habrían sido desarrollados por la energía universal con el fin de relacionarse con todas las formas de las cosas que esta energía habría creado a partir de los cinco estados elementales. Estos últimos junto con las cinco relaciones sensoriales, a través de las cuales conocemos la Materia, darían lugar al despliegue de “lo que denominaríamos en el lenguaje moderno el aspecto objetivo de la existencia cósmica” (Aurobindo, 2011, p. 91). En la Gita, se recoge cómo actúan la Presencia y el Poder divinos en estas cinco condiciones elementales de la materia: “Yo soy el sabor en las aguas, el sonido en el éter, el perfume en la tierra, la energía de la luz en el fuego, y puede añadirse, para completar más, el tacto, o el contacto en el aire.” (Aurobindo, 2016, p. 20). La doctrina de los cinco elementos aparece en la tradición de la India. Se dice que habría sido estudiada por Buda y es tradicionalmente atribuida a Kapila, un sabio que vivió en el siglo VIII a. C. En esta tradición, los cinco elementos se asocian con los cinco sentidos: el éter es el elemento asociado al oído; el aire se relacionaría con el elemento del tacto; el fuego con la vista; el agua con el gusto y la tierra con el olfato. En cambio, en Occidente, desde la época de Empédocles, quien era contemporáneo de Buda “sólo hemos oído hablar de cuatro elementos: fuego (que es caliente y seco), aire (que es caliente y húmedo), agua (que es frío y húmedo) y tierra (que es frío y seco). Los sistemas difieren, sin embargo, proceden de la misma raíz” (Campbell, 1991, pp. 511-512).

G. Bachelard señala cómo en la búsqueda de nuestra imaginación aparecen los cuatro elementos como unificadores del mundo. Estas imágenes van creciendo hasta alcanzar lo universal, de manera que cuando soñamos estar “ante una fuente, la imaginación descubre que el agua es la sangre de la tierra, que la tierra tiene una profundidad viva” (Bachelard, 2019, p. 265). En la alquimia, Adán se identifica con la prima materia, ya que los dos estarían formados por los cuatro elementos o que de ellos surgen estos elementos, así en la Turba dice: “De los cuatro elementos fueron creados nuestro padre Adán y sus hijos.” (como se citó en Jung, 2007,

p. 374) Mientras que en el Livre des Balances menciona como en el Pentateuco hay una descripción que relata como en la creación del cuerpo del primer ser se compuso de cuatro cosas que se transmitían por herencia, siendo éstas “el calor, el frio, la humedad y lo seco. En efecto, fue compuesto de tierra y agua, de un espíritu y un alma. La sequedad le viene de la tierra; la humedad, del agua; el calor, del espíritu; y el frio, del alma” (como se citó en Jung, 2007, p. 374).

Platón en el Timeo narra como el Demiurgo que habría configurado el mundo físico, crea el orden a partir del caos primordial mediante los cinco sólidos regulares: “El ordenamiento según número y forma en un plano superior culminó en la disposición deseada de los cinco elementos en el universo físico. Las formas y números esenciales actúan entonces como interconexión entre el reino superior y el inferior.” (Lawlor, 1993, p. 96) Estos cinco sólidos geométricos estarían constituidos por el tetraedro que representa el elemento fuego y está conformado por cuatro vértices y cuatro caras que son triángulos equiláteros. El octaedro que simboliza el aire, formado por seis vértices y ocho triángulos equiláteros. El cubo que encarna a la tierra con ocho vértices y seis caras cuadradas. El icosaedro imagen del elemento agua con doce vértices y doce caras que son triángulos equiláteros y el dodecaedro, formado por doce pentágonos regulares y veinte vértices que representa el éter. A. Daniélou dice como el símbolo del éter se correspondería con el oído debido a su forma laberíntica, teniendo este símbolo relación con “la evolución del espacio y el tiempo, de la expansión del universo, es la espiral que, partiendo del punto inicial, se despliega indefinidamente en movimientos circulares, como el propio universo” (Daniélou, 2012, p. 270).

Luca Pacioli en la Divina proportione señala como al igual “que Dios insufla vida en el cosmos a través de la quinta esencia, en los cuatro elementos terrenales y en todas las cosas de la naturaleza” (Hemenway, 2008, p. 109), también la divina proporción introduce vida en el dodecaedro. Esta última figura es la forma geométrica del universo como atestiguan las investigaciones actuales de Jean-Pierre Luminer y su equipo del Observatorio de Paris que afirman como el universo es finito y tendría forma de dodecaedro: “Este espacio cerrado mediría unos 30.000 millones de años luz de un lado a otro.” (Hemenway, 2008, p. 109) Esta teoría coincide con Platón que “menciona cierta <quinta composición> utilizada por el creador en su formación del universo. Así pues, el dodecaedro vino a estar asociado con el quinto elemento, el éter (prana)” (Lawlor, 1993, p. 96). Este último concepto es recogido por Aristóteles que decía cómo la Luna, los planetas y las estrellas residen en un reino celestial compuesto por un material distinto al de nuestro mundo y cómo la naturaleza al aborrecer el vacío no podría contener espacios celestiales que estuviesen desocupados: “Así que la consistencia requería un quinto elemento, o quintaesencia, diferente de tierra, aire, fuego y agua para rellenar el reino celeste. Los dodecaedros, por tanto, encuentran su lugar como los átomos de la quintaesencia, o el éter.” (Wilczek, 2016, p. 56) Esta concepción dodecaédrica de Platón contenida en el universo aparece representada en la obra de Dalí titulada La Última cena (1995), en esta pintura se pueden apreciar varios pentágonos que envuelven espacio arquitectónico donde Cristo está celebrando el sacramento eucarístico por lo que la escena se desarrollaría dentro de un gran dodecaedro como imagen simbólica del universo y que Dalí utiliza “para expresar una conexión cósmica que de otro modo sería difícil de pintar en un lienzo” (Wilczek, 2016, p. 303).

F. Wilczek llama la atención de como Platón propuso una teoría geométrica de los átomos y el universo que basó en las cinco formas simétricas o sólidos regulares que inspiraría más tarde a Euclides o Kepler, anticipando que los átomos pueden tener subcomponentes que no existen normalmente como objetos separados, sino formando parte de objetos más complejos que se materializan en la actualidad en los quarks y gluones que se encuentran en el interior de los núcleos atómicos. Así las teorías de Platón relativas a los sólidos regulares coincidirían con las ideas más vanguardistas de la ciencia actual, ya que estas figuras geométricas tienen la capacidad de capturar mediante la intuición, la idea de una “regularidad ideal para los <átomos> planos” (Wilczek, 2016, p. 49), por lo que estos polígonos regulares pueden servir para representar conceptualmente a los átomos y así poder construir “unas ideas de orden y simetría cada vez más ricas y más complejas” (Wilczek, 2016, p. 49). En este sentido E. Pérez de Carrera afirma como la realidad aparencial estaría constituida por un mosaico basado en formas geométricas a los que describe como:

diminutos y distanciados núcleos de micromateria, almidonados por una red energética que define órbitas y trazados perfectos. Nos engaña la imagen de como los hombres peregrinan como seres perdidos, desperdigados y errantes, buscando afanosos completar el dibujo desconocido del que se ignora hasta la propia forma. (Pérez de Carrera, 2004, p. 127)

Las teorías de Platón han inspirado a autores como Rupert Sheldrake que afirma como existiría una resonancia interna entre los campos de estructuras simétricas de los organismos, siendo esta autorresonacia comparable con las ideas formas platónicas que constituiría una memoria presente en la naturaleza que autoestabiliza la forma de la materia mediante los “campos mórficos”, estos serían como estructuras organizativas invisibles que moldean no sólo a los organismos vivos, sino también la naturaleza de cristales, moléculas y átomos, conteniendo información recopilada de toda la historia y la evolución pasada. Este bioquímico cree que al igual que las formas atómicas se pueden considerar desde el punto de vista platónico, el sistema periódico de elementos ya preexistiría antes del Bing Bang, de manera que en el transcurso de la evolución del universo los distintos tipos posibles de la forma atómica fueron consiguiendo una existencia material: “Es como si la Formas eternas de los átomos estuviesen esperando la ocasión de ser actualizadas en el tiempo y el espacio.” (Sheldrake 2006, p. 107) Estas teorías coinciden con los antiguos pensadores de la India que tenían en cuenta según Sri Aurobindo no sólo la acción cuantitativa de la Naturaleza (matra), es decir el aspecto cuantitativo de sus operaciones además de la dependencia que la Naturaleza posee en relación con las combinaciones y las disposiciones cuantitativas para la creación de formas, sino que también contemplaban que la Naturaleza tiene un poder ejecutivo e ideativo que sería innato y con poder para disponer las cosas según la cualidad de su ser y de su energía (guna swabhava), siendo el determinante primario que subyacería a la totalidad de las disposiciones cuantitativas exteriores, de manera que existe una oculta capacidad ideativa de la energía indivisa o universal (vijana) “que fija las matemáticas y decide los resultados de estas disposiciones más exteriores” (Aurobindo, 2016, p. 201).

De esta energía no manifestada habría salido la evolución objetiva de los cinco estados elementales de la materia, junto con “la evolución subjetiva de los sentidos,de la inteligencia y del ego” (Aurobindo, 2016, p. 186). Para Sri Aurobindo esta Idea suprema en el espíritu es la que concibe estos procesos y pone en uso de estas estrategias:

Solamente el Espíritu, que por el poder de su idea-ser y de su idea-fuerza, denominadas mahat y vijana, establece estas condiciones, no está de ese modo determinado ni sometido a limitación alguna, ya sea de cualidad o de cantidad, porque su infinitud inmensurable e indeterminable es superior a los modos que él desarrolla y utiliza para su creación. (Aurobindo, 2016, p. 201)

En el mito egipcio de Nun describe como el primer volumen creado fue a partir del océano cósmico o “el espíritu-espacio puro, indiferenciado, sin límites ni forma” (Lawlor, 1993, p. 96). Esta potencialidad en estado puro es impulsada para que se contraiga y se coagule a través de la semilla y la voluntad de Atón, el creador que esta implícita en Nun, el cual adquiere un volumen al distinguirse y crearse a sí mismo iniciándose así la creación. Este primer volumen establecido a partir de Nun poseía las formas esenciales de los cinco sólidos platónicos los cuales “tienen sus aristas y todos sus ángulos internos iguales” (Lawlor, 1993, p. 96). Según A. Speiser la construcción de los cinco sólidos regulares será un tema geométrico fundamental en Grecia como vemos en el sistema deductivo de la geometría griega expuesta “de forma canónica por Euclides en sus Elementos” (Weyl, 1990, p. 61), mientras que en el Renacimiento siguen estando de boga estas cuestiones como se refleja en la colección de dibujos del Códice Atlántico de Leonardo donde representa los cinco sólidos regulares platónicos y los trece semirregulares, apareciendo también esta geometría en el tratado la Divina Proportione de Luca Paccioli en el cual encontramos la ilustración llevada a cabo por Leonardo de las teorías platónicas sobre “las proporciones, de la función de la Sección Dorada como vínculo entre los 5 cuerpos platónicos” (Ghyka, 1998, p.106). El Libro Segundo de Alberto Durero presta especial atención al tema de la cuadratura del círculo y a la construcción de polígonos regulares desarrollables a partir del cuadrado y el triángulo equilátero además del pentágono o el eneágono. Según E. Panofsky en la Edad Media este tipo de desarrollos geométricos tenía una gran aplicación práctica como ocurre en la decoración islámica y la gótica, planteándose más tarde este tipo de cuestiones con la invención de armas de fuego o la edificación de fortificaciones, las cuales precisaban de la construcción de todo tipo de polígonos regulares por lo que Durero “pasa en seguida a desarrollar éstos en forma de esquemas de tracería y a combinarlos a modo de <pavimentos> que se anticipan a la <Congruentia figurarum harmonicarum> de Kepler en el libro Segundo de sus Harmonices mundo libri V” (Panofsky, 1989, pp. 265-266).

R. Lawlor señala como Luca Paccioli impartía la disciplina llamada corpo transparente a los artistas de su época entre los que se encontraban Leonardo, Brunelleschi o Fillide Giorgi, esta enseñanza se basaba en la contemplación de los cinco volúmenes regulares mediante la colocación de los sólidos uno dentro de otro mediante un material que transparentaba estas formas geométricas. Los sólidos se dibujaban clásicamente de manera que estuviesen contenidos dentro de nueve círculos concéntricos donde cada sólido tocaba la esfera que circunscribía el sucesivo sólido que estaba inscrito en él. Maurits Cornelis Escher representa estas figuras en su obra titulada Cuatro sólidos regulares de 1961, diciendo como los sólidos platónicos simbolizan de forma inigualable nuestra aspiración hacia la armonía y el orden,aunque “al mismo tiempo, su perfección nos infunde una sensación de impotencia” (como se citó en Odifreddi, 2017, p. 32). Escher investigó la teselación del espacio mediante el relleno de todo el espacio con estos solidos en sus obras División cubica del espacio de 1952 y Platelmintos de 1959.

Los sólidos platónicos serían los únicos sólidos regulares de tres dimensiones, ya que todos tienen aristas iguales y cada una de sus caras es un polígono regular. Todos sus vértices serían equidistantes del centro, no existiendo otra posibilidad siendo los únicos sólidos regulares finitos, ya que, si “intentamos juntar más de seis triángulos equiláteros, más de cuatro cuadrados, o más de tres de cualquiera de los polígonos de más lados, nos quedamos sin espacio: simplemente, no podemos acomodar los ángulos acomodados” (Wilczek, 2016, p. 50). P. Odifreddi señala como Teeteto descubrió como estas figuras tendrían el mismo número de caras en cada vértice de forma que todas sus caras son el mismo polígono regular: “El cubo y el octaedro se llaman duales porque uno tiene tres caras cuadradas en cada vértice y el otro, cuatro caras triangulares.” (Odifreddi, 2017, p. 32) Escher decía sobre este hecho como no existiría una fusión entre un cubo y el octaedro, pero no descartaba que se produjera, por lo que a lo largo de su obra siempre buscó de forma incansable este tipo de fusiones estudiando la lacería de los muros de la Alhambra, como el mismo escribe en 1941: “El problema de como encajar figuras congruentes… comenzó a intrigarme aún más tras mi vista a España en 1922.” (como se citó en Costa y Grasselli, 2017, p. 16) La teselación islámica basada en el pentágono será frecuente, así la estrella pentagonal cóncava aparece en la decoración de los baños, palacios y mezquitas, convirtiéndose “en el tema central del desarrollo de toda la decoración arquitectónica como puede ser un artesonado de madera o una pared de azulejos” (de la Torre Bravo, 2003, p. 125).

En el Islán la repetición de la estrella desarrolla simbólicamente la imagen primordial de que “la multiplicidad demuestra la Unicidad de Dios” (de la Torre Bravo, 2003,p. 125).

En la actualidad artistas como Monir Shahroudy Farmanfarmaian llevará a cabo una obra inspirada en este tipo de teselación como vemos en su obra titulada Grupo 4 [Serie combertible] de 2010 donde presenta una combinación de un patrón geométrico basado en el pentagrama, diciendo sobre la cúpula con espejos de la mezquita y monumento funerario Shāh Chérāgh del siglo XIV: “Era un universo en sí misma, la arquitectura se había transformado en espectáculo, todo era movimiento y flujo de luz, todos los sólidos se habían fracturado y disuelto en la brillantez del espacio, en la oración.” (como se citó en Straine, 2020, p. 100) Esta coleccionista de arte iraní desarrolla su obra mediante vidrio cortado donde fusiona la tradición persa del mosaico con una geometría contemporánea de carácter abstracto utilizando patrones geométricos como vemos en su obra Sunrise de 2015 (Fig. 1).

Figura 1: Monir Shahroudy Farmanfarmaian, Sunrise 2015. Fotografía de Aziza.

También el artista estadounidense Matt Shlian investiga este tipo de fusiones mediante las formas geométricas resultantes del plegado del papel, este creador realiza su obra mediante dobleces iniciales que le llevan a retículas intrincadas de formas tridimensionales creando así esculturas cinéticas. Estas investigaciones se traducen en su colaboración con la Universidad de Michigan donde trabaja a nano escala con estructuras de papel y micropliegues para visualizar entre otras cosas la división celular o desarrollar a partir de esta técnica células solares, convirtiéndose así el papel en una metáfora de los principios que rigen la ciencia. Otros artistas contemporáneos como Olafur Eliasson efectúa su obra mediante una red de casillas dodecaedricas como vemos en su obra titulada Quasi brick wall (2002) ubicada en la Fundación NMAC (Fundación Montenmedio Contemporánea) en Cádiz (España).

Ya en los años sesenta artistas como Mary Martín presenta relieves en metal donde juega con el aspecto reflectante del material mediante retículas de elementos geométricos cuadrangulares como vemos en su obra titulada Ritmos compuestos (1966) realizada en acero y aluminio. El pintor francés François Morelletç se interesa por la teselación en sus pinturas coloristas en obras como Mosaico azul, verde, amarillo, naranja, rojo de 1953. En esta misma época el pintor y escultor estadounidense Ellsworth Kelly lleva a cabo su lienzo titulado Colores para una pared grande de 1951 basado en la repetición patrones geométricos cuadrados (Fig. 2). Mientras que Sol LeWitt elige el cubo, símbolo más básico del mundo visible de las formas volumétricas como modulo constructivo en su obra titulada Construcción cubista: diagonal 4 esquinas opuestas, unidades 1 y 4 de 1971. En sus investigaciones sobre la figura del cuadrado vemos como lo representa junto con su diagonal como símbolo de “la extrema polaridad del universo, la unidad y la multiplicidad” (Lawlor, 1993, p. 31).

Figura 2: Ellsworth Kelly, Colores para una pared grande, 1951.

Figura 2. Ellsworth Kelly, Colores para una pared grande, 1951.

Fotografía de Ainhoa Díaz https://commons.wikimedia.org/wiki/File:Colors_for_a_Large_Wall_%28Ellsworth_Kelly,_1 951%29.jpg

M. Martínez Vela señala como solamente existen ocho teselados con polígonos regulares que fueron descubiertos por Kepler, los cuales estarían compuestos por diferentes combinaciones con las figuras geométricas del triángulo, del cuadrado, del hexágono, del octógono y del dodecágono, siendo condición previa que cada vértice debe estar rodeado por el mismo conjunto de formas. Los polígonos irregulares también pueden formar redes de mosaicos semirregulares mientras no dejen huecos entre ellos y no se superpongan como ocurre con el rectángulo, el rombo u otro cuadrilátero. Asimismo, el triángulo entraría también en este grupo “pues con dos iguales podemos formar un cuadrilátero. Además, se pueden usar otros polígonos tanto convexos como cóncavos” (Mártinez Vela, 2019, p. 19).

R. Lawlor afirma como los mosaicos semirregulares que permitirían dos tipos de vértice, forman la base de los patronos constructivos de gran parte de las tradiciones de las artes sagradas y decorativas como podemos ver en las decoraciones celtas e islámicas, apareciendo igualmente en la naturaleza en las estructuras celulares y en las cristalográficas. Mientras que el cinco es dominante en la estructura de las formas vivas, el seis y el ocho son más característicos de la geometría de las estructuras minerales e inanimadas. Todo sistema material fisicoquímico inorgánico como las formaciones cristalinas estaría regido por el principio de mínima acción o de Hamilton, que hace evolucionar el sistema hacia estados finales de equilibrio que convergerían en esquemas geométricos regulares de redes planas cuadradas o conjuntos cúbicos en el espacio, pudiendo converger además en el tipo exagonal mediante redes planas de triángulos o exágonos e incluso conjuntos cuboctaédricos en el espacio. El mundo inorgánico la simetría exagonal se correspondería con el “equilibrio inerte (cuyos cauces ideales son: relleno del plano o del espacio, isotropismo, periodicidad estática, yuxtaposición del mismo motivo intercambiable, sin dirección favorecida)” (Ghyka, 1968, pp. 54-55). Los sistemas materiales organizados que poseen vida como el ser humano, los vegetales o los animales pueden derogar “el principio de mínima acción” (Ghyka, 1968, p. 54) donde aparecen formas que se basan en el sistema pentagonal o asimétrico de la sección áurea:

El fenómeno causal de la asimetría es, en este caso, el crecimiento de los seres vivos, crecimiento que actúa de dentro hacia fuera, como por imbibición, turgencia, y no por aglutinación, como en los cristales, y en este crecimiento vivo tiende a producir formas sucesivas homotéticas, es decir, semejantes a sí mismas. (Ghyka, 1968, p. 54)

2. La sección áurea y los sólidos platónicos en el arte. M. C. Ghyka afirma como la arquitectura de la antigüedad contemporánea de la matemática pitagórica y de la religión de Eleusis se fundaba en diversas teorías como las basadas en las proporciones armónicas y las geométricas que se relacionaban a la década y a la tetracto junto con el estudio de los volúmenes, de los cinco cuerpos regulares, de los ritmos astronómicos y biológicos. El alemán E. Moessel señala como en la composición del arte de la Antigüedad hasta finales de la Edad Media no sería aritmética sino geométrica en la mayoría de los casos, teniendo los cuerpos platónicos un gran protagonismo tanto en la parte teórica como en la práctica, en las cuales habría una concepción de carácter cosmogónico que procedería de las diferentes particiones del círculo, ya que de estas segmentaciones angulares regulares del círculo derivarían a “sistemas de rectángulos triángulos, polígonos convexos y estrellados, que representan redes que tienen la forma y el significado de los sistemas de coordenadas” (como se citó en Ghyka, 1968, p. 110). Según M. C. Ghyka, esta geometría estaría como proyectada en el espacio, siendo estas ordenaciones geométricas los elementos composicionales tanto de la arquitectura como de la pintura y la escultura en bajorrelieve, señalando este autor como estas “particiones específicas del círculo y las razones numéricas que las caracterizan aparecen en las proyecciones planas de los cuerpos regulares inscritos en la esfera, tetraedro, octaedro, cubo, dodecaedro e icosaedro” (como se citó en Ghyka, 1968, p. 110), poniendo de ejemplo las investigaciones del arqueólogo Lund que estudió los planos de gran parte de las catedrales góticas, hallando en su composición el doble cuadrado y la sección áurea, figura geométrica que produciría en estos edificios un ritmo vivo y sutiles armonías, por lo que este autor llega a la conclusión de como existiría una “transmisión ininterrumpida, aunque por un número reducidísimo de iniciados, del esoterismo matemático platónico y neoplatónico y en particular de los trazados inspirados en el pentagrama y la sección áurea” (Ghyka, 1983, p. 218).

Según P. Hemenway habría una relación del dodecaedro con la sección áurea que se refleja en los pentágonos que constituyen las doce caras del dodecaedro: “Empezando por el pentágono, prolongando las líneas hasta formar una estrella de cinco puntas, las razones de la longitud de los segmentos lineales resultantes están todas basadas en Φ.” (Hemenway, 2008, p. 149). En las proporciones de los arcos perpiaños de la bóveda de la ojiva de Chartres, L. Charpentier ha comprobado cómo está basada en representación del hombre en la estrella de cinco puntas o pentagrama que se relaciona con el número áureo. Las dos puntas bajas de esta estrella inscrita en el círculo serían los centros de los arcos de círculo que forman los dos lados de la ojiva: “Estos arcos cortan el círculo en las dos puntas altas laterales.

La piedra angular está situada en la punta superior de la estrella.” (Charpentier, 1969, p. 56) Ya en Egipto encontramos esta concepción en la geometría del gran templo subterráneo de Osirión que personifica simbólicamente el mito de Osiris donde se representa su tumba cuya geometría se basa en la sección áurea y en el pentágono, simbolizando así la creencia de que el rey al morir se convertía en una estrella de cinco puntas. Esta estrella que surge del interior del pentágonosería “la configuración del hombre cósmico, el perfeccionador de la vida, la proporción áurea” (Lawlor 1993, p. 106). (Fig. 3)

Figura 3: Estrella de cinco puntas. Fuente: Imagen tomada del sitio web: https://publicdomainvectors.org/photos/1499541060.png

Figura 3. Estrella de cinco puntas. Fuente: Imagen tomada del sitio web: https://publicdomainvectors.org/photos/1499541060.png

La proporción áurea constituye la relación más esencial del universo “con la unidad, la división primera o primaria del uno” (Lawlor 1993, p. 46), siendo la única dualidad creativa que se puede dar dentro de la unidad, estando formada por tres términos como símbolo de la Santa Trinidad. Esa proporción trinitaria está relacionada con la consciencia perceptiva donde se integraría y se sintonizaría nuestro campo vibratorio externo y nuestro campo interior donde nos volveríamos conscientes “de que extraemos el objeto externo de la totalidad de nuestro espacio interior, fundiendo así la contemplación de uno mismo y el mundo” (Lawlor 1993, p. 45). Esta vivencia importante en el desarrollo evolutivo de la persona es lo que Sri Aurobindo llamó el “conocimiento por identidad”, una experiencia del mundo que en su naturaleza secreta sería un conocimiento directo e inmediato:

pero su carácter verdadero se nos oculta porque nos hemos separado por exclusión del resto del mundo, por la distinción entre nosotros como sujeto y todo lo demás como objeto, y nos vemos empujados a desarrollar procesos y órganos que nos ayuden a entrar nuevamente en comunión con todo lo que hemos excluido. (Aurobindo, 2008, p. 89)

R. Lawlow señala como en nuestra visión del ser humano como antropocosmos, la geometría sagrada se convierte en un cosmograma que nos revela “el drama de este nacimiento divino, y en el transcurso de todas las épocas de edificación de templos, la arquitectura sagrada basada en esta geometría ha sido un libro abierto que revela ese eterno drama” (Lawlor 1993,p.92).

Así en la India los templos y edificaciones de carácter sagrado “sigue viva la Vastupurushamandala, la tradición del diseño de los templos basado en el hombre cósmico” (Lawlor 1993, p. 92). La investigadora y divulgadora del arte indio, Bettina Baümer a través de su libro The Living Temple. Aesthetics in Śilpaśastras presenta mediante gran cantidad “de referencias a textos canónigos y ejemplos de diversas artes, una idea común: el carácter holístico de las artes vinculadas a lo sagrado en India” (como se citó en Fernández Gómez, 2021, p. 359). Para esta autora los cinco componentes de la planta de los templos de la India se

identifican con los cinco elementos cósmicos, siendo de gran importancia en esta arquitectura la montaña cósmica que tendría que ver con el cuerpo sutil. Según R. Lawlor, esta geometría sagrada sería inherente al cuerpo humano como vemos en las primeras etapas de la división celular donde se perciben todos los sólidos geométricos regulares. En la metafísica hindú cada uno de estos sólidos regulares sería el símbolo de las distintas capas invisibles y sutiles que envuelven al cuerpo humano y que además actúan sobre él, siendo estas asociaciones las siguientes:

El pequeño icosaedro central con la perfección final del cuerpo en su manifestación física; el octaedro con el cuerpo físico o nutricio (sede de la mente instintiva); el tetraedro con el cuerpo etéreo o energético (sede de la facultad mental intuitiva); el cubo con el cuerpo- mente de la “razón pura”; el dodecaedro con el cuerpo conocimiento (sede del innato conocimiento por identidad); el icosaedro con el cuerpo éxtasis (el de la unión meditativa). (Lawlor, 1993, p. 108)

Las tres raíces sagradas y los sólidos geométricos: la Vesica Piscis en las artes visuales. En la geometría sagrada la relación existente entre lo fijo y lo volátil, es decir entre la proporción y la progresión sería una clave fundamental de manera que todo lo manifiesto tanto en el mundo físico como en el mundo mental y de las imágenes pertenece “al incesante flujo de las progresiones en constante cambio; es solo el reino no manifiesto de los principios el que es inmutable” (Lawlor, 1993, p. 27). Platón en el Timeo relata que cuando el Demiurgo emprendió la unión del cuerpo del mundo, lo creó de fuego y tierra, buscando en esta operación un lazo intermedio para que esta unión fuera duradera: “La proporción (geométrica progresiva) es, por su esencia, lo que mejor puede hacerlo.” (como se citó en Jung, 1962, p. 237). C. G. Jung señala en relación con esta cuestión como la triada sería “un paso adelante del uno hacia su percepción. Tres es el <uno> vuelto perceptible, que sin la desaparición de la antítesis del <uno> y el <otro> hubiera permanecido en un simple estado de determinabilidad” (Jung, 1962, p. 237). El tres aparece como un sinónimo apropiado que representa el proceso del devenir temporal siendo una imagen paralela “de la autorrevelación de Dios como Uno absoluto en el despliegue del tres” (Jung, 1962, p. 237). Esta relación de la tríada con el Uno se puede formular mediante “el triángulo equilátero: a = b =c, o sea, por medio de la identidad de los tres, en el cual, en cada uno de los ángulos, que tienen una designación diferente, se da en cada caso la triada total” (Jung, 1962, p. 237). Según C. G. Jung para la realidad física se necesitarían “tres dimensiones y por lo tanto dos términos intermedios” (Jung, 1962, p. 238), ya que como dice el Timeo: “Si el cuerpo del mundo hubiera tenido solo una superficie plana, sin profundidad, hubiera bastado un solo término intermedio para unirlo con los otros dos.” (como se citó en Jung, 1962, p. 238)

R. Lawlor señala como este concepto trinitario de nuestra naturaleza se manifiesta en la geometría sagrada que tendría como elementos principales al círculo y al cuadrado de manera que en el acto de dividirse darían lugar a las tres raíces sagradas o “trinidad de principios generativos” siendo todo lo que se necesita para la formación de los cinco sólidos regulares, los cuales constituirían la base de todas las formas volumétricas: “Las raíces se consideran poderes generativos, o principios dinámicos mediante las cuales las formas aparecen y se transforman en otras formas.” (Lawlor, 1993, p. 36) Según este autor la raíz cuadrada de dos, la raíz cuadradade tres y la raíz cuadrada de cinco en todas las tradiciones de la geometría sagrada serían poderes que constituyen metáforas geométricas que representan “el momento suprarracional de la transformación” (Lawlor, 1993, p. 31).

Este instante transformador de carácter suprarracional se llevaría a cabo mediante tres procesos generales, siendo uno el generador que se simboliza por la raíz cuadrada de dos, el formativo que se simboliza por la raíz cuadrada de tres y el regenerativo que se simboliza por la raíz cuadrada de cinco cuya función se corresponde con phi (Φ) o número áureo. La raíz cuadrada de dos dividiría la superficie del cuadrado siendo un medio a través del cual la sección áurea o phi (Φ) actuaría en la naturaleza, Así la división de la altura del cuerpo humano basado en las proporciones armónicas de la raíz cuadrada de dos, tomando la altura total como unidad daría lugar a la localización de una serie de centros vitales que en la práctica zen se llaman “hará (vientre), un sutil centro físico, justo debajo del ombligo” (Lawlor, 1993, p. 30). En esta vía iniciática este centro se asocia con la meditación cuyo fin es producir una enraización mediante la potenciación del autocontrol y de la autotransmutación. Esta función también estaría presente en el tantrismo donde se trata de elevar la raíz o serpiente para que preste su energía a los centros glandulares principales de transformación como escribe Sri Aurobindo en su poema Savitri, Libro VII, Canto V:

Mas cuando sus pies habían tocado la trémula flor,

un poderoso movimiento estremeció su espacio interior como si un mundo fuera sacudido y encontrara su alma:

desde la noche sin alma y sin mente de lo Inconsciente una flamígera Serpiente ascendió liberada del sueño.

Se levantó henchiendo sus anillos y erguida

y ascendiendo poderosa tempestuosamente en su camino tocó sus centros con su llameante boca:

como si un ardiente beso hubiera interrumpido su sueño,

florecieron y rieron colmados de luz y de gozo. (Aurobindo, 2017, p. 528)

La raíz cuadrada de dos constituye la función geométrica que representa el símbolo universal de la raíz, la cual poseería propiedades divisorias y transformadoras que se consideran igualmente propiedades de unión y sinterización debido a que estos principios demuestran la mayoría de las veces los dos extremos de esta oposición. Estos principios de la raíz se simbolizan en la función intestinal del ser humano que transforma la sustancia alimenticia en energía, expresándose también en las circunvoluciones del cerebro, ya que, como los intestinos, estos giros del cerebro transforman “la materia prima mental, amorfa, en razón y entendimiento” (Lawlor, 1993, p. 30). El poder fálico o procreador también estaría implícito en la raíz, ya que la función sexual al igual que la función digestiva, operan para cuidar nuestro arraigo al mundo físico, siendo nuestros procesos mentales como procesos de “digestión, asimilación y transmutación” (Lawlor, 1993, p. 92).

La raíz cuadrada de dos constituye la función geométrica que representa el símbolo universal de la raíz, la cual poseería propiedades divisorias y transformadoras que se consideran igualmente propiedades de unión y sinterización debido a que estos principios demuestran la mayoría de las veces los dos extremos de esta oposición. Estos principios de la raíz se simbolizan en la función intestinal del ser humano que transforma la sustancia alimenticia en energía, expresándose también en las circunvoluciones del cerebro, ya que, como los intestinos, estos giros del cerebro transforman “la materia prima mental, amorfa, en razón y entendimiento” (Lawlor, 1993, p. 30). El poder fálico o procreador también estaría implícito en la raíz, ya que la función sexual al igual que la función digestiva, operan para cuidar nuestro arraigo al mundo físico, siendo nuestros procesos mentales como procesos de “digestión, asimilación y transmutación” (Lawlor, 1993, p. 92).La raíz cuadrada de cinco representa el cruce de dos mundos o extremos cósmicos mediante el cuadrado superior imagen del espíritu y el cuadrado inferior imagen del cuerpo de manera que las formas de relacionar ambos mundos o los principios mediadores de éstos se simbolizanmediante el “principio crístico” (Lawlor 1993, p. 37). R. Lawlor llama la atención de como la raíz cuadrada de tres aparece mediante dos configuraciones geométricas de gran importancia que tendrían un carácter formativo, una configuración es la Vesica Piscis y la segunda sería el cubo cortado por la diagonal. La raíz cuadrada de tres dividiría el volumen-forma del cubo, esta última raíz estaría relacionada con el proceso formativo, siendo este hecho más claro cuando vemos la vinculación de la vesica y la raíz cuadrada de tres con el hexágono que constituiría la simetría del orden para la medida no solo de la tierra, sino también “la medida del tiempo mediante 360º del de los cielos)” (Lawlor 1993, p. 35).

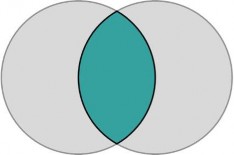
Todos los polígonos regulares se pueden obtener mediante una sucesión de construcciones a partir de la vesica la cual sería generadora de forma. Así las raíces dos y cinco se pueden derivar de este “cosmograma de la vesica, ya que no hay simbolización sintética de la unidad que no evoque todos los principios básicos” (Lawlor 1993, p. 35). La Vesica Piscis sería una vejiga (vesica) que al llenarse de aire tomaría la forma de pez (piscis) constituyendo un símbolo geométrico central en la mística medieval como podemos ver en la portada románica de la Iglesia de San Juan de Moarves de Ojeda (Palencia) del último tercio del siglo XII donde aparece el Pantocrátor dentro de la mandorla mística rodeado por los cuatro evangelistas que se remontan a las antiguas representaciones egipcias del dios Horus y sus cuatro hijos (Fig. 4-5).

Figura 4: Vesical aplanada. https://upload.wikimedia.org/wikipedia/commons/thumb/a/a7/Vesica_piscis_circles.svg/1280 px-Vesica_piscis_circles.svg.png

Figura 5: Detalle de la portada románica de la Iglesia de San Juan de Moarves, Ojeda (Palencia), último tercio del siglo XII.

En estos mandalas, según R. Lawlor, la Vesica Piscis se compone de dos círculos que tendrían por centro respectivamente un punto de la circunferencia del otro círculo, siendo una de las primeras formas que se obtienen a partir de círculos. En ella se pueden ver cómo quedan definidos en el interior de la vesica, dos triángulos equiláteros y si se añade un tercer círculo al lado contrario del primer círculo, quedan definidos los seis puntos de un hexágono regular, de manera que los círculos alumbrarían triángulos y hexágonos regulares. Esta figura ha sido motivo de inspiración de artistas del siglo pasado como vemos en la serie de dibujos sobre la vesica realizada por el bailarín polaco Vaslav Nijinsky entre 1917 y 1920 titulada Figuras geométricas, apareciendo igualmente en Soy radio (1924) de la creadora autodidacta Jeanne Natalie Wintsch que representa mediante esta forma geométrica las frecuencias de onda invisibles que nos rodean. I. Müller-Westerman señala como en la parte central de este trabajo bordado con hilos de colores sobre fondo blanco se puede apreciar una serie de círculos y figuras geométricas que se cortan formando “un ojo en el que se entrelazan las informaciones que llegan” (Müller-Westermann, 2013, p. 48). Esta forma arquetípica vesical aplanada será numerosa asimismo en la obra de Hilma af Klint en su serie iniciada en 1907 donde ilustrará las cuatro edades del ser humano, caracterizándose por contener arquetipos muy recurrentes como los mandalas, los símbolos tríadicos, ruedas, arabescos, formas helicoidales, el ocho, configuraciones circulares de siete elementos, flores etc.; todo ello representado por colores puros y en grades formatos que envuelven al espectador como vemos en Los diez mayores nº9 Ancianidad grupo IV de 1907 (Fig. 6).

Figura 6: Hilma af Klint. Los diez mayores nº9 Ancianidad grupo IV, 1907. h ttp://www.arteidolia.com/spiritualism-aesthetics/

En esta obra de Hilma af Klint estos círculos traslapados pueden representar una célula o una unidad cualquiera en proceso de hacerse dual formando en este proceso una zona central o vesica, la cual puede representar la simiente: “Mediante su germinación surgen las líneas de color (la raíz) y los polígonos (el germen, que da origen a las ramas).” (Lawlor 1993, p. 34)

R. Lawlor señala como a través del volumen podemos ver una metáfora del “acto creador, original y continuo de la materialización del espíritu y la creación de la forma” (Lawlor, 1993,p.96).

Así las relaciones geométricas de los sólidos regulares tendrían que ver simbólicamente con Purusha y Prakriti, la eterna dicotomía creadora de la mitolgía hindú. El Purusha es el hombre antropocósmico, el inmanifiesto e intocado por la creación, al igual que la figura del icosaedro es intocada por las demás formas, mientas que el dodecaedro simboliza a Prakriti el poder femenino de la creación y la manifestación de la Madre Universal en cuya matriz Purusha proyecta su semilla con el fin de concebir su propia encarnación en el mundo de la forma. Prakriti la quinta esencia del universo natural representada por el dodecaedro toca todas las formas de la creación desde el interior del icosaedro. Los tetraedros entrelazados se consideran como el yin y el yang, ya que el tetraedro es el volumen de la trinidad, siendo un símbolo primario de una función acompañada por su recíproca:

El resultado de esta interacción armónica de opuestos le confiere al cubo, símbolo de la existencia material, los cuatro estados de la materia, la tierra, el aire, el fuego y el agua. Tanto el cubo como los tetraedros entrelazados tocan al dodecaedro. En el corazón de este tetraedro está el octaedro, y como el cubo es una formación de sus extremidades, el octaedro simboliza la cristalización, la perfección estática de la materia. Es el diamante, elcorazón del sólido cósmico, la lente transformada y clarificada de luz, la doble pirámide. (Lawlor, 1993, p. 103)

Conclusiones

Las teorías de Platón, según las cuales la filosofía y la estética estarían basadas en el número y la geometría, están siendo recogidas por físicos actuales como Frank Wilczek. Este sugiere que existiría una simetría subyacente en la naturaleza que estaría ayudando a comprender la realidad física, ya que la simetría establecería la estructura, como se puede comprobar a través de los sólidos regulares. Estos sólidos habrían causado una gran fascinación en los artistas a lo largo de los siglos, como vemos durante el Renacimiento, cuando los tratadistas investigan las leyes de la geometría como los cinco volúmenes regulares llegando este interés hasta el siglo XX con creadores como Escher que analizó con gran fruición la teselación del espacio mediante el relleno de todo el espacio con los sólidos platónicos, apareciendo igualmente este interés por los teselados con polígonos regulares en la obra de Monir Shahroudy Farmanfarmaian, Matt Shlian, Mary Martín, François Morelletç, Ellsworth Kelly, Sol LeWitt o Olafur Eliasson.

La proporción aurea y la simetría pentagonal presente en la bóveda de la catedral de Chartres y en otros edificios de la antigüedad como el pentágono estrellado inscrito en el círculo, serían construcciones capaces de integrar y sintonizar nuestro campo vibratorio externo con nuestro campo interior, este conocimiento integral estaría estrechamente unido a nuestra forma de percibir el mundo produciéndose lo que Sri Aurobindo llamó el “conocimiento por identidad”, un conocimiento directo e inmediato o consciencia supramental que constituiría una percepción pura que captaría la esencia de las cosas, esta función intuitiva que estaría por encima de nuestro pensamiento es fundamental en los procesos artísticos, ya que elevaría la consciencia del ser humano.

Los cinco componentes de la planta de los templos de la India se identifican con los cinco elementos cósmicos figurados mediante los sólidos geométricos que tienen a su vez conexión con las cinco relaciones sensoriales a través de las cuales conocemos el mundo real de la materia como vemos a través de los estudios de Bettina Baümer siendo esta geometría sagrada inherente al cuerpo humano como recoge la metafísica hindú donde cada uno de estos sólidos regulares sería el símbolo de las distintas capas invisibles y sutiles que nos envuelven.

La raíz cuadrada de tres está contenida en la vesica siendo el poder formativo que da origen al universo poligonal. Mediante la división del círculo y del cuadrado se forman las tres raíces sagradas, poderes generativos o principios dinámicos a partir de las cuales surgirían los cinco sólidos regulares los cuales constituyen la base de todas las formas volumétricas. Esta forma vesical aplanada será un símbolo arquetípico fundamental en las creaciones de artistas como Vaslav Nijinsky, Hilma af Klint o Jeanne Natalie Wintsch cuya obra expresa metafóricamente los poderes de la naturaleza, esta geometría en el arte se puede convertir en un puente capaz de relacionar las ideas y las formas como una guía ideal capaz de canalizar la consciencia del ser humano hacia su totalidad.