DOI:
https://doi.org/10.14483/udistrital.jour.reving.2016.3.a05Published:
2016-10-09Issue:
Vol. 21 No. 3 (2016): September - DecemberSection:
Computational IntelligenceAnálisis y simulación del comportamiento de vorticidad para el modelo de partícula auto-propulsada
Analysis and simulation of vortex behavior for self-propelled particle model
Keywords:
Autopropulsión, modelo, partícula, vórtice. (es).Keywords:
Model, particle, self-propelled, vortex (en).Downloads
References
A. Czir´ok, T. Vicsek, “Collective behavior of interacting self-propelled particles”. Physica A, vol. 281, num. 1-4,
, pp. 17-29.
T. Vicsek, “Universal patterns of collective motion from minimal models of flocking”. Second IEEE International
Conference on Self-Adaptive and Self-Organizing Systems, 2008, pp. 3-11.
A. Mikhailov, V. Calenbuhr, “From cells to societies: Models of complex coherent action”. Springer Series in
Synergetics, 2002, pp. 33-68.
W. Ebeling, “Active brownian motion of pairs and swarms of particles”. Acta Physica Polonica B, vol. 38, 2007,
pp. 1657-1671.
U. Erdmann,W. Ebeling, V. Anishchenko, “Excitation of rotational modes in two-dimensional systems of driven
Brownian particles Physical”. Physical Review E, vol. 65, 2002, pp. 061106 1-9.
H. Espitia, J. Sofrony, “Path planning of mobile robots using potential fields and swarms of brownian particles”.
IEEE Congress on Evolutionary Computation (CEC), June 5-8, 2011.
H. Espitia, J. Sofrony, “Vortex Particle Swarm Optimization”. IEEE Congress on Evolutionary Computation
(CEC), June, 2013.
H. Espitia, J. Sofrony, “Algoritmo de optimizaci´on basado en enjambres de part´ıculas con comportamiento de
vorticidad y b´usqueda individual y grupal”. Tecnura, vol. 18, no. 42, 2014, pp. 24-37.
H. Espitia, J. Sofrony, “Vortex Particle Swarm Optimization in 2D Cases”. International Conference on Mechatronics,
Electronics and Automotive Engineering (ICMEAE), November, 2015.
H. Espitia, J. Sofrony, “Proposal for Parameter Selection of the Vortex Particle Swarm Optimization During
the Dispersion Stage”. International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE),
November, 2013.
H. Espitia, J. Sofrony, “Dispersion as Stopping Criterion for Vortex Particle Swarm Optimization”. 2nd International
Symposium on Instrumentation and Measurement, Sensor Network and Automation (IMSNA), December
-24, 2013.
D. Sumpter, “The principles of collective animal behaviour”. Philosophical Transactions of the Royal Society B,
vol. 361, num. 1465, 2006, pp. 5-22.
T. Vicsek, A. Czir´ok, E. Ben-Jacob, I. Cohen, O. Shochet, “Novel type of phase transition in a system of selfdriven
particles”. Physical Review Letters, vol. 75, 1995, pp. 1226-1229.
I. Couzin, J. Krause, N. Franks, S. Levin, “Effective leadership and decision making in animal groups on the
move”. Letters to nature, vol. 433, 2005, pp. 513-516.
I. Bajec, F. Heppner, “Organized flight in birds”. Animal Behaviour, vol. 78, num. 4, 2009, pp. 777-789.
H. Zhang, M. Chen, G. Stan, T. Zhou, J. Maciejowski, “Collective behavior coordination with predictive mechanisms”.
IEEE Circuits and Systems Magazine, vol. 8, num. 3, 2008, pp. 67-85.
H. Berg, Random walks in biology, Princeton University Press, 1983.
Y. C¸ engel, J. Cimbala, Mec´anica de fluidos, Fundamentos y Aplicaciones, McGraw-Hill, 2006.
H. Levine, W. Rappel, I. Cohen, “Self-organization in systems of self-propelled particles”. Physical Review E,
vol. 63, num. 1, 2001.
M. D’Orsogna, Y. Chuang, A. Bertozzi, L. Chayes, “Self-propelled particles with soft-core interactions: patterns,
stability, and collapsel”. Physical Review Letters, vol. 96, 2006, pp. 104302 1-4.
W. Ebeling, U. Erdmann, “Nonequilibrium Statistical Mechanics of Swarms of Driven Particles”. Physica A:
Statistical Mechanics and its Applications, vol. 314, num. 1-4, 2002, pp. 92-96.
U. Erdmann, W. Ebeling, A. Mikhailov, “Noise Induced Transition from Translational to Rotational Motion of
Swarms”. Physical Review E, vol. 71, num. 5, 2005, pp. 051904 1-7.
A. Ordemann, “Vortex-swarming of the zooplankton Daphnia”. The Biological Physicist, vol. 2, num. 3, 2002,
pp. 5-10.
C. Reynolds, “Flocks, herds, and schools: A distributed behavioral model, in computer graphics”. SIGGRAPH’
Conference Proceedings, 1987.
F. Schweitzer, “Active Brownian particles with internal energy depot”. Traffic and Granular Flow’99, 2000, pp.
-172.
F. Schweitzer, W. Ebeling, B. Tilch, “Statistical mechanics of canonical dissipative systems and applications to
swarm dynamics”. Physical Review E, vol. 64, num. 2, 2001, pp. 021110 1-12.
R. Mach, F. Schweitzer, “Multi-agent model of biological swarming”. Lecture Notes in Artificial Intelligence
(LNAI), vol. 2801, 2003, pp. 810-820.
K. Alligood, T. Sauer, J. Yorke, An introduction to dynamical systems, Springer, 1st edition, 1997.
C. McInnes, “Vortex formation in swarms of interacting particles”. Physical Review E, vol. 75, num. 3, 2007,
pp. 032904 1-3.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.3.a05
Análisis y Simulación del Comportamiento de Vorticidad para el Modelo de Partícula Auto-propulsada
Analysis and Simulation of Vortex Behavior for Self-propelled Particle Model
Helbert Eduardo Espitia Cuchango
Universidad Distrital Francisco José de Caldas,Bogotá, Colombia. heespitiac@udistrital.edu.co
Jorge Iván Sofrony Esmeral
Universidad Nacional de Colombia, Colombia.jsofronye@unal.edu.co
Recibido: 16-03-2016. Modificado: 16-06-2016. Aceptado: 26-07-2016
Resumen
Contexto: En este documento se realizan varios análisis a un modelo de partículas autopropulsadas; dicho modelo permite describir el comportamiento de grupos de individuos. Se caracteriza por presentar movimientos lineales y circulares lo cuales son empleados para la búsqueda de alimento, así como también para evadir obstáculos y depredadores.
Método: Se realizó en primer lugar el cálculo de puntos de equilibrio, posteriormente se observa la conservación de energía y momento angular, finalmente se realiza la estimación del radio de giro de las partículas cuando estas realizan movimientos circulares. Las simulaciones se realizan considerando los análisis de tal forma que se pueden observar las características mas relevantes.
Resultados: De los análisis realizados se aprecia que el componente de interacción entre partículas actua como una fuerza centrípeta dirigida al centro de rotación del enjambre, de tal forma que las partículas pueden describir una trayectoria circular a una velocidad constante.
Conclusiones: Mediante los análisis realizados se identificaron varias características importantes del modelo estudiado, las cuales son presentadas de forma cualitativa con simulaciones. Principalmente se pudo observar la capacidad del modelo para describir movimientos lineales y circulares dependiendo de la configuración de sus parámetros.
Palabras claves: Auto-propulsión, modelo, partícula, vórtice.
Idioma: Español.
Abstract
Context: In this paper several analyzes are performed to a self-propelled swarm model; this model permits to describe the swarm behavior. It is characterized by having both, linear and circular movements which are utilized to search nourishment as well as to evade obstacles and predators.
Method: In regard of the analyzes performed, it is first calculated the equilibrium points, then the conservation of energy and angular momentum is observed. Finally, it is performed an estimate of the rotation radius when the particles made circular motions. The simulations were made considering the analyzes in order to observe the most important characteristics of the studied model.
Results: From the analyzes, it is seen that the interaction among particles acts as a centripetal force directed to the rotation center of the swarm, such that the particles can describe a circular trajectory at a constant speed.
Conclusions: Through the analysis some important features of the model were identified, these features were presented via simulations. It was mainly observed the capacity of the model to describe linear and circular movements depending on parameters configuration.
Keywords: Model, particle, self-propelled, vortex.
1. Introducción
El comportamiento de muchos seres vivos esta sujeto a la interacción que se presenta con sus vecinos, lo cual es útil tanto para la búsqueda de alimento como también para evadir depredadores. El modelado de estos comportamientos ha sido de atención en áreas como matemática, física, biología e ingeniería. Particularmente, en ingeniería se ha buscado emplear tal comportamiento como inspiración para solucionar problemas de optimización.
En el campo de la biología resulta de importancia el planteamiento de modelos que representen los comportamientos de seres vivos tales como aves, peces, hormigas y bacterias, entre otros. Cuando se trata de comportamientos colectivos se busca modelar las interacciones de los individuos para reproducir comportamientos emergentes; algunos comportamientos que son de resaltar corresponden a la capacidad de los individuos para evadir obstáculos y depredadores.
1.1 Modelos de partículas
Una forma empleada para describir el comportamiento de grupos de individuos corresponde al modelo de partículas activas Brownianas; en particular, con este modelo se busca explotar la característica de la formación de vórtices. Son de resaltar los modelos realizados para describir el comportamiento del zooplancton Daphnia, puesto que su desplazamiento le permite evadir obstáculos. El modelo de partícula autopropulsada corresponde a uno de los más representativos del zooplancton Daphnia, donde se considera que el individuo posee una fuente interna para lograr desplazarse de forma autónoma [1].
El modelo de partículas autopropulsadas (Self-Propelled Particles) fue propuesto para estudiar el movimiento colectivo de grandes grupos de organismos [2]. Segun [1] el movimiento de los individuos se encuentra regido por la interacción entre vecinos. Por su parte, los modelos de partículas autopropulsadas están formados por partículas que interactúan a nivel local mediante un componente de propulsión intrínseca a la partícula [1]. Adicionalmente, el fenómeno de auto-propulsión se observa en procesos físico-químicos, donde se tienen partículas pequeģas con fuerzas superficiales sensibles a ciertas temperaturas y concentraciones químicas [3].
Por otra parte, en [4] y [5] se han realizado análisis sobre el comportamiento de vorticidad asociado a un ciclo límite en su comportamiento dinámico, dicho análisis es realizado para dos partículas en dos dimensiones.
El comportamiento emergente que se estudia en este documento consiste en un movimiento circular de partículas con la formación de un vórtice, ya que esta estrategia de locomoción que emplean algunos seres vivos para buscar alimento y evadir obstáculos puede ser empleada en otros campos para la solución de problemas de búsqueda y exploración.
1.2 Antecedentes
En el presente documento se lleva a cabo el análisis y simulación de un modelo compacto de partículas autopropulsadas que emplea un potencial parabólico de interacción. Este modelo se caracteriza por describir movimientos lineales y circulares; mediante análisis y simulaciones se valida el comportamiento del modelo y el efecto que tienen sus parámetros.
El modelo ha sido utilizado en varios trabajos; en primer lugar, para el planteamiento de un algoritmo de planeación de trayectorias de robots móviles tal como se observa en [6] y posteriormente para el desarrollo de un algoritmo de optimización basado en un enjambre de partículas con comportamiento de vorticidad [7], [8], [9]. La importancia del análisis del modelo para el desarrollo del algoritmo se puede apreciar en [10] y [11]. En estos documentos se ha empleado el modelo considerando análisis parciales; en consecuencia, el objetivo en esta oportunidad consiste en extender tales análisis y simulaciones.
En trabajos futuros, se espera que con dichos análisis se pueda mejorar la selección de parámetros así como también el comportamiento del algoritmo basado en el modelo considerado. Con una buena identificación y análisis de los parámetros del modelo, estos se podrían manipular de tal forma que el enjambre logre realizar procesos de exploración y explotación. El proceso de exploración estaría directamente relacionado con la dispersión que puede lograr el enjambre de partículas y la explotación con la convergencia del enjambre a un determinado punto.
2. Comportamiento de enjambres
En relación a las diferentes conductas que se pueden evidenciar en la naturaleza, las congregaciones de individuos son una temática interesante dados los comportamientos emergentes que se observan [12]. Aquellos han sido estudiados y representados de forma analítica, siendo de resaltar el trabajo presentado en [13] que se enfoca en desarrollar un modelo básico para representar un enjambre de individuos. Un trabajo relacionado se puede apreciar en [2] donde se describen varios patrones representativos de los enjambres. Adicionalmente, en [12] se hace una revisión del comportamiento colectivo para la formación de enjambres, observando las propiedades de la auto-regulación y algunos principios del comportamiento colectivo como: realimentación positiva, realimentación negativa, dirección, sincronización, integridad, redundancia, umbrales de respuesta, variabilidad, inhibición, egoísmo y variabilidad.
Sobre los diferentes enfoques considerados para modelos de enjambres, en [14] se analiza el efecto que tiene el liderazgo de un individuo; en [15] se consideran las diferentes formas de organización que presentan las aves [15] y en [16] se observa el efecto que tiene incorporar mecanismos de predicción en un modelo de enjambre. Adicionalmente se tiene modelos de enjambres (como hormigas) basados en el proceso de dispersión y detección de feromonas para la comunicación entre individuos, principalmente para la búsqueda de alimento. Un trabajo relacionado se puede apreciar en [17], donde se propone un sistema embebido para la simular el aprovisionamiento de alimentos en colonias de hormigas artificiales.
2.1 Modelos de partículas con comportamiento de vorticidad
El comportamiento de vorticidad es un fenómeno que se presenta con frecuencia en los fluidos y se debe a la interacción que existe entre las fuerzas inerciales y viscosas (se suele cuantificar mediante el número de Reynolds [18]). El fenómeno de vorticidad consiste en el movimiento de forma rotacional (circular) de partículas alrededor de un punto denominado vórtice. En dinámica de fluidos se efectúa el análisis de este fenómeno mediante las ecuaciones de Navier Stokes [19]. Además de los fluidos, este tipo de comportamiento se presenta en enjambres como cardúmenes de peces, bandadas de aves y colonias de bacterias, entre otros. Para modelar este comportamiento se tienen dos enfoques representativos; el primero consiste en el modelo de partícula autopropulsada [20], [21]; en segundo lugar se tiene el modelo de partícula activa Browniana [22]. Este último considera una componente estocástica. Tales modelos suelen incorporar potenciales de Morse a fin de representar la interacción entre individuos; sin embargo, también se pueden observar modelos que emplean un potencial parabólico [23].
Por su parte, en [24] se comenta que los patrones globales de los enjambres se presentan por las interacciones internas de los individuos. También se expone que el comportamiento circular de un solo individuo no constituye un comportamiento colectivo de enjambre. Sobre algunos enfoques empleados para un modelo de enjambre de partículas se tiene:
- Modelo computacional Boids desarrollado para simular congregaciones de individuos (Craig Reynolds 1986) [25].
- Modelo de interacción de partículas autopropulsadas (Self-Propelled Interacting Particles), (Vicsek 1995) [13].
- Modelo de interacción de partículas autopropulsadas con rango largo de atracción y rango corto de repulsión (Levine 2001) [20].
- Modelo de interacción de partículas Brownianas activas con depósitos internos de energía (Interacting Active Brownian Particles with Internal Energy Depot) [26], [27], [28].
3. Movimiento activo
En un caso escalar, el movimiento activo se encuentra basado en la ecuación ( 1), la cual presenta
una bifurcación supercrítica con velocidad ν igual a cero debajo del punto de bifurcación, siendo
el movimiento activo asintóticamente estable con 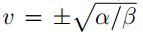 . En esta ecuación α y β son párametros de propulsión y frenado respectivamente.
. En esta ecuación α y β son párametros de propulsión y frenado respectivamente.
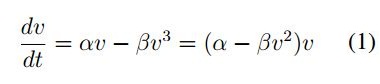
Considerando que una bifurcacion consiste en el cambio de la dinámica y estabilidad del sistema
dependiendo de sus parámetros, para la ecuación ((1)) en estado estable 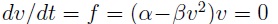 se tienen las soluciones
se tienen las soluciones 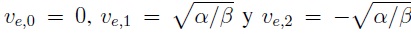 .Para determinar el tipo de comportamiento que presentan los puntos de equilibrio se emplea el Jacobiano obteniendo:
.Para determinar el tipo de comportamiento que presentan los puntos de equilibrio se emplea el Jacobiano obteniendo:
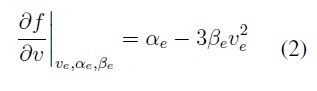
Del cálculo anterior se aprecia que el valor propio del sistema es 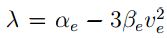 .
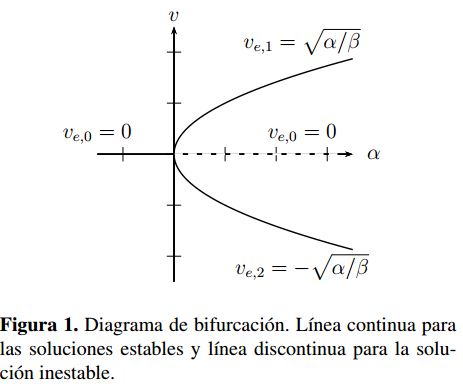
A modo de ejemplo, considerando β > 0 cuando α < 0 solo se tiene una solució real igual a νe =0 la
cual es estable,por otro lado si α> 0 se tienen tres soluciones reales: una para ν e =0 la cual es inestable,
las otras dos para
.
A modo de ejemplo, considerando β > 0 cuando α < 0 solo se tiene una solució real igual a νe =0 la
cual es estable,por otro lado si α> 0 se tienen tres soluciones reales: una para ν e =0 la cual es inestable,
las otras dos para 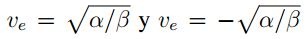 las cuales son estables.En la Figura 1 se puede apreciar el diagrama
de bifurcación para estas soluciones.
las cuales son estables.En la Figura 1 se puede apreciar el diagrama
de bifurcación para estas soluciones.
La ecuación (1) según [4] corresponde a una aproximación por expansión en series de Taylor para la descripción de un modelo de partículas con un depósito interno de energía. Por otro lado, en [3] se presenta que el comportamiento de auto-propulsión ocurre en procesos físicoquímicos, donde se tienen partículas pequeñas con fuerzas superficiales sensibles a concentraciones químicas y temperaturas, presentándose la interacción de fuerzas capilares y viscosas. La capilaridad ocurre cuando las fuerzas intermoleculares adhesivas entre un líquido y un sólido son mayores que las fuerzas intermoleculares cohesivas del líquido. Esto tiene como efecto la absorción del líquido lo cual puede estar en contra de la fuerza de gravedad [3] (la viscosidad consiste en la propiedad que presenta un fluido para oponerse a deformaciones tangenciales [3]).
4. Modelo de párticulas auto-propulsadas
El modelo considerado está formado por la menor cantidad de componentes que permitan describir una forma de locomoción con movimientos circulares. Las ecuaciones del modelo considerado son:
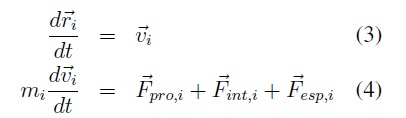
Con la primera ecuación se puede establecer la posición 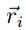 de la partícula conociendo la velocidad
de la partícula conociendo la velocidad
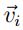 . Mediante la segunda ecuación se puede calcular la velocidad de la partícula conociendo las
fuerzas que actuan sobre ella.
. Mediante la segunda ecuación se puede calcular la velocidad de la partícula conociendo las
fuerzas que actuan sobre ella.
La ecuación correspondiente al balance de fuerzas presenta las siguientes componentes:
- Término de inercia
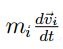 .
. - Componente de fuerzas disipativas y de propulsión
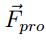 .
. - Término de relaciones entre individuos
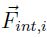 .
. - Componente de fuerzas dadas por el entorno
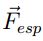 .
.
La fuerza de auto-propulsión se considera como:
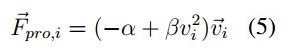
El término anterior es similar al presente en la ecuación de Van der Pol, esta ecuación se caracteriza
por tener un comportamiento de ciclo límite [29]. Segun [21] y [20] cuando se tiene este
término, la velocidad de las partículas en estado estable tiende a ser 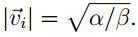
Con el fin de representar la interaccion entre individuos, el centro de masa del enjambre corresponde a:
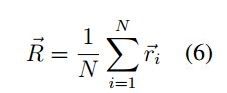
El factor dado por las interacciones de partículas se considera mediante un potencial parabólico de la forma [27]:
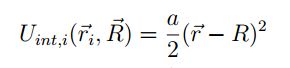
Mediante este potencial se tienen fuerzas que actúan directamente hacia el centro de masa del enjambre, lo cual permite tener un acople global de las partículas al centro de rotación de estas. Dichas fuerzas se pueden emplear para controlar la cohesión del enjambre. La fuerza de interacción asociada a este potencial es:
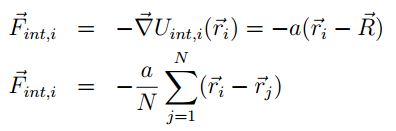
La información del entorno o espacio donde se desplazan las partículas se encuentra dada el campo potencial Uesp. La fuerza sobre cada partícula que se produce por el potencial Uesp es:
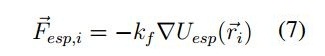
Donde, kf
5. Anális del modelo
En esta sección se realizan diferentes análisis y simulaciones con los cuales se muestran las características más relevantes del modelo. En primer lugar se establecen los puntos de equilibrio del enjambre, luego se realiza un análisis de conservación de energía y momento angular, con la finalidad de mostrar que el enjambre es capaz de realizar movimientos circulares. Finalmente se realiza la estimación del radio de giro del enjambre. Con las simulaciones se busca evidenciar las características identificadas mediante el análisis realizado.
5.1 Puntos de equilibrio
Los puntos de equilibrio se pueden establecer como:
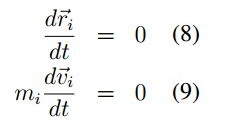
es decir
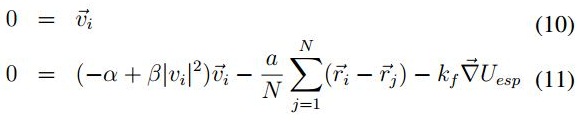
de lo anterior se tiene que 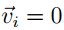 , por lo cual:
, por lo cual:
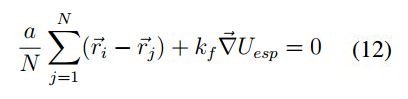
En el caso que Uesp tenga un valor mínimo 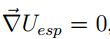 ,
por lo cual se tiene que
,
por lo cual se tiene que 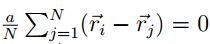 , es decir
, es decir 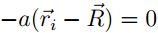 y finalmente
y finalmente 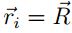 . Particularmente de la suposición
. Particularmente de la suposición 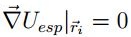 esto se cumple si
esto se cumple si 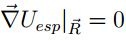 es decir que
es decir que 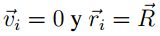 es un punto de equilibrio.
es un punto de equilibrio.
5.2 Anális de energía
El análisis de estabilidad se hace considerando el procedimiento empleado en [30]. Partiendo de la ecuación dinámica del modelo:
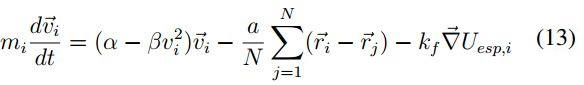
En primer lugar se realiza el cálculo de la energía cinética Ti y potencial Ui para una partícula de tal forma que se tiene:
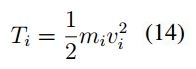
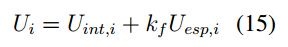
Tomando la derivada de la energía total Ei = Ti + kf Uesp,i :
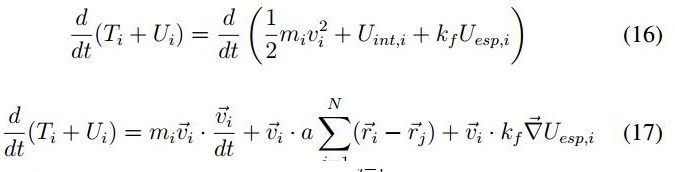
De la ecuació (13) es posible calcular:
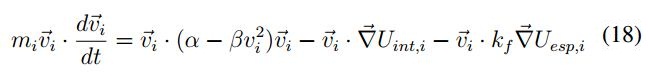
Sustituyendo la ecuación (18), en (17) se obtiene:
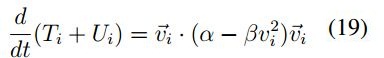
Sumando las contribuciones de todas las partículas:
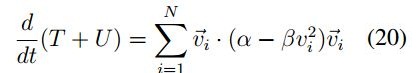
De lo anterior se tiene que el enjambre de partículas se encuentra en un estado de energía constante si:
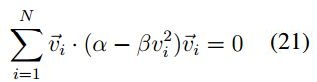
Por lo tanto, se puede tener un estado de equilibrio cuando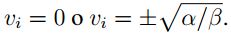
5.2.1 Análisis de momento angular
Mediante este análisis se busca evidenciar el comportamiento de vorticidad asociado al modelo, para esto se lleva a cabo un analisis de conservación de momento angular.
De forma general, el análisis de momento angular permite observar en los sistemas físicos las simetrías rotacionales. En algunos casos esta simetría permanece constante dando lugar a la ley de conservacion de momento angular.
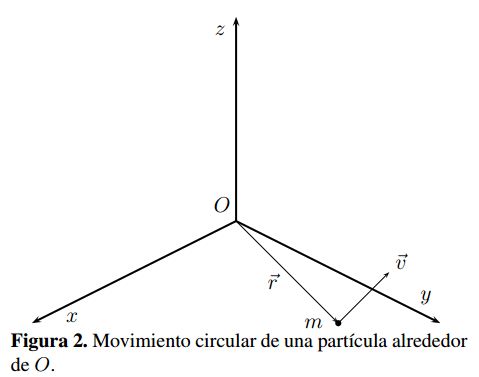
Considerando una partícula como la mostrada en la Figura 2, la cual se mueve en relación a un punto O, el momento angular de la partícula respecto a este punto corresponde a:
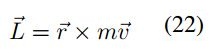
En este análisis se busca establecer cuando 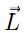 es constante es decir
es constante es decir 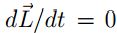 , entonces, en
primer lugar se tiene:
, entonces, en
primer lugar se tiene:
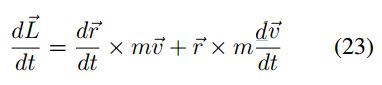
Puesto que 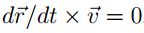 , entonces:
, entonces:
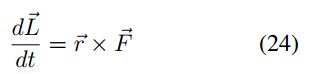
Considerando lo anterior, la conservacion del momento angular se tiene cuando 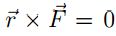 , lo
cual se presenta en alguna de las siguientes situaciones:
, lo
cual se presenta en alguna de las siguientes situaciones:
- La magnitud de la fuerza es cero.
- La fuerza que se ejerce sobre la partícula pasa por el radio de giro de esta.
La segunda situación ocurre con partículas que giran respecto a un punto fijo a velocidad constante.
Para el modelo en consideración, las condiciones de conservación del momento angular se pueden
establecer realizando el producto vectorial de 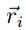 con la segunda ecuación de movimiento del modelo
de tal forma que se tiene:
con la segunda ecuación de movimiento del modelo
de tal forma que se tiene:
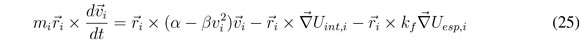
Tomando la suma para todas las partículas se tiene:
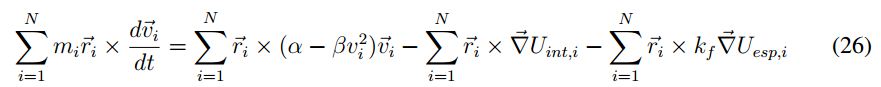
Empleando la identidad 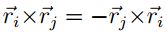 se puede comprobar que los torques internos producidos
por las interacciones de dos partículas se anulan:
se puede comprobar que los torques internos producidos
por las interacciones de dos partículas se anulan:
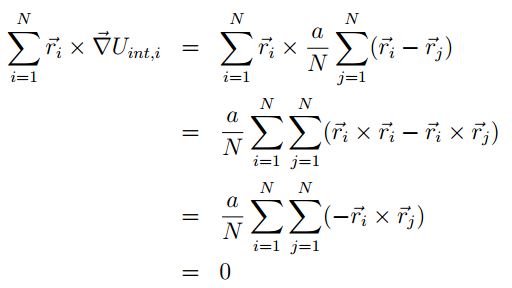
Como es de apreciar, la fuerza Fint,i está dada por la interacción de pares de partículas a lo largo
de  , de tal forma que debido a la simetría de las interacciones internas, este término tiende a ser
nulo. Para evidenciar el anterior resultado es posible desarrollar estas sumas de la siguiente forma:
, de tal forma que debido a la simetría de las interacciones internas, este término tiende a ser
nulo. Para evidenciar el anterior resultado es posible desarrollar estas sumas de la siguiente forma:
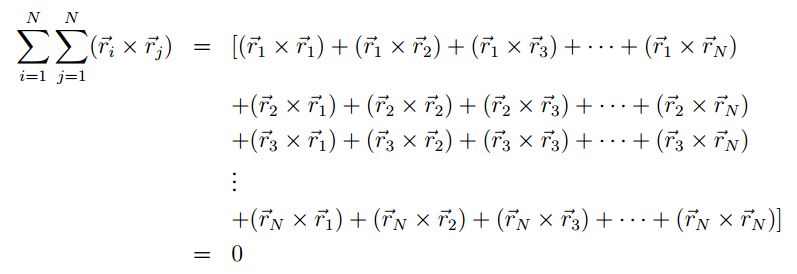
Considerando que el momento angular asociado a una partícula es:
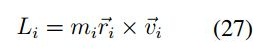
Para establecer la condición de la conservación del momento angular se tiene:
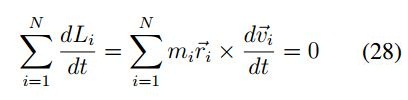
Reemplazando la ecuación ( 26), en (28) se tiene:
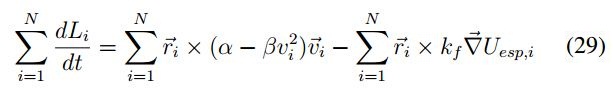
Considerando el resultado obtenido del análisis de energía donde se tiene un estado constante
de energía cuando 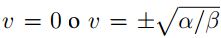 , al reemplazarlo en la ecuación ( (9)), el componente de auto-propulsión se elimina. De otro lado, considerando un potencial
, al reemplazarlo en la ecuación ( (9)), el componente de auto-propulsión se elimina. De otro lado, considerando un potencial 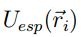 con simetría cónica que produce fuerzas radiales paralelas a
con simetría cónica que produce fuerzas radiales paralelas a 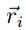 se establece que:
se establece que:
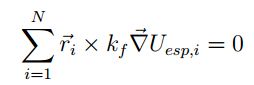
Bajo las anteriores consideraciones se tiene que:
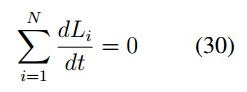
de tal forma que el momento angular se conserva; por lo tanto, en un estado constante de energía y
bajo la influencia de una función 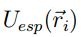 con simetría cónica, el enjambre de partículas describe un
movimiento circular con la presencia de un vórtice. Adicionalmente, es de notar que al tener kf = 0
se mantiene la conservación del momento angular, por lo que también se presentan movimientos
circulares en la ausencia de
con simetría cónica, el enjambre de partículas describe un
movimiento circular con la presencia de un vórtice. Adicionalmente, es de notar que al tener kf = 0
se mantiene la conservación del momento angular, por lo que también se presentan movimientos
circulares en la ausencia de 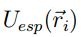 .
.
6. Estimación del radio del enjambre
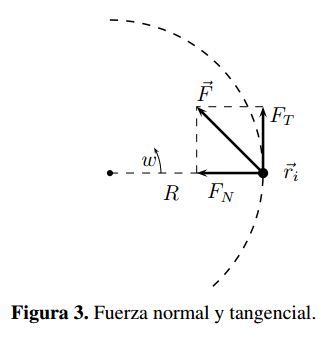
Considerando un movimiento circular uniforme para una partícula i como el mostrado en la Figura 3, se tiene una fuerza tangencial FT y normal FN tal que:
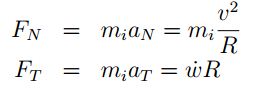
donde αT αT son las aceleraciones normal y tangencial, v la velocidad lineal, ω la velocidad angular, ώ la aceleracion angular y R el radio.
Para un movimiento circular uniforme se tiene en primer lugar que ώ = 0 y considerando los
resultados del análisis de energía, la velocidad se puede tomar como 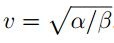 .
.
Teniendo en cuenta la fuerza de interacción (sin potencial externo) y las partículas efectuando un movimiento circular con radio R, se tiene entonces que la fuerza tangencial corresponde a FT = α R. Bajo estas consideraciones se tiene:
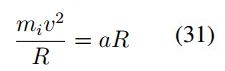
con 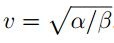 , se establece que:
, se establece que:
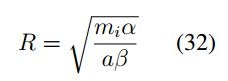
En un caso más general, donde se presenta un potencial externo Uesp se tiene que la fuerza producida
por este potencial está dada por 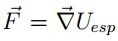 , considerando que este potencial presenta una
fuerza normal FN , entonces:
, considerando que este potencial presenta una
fuerza normal FN , entonces:
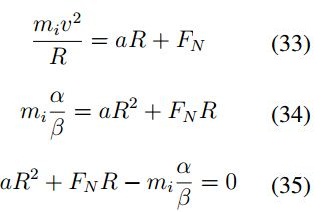
por lo cual se tiene:
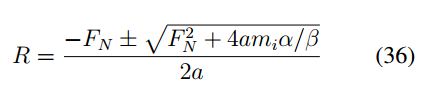
Para determinar el signo de la raíz se considera el caso cuando σ = 0 en el cual el radio debe tender a ser cero, por lo tanto se concluye que el signo del radical es positivo.
En el caso de tener Fn = 0 la expresión coincide con el análisis inicial donde:
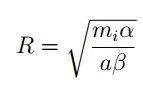
A manera de ejemplo se puede considerar un potencial Uesp con simetría cónica de la forma
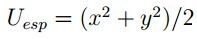 , entonces, Fn = R, por lo cual:
, entonces, Fn = R, por lo cual:
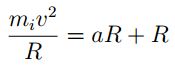
es decir:
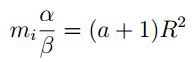
despejando el radio de giro se tiene:
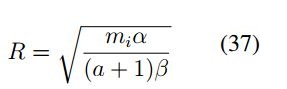
7. Simulación del modelo
Con el fin de realizar la simulacion del modelo las ecuaciones diferenciales ( (3)) y ( (4)) se convierten a tiempo discreto, empleando una aproximacion de Euler de primer orden con un intervalo de tiempo Δt, de tal forma que se tiene:
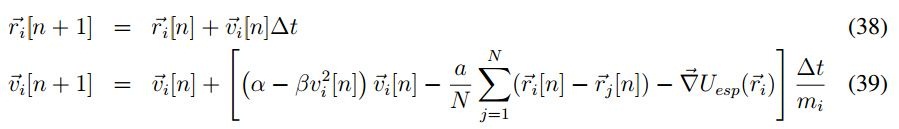
Como es de apreciar, los parámetros más representativos del modelo son N,α α , y β, por lo que en primer lugar se realiza un grupo de simulaciones donde se consideran diferentes valores de estos parámetros. Así, con este grupo de simulaciones se busca observar las características mas dominantes del modelo.
Una de las primeras características a observar se encuentra asociada con la fuerza de autopropulsión
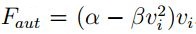 . Desde un punto de vista práctico, esta se puede considerar como
una fuerza de tipo disipativa
. Desde un punto de vista práctico, esta se puede considerar como
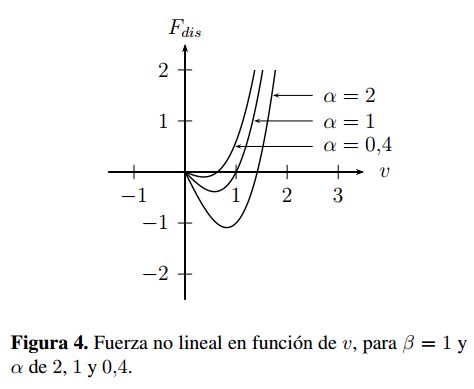
una fuerza de tipo disipativa 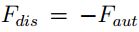 . En la Figura 4 se puede observar su efecto para diferentes valores de α al incrementar su valor la fuerza de propulsion aumenta. En esta figura los valores negativos corresponden a la propulsión suministrada, mientras que los valores positivos se encuentran asociados con la acción de frenado.
. En la Figura 4 se puede observar su efecto para diferentes valores de α al incrementar su valor la fuerza de propulsion aumenta. En esta figura los valores negativos corresponden a la propulsión suministrada, mientras que los valores positivos se encuentran asociados con la acción de frenado.
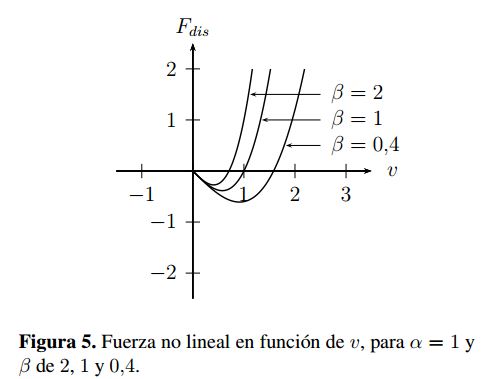
Adicionalmente en la Figura 5 se puede observar el comportamiento de Fdis para diferentes valores de β. Como es de apreciar, al incrementar el valor de β la fuerza de propulsión disminuye mientras se incrementa el efecto de la fuerza de frenado. También se puede notar que existen valores de v donde esta fuerza es negativa produciendo en este caso una propulsión de la partícula.
8. Simulación del modelo sin potencial externo
En este grupo de simulaciones se considera que no existe el potencial externo asociado al ambiente. Principalmente se observa el efecto que tienen los parametros N,α α , y β en la distribución final del enjambre. La simulación se realiza empleando un paso fijo de Δt = 0,1.
8.1 Simulación con movimiento de rotación
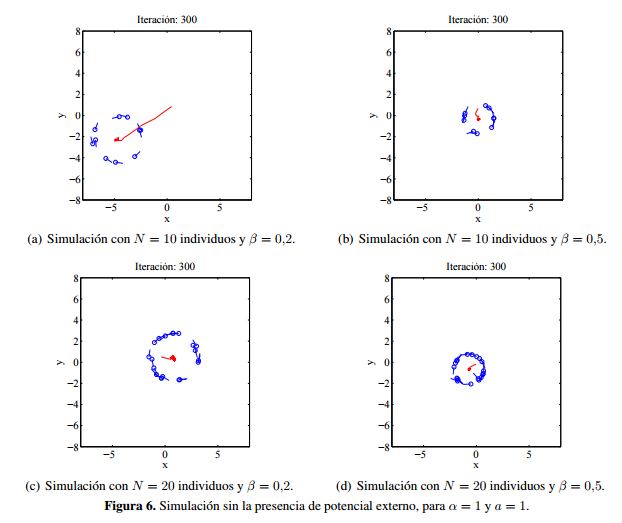
Considerando condiciones iniciales aleatorias tanto para la posición como para la velocidad, se tienen los resultados presentados en la Figura 6, donde se observa que el enjambre describe una trayectoria circular, apreciándose diferentes radios de giro según los parámetros considerados; adicionalmente, es de notar que el sentido de giro no es el mismo para todas las partículas.
En la Figura 6 se puede observar que el centro de rotación de las partículas depende de las condiciones iniciales, debido a la falta de un potencial externo que influya en el desplazamiento de estas. También es de apreciar en las simulaciones de la Figura 6, que el sentido de giro de las partículas no presenta la misma dirección para todas, ya que no se considera ninguna fuerza de alineamiento en el modelo seleccionado. Finalmente, es de resaltar que al tener un valor mayor de β el radio de giro tiende a disminuir, lo cual se considera con mayor detalle en simulaciones posteriores.
8.2 Simulación con movimiento de traslación
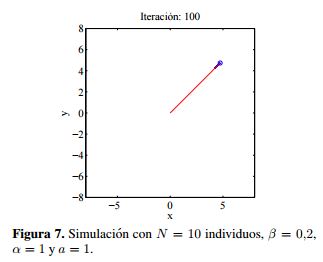
Esta simulación corresponde a un caso particular donde el enjambre realiza un movimiento de traslación. Este tipo de movimiento se presenta cuando la posición y velocidad inicial de las partículas es la misma. La posición inicial corresponde al punto [0, 0] origen del sistema de referencia y la velocidad se toma como [vxi,0, vyi,0] = [0,001, 0,001]. De esta forma, en la figura 7 es posible apreciar el movimiento de traslación que describen las partículas cuando las condiciones iniciales son iguales para la posición y la velocidad.
Como se ve en la Figura 7 la posición de las partículas coincide describiendo un movimiento lineal en dirección de la velocidad inicial. En este caso, el enjambre se comporta como una sola partícula presentándose un colapso del enjambre, producido por las condiciones iniciales de las partículas.
9. Simulación del modelo con potencial externo
En este conjunto de simulaciones se observa el efecto que tiene el potencial asociado al espacio o ambiente donde se desplazan las partículas. Este potencial puede ser empleado para guiar el enjambre. Para garantizar la convergencia del enjambre a un mismo punto, el potencial debe ser monomodal, es decir que solo presenta un punto mínimo.
El potencial considerado en dos dimensiones presenta simetría cónica de la forma Uesp = kx x2 + kx y 2, para el caso donde kx = kx se tiene un potencial "parabólico" (paraboloide de revolución), por otro lado cuando kx ≠ kx se presenta un potencial "elíptico" (paraboloide elíptico).
9.1 Combinación de movimientos de traslación y rotación
En esta simulación se puede apreciar que el enjambre presenta dos comportamientos, un movimiento
de traslación y otro de rotación alrededor de un punto (vórtice). Para ilustrar este hecho, se
tiene un espacio de dos dimensiones tal que 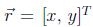 y un enjambre sometido a un potencial parabólico de la forma
y un enjambre sometido a un potencial parabólico de la forma 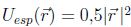 ,
el cual se encuentra centrado en el origen.Las partículas tienen condiciones iniciales
,
el cual se encuentra centrado en el origen.Las partículas tienen condiciones iniciales 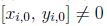 para la posición y
para la posición y 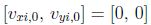 para la velocidad, donde las posiciones iniciales
son elegidas al azar. Los parámetros del modelo en esta simulación son
para la velocidad, donde las posiciones iniciales
son elegidas al azar. Los parámetros del modelo en esta simulación son 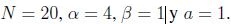 .
.
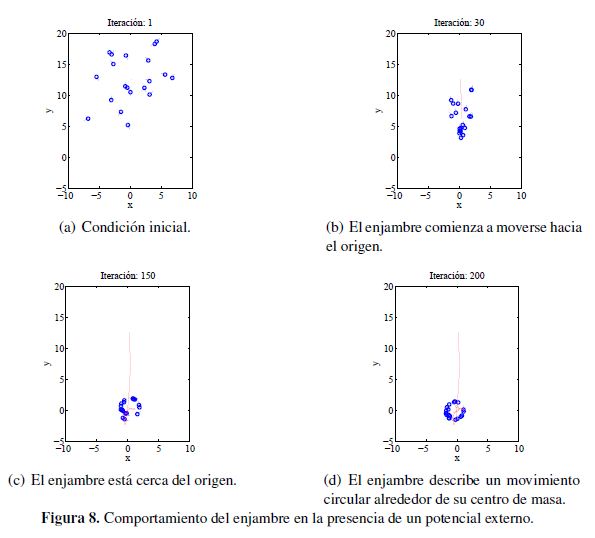
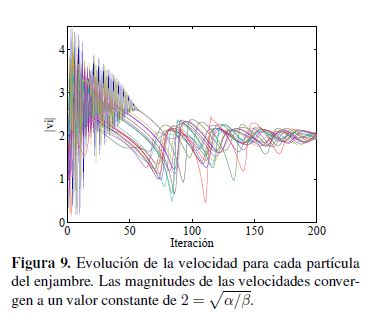
En la Figura 8, es posible observar cómo las partículas se desplazan primero al origen (punto
mínimo de Uesp) y una vez que el enjambre está lo suficientemente cerca de este punto, realiza movimientos
circulares (comportamiento asociado a un ciclo límite) donde la magnitud para la velocidad de cada partícula tiende a ser
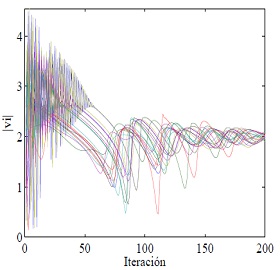
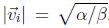 lo cual se puede apreciar en la Figura 9.
lo cual se puede apreciar en la Figura 9.
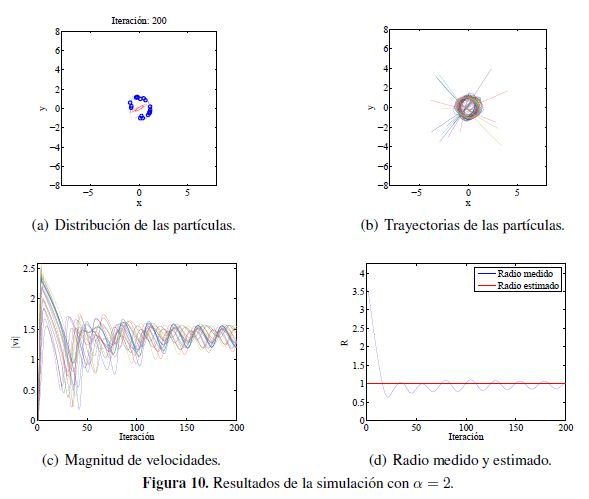
9.2 Velocidad y distribución del enjambre
Con el propósito de observar la distribución de las partículas, así como la velocidad de estas cuando
se tiene un potencial externo, se realiza un conjunto de simulaciones considerando un potencial parabólico
 tomando
tomando 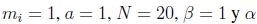 para 2 y 4, los resultados obtenidos para estos casos se muestran en las figuras 10 y 11. En la Figura 10 se presentan los resultados para 200
iteraciones con
para 2 y 4, los resultados obtenidos para estos casos se muestran en las figuras 10 y 11. En la Figura 10 se presentan los resultados para 200
iteraciones con  y condiciones iniciales aleatorias para la posición.
y condiciones iniciales aleatorias para la posición.
La figura (a) muestra la localización y orientación final de las partículas observándose la formación de un vórtice. Por su parte en (b) se tiene el recorrido de las partículas, (c) muestra la magnitud de las velocidades y en (d) se puede apreciar el valor del radio medido y del estimado para el enjambre de partículas.
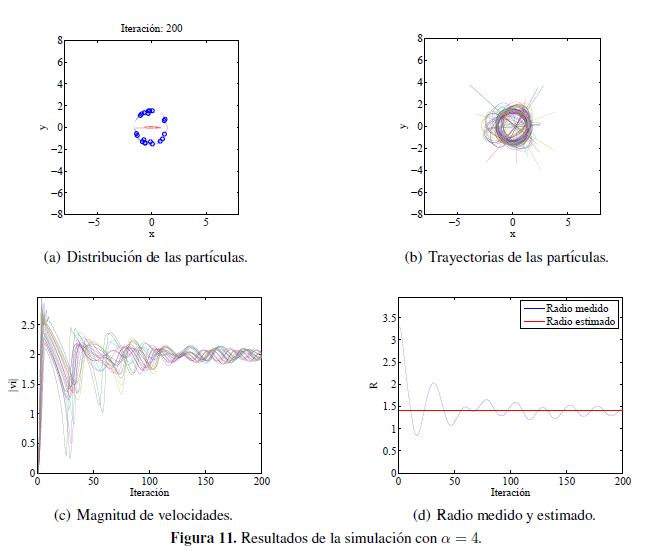
Considerando la ecuación (37) se puede establecer el radio de giro de tal forma que para α = 2 se tiene un radio estimado de 1,0 y para α = 4 se tiene un radio estimado de 1,4142.
En la Figura 11 se pueden observar los resultados de la simulación en el caso de tener α= 4. En
estas figuras se aprecia que el enjambre logra tener una distribución circular donde su radio de giro
se encuentra cerca del valor estimado. Adicionalmente se puede apreciar de nuevo que la magnitud
de la velocidad de las partículas tiende a ser 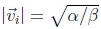 .
.
9.3 Simulación para un potencial no simétrico
En este caso se considera un potencial de la forma 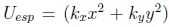 y los parámetros del modelo con
y los parámetros del modelo con 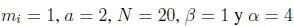 . Las condiciones iniciales de las
partículas se consideran aleatorias para las posiciones y cero para las velocidades.
. Las condiciones iniciales de las
partículas se consideran aleatorias para las posiciones y cero para las velocidades.
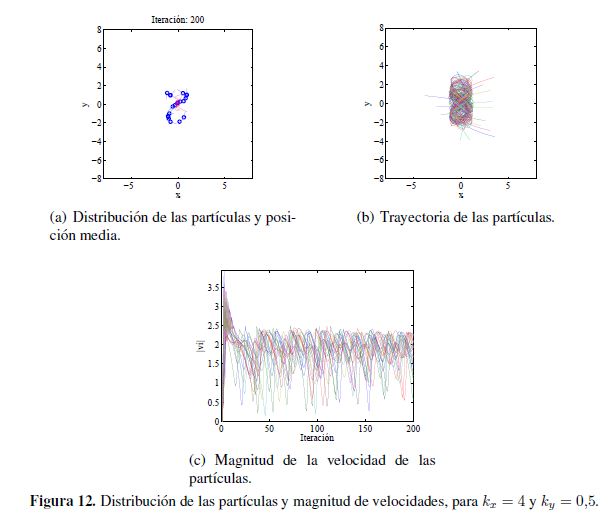
En la Figura 12 se pueden apreciar los resultados de la simulación cuando se toma kx = 4 y ky = 0,5. En (a) se muestra la posición media de las partículas y la distribución de estas en la última iteración. Por su parte, en la figura (b) se tiene la posición de todas las partículas y en la figura (c), se muestra la magnitud de la velocidad de las partículas.
En estas simulaciones se aprecia que no se presentan movimientos circulares perfectos. Sin embargo, al seguir teniendo un potencial monomodal, las partículas describen movimientos oscilatorios alrededor del punto donde el potencial tiene su menor valor.
10. Simulación del modelo para cuatro dimensiones
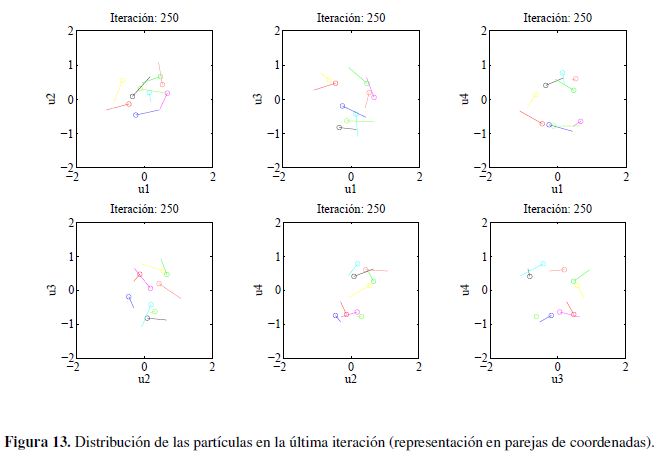
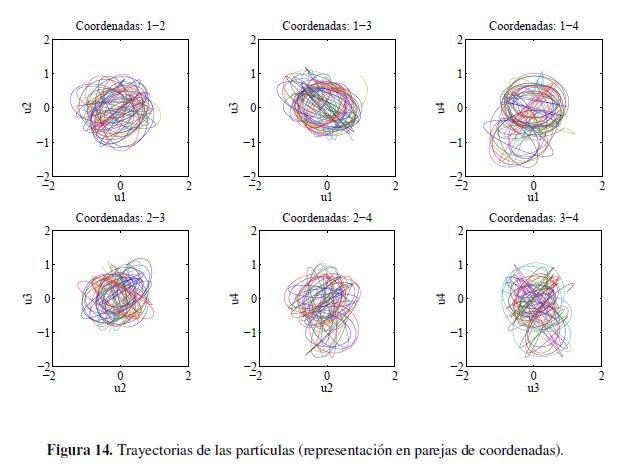
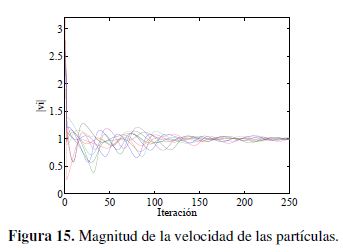
Con el propósito de apreciar el comportamiento del enjambre en varias dimensiones se realiza una simulación para cuatro dimensiones teniendo el resultado mostrado en las Figuras 13,14 y 15. Para la visualización de estos resultados, se toman las diferentes parejas de ejes coordenados que se pueden tener y se presentan en los respectivos planos el desplazamiento y orientación de las partículas.
En la Figura 13 se muestra la posición media de las partículas, así como la distribución y orientación de estas en la última iteración para los diferentes pares de ejes coordenados. En la Figura 14 se tiene la posición de todas las partículas y en la Figura 15 se muestra la magnitud de la velocidad de las partículas.
Con las simulaciones de las Figuras 13 y 14 se observa que el modelo permite describir comportamientos cíclicos (cercanos a movimientos circulares) en las cuatro dimensiones. Es de apreciar un comportamiento similar para los diferentes pares de ejes coordenados que se tomaron para la presentación de los resultados. Adicionalmente, en la Figura 15 se comprueba que la magnitud de la velocidad de las partículas tiene a ser 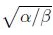 .
.
11. Conclusiones y expectativas futuras
Con el análisis realizado se mostró que el enjambre de partículas puede describir comportamientos circulares con la presencia de un vórtice. Adicionalmente mediante las simulaciones se corroboró de forma cualitativa los resultados obtenidos del análisis. Se espera que estos análisis se puedan emplear en trabajos futuros para mejorar la selección de parámetros, así como el comportamiento del enjambre.
Para una situación donde las velocidades y posiciones iniciales de las partículas son iguales, se presenta un movimiento lineal de las partículas. Cuando las posiciones y velocidades iniciales de las partículas se consideran aleatorias el enjambre logra describir un movimiento con características de vorticidad.
Mediante simulación se puede observar que la estimación del radio del giro del enjambre se acerca al valor real medido del enjambre. Este resultado permite establecer un mecanismo para controlar de forma aproximada el comportamiento del enjambre al modificar sus parámetros.
Aunque la presentación de los resultados de la simulación en más de tres dimensiones puede limitar la observación completa del comportamiento del enjambre, con la metodología empleada se puede apreciar de forma aproximada el movimiento que tienen las partículas.
Este tipo de comportamiento se puede emplear para el desarrollo de algoritmos de optimización de tal forma que se pueda mejorar la capacidad de exploración y explotación al incluir movimientos circulares y lineales del enjambre. La exploración se relaciona con la dispersión que puede lograr el enjambre de partículas y la explotación con la convergencia del enjambre a un determinado punto.
Referencias
[1] A. Czirók, T. Vicsek, "Collective behavior of interacting self-propelled particles". Physica A, vol. 281, num. 1-4, 2000, pp. 17-29.
[2] T. Vicsek, "Universal patterns of collective motion from minimal models of flocking". Second IEEE International Conference on Self-Adaptive and Self-Organizing Systems, 2008, pp. 3-11.
[3] A. Mikhailov, V. Calenbuhr, "From cells to societies: Models of complex coherent action". Springer Series in Synergetics, 2002, pp. 33-68.
[4] W. Ebeling, "Active brownian motion of pairs and swarms of particles". Acta Physica Polonica B, vol. 38, 2007, pp. 1657-1671.
[5] U. Erdmann,W. Ebeling, V. Anishchenko, "Excitation of rotational modes in two-dimensional systems of driven Brownian particles Physical". Physical Review E, vol. 65, 2002, pp. 061106 1-9.
[6] H. Espitia, J. Sofrony, "Path planning of mobile robots using potential fields and swarms of brownian particles". IEEE Congress on Evolutionary Computation (CEC), June 5-8, 2011.
[7] H. Espitia, J. Sofrony, "Vortex Particle Swarm Optimization". IEEE Congress on Evolutionary Computation (CEC), June, 2013.
[8] H. Espitia, J. Sofrony, "Algoritmo de optimización basado en enjambres de partículas con comportamiento de vorticidad y búsqueda individual y grupal". Tecnura, vol. 18, no. 42, 2014, pp. 24-37.
[9] H. Espitia, J. Sofrony, "Vortex Particle Swarm Optimization in 2D Cases". International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), November, 2015.
[10] H. Espitia, J. Sofrony, "Proposal for Parameter Selection of the Vortex Particle Swarm Optimization During the Dispersion Stage". International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), November, 2013.
[11] H. Espitia, J. Sofrony, "Dispersion as Stopping Criterion for Vortex Particle Swarm Optimization". 2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation (IMSNA), December 23-24, 2013.
[12] D. Sumpter, "The principles of collective animal behaviour". Philosophical Transactions of the Royal Society B, vol. 361, num. 1465, 2006, pp. 5-22.
[13] T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, O. Shochet, "Novel type of phase transition in a system of selfdriven particles". Physical Review Letters, vol. 75, 1995, pp. 1226-1229.
[14] I. Couzin, J. Krause, N. Franks, S. Levin, "Effective leadership and decision making in animal groups on the move". Letters to nature, vol. 433, 2005, pp. 513-516.
[15] I. Bajec, F. Heppner, "Organized flight in birds". Animal Behaviour, vol. 78, num. 4, 2009, pp. 777-789.
[16] H. Zhang, M. Chen, G. Stan, T. Zhou, J. Maciejowski, "Collective behavior coordination with predictive mechanisms". IEEE Circuits and Systems Magazine, vol. 8, num. 3, 2008, pp. 67-85.
[17] C. Rodríguez, M. Melgarejo, "Arquitectura FPGA para simulación de aprovisionamiento de alimentos en colonias de hormigas artificiales". Ingeniería, vol. 20, num. 2, 2015, pp. 245-260.
[18] H. Berg, Random walks in biology, Princeton University Press, 1983.
[19] Y. Cengel, J. Cimbala, Mecánica de fluidos, Fundamentos y Aplicaciones, McGraw-Hill, 2006.
[20] H. Levine, W. Rappel, I. Cohen, "Self-organization in systems of self-propelled particles". Physical Review E, vol. 63, num. 1, 2001.
[21] M. D’Orsogna, Y. Chuang, A. Bertozzi, L. Chayes, "Self-propelled particles with soft-core interactions: patterns, stability, and collapsel". Physical Review Letters, vol. 96, 2006, pp. 104302 1-4.
[22] W. Ebeling, U. Erdmann, "Nonequilibrium Statistical Mechanics of Swarms of Driven Particles". Physica A: Statistical Mechanics and its Applications, vol. 314, num. 1-4, 2002, pp. 92-96.
[23] U. Erdmann, W. Ebeling, A. Mikhailov, "Noise Induced Transition from Translational to Rotational Motion of Swarms". Physical Review E, vol. 71, num. 5, 2005, pp. 051904 1-7.
[24] A. Ordemann, "Vortex-swarming of the zooplankton Daphnia". The Biological Physicist, vol. 2, num. 3, 2002, pp. 5-10.
[25] C. Reynolds, "Flocks, herds, and schools: A distributed behavioral model, in computer graphics". SIGGRAPH’ Conference Proceedings, 1987.
[26] F. Schweitzer, "Active Brownian particles with internal energy depot". Traffic and Granular Flow’99, 2000, pp.161-172.
[27] F. Schweitzer, W. Ebeling, B. Tilch, "Statistical mechanics of canonical dissipative systems and applications to swarm dynamics". Physical Review E, vol. 64, num. 2, 2001, pp. 021110 1-12.
[28] R. Mach, F. Schweitzer, "Multi-agent model of biological swarming". Lecture Notes in Artificial Intelligence (LNAI), vol. 2801, 2003, pp. 810-820.
[29] K. Alligood, T. Sauer, J. Yorke,An introduction to dynamical systems, Springer, 1st edition, 1997.
[30] C. McInnes, "Vortex formation in swarms of interacting particles”. Physical Review E, vol. 75, num. 3, 2007, pp. 032904 1-3.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)










