DOI:
https://doi.org/10.14483/udistrital.jour.reving.2017.2.a03Published:
2017-05-05Issue:
Vol. 22 No. 2 (2017): May - AugustSection:
Environmental EngineeringEstimación Espectral de Series de Tiempo de Absorbancia Uv-Vis para el Monitoreo de Calidad de Aguas
Spectral Estimation of UV-Vis Absorbance Time Series for Water Quality Monitoring
Keywords:
Box-Cox Transformation, Periodogram, Principal Components Analysis, Power spectral density, Stationarity, UV-Vis sensor (en).Keywords:
Análisis por Componentes Principales, Captor UV-Vis, Densidad espectral de potencia, Estacionariedad, Periodograma, Transformación Box-Cox. (es).Downloads
References
Poch, M., Cortés, U., Comas, J., Rodríguez-Roda, I. and Sànchez-Marrè, M., “Decisions on urban water systems: some support”. University of Girona, First Edition, Servei de Publicacions, Spain 2012.
Garcia, X., Barceló, D., Comas, J., Hadjimichael, A., Page, T. and Acuña, V., “Placing ecosystem services at the heart of urban water systems management”. Science of the Total Environment 563–564, 2016, pp. 1078–1085.
Morales-Torres, A., Escuder-Bueno, I., Andrés-Doménech, I. and Perales-Momparler, S., “Decision Support Tool for energy-efficient, sustainable and integrated urban stormwater management”. Environmental Modelling & Software 84, 2016, pp. 518-528.
Akan, A. and Houghtalen, R., Urban Hydrology, Hydraulics, and Stormwater Quality: Engineering applications and computer modelling. John Wiley &Sons, Inc. Hoboken, USA. 2003.
Dirckx, G, van Daele, S. and Hellinck, N., “Groundwater Infiltration Potential (GWIP) as an aid to determining the cause of dilution of waste water”. Journal of Hydrology, 542, 2016, pp. 474-486.
Marsalek, J., Jiménez-Cisneros, B., Malmquist, P.-A., Karamouz, M., Goldenfum, J. and Chocat, B., “Urban water cycle processes and interactions”. Pub-lished by the International Hydrological Programme (IHP) of the United Nations Educational, Scientific and Cultural Organization (UNESCO). Paris 2006.
Gosset, A., Ferro, Y. and Durrieu, C., “Methods for evaluating the pollution impact of urban wet weather discharges on biocenosis: a review”. Water Research, 89, 2016, pp. 330–354.
Palla, A. and Gnecco, I., “Hydrologic modelling of Low Impact Development systems at the urban catchment scale”. Journal of Hydrology, 528, 2015, pp. 361-368.
Fazi, S., Bandla, A., Pizzetti, I. and Swarup, S., “Microbial biofilms as one of the key elements in modulating ecohydrological processes in both natural and urban water corridors”. Ecohydrology & Hydrobiology 16, 2016, pp. 33-38.
von Sperling, M. and de Lemos., C., Wastewater Characteristics, Treatment and Disposal. First Edition. IWA Publishing. UK 2007.
Francois, C., Gondran, N., Nicolas, J.-P. and Parsons, D. “Environmental assessment of urban mobility: Combing life cycle assessment with land-use and transport interaction modelling-Application to Lyon (France)”. Ecological Indicators, 72, 2017, pp. 597-604.
van den Broeke, J., “On-line and In-situ UV/Vis Spectroscopy: Real time multi parameter measurements with a single instrument”. AWE International, 2007, pp. 55-59.
Gruber, G., Bertrand-Krajewski, J.-L., De Beneditis, J., Hochedlinger, M., & Lettl, W., “Practical aspects, experiences and strategies by using UVVIS sensors for long-term sewer monitoring”. Water Practice & Technology, 2006, pp. 1-8.
Rieger, L., Langergraber, G., Thomann, M., Fleischmann, N., and Siegrist, H. “Spectral in-situ analysis of NO2, NO3, COD, DOC and TSS in the effluent of a WWTP”. Proccedings of AutMoNet – 2nd IWA Conference on Automation in Water Quality Monitoring, Vienna, 2004, pp. 29-36.
Matsumoto, T. and Sánchez, I. "Desempeño de la Planta de Tratamiento de Aguas Residuales de São João de Iracema (Brasil)”. Revista Ingeniería 21(2), 2016, pp. 176-186.
Salgado, R., Pinheiro, H. M., Ferreira, F., Saldanha, J., & Louren, N. “In situ UV-Vis spectroscopy to estimate COD and TSS in wastewater drainage sys-tems”. Urban Water Journal, 2013, pp. 1-12.
Torres, A., Lepot, M., & Bertrand-Krajewski, J.-L. “Local calibration for a UV/Vis spectrometer: PLS vs. SVM. A case study in a WWTP”. Proccedings of 7th International Conference on Sewer Processes & Networks, 28 - 30 August – 2013, Sheffield, UK.
Lepot M., Torres A., Hofer T., Caradot N., Gruber G., Aubin J.-B., Bertrand-Krajewski J.-L. “Calibration of UV/Vis spectrophotometers: A review and comparison of different methods to estimate TSS and total and dissolved COD concentrations in sewers, WWTPs and rivers”. Water Research 101, 2016, pp. 519–534.
Fei, W., & Bai, L. “Auto-Regressive Models of Non-stationary time series with finite length”. Tsinghua Science and Technology 10(2), 2005, pp. 162-168.
Kamarzarrin, M., Hosseini, S., Mehdi, M. and Kamarzarrin, M. “Designing and implementing of improved cryptographic algorithm using modular arith-metic theory”. Journal of Electrical Systems and Information Technology, 2, 2015, pp. 14–17.
Plazas-Nossa, L., Avila, M. and Torres, Andres. "Detection of Outliers and Imputing of Missing Values for Water Quality UV-VIS Absorbance Time Series”. Revista Ingeniería, 2016, In press.
Salcedo, G., Porto, R., and Morettin, P. “Comparing non-stationary and irregularly spaced time series”. Computational Statistics and Data Analysis 56, 2012, pp. 3921-3934.
Huang, J., Kobayashi, M., and McAleer, M. “Testing for the Box–Cox parameter for an integrated process”. Mathematics and Computers in Simulation, 83, 2012, pp. 1-9.
Bicego, M. and Baldo, S. "Properties of the Box–Cox transformation for pattern classification”. Neurocomputing, 218, 2016, pp. 390-400.
Tsiotas, G. “On the use of the Box–Cox transformation on conditional variance models”. Finance Research Letters, 4, 2007, pp. 28-32.
Proietti, T., and Lütkepohl, H. “Does the Box–Cox transformation help in forecasting macroeconomic time series?”. International Journal of Forecasting 29, 2013, pp. 88-99.
Langergraber, G., Fleischmann, N., Hofstaedter, F., & Weingartner, A. “Monitoring of a paper mill wastewater treatment plant using UV/VIS spectros-copy”. IWA Water Science and Technology, 49(1), 2004, pp. 9-14.
s::can. “Manual ana::pro Version 5.3 September 2006 Release”. Messtechnik GmbH, Vienna, Austria 2006.
Zamora, D., Métodos Machine Learning aplicados para estimar la concentración de los contaminantes de la DQO y de los SST en hidrosistemas de saneamiento urbano a partir de espectrometría UV-Visible. Tesis de Maestría, 2013, Pontificia Universidad Javeriana, Bogotá-Colombia.
Winkler, S., Saracevic, E., Bertrand-Krajewski, J.-L. and Torres, A., “Benefits, limitations and uncertainty of in situ spectrometry”. Water science and technology 57(10), 2008, pp. 1651–8.
Harjula, I., Hekkala, A., Matinmikko, M., and Mustonen, M., “Performance Evaluation of Spectrum Sensing Using Welch Periodogram for OFDM Signals”. IEEE 73rd Vehicular Technology Conference (VTC Spring), 2011, pp. 1-5.
Zhang, S., "Adaptive spectral estimation for nonstationary multivariate time series”. Computational Statistics and Data Analysis 103, 2016, pp. 330–349.
Chong, T.-L., “Estimating the differencing parameter via the partial autocorrelation function”. Journal of Econometrics, 97, 2000, pp. 365-381.
Hassler, U., “Persistence under temporal aggregation and differencing”. Economics Letters, 124, 2014, pp. 318-322.
Shen, Ch. “A comparison of principal components using TPCA and nonstationary principal component analysis on daily air-pollutant concentration series”. Physica A, 467, 2017, pp. 453-464.
Stavropoulos, C., and Fassois, S., “Non-stationary functional series modeling and analysis of hardware reliability series: a comparative study using rail vehicle interfailure times”. Reliability Engineering and System Safety, 68, 2000, pp. 169-183.
Shlens, J., “A Tutorial on Principal Component Analysis”. La Jolla, California, USA: Salk Institute for Biological Studies, 2009, pp. 1-13.
Barbour, A., and Parker, R., “psd: Adaptive,sine multitaper power spectral density estimation for R”. Computers and Geosciences, 63, 2014, pp. 1-8.
Bogdan,I. and Istrate, C. “The analysis of the principal components of the financial reporting in the case of Romanian listed companies”. Procedia Economics and Finance, 20, 2015, pp. 553–561.
Plazas-Nossa, L., Ávila, M. and Moncada, G. “Estimación del Exponente de Hurst y Dimensión Fractal para el análisis de series de tiempo de Absorbancia UV-VIS”. Ciencia e Ingeniería Neogranadina, 42(2), 2014, pp. 133-143.
Lee, D., and Baldick, R., “Future Wind Power Scenario Synthesis Through Power Spectral Density Analysis”. IEEE Transactions on Smart Grid, 5(1), 2014, pp. 490-500.
Bach, F. and Jordan, M., “Learning Graphical Models for Stationary Time Series”. IEEE Transactions on Signal Processing, 52(8), 2004, pp. 2189-2199.
Lv, P., and Yue, L., “Short-Term Wind Speed Forecasting Based on Non-stationary Time Series analysis and ARCH model”. Proccedings of International Conference on Multimedia Technology (ICMT), Hangzhou, China, 2011, pp. 2549-2553.
Proakis, J., and Manolakis, D. “Digital signal processing principles, algorithms, and applications”. Fourth Edition. Pearson Prentice Hall, New Jersey, USA 2007.
Tuffner, F., Pierre, J., and Kubichek, R. “Computationally Efficient Updating of a Weighted Welch Periodogram for Nonstationary Signals”. 51st Midwest Symposium on Circuits and Systems MWSCAS-2008, pp. 799-802.
Diebold, F., “Elements of Forecasting”. Second Edition. Thomson/South Western Publishing an ITP Company. Department of Economics University of Pennsylvania, 2001.
Gujarati, D. and Porter, D., “Basic Econometrics”. 5th Edition. McGraw-Hill Higer Education/Irwin. New York-USA. 2008.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Estimación Espectral de Series de Tiempo de Absorbancia UV-Vis para el Monitoreo de Calidad de Aguas
Spectral Estimation of UV-Vis Absorbance Time Series for Water Quality Monitoring
Leonardo Plazas Nossa
Universidad Distrital Francisco José de Caldas. Bogotá - Colombia,
lplazasn@udistrital.edu.co
Miguel A. Ávila A.
Universidad Distrital Francisco José de Caldas. Bogotá - Colombia,
maavila@udistrital.edu.co
Andres Torres
Pontificia Universidad Javeriana,
andres.torres@javeriana.edu.co
Recibido: 22/06/2016. Modificado: 20/01/2017. Aceptado: 20/02/2017.
Abstract
Background: Signals recorded as multivariate time series by UV-Vis absorbance captors installed in urban sewer systems, can be non-stationary, yielding complications in the analysis of water quality monitoring. This work proposes to perform spectral estimation using the Box-Cox transformation and differentiation in order to obtain stationary multivariate time series in a wide sense. Additionally, Principal Component Analysis (PCA) is applied to reduce their dimensionality.
Method: Three different UV-Vis absorbance time series for different Colombian locations were studied: (i) El- Salitre Wastewater Treatment Plant (WWTP) in Bogotá; (ii) Gibraltar Pumping Station (GPS) in Bogotá; and (iii) San-Fernando WWTP in Itagüí. Each UV-Vis absorbance time series had equal sample number (5705). The estimation of the spectral power density is obtained using the average of modified periodograms with rectangular window and an overlap of 50 %, with the 20 most important harmonics from the Discrete Fourier Transform (DFT) and Inverse Fast Fourier Transform (IFFT).
Results: Absorbance time series dimensionality reduction using PCA, resulted in 6, 8 and 7 principal components for each study site respectively, altogether explaining more than 97 % of their variability. Values of differences below 30 % for the UV range were obtained for the three study sites, while for the visible range the maximum differences obtained were: (i) 35 % for El-Salitre WWTP; (ii) 61 % for GPS; and (iii) 75 % for San-Fernando WWTP.
Conclusions: : The Box-Cox transformation and the differentiation process applied to the UV-Vis absorbance time series for the study sites (El-Salitre, GPS and San-Fernando), allowed to reduce variance and to eliminate tendency of the time series. A pre-processing of UV-Vis absorbance time series is recommended to detect and remove outliers and then apply the proposed process for spectral estimation.
Keywords:Box-Cox Transformation, Periodogram, Principal Components Analysis, Power spectral density, Stationarity, UV-Vis sensor.
Language: Spanish
Resumen
Contexto: Las señales registradas como de series de tiempo por sensores de espectrometría UV-Vis en diferentes instalaciones de saneamiento urbano, pueden ser no estacionarias, lo cual complica el análisis del monitoreo de la calidad del agua. Este trabajo propone realizar la estimación espectral aplicando la transformación de Box-Cox y la diferenciación con el fin de obtener series de tiempo estacionarias en sentido amplio y reducir su dimensionalidad con base en el análisis de componentes principales (PCA, por sus siglas en inglés).
Método:La metodología se aplica a series de tiempo de absorbancia UV-Vis para tres sitios de estudio en Colombia: (i) Planta para el tratamiento de agua residual (PTAR) El-Salitre (Bogotá); (ii) Estación de Bombeo Gibraltar (EBG) (Bogotá); y (iii) Planta para el tratamiento de agua residual (PTAR) SanFernando (Itagüí). Las series de tiempo de absorbancia UV-Vis se registran con igual tamaño de 5705 muestras. Se realiza la estimación de la densidad espectral mediante el promedio de eriodogramas modificados con ventana rectangular con un traslape del 50 %, utilizando en el procedimiento DFT (Discrete Fourier Transform) e IFFT (Inverse Fast Fourier Transform) con los veinte armónicos más relevantes.
Resultados:Al reducir la dimensionalidad de las series de tiempo de absorbancia con PCA, se obtienen para cada sitio de estudio seis, ocho y siete componentes principales respectivamente, explicando en conjunto más del 97 % de la variabilidad. Para los tres sitios de estudio, se obtuvieron valores de diferencias inferiores al 30 % para el rango UV, mientras que para el rango visible se obtiene máximas diferencias de: (i) 35 % para El-Salitre; (ii) 61 % para EBG; y (iii) 75 % para San-Fernando.
Conclusiones:Con la transformación de Box-Cox y el proceso de diferenciación aplicado a tres series de tiempo de absorbancia UV-Vis para los sitios propuestos de estudio, se logra reducir la varianza y se elimina la tendencia de las series de tiempo. Se recomienda realizar un pre-procesamiento de las series de tiempo de absorbancia UV-Vis para detectar y remover los valores extremos y posteriormente aplicar el proceso propuesto para la estimación espectral.
Palabras clave:Análisis por componentes principales, densidad espectral de potencia, estacionariedad, periodograma, sensor UV-Vis, transformación Box-Cox.
Idioma: Español
1. Introducción
El ciclo natural del agua se altera y se transforma en el ciclo urbano del agua. En este ciclo urbano el agua se utiliza en los asentamientos humanos (ciudades pequeñas, medianas y grandes) y se devuelve al ambiente con una calidad inferior [1]-[3]. Las actividades humanas han generado procesos que cambian el ciclo natural del agua tales como: (i) el agua se retira de un curso superficial (ríos), de un sistema subterráneo (pozos profundos) y de embalses naturales o construidos; (ii) es transportada a las plantas de tratamiento con el fin de lograr un nivel de calidad que permite su distribución (agua tratada se transportará a los usuarios por medio de bombas, tuberías y almacenes); (iii) se utiliza para diversas actividades de consumo humano; (iv) es recogida y transportado a través de un sistema de alcantarillado (aguas residuales); y (v) se envía a una Planta de Tratamiento de Aguas Residuales (PTAR), sometiéndola a diferentes procesos hasta llegar a un nivel de calidad que permite su retorno al medio ambiente [1]-[3]. Son posibles dos infraestructuras diferentes: sistema combinado o sistema separado [4], [5]. En el sistema combinado, el agua de lluvia y el agua residual utilizan el mismo sistema. En tiempo seco, todo el flujo es transportado y tratado en la PTAR, mientras que, en clima húmedo, como la escorrentía aumenta y puede superar la capacidad del sistema, los flujos de exceso son vertidos directamente (sin tratamiento) a las aguas receptoras a través de aliviaderos Combined Sewer Overflows (CSOs, por sus siglas en inglés) [1]. Así, agua de escorrentía se devuelve al medio natural con o sin tratamientos limitados (estanques de retención, cuencas de infiltración, sistemas de bio-filtración, sistemas de humedales, etc.), debido al alto volumen a tratar [6], [7].
La creciente impermeabilidad en las zonas urbanas trae cambios significativos en las propiedades de la tierra. En particular, la vegetación nativa se reduce y se limitan los patrones de drenaje natural que interceptan, almacenan e infiltran el agua lluvia [8]. Elárea impermeable efectiva en una cuenca hidrográfica es elárea impermeable conectada directamente con el sistema de drenaje de escorrentía y que contribuye a aumentar los volúmenes hidrológicos. La creciente urbanización genera impactos ambientales negativos en los ecosistemas acuáticos desde el punto de vista hidrológico, físico-qu ímico y biológico. En efecto, diferentes productos químicos (contaminantes) se han identificado en aguas residuales y de escorrentía pluvial que podr ían afectar a la salud humana y la vida acuática, tales como sólidos, trazas de metales, cloruro, nutrientes (N y P), pesticidas, hidrocarburos aromáticos policíclicos y bacterias, entre otros [6], [9]. Además, la calidad del agua es consecuencia de fenómenos naturales y el actuar del ser humano, además es una función de uso del suelo en el área de captación. Hoy en día se reconoce que la forma en que los seres humanos utilizan y ocupan la tierra tiene una implicación directa en la calidad del agua y, por lo tanto, se preconiza que el control de calidad del agua se asocia con una planificación global a nivel deárea de captación entera y no de forma individual para cada fuente que recibe un impacto directo [10], [11].
Por otro lado, los avances relacionados con laóptica y la electrónica en lasúltimas décadas, han permitido obtención de instrumentos robustos a pequeña escala aplicados a la espectrometría Ultravioleta y Visible (UV-Vis) de espectro completo. Tales instrumentos o sensores se utilizan en el monitoreo de la calidad de aguas en línea [12]. Los sensores o captores de espectrometría UV-Vis (rango entre 200 nm y 745 nm, son 219 longitudes de onda, con separación de 2,5 nm) son dispositivos que registran la atenuación de la luz, este proceso se conoce como absorbancia y registran valores de calidad de aguas en tiempo cuasi-continuo (espectro de absorbancia registrado por minuto). Se utilizan estos captores UV-Vis in-situ y en línea en las plantas para el tratamiento de agua residual (PTAR) en el monitoreo de las entradas y las salidas en estas, también en el monitoreo de iferentes etapas de tratamiento de la calidad del agua, con el objetivo de determinar la dinámica de cargas contaminantes y eficiencia en los procesos de remoción o de eliminación de nitratos, nitritos, materiales orgánicos (v.g. demanda química orgánica y demanda bioquímica de ox ígeno) y sólidos totales en suspensión [13]-[15]; se pueden ajustar diferentes escalas de tiempo y utilizar esa información como herramienta complemento en sistemas de toma de decisiones en tiempo real.
En estos sensores se deben realizar procesos para su calibración, esta puede ser de tipo global o de tipo local [16]-[18]. Se debe realizar el procesamiento y análisis de dichas series de tiempo con el fin de estimar la densidad espectral para descubrir su comportamiento periódico que puede estar oculto [19]-[21]. Si estas series de tiempo son no estacionarias en media y varianza, será necesario realizar las respectivas transformaciones sobre estas para obtener series de tiempo estacionarias en sentido amplio y poder aplicar procesos lineales, comprendiendo el comportamiento del fenómeno que las genera y si es posible aplicar técnicas de pronóstico para complementar procesos de control en tiempo real en las PTAR [22].
Este trabajo propone analizar los espectros de absorbancia UV-Vis que son registrados por los sensores instalados en diferentes sistemas utilizados para el saneamiento urbano, por medio de la transformación de Box-Cox para reducir la varianza y eliminar la tendencia [23], [24], también realizar la estimación espectral de series de temporales y poder interpretar el comportamiento que puede estar oculto [25], [26]. El análisis propuesto se aplicó a tres diferentes series de tiempo multivariadas de espectros UV-Vis registrados en tres diferentes sitios de estudio: (i) entrada PTAR El-Salitre (Bogotá); (ii) EBG (Bogotá); (iii) entrada PTAR San-Fernando (Itagüí).
2. Materiales y métodos
2.1. Sensores UV-Vis
Se utilizaron sensores UV-Vis de la compañía austriaca s::can (spectro::lyserTM) son instrumentos sumergibles de 44 mm de diámetro y de 64,7 cm de longitud, una lámpara de Xenón que actúa como fuente luminosa y un conjunto de foto-detectores que registran la absorbancia en un aproximado tiempo continuo (un espectro de absorbancia por minuto). Los espectros de absorbancia se encuentran en el rango desde el Ultravioleta-UV y Visible-Vis (200 nm - 750 nm) con pasos de 2,5 nm para un total de 219 longitudes de onda y ofrecen resultados en tiempo real [27], [28]. Los espectrómetros UV-Vis realizan una medición de la absorbancia de la luz en longitudes de onda desde ultravioleta a visible. La absorbancia es generada por partículas disueltas o en suspensión. Estos sensores son capaces de registrar y proporcionar información del orden de una medición por minuto, que puede traducirse en términos de concentraciones equivalentes tales como Sólidos Suspendidos Totales (SST), Demanda Química de Oxígeno (DQO), nitratos, nitritos, entre otros. Además, cuenta con un sistema de limpieza automática por aire o agua [27]-[29]. La medición es realizada directamente en el sitio (in situ) sin necesidad de realizar el muestreo y el tratamiento a las muestras. Por lo tanto, mediante estos sensores es posible obtener una medición confiable y a alta resolución, puesto que una sola medición toma generalmente cerca de quince segundos [17], [29], [30].
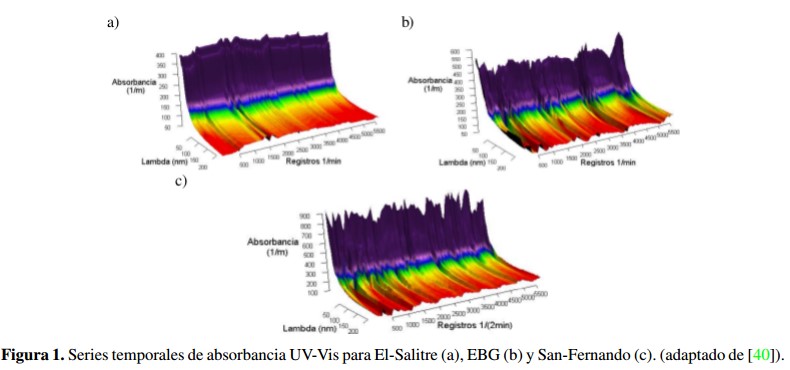
El proceso de análisis propuesto se aplicó en series temporales con una longitud de 5705 espectros de absorbancia para cada uno de los sitios de estudio: (i) El-Salitre, desde 29-06-2011 -09:03 h hasta 03-07-2011 - 17:33 h con una configuración temporal de un espectro por minuto; (ii) Estación Bombeo Gibraltar (EBG) desde 18-10-2011 - 11:08 h hasta 22-10-2011 -15:21 con una configuración temporal de un espectro por minuto; y (iii) San-Fernando desde 24-09-2011 - 06:04 h hasta 02-10-2011 - 09:16 h con una configuración temporal de un espectro por cada dos minutos como se observa en la Figura 1.
2.2. Series de tiempo estacionarias y no estacionarias
Cuando se analizan series de tiempo, estas pueden clasificarse en estacionarias y no estacionarias. Una serie de tiempo estacionaria es estable a lo largo del tiempo, es decir, su media y su varianza son constantes en el tiempo [19], [22], [35], [36]: los valores de la serie de tiempo tienden a oscilar alrededor de una media constante y la variabilidad respecto a la media también permanece constante en el tiempo. Una serie de tiempo no estacionaria se caracteriza porque la tendencia o variabilidad cambian en el tiempo [22]. Los cambios en la media determinan una tendencia a crecer o decrecer a largo plazo, por lo que la serie no oscila alrededor de un valor constante [44], [46]. Pueden permanecer durante periodos largos con valores por encima o por debajo de la media, debido a la presencia de una tendencia determin ística, al problema de ra íces unitarias o a la presencia de una varianza heterocedástica. Las series de tiempo no estacionarias pueden transformarse en series de tiempo estacionarias aplicando los correspondientes procedimientos. Las series de tiempo pueden ser no estacionarias en media y no estacionarias en varianza [36].
A las series de tiempo no estacionarias en varianza se requiere realizar la transformación de estabilización de su varianza, para que esta sea constante. George E. P. Box y David Cox en 1964, propusieron aplicar transformaciones de potencias [23], [24], como se indica en la ecuación 1.
donde, xt es la serie de tiempo y lambda λ es el parámetro que se agrega para obtener la estabilización en varianza [23]-[25].
Se realiza la transformación a cada una de las 219 series de temporales para cada sitio de estudio; siendo estas series de tiempo no estacionarias. Se reduce la varianza calculando el logaritmo natural a cada dato de la serie de tiempo. Cuando la serie de tiempo es no estacionaria en varianza, es posible transformarla en una serie de tiempo estacionaria en media utilizando la ecuación 2. En este proceso la longitud de valores de la serie de tiempo se reduce en uno. Cuando se realiza el proceso inverso, la longitud de la serie de tiempo vuelve a tener el valor original [33], [34].
2.3. Análisis por componentes principales - adaptado de [37], [39]
Con las series de temporales UV-Vis estacionarias en media y varianza, el siguiente paso consta en realizar la correspondiente transformación de tipo lineal, hallando un nuevo sistema de ejes coordenados utilizando de los valores originales. En el nuevo sistema de ejes coordenados, la mayor variabilidad de la información es retenida por el primer eje, que es conocido como primer componente principal; la siguiente mayor variabilidad es retenida por el segundo eje, la tercer siguiente variabilidad es retenida por el tercer eje y se continua con todas las demás variabilidades de los valores originales. Esta transformación de tipo lineal se base en la matriz de covarianza. Por consiguiente, se transforma conjunto de datos X que tiene dimensiones n x m, donde n es el número de observaciones y m el número de variables, a otro conjunto de datos de menor dimensión n x l, donde n sigue siendo el número de observaciones y l es el número de componentes principales. Este nuevo conjunto de datos es menor que m y presenta la mínima pérdida en la cantidad de informaciónútil. El proceso comienza encontrando la matriz de covarianzas que relaciona todas las variables de los valores originales como lo indica la ecuación 3.
donde N indica el número total de datos y n es cada uno de los valores en la matriz.
Es sugerido que para la transformación los valores no deben tener media diferente de cero, esto se consigue restando cada valor del promedio en cada columna (variable) como se muestra en la ecuación 4
donde i es cada uno de los valores por cada columna en la matriz de datos.
El proceso continúa obteniendo los datos normalizados, se utiliza la ecuación 5.
donde i hace referencia a los valores en cada una de las columnas en la matriz y es la desviación estándar de cada columna en la matriz de datos.
Se obtienen los autovalores y los autovectores de la matriz de covarianza, esto permite obtener las componentes principales (Principal Component-PC) como lo indica la ecuación 6.
Después de cualquier proceso realizado sobre las componentes principales, es necesario hacer la transformación inversa reconstruyendo los datos con el fin de retornar a las dimensiones originales mediante la ecuación 7; esta ecuación se aplicará después de haber realizado el proceso de transformación del dominio del tiempo al dominio de la frecuencia, realizar el pronóstico y aplicar la transformada inversa del dominio de la frecuencia al dominio del tiempo.
2.4. Análisis espectral
La estimación de la densidad espectral de potencia, Power Spectral Density (PSD, por sus siglas en inglés) de una señal estacionaria permite identificar periodicidades ocultas, estimar la entropía de la señal para comprimirla con o sin pérdidas, o proporcionar información sobre la dinámica interna de un sistema (su función de transferencia). Se realiza una estimación de la PSD de la señal, porque según la naturaleza estocástica de la señal, no es posible determinar la PSD con exactitud [38], [41].
Se puede realizar la estimación espectral por uno de dos posibles métodos: (i) clásicos o no paramétricos, para los cuales se estima la secuencia de autocorrelación a partir de un conjunto de datos y calculando la transformada de Fourier de la secuencia de autocorrelación estimada se obtiene una estimación del espectro; y (ii) no clásicos o paramétricos, los cuales utilizan un modelo (AR, MA, ARMA, etc.) determinado del proceso para estimar el espectro de potencia [42], [43].
La estimación espectral se realiza por medio del método clásico o no paramétrico, asumiendo que la señal es estacionaria en el sentido amplio (Wide-Sense Stationarity WSS). Una señal es estacionaria en sentido amplio, si esta tiene media constante y su función de autocorrelación solo depende del lapso de tiempo transcurrido entre dos periodos [42]. Cuando se tiene una señal discreta (con tiempo determinado), para estudiar e inferir las propiedades del proceso que la genera, un estimado de la densidad espectral es el periodograma, siendo este estimado la magnitud al cuadrado de la transformada discreta de Fourier (DFT) [42], [44] de la secuencia de datos como se indica en la ecuación 8.
donde N es el número de datos y Xk es la DFT de la secuencia de datos como lo indica la ecuación 9.
Con la estimación del periodograma se presenta el problema de enmascaramiento espectral y es necesario realizar otro proceso con el fin de obtener el decremento de la varianza del periodograma. Los algoritmos de Barlett y de Welch calculan la media de múltiples periodogramas de D segmentos de longitud L, estos pueden o no estar traslapados, a partir de los cuales se debe obtener valor promedio de los periodogramas obtenidos en cada segmento [45]. El proceso aplicado es el de promedio de periodogramas modificados con ventana rectangular con un traslape del 50 %. Se aplica la matemática modular para determinar el número de segmentos D con tamaño L [31].
Al realizar la estimación espectral de la señal en el dominio de la frecuencia es necesario realizarel proceso de transformación inversa utilizando la IFFT (Inverse Fast Fourier Transform) [44], como lo indica la ecuación 10.
Para comparar los resultados obtenidos se utiliza el cálculo del porcentaje de diferencia absoluto o APD (Absolute Percentage Difference) como lo indica la ecuación 11.
donde Valoriginal es el valor de absorbancia original de cada serie de tiempo y Val obtenido es el valor resultante de absorbancia al aplicar el proceso de análisis espectral [46], [47].
3. Metodología de aplicación del modelo AHP
Antes de presentar los resultados de este trabajo se realizará una discusión del método propuesto según los trabajos y resultados obtenidos por otros investigadores. El método propuesto es considerado como el pre-procesamiento que se debe aplicar a las series de tiempo multivariadas. Las series de tiempo de absorbancia UV-Vis analizadas no son estacionarias y, como varios trabajos lo indican, estas deben ser sometidas a procesos de transformación con el fin de estabilizarlas en varianza y obtener una distribución normal tal como lo indican [24] y [26]. En estos trabajos los autores pre-procesan diferentes series de tiempo (financieras, imágenes, enfermedades, etc.) utilizando la transformación de Box-Cox y varios procesos para encontrar el mejor valor para el parámetro. Los estudios indican que si el valor para es mayor a 1 el resultado de la transformación es de tipo convexo, si el valor es igual a 1 los datos no sufren cambios y si el valor está entre 0 y 1 el resultado de la transformación es de tipo cóncavo. Existen alternativas para obtener elóptimo valor de: los autores del trabajo [26] indican que para predicción en series de tiempo de tipo financieras el mejor valor es 0,5 y que para el caso lognormal el valor a utilizar es 0. Cuando las series de tiempo son multivariadas es necesario realizar la reducción de la dimensionalidad con el fin de procesar más rápido las series de tiempo: el trabajo presentado por [24] utiliza imágenes con resolución de 64x64 y aplica PCA para reducir la dimensionalidad a 158 componentes capturando una variabilidad del 99 %. Respecto al análisis espectral, los autores del trabajo [31] aplican el análisis espectral a sistemas de comunicación basados en OFDM. Los autores indican que utilizando periodogramas Barlett-Welch, el valoróptimo (reducciónóptima de la estimación de la varianza) del traslape de estos es del 50 %. Este valor garantiza que el promedio de los periodogramas obtenidos con la FFT permite encontrar los harmónicos relevantes que en el dominio de la frecuencia representa la serie de tiempo analizada. Después se aplica la transformación inversa IFFT para retornar al dominio del tiempo y obtener la serie de tiempo que representa el fenómeno en estudio. Si se ha aplicado PCA se debe realizar la transformación inversa PCA-1.
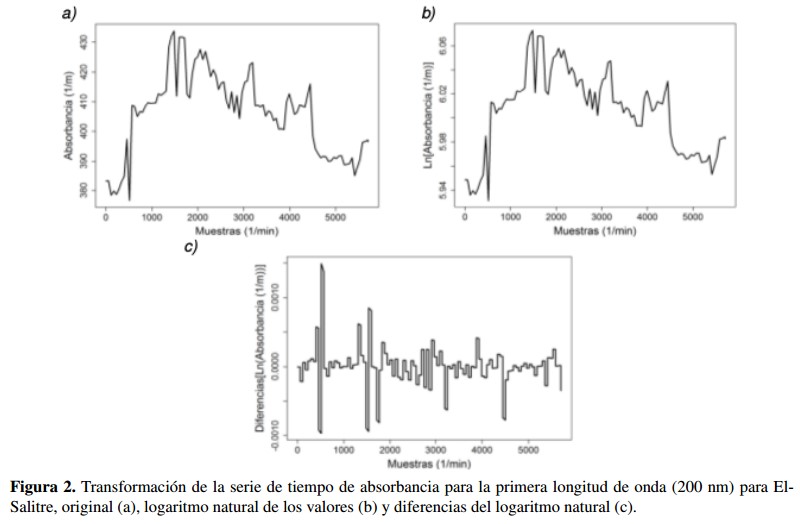
Se aplica el proceso descrito en la sección 2.2 a todas las series de temporales de absorbancia registradas por los sensores instalados en los sitios para el presente estudio. Como ejemplo, la Figura 2 muestra la transformación realizada a la primera longitud de onda (200 nm) para el sitio de estudio El-Salitre.
La Figura 2a muestra que la serie de tiempo original tiene un rango de valores desde 370 a 441 unidades de absorbancia UA (1/m). En la Figura 2b se observa la transformación para la reducción de la varianza teniendo la nueva serie de datos un rango de valores desde 5.93 UA a 6.07 UA y finalmente en la Figura 2c se observa que el resultado de la diferenciación de la serie de tiempo, esta se encuentra oscilando alrededor del valor 0.0 UA. Igual proceso se aplicó a las demás longitudes de onda y a los otros sitios de estudio.
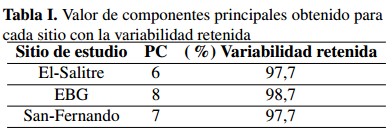
Con la series de tiempo de absorbancia se rea-liza la transformación lineal por el análisis de componentes principales para reducir la dimen-sionalidad del problema. La Tabla I muestra el número de componentes principales (PC) utili-zados para cada sitio de estudio con el porcen-taje de variabilidad que recogen estas PC.
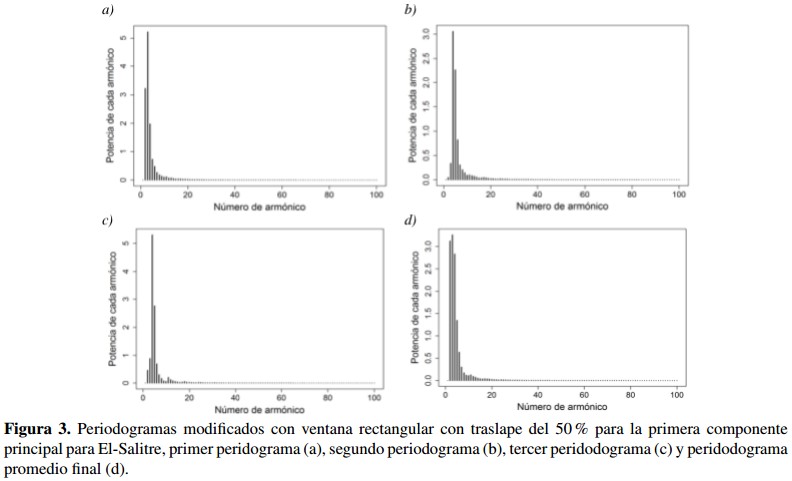
Con el número de componentes principales establecido, se realiza el proceso del análisis espectral para cada una de estas y para cada sitio de estudio. Se determinan 30 segmentos cada uno con 368 valores y con un traslape de 184 valores. La Figura 3 se muestra, como ejemplo, los periodogramas obtenidos para la primera componente principal y para el sitio de estudio El-Salitre.
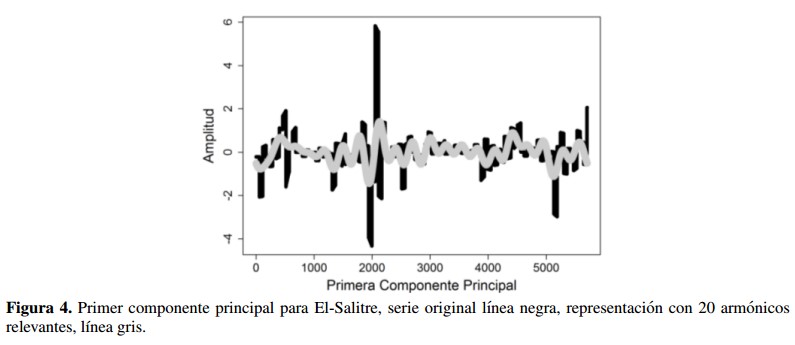
En la Figura 3 se muestran como ejemplo los tres primeros periodogramas (3a, 3b y 3c) para la primera componente principal y el periodograma promedio para El-Salitre. También se obtienen los periodogramas promedio finales para el resto de las componentes principales para este sitio de estudio y para los otros dos sitios de estudio. Entonces de cada periodograma promedio se toman los veinte armónicos más relevantes en el dominio de la frecuencia y se realiza el proceso inverso utilizando la IFFT retornando al dominio del tiempo como se observa en la Figura 4.
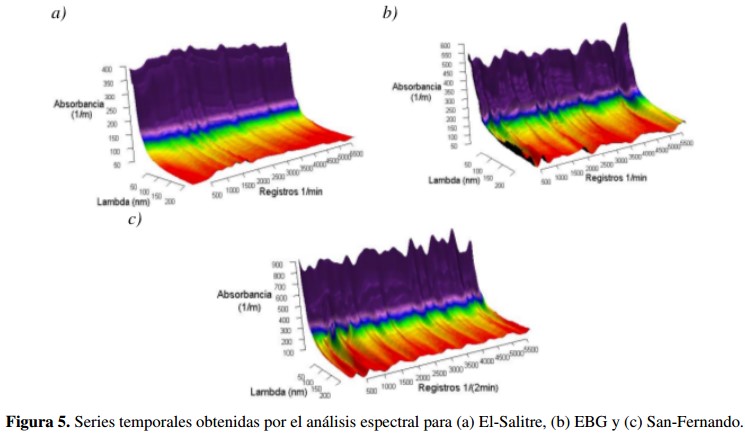
La Figura 4 muestra para la primera componente principal del sitio El-Salitre, el resultado al utilizar veinte armónicos más relevantes del dominio de la frecuencia en el análisis espectral para representar la señal. Finalmente se realiza el proceso de transformación de Box-Cox inverso para obtener los valores de absorbancia resultantes, como se observa en la Figura 5.
La Figura 5 muestra el resultado del proceso de análisis espectral para encontrar el periodograma y los valores de los armónicos que representan las series de tiempo en el dominio de la frecuen-cia. En este proceso se han utilizado los veinte armónicos más relevantes para cada componente principal que representan la serie de tiempo para cada uno de los sitios de estudio.
En la Figura 5 las series temporales obtenidas son similares a las presentadas en la Figura 1 pero son el resultado del proceso de estimación espectral utilizando el PCA. Lo anterior permite utilizar esta información, reducida en dimensionalidad y cantidad de armónicos, en proceso o metodología para realizar el pronóstico de la calidad del agua.
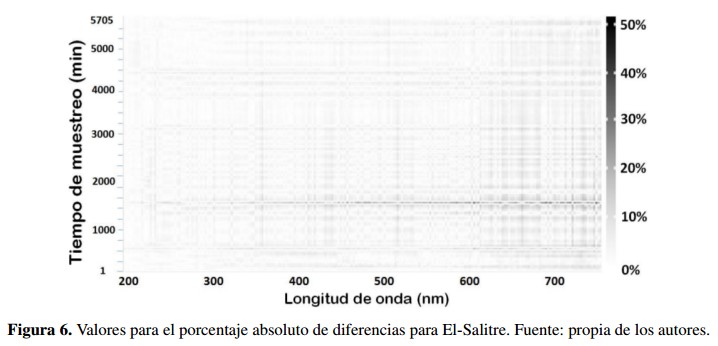
La Figura 6 muestra la distribución de los valores de los porcentajes absolutos de diferencia obtenidos (diferencia entre los valores de absorbancia originales y los obtenidos al aplicar el proceso de análisis espectral) para el sitio de estudio PTAR Salitre.
La Figura 6 muestra la distribución de los valores de los porcentajes absolutos de diferencia para el sitio estudio El-Salitre. Estos valores están en el rango de 0.0 % hasta el 34.9 %. Se observa que para las longitudes de onda en al rango UV (200.0 nm - 380.0 nm) los porcentajes de error absoluto no superan el 17.4 %. También se observa que para el rango Visible (382.5 nm - 745.0 nm) y para los tiempos de muestreo de 1530 a 1550 min, se encuentran los mayores valores de diferencia (de 2.5 % a 34.9 %). Para el resto de los tiempos de muestreo los errores no superaron el 27 %.
Para la EBG los valores de APD están en el rango de 0.0 % hasta el 60.8 %. Sin embargo para los tiempos de muestreo de 3750 a 3780 los valores de diferencia superaron el 30 %, para el resto de los tiempos de muestreo las diferencias no superaron el 30 %.
Para San-Fernando los valores están en el rango de 0.0 % hasta el 75.5 %. Estos resultados se pueden deber por las características de las series de tiempo de absorbancia, dado que en los tiempos de muestreo 408 a 474 min, los valores de diferencia superaron el 40 %. Para el resto de los tiempos de muestreo las diferencias no superaron el 40 %.
4. Conclusiones
Con la transformación de Box-Cox y el proceso de diferenciación aplicado a las series temporales UV-Vis para los sitios de estudio (El-Salitre, EBG y San-Fernando), se logra reducir la varianza y se elimina la tendencia de las series de tiempo. Esto implica que se obtienen señales estacionarias en el sentido amplio y a estas se les puede aplicar diferentes transformaciones lineales.
Se utiliza el proceso PCA (como transformación de tipo lineal con base en la matriz de covarianza) a las series temporales reduciendo su dimensionalidad para los sitios de estudio, se utilizan seis componentes principales para El-Salitre, ocho componentes principales para EBG y siete componentes principales para San-Fernando. Consecuentemente, las componentes principales explican (capturan) más del 97 % de la variabilidad para todas las series temporales estudiadas. Esto implica que se reduce el análisis y procesamiento de las series temporales UV-Vis en tiempo y se podría utilizar en procesos de tratamiento del agua en tiempo real.
El proceso aplicado es el promedio de periodogramas modificados con ventana rectangular con un traslape del 50 %; se puede estimar el comportamiento periódico que podría estar oculto si no se realiza este procedimiento. Se utilizan los veinte armónicos relevantes en el dominio de la frecuencia para representar el comportamiento de las series temporales UV-Vis para cada sitio de estudio. Esto implica que además de realizar la estimación espectral, el procedimiento se puede utilizar como un filtro para detectar valores atípicos (outliers).
Los valores de porcentaje absoluto en los que difieren los valores originales y los obtenidos por el proceso de estimación espectral para los tres sitios de estudio indican que para el espectro UV se obtiene las menores diferencias con valores menores al 30 % y para el rango Visible se obtienen los mayores valores. Esto implica que al obtener los mayores valores de porcentaje absoluto en las diferencias, podría indicar la presencia de un valor o valores atípicos (outliers). Se recomienda realizar un pre-procesamiento de series temporales UV-Vis con el fin de detectar y remover los valores atípicos y posteriormente aplicar el proceso propuesto para la estimación espectral.
El método de estimación espectral se puede utilizar como primer paso de pre-procesamiento en un sistema de pronóstico de la calidad del agua en tiempo real debido a que su implementación no es compleja ni costosa computacionalmente, lo cual es un aspecto clave si se tiene en cuenta el periodo de muestreo del sensor (una medición por minuto).
5. Agradecimientos
Los autores agradecen a la Empresa de Acueducto y Alcantarillado de Bogotá - EAAB (Contrato Administrativo No. 9- 0725100-0763-2010), a Empresas Públicas de Medellín (EPM) por suministrar las series temporales utilizadas en este trabajo. El procesamiento de la información se realizó en la colaboración del Centro de Computación de Alto Desempeño (CECAD) de la Universidad Distrital Francisco José de Caldas, Bogotá D.C., Colombia. (https://cecad.udistrital.edu.co).
Referencias
[1] Poch, M., Cortés, U., Comas, J., Rodríguez-Roda, I. and Sanchez-Marre, M., "Decisions on urban water systems: some support". University of Girona, First Edition, Servei de Publicacions, Spain 2012. "212, 213
[2] Garcia, X., Barceló, D., Comas, J., Hadjimichael, A., Page, T. and Acuña, V., "Placing ecosystem services at the heart of urban water systems management". Science of the Total Environment 563-564, 2016, pp. 1078-1085. "212
[3] Morales-Torres, A., Escuder-Bueno, I., Andres´-Domenech, I. and Perales-Momparler, S., "Decision Support Tool for energy-efficient, sustainable and integrated urban stormwater management". Environmental Modelling & Soft-ware 84, 2016, pp. 518-528. "212
[4] Akan, A. and Houghtalen, R., Urban Hydrology, Hydraulics, and Stormwater Quality: Engineering applications and computer modelling. John Wiley & Sons, Inc. Hoboken, USA. 2003. "212
[5] Dirckx, G, van Daele, S. and Hellinck, N., "Groundwater Infiltration Potential (GWIP) as an aid to determining the cause of dilution of waste water". Journal of Hydrology, 542, 2016, pp. 474-486. "212
[6] Marsalek, J., Jimenez´-Cisneros, B., Malmquist, P.-A., Karamouz, M., Goldenfum, J. and Chocat, B., "Urban water cycle processes and interactions". Published by the International Hydrological Programme (IHP) of the United Nations Educational, Scientific and Cultural Organization (UNESCO). Paris 2006."213
[7] Gosset, A., Ferro, Y. and Durrieu, C., "Methods for evaluating the pollution impact of urban wet weather discharges on biocenosis: a review". Water Research, 89, 2016, pp. 330-354 "213
[8] Palla, A. and Gnecco, I., "Hydrologic modelling of Low Impact Development systems at the urban catchment scale". Journal of Hydrology, 528, 2015, pp. 361-368. "213
[9] Fazi, S., Bandla, A., Pizzetti, I. and Swarup, S., "Microbial biofilms as one of the key elements in modulating ecohydrological processes in both natural and urban water corridors". Ecohydrology & Hydrobiology 16, 2016, pp. 33-38."213
[10] Von Sperling, M. and de Lemos., C., Wastewater Characteristics, Treatment and Disposal. First Edition. IWA Publishing. UK 2007."213
[11] Francois, C., Gondran, N., Nicolas, J.-P. and Parsons, D. "Environmental assessment of urban mobility: Combing life cycle assessment with land-use and transport interaction modelling-Application to Lyon (France)". Ecological Indicators, 72, 2017, pp. 597-604. "213
[12] Van den Broeke, J., "On-line and In-situ UV/Vis Spectroscopy: Real time multi parameter measurements with a single instrument". AWE International, 2007, pp. 55-59."213
[13] Gruber, G., Bertrand-Krajewski, J.-L., De Beneditis, J., Hochedlinger, M., & Lettl, W., "Practical aspects, ex-periences and strategies by using UVVIS sensors for long-term sewer monitoring". Water Practice & Technology, 2006, pp. 1-8. "213
[14] Rieger, L., Langergraber, G., Thomann, M., Fleischmann, N., and Siegrist, H. "Spectral in-situ analysis of NO 2 , NO 3 , COD, DOC and TSS in the effluent of a WWTP". Proccedings of AutMoNet - 2nd IWA Conference on Automation in Water Quality Monitoring, Vienna, 2004, pp. 29-36. "213
[15] Matsumoto, T. and Sanchez,´ I. "Desempeno˜ de la Planta de Tratamiento de Aguas Residuales de Sao˜ Joao˜ de Iracema (Brasil)". Revista Ingenier´?a 21(2), 2016, pp. 176-186. "213
[16] Salgado, R., Pinheiro, H. M., Ferreira, F., Saldanha, J., & Louren, N. "In situ UV-Vis spectroscopy to estimate COD and TSS in wastewater drainage sys- tems". Urban Water Journal, 2013, pp. 1-12. "213
[17] Torres, A., Lepot, M., & Bertrand-Krajewski, J.-L. "Local calibration for a UV/Vis spectrometer: PLS vs. SVM. A case study in a WWTP". Proccedings of 7th International Conference on Sewer Processes & Networks, 28 - 30 August - 2013, Sheffield, UK."213, 214
[18] Lepot M., Torres A., Hofer T., Caradot N., Gruber G., Aubin J.-B., Bertrand-Krajewski J.-L. "Calibration of UV/Vis spectrophotometers: A review and comparison of different methods to estimate TSS and total and dissolved COD concentrations in sewers, WWTPs and rivers". Water Research 101, 2016, pp. 519-534. "213
[19] Fei, W., & Bai, L. "Auto-Regressive Models of Non-stationary time series with finite length". Tsinghua Science and Technology 10(2), 2005, pp. 162-168."213, 215
[20] Kamarzarrin, M., Hosseini, S., Mehdi, M. and Kamarzarrin, M. "Designing and implementing of improved cry-ptographic algorithm using modular arithmetic theory". Journal of Electrical Systems and Information Technology, 2, 2015, pp. 14-17. "213
[21] Plazas-Nossa, L., Avila, M. and Torres, Andres. "Detection of Outliers and Imputing of Missing Values for Water Quality UV-VIS Absorbance Time Series". Revista Ingeniería, 2016, In press. "213
[22] Salcedo, G., Porto, R., and Morettin, P. "Comparing non-stationary and irregularly spaced time series". Computational Statistics and Data Analysis 56, 2012, pp. 3921-3934. "213, 215
[23] Huang, J., Kobayashi, M., and McAleer, M. "Testing for the Box-Cox parameter for an integrated process". Mathematics and Computers in Simulation, 83, 2012, pp. 1-9. "214, 215
[24] Bicego, M. and Baldo, S. "Properties of the Box-Cox transformation for pattern classification". Neurocomputing, 218, 2016, pp. 390-400. "214, 215, 218
[25] Tsiotas, G. "On the use of the Box-Cox transformation on conditional variance models". Finance Research Letters, 4, 2007, pp. 28-32. "214, 215
[26] Proietti, T., and Lutkepohl,¨ H. "Does the Box-Cox transformation help in forecasting macroeconomic time series?". International Journal of Forecasting 29, 2013, pp. 88-99. "214, 218
[27] Langergraber, G., Fleischmann, N., Hofstaedter, F., & Weingartner, A. "Monitoring of a paper mill wastewater treatment plant using UV/VIS spectroscopy". IWA Water Science and Technology, 49(1), 2004, pp. 9-14."214
[28] s::can. "Manual ana::pro Version 5.3 September 2006 Release". Messtechnik GmbH, Vienna, Austria 2006."214
[29] Zamora, D., Métodos Machine Learning aplicados para estimar la concentración de los contaminantes de la DQO y de los SST en hidrosistemas de saneamiento urbano a partir de espectrometría UV-Visible. Tesis de Maestría, 2013, Pontificia Universidad Javeriana, Bogotá -Colombia. "214
[30] Winkler, S., Saracevic, E., Bertrand-Krajewski, J.-L. and Torres, A., "Benefits, limitations and uncertainty of in situ spectrometry". Water science and technology 57(10), 2008, pp. 1651-8. "214
[31] Harjula, I., Hekkala, A., Matinmikko, M., and Mustonen, M., "Performance Evaluation of Spectrum Sensing Using Welch Periodogram for OFDM Signals". IEEE 73rd Vehicular Technology Conference (VTC Spring), 2011, pp. 1-5. "217, 218
[32] Zhang, S., .Adaptive spectral estimation for nonstationary multivariate time series". Computational Statistics and Data Analysis 103, 2016, pp. 330- 349. "
[33] Chong, T.-L., "Estimating the differencing parameter via the partial autocorrelation function". Journal of Econo-metrics, 97, 2000, pp. 365-381."215
[34] Hassler, U., "Persistence under temporal aggregation and differencing".Economics Letters, 124, 2014, pp. 318-322."215
[35] Shen, Ch. "A comparison of principal components using TPCA and nonstationary principal component analysis on daily air pollutant concentration series". Physica A, 467, 2017, pp. 453-464."215
[36] Stavropoulos, C., and Fassois, S., "Non-stationary functional series modeling and analysis of hardware reliability series: a comparative study using rail vehicle interfailure times". Reliability Engineering and System Safety, 68, 2000, pp. 169-183."215
[37] Shlens, J., "A Tutorial on Principal Component Analysis". La Jolla, California, USA: Salk Institute for Biological Studies, 2009, pp. 1-13."215
[38] Barbour, A., and Parker, R., "psd: Adaptive,sine multitaper power spectral density estimation for R". Computers and Geosciences, 63, 2014, pp. 1-8"217
[39] Bogdan,I. and Istrate, C. "The analysis of the principal components of the financial reporting in the case of Romanian list ed companies". Procedia Economics and Finance, 20, 2015, pp. 553-561."215
[40] Plazas-Nossa, L., Ávila, M. and Moncada, G. "Estimación del Exponente de Hurst y Dimensión Fractal para el análisis de series de tiempo de Absorbancia UV-VIS". Ciencia e Ingeniería Neogranadina, 42(2), 2014, pp. 133-143."214
[41] Lee, D., and Baldick, R., "Future Wind Power Scenario Synthesis Through Power Spectral Density Analysis". IEEE Transactions on Smart Grid, 5(1), 2014, pp. 490-500."217
[42] Bach, F. and Jordan, M., "Learning Graphical Models for Stationary Time Series". IEEE Transactions on Signal Processing, 52(8), 2004, pp. 2189-2199."217
[43] Lv, P., and Yue, L., "Short-Term Wind Speed Forecasting Based on Non-stationary Time Series analysis and ARCH model". Proccedings of International Conference on Multimedia Technology (ICMT), Hangzhou, China, 2011, pp. 2549-2553."217
[44] Proakis, J., and Manolakis, D. "Digital signal processing principles, algorithms, and applications". Fourth Edition. Pearson Prentice Hall, New Jersey, USA 2007."215, 217
[45] Tuffner, F., Pierre, J., and Kubichek, R. "Computationally Efficient Updating of a Weighted Welch Periodogram for Nonstationary Signals". 51st Midwest Symposium on Circuits and Systems MWSCAS-2008, pp. 799-802."217 [46]
[46] Diebold, F., "Elements of Forecasting". Second Edition. Thomson/South Western Publishing an ITP Company. Department of Economics University of Pennsylvania, 2001."215, 218
[47] Gujarati, D. and Porter, D., "Basic Econometrics". 5 th Edition. McGraw-Hill Higer Education/Irwin. New York-USA. 2008."218
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.


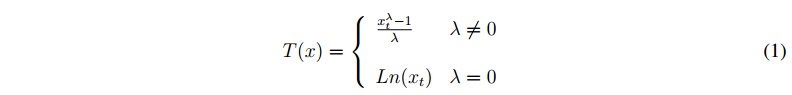
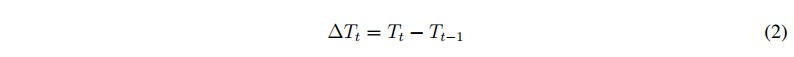
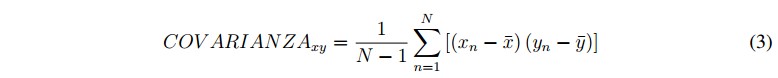
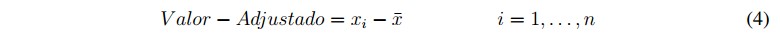
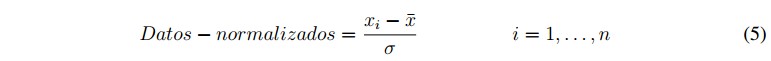
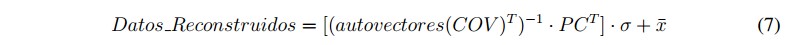
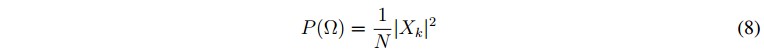
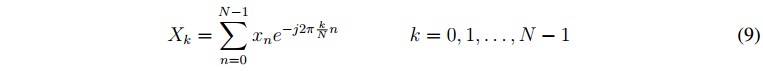

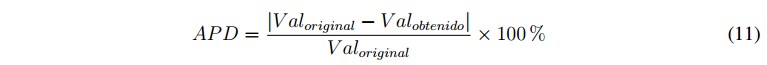



2.jpg)










