DOI:
https://doi.org/10.14483/udistrital.jour.reving.2017.1.a02Published:
2017-01-30Issue:
Vol. 22 No. 1 (2017): January - AprilSection:
Computational IntelligenceDel Operador Apertura en la Matemática Morfológica Difusa
On the Fuzzy Opening Morphological Operator
Keywords:
Erosion, interior, mathematical morphological, opening, operator (en).Keywords:
Operador Apertura, Erosión, Morfologia difusa (es).Downloads
References
J. Aguillón, S. Duarte, R. Herrera, Realce de candidatos a nódulo pulmonar en radiografías de tórax por medio de filtros de convergencia, Ingeniería, Universidad Distrital Francisco José de Caldas, 2014.
A. P. Ballesteros, L. C. López, R. Herrera Segmentación y conteo de las líneas de la nariz del feto en imágenes ecográficas de las 11-13+6 semanas de gestación, Ingeniería, Universidad Distrital Francisco José de Caldas, 2015.
R. Belohlávek, Fuzzy relational systems, Foundations and Principles, IFSR International Series on Systems, Science and Engineering, vol.20, Kluwer Academic/ Plenum Publishers, NewYork, 2002.
R. Belohlávek, T. Funiokova, Fuzzy Interior Operators, International Journal of General Systems, 2004.
N. Bunce, R. Mohiaddin, An Atlas of CONTRAST-ENHANCED ANGIOGRAPHY, The Parthenon Publishing Group, 2003.
N. Carmona, J. Elorza, J. Recasens, J. Bragard, Permutable fuzzy consequence and interior operators and their connection with fuzzy relations, Information Sciences, Volumen 310, 20 Julio 2015.
E. Dougherty, R. Lotufo, Hands on Morphological Image Processing, SPIE Publications, 2003.
J. Elorza, R. Fuentes-Gonzalez, J. Bragard, P. Burrillo, One relation between fuzzy closing morphological operators, fuzzy consequence operators induced by fuzzy preorders and fuzzy closure and co-closure systems, Fuzzy sets and systems, 2013.
W. Forero, Relaciones difusas inducidas por el operador morfológico clausurativo difuso, Trabajo de Grado, Universidad Distrital Francisco José de Caldas, 2015.
U. Höhle, Non-Classical Logics and their Applications to Fuzzy Subsets, Springer Science+Business Media, 1995.
A. R. Iturralde, Urgencias Urologicas, Ciencias Medicas, La Habana 2008.
J. Luna, C. Ochoa, Interior Operators and Topological Categories, Advances and Applications in Mathematical Sciences, vol. 10, Issue 2, 2011, pages 189-206, Mili Publications, Allahabad, India, 2011.
D. Pei, Fuzzy logic Algebras on Residuated Lattices, Southeast Asian Bulletin of Mathematics, 2004.
O. Salazar, J. Soriano, Las leyes de tercero excluido y contradicción como valores límite en lógica difusa, Ingeniería, Universidad Distrital Francisco José de Caldas, 2011.
G. Torrijos, Extracción de cuerpo de agua utilizando técnicas de análisis de mezcla y morfología matemática, Revista de Topografía Azimut, 2012.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2017.1.a02
Del Operador Apertura en la Matemática Morfológica Difusa
On the Fuzzy Opening Morphological Operator
Carlos Orlando Ochoa Castillo
Universidad Distrital Francisco José de Caldas.Bogotá-Colombia. karlos8ac@gmail.com
Wilson Javier Forero Baquero
Universidad Nacional de Colombia. Bogotá-Colombia. wilsonforerob@gmail.com
Recibido: 23-11-2015. Modificado: 13-04-2016. Aceptado: 25-07-2016
Resumen
Contexto: Las propiedades que posee un operador de interior se pueden trasladar a la determinación de características específicas de imágenes, las cuales, desde la matemática morfológica difusa pueden llegar a ser analizadas por medio del operador erosión y apertura, al conjugar estas ideas es pertinente indagar en torno a la naturaleza de estos operadores.
Método: Gracias a las propiedades reticulares que posee el análisis matemático de una imagen por medio de matemática morfológica difusa, se busca dotar de restricciones al elemento estructural con el cual se desea filtrar la imagen para así obtener caracterizaciones del operador apertura y erosión.
Resultados: Se demuestre que si la relación estructural es reflexiva o *-antitransitiva el operador apertura es interior; en caso que la relación cumpla ambas, la erosión es un operador interior.
Conclusiones:Los operadores morfológicos difusos permiten obtener información relevante sin alterar la estructural global de la imagen; arrojando mayor calidad que los métodos clásicos, en especial si se emplea el operador apertura difuso con una relación estructural adecuada.
Palabras clave: Apertura, erosión, interior, matemática morfológica, operador.
Idioma:Español.
Abstract
Context: Interior operators have interesting properties that can be used in detecting relevant features in digital images. In this respect, it is pertinent to study the behaviour of the opening and erosion operators from the perspective of fuzzy morphological mathematics.
Method: Bearing in mind the reticular properties inherent to the mathematical anaysis of an image by fuzzy morphological mathematics we seek to find restrictions on the structural element intended to filter the image so as to obtain characterizations of the opening and erosion operators.
Results: We prove that if the structural relationship is reflexive or *-antitransitive the opening operator is interior. On the other hand, we found that if the relationship meets both erosion is a interior operator.
Conclusions: The fuzzy morphological operators can give us more information than the classical methods when we filter an image, especially if we implement the opening operator with a right structural element.
Keywords:Erosion, interior, mathematical morphological, opening, operator.
1. Introducción
El estudio de imágenes diagnósticas por medio de contraste consiste en inyectar una tinta en el sistema circulatorio del paciente observando su flujo y posibles obstrucciones que determinan anomalías en el sujeto; de esta forma se buscan diseñar instrumentos y estrategias para la solución de tal problemática. En la matemática morfológica se han encontrado algunas respuestas de los análisis de las imágenes de operadores, filtros, entre otros [8], [1] pero la lógica clásica implementada en estos procesos limita la calidad de los resultados, como lo estudiado en [2], donde los autores describen problemas de ruido, detección de regiones apropiadas para realizar el análisis, debido a que la imagen está en una escala de grises y no solo en blanco o negro. Es por ello que la lógica difusa se convierte en un instrumento que ofrece la mayor información en la escala que se construya y al aplicar ciertos operadores, se obtendrá la información relevante para el diagnóstico perdiendo la menor cantidad de datos pero eliminando los posibles ruidos.
Un posible camino es estudiar los operadores de erosión y apertura para obtener la mayor cantidad de información en la menor cantidad de iteraciones en el proceso como se sugiere en [8].
2. Preliminares
Los operadores de erosión y apertura junto con sus propiedades demandan la presentación de algunos conceptos inherentes a la teoría de retículos y la lógica difusa, entre otros.
2.1 Retículos residuales
Definición 1: Sea 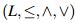 un retículo y * una operación binaria definida en L, se dice que
un retículo y * una operación binaria definida en L, se dice que
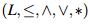 es un retículo residuado si existe una operació binaria
es un retículo residuado si existe una operació binaria 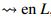 en L
, que satisface:
en L
, que satisface:
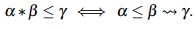
En caso de que 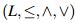 sea un retículo completo, entonces
sea un retículo completo, entonces 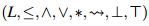 es un retículo residuado completo. La estructura anterior posee las siguientes propiedades
es un retículo residuado completo. La estructura anterior posee las siguientes propiedades
Lema 1. [11] , [14;] Sea 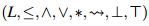 un retículo residuado completo, entonces para x, y,z elementos de L, se tiene que:
un retículo residuado completo, entonces para x, y,z elementos de L, se tiene que:
2.2 T- normas
Las normas triangulares [15], mejor conocidas como t-normas permiten una generalización de la intersección entre conjuntos difusos.
Definición 2. Una t- norma es una operación 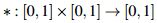 que satisface:
que satisface:
- Para todo x, y , z &# [ 0 ,1 ]
- * no es decreciente en ambos argumentos, es decir,
- 1 *x =x y 0*x=0 para todo x en [ 0 , 1 ]
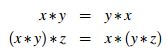

El concepto anterior, se relaciona con el de continuidad en [0,1] x [0,1], tal como se presenta en el siguiente,
Lema 2. [3] Sea 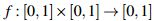 una operación binaria, si f es no decreciente en x entonces
f es continua a izquierda en x si y solo si para cualquier
una operación binaria, si f es no decreciente en x entonces
f es continua a izquierda en x si y solo si para cualquier 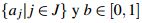 se cumple que :
se cumple que :
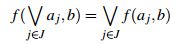
De la misma forma, f es continua a derecha si:
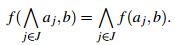
Dada la estructura de orden y topológica que el intervalo [0,1] posee como subespacio de ℝ, es
posible considerar la naturaleza de * con respecto al concepto de continuidad; desde esta perspectiva,
siguiendo a [3] se tiene que 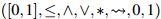 es un retículo residuado completo con *
una t-norma continua a izquierda.
es un retículo residuado completo con *
una t-norma continua a izquierda.
2.3 Relaciones difusas
En el desarrollo de la matemática difusa uno de los conceptos fundamentales es la de membresía o pertenencia de un elemento a un conjunto, el cual no está determinado únicamente con 0,1 sino que es multivaluado [11] modificando así la concepción de algunos conceptos entre los cuales se encuentran las relaciones internas de un conjunto.
Se define una relación difusa R mediante una función 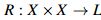 ;
igual que en el caso clásico es posible caracterizar las propiedades que posea, es por ello que se extiende el concepto de
preorden al ambiente difuso, con
;
igual que en el caso clásico es posible caracterizar las propiedades que posea, es por ello que se extiende el concepto de
preorden al ambiente difuso, con 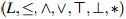 un retículo residuado completo (se entenderá
por
un retículo residuado completo (se entenderá
por 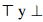 , el elemento máximo y mínimo respectivamente de la estructura).
, el elemento máximo y mínimo respectivamente de la estructura).
Definición 3 Sea 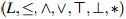 y X un conjunto, una relación difusa (binaria) R en X es un *-preorden difuso si satisface:
y X un conjunto, una relación difusa (binaria) R en X es un *-preorden difuso si satisface:
- R(x, x) = > para todo x ∈ X (Reflexiva)
- R(x, y) *R(y,z) = R(x,z) para todo x, y,z ∈ X (Transitiva).
Además del concepto de *-preorden difuso, aparecen de manera natural los conceptos de relación * -tolerante cuando R es reflexiva y simétrica i.e. R(x, y) = R(y, x) para todo x, y ∈ X; R es una relación * -equivalente si es un * - preorden difuso y es simétrica, junto a ello Rop es la relación opuesta de R, i.e. Rop (x, y) = R(y, x), en caso que se satisfaga que R(x, y)*R(y,z) ≥ R(x,z) se dirá que R es antitransitiva respecto a *.
3. Algunos operadores morfológicos difusos
Por medio de los operadores morfológicos es posible abarcar el reconocimiento de imágenes con el estudio de ciertos detalles específicos sin llegar a alterar la imagen global, sino actuando en elementos estructurales que se definan previamente; esto se logra a partir de los operadores de dilatación y erosión, los cuales son los elementos constitutivos de cualquier otro operador que se pueda definir. En las líneas que siguen, se entiende por elemento estructural a un subconjunto del conjunto en estudio.
En [9] se definen los operadores erosión y dilatación en 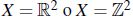 respectivamente por,
respectivamente por,
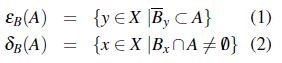
donde 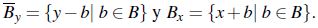
Se extienden las ideas anteriores tomando un conjunto arbitrario X y una relación difusa R la
cual es la proyección del concepto de elemento estructural y en consecuencia se denomina relación
estructural, así las ecuaciones (1) y (2) se definen en un contexto difuso por medio de  , se
denota a LX como el conjunto de todas las funciones de X en L, esto es, el conjunto de todos los
subconjuntos L.-difusos de X.
, se
denota a LX como el conjunto de todas las funciones de X en L, esto es, el conjunto de todos los
subconjuntos L.-difusos de X.
Definición 4.Dada una relación difusa 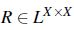 , los operadores erosión y dilatación de
, los operadores erosión y dilatación de 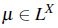 son,
son,
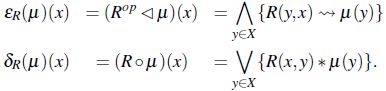
Con la composición de los operadores antes definidos es posible crear operadores que nos brinden
mayor exactitud en el reconocimiento de detalles específicos de una imagen [9], uno de ellos es el
operador apertura el cual consta de la composición del operador erosión seguido del operador dilatación,i.e.
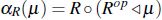 ; dicho operador es usado especialmente para eliminar regiones pequeñas y protuberancias.
; dicho operador es usado especialmente para eliminar regiones pequeñas y protuberancias.
Si se sustituye a 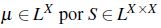 los conceptos previos se extienden como sigue,
los conceptos previos se extienden como sigue,
Definición 5. Sean 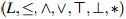 , X un conjunto y R, S
relaciones difusas en X. Las operaciones
, X un conjunto y R, S
relaciones difusas en X. Las operaciones 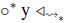 entre R y S
se define como,
entre R y S
se define como,
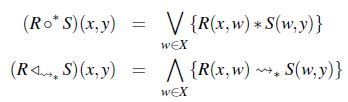
Por lo demostrado en [9] se tiene que 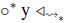 forman un par adjunto, esto es:
forman un par adjunto, esto es:
Teorema 1. ([9])Sean 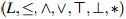 , X un conjunto y Q,R,S relaciones bonarias difusas en X entonces
, X un conjunto y Q,R,S relaciones bonarias difusas en X entonces
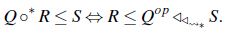
4. Relación estructural en los operadores de interior morfológicos difusos
Al abordar el estudio de las propiedades de los operadores apertura y erosión definidos en la sección anterior, se presentan otros objetos relacionados.
Definición 6: ([13],[15]) Un operador 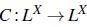 es un operador interior difuso en X si se verifica:
es un operador interior difuso en X si se verifica:
-
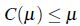 para todo subconjunto difuso
para todo subconjunto difuso 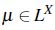 ,
, -
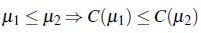 para todo
para todo 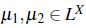 ,
, -
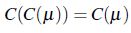 para todo
para todo 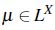 .
.
Se presenta el concepto de operador .-coherente con 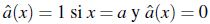 en otro caso
en otro caso
Definición 7. Sean 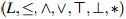 , X un conjunto y un operador
, X un conjunto y un operador 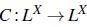 ; se dice que C es *-coherente si
; se dice que C es *-coherente si
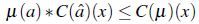
para todo 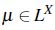 y para todo
y para todo 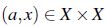 .
.
Lo anterior conlleva el siguiente enunciado,
Teorema 2. Sean 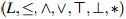 X un conjunto y
X un conjunto y 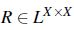 , los operadores
, los operadores 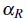 apertura y
apertura y 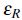 erosión son *-coherentes.
erosión son *-coherentes.
Demostración . Sea 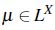 y
y 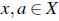
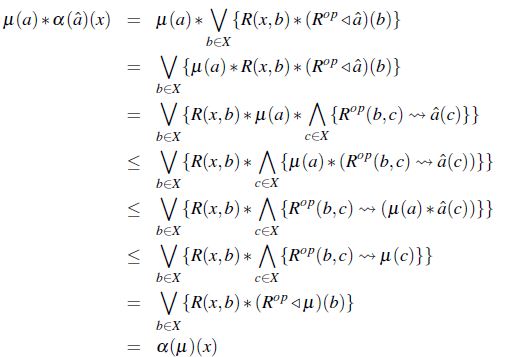
por lo tanto,
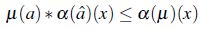
De manera análoga se tiene para 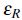 .
.
Es oportuno notar que lo afirmado es independiente de la relación estructural R que se tome, lo cual no ocurre al estudiar el concepto de interior con los operadores morfológicos en general, es necesario restringir a R, con lo cual se tiene que,
Teorema 3. Si R es reflexiva y Rop es *- antitransitiva entonces 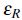 es un operador interior.
es un operador interior.
Demostración. Si 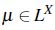 y
y 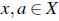
- De la definición de t-norma y la monotonía en el segundo argumento de
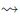 se satisface: si
se satisface: si
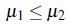 entonces
entonces 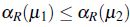 .
. - Por lo anterior solo resta verificar que
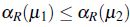 si R es reflexiva,
si R es reflexiva,
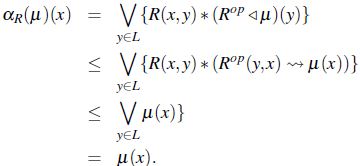
por tanto, 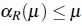
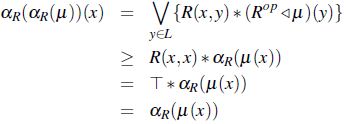
ahora si R es .-antitransitiva,
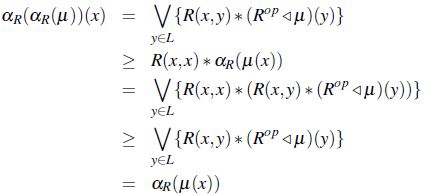
por lo tanto, en caso que R sea reflexiva o *-antitransitiva se satisface que:
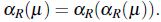
Los anteriores resultados, llevan a formularse la cuestión en torno a la relación entre los operadores erosión y apertura, con facilidad se tiene que
Corolario 1. Sea 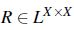 se tiene que para todo
se tiene que para todo 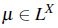
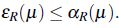
Al profundizar en las relaciones de *-equivalencia, se encuentra en [6] que el operador erosión posee las siguientes propiedades,
Lema 3. Sea R una relación de *-equivalencia, se satisfacen las siguientes propiedades,
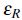 es un operador interior,
es un operador interior,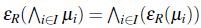 para cualquier
para cualquier 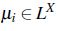 ,
,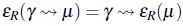 para cualquier constante
para cualquier constante 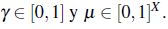
Tratando de formular lo correspondiente al operador apertura, se tiene el siguiente lema,
Lema 4. Sea R una relación de *-equivalencia, se satisfacen las siguientes propiedades,
-
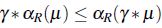 para cualquier
para cualquier 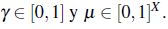
-
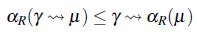 para cualquier constante
para cualquier constante 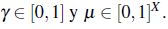
-
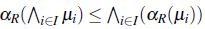 para cualquier
para cualquier 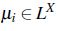 ,
,
Demostración. Con base en las propiedades del corolario 1 y el lema 3,
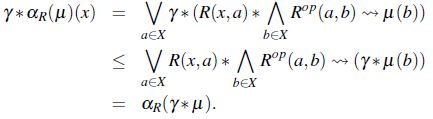
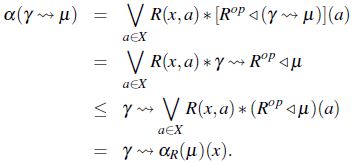
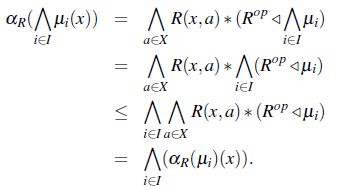
Con el objeto de relacionar los lemas anteriores se componen los operadores apertura y erosión,
Teorema 5. Sea R un *-equivalencia se tiene que,
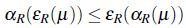
Demostración Es evidente que 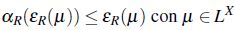 , además se tiene,
, además se tiene,
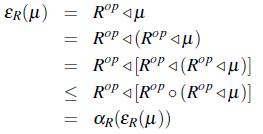
de lo anterior se tiene que,
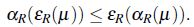
5. Aplicación
5.1. Materiales y Métodos
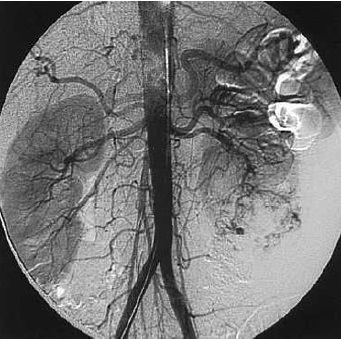
Un uso de los resultados presentados en la sección anterior se encuentra en el filtro de imágenes en escala de grises, lo cuál fue explorado por Forero en [10], en este caso se enfocará en imágenes médicas obtenidas por medio de contraste, la imagen que se implementará es una arteriografía por substracción digital con el método de Seldinger tomada de la Figura 1.7 de [12] en formato JPEG, con dimensiones 1441 x 1441 pixeles, para ello se implementó el lenguaje Python y el paquete pymorph el cual permite aplicar los operadores erosión y apertura en el caso clásico, admitiendo un elemento estructural binario.
Con el propósito de entender la interpretación que realiza el computador de la imagen de estudio es necesario observar la Figura 2, en ella se tiene la implementación de los operadores, erosión, apertura y dilatación en el caso clásico, lo cual consiste en trasladar el elemento estructural a la imagen original, en la Figura 2, el elemento estructural (observe el círculo rojo en la Figura 2) se sitúa en cada píxel; se toma en el caso de la dilatación la intersección del elemento estructural con la imagen y en caso de que alguno de los píxeles este pintando, se colorea el píxel, en caso contrario se deja en blanco, una explicación mas detallada del caso clásico de la implementación de cada uno de los operadores antes mencionados en lenguaje Matlab - Ptyhon puede verse en [7].

En algunos casos es complicado determinar la diferencia entre las líneas sanguíneas y los órganos, para ello se debe tener un rango en el cual se pueda filtrar qué elementos de la imagen son vitales para el diagnóstico del médico, esto se logra por medio del paquete OPENCV en Python, específicamente el comando inRange el cual permite filtrar la imagen extrayendo los colores que se determinen; en este caso se optó por una escala de grises obtenidas con ayuda de la conversión de la imagen en formato HSV con el comando COLOR_BGR2HSV del mismo paquete, lo anterior simula la función de pertenencia del conjunto difuso que se está formando, cuyos elementos son los píxeles de la imagen y su rango de pertenencia es obtenida tras la implementación del comando inRange.
Con los datos resultantes se procede a implementar el paquete pymorph y los códigos del operador apertura y erosión, con un elemento estructural generado por un arreglo de 4.4 píxeles ajustado de forma adecuada para comprobar los resultados teóricos presentados en la sección anterior (se tomo el paquete pymorph sin modificar el código fuente debido a que la t-norma que implementa es la del mínimo).
5.2 Resultados
Se tiene presente que al filtrar imágenes de resonancia por medio de contraste del tórax con el paquete pymorph se debe tomar un elemento estructural adecuado. Si se quiere observar rastros sanguíneos es óptimo utilizar líneas dentro de un arreglo de píxeles.
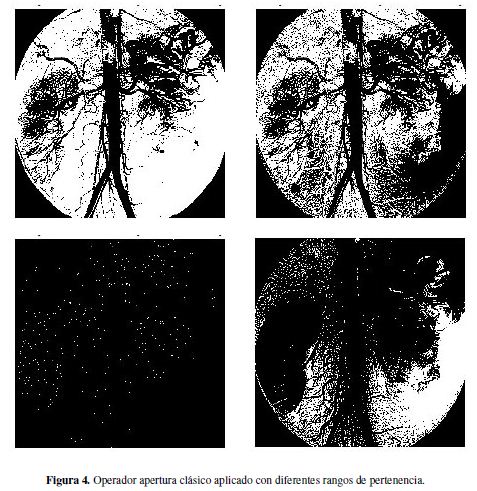
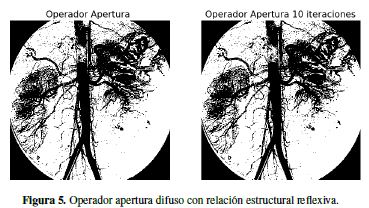
Es oportuno preguntar quí ocurre si solo se tiene el caso clásico de blanco y negro o una tonalidad de gris y negro. La Figura 4 se construye al tomar un rango de pertenencia dada por una tonalidad clara (inferior izquierda), oscura (inferior derecha) y media (superior derecha) del color gris (en formato RGB son respectivamente, (211,211,211), (120,120,120) y (173,173,173)) y se aplica el operador apertura a cada una de las imágenes generadas al aplicar el rango de pertenencia a la imagen original. Al unir estos intervalos de pertenencia en la escala (superior izquierda) se obtiene que la superposición de una con la otra da un mejor panorama de la imagen a analizar. Es así como se hace necesario una lógica de más de dos valores. Como se mostró en el sección anterior, si se aplica un número par de veces el operador apertura siempre que la relación estructural cumpla las condiciones del Teorema 4 es lo mismo que aplicarlo dos veces (debido a la idempotencia del operador), lo cual deviene en una reducción en las iteraciones que debe realizar el ordenador para arrojar la resonancia aplicando un filtro que genere como resultado tan solo las cavidades sanguíneas del paciente. En este caso se toma una relación estructural clásica, donde el elemento estructural es un cuadrado de 2.2 píxeles. En la Figura 5, se exhibe la imagen original y el operador apertura aplicado una y diez veces.
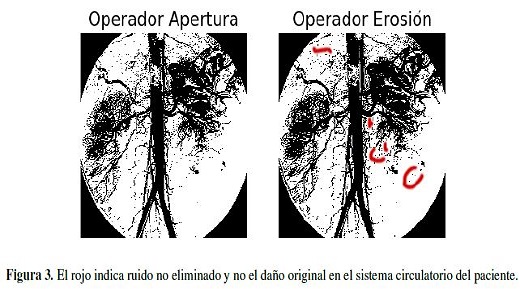
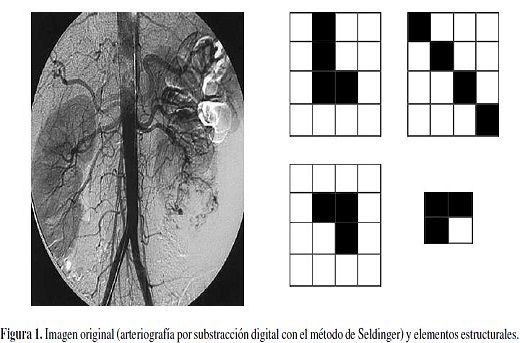
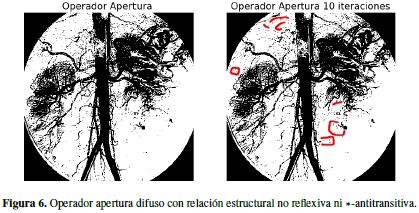
Ahora, la Figura 6 se obtiene al filtrar con una relación (elemento estructural forma de L dentro de un cuadro de 4.4 píxeles) que no satisface las condiciones del Teorema 4, para así resaltar la pérdida de información en el resultado que incide negativamente en el juicio del facultativo; al evaluar que elementos son taponamientos y cuáles son naturales del sistema circulatorio del paciente; el ruido que aparece está resaltado en rojo.
6.Discusión
En el estudio de imágenes diagnósticas es necesario la eliminación de ruidos para determinar anomalías del paciente, sea en la búsqueda de deformidades del feto como lo estudiaron A. P. Ballesteros, L. C. López, R. Herrera en [2] o taponamientos sanguíneos vistos en la sección anterior; esto último no es posible al aplicar los operadores morfológicos clásicos en Python por medio del paquete pymorph, debido a que admite tan solo un elemento estructural bivaluado. Es allí donde la contemplación de una relación estructural y la aplicación del rango de pertenencia de los valores a filtrar es necesario, en dicha búsqueda se encuentran los operadores morfológicos difusos y el intervalo de pertenencia se determina a partir del mínimo y máximo valor en la escala de grises de la imagen de estudio.
Además si se pregunta que operador aplicar a una imagen médica por medio de contraste en escala de grises es pertinente recordar por lo demostrado en el Coralario 1 que el operador apertura poseerá mayor información que la erosión; y, si se tiene en cuenta una relación estructural adecuada, a su vez tendrá toda la información relevante con el menor ruido posible ya que podrá tener mayor información el operador apertura; pero si esta en su gran mayoría es ruido es infructuosa dicha información por lo tanto si se conjuga el Corolario 1 y el Teorema 4 se tendrá que la mejor opción es el operador apertura con una relación estructural bien sea reflexiva o -*antitransitiva.
7. Conclusiones
La importancia de la matemática morfológica radica en el uso práctico que se le dé. Para mencionar solo un par de posibles aplicaciones en campos diferentes, ver por ejemplo su utilización en la detección de nódulos pulmonares en radiografías de tórax [1] o la identificación de lagunas y cuerpos de agua en imágenes geo-satélitales de alta resolución [16]. Un ejemplo mas concreto del uso de los operadores propuestos, se presentó en la sección 5 en imágenes en escala de grises muy usadas en diagnósticos de artereografía. Es por ello que si se tienen presentes los resultados en la elección de una relación estructural adecuada reducirá las iteraciones que deba realizar el computador para arrojar la imagen con la eliminación del ruido y perdida mínima de información relevante, además si se trabaja con el operador apertura es posible obtener menor ruido en la imagen que lo arrojado por la erosión.
Las implicaciones centrales en este artículo son:
- Si
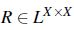 se tiene que para todo
se tiene que para todo 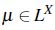 , se satisface que
, se satisface que 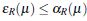 .
. - Si R es reflexiva y Rop es *- antitransitativa entonces
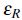 es un operador interior,además, si R es reflexiva o *-antitransitativa entonces
es un operador interior,además, si R es reflexiva o *-antitransitativa entonces
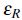 es un operador interior.
es un operador interior. - Si R un *-equivalencia entonces
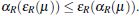
Agradecimientos
Los aportes brindados por los evaluadores permitieron el crecimiento del presente artículo, por ese motivo extendemos nuestros más sinceros agradecimientos, además a los editores de la revista por su paciencia durante el proceso de publicación.
Referencias
[1] J. Aguillón, S. Duarte, R. Herrera, “Realce de candidatos a nódulo pulmonar en radiografías de tórax por medio de filtros de convergencia”. Revista de Ingeniería, vol. 19, No. 2, pp. 85-104, 2014
[2] A. P. Ballesteros, L. C. López, R. Herrera,“Segmentación y conteo de las líneas de la nariz del feto en imágenes ecográficas de las 11-13+6 semanas de gestación”. Revista de Ingeniería, vol. 20, No. 1, pp. 65-78, 2015.
[3] R. Belohlávek, “Fuzzy relational systems, Ingeniera and Principles”. IFSR International Series on Systems Science and Engineering, vol.20, Kluwer Academic/ Plenum Publishers, NewYork, 2002.
[4] N. Bunce, R. Mohiaddin, “An Atlas of Contrast-Enhanced Angiography”, The Parthenon Publishing Group, 2003.
[5] R. Belohlávek, T. Funiokova, “Fuzzy Interior Operators”, International Journal of General Systems, 2004.
[6] N. Carmona, J. Elorza, J. Recasens, J. Bragard, “Permutable fuzzy consequence and interior operators and their connection with fuzzy relations”. Information Sciences, Volumen 310, 20 July 2015.
[7] R. Chityala, S. Pudipeddi, “Image Processing and Acquisition using Python”. Chapman Hall CRC Mathematical and Computational Imaging Sciences, 2014.
[8] E. Dougherty, R. Lotufo, “Hands on Morphological Image Processing”. SPIE Publications, 2003.
[9] J. Elorza, R. Fuentes-Gonzalez, J. Bragard, P. Burrillo, “One relation between fuzzy closing morphological operators, fuzzy consequence operators induced by fuzzy preorders and fuzzy closure and co-closure systems”. Fuzzy sets and systems, pp. 73-89, May 2013.
[10] W. Forero, “Relaciones difusas inducidas por el operador morfológico clausurativo difuso”. Trabajo de Grado, Universidad Distrital Francisco José de Caldas, 2015.
[11] U. Hohle, “Non-Classical Logics and their Applications to Fuzzy Subsets”. Springer Science+Business Media, 1995.
[12] A. R. Iturralde, “Urgencias urológicas”. Ciencias Médicas, 2008.
[13] J. Luna, C. Ochoa, “Interior Operators and Topological Categories”. Advances and Applications in Mathematical Sciences, vol. 10, Issue 2, 2011, pp. 189-206, 2011.
[14] D. Pei, “Fuzzy logic Algebras on Residuated Lattices”. Southeast Asian Bulletin of Mathematics, 2004.
[15] O. Salazar, J. Soriano, “Las leyes de tercero excluido y contradicción como valores límite en lógica difusa”. Revista de Ingeniería, vol 16, No. 1, pp. 50-59, 2011.
[16] G. Torrijos, “Extracción de cuerpo de agua utilizando técnicas de análisis de mezcla y morfología matemática”. Revista de Topografía Azimut, vol 4, pp. 53-60, 2012.
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

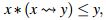
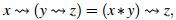
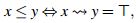
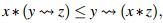
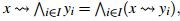
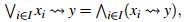
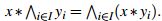



2.jpg)










