DOI:
https://doi.org/10.14483/udistrital.jour.reving.2017.2.a06Published:
2017-05-05Issue:
Vol. 22 No. 2 (2017): May - AugustSection:
Special Section: Best Extended Articles - WEA 2016Operation of a Photovoltaic Microinverter as Active Power Filter using the single phase P-Q Theory and Sliding Mode Control
Operación de un Microinversor Fotovoltaico como Filtro Activo de Potencia Usando la Teoría P-Q Monofásica y Control en Modo Deslizante
Keywords:
Microinverter, Active power filter, Single-phase PQ theory, Sliding-mode control, Nonlinear control (en).Keywords:
Microinversor, Filtro activo de potencia, Teoría P-Q monofásica, Control en modo deslizante, Control no lineal (es).Downloads
References
H. A. Sher, and K.E. Addoweesh, “Micro-inverters - Promising Solutions in Solar Photovoltaics,” Energy for Sustainable Development, vol. 16, pp. 389-400, Dec. 2012.
F. Blaabjerg, Z. Chen, and S.B. Kjaer, "Power electronics as efficient interface in dispersed power generation systems," IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1184-1194, Sep. 2004.
Y. Xue, L. Chang; S.B. Kjaer, J. Bordonau, and T. Shimizu, "Topologies of single-phase inverters for small distributed power generators: an overview," IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1305-1314, Sep. 2004.
J.D. Bastidas, C.A. Ramos-Paja, and E. Franco, "Modeling and parameter calculation of photovoltaic fields in irregular weather conditions," Revista INGENIERÍA, vol. 17, no. 1, pp. 37-48, Jun. 2012.
M. Molinas and J. Kondoh, "Power electronic loads as providers of reactive power ancillary service to the grid: Analytical and experimental study," in Proc. 13th European Conference on Power Electronics and Applications (EPE), Barcelona, 2009, pp. 1-10.
W. Abbas and M. A. Saqib, "Effect of Nonlinear Load Distributions on Total Harmonic Distortion in a Power System," in Proc. International Conference on Electrical Engineering (ICEE), Lahore, 2007, pp. 1-6.
C. H. Chang, Y. H. Lin, Y. M. Chen and Y. R. Chang, "Simplified Reactive Power Control for Single-Phase Grid-Connected Photovoltaic Inverters," IEEE Trans. Ind. Electron., vol. 61, no. 5, pp. 2286-2296, May 2014.
M. Islam, N. Afrin and S. Mekhilef, "Efficient Single Phase Transformerless Inverter for Grid-Tied PVG System With Reactive Power Control," IEEE Trans. Sustainable Energy, vol. 7, no. 3, pp. 1205-1215, July 2016.
I. Bouloumpasis, P. Vovos, K. Georgakas, and N.A. Vovos, “Current harmonics compensation in microgrids exploiting the power electronics interfaces of renewable energy sources,” Energies, vol. 8, no. 4, pp. 2295-2311, Aug. 2015.
F.P. de Souza and I. Barbi, "Single-phase active power filters for distributed power factor correction," in Proc. IEEE 31st Annual Power Electronics Specialists Conference (PESC), Galway, 2000, pp. 500-505.
O. Lopez-Santos. “Filtro activo paralelo para compensación̤ de factor de potencia y distorsión̤ armónica en aplicaciones industriales,” Master thesis, Universidad Nacional de Colombia, 2010.
F.R. Jimenez, J.M. Salamanca, & P.F. Cardenas, “Modeling and circuital analysis of a Single Phase Shunt Active Power Filter,” In 2014 IEEE 5th Colombian Workshop on Circuits and Systems (CWCAS), Barranquilla, 2014.
Hua, C-C. Li, C-H. Lee, C-S. Control Analysis of an active power filter using Lyapunov candidate. IET Power Electron., vol. 2. no. 4, April 2009.
O. Lopez-Santos, L. Martinez-Salamero, G. Garcia, & H. Valderrama-Blavi, “Sliding-mode control of a transformer-less dual-stage grid-connected photovoltaic micro-inverter,” In Proc. 10th IEEE International Multi-Conference on Systems, Signals & Devices (SSD), pp. 1-6, 2013.
O. Lopez-Santos, G. Garcia, J.C. Avila-Martinez, D.F. Gonzalez-Morales, & C. Toro-Zuluaga. “A simple digital sinusoidal reference generator for grid-synchronized power electronics applications,” In Proc. IEEE Workshop on Pow-er Electronics and Power Quality Applications (PEPQA), pp. 1-6, 2015.
O. Lopez-Santos, “Contribution to the DC-AC conversion in photovoltaic systems: Module oriented converters,” Doctoral dissertation, INSA de Toulouse, pp. 1-248, 2015.
A. Cid-Pastor, L. Martinez-Salamero, A. El Aroudi, R. Giral, J. Calvente, R. Leyva, "Synthesis of loss-free-resistors based on sliding-mode control and its applications in power processing," Control Engineering Practice, vol. 21 no. 5 pp. 689-699. May. 2013.
O. Lopez-Santos, G. Garcia and L. Martinez-Salamero, "Derivation of a global model of a two-stage photovoltaic microinverter using sliding-mode control," in Proc. IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, 2015, pp. 1-6.
M.T. Haque, "Single-phase PQ theory," in Proc. IEEE 33rd Annual Power Electronics Specialists Conference (PESC), Cairns, 2002, pp. 1815-1820.
M.T. Haque and T. Ise, "Implementation of single-phase pq theory," in Proc. of the Power Conversion Conference (PCC), Osaka, 2002, pp. 761-765.
M.T. Haque, "Single-phase pq theory for active filters," in Proc. IEEE Region 10 Conference on Computers, Communications, Control and Power Engineering (TENCON), 2002, pp. 1941-1944.
V. Khadkikar, A. Chandra and B. N. Singh, "Generalised single-phase p-q theory for active power filtering: simulation and DSP-based experimental investigation," IET Power Electron., vol. 2, no. 1, pp. 67-78, January 2009.
S. Golestan, M. Ramezani, J. M. Guerrero, F. D. Freijedo and M. Monfared, "Moving Average Filter Based Phase-Locked Loops: Performance Analysis and Design Guidelines," in IEEE Transactions on Power Electronics, vol. 29, no. 6, pp. 2750-2763, June 2014.
S.W: Smith, The scientist and engineer's guide to digital signal processing. 2d. Edition. San Diego: California Technical Publishing. 1999.
O. Lopez-Santos, G. Garcia, L. Martinez-Salamero, & L. Cortes-Torres, “Suppressing the effect of the DC-link voltage ripple on the current control of a sliding-mode controlled microinverter,” in Proc. Chilean Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), pp. 447-452, 2015.
H. Jiabing, Z.Q. Zhu, H. Nian, L. Shang, Y. He, “Sliding mode current control of grid-connected voltage source converter,” in proc. of the IEEE Energy Conversion Congress and Exposition (ECCE), pp. 912-919, Sep. 2010.
I.-S. Kim, “Sliding mode controller for the single-phase grid-connected photovoltaic system,” Applied Energy, vol. 83, Oct. 2006, pp. 1101-1115.
J. Matas, L. García, J. Miret, J. Guerrero, and M. Castilla, “Feedback Linearization of a Single-Phase Active Power Filter via Sliding Mode Control,” IEEE Trans. Power Electron., vol.23, no.1. Jan. 2008.
V. Utkin, J. Guldner and J. Shi, Sliding mode control in electromechanical systems, CRC Press, 2th. Edition, Taylor and Francis Group, 2009.
D. G. Montoya, C. A. Ramos-Paja and R. Giral, "Improved Design of Sliding-Mode Controllers Based on the Requirements of MPPT Techniques," in IEEE Trans. Power Electron., vol. 31, no. 1, pp. 235-247, Jan. 2016.
O. Lopez-Santos, G. Garcia, L. Martinez-Salamero, J.C. Avila-Martinez, & L. Seguier, “Non-linear control of the output stage of a solar microinverter,” International Journal of Control, pp. 1-20, 2015.
H. Panagopoulus, K.J. Astrom and T. Hagglund, “Design of PID controllers based on constrained optimization," IEE Proc. on Control Theory Appl., vol. 149, no. 1, pp. 32-40, 2002.
O. Lopez-Santos, L. Martinez-Salamero, G. Garcia, H. Valderrama-Blavi and T. Sierra-Polanco, "Robust Sliding-Mode Control Design for a Voltage Regulated Quadratic Boost Converter," IEEE Trans. Power Electron., vol. 30, no. 4, pp. 2313-2327, Apr. 2015.
IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems, IEEE Std 519-2014, 2014.
IEEE Recommended Practice for Utility Interface of Photovoltaic (PV) Systems, IEEE Std 929-2000, 2000.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Operation of a Photovoltaic Microinverter as Active Power Filter using the single phase P-Q Theory and Sliding Mode Control
Operación de un Microinversor Fotovoltaico como Filtro Activo de Potencia Usando la Teoría P-Q Monofásica y Control en Modo Deslizante
Oswaldo Lopez Santos
Universidad de Ibagué. Tolima - Colombia,
oswaldo.lopez@unibague.edu.co
Sebastian Tilaguy Lezama
Universidad de Ibagué. Tolima - Colombia,
2420111017@estudiantesunibague.edu.co
Sandra Patricia Rico Ramirez
Universidad de Ibagué. Tolima - Colombia,
2420071007@estudiantesunibague.edu.co
Luis Dario Cortes Torres
Universidad de Ibagué. Tolima - Colombia,
2420111040@estudiantesunibague.edu.co
Recibido: 27/12/2016. Modificado: 15/02/2017. Aceptado: 28/03/2017.
Abstract
Context: Microinverters are widely used in modular photovoltaic installations but its operation with reduced power is limited to inject real power into the grid. One way to optimize the use of microinverters consist of providing them the Active Power Filtering (APF) capability, which allows its use as both distributed generation and compensation unit even under unfavorable conditions of insolation. With this approach, the output stage of the microinverter can provide reactive and distortive components of power in order to compensate power quality defects of a localized load.
Method: This paper proposes a non-linear control strategy to integrate the APF function in a singlephase two-stage photovoltaic microinverter. The proposal involves the use of the single-phase P-Q theory to generate the current reference, sliding mode control to achieve a robust tracking of that reference and linear robust control to maintain the power balance regulating the DC-link voltage of the microinverter. The proposed control does not require the use of low-pass filters and in turn uses a recursive average computation improving the general performance of the system.
Results: The theoretical approach is validated by means of simulation results in which appropriate levels of harmonic distortion are obtained in the grid-side current for different load types and power levels. The robustness of the control system is tested by applying disturbances in the harmonic content of the load current and its power level obtaining an appropriate dynamic performance adapted to the demands of the application.
Conclusions: The main advantage of this proposal is the possibility to add the active filter function to coventional microinverters extending its capability to power conditioning only integrating some algorithms. A simple design method to ensure reliability, robustness and high power quality is detailed.
Keywords: Microinverter, Active power filter, Single-phase PQ theory, Sliding-mode control, NonLinear control
Acknowledgements: This research is being developed with the partial support of the Gobernacion del Tolima - Convenio de cooperacion 1026- 2013 - Research Culture and the Universidad de Ibagué under project 16-406-SEM with the assistance of students from the Research Hotbed on Control and Power Electronics (SICEP), Research Group D+TEC.
Language: English
Resumen
Contexto: Los microinversores son ampliamente utilizados en instalaciones fotovoltaicas modulares pero su operacion con potencia reducida es limitada a inyectar potencia real en la red. Una forma de optimizar el uso de los microinversores consiste en proveerles la capacidad para realizar Filtrado Activo de Potencia (FAP), lo que permite su uso como una unidad tanto de generacion como de compensación distribuida, incluso en condiciones desfavorables de irradiacion solar. Con esta propuesta, la etapa de salida del microinversor puede suministrar componentes de potencia reactiva y de distorsion para compensar defectos en la calidad de energia de una carga localizada.
Método: Se propone una estrategia de control no lineal para integrar la funcion FAP en un microinversor fotovoltaico monofasico de dos etapas. La propuesta involucra el uso de la teoria P-Q monofasica para generar la referencia de corriente, control en modo deslizante para conseguir un seguimiento robusto de dicha referencia y control lineal robusto para mantener el balance de potencia regulando el voltaje del bus DC intermedio del microinversor. El control propuesto no requiere del uso de filtros pasa-bajos y en cambio usa un computo recursivo de valor promedio, mejorando el desempeno general del sistema.
Resultados: La propuesta teorica es validada usando resultados de simulación en los que se evidencian niveles apropiados de distorsion armónica en la corriente de la red, los cuales se obtienen para diferentes tipos de carga y niveles de potencia. La robustez del sistema de control es puesta a prueba aplicando perturbaciones en el contenido armonico de la corriente de la carga y su nivel de potencia obteniendo un desempeno dinámico adecuado para las exigencias de la aplicación.
Conclusiones: La principal ventaja obtenida con el sistema de control propuesto es la posibilidad de adicionar la funcion de filtrado activo a los microinversores convencionales para extender su contribución hacia el acondicionamiento electrico con la integracción de algunos algoritmos. Se detalla un diseño simple para asegurar confiabilidad, robustez y altos niveles de calidad de potencia.
Palabras clave: Microinversor, Filtro activo de potencia, Teoría P-Q monofasica, Control en modo deslizante, Control no lineal.
Agradecimientos: Esta investigacion ha sido financiada parcialmente por la Gobernacion del Tolima segun el Convenio de cooperación 1026- 2013 - Cultura científica y la Universidad de Ibagué a traves del proyecto 16-406-SEM con la asistencia de estudiantes del Semillero de Investigacion en Control y Électronica de Potencia (SICEP) del Grupo de investigación D+TEC.
Idioma: Inglés
1. Introduction
The photovoltaic microinverter technology is a recent development in the field of power electronics which has allowed the modularization of the photovoltaic installations and in consequence has disseminated the proliferation of the distributed generation around the world [1]-[3]. This technology allows overlooking, at least to a large extent, the problems related with the use of photovoltaic arrays such as mismatching and partial shading [4]. Nevertheless, the functionality of the microinverters remains limited to inject into the grid the real power obtained from solar modules what is insufficient when there are no other representative power sources supporting the further power components. This aspect motivates the research dedicated to expand the capabilities of the microinverters including the generation of reactive and harmonic power with the aim to cover the requirements of reactive and nonlinear loads [5], [6].
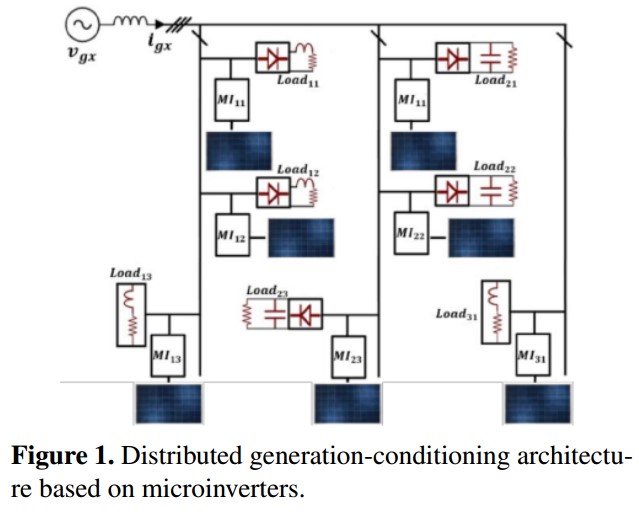
The current motivation is to achieve that the microinverter technology play a new role in AC distribution systems complementing their main objective of real power injection with capabilities of power conditioning [7]-[9]. This new approach introduces the distributed generation- conditioning concept, taking full advantage of the converters on the microinverter devices [10]. Thus, microinverters will be capable to generate a programmed amount of reactive power, a programmed harmonic content, or as it is presented in this paper, they can compensate the reactive and distortive power of localized loads. As a drawback, it is worth mentioning that the measurement of an additional current increases the cost of the system.
[13], which simultaneously injects the generated power into the grid reducing the amount of power delivered by it to fed the load. In other words, if the power produced by the solar panel is enough to cover the consumption of the load, the grid does not provide power, and, on the contrary, if the power produced by the solar panel is not sufficient, the grid will assume the contribution of the missing power. The worst case consists on the grid supplying the power demanded by the load and the power losses associated to the operation of the microinverter as an active power filter. The power requirements of the proposed device are covered with the same architecture of a two-stage microinverter which normally is composed by a DC-DC converter and a DC-AC converter in cascade connection interacting through a common DC-link [14].
The single-phase P-Q theory is used in order to calculate the current waveform required to compensate the power quality of the localized load. The tracking of that current reference is accomplished by means of a simple controller enforcing a first order sliding surface on the output current of the microinverter. The average voltage of the DC-link is regulated by means of a ProportionalIntegral (PI) controller affecting the fundamental component of the injected current. Then, this controller establishes the energy balance within the microinverter. The changes between operational modes take place without exhibiting commutation between modes.
Because of the number and complexity of mathematical operations required to implement the control, this paper assume that the proposed strategy can be implemented in both completely digital and hybrid analogue-digital form. In both cases, the proposal takes advantage of a novel and simple synchronization technique which fi- xes the number of samples per grid period regar dless the current value of the grid frequency [15]. Advantages and particularities of the proposed implementation are detailed and validated later.
The rest of the paper is organized as follows. Section 2 gives a general description of the system and its main characteristics whereas section 3 details the components of the proposed control. After that, several simulation results validating theoretical analysis are presented in section 4. Finally, conclusions are presented in section 5.
2. General Description
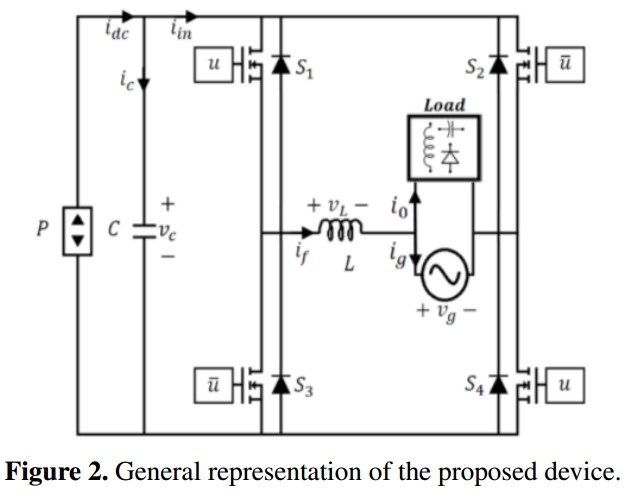
The output stage of a two-stage microinverter is a conventional full-bridge grid-connected DCAC converter. To separate the analysis of both stages of the microinverter, the set consisting of the solar panel and the DC-DC stage can be considered as a power source as was introduced in [16], [17]. The circuit configuration takes the form represented in Figure 2. The power source P represents the power available at the DC-link which is sourced by the solar panel through the DC-DC converter. The capacitor C serves as coupling element between DC-DC and DC-AC converters while the inductor L serves as coupling element between the DC-AC converter and the grid. The voltage vg is the grid voltage which is the same output voltage of the microinverter and input voltage of the compensated load. The output current of the microinverter, the current of the load and the resulting current of the grid were named as if, io and ig respectively. The bridge is controlled by means of the signal u applied directly to the interrupters S1 and S4 , and the complementary signal û = 1 - u applied to the interrupters S2 and S3, this control inducing bipolar commutation. The current idletra con gorrito represents the current given by the power source P while the current iin represents the input current of the full bridge.
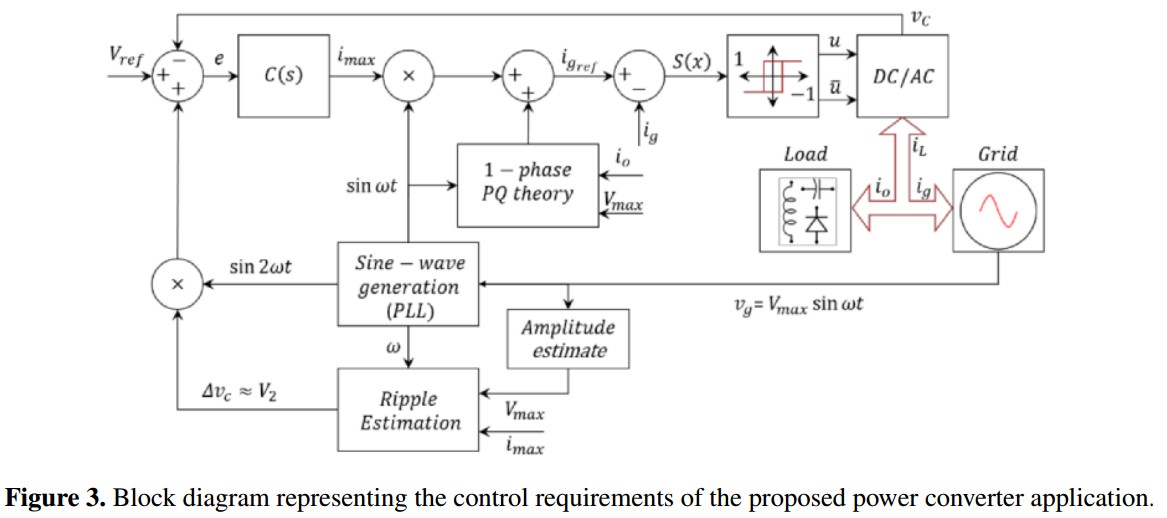
Taking as starting point strategy proposed in [18] to control the output stage of a solar microinverter, the functions related with the active power filter capability were integrated, obtaining the block diagram depicted in Figure 3. The blocks of single-phase P-Q theory, synchronization and sine-wave reference generation, ripple estimation, amplitude estimation and DC-link control are explained in detail in the following section.
3. Calculations, modeling and control
3.1. Modified single phase PQ theory
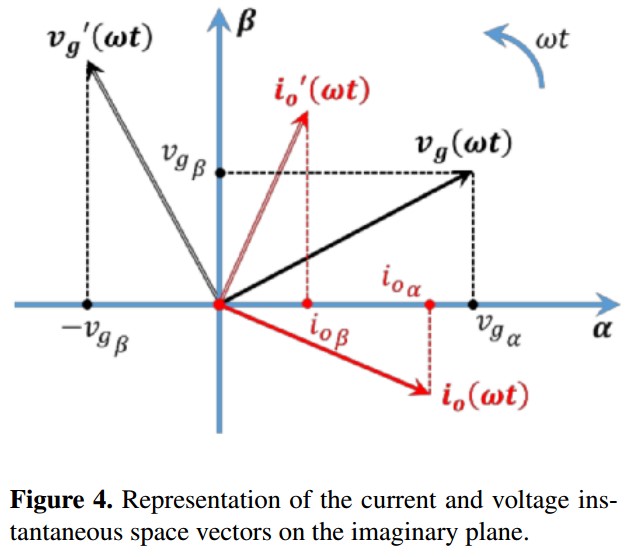
The P-Q theory originally developed for three phase systems uses the Clarke transform in order to obtain the representation of the current and voltage components in the complex plane. As it is introduced in [19]-[21], to obtain the same representation for single-phase systems, the fictitious vectors v�g(t) and i�o(t) are created by applying a phase shift of p/2 to the original signals as it is represented in the complex plane of Figure 4. Thus, the real components of current and voltage are the instantaneous values of each vg(t) and io(t) whereas the imaginary components are instantaneous values of its orthogonal versions v�g(t) and i�o(t).
With base on the above definition, it is possible to derivate the matrix expression obtaining the components of the instantaneous complex power:
The active power p(?t) can be also expressed as p(?t) = Pg+ p(?t) , where P represents the perperiod average of the power p(?t) and p(?t) the alternating component of p(?t). As a consequence, the compensating current reference is:
On the other hand, the current related with the real power delivered by the grid can be deduced using the expression (3)
The use of (2) o (3) to control an active power filter are differentiated by using the terms direct current or indirect current control respectively. In our work, we are interested in implementations, its advantages and drawbacks; however, this paper focuses on the indirect technique considering the fact that the performance is higher than in the case of the direct technique because the feedback signal is the same variable in which the desired behavior is really induced.
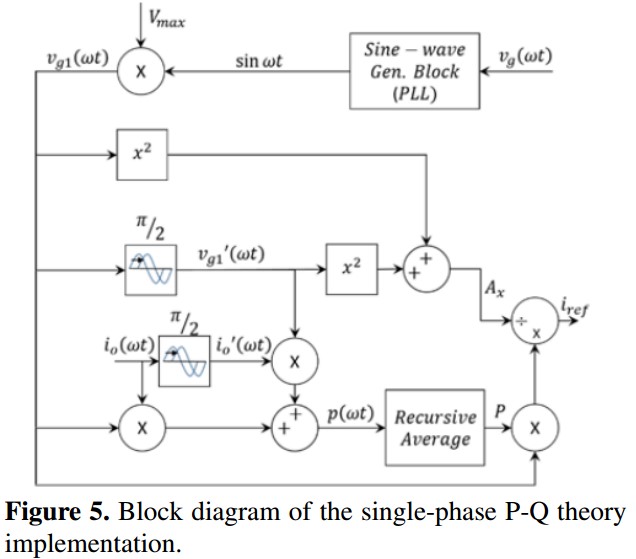
The fundamental difference between the original P-Q theory and the modified P-Q theory is the use of a phase looked loop (PLL) to obtain the measured voltage vg1(?t) which allows overcomes the negative effects of distortions in the estimation of the compensation current [22]. As it is detailed below, the use of a specific kind of PLL brings some relevant advantages to the system. The block diagram representing the applied P-Q theory is shown in Figure 5. It is worth to highlight that the term vg1(?t)2 + v�g1(?t)2 becomes V2gmax because both vg1(?t) and v�g1(?t) are pure sine waveforms generated by the PLL.
3.2. Synchronization and sine-wave generation
IThe P-Q theory was implemented with base on the grid synchronization system proposed in [15]. In this system, it is generated a sine waveform synchronized in frequency and phase with the grid using N = 1024 samples per period and consequently a high frequency N times higher than the grid frequency. That frequency is used to synchronize the execution of the control algorithms into the digital device with the following advantages:
- The commonly used low-pass filter required extracting the average power component and its delay effect are replaced by a recursive moving average filter (RMAF) improving noise and harmonic rejection, and reducing computational cost [23], [24]. The number of samples in the average is equal to N (1024) which is the same number of samples for a grid period; therefore, it is ensuring a high accuracy of the average computation and in consequence a high quality in the reference generation.
- The phase displacements required to generate the fictitious vector of the P-Q theory are highly accurate and no dependent of the grid frequency. A phase shift of 90? simply corresponds to a delay of 256 samples in the waveforms.
- Computations based on integrals averaged for a period of the grid frequency (average, RMS or FFT calculations) has a lower computational cost facilitating the optimization of execution time of per sample algorithm.
The same synchronization system provides the fundamental component required to inject the generated real power into the grid or in other case to extract the power to cover the power losses of the inverter. Complementarily, the PLL generates a double frequency component in order to estimate and cancel the effect of the voltage ripple of the DC-link in the control loops [25]. It is worth to mention that, the loop controller of the PLL also uses the RMAF instead of conventional low-pass filters.
3.3. Tracking of the current reference
The model of the grid-connected power converter can be expressed with the bilinear equation system:
The tracking of the current reference is accomplished by means of a sliding-mode controller. This kind of control has been used with the same purpose by other authors [26]-[28] and it is selected considering its advantages such as rapid response, robustness against external disturbances and parameter uncertainty, despite of the well know disadvantage of variable frequency commutation when it is implemented using a hysteresis comparator with constant band.
The following first order sliding surface is defined:
where igref is the reference current given by the P-Q theory computation. Analyzing the stability of sliding mode control the design requires fulfilling the transversality and reachability conditions. The transversality condition guarantees that the control variable u is present in the switching function derivate, or in other words to satisfy that dS(x)⁄du ≠ 0. To analyze this condition, time derivative of the sliding surface is obtained from (7) and (4) and after that the derivative of this result with respect to the control signal is obtained as follows:Then, it was established that the transversality condition is fulfilled while the voltage of the DC link is different to zero which is true for every operational condition. In the worst case, the absence of control signals enforces the converter to operate as a diode bridge rectifier with an output capacitance ensuring a minimum voltage near to the peak value of vg. The sign of transversality is negative and then, the sliding motion around the current reference is obtained by applying the following control law:
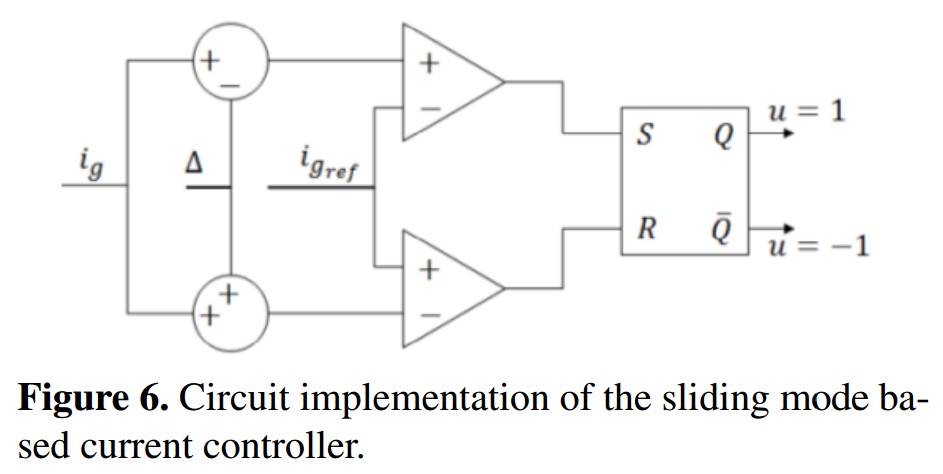
Because of the limitations of the electronic power devices to obtain infinite frequency commutation as suggest the application of sliding mode control, the control law (7) cannot be implemented directly and the switching frequency must be limited below admissible values. Then, the controller is implemented using a hysteresis comparator with a band of ± ∆ as it is depicted in Figure 6.
The reachability condition is used to determinate the capacity of system to reach the sliding surface from whatever arbitrary point. The reachability depends of the sign of transversality [30], and therefore its definition is:
By applying the above definition in the system equations, the following condition is obtained:
In general terms, expression (10) shows that the value of Vref must be selected is such a way that a considerable difference exist between the minimum value of vc including its ripple component and the maximum value of vg. Beyond to satisfy (10), the possible deviation of vc during transitory disturbance events must be even considered.
Finally, applying the invariance conditions defined as S(X) = 0 and S�(x) = 0|u=ueq and the equivalent control method [29], the resulting dynamics is:
By averaging expressions for a half grid period, linearizing and applying the Laplace transform, it is obtained that:
From (13), the transfer function of the DC link voltage to the output corrent amplitude can be used to synthesize a voltage regulator considering both the load current and the input power as disturbances.
3.4. DC-link voltage regulation
As it is explained in [31], a PI controller with a low-pass filter term can be applied in order to obtain zero error regulation of the DC-link voltage. This simple linear controller can reduce the effect of the double grid frequency component in the measurement of the DC link voltage and reject the possible power disturbances of power and load current. The controller has the form:
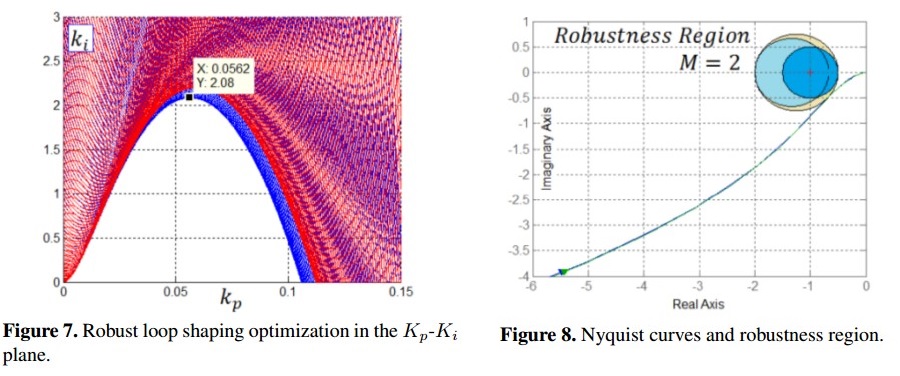
The value of Tf is selected in order to considerable decrease the ripple component of 120 Hz in the DC link voltage. The Kp and Ki parameters are selected in order to ensure robustness against disturbances and parameter uncertainties. This objective can be accomplished by using the loop shaping method introduced in [32]. A value of 2 is selected for the combined sensitivity M following criteria presented in [33].
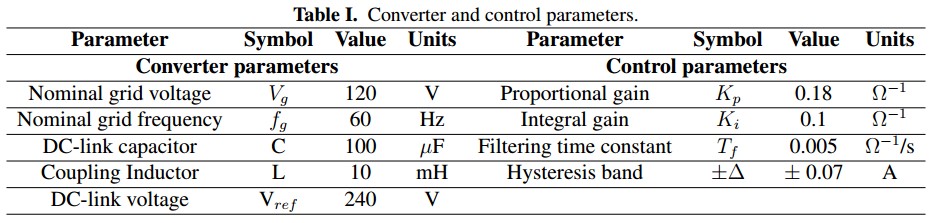
Figure 7 shows the two envelopes resulting after generate the whole space of solutions in the Kp - Ki plane ensuring robustness for input power values of 10 W (red color) and 100 W (blue color). The best solution is that which maximizes Ki outside of the shaded areas which results in Kp = 0,0562 and Ki = 2,08 for the set of converter parameters in Table I. With these parameters, the Nyquist curves of the loop transfer function L(s) = Igmax(s) -1Vc(s)C(s) for the two limit values of power are depicted in Figure 8. As it can be noted the robustness constrain was fulfilled with the selected controller parameters.
4. Simulation results
In order to validate the entire proposal and the applied concepts, several simulations have been implemented. Two type of load with two different power levels for each one have been used, an inductive-resistive load and a nonlinear load composed by a diode bridge rectifier with an inductiveresistive load at the DC side. The parameters used are listed in Table I.
4.1. Steady-state performance (PF and THD)
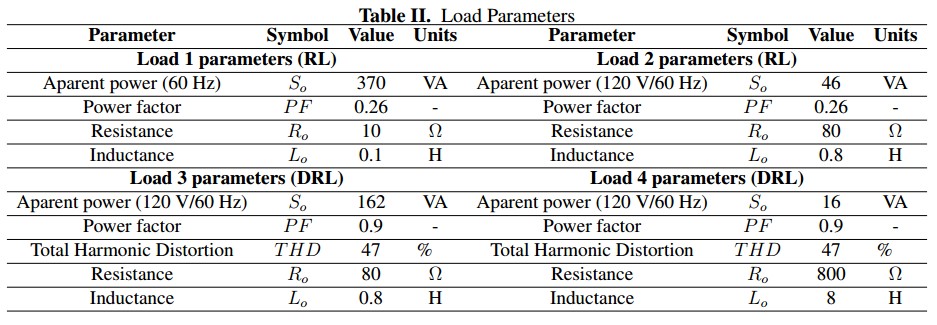
Figure 9shows simulated results evaluating the steady-state performance of the control system fortwo of the selected loads defined in Table II(Load 1 and Load 3) when the microinverter operates as an active filter because of the absence of input power. The THD of the waveforms is given in order to show the effect of the compensation algorithm. In the first case, the RL load is demanding reactive power which is entirely delivered by the microinverter obtaining unitary DPF and PF.
Figure 9a show the way in that the grid delivers a sinusoidal current without any phase shift respect to the voltage. The THD only increases a 0.30 % because of the high frequency component introduced by the microinverter. In the second case which is shown in Figure 9b, the nonlinear load has not phase displacement but has a high harmonic content (47.3 %). The microinverter compensates the load allowing to obtain unitary PF. The THD of the grid current is reduced below 4 %. In both cases the THD of the current is below of 5 % which corresponds to a permissive value according to the actual normativity [34], [35]. Also in both cases, the power factor is compensated.
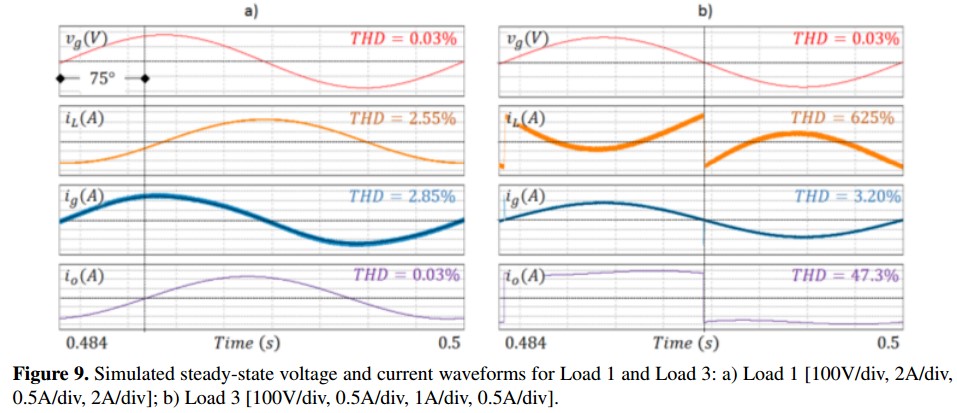
Figure 10 shows a complete analysis of the THD and PF obtained with the active filtering function of the microinverter for the overall operational range of load power and AC input voltage. Information was organized in 3D surfaces showing the simultaneous relation of each power quality indicator as function of both selected parameters. The first case corresponds to a RL load and the second case corresponds to a nonlinear load obtained with a diode bridge feeding a RL load. Points in surfaces were obtained using input voltage values between 110 and 130 V with steps of 5 V, and load impedances between 5 and 55 ? for the first case and between 60 and 110 ? for the second case, considering steps of 5 ? in both cases.
4.2. Transient response to input power and load disturbances
Figure 11 shows simulated results evaluating the transient response of the system when input power disturbances are applied. In subfigures 10a and 10b an input power change is applied at 0.4 s changing its value from 20 to 100 W. After that at 0.6 s, input power suddenly reduces to zero. The voltage of the DC-link absorbs the power disturbance returning to the desired value in less than 75 ms in both cases with voltage deviations lower than 10 %. This results show the robust response of the system rejecting power disturbances.
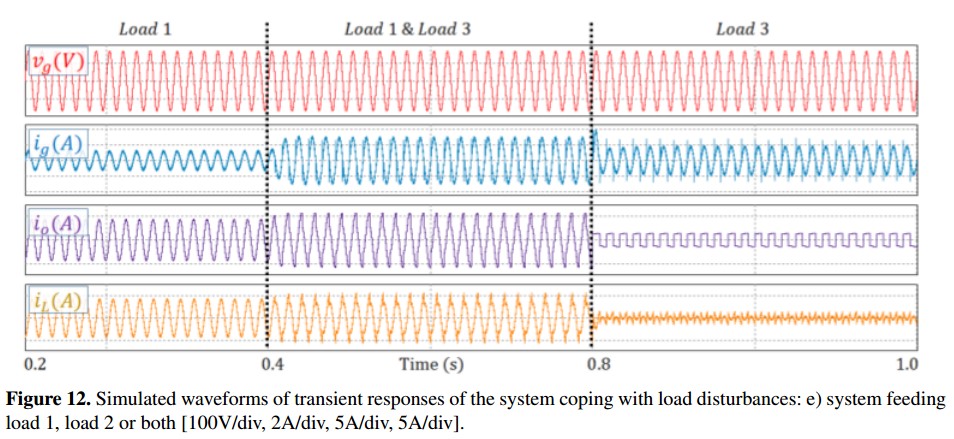
Figure 12 shows simulated results evaluating the transient response of the system when load changes are applied. The system operates with the load 1 0.4 s when the load 3 is added. After that, at 0.8 s, the load 1 is disconnected and the load 3 keeps connected. As it is can be noted, the system has the ability to cope with load changes without problem.
5. Conclusions
A new distributed power generation-compensation architecture based on single-phase microinverters has been presented. The main idea is to integrate the active power factor correction function in these devices taking advantage of the output-stage even if there is no production of photovoltaic solar energy. The proposal was validated by means of several simulation results evaluating the steady-state and dynamic performance of the converter working with different types of electrical loads and two different power levels for each of them. In the steady state, the obtained power factor is unitary and the THD in the grid current is reduced always below 5 % what is in good agreement with the established standards. The performance of the microinverter coping with transient events was evaluated by applying disturbances in both input power and power load. The design of the DC link voltage regulator using the robust loop shaping technique allowed to reduce the impact of disturbances obtaining voltage deviations below 10 % and reduced settling times below 75 ms. Compatibility of the P-Q theory in the reference generation, sliding mode control in the current controller and robust PI compensation in the DC link voltage control was facilitated by the use of a recursive moving average filter in which the number of samples is constant in a grid period despite of changes in the grid frequency. The current and future efforts are concentrated obtaining an experimental validation of the overall approach in which all control function are embedded in a digital signal processing device looking for a really optimized utilization of the computation and memory resources.
References
[1] H. A. Sher, and K.E. Addoweesh, "Micro-inverters - Promising Solutions in Solar Photovoltaics," Energy for Sustainable Development, vol. 16, pp. 389-400, Dec. 2012. ↑255
[2] F. Blaabjerg, Z. Chen, and S.B. Kjaer, "Power electronics as efficient interface in dispersed power generation systems," IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1184-1194, Sep. 2004. ↑255
[3] Y. Xue, L. Chang; S.B. Kjaer, J. Bordonau, and T. Shimizu, "Topologies of single-phase inverters for small distributed power generators: an overview," IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1305-1314, Sep. 2004. ↑ 255
[4] J.D. Bastidas, C.A. Ramos-Paja, and E. Franco, "Modeling and parameter calculation of photovoltaic fields in irregular weather conditions," Revista INGENIERIA, vol. 17, no. 1, pp. 37-48, Jun. 2012. ↑255
[5] M. Molinas and J. Kondoh, "Power electronic loads as providers of reactive power ancillary service to the grid: Analytical and experimental study," in Proc. 13th European Conference on Power Electronics and Applications (EPE), Barcelona, 2009, pp. 1-10. ↑255
[6] W. Abbas and M. A. Saqib, "Effect of Nonlinear Load Distributions on Total Harmonic Distortion in a Power System," in Proc. International Conference on Electrical Engineering (ICEE), Lahore, 2007, pp. 1-6. ↑255
[7] C. H. Chang, Y. H. Lin, Y. M. Chen and Y. R. Chang, "Simplified Reactive Power Control for Single-Phase GridConnected Photovoltaic Inverters," IEEE Trans. Ind. Electron., vol. 61, no. 5, pp. 2286-2296, May 2014. ↑256
[8] M. Islam, N. Afrin and S. Mekhilef, "Efficient Single Phase Transformerless Inverter for Grid-Tied PVG System With Reactive Power Control," IEEE Trans. Sustainable Energy, vol. 7, no. 3, pp. 1205-1215, July 2016. ↑256
[9] I. Bouloumpasis, P. Vovos, K. Georgakas, and N.A. Vovos, "Current harmonics compensation in microgrids exploiting the power electronics interfaces of renewable energy sources," Energies, vol. 8, no. 4, pp. 2295-2311, Aug. 2015. ↑256
[10] F.P. de Souza and I. Barbi, "Single-phase active power filters for distributed power factor correction," in Proc. IEEE 31st Annual Power Electronics Specialists Conference (PESC), Galway, 2000, pp. 500-505. ↑256
[11] O. Lopez-Santos, "Filtro activo paralelo para compensacion de factor de potencia y distorsi on arm onica en apli- caciones industriales," Master thesis, Universidad Nacional de Colombia, 2010. ↑256
[12] F.R. Jimenez, J.M. Salamanca, & P.F. Cardenas, "Modeling and circuital analysis of a Single Phase Shunt Active Power Filter," In 2014 IEEE 5th Colombian Workshop on Circuits and Systems (CWCAS), Barranquilla, 2014. ↑ 256
[13] Hua, C-C. Li, C-H. Lee, C-S. "Control Analysis of an active power filter using Lyapunov candidate," IET Power Electron., vol. 2. no. 4, April 2009. ↑256
[14] O. Lopez-Santos, L. Martinez-Salamero, G. Garcia, & H. Valderrama-Blavi, "Sliding-mode control of a transformerless dual-stage grid-connected photovoltaic micro-inverter," In Proc. 10th IEEE International Multi-Conference on Systems, Signals & Devices (SSD), pp. 1-6, 2013. ↑256
[15] O. Lopez-Santos, G. Garcia, J.C. Avila-Martinez, D.F. Gonzalez-Morales, & C. Toro-Zuluaga. "A simple digital sinusoidal reference generator for grid-synchronized power electronics applications," In Proc. IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), pp. 1-6, 2015. ↑257, 259
[16] O. Lopez-Santos, "Contribution to the DC-AC conversion in photovoltaic systems: Module oriented converters," Doctoral dissertation, INSA de Toulouse, pp. 1-248, 2015. ↑257
266 INGENIERIA • VOL. 22 • NO. 2 • ISSN 0121-750X • E-ISSN 2344-8393 • UNIVERSIDAD DISTRITAL FRANCISCO JOSE DE CALDAS O. Lopez • S. Tilaguy • S. P. Rico • L. Cortes[17] A. Cid-Pastor, L. Martinez-Salamero, A. El Aroudi, R. Giral, J. Calvente, R. Leyva, "Synthesis of loss-freeresistors based on sliding-mode control and its applications in power processing," Control Engineering Practice, vol. 21 no. 5 pp. 689-699. May. 2013. ↑257
[18] O. Lopez-Santos, G. Garcia and L. Martinez-Salamero, "Derivation of a global model of a two-stage photovoltaic microinverter using sliding-mode control," in Proc. IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, 2015, pp. 1-6. ↑257
[19] M.T. Haque, "Single-phase PQ theory," in Proc. IEEE 33rd Annual Power Electronics Specialists Conference (PESC), Cairns, 2002, pp. 1815-1820. ↑258
[20] M.T. Haque and T. Ise, "Implementation of single-phase pq theory," in Proc. of the Power Conversion Conference (PCC), Osaka, 2002, pp. 761-765. ↑258
[21] M.T. Haque,"Single-phase pq theory for active filters," in Proc. IEEE Region 10 Conference on Computers, Communications, Control and Power Engineering (TENCON), 2002, pp. 1941-1944. ↑258
[22] V. Khadkikar, A. Chandra and B. N. Singh, "Generalised single-phase p-q theory for active power filtering: simulation and DSP-based experimental investigation". IET Power Electron., vol. 2, no. 1, pp. 67-78, January 2009. ↑259
[23] S. Golestan, M. Ramezani, J. M. Guerrero, F. D. Freijedo and M. Monfared, "Moving Average Filter Based Phase-Locked Loops: Performance Analysis and Design Guidelines," in IEEE Transactions on Power Electronics, vol. 29, no. 6, pp. 2750-2763, June 2014. ↑259
[24] S.W: Smith, The scientist and engineer�s guide to digital signal processing. 2d. Edition. San Diego: California Technical Publishing. 1999. ↑259
[25] O. Lopez-Santos, G. Garcia, L. Martinez-Salamero, & L. Cortes-Torres, "Suppressing the effect of the DC-link voltage ripple on the current control of a sliding-mode controlled microinverter," in Proc. Chilean Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), pp. 447-452, 2015. ↑259
[26] H. Jiabing, Z.Q. Zhu, H. Nian, L. Shang, Y. He, "Sliding mode current control of grid-connected voltage source converter," in Proc. of the IEEE Energy Conversion Congress and Exposition (ECCE), pp. 912-919, Sep. 2010. ↑ 260
[27] I.-S. Kim, "Sliding mode controller for the single-phase grid-connected photovoltaic system," Applied Energy, vol. 83, Oct. 2006, pp. 1101-1115 ↑260
[28] J. Matas, L. Garcia, J. Miret, J. Guerrero, and M. Castilla, "Feedback Linearization of a Single-Phase Active Power Filter via Sliding Mode Control," IEEE Trans. Power Electron., vol.23, no.1. Jan. 2008. ↑260
[29] V. Utkin, J. Guldner and J. Shi, Sliding mode control in electromechanical systems, CRC Press, 2th. Edition, Taylor and Francis Group, 2009. ↑261
[30] D. G. Montoya, C. A. Ramos-Paja and R. Giral, "Improved Design of Sliding-Mode Controllers Based on the Requirements of MPPT Techniques," in IEEE Trans. Power Electron., vol. 31, no. 1, pp. 235-247, Jan. 2016. ↑261
[31] O. Lopez-Santos, G. Garcia, L. Martinez-Salamero, J.C. Avila-Martinez, & L. Seguier, "Non-linear control of the output stage of a solar microinverter," International Journal of Control, pp. 1-20, 2015. ↑261
[32] H. Panagopoulus, K.J. Astrom and T. Hagglund, "Design of PID controllers based on constrained optimization," IEE Proc. on Control Theory Appl., vol. 149, no. 1, pp. 32-40, 2002. ↑262
[33] O. Lopez-Santos, L. Martinez-Salamero, G. Garcia, H. Valderrama-Blavi and T. Sierra-Polanco, "Robust Sliding Mode Control Design for a Voltage Regulated Quadratic Boost Converter," IEEE Trans. Power Electron., vol. 30, no. 4, pp. 2313-2327, Apr. 2015. ↑262
[34] IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems, IEEE Std 519- 2014, 2014. ↑263
[35] IEEE Recommended Practice for Utility Interface of Photovoltaic (PV) Systems, IEEE Std 929-2000, 2000. ↑ 263
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.


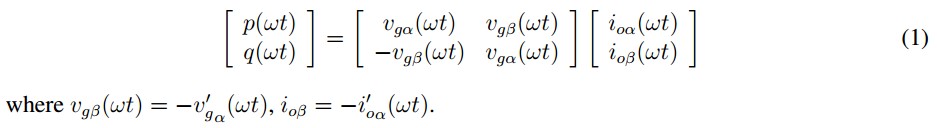
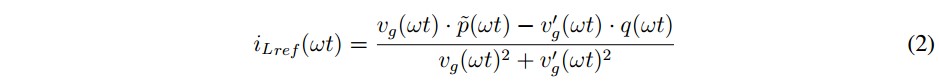
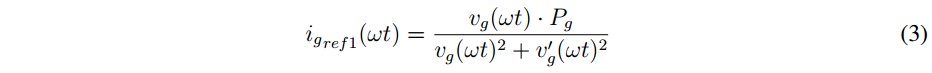
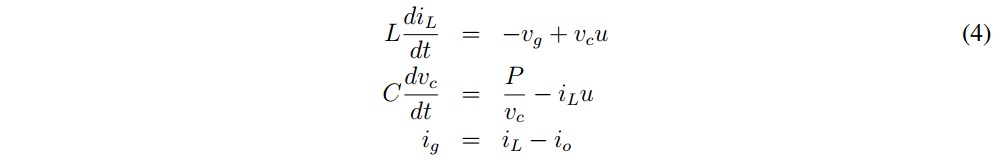
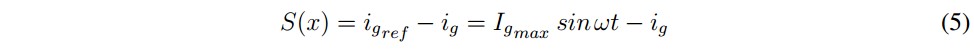
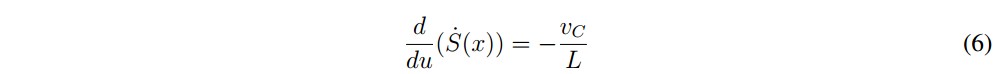
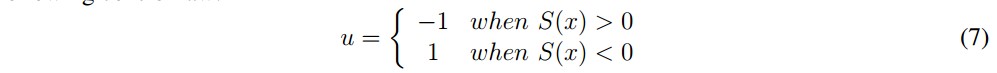
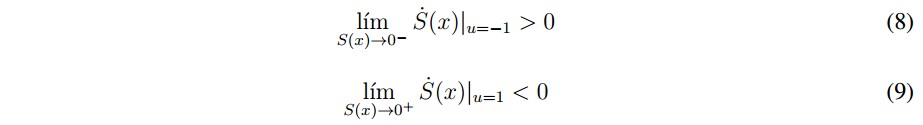
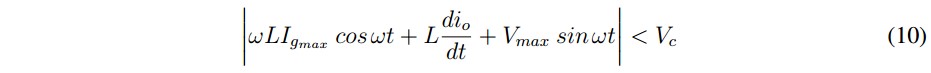
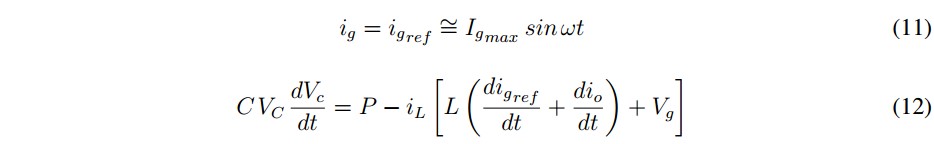
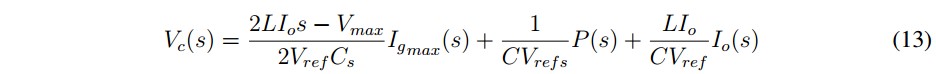
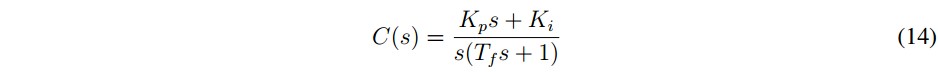



2.jpg)










