Ciencia, Investigación y Desarrollo

Ingeniería, 2001-00-00 vol:6 nro:1 pág:73-76

Técnicas de simulación y filtrado de ruido en señales de espectroscopía RMN mediante transformadas wavelets

Héctor Fernando Cancino de Greiff

Juan Valentín Lorenzo Ginori

Resumen

En este artículo se muestra el desarrollo de programas de simulación para estudiar técnicas de filtrado de ruido en señales de Espectroscopia de Resonancia Magnética Nuclear Pulsada (RMN), conocidas por la sigla FID (del inglés, Free Induction Decay). Estas señales son generadas al excitar núcleos resonantes con pulsos de radiofrecuencia en presencia de un campo magnético externo, y presentan una forma de onda exponencial compleja decreciente con ruido gaussiano añadido.

Los programas de computación realizados permiten generar señales FID con parámetros definibles por el usuario, y adicionarles ruido gaussiano con una relación señal a ruido (SNR) determinada. Las señales con pobre SNR pueden ser tratadas por el método tradicional de acumulaciones. Otra alternativa considerada es la supresión de ruido mediante Wavelets ("Wavelet shrinkage denoising"). Esta novedosa técnica promete ser rápida y eficiente. Los programas creados sirven de base para el estudio y desarrollo ulterior de estas técnicas, facilitando la evaluación de los resultados mediante el método de Monte Carlo.

Se posibilita el cálculo en diferentes casos de la relación señal a ruido residual en dB, que establece la diferencia de la señal sin ruido con la ruidosa, tanto para el método de filtrado que emplea acumulaciones como mediante las Transformadas Wavelets (WT) y Wavelet Packets (WPT). A partir de estos programas y de la metodología asociada, se facilita la investigación de las mejores variantes de filtrado para supresión de ruido en las señales FID.

Palabras Claves: supresión de ruido, denoising, wavelets, free induction decay, noise filtering.

Abstract

In this article is shown the development of simulation programs for studying the techniques of noise filter in NMR (Nuclear Magnetic Resonance) signals, known as FID (Free induction decay). This signals are generated by exciting resonant nucleus with radio frequency pulses in an exterior magnetic field, presenting a complex exponential wave with gaussian noise.

The computed programs may generate FID parameters signals definable by the user, add gaussian noise with a SNR determined. The signals with a low SNR may be treated by the traditional method of accumulations. Another considered alternative is the noise suppression through wavelets. This innovated technique promises to be quick and efficient. The created programs are used for the study and further development of these techniques, making more easy the results evaluation through the Monte Carlo method.

The calculus is easier in different cases of the relation signal to noise residual in dB, establishing the difference signal without noise and with noise, also for the filtered method using accumulations so WT and WPT. From these programs and the associated methodology the investigations of better filtration variables for noise suppression in the FID signals is easier.

INTRODUCCIÓN

En la espectroscopia de Resonancia Magnética Nuclear Pulsada (RMN) se producen las señales conocidas como FIDs, las cuales son generadas al observar núcleos resonantes previamente excitados con pulsos de radiofrecuencia (R. F.) en presencia de un campo magnético externo. Las mismas presentan una forma de onda de decaimiento libre con ruido gaussiano aditivo [1].

Estas señales generalmente se presentan con una pobre relación señal a ruido (SNR) lo cual afecta el análisis a partir de las mismas. Los parámetros que las caracterizan son: frecuencia, fase, constante de decaimiento y amplitud. El objetivo de los métodos de supresión de ruido es obtener una función de decaimiento libre (FID) en lo posible depurada de ruido, posibilitando así una adecuada estimación de los parámetros de las mismas a partir de la forma de onda. La obtención de una señal FID ha sido descrita entre otros autores por de Beer [1] de la forma que se expone a continuación.

El movimiento del vector de magnetización nur clear M en un campo magnético B₀ constante y un campo magnético oscilatorio de RF B₁ , perpendicular a B₀ girando a una velocidad angular ω , se describe mediante las ecuaciones de Bloch:

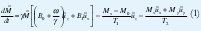
donde: t variable tiempo, γ la razón giromagnética u_x , u_yu_z , los vectores unitarios a lo largo del marco rotante M₀, la magnetización de equilibrio en t = 0, T₁ el tiempo de relajación longitudinal y T₂ el tiempo de relajación transversal.

El tiempo de duración del campo de R.F. B₁ es mucho más corto que T₁ o T₂ .

Durante el pulso de R.F. larmagnetización efectúa una precesión alrededor de B₁ en el marco rotante. El pulso es llamado de 90° (o π/2) si la precesión de los espines nucleares es de 90°. Una vez que el pulso es apagado, la magnetización comienza a precesar alrededor del eje z con una velocidad angular Δω = (&oemga; - ω₀ ) , donde ω₀ es la velocidad angular de resonancia, definida por:

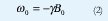
La magnetización al precesar induce una señal en el dominio del tiempo en un sistema de demodulación de RMN. Esta señal, después de ser detectada, se obtiene según la siguiente expresión:

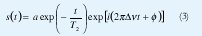
donde la amplitud α es proporcional al número de núcleos concernientes Δω= 2πΔv , e i² = -1 .

En consecuencia, en el caso ideal del FID de RMN de un cierto núcleo, éste puede ser descrito por una sinusoide con decaimiento exponencial complejo, de amplitud proporcional al número de núcleos, la constante de decaimiento es igual al recíproco del tiempo de relajación transversal de ese núcleo, y la frecuencia es igual a la diferencia entre la frecuencia del espectrómetro de RMN y la frecuencia de resonancia de ese núcleo.

La técnica de supresión de ruido que se aplica tradicionalmente a las señales FID consiste en la acumulación (suma coherente) de dichas señales, considerando la repetición de los experimentos sin ninguna alteración en el tiempo de los parámetros externos tales como la inducción magnética o la frecuencia de R.F. Por este método de acumulaciones, ampliamente conocido, se logra una mejora en la SNR proporcional a √n , donde n es el número de acumulaciones. No obstante, existen situaciones, como es el caso de la espectroscopia in vivo, en las que no resulta posible realizar una gran cantidad de acumulaciones, por lo que deben aplicarse métodos alternativos para filtrar el ruido.

El uso de métodos de computación para estudiar las señales RMN, así como las técnicas de supresión (filtrado) de ruido en señales de diversa naturaleza mediante la aplicación de WT y WPT ("Wavelet shrinkage denoising"), han probado tener una gran efectividad y constituyen un tema actual de investigación [2, 3].

Este método consiste en esencia en realizar una descomposición de la señal dada en diferentes niveles mediante WP o WPT, y aplicar un umbral de modo que se supriman aquellos coeficientes cuya pequeña amplitud (baja correlación con la wavelet utilizada) permita presumir que se deben al ruido y por tanto pueden ser suprimidos, permitiendo una reducción del nivel de ruido en la señal reconstruida a partir de los coeficientes remanentes. Una descripción detallada del método puede encontrarse en los textos de Wickerhauser [4] y Teolis [5].

Otros trabajos tratan el problema de la estimación espectral y el análisis en espectroscopia RMN [6, 7, 8]. Sistemas como los descritos en estos trabajos, pueden resultar mejorados por la inclusión de herramientas efectivas de filtrado de ruido. El objetivo de esta investigación ha sido la creación de herramientas computacionales en MATLAB, las cuales sirven de base para el desarrollo de métodos de supresión de ruido en señales de espectroscopia RMI. La efectividad de estas herramientas ha sido comprobada mediante experimentos de simulación.

MATERIALES Y MÉTODOS

En este trabajo se utilizó la programación en MATLAB así como las facilidades que ofrece el Matlab Wavelet Toolbox para el estudio de aplicaciones con WT y WPT, como es el caso objeto de estudio. Como señales de prueba se han simulado ejemplos de experimentos de espectroscopia RMN "in vivo" según De Beer [1].

Para realizar la simulación de las señales FID se utilizó la siguiente expresión:

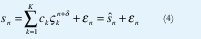
donde

n = 0, . . . . N - 1 : índice de muestreo.
C_k = α _k exp( jφ_k) : amplitud compleja de la componente k-ésima.
ζ_k = exp[(-α_k + j2πv_k)T : k-ésimo polo de señal.
T : Intervalo de muestreo.
δ: retardo en nro. de muestras, t_inicial = T = T_i.
Sn : señal FID.
ε_n : ruido gaussiano aditivo.

TRATAMIENTO TRADICIONAL DEL PROBLEMA DE LA SUPRESIÓN DE RUIDO EN SEÑALES DE RMN.

Para esta técnica, se realizó un programa que permite determinar las mejoras en cuanto a la relación señal a ruido en función de la cantidad de acumulaciones. El parámetro de referencia utilizado a lo largo de este trabajo para caracterizar la efectividad de un método dado de supresión de ruido, es la relación señal a ruido residual rnsr, definida como:

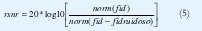
Esta función está configurada en un programa Matlab como la función "residual" y tiene como argumentos los dos vectores a comparar y la salida es la relación en dB de señal a ruido entre el vector original (sin ruido) y el vector diferencia.

Para generar las señales de prueba, se crearon los siguientes programas:

1. FIDGEN para la generación de señales FID unidimensionales multicomponentes.

2. FIDRUID para generar y crear registros FID contaminados con ruido.

Para establecer la mejoría de la SNR mediante acumulaciones, se crearon los siguientes programas:

3. ACUM: función para realizar acumulaciones en el cálculo de espectros RMN y evaluación de métodos de supresión de ruido en las señales FID para espectroscopía de RMN.

4. RESIDUAL: Función para la determinación de la relación señal a ruido residual.

SUPRESIÓN DE RUIDO MEDIANTE WAVELETS

Con el propósito de desarrollar la aplicación de las técnicas de "denoising" o supresión de ruido mediante WP y WPT, se crearon funciones que permiten aplicar estas técnicas a las señales FID creadas mediante los programas antes descritos. Para este fin, se desarrollaron las siguientes funciones y aplicaciones que permiten aplicar tanto diferentes parámetros definidos para las funciones de MATLAB, como diferentes tipos de Wavelets o Wavelets Packets:

1. WDENFID: Función para obtener el registro FID tratado por medio de wavelets para la supresión de ruido. Se basa por completo en la función "wdencmp" de MATLAB.

2. WFIDS: Programa completo de procesamiento de FIDs con Transformadas Wavelets. Este programa comprende las siguientes operaciones:

1. Generacion de fids ruidosos (función "fidruid").
2. Definición del umbral (función "umbral").
3. Supresión de ruido con wavelets ("función wdenfid").
4. Determinación de la relación señal a ruido residual (mediante la función "residual").

3. WPFIDS: Programa de supresión de ruido en señales FID mediante wavelets packets. Su estructura es análoga a la de WFIDS.

RESULTADOS

Se realizó la comprobación del funcionamiento de los diferentes programas: Generación de señales FID limpias y contaminadas con ruido para diferentes conjuntos de parámetros, filtrado de ruido mediante acumulaciones y filtrado de ruido mediante WP y WPT. A continuación se muestra una selección de resultados, que refleja el comportamiento de dichos programas de simulación.

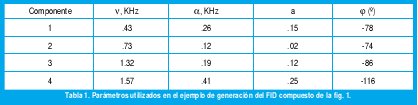
La figura 1 muestra el resultado de generar mediante los programas FIDGEN y FIDRUID la parte real de un registro FID de cuatro componentes y una versión ruidosa del mismo (snr = 5 dB), para el conjunto de parámetros que se muestra en la tabla 1, los que han sido tomados de un ejemplo real que aparece en la referencia [1]. Los otros parámetros utilizados fueron:

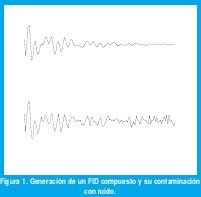
N (número de muestras) = 125.

Ts (intervalo de muestreo en ms) = 0.13.

Tinicial = Ti,( inicio de la señal, ms) = 0.39.

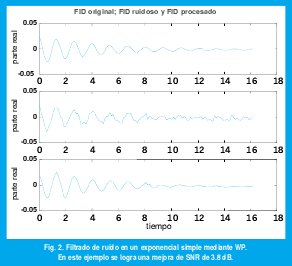
Fueron comprobados mediante simulación los programas WFIDS y WPFIDS para filtrado de ruido. Como ejemplo de la ejecución de estos programas se muestra el resultado de aplicar WFIDS a un exponencial simple (parte real), cuyos parámetros son:

V= 0.74 KHz; α= 0.21 KHz; a = 0.03; φ = -81º; N = 125; Ts = 0.13; Ti = δT = 0.39; SNR = 7 dB.

Se utilizó una Wavelet de Meyer con 5 niveles de descomposición, que con un umbral global adecuado permite lograr una mejora cercana a 4 dB en la relación señal a ruido para esta realización específica. Este resultado se ilustra gráficamente en la figura 2.

CONCLUSIONES

En este trabajo se ha creado un conjunto de programas para la simulación de señales FID de espectroscopia RMN, así como la contaminación controlada de estas señales con ruido para posteriormente emplear el filtrado de ruido mediante acumulaciones que es el método tradicional y además utilizando las técnicas basadas en WP y WPT. Se comprobó la efectividad de los programas bajo diferentes situaciones que simulan señales reales.

Los programas desarrollados han permitido las condiciones para investigar de la manera más efectiva la aplicación de métodos de supresión de ruido en señales FID basados en WP y WPT, utilizando técnicas de Monte Carlo [1]. En investigaciones futuras y mediante la aplicación de los programas desarrollados será posible evaluar la efectividad de diferentes Wavelets y Wavelets Packets, determinar la cantidad más adecuada de niveles de descomposición y las mejores estrategias de establecimiento de los umbrales, así como posibles correlaciones de éstos con los parámetros de las señales a procesar.

El método de estudio propuesto contribuirá a obtener, en investigaciones futuras, una metodología de supresión de ruido en las señales FID con baja distorsión residual, que permita lograr una efectiva estimación de los parámetros de la señal.

REFERENCIAS

[1] R de Beer. "c59 Quantitative In Vivo NMR". University of technology Delft, Department of Applied Physics, August 3, 1994.

[2] C. Taswell. "Randomized signal classes for evaluating the performance of Wavelet Shrinkage denoising methods". Proceedings of the IASTED International Conference Signal and Image Processing (SIP'99). Oct.18-21. 1999.

[3] M. Wachowiak, G. Rash, P. Quesada and A.Desoky "WaveletBased Noise Removal for Based Noise Removal for Biomechanical Signals: A Comparative Study". IEEE Transactions on Biomedical engineering, Vol 47, N° 3, March 2000.

[4] M. V. Wickerhauser, "Adapted Wavelet Analysis from Theory to Software", NY, IEEE Press, 1994.

[5] A. Teolis, "Computational Signal Processing with Wavelets", Birkhäuser, Boston, 1998.

[6] J.Shoolery "The development of experimental and analytical high resolution NMR". Progress in Nuclear Magnetic Resonance Spectroscopy 28 (1995) 37-52.

[7] D. Naugler, R.Cushley. "Spectral Estimation of NMR Relaxation" Journal of Magnetic Resonance". Vol 145, N° 2, August 2000. pp 209-215.

[8] K. Keating, J. Myers,.. "Development and use of Virtual NMR Facility. Journal of Magnetic Resonance". Vol 143, N° 1, March 2000. pp 172-183.

Héctor F. Cancino De Greiff
Ingeniero Electrónico U. Distrital, Msc. Sistemas Digitales U. Central de Venezuela Ms. C. Profesor Asociado Universidad Distrital. Candidato a Doctor en Telecomunicaciones. fcancino@atlas.udistrital.edu.co

Juan V. Lorenzo Ginori Dr. Profesor Titular de la Universidad Central de las Villas. Cuba. juanl@uclv.etecsa.cu