Ingeniería, 2005-00-00 vol:10 nro:1 pág:41-47

Reconstrucción no lineal de imágenes por resonancia magnética de datos no cartesianos en espacio K

NON-LINEAR RECONSTRUCTION OF MAGNETIC RESONANCE IMAGING OF NON-CARTESIAN K-SPACE DATA

Héctor Cristyan Manta Caro
Miembro Grupo de investigación Resonancia Magnética RM-UD
Héctor Fernando Cancino de Greiff
Director Grupo de investigación Resonancia Magnética RM-UD

Resumen

En este artículo, se presentan dos métodos novedosos de reconstrucción no lineal de imágenes por resonancia magnética de datos no cartesianos en Espacio K, esto es, muestras no uniformes en el dominio espacio-frecuencia. En primera instancia, el método de reconstrucción por interpolación en el dominio de la frecuencia, Gridding, y en segundo lugar, el método de reconstrucción iterativa mediante la pseudo-inversión de la transformada rápida no uniforme de Fourier con la técnica no lineal del gradiente conjugado.

La investigación se enfoca en la elección de parámetros eficientes para la minimización de la función error cuadrático medio de reconstrucción y su posterior caracterización mediante técnicas de simulación de Montecarlo. Con el fin de simplificar y estandarizar el análisis y aplicación de los métodos dichas técnicas se realizan sobre una imagen antropogénica de tipo numérica, conocida como el phantom de Shepp y Logan.

Palabras clave:
métodos de reconstrucción, imágenes por resonancia magnética, transformada rápida no uniforme de Fourier.

Abstract

In this paper, two novel methods of non-linear reconstruction of magnetic resonance imaging of non-Cartesian K-Space data are presented. That is non-uniform samples at space-frequency domain. In the first place, the reconstruction method by interpolation at frequency domain, Gridding, and on the other hand, the iterative reconstruction method by means of the pseudoinversion of non-uniform fast Fourier transform with the non-linear technique of the conjugate gradient.

The investigation is focused in the election of efficient parameters to minimize the reconstruction mean squared error function and its subsequent characterization through Montecarlo simulation techniques. All of this, to simplify and standardize the analysis and application of these methods, which are applied over an anthropogenic image of numerical type, known as the phantom of Shepp and Logan.

Key words:
reconstruction methods, magnetic resonance imaging, non-uniform fast Fourier transform.

1. INTRODUCCIÓN

En la actualidad han surgido métodos de adquisición de imágenes por resonancia magnética más sofisticados que las convencionales adquisiciones cartesianas, en los cuales los datos colectados de la transformada continua de Fourier en el dominio espacio-frecuencia se encuentran muestreados de manera no uniforme [2].

Estas estrategias de muestreo están basadas en adquisiciones espirales y radiales del Espacio K y proporcionan ventajas y propiedades de movimiento comparadas con los métodos convencionales. Así, la imagen no puede ser reconstruida por simple aplicación de la transformada inversa rápida de Fourier y deben implementarse estrategias de reconstrucción más sofisticadas.

De esta forma, se han presentado algoritmos de reconstrucción con base en operadores de interpolación en el dominio de la frecuencia, y así emplear las ventajas computacionales de algoritmos como la FFT [8], con complicaciones en el manejo de la no uniformidad del muestreo, que conlleva la generación de zonas sobremuestreadas, y factores que reducen la calidad de la imagen reconstruida como el aliasing, y las réplicas.

Los intentos por solucionar estos problemas en la reconstrucción de imágenes médicas han llevado a la búsqueda de la llamada transformada rápida no uniforme de Fourier [1], [9], la cual podría tener la complejidad de los algoritmos de Cooley y Tukey [4] y ser exacta. Sin embargo, las soluciones actuales de transformada rápida no uniforme son soluciones aproximadas [5].

Así pues, se presenta una comparación entre métodos convencionales de reconstrucción basados en operadores de interpolación y el algoritmo de reconstrucción iterativa a fin de establecer parámetros eficientes para la minimización del error cuadrático medio de reconstrucción en ausencia de ruido, y en presencia de ruido blanco gaussiano de media cero.

2. ADQUISICIÓN DE IMÁGENES POR RESONANCIA MAGNÉTICA

La técnica de adquisición de Imágenes por Resonancia Magnética (IRM) [13] usada principalmente en los campos de la medicina comenzó con la tomografía, la cual consiste en producir imágenes en una delgada sección a lo largo del volumen del cuerpo humano. Durante la adquisición de imágenes IRM, el objeto se coloca en un campo magnético constante B0 , al irradiar el objeto con un pulso de radiofrecuencia con una banda de frecuencia angosta, sólo los espines en la frecuencia de resonancia serán excitados, los cuales se encuentran en una delgada sección perpendicular a la dirección del gradiente. Los gradientes de campo son controlables en tres ejes ortogonales entre sí G = (G_x, G_y , G_z) .

Debido a los gradientes de campo, la frecuencia de resonancia del espín depende de su posición, frequency encoding. Por desplazamiento del gradiente de sección G_z durante el tiempo de excitación, una angosta sección perpendicular al eje z se excita. La codificación espacial con el plano seleccionado se realiza mediante modificación de los gradientes en función del tiempo: G (t) = (G_x(t), G y (t)). La señal recibida, FID Free Induction Decay, resultante de modificar los gradientes controlables de campo magnético es igual a la transformada continua de Fourier de la imagen de la sección, a lo largo de la trayectoria K (t).

2.1. Trayectorias del Espacio K

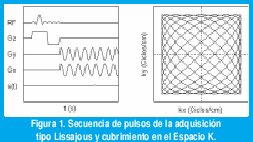
La secuencia de frecuencias espaciales muestreadas durante la adquisición de datos IRM se conoce por trayectorias del Espacio K, estas poseen un alto valor informativo, ya que muestran el momento en que se mide cada frecuencia espacial. En la Figura 1 se muestra una trayectoria tipo Lissajous, determinada en el espacio k por:

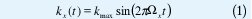
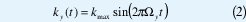
Donde k_max es la máxima frecuencia espacial muestreada,Ω la frecuencia de variación de campo magnético y en la Figura 2, se muestra un patrón de trayectoria espiral con desfase β, determinada por:

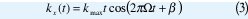
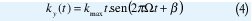
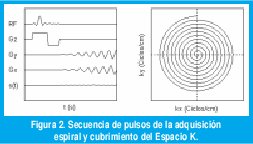
2.2. Phantom de Shepp Logan

El Phantom de Shepp Logan [11] es una superposición de 10 elipses, ver Figura 3, las cuales representan características del cerebro humano.

Su principal ventaja es tener una expresión analítica simple para su transformada continua de Fourier. La transformada continua de Fourier 2D en este caso _E de una elipse de intensidad P, semiejes de longitud A y B, ángulo de orientación φ y centrada en el punto x₀, y₀ está dada por:

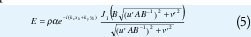
en donde u'=K,Cosφ,v= -K Sinφ, + K Cosφ y J₁ es la función de Bessel de primer orden y primer tipo. Así pues, la transformada continua de Fourier del Phantom completo se describe por:

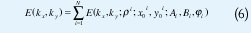
3. MÉTODOS DE RECONSTRUCCIÓN

Los algoritmos de reconstrucción se agrupan en tres grandes áreas:

•Grid-Driven: los valores de cada punto en la cuadrícula son interpolados de los datos vecinos en el Espacio K.

•Data-Driven: la contribución de cada dato es sumado al punto de la cuadrícula Cartesiana adyacente. Ejemplo: el algoritmo Gridding.

•Finalmente, existe un grupo de algoritmos que calculan aproximaciones locales a fin de minimizar el error de interpolación en localizaciones específicas de los datos muestreados y los puntos de la cuadrícula.

3.1. Reconstrucción Gridding

La idea fundamental del método de reconstrucción Gridding [8] es como sigue: sea m(x,y)una función bidimensional con transformada de Fourier M (k_x, k_y) y S (k_x, k_y) una función de muestreo no Cartesiano, los datos muestreados en el dominio de Fourier están dados por:

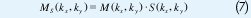
los cuales se convolucionan con una función C (k_x , k_y), Gridding Kernel, posteriormente, se muestrean sobre una cuadricula Cartesiana III (k_x, k_y) con separación entre puntos Δk de forma:

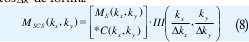
en donde el símbolo* corresponde al operador convolución bidimensional. Después que todos los datos muestreados son procesados, se aplica la transformada inversa discreta de Fourier 2D, para producir la imagen.

3.2. Compensación de la densidad no uniforme del muestreo

La transformada inversa de la función de muestreo no uniforme S (k_x, k_y), es la respuesta al impulso del sistema s (x, y) , la cual afecta con aliasing por los lóbulos laterales a la imagen. La solución para corregir la densidad no uniforme de muestreo en la operación Gridding que tiene dos opciones:

Una es la precompensación:

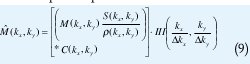
La otra es la postcompensación:

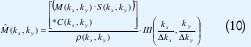
Así, existen muchas alternativas para estimar la función de compensación (k x , k y ) : una alternativa es calcular numéricamente las áreas asociadas con cada muestra. Para este fin, se describe un algoritmo llamado diagrama de Voronoi [10]. Así, la inversa de la función de densidad de área es equivalente a la función de compensación, ver Figura 4.

3.3. Función de convolución Gridding Kernel y función de apodization

La función de convolución ideal es sinc(k_x /Δk_x)sinc(k_y/Δ k_y), la cual es una función de extensión infinita y debe truncarse en algún punto. Un primer procedimiento es realizar un ventaneo de la función. Un segundo procedimiento es la reducción del ancho de la función de convolución. Esta convolución en el algoritmo Gridding tiene un doble efecto: un resultado indeseable al producir una atenuación no uniforme o apodization, y una supresión de los lóbulos laterales generados por la función de muestreo no Cartesiana.

La función de apodization c(x, y) es la transformada de Fourier de la función de convolución, Gridding kernel, la cual puede calcularse analíticamente para una gran variedad de ventanas. De este modo, la apodization puede corregirse al dividir la imagen por la función de deapodization. En la práctica, es frecuente dividir la imagen solo por una parte de la función de apodization. Una forma de limitar la deapodization es dividir la imagen en todo el campo de vista de la imagen FOV field of view por la función c(x, y) + a con a constante, en lugar de c(x,y), de tal modo que la imagen reconstruida es:

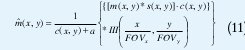
3.4. Sobremuestreo del Espacio K

En los casos considerados, se tiene el problema de la réplica de los lóbulos laterales, los cuales tiene la misma amplitud de la imagen deseada, en los bordes del FOV , el cual es una medida de la dimensión de la imagen. El problema consiste en la inexistencia de una banda de transición, esto es consecuencia directa de la reconstrucción de la imagen a partir de una cuadrícula del mismo número de muestras, que los datos en el espacio k, denominada cuadrícula 1X. Así, la densidad de la cuadricula se selecciona a un tamaño mayor que la densidad de los datos del espacio k, de tal forma se reduce tanto el efecto de apodization como el aliasing. Se introduce un factor de incremento de densidad de la cuadricula, de modo que ahora se emplea una cuadricula en el espacio k:

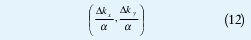
4. TRANSFORMADA RÁPIDA NO UNIFORME DE FOURIER (NUFFT)

El corazón de la reconstrucción iterativa de imágenes de muestras no uniformes en la frecuencia es la NUFFT hacia delante [3]. La cual puede ser definida de la siguiente forma: Definiendo ξ= (ξ1,...,ξk) donde ξ_k ∈[-π,π] como un vector de frecuencias no uniformemente distribuidas y f = (f-_{N /2},..., f_{( N / 2 ) -1}) donde f_n ∈ C como un vector de muestras de la señal complejo. La Transformada No Uniforme de Fourier está definida por [6]:

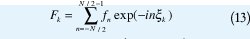
con n entero, en notación matricial:

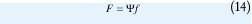
donde ψ ∈ C^KxN (K≥N) es una matriz de rango completo que contiene K funciones exponenciales discretas en sus filas.

Una aproximación rápida T del operador no uniforme de Fourier puede ser realizada proyectando la señal f en alguna base uniforme sobremuestrada de Fourier Φ ∈ C^qKxN usando la FFT estándar y empleando luego un método de interpolación.

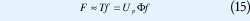
donde U_p denota el operador interpolación. Recientemente, Fessler y Sutton [5], [6] proponen obtener coeficientes de interpolación que minimizan el máximo error de aproximación. Este acercamiento puede ser formulado como un problema min.-máx.

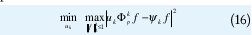
donde u_k es la parte no cero de la fila k-ésima de la matriz de interpolación U_p, Φ ^k_p es la parte de la base sobremuestreada de Fourier Φ, conteniendo p vecinos más cercanos de los elementos de la base no uniforme ψ_k y |f|²₂ (f)½ denota la norma sub-dos de f.

4.1. Transformada inversa rápida no uniforme de Fourier

Una solución sencilla del problema inverso de la Ec. (14) es una operación computacionalmente extensa, la cual está dada por la pseudo inversa Moore-Penrose:

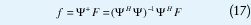
el superíndice H denota transpuesta Hermitiana. Sin embargo, tal solución es prácticamente imposible cuando el número total de muestra N es grande, puesto que necesita de la inversión de una matriz de N² xN² en el caso 2D. Alternativamente, la Ec. (17) puede ser reformulada como un problema de minimización del error de la señal reconstruida:

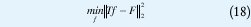
El problema puede ser resuelto iterativamente con varias técnicas de resolución de ecuaciones integro-diferenciales no lineales, dentro de tales métodos se propone en la presente investigación el uso del método no lineal del Gradiente Conjugado [7] con la fórmula de actualización de Fletcher Reeves.

5. SIMULACIONES DE MONTECARLO

La palabra simulación se refiere a un programa de tipo computacional, basado en modelos probabilísticos a fin de imitar un sistema real, caracterizar o establecer relaciones entre variables especialmente cuando otros tipos de análisis son complejos matemáticamente o existen dificultades para reproducir un experimento y los métodos de Montecarlo abarcan una colección de técnicas estocásticas.

5.1. Ruido en IRM

Recientes investigaciones se refieren al ruido térmico como principal elemento perturbador en el sistema de recepción de la señal de resonancia magnética [12]. Además, puede mostrarse que el ruido térmico se caracteriza por una función de densidad de probabilidad Gaussiana con media nula [12]. Por tal razón las simulaciones de Montecarlo se realizan con señales contaminadas con ruido Gaussiano.

5.2. Reconstrucción de IRM

Las reconstrucciones se realizan sobre el phantom de Shepp-Logan y un phantom compuesto por seis circunferencias. La Ec. (6) determina la expresión analítica de la transformada continua de Fourier de cualquier phantom, la cual es la base para la adquisición no uniforme de los datos IRM, mediante muestreo en trayectoria espiral. La reconstrucción Gridding simple sobre una cuadricula 1X, es un operador que no realiza la corrección de la densidad de muestreo, ni deapodization [8], Figura 5(a).

Una reconstrucción Gridding con precompensación de la densidad de muestreo se muestra en la Figura 5 (b). La función de compensación de densidad se calculó mediante el diagrama de Voronoi [10], ver Tabla I. La Figura 5 (c) muestra la reconstrucción Gridding 2X. Cabe notar que es posible incrementar la densidad de la cuadrícula cartesiana a un valor mayor e incluso en valores no enteros.

La Figura 5 (d) muestra la reconstrucción Gridding 2X con precompensación de densidad de muestreo mediante diagramas de Voronoi, y deapodization parcial. Se introduce un índice de deapodization , tal como se describe en la Ec. (11). Ver Tabla II.

En la Tabla I, se muestran los valores de error cuadrático medio para distintos índices de precompensación, esto es, la variación o delta de la función de precompensación entre sus niveles máximo y mínimo, sin supresión del nivel D.C. de la señal.

En la Tabla III, se muestran los valores del error cuadrático medio de reconstrucción, empleando el método convencional Gridding, para una adquisición sin ruido.

5.3. Reconstrucción iterativa

En la Tabla IV se listan los 20 primeros valores del error cuadrático de reconstrucción en el método iterativo, empleando el método del gradiente conjugado con la fórmula de actualización de

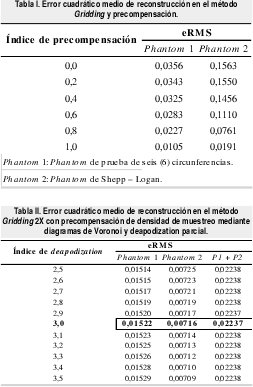
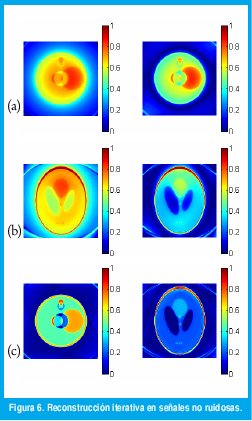
FletcherReeves para la minimización del error de reconstrucción mediante aplicación del operador directo rápido no uniforme de Fourier, así se observa que este error posee un valor asintótico, que evidencia el error de aproximación en la aplicación del operador rápido no uniforme de Fourier. Así mismo en la Figura 6 se muestra las imágenes en la 1ª, 2ª (a), (b) y 15ª (c) iteración.

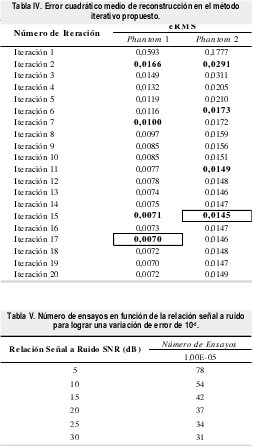
5.4. Reconstrucción en presencia de ruido

Las muestras no uniforme se contaminan con ruido blanco Gaussiano a valores de relación señal a ruido de 5, 10, 15, 20, 25 y 30 dB. Se caracteriza la función aleatoria de error cuadrático de reconstrucción, mediante la aplicación de métodos de simulación de Montecarlo.

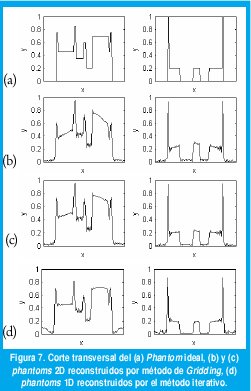
El número de ensayos para calcular los promedios estadísticos se determina mediante observación de la variación de los promedios estadísticos en función del número de ensayos, lo que corresponde a determinar el k-ésimo ensayo en el que la derivada de la esperanza y la varianza sea aproximan a cero, en el caso especifico un valor de variación igual a 10-5 determina este número de ensayos, Tabla V. En la Figura 7 se muestran los cortes transversales de los phantoms 2D reconstruidos por ambos métodos: el método iterativo y el método convencional Gridding.

6. CONCLUSIONES

El problema dominante en el operador Gridding simple es el excesivo componente D.C. debido a que la trayectoria espiral sobremuestrea las bajas frecuencias. Se observa además el efecto de réplicas y aliasing por causa de la convolución entre la imagen ideal y la transformada de Fourier de la función de muestreo no uniforme y el re-muestreo rectilíneo en el espacio k. Las réplicas que se presentan en la imagen producto del re-muestreo cartesiano, pueden reducirse por medio de un sobremuestreo en el espacio k.

La elección del índice de deapodization en el método de reconstrucción convencional es un compromiso entre compensar los efectos del remuestreo cartesiano (réplicas) o los efectos de la función de convolución (apodization). En el método de reconstrucción Gridding se observa una disminución del error cuadrático medio de reconstrucción a medida que aumenta la variación de valor pico a pico de la función de precompensación, siempre que el valor mínimo de la función sea estrictamente igual a 0, eliminación de la componente D.C. de la señal.

El error de reconstrucción en el método iterativo posee un valor asintótico, que evidencia el error de aproximación en la aplicación del operador rápido no uniforme de Fourier. Es de anotar que en el método iterativo propuesto no se realiza precompensación de la densidad de muestreo, lo cual constituye una de las ventajas del método iterativo en comparación al método convencional. Así mismo tampoco se realiza deapodization de la imagen reconstruida.

Sin embargo, existe un aumento en las réplicas debidas al muestreo no uniforme en trayectoria espiral, aún así se logra obtener mejores resultados y se reduce la complejidad de la técnica de reconstrucción en este aspecto, aunque se agregan técnicas adicionales en la actualización de la dirección del gradiente conjugado de búsqueda, pero esencialmente se incrementa la complejidad en la incorporación de la técnica de búsqueda lineal. El número de ensayos es función de la mínima variación permitida en las observaciones y la relación señal a ruido.

REFERENCIAS BIBLIOGRÁFICAS

[1]. Bagchi, S., Mitra, S.K., «Nonuniform Discrete Fourier Transform and its Signal Processing Applications», Norwell, M.A.: Kugler, 1999.

[2]. Bronstein, M. Bronstein, A. Zibulevsky, M. Azhari, H. «Reconstruction in ultrasound diffraction tomography using non-uniform FFT», IEEE Transaction on Medical Imaging, Vol. 21 No. 11, pp. 1395-1401, November 2002.

[3]. Bronstein, M. Bronstein, A. Zibulevsky, M., «The non-uniform FFT and some of its applications», pp. 1-51, November 2002.

[4]. Cooley, J. W. Tukey, J.W. «An algorithm for the machine calculation of complex Fourier Series». Mathematical computation, Vol. 19, pp 297-301, April 1965.

[5]. Fessler, J.A. Sutton, B.P., «Nonuniform Fast Fourier Transforms Using Min-Max Interpolation». IEEE Transaction on Signal Processing, Vol. 51, pp 560-574, February 2003.

[6]. Fessler, J.A. Sutton, B.P. «A min-max approach to the multidimensional nonuniform FFT: Application to tomographic image reconstruction,» Proceedings IEEE International Conference on Image Processing, Vol. 1, pp. 706­9, 2002.

[7]. Gilbert, J.C. Nocedal, J., «Global Convergence Properties of Conjugate Gradient Methods for Optimization». SIAM Journal on Optimization, Vol. 2, No. 1, pp. 21-42, 1992.

[8]. Jackson, J.I. Meyer, C.H. Nishimura, Dwight G. Macovski, Albert. «Selection of a Convolution Function for Fourier Inversion Using Gridding». IEEE Transactions on Medical Imaging, Vol. 10, No. 3, pp 473 ­ 478, September 1991.

[9]. Oppenheim, A. Johnson, D, «Computation of spectra with unequal resolution using the fast Fourier transform», Proceedings. IEEE, Vol. 59, pp. 299­301, 1971.

[10]. Rasche, V., Proska, R., Sinkus, R., Boernert, P., Eggers, H. «Resampling of data between arbitrary grids using convolution interpolation», IEEE Transactions on Medical Imaging, Vol. 18, No. 5, pp 385-392, 1999.

[11]. Shepp, Lawrence. A. Logan B. F. «The Fourier reconstruction of a head section», IEEE Transactions on Nuclear Sciences, Vol. 21, No. 3, pp. 21­43, June 1974.

[12]. Sijbers, J, «Signal and Noise Estimation from Magnetic Resonance Images», Ph.D. Thesis, Department of Physics, University of Antwerp, Antwerp (Belgium), 1999.

[13]. Stuart, C. «Functional MRI: Methods and Applications». www.fmrib.ox.ac.uk/~stuart, September 2000.

Héctor Cristyan Manta Caro
Ingeniero Electrónico - U. Distrital. Estudiante Maestría en Ciencias de la Información y las Comunicaciones - U. Distrital. hcmantac@udistrital.edu.co

Héctor Fernando Cancino de Greiff
Ingeniero Electrónico - U. Distrital, MSc. Sistemas Digitales -U. Central de Venezuela. Dr. en Ciencias Técnicas -U. Central de las Villas, Cuba. Profesor Asociado - U. Distrital. fcancino@udistrital.edu.co