DOI:
https://doi.org/10.14483/23448393.2161Published:
2006-11-30Issue:
Vol. 12 No. 2 (2007): July - DecemberSection:
Science, research, academia and developmentAnálisis del Problema del Ruido en Sistemas TS-OCDMA Coherentes
Analisis del Problema del Ruido en Sistemas TS-OCDMA Coherentes
Keywords:
Acceso Múltiple, BER, interferencia de múltiple acceso, OCDMA, ruido de batido (es).Downloads
References
P. R. Prucnal, M. A. Santoro, and T. R. Fan, "Spread spectrum fiber-optic local area network using optical processing," J. Lightwave Technol., vol. 4, May 1986, pp. 547554,.
Amaya W., Gómez J. C. "Modelado de un sistema de Acceso Múltiple por división de código en el entorno óptico.", Revista de Ingenierías Universidad Distrital, Vol 2, 2006.
K. I. Kitayama, "Code division multiplexing lightwave networks based upon optical code conversion," IEEE J. Select. Areas Commun., vol. 16, Sept. 1998, pp. 1209 1319.
H. Sotobayashi, W. Chujo, K. Kitayama, "1.6-b/s/Hz 6.4Tb/s QPSK-OCDMA/WDM (4 OCDM x 40 WDM x 40Gb/ s) Transmisión Experiment Using Optical Hard Thresholding", IEEE Photon. Technol. Lett., vol. 14, no.4, April 2002, pp. 555-557.
P. C. Teh, M. Ibsen, J. H. Lee, P. Petropoulos and D.J. Richardson, "Demonstration of a Tour-Channel WDM/ OCDMA System Using 255-Chip 320-Gchip/s Quaternary Phase Coding Gratings", IEEE Photon. Technol. Lett., vol. 14, February 2002, pp. 227-229, no. 2.
X. Wang, K. I. Kitayama,"Analysis of Beat Noise in Coherent and IncoherentTime-Spreading OCDMA",J. Lightwave Technol., vol. 22, October 2004, pp. 2226 2235.
Goodman J. W., "Statistic Optics". New York: Wiley, 1985.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2007-00-00 vol:12 nro:2 pág:30-38
Análisis del problema de ruido en sistemas TS-OCDMA coherentes
Waldimar Amaya Ocampo
Ingeniero Electrónico y Magíster en Teleinformática de la Universidad Distrital,pertenece al grupo de investigación TEAM, Universidad Politécnica de Valencia.
Juan Carlos Gómez Paredes
Ingeniero en Telecomunicaciones. Profesor de la Facultad de Ingeniería de la Universidad Distrital, pertenece al grupo de investigaciones GITUD.
Resumen
El presente artículo describe el análisis del problema de ruido en los sistemas TS-OCDMA (Time Spreading - Optical Code Division Multiple Access). El ruido total en este tipo de sistemas esta compuesto por ruido de batido, ruido de interferencia de múltiple acceso (MAI) y por el ruido térmico y shot propios de de los elementos electrónicos presentes en el proceso de detección. El modelo del ruido que se plantea en este artículo es evaluado mediante simulaciones en donde los principales parámetros a considerar son la penalización de potencia, la razón de error de bit (BER) y la diafonía.
Palabras clave:
Acceso Múltiple, BER, interferencia de múltiple acceso, OCDMA, ruido de batido.
Abstract
This paper describes the analisys related to the noise problems that exist in the TS-OCDMA Systems (Time Spreading - Optical Code Division Multiple Access). This noise is composed by the Beat Noise, Multiple Access Interference Noise, thermal and Shot Noise of the electronics devices presents in the detection process. The model of noise in this paper is evaluated through simulations in which the main parameters to be considered are the power penalty, the BER and the crosstalk.
Key words:
Beat noise, BER, OCDMA systems, multiple access, multiple-access interference.
1. Introducción
Los sistemas con multiplexación por división en código óptico (OCDMA) son objeto de estudio constante pese al dominio de los sistemas WDMA (Wavelenght Division Multiple Access). Hoy en día se observan los sistemas OCDMA no como competidores en ancho de banda, sino como posibles complementos de los sistemas WDMA, sobretodo en la red de acceso, y atendiendo a su potencial de flexibilidad, seguridad, granularidad, escalabilidad, etc. [1]-[3]. Este artículo se centra en los sistemas Time-Spreading OCDMA en régimen coherente, en los que se puede aprovechar al máximo las características de codificación no sólo de la amplitud, sino también de la fase, generando códigos bipolares o de múltiples niveles de fase [4]-[5].
Los sistemas coherentes TS-OCDMA tienen múltiples ventajas sobre los sistemas incoherentes, entre ellas, una mayor eficiencia en el uso del ancho de banda y de la potencia, mayor correlación y en general códigos con mejor desempeño. No obstante, existe un problema en los sistemas coherentes, y es el ruido inherente que se presenta en el momento de la fotodetección. Este ruido es producto del batido en campo de las señales que llegan al fotodetector. Además de este ruido, en los sistemas coherentes también esta presente la interferencia de múltiple acceso (MAI) y los ruidos propios de los dispositivos eléctricos (ruido térmico, shot, etc.). Como se vio en [2] el ruido presente provoca que exista incertidumbre en el momento de recuperar la señal.
Los sistemas TS-OCDMA coherentes utilizan como función de entrada pulsos muy estrechos, normalmente con duraciones que no superan los 5 ps. Por otra parte el dispositivo más usado para realizar la codificación son las redes de difracción de Brag g superestructuradas (SSFBG). De esta forma existirá una SSFBG con un código grabado en el extremo del transmisor y una SSFBG en el extremo receptor con el código conjugado, para realizar la decodificación. Cada código tienen un número N de chips, por lo tanto la señal codificada tendrá una duración de N veces el tiempo del chip (T c ). Y la señal decodificada, al ser producto de la correlación entre las dos señales, una duración de (2N1)×Tc. En [6] se presenta un modelo que permite estudiar el fenómeno del ruido en los sistemas OCDMA, sin embargo, como se podrá ver en el apartado 2, este modelo no tiene en cuenta algunos de los aspectos anteriormente mencionados. Por esta razón, hemos querido realizar primero una generalización de dicho modelo y posteriormente modelarlo bajo la hipótesis de sistema asíncrono. De esta manera en el apartado 2 se describirá de forma resumida el estudio en el que se ha basado este artículo con el objeto de hacerlo más comprensible, mostrando las consideraciones con las que se realizó. En el apartado 3 se incluirán dentro del modelo algunos aspectos importantes como son, la posibilidad de una forma arbitraria del pulso (bit) de la señal de entrada y la consideración del ruido no solo en el tiempo de chip de datos si no en la totalidad del tiempo de bit. En 4, y siguiendo con la misma línea, se propone un estudio del sistema bajo hipótesis asíncrona. Esta hipótesis se plantea con base en que los tráficos aportados por cada usuario están incorrelados. Finalmente en 5 se evalúa cada modelo y se muestra el efecto de la inclusión de cada una de las características adicionadas. Nos centraremos especialmente en la mejora que implica la consideración de una hipótesis asíncrona. Mediante esta evaluación pretendemos dar una visión lo más realista posible de los problemas de ruido en los sistemas OCDMA y las limitaciones que esto implica.
2. Modelo básico del sistema TS OCDMA
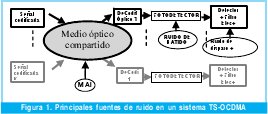
Las principales fuentes de ruido en un sistema TS-OCDMA se muestran en la figura 1, allí podemos ver que lo primero que afecta la señal es la MAI (Multiple Access Interference noise). Esta primera interferencia se presenta al mezclar las señales de los diferentes usuarios. El ruido de batido aparece después cuando se realiza la fotodetección y finalmente la ultima fuente de ruido son los dispositivos electrónicos en el receptor, que entregan ruido térmico y ruido de disparo.
Para el análisis de este sistema se toman en [6] las siguientes consideraciones:
1. Se utiliza lo que se conoce como Time Gating de tal forma que la interferencia multiacceso (MAI) y el ruido de batido solo es considerado dentro del instante o "chip" central del bit, equivalente a un Tc.
2. Supone los chips constantes en la anchura Tc.
3. Todos los chips caen perfectamente solapados.
4.Los estados de polarización de la señal de dato e interferente se asumen iguales (peor caso).
5. No se incluyen técnicas de thresholding lo que en principio podría mejorar los resultados del modelo.
En la figura 2. se representa el modelo de los chips recibidos tendiendo en cuentas las pautas del párrafo anterior.
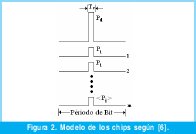
Para el análisis se supone que existen K usuarios en el sistema. En un instante determinado m (0<m<k-1) son usuarios interferentes del usuario deseado. De esta manera el campo eléctrico a la entrada del detector es:
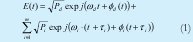
donde Pd y Pi son las intensidades ópticas de la señal objetivo decodificada y de los usuarios interferentes respectivamente, d y i son las frecuencias ópticas, d y i son las fases ópticas relativas respectivas de estas señales y i es el retardo relativo de tránsito a lo largo de la red óptica entre la señal de datos y cada uno de los diferentes usuarios interferentes.
Se asume que d y i son mutuamente independientes que siguen un proceso estocástico con distribución gausiana. Si empleamos un fotodetector de ley cuadrática la señal a la salida del integrador será:

Donde ℜ es la responsividad del fotodetector,Tc es el tiempo de chip η es el ruido del receptor.
En la Ecuación 2, el primer término corresponde a la señal deseada, el segundo a la interferencia MAI, el tercero al ruido producido por el batido de los pulsos de los usuarios interferentes con el pulso de datos objetivo, conocido como batido de primer orden. El cuarto término corresponde al batido de los interferentes entre si, llamado batido de segundo orden y finalmente la ultima fuente de ruido correspondiente al receptor.
El tercer y cuarto término determinan si el sistema que consideramos es un sistema coherente o incoherente, puntualmente φ (t-τ)≡ δ φij(t) que es fuertemente dependiente de la coherencia del pulso óptico dentro del tiempo de integración. Así podemos tener 3 casos a saber:
Régimen Incoherente: aquí se asume que tc (tiempo de coherencia de la luz [7]) es mucho menor que Tc, (tc <<Tc). En este régimen δ φij(t) es un proceso aleatorio uniformemente distribuido sobre [π-π,] durante el intervalo de integración Tc. Las integrales de la función coseno son iguales a 0, con lo cual Z se puede simplificar a:
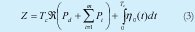
En este régimen el ruido dominante es el ruido MAI ya que el ruido de batido puede ser ignorado debido a que se promedia en la detección.
Régimen Coherente: la coherencia de la luz debe ser mantenida por lo menos dentro de cada chip, dado que precisamente se busca la interacción coherente de los chips en el decodificador para "alimentar" el pico de autocorrelación. En esta situación, es decir (tc ≥Tc), δ φij(t) es una constante dentro de la duración de la integral, convirtiendo a Z en:

donde Δ Φi ≡ √t (δ Φ)id Tc + ωi τi denotan el ruido de fase total.Δ Φi y Δ Φiij son procesos aleatorios que varían sobre [-π,π] de bit a bit, lo cual resulta en el ruido de batido de los sistemas coherentes.
Régimen Parcialmente Coherente: el modelo se puede simplificar asumiendo que la fase relativa Δ Φi y Δ Φii se mantienen constantes dentro de cada ranura de tiempo del tiempo de coherencia τ, y que son procesos aleatorios mutuamente independientes distribuidos sobre [π,-π] para diferentes ranuras de tiempo. Bajo esta suposición podemos decir que Z puede ser expresado como:
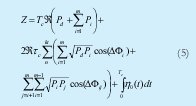
La constante de coherencia kt≡Tc/τc indicara en que grado el sistema es más ó menos coherente de tal forma que esta ecuación cuando kt=1 es la misma que en un sistema coherente y cuando kt⇒ ∞ entonces las ecuación se convertirá en la mismas de un sistema incoherente.
Este artículo se centra en los sistemas TimeSpreading OCDMA en régimen coherente, en los que se puede aprovechar al máximo las características de codificación no sólo de la amplitud sino de la fase, generando códigos bipolares o de múltiples niveles de fase [4]-[5].
Si queremos ver el efecto de esta interferencia apelaremos a la medida de BER que se considera como la más representativa.
La BER promedio del sistema depende del número m de usuarios interferentes de los K 1 posibles, de tal manera que se puede escribir:
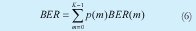
donde p(m) es la probabilidad que m de los K-1 usuarios interferentes estén simultáneamente enviando un 1, lo cual obedece una distribución binomial
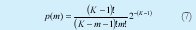
BER(m) es la BER que experimentará el canal de "datos" con m señales interferentes. Si los bits son equiprobables entonces podemos expresarla como:
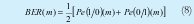
donde Pe(1|0)(m) y Pe(0|1)(m) son las probabilidades de error condicionales de los símbolos cero y uno respectivamente.
Si se asume que la MAI y el ruido del receptor tienen una distribución gausiana, las probabilidades de error son:
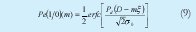
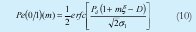
donde 0<D<1+mx es el umbral de decisión y x es la diafonía definida como x=<Pi>/Pd. Adicionalmente s0 y s1 son las varianzas del ruido en un sistema coherente para los símbolos 0 y 1 respectivamente.
Cabe anotar que para la deducción de estas formulas se usó una aproximación gausiana de la función de densidad de probabilidad del total de la señal recibida, que es valida cuando los valores de m son mayores a 4, lo cual esta bien ya que el objetivo es tener un sistema con la máxima cantidad de usuarios posibles.
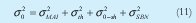
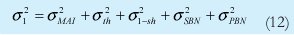
Siendo:
la varianza o potencia de ruido MAI total del sistema: σ2MAI= mσ2MAI-0Los términos σ2th y σ2sh son las varianzas de ruido térmico y ruido shot respectivamente.
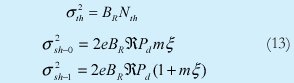
BR=1/(2Tc) es el ancho de banda del receptor,y Nth es la densidad espectral de ruido térmico.
Usualmente en redes TS-OCDMA el nivel de diafonía es muy bajo ( ξ <<1). La relación entre la varianza del batido primario y el ruido del batido secundario esta alrededor de 2/m√, de tal forma que si m no es muy grande (m √ξ <<1), el batido secundario puede ser ignorado. En nuestro caso el batido secundario no puede ser ignorado ya que estamos buscando modelar un sistema en donde queremos tener una gran cantidad de usuarios.
En la varianza σ20 se ha incluido el término σ2 SBN, el cual corresponde a la varianza del ruido de batido secundario, y podemos deducirlo sabiendo Pi = Pj = ξPd que y reemplazando en el 4to término de la ecuación 4. tendremos la corriente de ruido de batido secundario
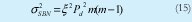
De la misma manera en la varianza de σ21 aparece el término σ2 PBN que corresponde a la varianza del ruido de batido primario, y que de manera similar a lo que se hizo con σ2 SBN se puede encontrar que es:
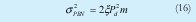
Obteniendo de esta manera todos los términos necesarios para realizar la evaluación. Hasta aquí el análisis que se ha descrito es el mismo que el planteado por [6]. Esto permite que sea más fácil el seguimiento de la contribución hecha a este modelo, la cual se plantea a continuación.
3. Forma de pulso arbitraria e inclusión de interferencia en todo el tiempo de BIT
Para realizar una generalización del modelo, se hacen las siguientes consideraciones:
- Forma de pulso arbitraria s(t).
- Ruido en todo el tiempo de bit y no solo en el tiempo del pulso.
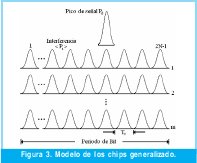
La forma de pulso puede ser como se muestra en la figura 3 de tipo gausiano, tal como fue simulado en [2], o de cualquier otra forma.
El campo recibido ahora será:
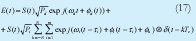
En donde S(t) es la función normalizada que describe la forma del chip y φk es la fase óptica relativa entre chips.
Para un sistema TS OCDMA que emplea fotodetección cuadrática (fotodetector seguidor normal), tomando módulo al cuadrado y aplicando una respuesta impulsional del receptor hRC(t) obtenemos la fotocorriente.
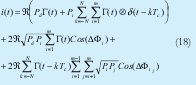
Se observa que la nueva sumatoria ya incluye la interferencia en todo el tiempo de bit y que la función ⌈(t)= s2 (t) ⊗ hRC (t) incluye tanto la forma de los pulsos de la fuente óptica codificada, como la respuesta concreta del receptor empleado. Ambas pueden ser por lo tanto arbitrarias.
Se muestrea en el instante central que ha sido tomado como referencia donde se produce el pico de Pd, es decir, t=0

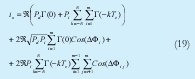
Los términos de fase siguen teniendo el mismo comportamiento del modelo anterior. Tomando como válida la aproximación gaussiana para todos los ruidos podemos aplicar el modelo de detector con umbral de decisión óptimo, cuyo parámetro de calidad se define como
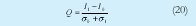
y por lo tanto a partir de éste la probabilidad de error de bit queda como:
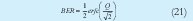
Las incógnitas ahora son I1, I0, σ1 y σ0 las cuales se hallan de manera similar al caso anterior, obteniendo:
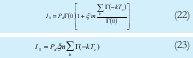
Para los ruidos de interferencia en el sistema quedara como:
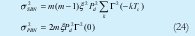
Estas ecuaciones incluyen ya a ⌈ (0) lo que hace que sean más generales.
Con el objeto de hacer una descripción más manejable se hace conveniente expresar los ruidos en términos de relaciones de señal a ruido.

Tomando en consideración el ruido shot sólo para el "1", tenemos
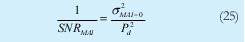
Así mismo la relación señal a ruido térmico es:
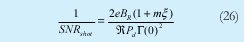
Así mismo la relación señal a ruido térmico es:
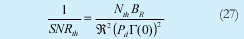
y unificando las dos anteriores en una tenemos:
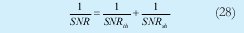
Llevando estos resultados a la ecuación 20 obtenemos que Q es:
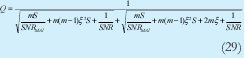
La diferencia de esta descripción de Q con la que podríamos obtener de 1 radica en el término S que esta definido como:
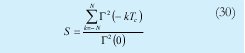
que a su vez depende de ⌈. Obsérvese que este término realmente es le que determina cuantas componentes de batido se tendrán en cuenta, en otras palabras el ancho de banda del filtro en le receptor.
El máximo ancho de banda que podemos considerar para seleccionar solo la información esencial es BR=1/2Tc, que equivale a utilizar la técnica de time gating. En este caso ⌈2 (-kTc) << (0) , para todo valor de k diferente de 0. Así, estaríamos eliminando todas las componentes interferentes que caen fuera del instante central del bit y por lo tanto en k=0, S será igual a 1 y la expresión para Q será exactamente igual que la encontrada por [6].
Por otra parte si comenzamos a disminuir el ancho de banda, S se hará mayor y Q disminuirá lo que ocasiona que la BER aumente, ya que estaremos considerando una mayor cantidad de componentes de ruido de batido secundario. El mínimo ancho de banda que podemos tener es BR=1/2Tbit. Si lo vemos en el dominio temporal estaríamos tomando todas las componentes de interferencia posible desde -Nchip hasta Nchip ya que Tbit=2NchipTc. En este caso ⌈ 2 (- kTc ) 0 para todo k en ese inter valo. Podemos suponer que ⌈2 (- kTc ) = cte = ⌈2 (0 ) con lo que obtendríamos que S= 2 Nchip que incluye toda la interferencia fuera del instante central del chip.
4. Reducción del impacto del ruido de batido primario en hipótesis asíncrona
En los modelos considerados hasta el momento se parte de la suposición de que existe un solapamiento total entre los chips del usuario objetivo como de los interferentes. Esta hipótesis aunque es fácil de analizar no es realista, ya que los tráficos de los usuarios están incorrelados tanto en tiempo como en fase. La incorrelación implica asincronía del sistema, lo cual tiene ventajas en lo que respecta al rechazo de ruido de batido tal como fue descrito en [2].
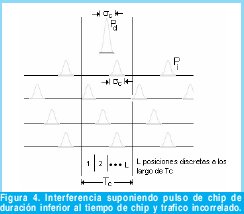
La situación representada en la Figura 4. introduce además una nueva hipótesis en el modelo y es que la duración temporal de los "chips" puede ser en general menor que la separación entre los mismos. En este escenario, la contribución de ruido de batido tanto primario como secundario se reduce al no existir un solapamiento constante entre señal e interferencia.
Se realizarán las siguientes suposiciones para poder tratar el problema de forma sencilla.
1. Se definen L posiciones discretas (slots) de caída de los pulsos-chips dentro del tiempo de chip Tc.
2. Los chips son de anchura σ= Tc /L. Y supondremos que no hay solapamientos parciales entre chips. Es decir ocupan posiciones discretas.
3. La probabilidad de que un chip (usuario) ocupe cualquiera de las posiciones (L) es uniforme α = 1 /L.
4. Definimos MB1= Número de chips interferentes del conjunto m total que caen sobre la posición del chip de datos (Pd), estos producen Ruido de batido Primario.
5. MB2(l) = Número de chips interferentes que caen en el tramo l-ésimo siendo l∈ [1'!(L1)]. Estos producen Ruido de batido Secundario(Beat Noise Secundary (B2)).
Como se puede entender el número de usuarios interferentes m ahora se divide entre los interferentes que caen directamente sobre el chip de dato y los que no lo interfieren directamente, de tal manera que podemos decir:
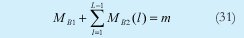
Para realizar el análisis con esta nueva situación podemos partir de la misma expresión de campo que en el caso anterior, y así encontrar que is (fotocorriente en el instante central) ahora es igual a:
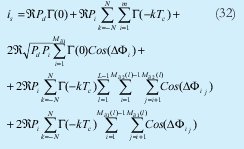
La diferencia con las expresión anteriormente hallada para is se nota a partir del tercer término, el cual corresponde al ruido de batido primario, la sumatoria ya no cubre a los m usuarios interferentes si no apenas a los que influyen al chip de datos, el siguiente término es el batido secundario producido por el batido entre las componentes de usuarios que caen dentro del tiempo de chip pero que no influyen el chip de dato y el ultimo término es el batido secundario producido entre los usuarios interferentes que caen directamente sobre el chip de datos.
De 32 podemos encontrar las expresiones para las varianzas de ruido de los chips 0´s y 1´s
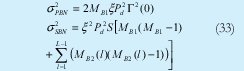
Como se puede deducir de estas expresiones, la fotocorriente, la interferencia por ruido de batido, y en definitiva la BER dependerán de las combinación concreta de posiciones de caída de los chips interferentes a lo largo del Tc (Tiempo de chip), es decir del valor concreto del vector de MB1 y del vector MB2(l). La BER conjunta en este caso se obtendría aplicando:
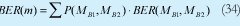
donde P(MB1,MB2) es la probabilidad de que las posibles combinaciones se den.
Suponiendo, como es natural, que los instantes de llegada al decodificador de los distintos usuarios son absolutamente independientes, podemos desglosar la probabilidad conjunta de que ocurra una combinación dada, como el producto:
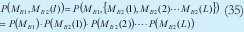
donde P(MB1) es la probabilidad de que en la posición del slot temporal que ocupa el chip de datos recaigan MB1 chips interferentes y P(MB2(l)) es la probabilidad de que en el slot temporal l-ésimo recaigan MB2(l) interferentes.
Como ejemplos extremos del impacto sobre el ruido de batido nos podemos fijar en el caso en que MB1=0 y por lo tanto no exista ningún interferente sobre el chip de datos haciendo que sPBN=0, o también que MB2=0, reduciendo al mismo problema que teníamos cuando no considerábamos la hipótesis asíncrona dentro del tiempo del chip.
Cada uno de los términos de P(MB1,MB2(l)) se puede hallar conociendo que la probabilidad de que X usuarios del conjunto m "caigan" en la misma posición es una distribución binomial.
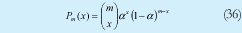
De tal forma que:
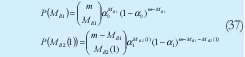
Y así sucesivamente hasta que se complete el valor de m, (Ec. 3.34). y en donde
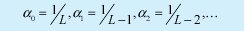
5. Resultados de evaluación de los diferentes modelos
La evaluación del modelo general, en función del número de usuarios del sistema K, diafonía de los codificadores-decodificadores (î), y número de slots temporales L, se ha llevado a cabo mediante el cálculo de la potencia de señal necesarias Pd a la entrada del decodificador para garantizar una BER= 10-9, y de éstas las penalizaciones de potencia.
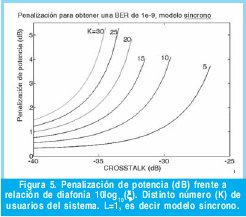
La Figura 5 muestra la penalización frente al valor de diafonía para diferente número de usuarios cuando se considera L=1 es decir el modelo simplificado síncrono (2)-(3) [6]. Es destacable como el nivel î máximo admisible incluso para 5 usuarios es de -30dB (requiere códigos de 1000 chips) o de - 36dB para 25 usuarios (requiere códigos de 4000 chips), lo que es prácticamente irrealizable.
La evaluación del modelo para L=6 (Figura 6), muestra una reducción sustancial del impacto del ruido de batido dominante (PBN), suavizando los estrictos requisitos de diafonía máximo a -26dB para K=5 y -32 dB para K=25. La Figura 7 sintetiza los distintos casos de L desde 1 hasta 10.
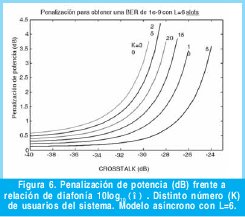
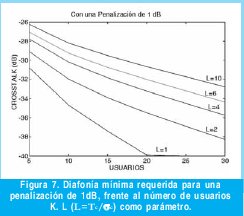
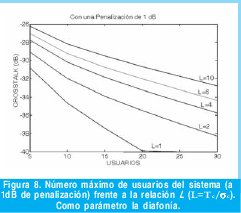
Desde el punto de vista de sistemas, se aprecia la diferencia en la evaluación del efecto de los ruidos de batido al considerar L>1 en la figura 8, donde se ha representado el número máximo de usuarios frente el número de slots L, para tres valores de diafonía.
Para -25dB de diafonía (caso excesivamente desfavorable) la mejora en función del número de slots L es inapreciable. Para un valor de -30dB pasamos de K=5 a K=18 al incrementar L desde1 hasta 10, y para -35dB el incremento es desde K=13 hasta K=40.
Las mejoras obtenidas para el modelo asíncrono obedecen a la distribución aleatoria de las señales de los canales interferentes a lo largo del tiempo de "chip" (Tc), siendo la anchura del mismo . Esta suposición por lo tanto fuerza la utilización de un mayor ancho de banda óptico para el sistema OCDMA (), que en el modelo es justamente un incremento L. La reducción de la duración del chip y el consiguiente aumento espectral ocupado es lo que podríamos llamar una alternativa de mitigación de ruido de batido por dispersión en el dominio temporal. Su alternativa opuesta consistiría en la división del sistema OCDMA completo en L porciones espectrales disjuntas conformando un sistema WDM-OCDMA. Cada subsistema OCDMA en este caso mantendría la condición de solapamiento temporal estricto entre datos e interferencia pero para un número de usuarios inferior.
6. Conclusiones
Partiendo del modelo planteado en [6], se ha realizado una formulación generalizada para las fuentes de ruido por interferencia de Batido y MAI en sistemas Time-Spreading OCDMA de tipo Coherente. La generalización permitió, entre otras, considerar un sistema real donde el receptor puede tener un ancho de banda menor que 1/2Tc. Bajo esta consideración, se disminuye el rendimiento del sistema, al incluir no solamente el ruido que cae directamente sobre el chip de datos, si no el que cae durante todo el tiempo de bit. También se ha extendido el modelo simplificado con superposición total de datos e interferencia (peor caso) a un modelo estadístico con duración de chip inferior a la separación entre chips. La evaluación del modelo extendido ha revelado importantes reducciones en el impacto del ruido de batido en el sistema permitiendo el aumento de usuarios o de la diafonía máxima permitida.
Referencias bibliográficas
[1] P. R. Prucnal, M. A. Santoro, and T. R. Fan, "Spread spectrum fiber-optic local area network using optical processing," J. Lightwave Technol., vol. 4, May 1986, pp. 547554,.
[2] Amaya W., Gómez J. C. "Modelado de un sistema de Acceso Múltiple por división de código en el entorno óptico.", Revista de Ingenierías Universidad Distrital, Vol 2, 2006.
[3] K. I. Kitayama, "Code division multiplexing lightwave networks based upon optical code conversion," IEEE J. Select. Areas Commun., vol. 16, Sept. 1998, pp. 1209-1319.
[4] H. Sotobayashi, W. Chujo, K. Kitayama, "1.6-b/s/Hz 6.4- Tb/s QPSK-OCDMA/WDM (4 OCDM x 40 WDM x 40Gb/ s) Transmisión Experiment Using Optical Hard Thresholding", IEEE Photon. Technol. Lett., vol. 14, no.4, April 2002, pp. 555-557.
[5] P. C. Teh, M. Ibsen, J. H. Lee, P. Petropoulos and D.J. Richardson, "Demonstration of a Tour-Channel WDM/ OCDMA System Using 255-Chip 320-Gchip/s Quaternary Phase Coding Gratings", IEEE Photon. Technol. Lett., vol. 14, February 2002, pp. 227-229, no. 2.
[6] X. Wang, K. I. Kitayama,"Analysis of Beat Noise in Coherent and IncoherentTime-Spreading OCDMA",J. Lightwave Technol., vol. 22, October 2004, pp. 2226 2235.
[7] Goodman J. W., "Statistic Optics". New York: Wiley, 1985.
Waldimar A. Amaya Ocampo
Ingeniero electrónico de la Universidad Distrital Francisco José de Caldas. Especialista en telecomunicaciones móviles de la misma universidad. Candidato al título de Magíster en Teleinformática en la Universidad Distrital. Se desempeñó como Director Técnico en Cablecentro S.A. durante 2 años. Posteriormente, ejerció el cargo de Docente en la Universidad Distrital y en la Universidad Santo Tomás. Actualmente realiza estudios de doctorado en Telecomunicaciones en la Universidad Politécnica de Valencia, España. Se desempeña como ingeniero de investigación y desarrollo en el Instituto de Telecomunicaciones y Aplicaciones Multimedia (ITEAM) de la misma universidad y pertenece como investigador al grupo de Comunicaciones Ópticas y Cuánticas donde realiza estudios sobre sistemas ópticos de acceso múltiple por división de código (OCDMA). walamoc@doctor.upv.es
Juan Carlos Gómez Paredes
Ingeniero en telecomunicaciones del Instituto Superior Politécnico José Antonio Echevarria de Ciudad de la Habana, Cuba. Especialista en Computación Aplicada a la Enseñaza de la Ingeniería y Magíster en Sistemas de Transmisión por Fibra &Oacuxte;ptica de la misma Universidad. Se desempeñó como coordinador del proyecto curricular de ingeniería electrónica de la Universidad Distrital. Actualmente se desempeña como profesor en el área de comunicaciones y de la especialización en comunicaciones móviles de la facultad de ingeniería de la Universidad Distrital. jcgomez95@hotmail.com
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










