DOI:
https://doi.org/10.14483/23448393.18002Published:
2022-01-04Issue:
Vol. 27 No. 1 (2022): January-AprilSection:
Industrial EngineeringSimulación de una política de inventario basada en la metodología Demand Driven MRP desde un enfoque de redes de Petri
Simulation of an Inventory Policy Based on the Demand Driven MRP Methodology from a Petri Nets Approach
Keywords:
Demand Driven MRP, Inventory, Petri nets (en).Keywords:
Demand Driven MRP, inventario, redes de Petri (es).Downloads
References
C. J. Vidal, Fundamentos de control y gestión de inventarios, Universidad del Valle, 2010.
D. Singh and A. Verma, “Inventory management in supply chain”, Mater. Today Proc., vol. 5, no. 2, pp. 3867-3872, 2018. https://doi.org/10.1016/j.matpr.2017.11.641 DOI: https://doi.org/10.1016/j.matpr.2017.11.641
A. M. Paredes Rodríguez, V. L. Chud Pantoja y J. C. Osorio, “Sistema de control de Inventarios multicriterio difuso para repuestos”, Sci. Tech., vol. 24, no. 4, pp. 595-603, 2019. DOI: https://doi.org/10.22517/23447214.22331
J. L. Cardona Tunubala, J. P. Orejuela Cabrera y C. A. Rojas-Trejos, “Gestión de inventario y almacenamiento de materias primas en el sector de alimentos concentrados”, Rev. EIA, vol. 15, no. 30, pp. 195-208, 2018. https://doi.org/10.24050/reia.v15i30.1066 DOI: https://doi.org/10.24050/reia.v15i30.1066
Z. Chen, and R. Rossi, “A dynamic ordering policy for a stochastic inventory problem with cash constraints”, Omega, vol. 102, 2021. https://doi.org/10.1016/j.omega.2020.102378 DOI: https://doi.org/10.1016/j.omega.2020.102378
R. Miclo, M. Lauras, F. Fontanili, J. Lamothe, and S. A. Melnyk, “Demand Driven MRP: Assessment of a new approach to materials management”, Int. J. Prod. Res., vol. 57, no. 1, pp. 166-181, 2019. https://doi.org/10.1080/00207543.2018.1464230 DOI: https://doi.org/10.1080/00207543.2018.1464230
R. Miclo, F. Fontanili, M. Lauras, J. Lamothe, and B. Milian, “An empirical comparison of MRPII and Demand-Driven MRP”, IFAC-PapersOnLine, vol. 49, no. 12, pp. 1725-1730, 2016. https://doi.org/10.1016/j.ifacol.2016.07.831 DOI: https://doi.org/10.1016/j.ifacol.2016.07.831
L. A. San-José, J. Sicilia, and B. Abdul-Jalbar, “Optimal policy for an inventory system with demand dependent on price, time and frequency of advertisement”, Comput. Oper. Res., vol. 128, 2021. https://doi.org/10.1016/j.cor.2020.105169 DOI: https://doi.org/10.1016/j.cor.2020.105169
Y. Chen, M. I. M. Wahab, and P. Ongkunaruk, “A joint replenishment problem considering multiple trucks with shipment and resource constraints”, Comput. Oper. Res., vol. 74, pp. 53-63, 2016. https://doi.org/10.1016/j.cor.2016.04.012 DOI: https://doi.org/10.1016/j.cor.2016.04.012
K. Labadi, H. Chen, L. Amodeo, and C. Chu, “Batch deterministic and stochastic petri nets: Modelling, analysis and application to inventory systems”, IFAC Proc. Vol., vol. 38, no. 1, pp. 343-348, 2005. https://doi.org/10.3182/20050703-6-CZ-1902.00341 DOI: https://doi.org/10.3182/20050703-6-CZ-1902.00341
M. Dotoli, M. P. Fanti, and A. M. Mangini, “Comparing management policies for supply chains via a hybrid Petri net model”, Conf. Proc. - IEEE Int. Conf. Syst. Man Cybern., pp. 3469-3474, 2007. https://doi.org/10.1109/ICSMC.2007.4413684 DOI: https://doi.org/10.1109/ICSMC.2007.4413684
N. R. S. Raghavan and D. Roy, “A stochastic Petri net approach for inventory rationing in multi-echelon supply chains”, J. Heuristics, vol. 11, pp. 421-446, 2005. https://doi.org/10.1007/s10732-005-1855-2 DOI: https://doi.org/10.1007/s10732-005-1855-2
L. Cui, J. Deng, L. Wang, M. Xu, and Y. Zhang, “A novel locust swarm algorithm for the joint replenishment problem considering multiple discounts simultaneously”, Knowledge-Based Syst., vol. 111, pp. 51-62, 2016. https://doi.org/10.1016/j.knosys.2016.08.007 DOI: https://doi.org/10.1016/j.knosys.2016.08.007
R. Ramanathan, “ABC inventory classification with multiple-criteria using weighted linear optimization”, Comput. Oper. Res., vol. 33, no. 3, pp. 695-700, 2006. https://doi.org/10.1016/j.cor.2004.07.014 DOI: https://doi.org/10.1016/j.cor.2004.07.014
A. Kortabarria, U. Apaolaza y A. Lizarralde, “Demand driven mrp - nuevo método para la gestión de la cadena de suministro: un estudio de caso”, Dir. y Organ., vol. 67, 2019. https://doi.org/10.37610/dyo.v0i6 DOI: https://doi.org/10.37610/dyo.v0i67.540
C. Ptak, and C. Smith, DDMRP: Demand Driven Material Requirements Planning, Industrial Press, 2016.
J. Sheng, and D. Prescott, “A coloured Petri net framework for modelling aircraft fleet maintenance”, Reliab. Eng. Syst. Saf., vol. 189, pp. 67-88, 2019. https://doi.org/10.1016/j.ress.2019.04.004 DOI: https://doi.org/10.1016/j.ress.2019.04.004
S. H. Zegordi, and H. Davarzani, “Developing a supply chain disruption analysis model: Application of colored Petri-nets”, Expert Syst. Appl., vol. 39, no. 2, pp. 2102-2111, 2012. https://doi.org/10.1016/j.eswa.2011.07.137 DOI: https://doi.org/10.1016/j.eswa.2011.07.137
L. H. Fierro, R. E. Cano, and J. I. García, “Modelling of a multi-agent supply chain management system using colored Petri nets”, Procedia Manuf., vol. 42, no. 2019, pp. 288-295, 2020. https://doi.org/10.1016/j.promfg.2020.02.095 DOI: https://doi.org/10.1016/j.promfg.2020.02.095
A. P. Velasco Acosta, C. Mascle, and P. Baptiste, “Applicability of Demand-Driven MRP in a complex manufacturing environment”, Int. J. Prod. Res., vol. 58, no. 14, pp. 4233-4245, 2020. https://doi.org/10.1080/00207543.2019.1650978 DOI: https://doi.org/10.1080/00207543.2019.1650978
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 14 de mayo de 2021; Revisión recibida: 28 de julio de 2021; Aceptado: 14 de septiembre de 2021
Resumen
Contexto:
En la actualidad, las compañías se enfrentan a una problemática asociada al control del inventario debido a que existe un alto número de referencias que se deben administrar con el objetivo de reducir las ventas perdidas y disminuir el inventario de baja rotación.
Método:
Demand Driven MRP (DDMRP) es una estrategia de control de inventarios innovadora que incorpora elementos de sistemas Lean y teoría de restricciones que llevan a introducir buffers dinámicos con el objetivo de controlar los niveles de inventario al tiempo que se responde a la demanda. El uso de redes de Petri se utilizan para simular y validar la aplicación de la metodología DDMRP en un inventario de producto terminado.
Resultados:
A partir de la simulación realizada se logra comprobar la efectividad de la metodología DDMRP para el caso de estudio, en el que se reduce el sobrestock de inventario, al mismo tiempo que se minimiza la posibilidad de agotados.
Conclusiones:
La simulación de la metodología DDMRP a través de redes de Petri permitió evaluar el funcionamiento de la política antes de su implementación, para validar la efectividad de la estrategia sobre indicadores de desempeño de la compañía como lo son el nivel de servicio y los costos de almacenamiento.
Palabras clave:
Demand Driven MRP, inventario, redes de Petri Idioma: Español..Abstract
Context:
Currently, companies are facing a problem associated with inventory control since there is a high number of references that they must manage to reduce lost sales and minimize low-turnover inventory.
Method:
Demand Driven MRP (DDMRP) is an innovative inventory control strategy that incorporates elements of Lean systems and theory of constraints which lead to the introduction of dynamic buffers with the purpose of controlling inventory levels while responding to the demand. Petri nets are used to simulate and validate the application of the DDMRP methodology in a finished product inventory.
Results:
From the conducted simulation, it is possible to verify the effectiveness of the DDMRP methodology for the case under study, where the overstock is reduced while the possibility of out-of-stock is minimized.
Conclusions:
The simulation of the DDMRP methodology through Petri nets allowed evaluating the performance of the policy before its implementation with the purpose of validating the effectiveness of the strategy on company performance indicators such as the level of service and costs storage.
Keywords:
Demand Driven MRP, Inventory, Petri nets. Language: Spanish..Introducción
En los últimos años, el control de inventarios se ha convertido en un tema apasionante y complejo debido a la gran incertidumbre que existe en el mercado y la naturaleza propia de los productos que se gestionan, lo que refleja que, después del transporte, el inventario es la actividad que mayor aporte tiene en los costos logísticos en la mayoría de organizaciones [1]. La gestión de inventarios es un reto que hoy enfrentan las pequeñas y medianas empresas debido a que esta actividad involucra la planeación y el control del inventario con el objetivo de minimizar la inversión al tiempo que se equilibran la oferta y la demanda, evitando costos asociados a exceso o faltante de inventario [2].
Diversas investigaciones han estudiado el efecto de la política de control de inventario sobre organizaciones pertenecientes a una cadena de abastecimiento. Paredes, Chud y Osorio [3] proponen una política de inventarios (s, Q) para un inventario de repuestos de un ingenio azucarero, con lo que logran disminuir el costo de almacenamiento de referencias críticas, a la vez que se incrementa el nivel de servicio prestado a los clientes en producción. Cardona, Orejuela y Rojas [4] construyen una metodología con el objetivo de gestionar de manera integrada el control de inventario y la ubicación de ítems en bodegas de materia prima en la industria de alimentos concentrados. Chen y Rossi [5] desarrollan un modelo de gestión de inventarios para un minorista pequeño que maneja productos con demanda no estacionaria y tiene limitaciones de efectivo que validan la necesidad de tener un control exhaustivo de las inversiones realizadas en la compra de inventario. Por el contrario, en este artículo se pretende simular la aplicación de una estrategia de inventario poco tradicional conocida como Demand Driven MRP (DDMRP) en una pequeña empresa que se dedica a la comercialización de artículos de ferretería.
Demand Driven MRP es un método de gestión de inventarios reciente y prometedor que se ha desarrollado e implementado en distintas organizaciones a nivel mundial, demostrando ser una metodología con un enfoque de planificación superior [6]. Esta metodología incorpora elementos de sistemas Lean y la teoría de restricciones que la llevan a introducir buffers dinámicos con el objetivo de controlar los niveles de inventario al tiempo que se responde a las demandas del cliente en un mercado cada más competitivo y dinámico. La ventaja que tiene Demand Driven MRP sobre sistemas tradicionales de gestión de inventarios es que no trabaja con base en pronósticos, por lo que la incertidumbre en la demanda es menor y existe un menor riesgo de generación del efecto látigo [7], el cual representa cómo pequeñas fluctuaciones en la demanda pueden generar enormes oscilaciones en los inventarios de toda la cadena de suministro, ocasionando pérdidas económicas a través de dos posibles escenarios: el primero asociado a un abastecimiento por encima de la cantidad demandada que genere excesos de inventario, aumentando los costos de almacenamiento, y en el segundo escenario, donde puede ocurrir desabastecimiento por una mala planificación de la demanda, que conlleve a la generación de ventas perdidas.
En [8] se desarrolla un modelo matemático basado en una amplia variedad de estrategias de inventario encontradas en la literatura, el cual busca determinar la frecuencia de la publicidad, el precio de venta y la duración del periodo de existencias para maximizar el beneficio promedio por unidad de tiempo, lo que conduce a un problema de inventario no lineal, que se resuelve utilizando un algoritmo eficiente desarrollado previamente por los autores. En [9] se define un modelo de abastecimiento conjunto teniendo en cuenta restricciones de capacidad de transporte, número de envíos y presupuesto asignado. Para la modelación del problema los autores utilizaron programación lineal entera mixta, pero debido a la complejidad del problema, la solución la obtuvieron a través de la aplicación de una heurística llamada algoritmo genético. Por el contrario, la presente investigación incluye como elemento innovador, el uso de la simulación, específicamente del enfoque de redes de Petri para validar la aplicación de la metodología DDMRP en una pequeña ferretería. Se debe tener en cuenta que aunque las redes de Petri se han utilizado previamente para el estudio de políticas de inventario en cadenas de abastecimiento ([10] - [12]), no existe un referente que haya simulado bajo este enfoque el uso de la metodología DDMRP.
El artículo se estructura de la siguiente forma: se presenta el planteamiento de problema de la compañía objeto de estudio, luego se describe la metodología DDMRP y se detalla el uso del enfoque de simulación de eventos discretos a través de redes de Petri, por último, se presentan resultados y conclusiones.
Planteamiento del problema
El constante cambio al que se encuentra sometido el mercado actual crea la necesidad de darle una administración diferente al inventario, debido a que el número de referencias que administran las compañías van en aumento con el tiempo y cada vez es más difícil tener un control sobre el inventario [13]. En la presente investigación se utilizará como caso de estudio una pequeña ferretería de la ciudad de Buga, la cual actualmente maneja más de 2000 artículos en su inventario y lleva más de tres años en el mercado.
Actualmente el control de inventarios dentro de la ferretería se maneja de forma empírica, esto conlleva a que los pedidos a los proveedores se hagan por intuición de la gerencia; este proceso genera un factor de riesgo importante a la hora de tomar decisiones para las diferentes actividades de los negocios, debido que una escasez de inventarios o un exceso de estos ocasiona en la empresa sobrecostos, bien sea por la disminución de ventas o por el incremento en costos de almacenaje, manipulación de mercancías, tiempos de preparación y recepción de pedidos.
Es importante tener en cuenta que, debido a la existencia de un gran número de referencias heterogéneas que administra la ferretería, existe la posibilidad de seleccionar distintos tipos de proveedores para el abastecimiento de los productos, lo que conlleva a que los tiempos de entrega, las condiciones de despacho y otros aspectos sean muy variados, dependiendo del tipo de proveedor y de la categoría de productos que maneje cada uno de ellos.
Metodología
La investigación se construye siguiendo la metodología expuesta en la Figura 1, donde se puede observar que inicialmente se realiza una clasificación ABC del inventario para priorizar aquellas referencias de mayor criticidad para la organización. Una vez se obtienen las referencias tipo A, se procede a establecer cada uno de los niveles de buffers por cada referencia, tal y como lo indica la metodología Demand Driven MRP. Por último, se procede a construir una red de Petri para la simulación de la estrategia de inventario. A continuación se explica en mayor detalle cada una de estas fases.
Figura 1: Metodología para la simulación de la metodología Demand Driven MRP
Clasificación ABC de productos en el inventario
La clasificación de productos dentro de un inventario ha ayudado a las compañías a centrar su atención en aquellos artículos más representativos y de esta forma tener una mayor eficiencia a la hora de gestionar su inventario. Uno de los esquemas más utilizados para la priorización de productos en un inventario se conoce como el análisis ABC [14], el cual se realiza de dos formas: con un solo criterio o con múltiples criterios. En esta investigación se utilizará una clasificación ABC tradicional, utilizando el criterio de ventas como principal insumo para identificar las referencias más importantes dentro del inventario y, a partir de ellas, establecer una política de control basándose en la metodología Demand Driven MRP.
Metodología Demand Driven MRP
Demand Driven MRP (DDMRP) es un método de gestión de almacenes reciente y prometedor que se ha desarrollado e implementado en distintos contextos empresariales [6], el cual incorpora elementos extraídos de sistemas Lean y teoría de restricciones al introducir buffers dinámicos para controlar las existencias de producto dentro del inventario, evitando acumular excesos de productos que conlleven mayores costos de almacenamiento, al mismo tiempo que ocurre la probabilidad de venta perdida. DDMRP incorpora conceptos innovadores permitiendo planificar y controlar el flujo de materiales de una cadena de suministro [15]. A continuación se describen los cinco pasos de los que se compone el DDMRP según Ptak y Smith [16]
Posicionamiento estratégico del inventario
Cuando la empresa cuenta con un inventario en toda la cadena de suministros genera un gran desperdicio de recursos. Sin embargo, deshacerse por completo del inventario conlleva riesgos a la hora de gestionar los suministros que varían en el tiempo. Cuando se piensa evitar estos problemas, el DDMRP propone ciertos factores para identificar el mejor orden que se le puede dar al inventario. De esta forma, el inventario permite desacoplar los procesos para absorber tanto la variabilidad de la demanda como la del suministro, evitando la transmisión de la incertidumbre.
Perfiles y niveles de buffer
Para poder nivelar los buffers y posicionar el inventario en la estructura de materiales es necesario dimensionarlos, para eso debe construirse cada producto teniendo lo que se conoce como el perfil del buffer. Los perfiles de buffer son familias o grupos de piezas para los cuales hay que idear un conjunto de reglas, directrices y procedimientos que se pueden aplicar de la misma manera a todos los miembros de un perfil dado. Una vez que se posicione el inventario en la estructura de materiales es necesario dimensionarlos. Para ello el DDMRP se basa en el consumo medio diario real de las referencias, el Lead Time de estas, o la existencia o no de una cantidad mínima de pedido definida. De esta forma los buffers se dimensionan considerando la demanda real y no con base en previsiones erróneas.
Para realizar el cálculo de los buffers y que esto facilite la implementación dentro del modelo de desacople propuesto se requiere primero tener conocimiento de algunos datos utilizados de referencia como se presenta a continuación:
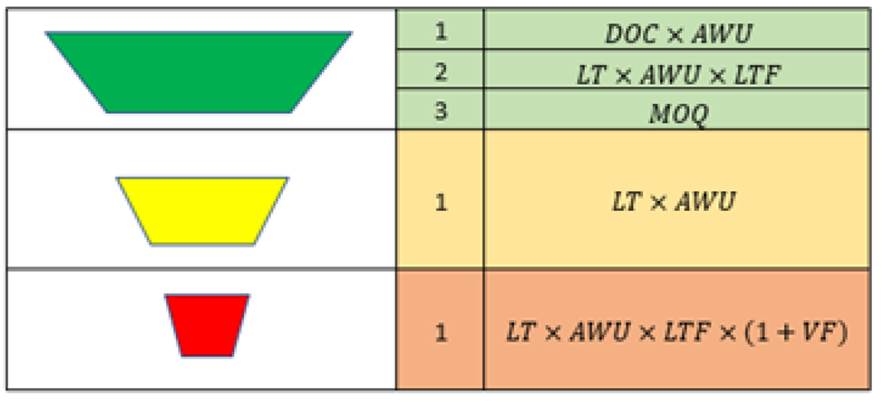
AWU: es el promedio semanal de demanda de cada producto, en este caso tomando 10 semanas pertenecientes a los meses de enero a marzo.
Lead Time (LT): es el tiempo invertido por los procesos previos a la posición del buffer, y que van hasta el buffer anterior. En este modelo se tomó el tiempo promedio de atención de los proveedores expresado en semanas.
Desired Order Cycle (DOC): tiempo deseado entre órdenes o que transcurre entre una revisión del estado del buffer y la siguiente revisión. Esto es un dato que puede ser dado subjetivamente para cada referencia o grupo de referencias; también puede ser una política que la empresa tenga.
Lead Time Factor (LTF): número que representa la variabilidad del tiempo de entrega del producto. Este valor depende del tipo de producto que maneja la compañía (maquilado, fabricado y comercializado) y el nivel de tiempo de entrega (Lead Time alto, medio o bajo).
Mínimum Order Quantity (MOQ): cantidad mínima a ordenar del producto terminado. O lo que es lo mismo, cada vez que se ordena de ese producto, cuánto es lo mínimo que se ordena, en caso de que este dato exista.
Variability Factor (VF): número que representa la variabilidad de la demanda (alta, media y baja) y del tipo de producto que maneja la compañía (maquilado, fabricado y comercializado). En la Tabla I se pueden observar los valores de LTF y VF según tipo de producto y tiempo de entrega.
Fuente: Demand Driven Institute.
Tabla I: Lead Time Factor and Variability Factor según características del producto y tiempo de entrega

Una vez se tiene la información completa por cada una de las referencias, se procede a calcular las zonas roja, amarilla y verde para consolidar los niveles del buffer (ver Figura 2).
Figura 2: Fórmulas para el cálculo de zona roja, amarilla y verde de los buffers
Ajustes dinámicos
Debido a los cambios tan repentinos del mercado, es necesario estar reajustando las dimensiones de los buffers para que su función no presente errores ante nuevas realidades. Esto se hace por la posibilidad de que el consumo varíe en el tiempo para alguna referencia, y que la empresa sea capaz de atender a tiempo las necesidades reales de dichas referencias. La metodología DDMRP permite hacer estos cambios para ajustar los buffers según sea necesario para la organización.
Planificación basada en la demanda
Este paso permite diagnosticar las posibles necesidades que la empresa tenga frente a los materiales y comprar según el tipo de referencia. La metodología DDMRP ha desarrollado el conceptde flujo neto, este se calcula considerando el stock físico como órdenes de compra abiertas y la demanda real. Cuando el valor de esta variable alcanza la zona de reposición del buffer, la empresa debe planificar una orden de compra hasta el nivel máximo del buffer correspondiente. Para facilitar dicha tarea, el DDMRP muestra la posición del flujo neto de cada buffer a través de una alerta codificada por colores [15]. Esta metodología permite identificar de manera fácil las referencias que deben ser tratadas.
Ejecución visible y colaborativa
Al tener las órdenes ya planificadas, se recomienda de forma primordial asegurarse de que todo avanza según lo previsto. El DDMRP incorpora diferentes alertas identificadas por colores, siendo el rojo el que representa que el material está agotado, el amarillo provoca una alerta que indica que se debe abastecer el material y el verde se considera como el rango de inventario óptimo. En caso de que algo se desvíe de lo planificado, esto se muestra a través de dichas alertas. De esta manera, el responsable de dar seguimiento puede identificar de forma sencilla qué referencias se encuentran en situación crítica y requieren atención. Esta ejecución permite a la empresa priorizar las referencias correctamente basándose en el estado de penetración de los buffers, evitando así la generación de prioridades erróneas basadas en la fecha de vencimiento
Simulación a través de redes de Petri
Las redes de Petri son potentes herramientas gráficas y matemáticas para modelar sistemas dinámicos complejos [17], y aunque su aplicación principal se encuentra dentro de los sistemas de producción, existen autores que han utilizado esta herramienta para modelar distintas decisiones de inventario en cadenas de abastecimiento [18], [19]. Una red de Petri es un caso particular de grafo dirigido, ponderado y bipartito con dos tipos de nodos: lugares y transiciones, donde los arcos pueden conectar desde los nodos lugar hasta los nodos transición o al revés. Una red de Petri tradicional está compuesta por cinco elementos (P, T, A, W, Mo), donde P se relaciona con los lugares, T representa las transiciones, A define los arcos, W los pesos que existen entre los arcos y, por último, Mo es el conjunto de tokens que circulan por el sistema.
En la Figura 3 se exhibe la red de Petri generada para la simulación de la estrategia Demand Driven MRP para producto terminado. Este proceso empieza con la transición T1, que viene siendo la llegada de los productos a la compañía, estos son llevados a la bodega donde se almacenan en P2, con la transición T3 se genera una demanda aleatoria representada por una distribución estadística, la cual se acumula en el lugar P1, y si hay unidades con las que se pueda responder al pedido se activa la transición T2, que permite generar la venta (P4). Si en este caso ocurre que no se cuenta con la cantidad requerida, se activa la transición T4, terminando las unidades en el lugar P3 que representa la venta perdida. Para la política del Demand Driven se genera un periodo de revisión para cada R semanas, en el que el ciclo se representa con la transición T6 y T7 que son respectivamente el inicio y el fin del periodo de revisión, esto permite saber que deben pasar R semanas para revisar el inventario, pasando un token al lugar P6 cuando sea momento de hacer la revisión. La transición T5 representa el momento del pedido cuando se tiene que validar si se encuentra en la semana de pedido y observar cómo está el nivel actual de inventario frente a los niveles de buffers que se determinaron. Al lugar P5 pasa el tamaño de pedido generado, el cual está representado por el nivel superior de la zona de verde del buffer, restando la cantidad actual en inventario. Una semana después, el producto llega al almacén, por lo que la transición T1 se activa y se cierra el ciclo.
Figura 3: Red de Petri construida para la simulación de la estrategia Demand Driven MRP
Resultados
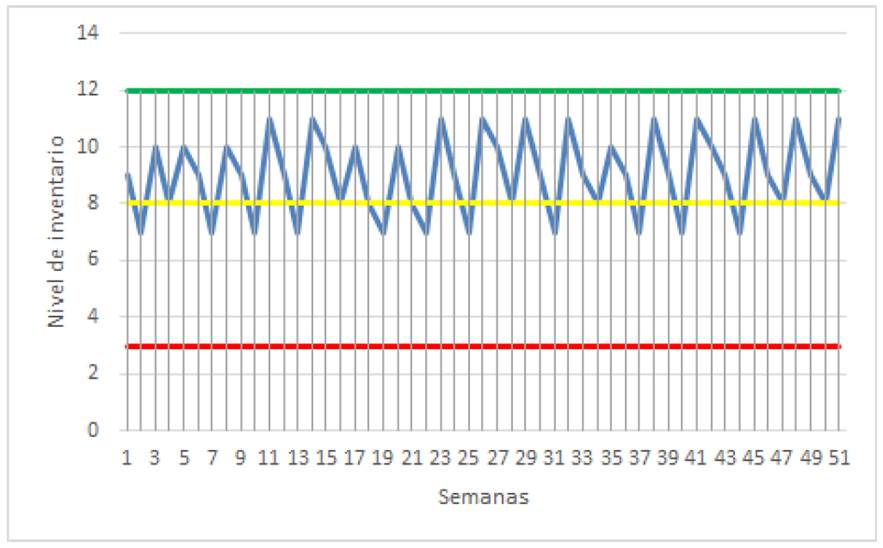
Para realizar la clasificación ABC en la compañía objeto de estudio se utilizaron valores de venta de los 2.728 artículos que ha manejado la ferretería en el último año de operación, luego de la aplicación de la regla de Pareto, se logró identificar un listado de 81 artículos críticos (considerados tipo A) que representan el 80 % de los ingresos de la compañía. Para cada uno de estos productos se realizó un levantamiento de la información necesaria para el cálculo de los niveles de buffer para el uso de la metodología Demand Driven MRP. La Tabla II muestra el cálculo de las zonas de buffer obtenidas para algunas referencias críticas de la organización teniendo en cuenta información como Lead Time, promedio de consumo semanal, cantidad mínima de pedido, entre otros. La red de Petri presentada en la Figura 3 fue simulada por un lapso de 52 semanas utilizando Visual Basic de Excel, para verificar el comportamiento de la estrategia propuesta comparado conlos datos históricos del año 2020. Se debe tener en cuenta que el periodo de revisión que se considera dentro de la simulación es de dos semanas, partiendo del hecho de que los proveedores de la ferretería tienen un tiempo de entrega estimado de una semana. Asimismo, se simula una demanda aleatoria para cada producto que se comporta siguiendo una distribución estadística que se obtuvo a partir de un análisis detallado del histórico de ventas del año 2020. En la Figura 4 se puede observar cómo el nivel de inventario de un producto referente para la organización (representado por la línea azul), en las 52 semanas de simulación, oscila entre la zona amarilla y verde del amortiguador diseñado, por lo que se demuestra que la red de Petri programada representa fielmente a la metodología Demand Driven MRP. Asimismo, se logra demostrar que la metodología DDMRP evita la generación de sobrestock de inventario (en ninguna de las semanas simuladas el nivel de inventario promedio supera la zona verde del buffer establecido), al tiempo que reduce la posibilidad de agotados (el inventario no llega a estar en la zona roja en ninguna de las 52 semanas de simulación).
Tabla II: Ejemplo del cálculo de zonas de buffer para algunos productos tipo A

Figura 4: Ejemplo de comportamiento del nivel de inventario para una referencia tipo A a partir de la simulación de la política de Demand Driven MRP
En la Figura 5 se presenta una comparación del nivel de servicio obtenido con la implementación de la estrategia Demand Driven MRP para cada una de las 81 referencias analizadas, comparado con el nivel de servicio real experimentado por la compañía para cada una de las referencias tipo A en el año 2020; se puede notar claramente cómo con la implementación de la metodología el nivel de servicio de la mayoría de referencias estaría cercano al 100 %, representando un incremento del 25 % comparado con el promedio general del nivel de servicio presentado en el año 2020, lo que comprueba que al usar dicha metodología se logrará cubrir las variaciones de demanda, evitando que el producto se agote y logrando como resultado el incremento de las ventas de la compañía.
Figura 5: Comparación entre el nivel de servicio real para el año 2020 y el nivel de servicio obtenido por la metodología DDMRP
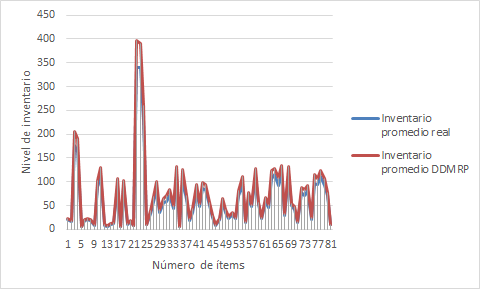
Otro aspecto a considerar luego de la simulación de la estrategia DDMRP es el hecho de que en la mayoría de los productos se incrementa la inversión en inventario para la compañía en comparación con el promedio de existencias que se tuvieron en el año 2020 (ver Figura 6), lo que implica para la compañía revisar una distribución de sus gastos para realizar una mayor inversión en aquellos productos más representativos para la empresa, al tiempo que se debe validar el espacio de almacenamiento disponible en su bodega para determinar la viabilidad de la implementación de la metodología.
Figura 6: Comparación entre inventario promedio para el año 2020 y el inventario simulado por la metodología DDMRP
Discusión
En este artículo se aborda la aplicación de la metodología de simulación redes de Petri, para analizar, modelar y estudiar el comportamiento de la implementación de una política de inventarios basada en la metodología Demand Driven MRP (DDMRP) en una pequeña empresa comercializadora de artículos ferreteros. Alineado al planteamiento de diferentes autores ( [6], [7], [16]), se logra demostrar la efectividad de la estrategia de inventario para el incremento del nivel de servicio, lo que conlleva a una reducción de los productos agotados y un aumento en el ingreso por ventas de la compañía. En un estudio reciente realizado por [20] se evalúa la aplicabilidad de la metodología DDMRP en un entorno de producción complejo, utilizando el software de simulación ARENA, se logra concluir que la estrategia implementada en la organización objeto de estudio previene el desabastecimiento y el exceso de inventario, reduce el tiempo de entrega en un 41 % y reduce los niveles de stock en un 18 %. En contraste, el presente estudio demuestra la adaptación que tiene la metodología DDMRP para una empresa comercializadora, encontrando igualmente beneficios asociados a la nivelación del inventario y al incremento en la satisfacción del cliente final.
Por otro lado, se considera fundamental para la implementación de la política de inventarios propuesta en este documento, un incremento en la capacidad de almacenamiento actual que permita garantizar los beneficios económicos y en términos de servicio que conlleva la adaptación de esta estrategia. Asimismo, se hace necesario que la gerencia aumente el capital disponible para la compra de los artículos de mayor criticidad dentro del inventario. Por último, un hallazgo de mucha relevancia está relacionado con que la metodología Demand Driven MRP ha sido implementada comúnmente en compañías manufactureras [20]. Sin embargo, dentro de la literatura se encontraron pocos casos en los cuales se analiza la efectividad de la estrategia DDMRP en empresas comercializadoras, como lo presenta el presente caso de estudio. Además, un elemento innovador y diferenciador dentro de la investigación realizada es la utilización de las redes de Petri para el modelamiento y el análisis de la política de inventarios basados en la metodología Demand Driven MRP (DDMRP).
Conclusiones
La estrategia de control de inventario Demand Driven MRP (DDMRP) demostró ser una metodología eficaz para el control de inventarios de producto terminado, evitando la acumulación de inventarios innecesarios y mejorando el nivel de servicio de atención al cliente final. Esta conclusión se logra obtener gracias a la simulación de la política en una pequeña ferretería de la ciudad de Buga, donde se incrementa aproximadamente en un 25 % el nivel de servicio de las referencias tipo A, alcanzado estándares entre 98 % y 100 %. No obstante, para llegar a este nivel de atención, la compañía debe garantizar un inventario promedio superior por cada referencia al que actualmente posee, lo que conlleva a tomar decisiones relacionadas con una redistribución de las compras y una validación de la capacidad de almacenamiento en la bodega. La simulación de la metodología DDMRP a través de redes de Petri permite evaluar el funcionamiento de la política antes de su implementación, para validar la efectividad de la estrategia sobre indicadores de desempeño de la compañía como lo son el nivel de servicio, los costos de almacenamiento, la utilización de los recursos, entre otros. La ventaja que ofrecen las redes de Petri en comparación con otras metodologías de simulación es su fácil adaptabilidad a restricciones particulares relativas a la gestión de sus inventarios que presente la compañía, lo que permite personalizar la política en el lenguaje Visual Basic de Excel sin incurrir en gastos de tiempo y recursos de programación para la ferretería. Como futura investigación se espera realizar una sensibilización de algunos parámetros críticos para el uso de la metodología DDMRP como lo son el tiempo de entrega y el periodo de revisión, con el propósito de validar la efectividad de la estrategia en condiciones de incertidumbre y riesgo. Asimismo, se propone incluir una restricción de almacenamiento en la red de Petri diseñada para verificar la viabilidad de la estrategia considerando limitaciones de recursos y dinero.
Referencias
License
Copyright (c) 2022 Andres Mauricio Paredes Rodriguez, Kevin Alexander Ciro Jaramillo, José Daniel Jaramillo Ceballos

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.








2.jpg)










